北师大版七年级下册三角形全等证明及其性质(试题集)

新北师大版七年级下数学三角形全等证明典型习题1.这个零件的形状如下图所示。

已知∠A=90º，∠C=25º，∠B=25º。

如果测量得到∠BCD=150º，那么可以判断这个零件是不合格的。

根据三角形的相关知识，我们可以解释这个不合格的原因。

2.已知如下图，在△ABC中，AD是高，AE是角平分线，∠B=30°，∠C=50°。

我们需要求出∠XXX的度数，并描述∠DAE与∠C-∠B之间的关系，不需要证明。

3.如下图所示，已知D是△ABC边BC延长线上的一点，DF⊥XXX于E，∠A=35°，∠D=42°。

我们需要求出∠ACD的度数。

4.如下图所示，在△ABC中，∠B=∠C，∠BAD=40°，且∠ADE=∠AED。

我们需要求出∠XXX的度数。

5.有一座小山，现在需要在小山A、B的两端开一条隧道。

施工队为了知道A、B两端的距离，在平地上选了一个可以直接到达A和B的点C，连接AC并延长到D使CD=CA，连接BC并延长到E，使CE=CB，连接DE。

那么量出DE的长度，就是A、B的距离。

这是因为DE是平面上的一条直线，而且△ABC和△CDE是相似的。

6.如下图所示，已知DC=BA，BE⊥AC于点E，DF⊥AC于点F，且BE=DF。

我们需要证明AB∥DC。

8.如下图所示，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

我们需要证明BC=AB+DC。

9.如下图所示，AE、BC交于点M，F点在AM上，BE∥CF，BE=CF。

我们需要证明AM是△ABC的中线。

10.已知AB=AC，DB=DC，F是AD的延长线上的一点。

我们需要证明BF=CF。

11.如下图所示，AB＝AD，BC＝DC，E、F分别是DC、BC的中点。

我们需要证明AE＝AF。

12.如下图所示，AB=AC，BD⊥AC，CE⊥AB，垂足分别为D、E，BD、CE相交于点F。

北师大版七年级数学下册专题训练系列（附解析专训3判定三角形全等的四种思路名师点金：全等三角形是初中几何的重要内容之一，是几何入门最关键的一步，学习了判定三角形全等的几种方法之后，如何根据已知条件说明三角形全等，掌握说明全等的几种思路尤为重要．条件充足时直接用判定方法1．【中考·武汉】如图，AC和BD相交于点O，OA＝OC，OB＝OD，试说明：AB∥CD.(第1题)条件不足时添加条件用判定方法2．如图，点A，F，C，D在一条直线上，AF＝DC，BC∥EF，请只补充一个条件，使得△ABC≌△DEF，并说明理由．(第2题)非三角形问题中构造全等三角形用判定方法3．如图是一个风筝模型的框架，由DE＝DF，EH＝FH，就能说明∠DEH＝∠DFH.试用你所学的知识说明理由．(第3题)4．如图，要测量AB的长，因为无法过河接近点A，可以在AB所在直线外任取一点D，在AB的延长线上任取一点E，连接ED和BD，并且延长BD到点G，使DG＝BD，延长ED到点F，使DF＝ED，连接FG，并延长FG到点H，使H，D，A在一条直线上，则HG＝AB，试说明理由．(第4题)答案1．解：在△AOB 和△COD 中，⎩⎪⎨⎪⎧OA ＝OC ，∠AOB ＝∠COD ，OB ＝OD ，所以△AOB ≌△COD.所以∠A ＝∠C.所以AB ∥CD.2．解：补充条件：EF ＝BC ，可使得△ABC ≌△DEF.理由如下：因为AF ＝DC ，点A ，F ，C ，D 在一条直线上， 所以AF ＋FC ＝DC ＋FC ，即AC ＝DF.因为BC ∥EF ，所以∠EFD ＝∠BCA.在△ABC 和△DEF 中，⎩⎪⎨⎪⎧BC ＝EF ，∠BCA ＝∠EFD ，AC ＝DF ，所以△ABC ≌△DEF(SAS)．点拨：答案不唯一．(第3题)3．解：如图，连接DH.在△DEH 和△DFH 中，⎩⎪⎨⎪⎧DE ＝DF ，EH ＝FH ，DH ＝DH ，所以△DEH ≌△DFH(SSS)．所以∠DEH ＝∠DFH(全等三角形的对应角相等)．4．解：在△DEB 和△DFG 中，因为DB ＝DG ，∠BDE ＝∠GDF ，DE ＝DF ， 所以△DEB ≌△DFG(SAS)．所以∠E ＝∠F.所以AE ∥FH.所以∠DBA ＝∠DGH.又因为DB ＝DG ，∠ADB ＝∠HDG ，所以△ADB ≌△HDG(ASA)．所以HG ＝AB.。

最新七年级下册三角形全等的证明试题1、如图，AB=DE，AC=EF，BE=CF，证明∠A=∠D。

2、如图，AB=CD，BE=DF，AF=EC，证明AB∥CD。

3、如图，AC=DF，EF=BC，AD=BE，证明∠F=∠C。

4、如图，AB=AC，AD=AE，BE=DC，证明∠ABD=∠AEC。

5、如图，AB=AD,AE=AC，BC=ED，证明∠ABE=∠ACD。

6、如图，AD=AB，DC=BC，证明∠B=∠D。

7、如图，AB=AC，BD=DC，证明∠1=∠2.8、如图，∠C=90°，AD=BD，DE=DC，AE=BC，说明AB和DE的关系。

9、如图，AB=DE，BC=EF，AF=CD，证明AB∥DE。

10、如图，AB=AC，D是BC的中点，证明AD⊥BC。

11、如图，AE=DF，AB=CD，CE=BF，证明AE∥DF。

12、如图，AB=AD，AE=AC，BC=DE，证明∠E=∠C。

13、如图，BC=BE，DE=DC，∠C=90°，证明（1）DE⊥AB（2）BD是∠ABC的角平分线。

14、如图，AB=EF，AD=CF，DE=BC，证明∠B=∠E。

15、如图，OA=OB，AC=BD，AD=BC，证明∠ACB=∠ADB。

16、如图，AD=BC，A0=OB，OC=OD，证明∠BAD=∠ABC。

17、如图，AD=BD，BE=AC，AD+DE=BC，AD⊥BC，证明BE⊥AC。

18、如图，AD=BC，AF=EC，DE=BF，证明DE∥BF，AD∥BC。

19、如图，AB=DC，AC=BD，AO=OD，证明∠B=∠C。

20、如图，AB=AD，AE=AC，BC=DE，证明∠1=∠2.21、如图，AC⊥CE，AC=CE，AB=CD，且AB+DE=BD，AB∥DE。

22、如图，AE=AB，AC=AF，EC=BF，证明∠BAE=∠CAF。

23、如图，AD=BC，AC=BD，证明∠ADO=∠BCO。

24、如图，AB=AC，BD=CE，AD=AE，证明∠ABC=∠ADE。

探索三角形全等的条件题组利用“SSS”判定三角形全等1.如图,E是BC的中点,连接AC,AE,若AB=AC,AE=CD,AD=CE,则图中的全等三角形有( )A.0对B.1对C.2对D.3对【解析】选D.在△ABE和△ACE中,AB=AC,AE=AE,BE=CE,所以△ABE≌△ACE(SSS),在△AEC和△CDA中,AE=CD,AC=CA,AD=CE,所以△AEC≌△CDA(SSS),所以△ABE≌△CAD.2.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )A.SASB.ASAC.AASD.SSS【解析】选D.在△ABC和△ADC中,所以△ABC≌△ADC(SSS).3.如图,AC=DC,BC=EC,请你添加一个适当的条件: ,使得△ABC≌△DEC. 【解析】添加条件是:AB=DE,在△ABC与△DEC中,所以△ABC≌△DEC.答案:AB=DE(本题答案不唯一)4.如图,在△ABC中,已知AD=DE,AB=BE,∠A=80°,则∠CED= 度.【解析】因为AD=ED,AB=EB,BD=BD,所以△ABD≌△EBD(SSS),所以∠A=∠DEB=80°,所以∠CED=180°-80°=100°.答案:100【方法技巧】如何寻找全等条件1.先找已知条件,已知条件包括两部分:已知给出的;图中隐含的(如公共边、公共角、对顶角等).2.由已知条件推导所需要的条件.5.如图,点B,E,C,F在一条直线上,AB=DF,AC=DE,BE=FC.试说明:△ABC≌△DFE.【解析】因为BE=FC,所以BC=EF,在△ABC和△DFE中,所以△ABC≌△DFE(SSS).【方法技巧】“SSS”的用法和注意事项(1)当要说明的两个三角形已经具备“两边对应相等”的条件时,可考虑运用“SSS”.(2)运用“SSS”判定两三角形全等时,要注意公共边的条件以及线段和差的使用.(3)根据条件判定三角形全等后,对应顶点要写在对应位置上.题组三角形的稳定性1.下列实际情景运用了三角形稳定性的是( )A.人能直立在地面上B.校门口的自动伸缩栅栏门C.古建筑中的三角形屋架D.三轮车能在地面上运动而不会倒【解析】选C.古建筑中的三角形屋架是利用了三角形的稳定性.2.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短【解析】选A.以A,O,B为顶点可构成一个三角形,三角形具有稳定性,所以利用的几何原理是三角形的稳定性.3.空调外机安装在墙壁上时,一般都会像如图所示的方法固定在墙壁上,这种方法是利用了三角形的.【解析】这种方法应用的数学知识是:三角形的稳定性.答案:稳定性如图,在△ABC和△AEF中,AB=AE,EF=BC,AF=AC,试说明,∠EAB=∠FAC.【解析】在△ABC和△AEF中,AB=AE,EF=BC,AF=AC,所以△AEF≌△ABC,所以∠EAF=∠BAC,所以∠EAF-∠BAF=∠BAC-∠BAF,所以∠EAB=∠FAC.【母题变式】[变式一]如图,在△ABC和△DEF中,AB=DE,AC=DF,且BE=CF,试说明:∠A=∠D.【解析】因为BE=CF,所以BE+EC=EC+CF,所以BC=EF,在△ABC和△DEF中,AB=DE,EF=BC,DF=AC,所以△DEF≌△ABC所以∠A=∠D.[变式二]如图,△ABC与△DCB中,AC与BD交于点E,且AC=DB,AB=DC.试说明:∠ABE=∠DCE.【解析】在△ABC与△DCB中,AC=DB,AB=DC,BC=CB,所以△ABC≌△DCB,所以∠ABC=∠DCB,∠ACB=∠DBC,所以∠ABC-∠DBC=∠DCB-∠ACB,所以∠ABE=∠DCE.[变式三]已知:如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.试说明:AD⊥AE.【解析】在△ABD和△ACE中,AB=AC,AD=AE,BD=CE,所以△ABD≌△ACE(SSS),所以∠EAC=∠DAB,所以∠DAE=∠BAC,因为AB⊥AC,所以∠BAC=90°,所以∠DAE=90°,即AD⊥AE.探索三角形全等的条件题组利用“ASA”判定三角形全等1.如图,∠1=∠2,BC=EF,欲证△ABC≌△DEF,则还需补充的一个条件是( )A.AB=DEB.∠ACE=∠DFBC.BF=ECD.∠ABC=∠DEF【解析】选D.根据“ASA”,另一组角必须是∠ABC和∠DEF,故它们必须相等.2.如图,已知∠ABC=∠D,∠ACB=∠CBD,关于图中的两个三角形的关系的说法中正确的是( )A.可用ASA说明它们全等B.可用AAS说明它们全等C.可用SSS说明它们全等D.不全等,缺少对应边相等的条件【解析】选D.图中的两个三角形不全等,因为缺少对应边相等的条件.3.如图,∠BAC=∠DAC,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.【解析】添加∠BCA=∠DCA.理由如下:在△ABC与△ADC中,因为∠BCA=∠DCA,AC=AC,∠BAC=∠DAC,所以△ABC≌△ADC(ASA).4.如图,已知EF∥MN,EG∥HN,且FH=MG,试说明:EF=NM.【解析】因为EF∥MN,EG∥HN,所以∠F=∠M,∠EGF=∠NHM,因为FH=MG,所以FH+HG=MG+HG,所以GF=HM,在△EFG和△NMH中,因为∠F=∠M,GF=HM,∠EGF=∠NHM,所以△EFG≌△NMH(ASA).所以EF=NM.5.如图,D,E分别在BC,AC边上,且∠B=∠C,AB=DC,∠BAD=∠CDE.试说明:△ADE是等腰三角形.【解析】因为在△ADB和△DEC中,∠BAD=∠CDE,AB=DC,∠B=∠C,所以△ADB≌△DEC(ASA).所以AD=DE,所以△ADE 是等腰三角形. 题组利用“AAS ”判定三角形全等1.如图,能用AAS 来判断△ACD ≌△ABE,需要添加的条件是 ( ) A.∠ADC=∠AEB,∠C=∠B B.∠AEB=∠ADC,CD=BE C.AC=AB,AD=AE D.AC=AB,∠C=∠B【解析】选 B.AAS 是根据两角及其中一角的对边对应相等判定三角形全等的方法.【知识归纳】(1)要说明两个三角形全等,只要这两个三角形中存在两个角对应相等,一条边对应相等,就可以考虑运用“角边角”或“角角边”.(2)如果两个三角形有两个角对应相等那么第三个角也必然对应相等,因此由“角边角”判定方法可以得到判定三角形全等的又一个方法,即“角角边”. (3)综合“角边角”和“角角边”这两个判定方法解决三角形全等问题. 2.如图,点B,F,C,E 在一条直线上,已知FB=CE,AC ∥DF,请你添加一个适当的条件使得△ABC ≌△DEF.【解析】添加∠A=∠D.理由如下: 因为FB=CE,所以BC=EF.又因为AC ∥DF,所以∠ACB=∠DFE.所以在△ABC 与△DEF 中,所以△ABC ≌△DEF(AAS). 答案:∠A=∠D(答案不唯一)3.如图,已知BD=CE,∠B=∠C,若AB=8,AD=3,则DC= . 【解析】在△ABD 和△ACE 中,∠A=∠A,∠B=∠C,BD=CE,所以△ABD≌△ACE(AAS),所以AC=AB=8,所以CD=AC-AD=8-3=5.答案:54.如图,四边形ABCD是正方形,G是BC上任意一点(点G与B,C不重合),AE⊥DG 于点E,CF∥AE交DG于点F.(1)在图中找出一对全等三角形,并加以说明.(2)试说明:AE=FC+EF.【解析】(1)△AED≌△DFC.因为四边形ABCD是正方形,所以AD=DC,∠ADC=90°.又因为AE⊥DG,CF∥AE,所以∠AED=∠AEG=∠DFC=90°,所以∠EAD+∠ADE=∠FDC+∠ADE=90°,所以∠EAD=∠FDC.所以△AED≌△DFC(AAS).(2)因为△AED≌△DFC,所以AE=DF,ED=FC.因为DF=DE+EF,所以AE=FC+EF.如图,已知∠1=∠2,∠3=∠4.试说明:BD=BC.【解析】因为∠ABD+∠3=180°,∠ABC+∠4=180°,且∠3=∠4,所以∠ABD=∠ABC,在△ADB和△ACB中,因为∠1=∠2,AB=AB,∠ABD=∠ABC,所以△ADB≌△ACB(ASA),所以BD=BC.【母题变式】[变式一]如图,已知∠C=∠D,∠3=∠4.试说明:BD=BC.【解析】因为∠ABD+∠3=180°,∠ABC+∠4=180°,且∠3=∠4,所以∠ABD=∠ABC,在△ADB和△ACB中,因为∠D=∠C,∠ABD=∠ABC,AB=AB,所以△ADB≌△ACB(AAS),所以BD=BC.[变式二]如图,已知AD=AC,BD=BC.试说明:∠3=∠4.【解析】在△ADB和△ACB中,因为AD=AC,BD=BC,AB=AB,所以△ADB≌△ACB(SSS),所以∠ABD=∠ABC,因为∠ABD+∠3=180°,∠ABC+∠4=180°,所以∠3=∠4.[变式三]如图:已知AE交BD于点C,∠DAC=∠EBC=∠BAC,AB=AC.试说明:DC与BE 有怎样的数量关系.【解析】DC=BE.因为∠EBC=∠BAC,∠ACD=∠BAC+∠ABC,∠ABE=∠EBC+∠ABC, 所以∠ACD=∠ABE,在△ACD和△ABE中,∠DAC=∠BAC,AC=AB,∠ACD=∠ABE,所以△ACD≌△ABE(ASA),所以DC=BE.如图,AC,BD相交于点O,且AB=DC,AC=DB.试说明:∠ABO=∠DCO.【解析】连接BC.在△ABC和△DCB中,AB=DC,AC=DB,BC=CB,所以△ABC≌△DCB(SSS),所以∠A=∠D,在△AOB和△DOC中,∠A=∠D,∠AOB=∠DOC,AB=DC,所以△AOB≌△DOC(AAS).所以∠ABO=∠DCO.探索三角形全等的条件题组利用“SAS”判定三角形全等1.如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )【解析】选B.A.与△ABC有两边相等,而夹角不一定相等,二者不一定全等;B.与△ABC有两边及其夹角相等,二者全等;C.与△ABC有两边相等,但两边的夹角不相等,二者不一定全等;D.与△ABC有两角相等,但边不对应相等,二者不一定全等.2.已知:如图,AC=AE,∠1=∠2,AB=AD,若∠D=25°,则∠B的度数为 ( )A.25°B.30°C.15°D.30°或15°【解析】选A.因为∠1=∠2,所以∠BAC=∠DAE,又因为AC=AE,AB=AD,所以△ABC≌△ADE,所以∠B=∠D=25°.3.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带去玻璃店.【解析】带第③块玻璃去,根据它能确定原来三角形的两角及其夹边的大小,从而根据“ASA”确定新的三角形与原来的三角形一样.答案:第③块玻璃4.如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.【解析】因为AE=BF,所以AE+EF=BF+EF,即AF=BE,在△ADF和△BCE中,所以△ADF≌△BCE.5.已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB,AC的中点,求证:BE=CD. 【解析】因为∠ABC=∠ACB,所以AB=AC,因为点D,E分别是AB,AC的中点.所以AD=AE,在△ABE与△ACD中,所以△ABE≌△ACD,所以BE=CD.题组三角形全等判定方法的综合应用1.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )A.AB=CDB.EC=BFC.∠A=∠DD.AB=BC【解析】选A.因为AE∥FD,所以∠A=∠D,因为AB=CD,所以AC=BD,在△AEC和△DFB中,AE=DF,∠A=∠D,AC=DB.所以△EAC≌△FDB(SAS).2.在△ABC中,AB=5,AC=3,AD是△ABC的中线,设AD长为m,则m的取值范围是.【解析】延长AD至点E,使DE=AD,连接EC,因为BD=CD,DE=DA,∠ADB=∠EDC,所以△ABD≌△ECD,所以CE=AB,因为AB=5,AC=3,所以CE=5,因为AD=m,所以AE=2m,所以2<2m<8,所以1<m<4.答案:1<m<43.如图,在四边形ABCD中,AB=CD,AD=BC,对角线AC,BD交于点O,则图中共有对全等三角形.【解析】因为在△ABD和△CDB中,AD=BC,AB=CD,BD=BD,所以△ABD≌△CDB(SSS),所以∠ADB=∠CBD,∠ABD=∠BDC,因为在△ABC和△CDA中,AD=BC,AB=CD,AC=CA,所以△ABC≌△CDA(SSS),所以∠DAC=∠BCA,∠ACD=∠BAC,因为在△AOB和△COD中,∠BAO=∠DCO,AB=CD,∠ABO=∠CDO,所以△AOB≌△COD(ASA),因为在△AOD和△COB中,∠ADB=∠DBC,AD=CB,∠DAC=∠BCA,所以△AOD≌△COB(ASA).答案:44.已知:如图,△AOC≌△BOD.试说明:△AOD≌△BOC.【解析】因为△AOC≌△BOD,所以OA=OB,OC=OD,∠AOC=∠BOD,所以∠AOC+∠COD=∠BOD+∠COD,即∠AOD=∠BOC,在△AOD和△BOC中,AO=BO,∠AOD=∠BOC,OD=OC,所以△AOD≌△BOC.5.在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.试说明:PB=PC,并直接写出图中其他相等的线段.【解析】在△ABF和△ACE中,AB=AC,∠BAF=∠CAE,AF=AE,所以△ABF≌△ACE(SAS),所以∠ABF=∠ACE(全等三角形的对应角相等),所以BF=CE(全等三角形的对应边相等),因为AB=AC,AE=AF,所以BE=CF,在△BEP和△CFP中,∠BPE=∠CPF,∠PBE=∠PCF,BE=CF,所以△BEP≌△CFP(AAS),所以PB=PC,因为BF=CE,所以PE=PF,所以图中相等的线段为PE=PF,BE=CF,EC=BF.【知识归纳】(1)首先观察待判断的线段(角),存在于哪两个可能全等的三角形之中.(2)根据题目中已有的条件,对照全等判定的定理,分析采用哪条定理易判断这两个三角形全等,看还缺什么条件.(3)设法判断出所缺条件,此时应注意所缺条件可能存在于另外一对易判断的全等三角形中.如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.试说明:BD=CE.【解析】因为BD,CE是高,所以∠ADB=∠AEC=90°,在△ABD和△ACE中,∠A=∠A.∠ADB=∠AEC,AB=AC,所以△ABD≌△ACE(AAS).所以BD=CE.【母题变式】[变式一]如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.试说明:BE=CD.【解析】因为BD,CE是高,所以∠ADB=∠AEC=90°,在△ABD和△ACE中,∠A=∠A,∠ADB=∠AEC,AB=AC,所以△ABD≌△ACE(AAS),所以AD=AE.因为AB=AC,所以BE=CD.[变式二]如图,已知△ABC中,BD,CE是高,BD与CE相交于点O,若∠A=80°,求∠BOC的度数.【解析】因为BD,CE是高,所以∠ADB=∠AEC=90°在△ABC中,∠A=80°,所以∠ABD=90°-80°=10°,所以∠BOE=90°-10°=80°,所以∠BOC=180°-80°=100°.[变式一]如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.试说明:△BEO≌△CDO.【解析】因为BD,CE是高,所以∠ADB=∠AEC=90°,在△ABD和△ACE中,∠A=∠A,∠ADB=∠AEC,AB=AC,所以△ABD≌△ACE(AAS),所以AD=AE.因为AB=AC,所以BE=CD.又因为∠BDC=∠BEC,∠BOE=∠COD,所以△BEO≌△CDO(AAS).[变式二]如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O. 试说明:△BEC≌△CDB.【解析】因为BD,CE是高,所以∠ADB=∠AEC=90°,在△ABD和△ACE中,∠A=∠A,∠ADB=∠AEC,AB=AC,所以△ABD≌△ACE(AAS),所以AD=AE,BD=CE,因为AB=AC,所以BE=CD.又因为BC=CB,所以△BEC≌△CDB(SSS).。

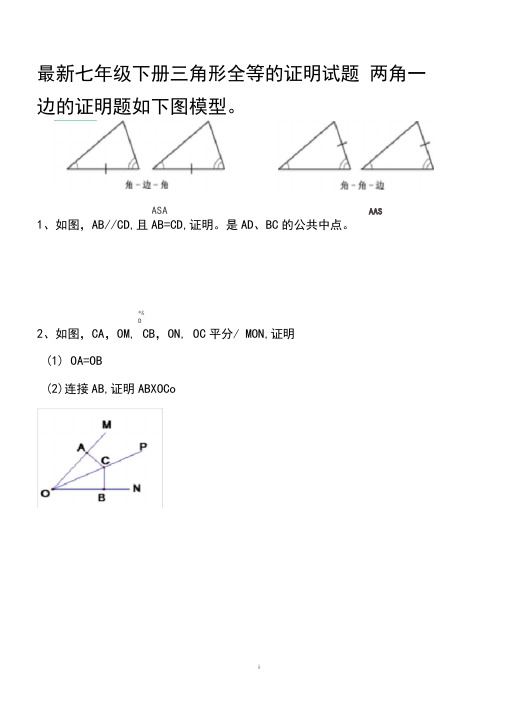
最新七年级下册三角形全等的证明试题两角一边的证明题如下图模型。

1、如图，AB//CD,且AB=CD,证明。

是AD、BC的公共中点。

*&D2、如图，CA，OM, CB，ON, OC平分/ MON,证明(1) OA=OB(2)连接AB,证明ABXOCoASA AAS3、如图，/ B=/C, AD=AE,证明BD=CE4、如图，AC平分/ BAD, AB± BC, AD，DC,证明CA平分/ BCD。

5、如图，AB//DE, BF=CE / A=/D,试着说明AC和DF的关系。

6、如图，AB=CD, /A=/D,证明/ 1 = /2./D, / BCE之ACD, CB=CE 证明AB=ED。

8、如图，DE，AB, DF，AC, D 是BC 的中点，/ BDF=/CDE 证明AB=ACoH a c9、如图，/ 1 = /2, AB=AE, / B=/E,证明/ D=/C10、如图，ABXBC, DC± BC, BE=CF / BED=/ ACF,证明AFXDE月E11、如图，CE、BD分别是三角形的两条高线，且AB=AC,证明/ CBD= / BCE12、如图，BE=CF /A=/D, AB II DE,说明AC 和DF 的关系13、如图，/ C=/ D, /ABD=/BAC,证明DE=CE14、如图，AB//CF, AD=CF,证明E是AC的中点15、如图，AF=CE ADU BC, DF// BE,说明AB 和CD 关系16、如图，BEIGE, ADXCE, AC，BC,且AC=BQ 说明线段BE、AD、17、如图，Z A+Z C=180 ,BD 平分/ ABC,证明AD=CDoDE之间的关系18、如图，/ 1 = /2, / E=/ D, AE=AD,证明EC=BD19、如图，AD=BC, /A=/C,说明A、C的连线和B、D的连线的关系。

D20、如图，/ 1 = /2, /D=/E, AB=AC,证明BD=CE21、如图，BD平分/ ABC, /A=/C,证明A、C的连线和BD垂直22、如图，△ ABD是以AB为斜边的等腰直角三角形，/C与/AEB互补，说明BE和AC的关系23、如图，ABXBC, FD，BC, EF± AC,且AB=ED,证明BC=DR24、如图，AC，CD, BD^CD, M、F分另是CF、BD的中点，证明AC=DR25、如图，DE=BF, ABH CD, / E=/ F,说明AE和CF关系。

最新七年级下册三角形全等的证明1、已知：如图，四边形ABCD中，AC平分角BAD，CE垂直AB 于E，且角B+角D=180度，求证：AE=AD+BEA B DCE 122、已知，如图，AB=CD，DF⊥AC于F，BE⊥AC于E，DF=BE。

求证：AF=CE。

FE A CDB3、已知，如图，AB ⊥AC ，AB ＝AC ，AD ⊥AE ，AD ＝AE 。

求证：BE ＝CD 。

AEDC B4、如图，DE⊥AB，DF⊥AC，垂足分别为E、F，请你从下面三个条件中任选出两个作为已知条件，另一个为结论，推出一个正确的命题。

①AB=AC ②BD=CD ③BE=CFBD C5、如图，△ABC中，AB=AC，过A作GE∥BC，角平分线BD、CF 交于点H，它们的延长线分别交GE于E、G，试在图中找出三对全等三角形，并对其中一对给出证明。

E G6、如图，在△ＡＢＣ中，点Ｄ在ＡＢ上，点Ｅ在ＢＣ上，ＢＤ＝ＢＥ。

（１）请你再添加一个条件，使得△ＢＥＡ≌△ＢＤＣ，并给出证明。

你添加的条件是：________ ___（2）根据你添加的条件，再写出图中的一对全等三角形：______________（不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）7、已知：如图，AB⊥BC，AD⊥DC，AB=AD，若E是AC上一点。

求证：EB=ED。

DA E CB8、已知：如图，AB、CD交于O点，CE//DF，CE=DF，AE=BF。

求证：∠ACE=∠BDF。

AB CDEFO9、已知：如图，△ABC中，AD⊥BC于D，E是AD上一点，BE的延长线交AC于F，若BD=AD，DE=DC。

求证：BF⊥AC。

AE FDB C10、. 已知：如图，△ABC 和△A ＇B ＇C ＇中，∠BAC=∠B ＇A ＇C ＇，∠B=∠B ＇，AD 、A ＇D ＇分别是∠BAC 、∠B ＇A ＇C ＇的平分线，且AD=A ＇D ＇。

求证：△ABC ≌△A’B’C’。

最新七年级下册三角形单元测试试题一、选择题1．一定在△ABC内部的线段是（）。

A．锐角三角形的三条高、三条角平分线、三条中线B．钝角三角形的三条高、三条中线、一条角平分线C．任意三角形的一条中线、二条角平分线、三条高D．直角三角形的三条高、三条角平分线、三条中线2．下列说法中，正确的是（）。

A．一个钝角三角形一定不是等腰三角形，也不是等边三角形B．一个等腰三角形一定是锐角三角形，或直角三角形C．一个直角三角形一定不是等腰三角形，也不是等边三角形D．一个等边三角形一定不是钝角三角形，也不是直角三角形3．如图，在△ABC中，D、E分别为BC上两点，且BD＝DE＝EC，则图中面积相等的三角形有（）。

A．4对 B．5对 C．6对 D．7对4．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A．锐角三角形 B．钝角三角形 C．直角三角形 D．无法确定5．下列各题中给出的三条线段不能组成三角形的是（）A．4厘米、5厘米、6厘米B．4厘米、4厘米、4厘米C．5厘米、13厘米、6厘米D．7厘米、9厘米、7厘米6．若等腰三角形的一边是7，另一边是4，则此等腰三角形的周长是（）。

A．18 B．15 C．18或15 D．无法确定7．两根木棒分别为6cm和9cm，要选择第三根木棒，将它们钉成一个三角形，如果第三根木棒长为偶数，那么第三根木棒的取值情况有（）种。

A．3 B．4 C．5 D．68．△ABC的三边a、b、c都是正整数，且满足a≤b≤c，如果b＝4，那么这样的三角形共有（）个。

A．4 B．6 C．8 D．109．各边长均为整数的不等边三角形的周长小于13，这样的三角形有（）A．1个 B．2个 C．3个 D．4个10．三角形所有外角的和是（）A．180° B．360° C．720° D．540°11．锐角三角形中，最大角α的取值范围是（ ） A ．0°＜α＜90°; B ．60°＜α＜180°; C ．60°＜α＜90°; D ．60°≤α＜90°12．如果三角形的一个外角不大于和它相邻的内角，那么这个三角形为（ ）A ．锐角或直角三角形;B ．钝角或锐角三角形C ．直角三角形;D ．钝角或直角三角形13．已知△ABC 中，∠ABC 与∠ACB 的平分线交于点O ，则∠BOC 一定（ ）A ．小于直角;B ．等于直角;C ．大于直角;D ．大于或等于直角 二、填空题1．如图:（1）AD ⊥BC ，垂足为D ，则AD 是________的高， ∠________＝∠________＝90°；（2）AE 平分∠BAC ，交BC 于点E ，则AE 叫________，∠________＝∠________＝∠________，AH叫________；（3）若AF ＝FC ，则△ABC 的中线是________；（4）若BG ＝GH ＝HF ，则AG 是________的中线，AH 是________的中线．212．如图，∠ABC＝∠ADC＝∠FEC＝90°．（1）在△ABC中，BC边上的高是________；（2）在△AEC中，AE边上的高是________；（3）在△FEC中，EC边上的高是________；（4）若AB＝CD＝3，AE＝5，则△AEC的面积为________．3．在等腰△ABC中，如果两边长分别为6cm、10cm，则这个等腰三角形的周长为________．4．五段线段长分别为1cm、2cm、3cm、4cm、5cm，以其中三条线段为边长共可以组成________个三角形．5．已知三角形的两边长分别为3和10，周长恰好是6的倍数，那么第三边长为________．6．一个等腰三角形的周长为5cm，如果它的三边长都是整数，那么它的腰长为________cm．7．在△ABC中，若∠A∶∠B∶∠C＝5∶2∶3，则∠A＝______；∠B ＝______；∠C＝______．8．如图，△ABC中，∠ABC、∠ACB的平分线相交于点I．（1）若∠ABC＝70°，∠ACB＝50°，则∠BIC＝________；（2）若∠ABC＋∠ACB＝120°，则∠BIC＝________；（3）若∠A＝60°，则∠BIC＝________；（4）若∠A＝100°，则∠BIC＝________；（5）若∠A＝n°，则∠BIC＝________．三、解答题1．在△ABC中，∠BAC是钝角．画出：（1）∠ABC的平分线；（2）边AC上的中线；（3）边AC上的高．2．△ABC 的周长为16cm ，AB ＝AC ，BC 边上的中线AD 把△ABC 分成周长相等的两个三角形．若BD ＝3cm ，求AB 的长．3．如图，AB ∥CD ，BC ⊥AB ，若AB ＝4cm ，，求△ABD 中AB 边上的高．212cm =∆ABCS4．学校有一块菜地，如下图．现计划从点D 表示的位置（BD ∶DC ＝2∶1）开始挖一条小水沟，希望小水沟两边的菜地面积相等．有人说：如果D 是BC 的中点的话，由此点D 笔直地挖至点A 就可以了．现在D 不是BC 的中点，问题就无法解决了．但有人认为如果认真研究的话一定能办到．你认为上面两种意见哪一种正确，为什么?5．在直角△ABC 中，∠BAC ＝90°，如下图所示．作BC 边上的高，图中出现三个直角三角形（3＝2×1＋1）；又作△ABD 中AB 边上的高，这时图中便出现五个不同的直角三角形（5＝2×2＋1）；按照同样的方法作、、……、．当作出时，图中共有多少个不同的直角三角形?1DD 21D D 32D D k k D D 1-k k D D 1-6．一块三角形优良品种试验田，现引进四个良种进行对比实验，需将这块土地分成面积相等的四块．请你制订出两种以上的划分方案．7．一个三角形的周长为36cm，三边之比为a∶b∶c＝2∶3∶4，求a、b、c．8．已知△ABC的周长为48cm，最大边与最小边之差为14cm，另一边与最小边之和为25cm，求△ABC各边的长．9．已知三角形三边的长分别为：5、10、a－2，求a的取值范围．10．已知等腰三角形中，AB＝AC，一腰上的中线BD把这个三角形的周长分成18cm和9cm两部分，求这个等腰三角形的底边的长．11．如图，已知△ABC中，AB＝AC，D在AC的延长线上．求证：BD－BC＜AD－AB．12．如图，△ABC 中，D 是AB 上一点．求证：（1）AB ＋BC ＋CA ＞2CD ；（2）AB ＋2CD ＞AC ＋BC ．13．如图，AB ∥CD ，∠BMN 与∠DNM 的平分线相交于点G ，（1）完成下面的证明：∵ MG 平分∠BMN （ ），∴ ∠GMN ＝∠BMN （ ），同理∠GNM ＝∠DNM ．∵ AB ∥CD （ ），∴ ∠BMN ＋∠DNM ＝________（ ）．∴ ∠GMN ＋∠GNM ＝________．2121∵∠GMN＋∠GNM＋∠G＝________（），∴∠G＝ ________．∴ MG与NG的位置关系是________．（2）把上面的题设和结论，用文字语言概括为一个命题：_________________________________________________．14．已知，如图D是△ABC中BC边延长线上一点，DF⊥AB交AB于F，交AC于E，∠A＝46°，∠D＝50°．求∠ACB的度数．15．已知，如图△ABC中，三条高AD、BE、CF相交于点O．若∠BAC ＝60°，求∠BOC的度数．16．已知，如图△ABC中，∠B＝65°，∠C＝45°，AD是BC边上的高，AE是∠BAC的平分线．求∠DAE的度数．17．已知，如图CE是△ABC的外角∠ACD的平分线，BE是∠ABC内任一射线，交CE于E．求证：∠EBC＜∠ACE．18．画出图形，并完成证明：已知：AD是△ABC的外角∠EAC的平分线，且AD∥BC．求证：∠B＝∠C．。

最新三角形全等的证明练习题1、已知:如图，四边形ABCD中，AB∥CD ∠A=∠C.求证：AD=BC、AB=CD。

A2、已知AD是⊿ABC的中线，BE⊥AD，CF⊥AD，试着说明DE、DF的关系。

FB CDE3、已知CD ∥AB ，DF ∥EB ，AF=CE ，证明AB=CD 。

4、已知∠1=∠2，∠3=∠4，证明AC=AD 。

A DC E F B5、已知∠A =∠B ，∠1=∠2，AB =CD ，说明BF=EC 。

6、已知ED ⊥AB ，EF ⊥BC ，BD =EF ，说明EM 、MD 和BF 的关系；。

A B C DE F 1 27、在⊿ABC 中，高AD 与高BE 相交于点H ，DH=CD ，证明：BH=AC 。

8、已知∠A =∠D ，AC ∥FD ，BF=CE ，问AB 、DE 的关系，并说明理由。

AB CEH AB CEF D9、已知∠AFE=∠BCD ，AF =CD ，AB ⊥BC ，DE ⊥EF ，10、已知AD =AE ，∠BDC =∠CEB ，证明∠B=∠C 。

A B C E D F A D E B C11、已知CE⊥AB，DF⊥AB，AC∥DB，AF=BE，说明CE、FD的关系。

12、已知DE=FE，FC∥AB，证明E是AC的中点。

AD BE FC13、如图，D ，E ，F ，B 在一条直线上，AB =CD ，∠B =∠D ，BF =DE ，问(1)AE =CF(2)AE ∥CF 。

14、已知，E 、F 是AB 上的两点，AE =BF ，又AC ∥DB ，AC =DB ，证明CF=DE 。

CD EFA BBA DFE C15、已知，点C 是AB 的中点，CD ∥BE ，且CD =BE ，证明∠D=∠E 。

16、已知AB =AC ，∠1=∠2，AD =AE ，证明BD=CE 。

A DB EC 1 2D AE C B 1 217、如图，AB =AE ，AC =AD ，证明：BC=DE 。

新北师大版七年级下数学三角形全等证明典型习题1．一个零件的形状如图，按规定∠A=90º ，∠ C=25º，∠B=25º， 检验已量得∠BCD=150º，就判断这个零件不合格， 运用三角形的有关知识说明零件不合格的理由。

2．已知，如图，在△ ABC 中，AD ，AE 分别是 △ ABC 的高和角平分线， 若∠B=30°，∠C=50°. （1）求∠DAE 的度数。

（2）试写出 ∠DAE 与∠C-∠B 有何关系?（不必证明）3.如图,已知D 为△ABC 边BC 延长线上一点,DF ⊥AB 于F 交 AC 于E,∠A=35°,∠D=42°,求∠ACD 的度数.4.如图,在△ABC 中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED, 求∠CDE 的度数.5、有一座小山，现要在小山A 、B 的两端开一条隧道，施工队要知道A 、B两端的距离，于是先在平地上取一个可以直接到达A 和B 的点C ，连接AC 并延长到D 使CD=CA ，连接BC 并延长到E ，使CE=CB ，连接DE ，那么量出DE 的长，就是A 、B 的距离，你能说说其中的道理吗？21．已知：如图，在△ABC 中，∠BAC=800，AD ⊥BC 于D ，AE 平分∠DAC ，∠B=600； 求∠AEC 的度数.CDAE CDBFDCBE ADCBEA6、已知：如图，AC BE BA DC ⊥=,于点AC DF E ⊥,于点F ，且BE=DF求证：AB ∥DCABCDE F8. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ， 且点E 在AD 上。

求证：BC=AB+DC 。

9、如图：AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

10、AB=AC ，DB=DC ，F 是AD 的延长线上的一点。