2011年河北中考数学试题(含答案)

2011年中考数学试题精选汇编《矩形、菱形、正方形》一、选择题1. （2011浙江省舟山，10，3分）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（ ）（A ）48cm（B ）36cm （C ）24cm （D ）18cm【答案】A 2. （2011山东德州8,3分）图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），……，则第n 个图形的周长是（A ）2n （B ）4n （C ）12n + （D ）22n +【答案】C3. （2011山东泰安，17 ，3分）如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S 1，S 2，则S 1+S 2的值为A.17B.17C.18D.19图1图2 图3……（第10题） FA B C D H E① ②③ ④ ⑤4. （2011山东泰安，19 ，3分）如图，点O是矩形ABCD的中心，E是AB上的点，沿CE 折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为A.23B. 332C. 3D.6【答案】A5. （2011浙江杭州，10，3）在矩形ABCD中，有一个菱形B F D E(点E，F分别在线段AB，CD上)，记它们的面积分别为ABCD BFDES S和．现给出下列命题：（）①若ABCDBFDESStan EDF∠=．②若2,DE BD EF=∙则2DF AD=．则:A．①是真命题，②是真命题 B．①是真命题，②是假命题C．①是假命题，②是真命题 D，①是假命题，②是假命题【答案】A6. （2011浙江衢州，1,3分）衢州市新农村建设推动了农村住宅旧貌变新颜，如图为一农村民居侧面截图，屋坡AF AG、分别架在墙体的点B、点C处，且AB AC=,侧面四边形BDEC为矩形，若测得100FAG∠=︒，则FBD∠=( )A. 35°B. 40°C. 55°D. 70°【答案】C7. （2011浙江温州，6，4分）如图，在矩形ABCD中，对角线AC，BD交于点O．已知∠AOB= 60°，AC＝16，则图中长度为8的线段有( )A．2条B．4条C．5条D．6条8. 2011四川重庆，10，4分）如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG ≌△AFG ；②BG ＝GC ；③AG ∥CF ；④S △FGC ＝3．其中正确结论的个数是( )A ．1B ．2C ．3D ．4【答案】C9. （2011浙江省嘉兴，10，4分）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（ ）（A ）48cm（B ）36cm （C ）24cm （D ）18cm【答案】A 10．（2011台湾台北，29）如图(十二)，长方形ABCD 中，E 为BC 中点，作AEC 的角平分线交AD 于F 点。

2018年河北省中考数学试卷一、选择题（本大题共16小题，共42分，1-10小题各3分，11-16小题各2分）1．（3分）下列图形具有稳定性的是（）A．B．C．D．2．（3分）一个整数815550…0用科学记数法表示为8.1555×1010，则原数中“0”的个数为（）A．4B．6C．7D．103．（3分）图中由“○”和“□”组成轴对称图形，该图形的对称轴是直线（）A．l1B．l2C．l3D．l44．（3分）将9.52变形正确的是（）A．9.52=92+0.52B．9.52=（10+0.5）（10﹣0.5）C．9.52=102﹣2×10×0.5+0.52D．9.52=92+9×0.5+0.525．（3分）图中三视图对应的几何体是（）A．B．C．D．6．（3分）尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅰ、作线段的垂直平分线；Ⅰ、过直线上一点作这条直线的垂线；Ⅰ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是（）A．①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣ⅠB．①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣ⅠC．①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣ⅠD．①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣Ⅰ7．（3分）有三种不同质量的物体“”“”“”，其中，同一种物体的质量都相等，现左右手中同样的盘子上都放着不同个数的物体，只有一组左右质量不相等，则该组是（）A．B．C．D．8．（3分）已知：如图，点P在线段AB外，且PA=PB，求证：点P在线段AB的垂直平分线上，在证明该结论时，需添加辅助线，则作法不正确的是（）A．作∠APB的平分线PC交AB于点CB．过点P作PC⊥AB于点C且AC=BCC．取AB中点C，连接PCD．过点P作PC⊥AB，垂足为C9．（3分）为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高（单位：cm）的平均数与方差为：x甲=x丙=13，x乙=x丁=15：s甲2=s丁2=3.6，s乙2=s丙2=6.3．则麦苗又高又整齐的是（）A．甲B．乙C．丙D．丁10．（3分）图中的手机截屏内容是某同学完成的作业，他做对的题数是（）A．2个B．3个C．4个D．5个11．（2分）如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时的航行方向为（）A．北偏东30°B．北偏东80°C．北偏西30°D．北偏西50°12．（2分）用一根长为a（单位：cm）的铁丝，首尾相接围成一个正方形，要将它按图的方式向外等距扩1（单位：cm）得到新的正方形，则这根铁丝需增加（）A．4cm B．8cm C．（a+4）cm D．（a+8）cm 13．（2分）若2n+2n+2n+2n=2，则n=（）A．﹣1B．﹣2C．0D．1 414．（2分）老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：接力中，自己负责的一步出现错误的是（）A．只有乙B．甲和丁C．乙和丙D．乙和丁15．（2分）如图，点I为△ABC的内心，AB=4，AC=3，BC=2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为（）A．4.5B．4C．3D．216．（2分）对于题目“一段抛物线L：y=﹣x（x﹣3）+c（0≤x≤3）与直线l：y=x+2有唯一公共点，若c为整数，确定所有c的值，”甲的结果是c=1，乙的结果是c=3或4，则（）A．甲的结果正确B．乙的结果正确C．甲、乙的结果合在一起才正确D．甲、乙的结果合在一起也不正确二、填空题（本大题有3个小题，共12分.17～18小题各3分：19小题有2个空，每空3分，把答案写在题中横线上）17．（3分）计算：√−12−3=．18．（3分）若a，b互为相反数，则a2﹣b2=．19．（6分）如图1，作∠BPC平分线的反向延长线PA，现要分别以∠APB，∠APC，∠BPC为内角作正多边形，且边长均为1，将作出的三个正多边形填充不同花纹后成为一个图案．例如，若以∠BPC为内角，可作出一个边长为1的正方形，此时∠BPC=90°，而90°2=45是360°（多边形外角和）的18，这样就恰好可作出两个边长均为1的正八边形，填充花纹后得到一个符合要求的图案，如图2所示．图2中的图案外轮廓周长是；在所有符合要求的图案中选一个外轮廓周长最大的定为会标，则会标的外轮廓周长是．三、解答题（本大题共7小题，共计66分）20．（8分）嘉淇准备完成题目：发现系数“”印刷不清楚．（1）他把“”猜成3，请你化简：（3x2+6x+8）﹣（6x+5x2+2）；（2）他妈妈说：“你猜错了，我看到该题标准答案的结果是常数．”通过计算说明原题中“”是几？21．（9分）老师随机抽查了本学期学生读课外书册数的情况，绘制成条形图（图1）和不完整的扇形图（图2），其中条形图被墨迹遮盖了一部分．（1）求条形图中被遮盖的数，并写出册数的中位数；（2）在所抽查的学生中随机选一人谈读书感想，求选中读书超过5册的学生的概率；（3）随后又补查了另外几人，得知最少的读了6册，将其与之前的数据合并后，发现册数的中位数没改变，则最多补查了人．22．（9分）如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着﹣5，﹣2，1，9，且任意相邻四个台阶上数的和都相等．尝试（1）求前4个台阶上数的和是多少？（2）求第5个台阶上的数x是多少？应用求从下到上前31个台阶上数的和．发现试用含k（k为正整数）的式子表示出数“1”所在的台阶数．23．（9分）如图，∠A=∠B=50°，P 为AB 中点，点M 为射线AC 上（不与点A 重合）的任意一点，连接MP ，并使MP 的延长线交射线BD 于点N ，设∠BPN=α．（1）求证：△APM ≌△BPN ；（2）当MN=2BN 时，求α的度数；（3）若△BPN 的外心在该三角形的内部，直接写出α的取值范围．24．（10分）如图，直角坐标系xOy 中，一次函数y=﹣12x +5的图象l 1分别与x ，y 轴交于A ，B 两点，正比例函数的图象l 2与l 1交于点C （m ，4）．（1）求m 的值及l 2的解析式；（2）求S △AOC ﹣S △BOC 的值；（3）一次函数y=kx +1的图象为l 3，且11，l 2，l 3不能围成三角形，直接写出k 的值．25．（10分）如图，点A 在数轴上对应的数为26，以原点O 为圆心，OA 为半径作优弧AB ̂，使点B 在O 右下方，且tan ∠AOB=43，在优弧AB ̂上任取一点P ，且能过P 作直线l ∥OB 交数轴于点Q ，设Q 在数轴上对应的数为x ，连接OP ．（1）若优弧AB̂上一段AP ̂的长为13π，求∠AOP 的度数及x 的值； （2）求x 的最小值，并指出此时直线l 与AB̂所在圆的位置关系； （3）若线段PQ 的长为12.5，直接写出这时x 的值．26．（11分）如图是轮滑场地的截面示意图，平台AB距x轴（水平）18米，与y轴交于点B，与滑道y=kx（x≥1）交于点A，且AB=1米．运动员（看成点）在BA方向获得速度v米/秒后，从A处向右下飞向滑道，点M是下落路线的某位置．忽略空气阻力，实验表明：M，A的竖直距离h（米）与飞出时间t （秒）的平方成正比，且t=1时h=5，M，A的水平距离是vt米．（1）求k，并用t表示h；（2）设v=5．用t表示点M的横坐标x和纵坐标y，并求y与x的关系式（不写x的取值范围），及y=13时运动员与正下方滑道的竖直距离；（3）若运动员甲、乙同时从A处飞出，速度分别是5米/秒、v乙米/秒．当甲距x轴1.8米，且乙位于甲右侧超过4.5米的位置时，直接写出t的值及v乙的范围．2018年河北省中考数学试卷参考答案与试题解析一、选择题（本大题共16小题，共42分，1-10小题各3分，11-16小题各2分）1．（3分）下列图形具有稳定性的是（）A．B．C．D．【解答】解：三角形具有稳定性．故选：A．2．（3分）一个整数815550…0用科学记数法表示为8.1555×1010，则原数中“0”的个数为（）A．4B．6C．7D．10【解答】解：∵8.1555×1010表示的原数为81555000000，∴原数中“0”的个数为6，故选：B．3．（3分）图中由“○”和“□”组成轴对称图形，该图形的对称轴是直线（）A．l1B．l2C．l3D．l4【解答】解：该图形的对称轴是直线l3，故选：C．4．（3分）将9.52变形正确的是（）A．9.52=92+0.52B．9.52=（10+0.5）（10﹣0.5）C．9.52=102﹣2×10×0.5+0.52D．9.52=92+9×0.5+0.52【解答】解：9.52=（10﹣0.5）2=102﹣2×10×0.5+0.52，故选：C．5．（3分）图中三视图对应的几何体是（）A．B．C．D．【解答】解：观察图形可知选项C符合三视图的要求，故选：C．6．（3分）尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅰ、作线段的垂直平分线；Ⅰ、过直线上一点作这条直线的垂线；Ⅰ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是（）A．①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣ⅠB．①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣ⅠC．①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣ⅠD．①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣Ⅰ【解答】解：Ⅰ、过直线外一点作这条直线的垂线；Ⅰ、作线段的垂直平分线；Ⅰ、过直线上一点作这条直线的垂线；Ⅰ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是：①﹣Ⅰ，②﹣Ⅰ，③﹣Ⅰ，④﹣Ⅰ．故选：D．7．（3分）有三种不同质量的物体“”“”“”，其中，同一种物体的质量都相等，现左右手中同样的盘子上都放着不同个数的物体，只有一组左右质量不相等，则该组是（）A．B．C．D．【解答】解：设的质量为x，的质量为y，的质量为：a，假设A正确，则，x=1.5y，此时B，C，D选项中都是x=2y，故A选项错误，符合题意．故选：A．8．（3分）已知：如图，点P在线段AB外，且PA=PB，求证：点P在线段AB的垂直平分线上，在证明该结论时，需添加辅助线，则作法不正确的是（）A．作∠APB的平分线PC交AB于点CB．过点P作PC⊥AB于点C且AC=BCC．取AB中点C，连接PCD．过点P作PC⊥AB，垂足为C【解答】解：A、利用SAS判断出△PCA≌△PCB，∴CA=CB，∠PCA=∠PCB=90°，∴点P在线段AB的垂直平分线上，符合题意；C、利用SSS判断出△PCA≌△PCB，∴CA=CB，∠PCA=∠PCB=90°，∴点P在线段AB的垂直平分线上，符合题意；D、利用HL判断出△PCA≌△PCB，∴CA=CB，∴点P在线段AB的垂直平分线上，符合题意，B、过线段外一点作已知线段的垂线，不能保证也平分此条线段，不符合题意；故选：B．9．（3分）为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高（单位：cm）的平均数与方差为：x甲=x丙=13，x乙=x丁=15：s甲2=s丁2=3.6，s乙2=s丙2=6.3．则麦苗又高又整齐的是（）A．甲B．乙C．丙D．丁【解答】解：∵x乙=x丁＞x甲=x丙，∴乙、丁的麦苗比甲、丙要高，∵s甲2=s丁2＜s乙2=s丙2，∴甲、丁麦苗的长势比乙、丙的长势整齐，综上，麦苗又高又整齐的是丁，故选：D．10．（3分）图中的手机截屏内容是某同学完成的作业，他做对的题数是（）A．2个B．3个C．4个D．5个【解答】解：①﹣1的倒数是﹣1，原题错误，该同学判断正确；②|﹣3|=3，原题计算正确，该同学判断错误；③1、2、3、3的众数为3，原题错误，该同学判断错误；④20=1，原题正确，该同学判断正确；⑤2m2÷（﹣m）=﹣2m，原题正确，该同学判断正确；故选：B．11．（2分）如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时的航行方向为（）A．北偏东30°B．北偏东80°C．北偏西30°D．北偏西50°【解答】解：如图，AP∥BC，∴∠2=∠1=50°．∠3=∠4﹣∠2=80°﹣50°=30°，此时的航行方向为北偏东30°，故选：A．12．（2分）用一根长为a（单位：cm）的铁丝，首尾相接围成一个正方形，要将它按图的方式向外等距扩1（单位：cm）得到新的正方形，则这根铁丝需增加（）A．4cm B．8cm C．（a+4）cm D．（a+8）cm 【解答】解：∵原正方形的周长为acm，∴原正方形的边长为a4 cm，∵将它按图的方式向外等距扩1cm，∴新正方形的边长为（a4+2）cm，则新正方形的周长为4（a4+2）=a+8（cm），因此需要增加的长度为a+8﹣A=8cm．故选：B．13．（2分）若2n+2n+2n+2n=2，则n=（）A．﹣1B．﹣2C．0D．1 4【解答】解：∵2n+2n+2n+2n=2，∴4•2n=2，∴2•2n=1，∴21+n=1，∴1+n=0，∴n=﹣1．故选：A．14．（2分）老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：接力中，自己负责的一步出现错误的是（）A．只有乙B．甲和丁C．乙和丙D．乙和丁【解答】解：∵x2−2xx−1÷x21−x=x2−2xx−1•1−xx2=x2−2xx−1•−(x−1)x2=x(x−2)x−1•−(x−1)x=−(x−2)x=2−x x，∴出现错误是在乙和丁，故选：D．15．（2分）如图，点I为△ABC的内心，AB=4，AC=3，BC=2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为（）A．4.5B．4C．3D．2【解答】解：连接AI、BI，∵点I为△ABC的内心，∴AI平分∠CAB，∴∠CAI=∠BAI，由平移得：AC∥DI，∴∠CAI=∠AID ，∴∠BAI=∠AID ，∴AD=DI ，同理可得：BE=EI ，∴△DIE 的周长=DE +DI +EI=DE +AD +BE=AB=4，即图中阴影部分的周长为4，故选：B ．16．（2分）对于题目“一段抛物线L ：y=﹣x （x ﹣3）+c （0≤x ≤3）与直线l ：y=x +2有唯一公共点，若c 为整数，确定所有c 的值，”甲的结果是c=1，乙的结果是c=3或4，则（ ）A ．甲的结果正确B ．乙的结果正确C ．甲、乙的结果合在一起才正确D ．甲、乙的结果合在一起也不正确【解答】解：∵抛物线L ：y=﹣x （x ﹣3）+c （0≤x ≤3）与直线l ：y=x +2有唯一公共点∴①如图1，抛物线与直线相切，联立解析式{y =−x(x −3)+c y =x +2得x 2﹣2x +2﹣c=0△=（﹣2）2﹣4（2﹣c ）=0解得c=1②如图2，抛物线与直线不相切，但在0≤x ≤3上只有一个交点此时两个临界值分别为（0，2）和（3，5）在抛物线上∴c 的最小值=2，但取不到，c 的最大值=5，能取到∴2＜c ≤5又∵c 为整数∴c=3，4，5综上，c=1，3，4，5故选：D．二、填空题（本大题有3个小题，共12分.17～18小题各3分：19小题有2个空，每空3分，把答案写在题中横线上）17．（3分）计算：√−12−3=2．【解答】解：√−12−3=√4=2，故答案为：2．18．（3分）若a，b互为相反数，则a2﹣b2=0．【解答】解：∵a，b互为相反数，∴a+b=0，∴a2﹣b2=（a+b）（a﹣b）=0．故答案为：0．19．（6分）如图1，作∠BPC平分线的反向延长线PA，现要分别以∠APB，∠APC，∠BPC为内角作正多边形，且边长均为1，将作出的三个正多边形填充不同花纹后成为一个图案．例如，若以∠BPC为内角，可作出一个边长为1的正方形，此时∠BPC=90°，而90°2=45是360°（多边形外角和）的18，这样就恰好可作出两个边长均为1的正八边形，填充花纹后得到一个符合要求的图案，如图2所示．图2中的图案外轮廓周长是14；在所有符合要求的图案中选一个外轮廓周长最大的定为会标，则会标的外轮廓周长是21．【解答】解：图2中的图案外轮廓周长是：8﹣2+2+8﹣2=14；设∠BPC=2x，∴以∠BPC为内角的正多边形的边数为：360180−2x=18090−x，以∠APB为内角的正多边形的边数为：360 x，∴图案外轮廓周长是=18090−x﹣2+360x﹣2+360x﹣2=18090−x+720x﹣6，根据题意可知：2x的值只能为60°，90°，120°，144°，当x越小时，周长越大，∴当x=30时，周长最大，此时图案定为会标，则会标的外轮廓周长是=18090−30+72030﹣6=21，故答案为：14，21．三、解答题（本大题共7小题，共计66分）20．（8分）嘉淇准备完成题目：发现系数“”印刷不清楚．（1）他把“”猜成3，请你化简：（3x2+6x+8）﹣（6x+5x2+2）；（2）他妈妈说：“你猜错了，我看到该题标准答案的结果是常数．”通过计算说明原题中“”是几？【解答】解：（1）（3x2+6x+8）﹣（6x+5x2+2）=3x2+6x+8﹣6x﹣5x2﹣2=﹣2x2+6；（2）设“”是a，则原式=（ax2+6x+8）﹣（6x+5x2+2）=ax2+6x+8﹣6x﹣5x2﹣2=（a﹣5）x2+6，∵标准答案的结果是常数，∴a﹣5=0，解得：a=5．21．（9分）老师随机抽查了本学期学生读课外书册数的情况，绘制成条形图（图1）和不完整的扇形图（图2），其中条形图被墨迹遮盖了一部分．（1）求条形图中被遮盖的数，并写出册数的中位数；（2）在所抽查的学生中随机选一人谈读书感想，求选中读书超过5册的学生的概率；（3）随后又补查了另外几人，得知最少的读了6册，将其与之前的数据合并后，发现册数的中位数没改变，则最多补查了3人．【解答】解：（1）抽查的学生总数为6÷25%=24（人），读书为5册的学生数为24﹣5﹣6﹣4=9（人），所以条形图中被遮盖的数为9，册数的中位数为5；（2）选中读书超过5（3）因为4册和5册的人数和为27，即最多补查了3人．故答案为3．22．（9分）如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着﹣5，﹣2，1，9，且任意相邻四个台阶上数的和都相等．尝试（1）求前4个台阶上数的和是多少？（2）求第5个台阶上的数x是多少？应用求从下到上前31个台阶上数的和．发现试用含k（k为正整数）的式子表示出数“1”所在的台阶数．【解答】解：尝试：（1）由题意得前4个台阶上数的和是﹣5﹣2+1+9=3；（2）由题意得﹣2+1+9+x=3，解得：x=﹣5，则第5个台阶上的数x是﹣5；应用：由题意知台阶上的数字是每4个一循环，∵31÷4=7…3，∴7×3+1﹣2﹣5=15，即从下到上前31个台阶上数的和为15；发现：数“1”所在的台阶数为4k﹣1．23．（9分）如图，∠A=∠B=50°，P为AB中点，点M为射线AC上（不与点A重合）的任意一点，连接MP，并使MP的延长线交射线BD于点N，设∠BPN=α．（1）求证：△APM≌△BPN；（2）当MN=2BN时，求α的度数；（3）若△BPN的外心在该三角形的内部，直接写出α的取值范围．【解答】（1）证明：∵P是AB的中点，∴PA=PB，在△APM和△BPN中，∵{∠A=∠BPA=PB∠APM=∠BPN，∴△APM≌△BPN（ASA）；（2）解：由（1）得：△APM≌△BPN，∴PM=PN，∴MN=2PN，∵MN=2BN，∴BN=PN，∴α=∠B=50°；（3）解：∵△BPN的外心在该三角形的内部，∴△BPN是锐角三角形，∵∠B=50°，∴40°＜∠BPN＜90°，即40°＜α＜90°．24．（10分）如图，直角坐标系xOy中，一次函数y=﹣12x+5的图象l1分别与x，y轴交于A，B两点，正比例函数的图象l2与l1交于点C（m，4）．（1）求m的值及l2的解析式；（2）求S△AOC ﹣S△BOC的值；（3）一次函数y=kx+1的图象为l3，且11，l2，l3不能围成三角形，直接写出k的值．【解答】解：（1）把C （m ，4）代入一次函数y=﹣12x +5，可得4=﹣12m +5，解得m=2， ∴C （2，4），设l 2的解析式为y=ax ，则4=2a ， 解得a=2，∴l 2的解析式为y=2x ；（2）如图，过C 作CD ⊥AO 于D ，CE ⊥BO 于E ，则CD=4，CE=2，y=﹣12x +5，令x=0，则y=5；令y=0，则x=10，∴A （10，0），B （0，5）， ∴AO=10，BO=5，∴S △AOC ﹣S △BOC =12×10×4﹣12×5×2=20﹣5=15；（3）一次函数y=kx +1的图象为l 3，且11，l 2，l 3不能围成三角形，∴当l 3经过点C （2，4）时，k=32；当l 2，l 3平行时，k=2；当11，l 3平行时，k=﹣12；故k 的值为32或2或﹣12．25．（10分）如图，点A 在数轴上对应的数为26，以原点O 为圆心，OA 为半径作优弧AB̂，使点B 在O 右下方，且tan ∠AOB=43，在优弧AB ̂上任取一点P ，且能过P 作直线l ∥OB 交数轴于点Q ，设Q 在数轴上对应的数为x ，连接OP ．（1）若优弧AB̂上一段AP ̂的长为13π，求∠AOP 的度数及x 的值； （2）求x 的最小值，并指出此时直线l 与AB̂所在圆的位置关系； （3）若线段PQ 的长为12.5，直接写出这时x 的值．【解答】解：（1）如图1中，由n⋅π⋅26180=13π，解得n=90°， ∴∠POQ=90°， ∵PQ ∥OB ， ∴∠PQO=∠BOQ ，∴tan ∠PQO=tan ∠QOB=43=OPOQ，∴OQ=392，∴x=392．（2）如图当直线PQ 与⊙O 相切时时，x 的值最小．在Rt△OPQ中，OQ=OP÷45=32.5，此时x的值为﹣32.5．（3）分三种情况：①如图2中，作OH⊥PQ于H，设OH=4k，QH=3k．在Rt△OPH中，∵OP2=OH2+PH2，∴262=（4k）2+（12.5﹣3k）2，整理得：k2﹣3k﹣20.79=0，解得k=6.3或﹣3.3（舍弃），∴OQ=5k=31.5．此时x的值为31.5．②如图3中，作OH⊥PQ交PQ的延长线于H．设OH=4k，QH=3k．在Rt△在Rt△OPH中，∵OP2=OH2+PH2，∴262=（4k）2+（12.5+3k）2，整理得：k2+3k﹣20.79=0，解得k=﹣6.3（舍弃）或3.3，∴OQ=5k=16.5，此时x的值为﹣16.5．③如图4中，作OH⊥PQ于H，设QH=4k，AH=3k．在Rt△OPH中，∵OP2=OH2+PH2，∴262=（4k）2+（12.5﹣3k）2，整理得：k2﹣3k﹣20.79=0，解得k=6.3或﹣3.3（舍弃），∴OQ=5k=31.5不合题意舍弃．此时x的值为﹣31.5．综上所述，满足条件的x的值为﹣16.5或31.5或﹣31.5．26．（11分）如图是轮滑场地的截面示意图，平台AB距x轴（水平）18米，与y轴交于点B，与滑道y=kx（x≥1）交于点A，且AB=1米．运动员（看成点）在BA方向获得速度v米/秒后，从A处向右下飞向滑道，点M是下落路线的某位置．忽略空气阻力，实验表明：M，A的竖直距离h（米）与飞出时间t （秒）的平方成正比，且t=1时h=5，M，A的水平距离是vt米．（1）求k，并用t表示h；（2）设v=5．用t表示点M的横坐标x和纵坐标y，并求y与x的关系式（不写x的取值范围），及y=13时运动员与正下方滑道的竖直距离；（3）若运动员甲、乙同时从A处飞出，速度分别是5米/秒、v乙米/秒．当甲距x轴1.8米，且乙位于甲右侧超过4.5米的位置时，直接写出t的值及v乙的范围．【解答】解：（1）由题意，点A （1，18）带入y=kx得：18=k1∴k=18设h=at 2，把t=1，h=5代入 ∴a=5 ∴h=5t 2（2）∵v=5，AB=1 ∴x=5t +1 ∵h=5t 2，OB=18 ∴y=﹣5t 2+18 由x=5t +1则t=15(x −1)∴y=﹣15(x −1)2+18=−15x 2+25x +895当y=13时，13=﹣15(x −1)2+18解得x=6或﹣4 ∵x ≥1 ∴x=6 把x=6代入y=18xy=3∴运动员在与正下方滑道的竖直距离是13﹣3=10（米） （3）把y=1.8代入y=﹣5t 2+18 得t 2=8125解得t=1.8或﹣1.8（负值舍去）∴x=10∴甲坐标为（10，1.8）恰好落在滑道y=18 x上此时，乙的坐标为（1+1.8v乙，1.8）由题意：1+1.8v乙﹣（1+5×1.8）＞4.5∴v乙＞7.52017年河北省中考数学试卷一、选择题（本大题共16小题，共42分。

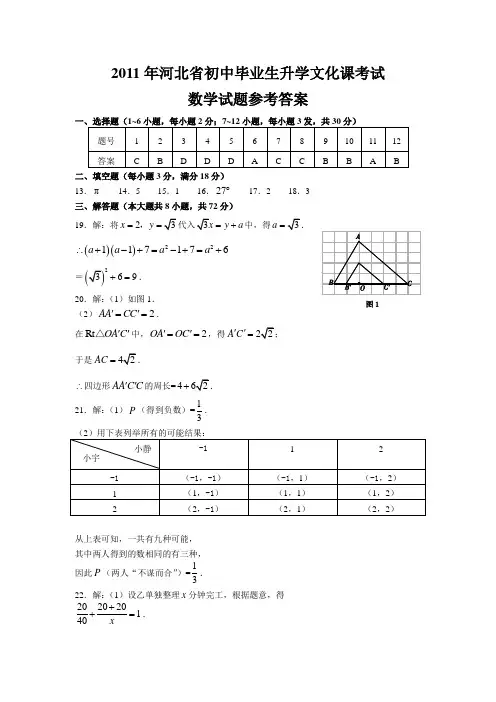
2011年河北省初中毕业生升学文化课考试数学试题参考答案二、填空题（每小题3分，满分18分）13．π 14．5 15．1 16．27︒ 17．2 18．3 三、解答题（本大题共8小题，共72分） 19．解：将2x y ==，y a =+中，得a =()()22117176a a a a ∴+-+=-+=+＝269+=．20．解：（1）如图1． （2）2A A C C ''==．在R t O A C ''△中，2O A O C ''==，得A C ''= 于是AC =∴四边形A A C C ''的周长=4+21．解：（1）P （得到负数）=13．从上表可知，一共有九种可能， 其中两人得到的数相同的有三种， 因此P （两人“不谋而合”）=13．22．解：（1）设乙单独整理x 分钟完工，根据题意，得202020140x++=．解得80x =．经检验80x =是原分式方程的解．答：乙单独整理80分钟完工．（2）设甲整理y 分钟完工，根据题意，得3018040y +≥．解得25y ≥．答：甲至少整理25分钟完工．23．解：（1）证明： 四边形A B C D 是正方形，90D C D A D C E D AG ∴=∠=∠=︒，．又C E A G D C E D A G =∴ ，△≌△． E D C G D A D E D G ∴∠=∠=，又90A D E E D C ∠+∠=︒ ，90A D E G D A ∴∠+∠=︒． D E D G ∴⊥．（2）如图2．（3）四边形C E F K 为平行四边形． 证明：设C K D E ，相交于M 点．ABCD DEFG 四边形和四边形都是正方形， AB C D AB C D EF D G EF D G ∴==∥，，，∥； BK AG K G AB C D =∴== ，，∴四边形C K G D 为平行四边形． C K D G EF C K D G ∴==，∥． 90K M E C D E D EF ∴∠=∠=∠=︒． 180K M E D E F ∴∠+∠=︒．C K E F ∴∥，∴四边形C E F K 为平行四边形．（注：由CK DG EF DG CK EF ∥，∥得∥也可）（4）221ABC D D EFGS nS n =+正方形正方形．24．解：（1）60，100． （2）依题意，得2402402520060y x x =⨯+⨯+汽，500200y x =+火．240240 1.652280100y x x =⨯+⨯+火．3962280y x =+汽．若y y >汽火，得5002003962280x x +>+,20x ∴>．（3）上周货运量()1720192222232472120x =++++++÷=>． 从平均数分析，建议预定火车费用较省．从折线图走势分析，上周货运量周四（含周四）后大于20且呈上升趋势，建议预定火车费用较省．25．解：思考 90，2． 探究一 30，2． 探究二（1）由已知得M P 与的距离为4，∴当M P AB ⊥时，点P 到A B 的最大距离是4，从而点P 到C D 的最小距离为642-=．当扇形M O P 在A B C D ，之间旋转到不能再转时， MP 与A B 相切， 此时旋转角最大，B M O ∠的最大值为90︒．（2）如图4，由探究一可知，点P 是 MP 与C D 的切点时，α达到最大，即O P C D ⊥．此时，延长P O 交A B 于点H ，α最大值为3090120O M H O H M ∠+∠=︒+︒=︒．如图5，当点P 在C D 上且与A B 距离最小时，M P C D ⊥，α达到最小，连接M P ，作O H M P ⊥于点H ，由垂径定理，得3M H =，在R t M O H △中，4M O =，3sin 4M H M O H O M ∴∠==，49M O H ∴∠=︒．M O H α=2∠ ，∴α最小为98︒．∴α的取值范围是98120︒α︒≤≤．26．解：（1）把00x y ==，代入2y x bx c =++，得0c =；再把0x t y ==，代入2y x b x =+，得200t bt t b t +=>∴=- ，，．（2）①不变．如图6，当1x =时，1y t =-，故()11-M t ，．tan 145AM P AM P ∠=∴∠=︒ ，． PAM AM N P S S S =-△四边形②=D PN PAM N D AM S S S +-△△梯形 =()()()()()()11144164161311222t t t t t t --+-+-⨯---⎡⎤⎣⎦=2315622t t -+． 解2315216228t t -+=，得121922t t ==，．11452t t <<∴= ，舍去，92t ∴=．（3）71123t <<．【注：下面是（3）的思考方法，供阅卷教师参考．当2y x tx =-经过点()23-，时，“好点”()()2221--，和，在抛物线上方，此时2322t -=-，732t x ∴==．时，32y =-，在12--和之间，说明“好点”()31-，也在抛物线上方．因此，抛物线要将这些“好点”分成数量相等的两部分时，必须72t >，如图7；当2y xt x=-经过点()32-，时，“好点”()31-，在抛物线上方，此时2112333t t -=-∴=，．当2x =时，103y =-，在34--和之间，说明“好点”()2-3，，()()2-22-1，和，也在抛物线上方．因此，抛物线要将这些“好点”分成数量相等的两部分时，必须113t <．综上所述，t 的取值范围是71123t <<．】。

2011河北省初中毕业生升学文化课考试数 学 试 卷本试卷分卷Ⅰ和卷Ⅱ两部分：卷I 为选择题，卷Ⅱ为非选择题. 本试卷满分为120分，考试时间为120分钟.卷Ⅰ（选择题，共30分）注意事项：1．答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡，考试结束，监考人员将试卷和答题卡一并收回.2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，答在试卷上无效.一、选择题（本大题共12个小题.1－6小题，每小题2分，7－12小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的 1．计算30的结果是A ．3B ．30C ．1D ．0 2．如图1，∠1＋∠2等于A ．60°B ．90°C ．110°D ．180°3．下列分解因式正确的是A ．－a ＋a 3=－a (1＋a 2)B ．2a －4b ＋2=2(a －2b )C ．a 2－4=(a －2)2D ．a 2－2a ＋1=(a －1)2 4．下列运算中，正确的是A ．2x －x =1B ．x ＋x 4=x 5C ．(－2x )3=－6x 3D ．x 2y ÷y =x 2 5．一次函数y =6x ＋1的图象不经过．．． A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限6．将图2①围成图2②的正方体，则图②中的红心“”标志所在的正方形是正方体中的 A ．面CDHE B ．面BCEFC ．面ABFGD ．面ADHG7．甲、乙、丙三个旅行团的游客人数都相等，且每团游客的平均年龄都是32岁，这三个团游客年龄的方并有分别是227S =甲，219.6S =乙，21.6S =丙，导游小王最喜欢带游客年龄相近的团队，若在这三个团中选择一个，则他应选A ．甲团B ．乙团C ．丙团D ．甲或乙团8．一小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下面的函数关系式：h =－5(t －1)2＋6，则小球距离地面的最大高度是 A ．1米 B ．5米 C ．6米 D ．7米9．如图3，在△ABC 中，∠C =90°，BC =6，D ，E 分别在AB ，AC 上，将△ABC 沿DE 折叠，使点A 落在A ′处，若A ′为CE 的中点，则折痕DE 的长为A ．12B ．5米C ．6米D ．7米10．已知三角形三边长分别为2，x ，13，若x 为正整数，则这样的三角形个数为A ．2B ．3C ．5D ．1311．如图4，在长形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆住的侧面，刚好能组合成圆住.设矩形的长和宽分别为y 和x ，则y 与x 的函数图象大致是图1① ②图212．根据图5中①所示的程序，得到了y 与x 的函数图象，如图5中②，若点M 是y 轴正半轴上任意一点，过点M作PQ ∥x 轴交图象于点P 、Q ，连接OP 、OQ ，则以下结论：①x ＜0时，y =2x②△OPQ 的面积为定值③x ＞0时，y 随x 的增大而增大 ④MQ =2PM⑤∠POQ 可以等于90° 其中正确结论是 A ．①②④ B．②④⑤C ．③④⑤D ．②③⑤2011年河北省初中毕业生升学文化课考试数学 试 卷卷Ⅱ（非选择题，共90分）注意事项：1．答卷Ⅱ前，将密封线左侧的项目填写清楚.2．答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题（本大题共6个小是，每小题3分，共18分，把答案写在题中横线上） 13π，－4，0这四个数中，最大的数是___________.14．如图6，已知菱形ABCD ，其顶点A 、B 在数轴上对应的数分别为－4和1，则BC =_____.15．若︱x －3︱＋︱y ＋2︱=0，则x ＋y 的值为_____________.16．如图7，点O 为优弧ACB 所在圆的心，∠AOC =108°，点D 在AB 的延长线上，BD =BC ，则∠D =____________. 17．如图8中图①，两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置得到图②，则阴影部分的周长为_________18．如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.如：小宇在编号为3的顶点时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.图6ABCD0 ① ②ABC DO 图7C① ②图8若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是____________.三、解答题（本大题共8个小题，共72分，解答应写出文字说明、证明过程 或演算步骤） 19．（本小题满分8分）已知2x y =⎧⎪⎨=⎪⎩x ，yy a =+的解.求(a ＋1)(a －1)＋7的值 20．（本小题满分8分）如图10，在6×8的网格图中，每个小正方形边长均为1，点O 和△ABC 的顶点均为小正方形的顶点. ⑴以O 为位似中心，在网格图．．．中作△A ′B ′C ′，使△A ′B ′C ′和△ABC 位似，且位似比为1：2 ⑵连接⑴中的AA ′，求四边形AA ′C ′C 的周长.21．（本小题满分8分）如图11，一转盘被等分成三个扇形，上面分别标有关－1，1，2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，鞭个扇形恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）.⑴若小静转动转盘一次，求得到负数的概率； ⑵小宇和小静分别转动一次，若两人得到的数相同，则称两人“不谋而合”，用列表法（或画树形图）求两人“不谋而合”的概率.图11小宇 小静22．（本小题满分8分）甲、乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工，若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工.⑴问乙单独整理多少分钟完工？⑵若乙因式作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？23．（本小题满分9分）如图12，四边形ABCD 是正方形，点E ，K 分别在BC ，AB 上，点G 在BA 的延长线上，且CE =BK =AG . ⑴求证：①DE =DG ；②DE ⊥DG ；⑵尺规作图：以线段DE ，DG 为边作出正方形DEFG （要求：只保留作图痕迹，不写作法和证明）；⑶连接⑵中的KF ，猜想并写出四边形CEFK 是怎样的特殊四边形，并证明你的猜想；⑷当1CE CB n 时，衣直接写出ABCD DEFGS S 正方形正方形的值.24．（本小题满分9分）已知A 、B 两地的路程为240千米，某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地，受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订.现在有货运收费项目及收费标准表，行驶路程S （千米）与行驶时间t （时）的函数图象（如图13中①），上周货运量折线统计图（如图13中②）等信息如下：⑴汽车的速度为__________千米/时，火车的速度为_________千米/时；设每天用汽车和火车运输的总费用分别为y 汽（元）和y 火（元），分别求y 汽、y 火与x 的函数关系式（不必写出x 的取值范围）及x 为何值时y 汽＞y 火；（总费用=运输费＋冷藏费＋固定费用）A B CDG 图11图13 ②⑶请你从平均数、折线图走势两个角度分析，建议该经销商应提前下周预定哪种运输工具，才能使每天的运输总费用较省？25．（本小题满分10分）如图14①至图14④中，两平行线AB、CD音的距离均为6，点M为AB上一定点.思考：如图14①中，圆心为O的半圆形纸片在AB、CD之间（包括AB、CD），其直径MN在AB上，MN=8，点P为半圆上一点，设∠MOP=α，当α=________度时，点P到CD的距离最小，最小值为____________.探究一在图14①的基础上，以点M为旋转中心，在AB、CD之间顺时针旋转该半圆形纸片，直到不能再转动为止.如图14②，得到最大旋转角∠BMO=_______度，此时点N到CD的距离是______________.探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉，使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.⑴如图14③，当α=60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值：⑵如图14④，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的取值范围.（参考数据：sin49°=34，cos41°=34，tan37°=34）BADC图14①BADC图14 ③BADC图14 ②BADC图14 ④M26．(本小题满分12分)如图15，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P.已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）.⑴求c、b（用含t的代数式表示）；⑵当4＜t＜5时，设抛物线分别与线段AB、CD交于点M、N.①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；②求△MPN的面积S与t的函数关系式，并求t为何值时，S=218；③在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接．．写出t的取值范围.。

2011河北省初中毕业生升学文化课考试数 学 试 卷本试卷分卷Ⅰ和卷Ⅱ两部分：卷I 为选择题，卷Ⅱ为非选择题. 本试卷满分为120分，考试时间为120分钟.卷Ⅰ（选择题，共30分）注意事项：1．答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡，考试结束，监考人员将试卷和答题卡一并收回.2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，答在试卷上无效.一、选择题（本大题共12个小题.1－6小题，每小题2分，7－12小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的 1．计算30的结果是A ．3B ．30C ．1D ．0 2．如图1，∠1＋∠2等于A ．60°B ．90°C ．110°D ．180°3．下列分解因式正确的是A ．－a ＋a 3=－a (1＋a 2)B ．2a －4b ＋2=2(a －2b )C ．a 2－4=(a －2)2D ．a 2－2a ＋1=(a －1)24．下列运算中，正确的是A ．2x －x =1B ．x ＋x 4=x 5C ．(－2x )3=－6x 3D ．x 2y ÷y =x 25．一次函数y =6x ＋1的图象不经过．．． A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限6．将图2①围成图2②的正方体，则图②中的红心“ ”标志所在的正方形是正方体中的A ．面CDHEB ．面BCEFC ．面ABFGD ．面ADHG7．甲、乙、丙三个旅行团的游客人数都相等，且每团游客的平均年龄都是32岁，这三个团游客年龄的方并有分别是227S =甲，219.6S =乙，21.6S =丙，导游小王最喜欢带游客年龄相近的团队，若在这三个团中选择一个，则他应选 A ．甲团 B ．乙团 C ．丙团 D ．甲或乙团8．一小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下面的函数关系式：h =－5(t －1)2＋6，则小球距离地面的最大高度是 A ．1米 B ．5米 C ．6米 D ．7米9．如图3，在△ABC 中，∠C =90°，BC =6，D ，E 分别在AB ，AC 上，将△ABC 沿DE 折叠，使点A 落在A ′处，若A ′为CE 的中点，则折痕DE 的长为A ．12B ．2C ．3D ．410．已知三角形三边长分别为2，x ，13，若x 为正整数，则这样的三角形个数为A ．2B ．3C ．5D ．13图1 ①②图211．如图4，在长方形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱.设矩形的长和宽分别为y 和x ，则y 与x 的函数图象大致是12．根据图5中①所示的程序，得到了y 与x 的函数图象，如图5中②，若点M 是y 轴正半轴上任意一点，过点M 作PQ∥x 轴交图象于点P 、Q ，连接OP 、OQ ，则以下结论：①x ＜0时，y =2x②△OPQ 的面积为定值③x ＞0时，y 随x 的增大而增大 ④MQ =2PM⑤∠POQ 可以等于90° 其中正确结论是 A ．①②④ B ．②④⑤C ．③④⑤D ．②③⑤2011年河北省初中毕业生升学文化课考试数 学 试 卷卷Ⅱ（非选择题，共90分）注意事项：1．答卷Ⅱ前，将密封线左侧的项目填写清楚.2．答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题（本大题共6个小是，每小题3分，共18分，把答案写在题中横线上） 13π，－4，0这四个数中，最大的数是___________.14．如图6，已知菱形ABCD ，其顶点A 、B 在数轴上对应的数分别为－4和1，则BC =_____.15．若︱x －3︱＋︱y ＋2︱=0，则x ＋y 的值为_____________. 16．如图7，点O 为优弧ACB 所在圆的心，∠AOC =108°，点D 在AB 的延长线上，BD =BC ，则∠D =____________.图6ABCD图40 ①②ABC DO 图7C① ②图817．如图8中图①，两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置得到图②，则阴影部分的周长为_________18．如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.如：小宇在编号为3的顶点时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”. 若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是____________.三、解答题（本大题共8个小题，共72分，解答应写出文字说明、证明过程 或演算步骤） 19．（本小题满分8分）已知2x y =⎧⎪⎨=⎪⎩x ，yy a =+的解.求(a ＋1)(a －1)＋7的值 20．（本小题满分8分）如图10，在6×8的网格图中，每个小正方形边长均为1，点O 和△ABC 的顶点均为小正方形的顶点.⑴以O 为位似中心，在网格图．．．中作△A ′B ′C ′，使△A ′B ′C ′和△ABC 位似，且位似比为1：2⑵连接⑴中的AA ′，求四边形AA ′C ′C 的周长.（结果保留根号）图9如图11，一转盘被等分成三个扇形，上面分别标有关－1，1，2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，鞭个扇形恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）.⑴若小静转动转盘一次，求得到负数的概率；⑵小宇和小静分别转动一次，若两人得到的数相同，则称两人“不谋而合”，用列表法（或画树形图）求两人“不谋而合”的概率.22．（本小题满分8分）甲、乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工，若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工.⑴问乙单独整理多少分钟完工？⑵若乙因式作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？23．（本小题满分9分）如图12，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE=BK=AG.⑴求证：①DE=DG；②DE⊥DG；⑵尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；⑶连接⑵中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；⑷当1CECB n时，衣直接写出ABCDDEFGSS正方形正方形的值.图11小宇小静AB CD图11已知A 、B 两地的路程为240千米，某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地，受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订.现在有货运收费项目及收费标准表，行驶路程S （千米）与行驶时间t （时）的函数图象（如图13中①），上周货运量折线统计图（如图13中②）等信息如下：⑴汽车的速度为__________千米/时，火车的速度为_________千米/时；设每天用汽车和火车运输的总费用分别为y 汽（元）和y 火（元），分别求y 汽、y 火与x 的函数关系式（不必写出x 的取值范围）及x 为何值时y 汽＞y 火；（总费用=运输费＋冷藏费＋固定费用）⑶请你从平均数、折线图走势两个角度分析，建议该经销商应提前下周预定哪种运输工具，才能使每天的运输总费用较省？图13①图13 ②如图14①至图14④中，两平行线AB、CD间的距离均为6，点M为AB上一定点.思考：如图14①中，圆心为O的半圆形纸片在AB、CD之间（包括AB、CD），其直径MN在AB上，MN=8，点P为半圆上一点，设∠MOP=α，当α=________度时，点P到CD的距离最小，最小值为____________.探究一在图14①的基础上，以点M为旋转中心，在AB、CD之间顺时针旋转该半圆形纸片，直到不能再转动为止.如图14②，得到最大旋转角∠BMO=_______度，此时点N到CD的距离是______________.探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉，使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.⑴如图14③，当α=60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值：⑵如图14④，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的取值范围.（参考数据：sin49°=34，cos41°=34，tan37°=34）BADC图14①BADC图14 ③BADC图14 ②BADC图14 ④M如图15，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P.已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）.⑴求c、b（用含t的代数式表示）；⑵当4＜t＜5时，设抛物线分别与线段AB、CD交于点M、N.①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；②求△MPN的面积S与t的函数关系式，并求t为何值时，S=218；③在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接．．写出t的取值范围.参考答案：1.C2.B3.D4.D5.D6.A7.C8.C9.B 10.B 11.A 12. B. 13. π 14. 5 15. 1 16. 27° 17. 2 18. 319.解：将2,x y =y a =+中，得a =∴22(1)(1)7176a a a a +-+=-+=+=269+= 20. 解：⑴如图1.⑵ ''2AA CC ==在Rt ⊿''OA C 中，''OA OC ==2，得''A C =AC =∴四边形''AA C C 的周长=4+21. 解：⑴ P （得到负数）=13⑵用下表列举所有的可能结果：从上表可知，一共有九种可能，其中两人得到的数相同的有三种， 因此 P （两人“不谋而合”）=13（注：画树状图正确也相应给分）22. 解：⑴ 设乙单独整理x 分钟完工，根据题意得：202020140x++= 解得：80x =.经检验80x =是原方程的解.答：乙单独整理80分钟完工.⑵ 设甲整理y 分钟完工，根据题意得：308040y +≥1， 解得：y ≥25答：甲至少整理25分钟完工.（注：以下解答也给分.设甲、乙分别整理,y z 分钟，得18040z y +=.∴802.z y =- ∵30z ≤，∴80230y -≤，∴y ≥25.）23. 解：⑴证明：∵ 四边形ABCD 是正方形 ，∴DC DA =，90DCE DAG ∠=∠=°. 又∵CE AG =，∴⊿D C E ≌⊿D A G .∴EDC GDA ∠=∠，DE DG =.又∵90ADE EDC ∠+∠= ,∴90ADE GDA ∠+∠= ,∴DE DG ⊥.⑵如图2（注：图3或其它画法正确的相应给分）⑶四边形CEFK 是平行四边形. 证明：设,CK DE 相交于M 点.∵四边形ABCD 和四边形DEFG 都是正方形，∴AB ∥CD , AB=CD , EF=DG , EF ∥DG , ∵BK=AG , ∴KG=AB=CD , ∴四边形CKGD 为平行四边形. ∴CK=DG=EF , CK ∥DG . ∴90KME GDE DEF ∠=∠=∠=.∴180KME DEF ∠+∠=.∴CK ∥EF , ∴四边形CEFK 是平行四边形.(注：由CK ∥DG , EF ∥DG 得CK ∥EF 也可)⑷22=1ABCD DEFG S n S n +正方形正方形. 24. 解： ⑴ 60，100. ⑵依题意，得240=2402520060y x x ⨯+⨯+汽. =500200y x +汽.240=240 1.652280100y x x ⨯+⨯+火. =3962280y x +火.若y 汽 >y 火,得500200x +>3962280x +， ∴x >20.⑶上周货运量(17201922222324)72120X =++++++÷=>. 从平均数分析，建议预定火车费用较省.从折线图走势分析，上周货运量周四（含周四）后大于20且呈上升趋势，建议预定火车费用较省.25. 解：思考 90，2. 探究一 30，2.探究二、⑴由已知得M 与P 的距离为4，∴当MP AB ⊥时，点P 到AB 的最大距离是4，从而点P 到CD 的最小距离为642-=.当扇形MOP 在,AB CD 之间旋转到不能再转时， MP与AB 相切，此时旋转角最大，BMO ∠的最大值为90°.⑵如图4，由探究一可知，点P 是 MP与CD 的切点时，a 达到最大，即OP CD ⊥.此时，延长PO 交AB 于点H ，a 最大值为3090120OMH OHM ∠+∠=+=.如图5，当点P 在CD 上且与AB 距离最小时，MP CD ⊥，a 达到最小，连接MP ，作OH MP ⊥于点H ，由垂径定理，得3MH =，在Rt ⊿MOH 中，MO =4， ∴3sin ,4MH MOH OM ∠==∴49MOH ∠= ，∵2a MOH =∠，∴a 最小为98 . ∴a 的取值范围是98120a ≤≤.26. 解：⑴把0,0x y ==代入2y x bx c =++，得0c =.再把x t =,0y =代入2y x bx =+，得20t bt +=，∵0t >，∴b t =-.⑵①不变.如图6，当1x =时，1y t =-，故(1,1)M t -. ∵tan 1AMP ∠=.∴45AMP ∠=②PAM AMNP -S S S = 四边形=DPN PAM NDAM +-S S S 梯形 =[]111(416)(1)3(1)(1)222t t t t -+-⨯---（t-4)(4t-16)+=2315622t t -+ 解2315622t t -+=218，得1219,22t t ==. ∵45t <<，∴112t =舍去，∴92t =. ⑶71123t <<。

2011年河北省初中毕业生升学文化课考试数学试卷卷Ⅰ（选择题，共30分）注意事项：1．答卷I前，考生务必将自己的姓名、准考证号、科目填涂在答题卡上，考试结束，监考人员将试卷和答题卡一并收回．2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．答在试卷上无效．一、选择题（本大题共12个小题，1~6小题，每小题2分；7~12小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．计算30的结果是的算术平方根是（）A．3 B．30 C．1 D．02. 如图1,∠1+∠2等于A．60°B．90°C．110°D．180°3．下列分解因式正确的是–A．–a+a3=–a(1+a2) B．2a–4b+2=2(a–2b)C．a2–4=(a–2)2D．a2–2a+1=(a–1)24．下列运算中，正确的是A．2x–x=1 B．x+x4=x5C．(–2x)3=–6x3 D．x2y÷y=x25．一次函数y=6x+1的图象不经过．．．A．第一象限B．第二象限C．第三象限D．第四象限6．将图2-1围成图2–2的正方体，则图2-1中的红心“”标志所在的正方形的是正方形是下文体中的Ａ．面CDHEＢ．面BCEFＣ．面ABFG D．面ADHG7．甲、乙、丙三个旅行团的游客人数相等，且每团游客的平均年龄都是32岁，这三个团游客年龄的方差分别是S 甲2=27，S 乙2=19.6，S 丙2=1.6．导游小王最喜欢带游客年龄相近的团队，若在三个团中选择一个，则他 应选 A ．甲团 B ．乙团 C ．丙团 D ．甲团或乙团8．一小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下面函数关系式：h =–5(t –1)2+6，则小球距离地面的最大高度是 A ．1米 B ．5米 C ．6米 D ．7米9．如图3，在△ABC 中，∠C =90°，BC =6，D 、E 分别在AB 、AC 上将△ABC 沿DE 折叠，使点A 落在点A ´处，若A ´为CE 的中点，则折痕DE 的度A ．1米B ．5米C ．6米D ．7米10．已知三角形三边长分别为2，x ，13，若x 为正整数，则这样的三角形个数为 A ．2 B ．3 C ．5 D ．1311．如图4，在矩形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为y 和x ，则y 与x 的函数图象大致是12.根据图5-1所示的程序，得到了y 与x 的函数图象，如图5-2.若点M 是y 轴正半轴上任意一点，过点M 作PQ ∥x 轴交图象于点P ，Q ，连接OP ，OQ .则以下结论： ①x ＜0时，y =2x②△OPQ 的面积为定值． ③x ＞0时，y 随x 的增大而增大 ④MQ =2PM⑤∠POQ 可以等于90°. 其中正确的是：A ．①②④B ．②④⑤C ．③④⑤D ．②③⑤2011年河北省初中毕业生升学文化课考试数 学 试 卷卷II （非选择题，共96分）注意事项：1．答卷II 前，将密封线左侧的项目填写清楚．2．答卷II 时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上．二、填空题（本大题共6个小题，每小题3分，共18分．把答案写在题中横线上） 13．35，π，–4，0这四个数中，最大的数是_________________14．如图6，已知菱形ABCD ，其顶点A ，B 在数轴上对应的数分别为–4和1,则BC ＝_____________ 15．若||x –3+||y +2=0，则x +y 的值为16．如图7，点O 为优级弧ACB ⌒所在圆的圆心，∠AOC ＝108°，点D 在AB 延长线上，BD ＝BC ，则∠D ＝ __________17. 如图8-1，两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ´B ´D ´的位置，得到图8-2，则阴影部分的周长为___________.18．如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是三、解答题（本大题共8个小题，共72分．解答应写出文字说明、证明过程或演算步骤） 19．（本小题满分8分）已知⎩⎨⎧x =2y =3是关于x ，y 的二元一次方程3x =y +a 的解.求（a +1）（a –1）+7的值20．（本小题满分8分）如图10，在6⨯8网格图中，每个小正方形的边长均为1，点O 和△ABC 的顶点均为小正方形的顶点．（1）以O 为位似中心，在网格图中．．．．作△A ´B ´C ´，使△A ´B ´C ´和△ABC 位似，且位似比为1：2；（2）连接（1）中的AA ´，求四边形AA ´C ´C 的周长.（结果保留根号）.如图11，一转盘被等分成三个扇形，上面分别标有–1，1，2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，某个扇形会恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）.（1）若小静转动转盘一次，求得到负数的概率；（2）小宇和小静分别转动转盘一次，若两人得到的数相同，则称两“不谋而合”.用列表法（或画树状图）求两人“不谋而合”的概率.22．（本小题满分8分）甲、乙两人准备整理一批新到的实验器材．若甲单独整理需要40分钟完工；若甲、乙共同事理20分钟后，乙需再单独整理20分钟才能完工．（1）问乙单独整理多少分钟完工？（2）若乙因工作需要，他整理时间不超过30分钟，则甲至少整理多少分钟才能完工？23．（本小题满分9分）如图12，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE＝BK＝A G．（1）求证：①DE＝DG；②DE⊥DG（2）尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；（3）连接（2）中KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；（4）当CECB＝1n时，请直接写出S正方形ABCDS正方形DEFG的值．24．（本小题满分9分）已知A 、B 两地的路程为240千米．某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地．受各各因素限制，下一周只采用汽车和火车中的一种进行运输，且须提前预订．现有货运收费项目及收费标准表、行驶路程s （千米）与行驶时间t （时）的函数图象（如图13-1）、上周货运量折线统计图（如图13-2）等信息如下： 货运收费项目及收费标准表（1）汽车的速度为___________千米/时， 火车的速度为___________千米/时； （2）设每天．．用汽车和火车运输的总费用分别为 y 汽 （元）和y 火 （元），分别求y汽、y 火与x的函数关系式（不必写出x 的取值范围），及x 为何值时y 汽 ＞y 火；（总费用＝运输费＋冷藏费＋固定费用） （3）请你从平均数、折线图走势两个角度分析，建议该经销商应提前为下周预定哪种运输工具，才能使每天的运输总费用较省？25．（本小题满分10分）如图14-1至14-4中，两平行线AB，CD间的距离均为6，点M为AB上一定点．思考如图14-1，圆心为O的半圆形纸片在AB，CD之间．．（包括AB，CD），其直径MN在AB上，MN＝8，点P为半圆上一点，设∠MOP＝α．当α＝_____度时，点P到CD的距离最小，最小值为_______探究一在图14-1的基础上，以点M为旋转中心，在AB，CD之间顺时针旋转该半圆形纸片，直到不能再转动为止，如图14-2，得到最大旋转角∠BMO＝_____度，此时点N到CD的距离是_______．探究二将图14-1中的扇形纸片NOP按下面对α的要求剪掉，使户型纸片MOP绕点M在AB，CD之间．．顺时外旋转．（1）如图14-3，当α＝60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值（2）如图14-4，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的取值范围．（参考数据：sin49°=34，cos41°=34，tan37°=34）26．（本小题满分12分）如图15，在平面直角坐标系中，点P 从原点O 出发，沿x 轴向右以每秒1个单位长的速度运动t 秒（t ＞0），抛物线y =x 2+bx +c 经过点O 和点P ．已知矩形ABCD 的三个顶点为A （1，0），B （1，–5），D （4，0）．（1）求c ，b （用含t 的代数式表示）；（2）当4＜t ＜5时，设抛物线分别与线段AB ，CD 交于点M ，N ．①在点P 的运动过程中，你认为∠AMP 的大小是否会变化？若变化，说明理由；若不变，求出∠AMP 的值；②求△MPN 的面积S 与t 的函数关系式，并求t 为何值时，S ＝218（3）在矩形ABCD 的内部（不含边界），把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接．．写出t 的取值范围．。

数学试卷第1页（共10页）准考证号：**市2011年初中毕业生学业考试数学试卷【说明】全卷分为第Ⅰ卷和第Ⅱ卷，第Ⅰ卷1－2页，第Ⅱ卷3－10页。

考试时间120分钟，满分150分。

考试结束后，第Ⅱ卷和答题卡按规定装袋上交。

第Ⅰ卷(选择题 共40分)注意事项：1．答第Ⅰ卷前，考生务必将自己的学校、姓名、准考证号、考试科目填涂在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡 皮擦干净后，再选涂其他答案，不能答在试题卷上。

3．考试结束后，本试卷由考场统一收回，集中管理。

一、选择题：本大题共10个小题，每小题4分，共40分，在每个小题给出的四个选项中，只有一个符合题目要求 1．－2的相反数A ．－2B ．2C ．2±D ．－2 2．下列分式是最简分式的Ａ．b a a 232 B ．a a a 32- C ．22b a b a ++ D ．222ba ab a -- 3．下列运算错误的是A ．235a a a ⋅=B ．347()m m =C ．3363282c b a bc a =）（ D ．624m m m ÷= 4．一幅扑克牌（不含大小王），任意抽取一张，抽中方块的概率是 A ．21 B ．521 C ．31 D ．415．函数31--=x x y 的自变量x 的取值范围是 A ．1x > B ．1x >且3x ≠ C ．1≥x D. 1≥x 且3x ≠数学试卷第2页（共10页）6．点（－2，3）关于原点对称的点的坐标是A ．(2,3)B ．(－2,－3)C ．(2,－3)D ．(－3,2) 7．如图：等腰梯形ABCD 中 ，AD ∥BC ，AB=DC ， AD=3，AB=4,∠B=60︒，则梯形的面积是 A.310 B.320 C.346+ D.3812+ 8．计算2sin30︒-sin 245︒+cot60︒的结果A.3321+ B.3321+ C.23+ D.23-1+ 9．如图：△ABC 中，DE ∥BC ，AD:DB=1:2,下列选项正确的是A ．DE:BC=1:2B ．AE:AC=1:3C ．BD:AB=1:3D ．S DE A ∆:S ABC ∆=1:4（ 第9题） （第10题）10．如图：在△ABC 中，∠ACB=90°,CD ⊥AB 于点D ，下列说法中正确的个数是①CD AB BC AC ⋅=⋅ ②DB AD AC ⋅=2③BA BD BC ⋅=2 ④DB AD CD ⋅=2A ．1个B ．2个C ．3个D ．4个CBEDABDAC数学试卷第3页（共10页）绝密★启用前【考试时间：2011年6月】**市2011年初中毕业生学业考试数学试卷第Ⅱ卷（非选择题 共110分）注意事项：1．第Ⅱ卷共8页，用钢笔或中性笔直接答在试卷上。

2011年河北省中考数学试卷及答案解析一、选择题（共12小题，1-6小题每小题2分，7-12小题，每题3分，满分30分）1、（2011•河北）计算30的结果是（）A、3B、30C、1D、0考点：零指数幂。

专题：计算题。

分析：根据零指数幂：a0=1（a≠0）计算即可．解答：解：30=1，故选C．点评：本题主要考查了零指数幂，任何非0数的0次幂等于1．2、（2011•河北）如图，∠1+∠2等于（）A、60°B、90°C、110°D、180°考点：余角和补角。

专题：计算题。

分析：根据平角的定义得到∠1+90°+∠2=180°，即由∠1+∠2=90°．解答：解：∵∠1+90°+∠2=180°，∴∠1+∠2=90°．故选B．点评：本题考查了平角的定义：180°的角叫平角．3、（2011•河北）下列分解因式正确的是（）A、﹣a+a3=﹣a（1+a2）B、2a﹣4b+2=2（a﹣2b）C、a2﹣4=（a﹣2）2D、a2﹣2a+1=（a﹣1）2考点：提公因式法与公式法的综合运用。

专题：因式分解。

分析：根据提公因式法，平方差公式，完全平方公式求解即可求得答案．解答：解：A、﹣a+a3=﹣a（1﹣a2）=﹣a（1+a）（1﹣a），故本选项错误；B、2a﹣4b+2=2（a﹣2b+1），故本选项错误；C、a2﹣4=（a﹣2）（a+2），故本选项错误；D、a2﹣2a+1=（a﹣1）2，故本选项正确．故选D．点评：本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，理解因式分解与整式的乘法是互逆运算是解题的关键．4、（2011•河北）下列运算中，正确的是（）A、2x﹣x=1B、x+x4=x5C、（﹣2x）3=﹣6x3D、x2y÷y=x2考点：整式的除法；合并同类项；幂的乘方与积的乘方。

2011河北中考数学试题及答案2011年河北省初中毕业生升学文化课考试数学试卷一、选择题（本题共10小题，每小题3分，共30分）1. 以下各数中，绝对值最小的数是（）A. -3B. -2C. 0D. 12. 以下各数中，是无理数的是（）A. 0.5B. πC. 0.3333…D. 0.56253. 以下各数中，是负数的是（）A. -2B. 0C. 2D. 14. 以下各数中，是正数的是（）A. -3B. 0C. 3D. -15. 以下各数中，是整数的是（）A. 0.5B. 3.14C. 0D. -26. 以下各数中，是分数的是（）A. 0.5B. 3.14C. 0D. -27. 以下各数中，是正有理数的是（）A. 0.5B. 3.14C. 0D. -28. 以下各数中，是负有理数的是（）A. 0.5B. 3.14C. 0D. -29. 以下各数中，是正无理数的是（）A. 0.5B. πC. 0D. -210. 以下各数中，是负无理数的是（）A. 0.5B. πC. 0D. -2二、填空题（本题共5小题，每小题3分，共15分）11. 一个数的相反数是-3，则这个数是____。

12. 一个数的绝对值是2，则这个数是____。

13. 一个数的倒数是2，则这个数是____。

14. 一个数的平方是4，则这个数是____。

15. 一个数的立方是-8，则这个数是____。

三、解答题（本题共6小题，共55分）16. 计算题（本题共2小题，每小题5分，共10分）（1）计算：(-3) + 2 × (-1) - 4 ÷ 2（2）计算：(-2)² - 3 × (-1) + (-4) ÷ (-2)17. 化简题（本题共2小题，每小题5分，共10分）（1）化简：-3a - 2a + 4a（2）化简：-2x² + 3x² - 5x² + 4x²18. 几何题（本题共2小题，每小题5分，共10分）（1）已知一个三角形的两边长分别为3和4，求第三边长的取值范围。

第4题图灯三角尺 投影湖北省荆门市二○一一年初中毕业生学业考试数 学 试 题注意事项：1.本卷满分为120分，考试时间为120分钟．2.本卷是试题卷，不能答题，答题必须写在答题卡上．解题中的辅助线和标注角的字母、符号等务必添在答题卡的图形上.3.在答题卡上答题，选择题必须用２Ｂ铅笔填涂，非选择题必须用0.5毫米黑色签字笔或黑色墨水钢笔作答．★ 祝 考 试 顺 利 ★一、选择题（本大题共12小题，每小题只有唯一正确答案，每小题3分，共36分） 1.有理数21-的倒数是（ ▲ ） A .2- B .2 C .21 D .21-2.下列四个图案中，轴对称图形的个数是（ ▲ ）A .1B .2C .3D .43.将代数式142-+x x 化成q p x ++2)(的形式为（ ▲ ）A .3)2(2+-x B .4)2(2-+x C .5)2(2-+x D .4)4(2++x4.如图，位似图形由三角尺与其灯光照射下的中心投影组成，相似比为2∶5，且三角尺的一边长为8cm ，则投影三角形的对应边长为（ ▲ ）A .8cmB .20cmC .3.2cmD .10cm5.有13位同学参加学校组织的才艺表演比赛，已知他们所得的分数互不相同，共设7个获奖名额.某同学知道自己的比赛分数后，要判断自己能否获奖，在下列13名同学成绩的统计量中只需知道一个量，它是（ ▲ ）A .众数B .方差C .中位数D .平均数 6.对于非零的两个实数a 、b ，规定11a b b a⊗=-.若1(1)1x ?=，则x 的值为（ ▲ ） 第2题图A .23 B .31 C .21 D .21- 7. 如图，P 为线段AB 上一点，AD 与BC 交于E ，∠CPD ＝∠A ＝∠B ，BC 交PD 于F ，AD 交PC 于G ，则图中 相似三角形有（ ▲ ）A .1对B .2对C .3对D .4对 8.若等式1)23(0=-x成立，则x 的取值范围是（ ▲ ） A .12x ≠ B .0x ≥且12x ≠ C .0x ≥ D .>0x 且12x ≠ 9.如图，长方体的底面边长分别为2cm 和4cm ，高为5cm .若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点，则蚂蚁爬行的最短路径长为（ ▲ ）A .13cmB .12cmC .10cmD .8cm 10.在△ABC 中，∠A ＝120°，AB ＝4，AC ＝2，则sin B 的值是（ ▲ ）A .51714B .35C .217D .211411.关于x 的方程0)1(2)13(2=+++-a x a ax 有两个不相等的实根1x 、2x ，且有a x x x x -=+-12211，则a 的值是（ ▲ ）A .1B .1-C . 1或1-D .212.图①是一瓷砖的图案，用这种瓷砖铺设地面， 图②铺成了一个2×2的近似正方形，其中完整 菱形共有5个；若铺成3×3的近似正方形图案 ③，其中完整的菱形有13个；铺成4×4的近 似正方形图案④，其中完整的菱形有25个； 如此下去，可铺成一个n n ⨯的近似正方形图 案.当得到完整的菱形共181个时，n 的值为 （ ▲ ）A .7B .8C .9D .10二、填空题（本大题共5小题，每小题3分，共15分）13.计算1112()2232----= ▲ .14.已知A ＝2x ，B 是多项式，在计算B +A 时，小马虎同学把B +A 看成了B ÷A ，结果得212x x +，则B +A ＝ ▲ .15.如图，⊙O 是△ABC 的外接圆，CD 是直径，∠B ＝40°，则∠ACD 的度数是 ▲ .16.请将含60°顶角的菱形分割成至少含一个等腰梯形且面积相等的六部分，用实线画出分PC ADBEFG第7题图2cm5cmQ第9题图第12题图OCD第15题图第16题图第17题图B'yxOCBA割后的图形. 17.如图，双曲线xy 2=(x ＞0）经过四边形OABC 的顶点A 、C ，∠ABC ＝90°，OC 平分OA 与x 轴正半轴的夹角，AB ∥x 轴，将△ABC 沿AC 翻折后得△AB C ¢，B '点落在OA上，则四边形OABC 的面积是 ▲ .三、解答题（本大题共7个小题，共69分）18.（本题满分8分）解不等式组，并把解集在数轴上表示出来.331 213(1)8. x x x x ì-+?ïíï---î； ①＜②19.（本题满分9分）如图，P 是矩形ABCD 下方一点，将△PCD 绕P 点顺时针旋转60°后恰好D 点与A 点重合，得到△PEA ，连接EB ，问△ABE 是什么特殊三角形？请说明理由.DCB APE第19题图20.（本题满分10分）2011年国家对“酒后驾车”加大了处罚力度，出台了不准酒后驾车的禁令.某记者在一停车场对开车的司机进行了相关的调查，本次调查结果有四种情况：①偶尔喝点酒后开车；②已戒酒或从来不喝酒；③喝酒后不开车或请专业司机代驾；④平时喝酒，但开车当天不喝酒.将这次调查情况整理并绘制了如下尚不完整的统计图，请根据相关信息，解答下列问题.（1）该记者本次一共调查了▲ 名司机； （2）求图甲中④所在扇形的圆心角，并补全图乙；（3）在本次调查中，记者随机采访其中的一名司机，求他属第②种情况的概率； （4）请估计开车的10万名司机中，不违反“酒驾”禁令的人数.21.（本题满分10分）某河道上有一个半圆形的拱桥，河两岸筑有拦水堤坝，其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME 、NF 与半圆相切，上、下桥斜面的坡度i ＝1∶3.7，桥下水深OP ＝5米，水面宽度CD ＝24米.设半圆的圆心为O ，直径AB 在坡角顶点M 、N 的连线上，求从M 点上坡、过桥、下坡到N 点的最短路径长.（参考数据：π≈3，3≈1.7，tan15°＝321 ）第21题图图乙27021201008060402029%③④③①4②①1%人数第20题图图甲22.（本题满分10分）如图，等腰梯形ABCD 的底边AD 在x 轴上，顶点C 在y 轴正半轴上，B (4,2)，一次函数1y kx =-的图象平分它的面积，关于x 的函数()232y mx m k x m k =-+++的图象与坐标轴只有两个交点，求m 的值.23.（本题满分10分）2011年长江中下游地区发生了特大旱情，为抗旱保丰收，某地政府制定了农户投资购买抗旱设备的补贴办法，其中购买Ⅰ型、Ⅱ型抗旱设备所投资的金额 型号 金额Ⅰ型设备Ⅱ型设备投资金额x （万元） x5x2 4 补贴金额y （万元）)0(1≠=k kx y2)0(22≠+=a bxax y2.43.2（1）分别求1和2的函数解析式；（2）有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买，请你设计一个能获得最大补贴金额的方案，并求出按此方案能获得的最大补贴金额.第22题图y =kx 1yxODC BA24.（本题满分12分）如图甲，分别以两个彼此相邻的正方形OABC 与CDEF 的边OC 、OA 所在直线为x 轴、y 轴建立平面直角坐标系（O 、C 、F 三点在x 轴正半轴上）.若⊙P 过A 、B 、E 三点(圆心在x 轴上)，抛物线214y x bx c =++经过A 、C 两点，与x 轴的另一交点为G ，M 是FG 的中点，正方形CDEF 的面积为1. （1）求B 点坐标；（2）求证：ME 是⊙P 的切线；（3）设直线AC 与抛物线对称轴交于N ，Q 点是此对称轴上不与N 点重合的一动点，①求△ACQ 周长的最小值；②若FQ ＝t ，S △ACQ ＝s ，直接写出．．．．s 与t 之间的函数关系式.图甲yxP OM GF E DCBA图乙（备用图）ABCDE FGO xy湖北省荆门市二○一一年初中毕业生学业考试数学试题参考答案及评分标准一、选择题 （每选对一题得3分，共36分）1.A2.C3.C4.B5.C6.D7.C8.B9.A 10.D 11.B 12.D二、填空题（每填对一题得3分，共15分）13.0 14.x x x 2223++ 15.50° 16.方法很多，参照给分 17.2三、解答题（按步骤给分，其它解法参照此评分标准给分）18.解：由①得：x ≤1 ………………………………………………………………………2分 由②得：x ＞2- …………………………………………………………………………4分 综合得：-2＜x ≤1 …………………………………………………………………………6分 在数轴上表示这个解集…………………………8分 【考点】解一元一次不等式组；在数轴上表示不等式的解集． 【专题】计算题；数形结合．【分析】先解每一个不等式，再求解集的公共部分即可．【点评】本题考查了解一元一次不等式组，解集的数轴表示法．关键是先解每一个不等式，再求解集的公共部分．19.解：△ABE 是等边三角形.理由如下：………………………………………………… 2分 由旋转得△P AE ≌△PDC∴CD =AE ，PD =P A ，∠1=∠2……………………4分 ∵∠DP A =60°，∴△PDA 是等边三角形…………5分 ∴∠3＝∠P AD ＝60°.由矩形ABCD 知，CD ＝AB ，∠CDA ＝∠DAB ＝90°． ∴∠1＝∠4＝∠2＝30° ………………………7分 ∴AE ＝CD ＝AB ，∠EAB ＝∠2+∠4＝60°，∴△ABE 为等边三角形.…………………………9分【考点】旋转的性质；全等三角形的判定与性质；等边三角形的判定；矩形的性质． 【专题】几何图形问题．第16题图【分析】根据旋转的性质，图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，旋转前后图形的大小和形状没有改变，根据图形求出旋转的角度，即可得出三角形的形状． 【点评】本题主要考查了图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，旋转前后图形的大小和形状没有改变，难度适中．20.解：（1）2÷1%=200 …………………………………………………………………… 2分（2）360°×70200＝126°，∴④所在扇形的圆心角为126° ………………………… 4分 200×9%=18（人）200－18－2－70=110（人）第②种情况110人，第③种情况18人．注：补图②110人，③18人………………………………………………………………6分（3）P （第②种情况）＝1101120020=∴他是第②种情况的概率为1120…………………………………………………………8分（4）10×（1-1%）＝9.9（万人）即：10万名开车的司机中，不违反“酒驾”禁令的人数为9.9万人 ………………10分 【考点】扇形统计图；用样本估计总体；条形统计图；概率公式． 【专题】图表型． 【分析】（1）从扇形图可看出①种情况占1%，从条形图知道有2人，所以可求出总人数． （2）求出④所占的百分比然后乘以360°就可得到圆心角度数，然后求出其他情况的人，补全条形图．（3）②种情况的概率为②中调查的人数除以调查的总人数．（4）2万人数减去第①种情况的人数就是不违反“酒驾”禁令的人数． 【点评】本题考查对扇形图和条形图的认知能力，知道扇形图表现的是部分占整体的百分比，条形图告诉我们每组里面的具体数据，从而可求答案．21.解：连接OD 、OE 、OF ，由垂径定理知：PD ＝12CD ＝12（m ） ………… 1分在Rt △OPD 中，OD ＝2222125+=+OP PD ＝13（m ）∴OE ＝OD ＝13m …………………………………………………………………………2分 ∵tan ∠EMO =i = 1∶3.7 ，tan15°＝321+=32-≈1：3.7∴∠EMO ＝15°……………………………………………………………………………4分 由切线性质知∠OEM ＝90°∴∠EOM =75°同理得∠NOF ＝75°∴∠EOF ＝180°-75°×2＝30° ………………………………6分在Rt △OEM 中，tan15°＝321+=32-≈1∶3.7∴EM ＝3.7×13＝48.1（m ） …………………………………………………………7分 又∵EF⌒ 的弧长＝1801330⋅π＝6.5（m ） ………………………………………9分 ∴48.1×2+6.5＝102.7（m ），即从M 点上坡、过桥、再下坡到N 点的最短路径长为102.7米. ……………… 10分（注：答案在102.5m —103m 间只要过程正确，不扣分）【考点】解直角三角形的应用-坡度坡角问题． 【专题】几何图形问题．【分析】首先明确从M 点上坡、过桥、下坡到N 点的最短路径长应为如图ME +EF ⌒ +FN ，连接如图，把实际问题转化为直角三角形问题，由已知求出OD 即半径，再由坡度i =1∶3.7和tan15°＝321+=32-≈1∶3.7，得出∠M =∠N =15°，因此能求出ME 和FN ，所以求出∠EOM =∠FON =90°-15°=75°，则得出EF ⌒ 所对的圆心角∠EOF ，相继求出EF ⌒ 的长，从而求出从M 点上坡、过桥、下坡到N 点的最短路径长．【点评】此题考查的知识点是解直角三角形的应用，解题的关键是由已知先求出半圆的半径和∠M 和∠N ，再由直角三角形求出MF 和FN ，求出EF⌒ 的长．22.解：过B 作BE ⊥AD 于E ，连接OB 、CE 交于点P ， ∵P 为矩形OCBE 的对称中心，则过P 点的直线平分矩形OCBE 的面积. ∵P 为OB 的中点，而B （4，2） ∴P 点坐标为（2，1）………………2分 在Rt △ODC 与Rt △EAB 中， OC ＝BE ，AB ＝CD∴Rt △ODC ≌Rt △EAB （HL ）， ∴S △ODC ＝S △EBA∴过点（0，-1）与P （2，1）的直线平分等腰梯形面积，这条直线为1y kx =-∴211k -=， ∴1k = ………………………………………………………………4分 ∵()232y mx m k x m k =-+++的图象与坐标轴只有两个交点，①当m ＝0时，1y x =-+，其图象与坐标轴有两个交点（0，1），（1，0） ………6分 ②当m ≠0时，函数()232y mx m k x m k =-+++的图象为抛物线，且与y 轴总有一个交点（0，2m +1）若抛物线过原点时，2m +1=0，即m =12-， EPy =kx 1yxODCBA此时2(31)4(21)m m m D=+-+=2(1)m +＞0∴抛物线与x 轴有两个交点且过原点，符合题意． ……………………………8分 若抛物线不过原点，且与x 轴只有一个交点，也合题意，此时2(31)4(21)m m m ¢D=+-+=0，∴121m m ==-综上所述，m 的值为m =0或21-或-1 …………………………………………10分 【考点】梯形的性质，函数与图象与坐标轴的交点． 【专题】图形与坐标．【分析】过B 作BE ⊥AD 于E ，连接OB 、CE 交于点P ，根据矩形OCBE 的性质求出B 、P 坐标，然后再根据相似三角形的性质求出k 的值，将解析式()232y mx m k x m k =-+++中的k 化为具体数字，再分m =0和m ≠0两种情况讨论，得出m 的值．【点评】此题考查了抛物线与坐标轴的交点，同时结合了梯形的性质和一次函数的性质，要注意数形结合，同时要进行分类讨论，得到不同的m 值．23.解：（1）由题意得：①5k =2，k =52， ∴ x y 521=……………………………………2分②42 2.4,164 3.2,a b a b +=⎧⎨+=⎩∴15a =-， 85b =. ∴x x y 585122+-=………………………4分（2）设购Ⅱ型设备投资t 万元，购Ⅰ型设备投资（10-t ）万元，共获补贴Q 万元．∴t t y 524)10(521-=-=，t t y 585122+-= ∴529)3(5145651585152422221+--=++-=+--=+=t t t t t t y y Q …………7分∵51-＜0，∴Q 有最大值，即当3t =时，Q 最大＝529∴107t -= (万元) ………………………………………………………………………9分 即投资7万元购Ⅰ型设备，投资3万元购Ⅱ型设备，共获最大补贴5.8万元………10分【考点】二次函数的应用． 【分析】（1）根据图表得出函数上点的坐标，利用待定系数法求出函数解析式即可； （2）根据12y y y =+得出关于x 的二次函数，求出二次函数最值即可．【点评】此题主要考查了待定系数法求一次函数和二次函数解析式以及二次函数的最值问题，利用函数解决实际问题是中考的热点问题．24.解：（1）如图甲，连接PE 、PB ，设PC ＝n ，∵正方形CDEF 面积为1，∴CD ＝CF ＝1． 根据圆和正方形的对称性知OP ＝PC ＝n ， ∴BC ＝2PC ＝2n ． ………1分 而PB ＝PE ，22222254n n n PC BC PB =+=+=，1)1(2222++=+=n EF PF PE ，x yxPOM GFE DC BA∴2251)1(n n =++， 解得1n = (21-=n 舍去) ． …………… 2分 ∴BC ＝OC ＝2，∴B 点坐标为(2,2)． ………3分 （2）如图甲，由（1）知A (0,2)，C (2,0)，∵A ，C 在抛物线上，∴2412++=bx x y ，∴23-=b ∴抛物线的解析式为223412+-=x x y即41)3(412--=x y …………………………………………………………… 4分∴抛物线的对称轴为3x =即EF 所在直线∵C 与G 关于直线3x =对称， ∴CF ＝FG ＝1，∴FM ＝12FG ＝12在Rt △PEF 与Rt △EMF 中，EF PF ＝2，221:1==FM EF ， ∴EF PF =FMEF，∴△PEF ∽△EMF …………5分 ∴∠EPF ＝∠FEM ，∴∠PEM ＝∠PEF +∠FEM ＝∠PEF +∠EPF ＝90°∴ME 与⊙P 相切． ……………………………………………………………………6分 （注：其他方法，参照给分）（3）①如图乙，延长AB 交抛物线于A '，连接A C '交对称轴x =3于Q ，连接AQ ， 则有AQ ＝A 'Q ，△ACQ 周长的最小值为（AC +A 'C ）的长．……7分 ∵A 与A '关于直线3x =对称， ∴A (0,2)，A '(6,2)，∴A 'C ＝522)26(22=+-，而AC =222222=+ …………………8分∴△ACQ 周长的最小值为2225+……9分 ②当Q 点在F 点上方时，1S t =+ ……10分 当Q 点在线段FN 上时，1S t =- ……11分当Q 点在N 点下方时，1S t =- ……12分【考点】二次函数综合题． 【分析】（1）如图甲，连接PE 、PB ，设PC =n ，由正方形CDEF 的面积为1，可得CD =CF =1，根据圆和正方形的对称性知：OP =PC =n ，由PB =PE ，根据勾股定理即可求得n 的值，继而求得B 的坐标；（2）由（1）知A （0，2），C （2，0），即可求得抛物线的解析式，然后求得FM 的长，则可得△PEF ∽△EMF ，则可证得∠PEM =90°，即ME 是⊙P 的切线； （3）①如图乙，延长AB 交抛物线于A ′，连CA ′交对称轴3x =于Q ，连接AQ ，则有AQ =A ′Q ，△ACQ 周长的最小值为AC +A ′C 的长，利用勾股定理即可求得△ACQ 周长的最小值； ②分别当Q 点在F 点上方时，当Q 点在线段FN 上时，当Q 点在N 点下方时去分析即可求得答案．【点评】此题考查了待定系数法求二次函数的解析式，圆的性质，相似三角形的判定与性质QN A'x =3ABCDE F GOxy图乙以及勾股定理等知识．此题综合性很强，题目难度较大，解题的关键是方程思想、分类讨论与数形结合思想的应用．。

2011年河北省中考数学试卷一、选择题（共12小题，1-6小题每小题2分，7-12小题，每题3分，满分30分） 1、计算30的结果是（ ） A 、3 B 、30 C 、1 D 、0 2、如图，∠1+∠2等于（ ） A 、60° B 、90° C 、110° D 、180° 3、下列分解因式正确的是（ ）A 、﹣a+a 3=﹣a （1+a 2）B 、2a ﹣4b+2=2（a ﹣2b ）C 、a 2﹣4=（a ﹣2）2D 、a 2﹣2a+1=（a ﹣1）2 4、下列运算中，正确的是（ ） A 、2x ﹣x=1 B 、x+x 4=x 5 C 、（﹣2x ）3=﹣6x 3 D 、x 2y÷y=x 2 5、一次函数y=6x+1的图象不经过（ ） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限 6、将图1围成图2的正方体，则图1中的红心“”标志所在的正方形是正方体中的（ ） A 、面CDHEB 、面BCEFC 、面ABFGD 、面ADHG7、甲、乙、丙三个旅行团的游客人数都相等，且毎团游客的平均年龄都是32岁，这三个团游客年龄的方差分别是S 甲2=27，S 乙2=19.6，S 丙2=1.6，导游小王最喜欢带游客年龄相近的团队，若在三个团中选择一个，则他应选（ ） A 、甲团 B 、乙团 C 、丙团 D 、甲或乙团8、一小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下面函数关系式：h=﹣5（t ﹣1）2+6，则小球距离地面的最大高度是（ ） A 、1米 B 、5米 C 、6米 D 、7米9、如图，在△ABC 中，∠C=90°，BC=6，D ，E 分别在 AB 、AC 上，将△ABC 沿DE 折叠，使点A 落在点A′处，若A′为CE 的中点，则折痕DE 的长为（ ）A 、12B 、2C 、3D 、410、已知三角形三边长分别为2，x ，13，若x 为正整数 则这样的三角形个数为（ ） A 、2 B 、3 C 、5 D 、1311、如图，在矩形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为y 和x ，则y 与x 的函数图象大致是（ ）A 、B 、C 、D 、12、根据图1所示的程序，得到了y 与x 的函数图象，如图2．若点M 是y 轴正半轴上任意一点，过点M 作PQ ∥x 轴交图象于点P ，Q ，连接OP ，OQ ．则以下结论： ①x ＜0 时，y =2x ②△OPQ 的面积为定值．③x ＞0时，y 随x 的增大而增大．④MQ=2PM ．⑤∠POQ 可以等于90°．其中正确结论是（ ）A 、①②④B 、②④⑤C 、③④⑤D 、②③⑤二、填空题（共6小题，每小题3分，满分18分） 13、√53，π，﹣4，0这四个数中，最大的数是 ．14、如图，已知菱形ABCD ，其顶点A ，B 在数轴上对应的数分别为﹣4和1，则BC= ． 15、若|x ﹣3|+|y+2|=0，则x+y 的值为 ．16、如图，点0为优弧ACB ̂所在圆的圆心，∠AOC=108°，点D 在AB 延长线上，BD=BC ，则∠D= ．17、如图1，两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A’B’D’的位置，得到图2，则阴影部分的周长为 ．18、如图，给正五边形的顶点依次编号为1，2，3，4，5．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”．如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”．若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是 ． 三、解答题（共8小题，满分72分）19、已知{x =2y =√3是关于x ，y 的二元一次方程√3x =y +a 的解，求（a+1）（a ﹣1）+7的值．20、如图，在6×8网格图中，每个小正方形边长均为1，点0和△ABC的顶点均为小正方形的顶点．（1）以O为位似中心，在网络图中作△A′B′C′，使△AA′B′C′和△ABC位似，且位似比为1：2；（2）连接（1）中的AA′，求四边形AA′C′C的周长．（结果保留根号）21、如图，一转盘被等分成三个扇形，上面分别标有﹣1，1，2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，某个扇形会恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形＞．（1）若小静转动转盘一次，求得到负数的概率；（2）小宇和小静分别转动转盘一次，若两人得到的数相同，则称两人“不谋而合”．用列表法（或画树状图）求两人“不谋而合”的概率．22、甲、乙两人准备整理一批新到的实验器材．若甲单独整理需要40分钟完工：若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工．（1）问乙单独整理多少分钟完工？（2）若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？23、如图，四边形ABCD 是正方形，点E ，K 分别在BC ，AB 上，点G 在BA 的延长线上，且CE=BK=AG ． （1）求证：①DE=DG ； ②DE ⊥DG（2）尺规作图：以线段DE ，DG 为边作出正方形DEFG （要求：只保留作图痕迹，不写作法和证明）； （3）连接（2）中的KF ，猜想并写出四边形CEFK 是怎样的特殊四边形，并证明你的猜想： （4）当CECB =1n 时，请直接写出S 正方形ABCDS正方形DEFG的值．24、已知A 、B 两地的路程为240千米．某经销商每天都要用汽车或火车将x 吨保鲜品一次 性由A 地运往B 地．受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订．现有货运收费项目及收费标准表、行驶路程s （千米）与行驶时间t （时）的函数图象（如图1）、上周货运量折线统计图（如图2）等信息如下：火车1.6 5 2280（1）汽车的速度为 千米/时，火车的速度为 千米/时： （2）设每天用汽车和火车运输的总费用分别为y 汽（元）和y 火（元），分别求y 汽、y 火与 x 的函数关系式（不必写出x 的取值范围），及x 为何值时y 汽＞y 火（总费用=运输费+冷藏费+固定费用）（3）请你从平均数、折线图走势两个角度分析，建议该经销商应提前为下周预定哪种运输工具，才能使每天的运输总费用较省？25、如图1至图4中，两平行线AB 、CD 间的距离均为6，点M 为AB 上一定点． 思考:如图1，圆心为0的半圆形纸片在AB ，CD 之间（包括AB ，CD ），其直径MN 在AB 上，MN=8，点P 为半圆上一点，设∠MOP=α．当α= 90 度时，点P 到CD 的距离最小，最小值为 2 ．探究一:在图1的基础上，以点M 为旋转中心，在AB ，CD 之间顺时针旋转该半圆形纸片，直到不能再转动为止，如图2，得到最大旋转角∠BMO= 30 度，此时点N 到CD 的距离是 2 ．探究二:将如图1中的扇形纸片NOP 按下面对α的要求剪掉，使扇形纸片MOP 绕点M 在AB ，CD 之间顺时针旋转． （1）如图3，当α=60°时，求在旋转过程中，点P 到CD 的最小距离，并请指出旋转角∠BMO 的最大值； （2）如图4，在扇形纸片MOP 旋转过程中，要保证点P 能落在直线CD 上，请确定α的取值范围． （参考数椐：sin49°=34，cos41°=34，tan37°=34．）26、如图，在平面直角坐标系中，点P 从原点O 出发，沿x 轴向右以毎秒1个单位长的速度运动t 秒（t ＞0），抛物线y=x 2+bx+c 经过点O 和点P ，已知矩形ABCD 的三个顶点 为 A （1，0），B （1，﹣5），D （4，0）． （1）求c ，b （用含t 的代数式表示）：（2）当4＜t ＜5时，设抛物线分别与线段AB ，CD 交于点M ，N ．①在点P 的运动过程中，你认为∠AMP 的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；②求△MPN 的面积S 与t 的函数关系式，并求t 为何值时，S =218；（3）在矩形ABCD 的内部（不含边界），把横、纵 坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t 的取值范围．2011年河北省中考数学试卷答案一、1、C ．2、B ．3、D ．4、D ．5、D ．6、A ．7、C ．8、C ．9、B ．10、B ．11、A ．12B ． 二、13、π14、5．15、1．16、27°．17、2．18、3． 三、19、解：∵{x =2y =√3是关于x ，y 的二元一次方程√3x =y +a 的解，∴2√3=√3+a ，a=√3，∴（a+1）（a﹣1）+7=a2﹣1+7=3﹣1+7=9．20、解：（1）如图所示：（2）AA′=CC′=2．在Rt△OA′C′中，OA′=OC′=2，得A′C′=2√2；同理可得AC=4√2．∴四边形AA′C′C的周长=4+6√2．21、解：（1）∵转盘被等分成三个扇形，上面分别标有﹣1，1，2，∴小静转动转盘一次，得到负数的概率为：13；（2）列表得：∴一共有9种等可能的结果，两人得到的数相同的有3种情况，∴两人“不谋而合”的概率为39=13．22、解：（1）设乙单独整理x分钟完工，根据题意得：20 40+20+20x=1解得x=80，经检验x=80是原分式方程的解．答：乙单独整理80分钟完工．（2）设甲整理y分钟完工，根据题意，得30 80+y40≥1解得：y≥25答：甲至少整理25分钟完工．23、（1）证明：∵四边形ABCD是正方形，∴DC=DA，∠DCE=∠DAG=90°．又∵CE=AG，∴△DCE≌△GDA，∴DE=DG，∠EDC=∠GDA，又∵∠ADE+∠EDC=90°，∴∠ADE+∠GDA=90°，∴DE⊥DG．（2）如图．（3）四边形CEFK为平行四边形．证明：设CK、DE相交于M点，∵四边形ABCD和四边形DEFG都是正方形，∴AB∥CD，AB=CD，EF=DG，EF∥DG，∵BK=AG，∴KG=AB=CD，∴四边形CKGD是平行四边形，∴CK=DG=EF，CK∥DG，∴∠KME=∠GDE=∠DEF=90°，∴∠KME+∠DEF=180°，∴CK∥EF，∴四边形CEFK为平行四边形．（4）S正方形ABCDS正方形DEFG=n2n2+1．24、解：（1）根据图表上点的坐标为：（2，120），（2，200），∴汽车的速度为60千米/时，火车的速度为100千米/时，故答案为：60，100；（2）依据题意得出：y汽=240×2x+24060×5x+200，=500x+200；y火=240×1.6x+240100×5x+2280，=396x+2280．若y汽＞y火，得出500x+200＞396x+2280．∴x＞20；（3）上周货运量x=（17+20+19+22+22+23+24）÷7=21＞20，从平均数分析，建议预定火车费用较省．从折线图走势分析，上周货运量周四（含周四）后大于20且呈上升趋势，建议预订火车费用较省．25、解：思考：根据两平行线之间垂线段最短，直接得出答案，当α=90度时，点P到CD的距离最小，∵MN=8， ∴OP=4，∴点P 到CD 的距离最小值为：6﹣4=2． 故答案为：90，2；探究一：∵以点M 为旋转中心，在AB ，CD 之间顺时针旋转该半圆形纸片，直到不能再转动为止，如图2， ∵MN=8，MO=4，OY=4， ∴UO=2，∴得到最大旋转角∠BMO=30度，此时点N 到CD 的距离是 2；探究二（1）由已知得出M 与P 的距离为4，∴PM ⊥AB 时，点MP 到AB 的最大距离是4，从而点P 到CD 的最小距离为6﹣4=2， 当扇形MOP 在AB ，CD 之间旋转到不能再转时，弧MP 与AB 相切， 此时旋转角最大，∠BMO 的最大值为90°；（2）如图3，由探究一可知，点P 是弧MP 与CD 的切线时，α大到最大，即OP ⊥CD ，此时延长PO 交AB 于点H ，α最大值为∠OMH+∠OHM=30°+90°=120°，如图4，当点P 在CD 上且与AB 距离最小时，MP ⊥CD ，α达到最小，连接MP ，作HO ⊥MP 于点H ，由垂径定理，得出MH=3，在Rt △MOH 中，MO=4， ∴sin ∠MOH=MH OM =34， ∴∠MOH=49°， ∵α=2∠MOH ， ∴α最小为98°，∴α的取值范围为：98°≤α≤120°． 26、解：（1）把x=0，y=0代入y=x 2+bx+c ，得c=0， 再把x=t ，y=0代入y=x 2+bx ，得t 2+bt=0， ∵t ＞0， ∴b=﹣t ；（2）①不变．如图6，当x=1时，y=1﹣t ，故M （1，1﹣t ）， ∵tan ∠AMP=1， ∴∠AMP=45°； ②S=S 四边形AMNP﹣S △PAM =S △DPN +S梯形NDAM﹣S △PAM =12（t ﹣4）（4t ﹣16）+12[（4t ﹣16）+（t ﹣1）]×3﹣12（t ﹣1）（t ﹣1）=32t 2﹣152t+6． 解32t 2﹣152t+6=218， 得：t1=12，t2=92， ∵4＜t ＜5，∴t1=12舍去，∴t=92． （3）72＜t ＜113．。

2011河北中考数学试题及答案一. 选择题1.若x+1<0，则x的取值范围是（）A. x>1B.x<-1C. x>0D. x<-2答案：B. x<-12.已知函数 y = 2x + b, 当 x = 3 时，y = 5，求 b 的值。

A. 4B. 5C. 6D. 7答案：C. 63.如图，已知矩形ABCD的周长为18cm，若BM = MC，那么矩形ABCD的面积为（）A. 18cm²B. 27cm²C. 36cm²D. 32cm²答案：B. 27cm²二．填空题：4.已知一次函数的图象经过点（2，3），斜率为5，则其方程为y = _________答案：y = 5x - 75.若两倍数5x － 6y＝ 1 .66 ，则 x ＋ y = _________答案： x ＋ y = 1.32三．解答题：6.某小组共有男生4人，女生5人，现将其中3名男生按任意顺序排列，3名女生按任意顺序排列。

问共有多少种不同的结果？解：男生共有4人，取3人排列共有4!/(4-3)!= 4! /1! = 4×3×2 = 24 种结果女生共有5人，取3人排列共有5! /(5-3)!= 5! /2! = 5×4×3= 60种结果根据乘法原理，男生和女生排列的结果数为 24 × 60 = 1440 种结果。

7.已知直线y = 2x + c 与曲线y = x²- c²相交于点A, B两点，且A, B两点间的距离为4，求常数c的值。

解：由于直线y = 2x + c与曲线y = x²- c²相交，则有 2x + c = x²- c²整理得，x²-2x- c²- c = 0对于二次方程，求解其判别式：Δ = (-2)²-4(1)(- c²- c) = 4 + 4c² + 4c由于A, B两点间的距离为4，说明其横坐标之差等于4，则有x₁-x₂ = 4。

解直角三角形的应用一、选择题A 组1. （2011年北京四中中考全真模拟15）从小明家到学校有两条路。

一条沿北偏东45度方向可直达学校前门，另一条从小明家一直往东，到商店处向正北走200米，到学校后门。

若两条路的路程相等，学校南北走向。

学校的后门在小明家北偏东67.5度处。

学校从前门到后门的距离是（ ）米.;D.200米 答案：B2.（2011.河北廊坊安次区一模）如图4，市政府准备修建一座高AB ＝6m 的过街天桥，已知天桥的坡面AC 与地面BC 的夹角∠ACB 的余弦值为45，则坡面AC 的长度为 A ．152m B ．10 m Cm D．2m 答案:B3. (2011浙江省杭州市10模)如图，小亮同学在晚上由路灯A 走向路灯B ，当他走到点P 时，发现他的身影顶部正好接触路灯B 的底部，这时他离路灯A 25米，离路灯B 5米，如果小亮的身高为1.6米，那么路灯高度为 ( ▲ ) A ．6.4米 B ． 8米 C ．9.6米 D ． 11.2米 答案:C（第3题）第2题图4. (浙江省杭州市瓜沥镇初级中学2011年中考数学模拟试卷) 如图所示，平地上一棵树高为6米，两次观察地面上的影子，•第一次是当阳光与地面成60°时，第二次是阳光与地面成30°时，第二次观察长…………………( )A. B. 3- 3答案：B5．(河北省中考模拟试卷)石家庄市在“三年大变样”城中村改造建设中，计划在一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米售价a 元，则购买这种草皮至少需要……（ ）A ．450a 元B ．225a 元C ．150a 元D ．300a 元 答案：CB 组1．（2011杭州上城区一模）Rt △ABC 中，∠C =90°，a 、b 、c 分别是∠A 、∠B 、∠C 的对 边，那么c 等于（ ）A.cos sin a A b B +B.sin sin a A b B +C.sin sin a b A B +D.cos sin a b A B +答案：B2．（2011浙江杭州义蓬一中一模）如图，小明发现电线杆AB 的影子落在土坡的坡面CD 和地面BC 上，量得CD=8米，BC=20米，CD 与地面成30º角，且此时测得1米杆的影长为2米，则电线杆的高度为( )A ．14米B ．28米C ．314+米D ．3214+米 答案：D3.（安徽芜湖2011模拟）小明沿着坡度为1:2的山坡向上走了1000m ，则他升高了 （ ）A ．500mB ．5200mC ．3500mD ．1000m 答案: B4.（浙江杭州进化2011一模）如图折叠直角三角形纸片的直角，使点C 落在斜边AB 上的点E 处. 已知AB=38, ∠B=30°, 则DE 的长是( ). A. 6 B. 4 C. 34 D. 23第5题（第1题）答案: B5、（2011年北京四中34模）如图，矩形ABCD 中，AB>AD ，AB=a ，过点A 作射线AM ，使得∠DAM=60°，DE ⊥AM 与E ，DF ⊥AM 与F ，则DE+CF 的值是7.13=）（ ） A ．a B ． a 2017 C ．a 275 D ． 2a答案：D6．（2011年浙江省杭州市模2）如图，在菱形ABCD 中，DE ⊥AB ，3cos 5A =，BE=2，则tan ∠DBE 的值是（ ）A．12B ．2 C答案：B二、填空题A 组1、（2011年北京四中模拟28）如图，一人乘雪橇沿坡比172米，那么他下降的高度为 __米． 答案：362. （2011浙江杭州模拟7）如图为护城河改造前后河床的横断面示意图，将河床原竖直迎水面BC 改建为坡度1：0．5的迎水坡AB ，已知AB=4 5 米，则河床 面的宽减少了_______ 米．(即求AC 的长)A CB．5 i 1：（第2题图）答案:43. (2011浙江省杭州市8模)如图，小明在A 时测得某树的影长为3米，B 时又测得该树的影长为12米，若两次日照的光线互相垂直，则树的高度为_____米.答案:64．(2011年宁夏银川)为了测量水塔的高度，取一根竹杆放在阳光下，已知2米长的竹杆投影长为1.5米，在同一时刻测得水塔的投影长为30米，则水塔高为_________米. 答案：40 B 组1.（2011灌南县新集中学一模）在△ABC 中，∠C ＝90°，AB ＝20，cosB ＝14，则BC 等于 . 答案：52.（2011灌南县新集中学一模）如图，在△ABC 中，∠C ＝90°，AC ＝8，CB ＝6，在斜边AB 上取一点M ，使MB ＝CB ，过M 作MN ⊥AB 交AC 于N ，则MN ＝ .答案： 33. （河南新乡2011模拟）如图，甲、乙两楼相距20米，甲楼高20米，小明站在距甲楼10米的A 处目测得点A 与甲、乙楼顶B C 、刚好在同一直线上，若小明的身高忽略不计，则乙楼的高度是 米． 答案：60米（第3题）A 时B 时 （第2题图）NMCBA4、（北京四中2011中考模拟13）如图，沿倾斜角为30º的山坡植树， 要求相邻两棵树间的水平距离AC 为m 2，那么相邻两棵树的斜坡距离 AB 约为_________m ;(结果精确到0.1m ，可能用到的数据：3≈1.732， 2≈1.414).答案：约为3.25.（北京四中2011中考模拟14）如图:为了测量河对岸旗杆AB 的高度,在 点C 处测得顶端A 的仰角为30°,沿CB 方向前进20m 达到D 处,在D 点测得 旗杆顶端A 的仰角为45°,则旗杆AB 的高度为__________m.(精确到0.1m)答案：27.36. （2011深圳市模四） 如图所示，太阳光线与地面成60°角，一棵倾斜的大树与地面成30°角，•这时测得大树在地面上的影子约为10米，则大树的高约为________米．（•保留根号） 答案：3107、（2011年北京四中33模）如图所示，某河堤的横断面是梯形ABCD ，BC//AD ，迎水坡AB 长10m ，且34tan =∠BAE ，则河堤的高BE 为 m 。

2024年河北省中考数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图显示了某地连续5天的日最低气温，则能表示这5天日最低气温变化情况的是（ ）A ．B ．C ．D ．【答案】A 【分析】本题考查了正负数的大小比较，熟练掌握正负数大小比较的方法解题的关键．由五日气温为2,4,0,1,1---℃℃℃℃℃得到24->-，401-<<，11>-，则气温变化为先下降，然后上升，再上升，再下降．【详解】解：由五日气温为2,4,0,1,1---℃℃℃℃℃得到24->-，401-<<，11>-∴气温变化为先下降，然后上升，再上升，再下降．故选：A ．2．下列运算正确的是（ ）A ．734a a a -=B ．222326a a a ⋅=C ．33(2)8a a -=-D ．44a a a÷=【答案】C【分析】本题考查整式的运算，根据合并同类项，单项式乘以单项式，积的乘方，同底数幂的除法依次对各选项逐一分析判断即可．解题的关键是掌握整式运算的相关法则．【详解】解：A ．7a ，4a 不是同类项，不能合并，故此选项不符合题意；B ．224326a a a ⋅=，故此选项不符合题意；C ．()3328a a -=-，故此选项符合题意；D ．441a a ÷=，故此选项不符合题意．故选：C ．3．如图，AD 与BC 交于点O ，ABO 和CDO 关于直线PQ 对称，点A ，B 的对称点分别是点C ，D ．下列不一定正确的是（ ）A ．AD BC⊥B ．AC PQ ⊥C ．ABO CDO △≌△D ．AC BD∥【答案】A 【分析】本题考查了轴对称图形的性质，平行线的判定，熟练掌握知识点是解题的关键．根据轴对称图形的性质即可判断B 、C 选项，再根据垂直于同一条直线的两条直线平行即可判断选项D ．【详解】解：由轴对称图形的性质得到ABO CDO △≌△，,AC PQ BD PQ ⊥⊥，∴AC BD ∥，∴B 、C 、D 选项不符合题意，故选：A ．4．下列数中，能使不等式516x -<成立的x 的值为（ ）A ．1B ．2C ．3D ．45．观察图中尺规作图的痕迹，可得线段BD 一定是ABC 的（ ）A ．角平分线B ．高线C ．中位线D ．中线【答案】B 【分析】本题考查的是三角形的高的定义，作线段的垂线，根据作图痕迹可得BD AC ⊥，从而可得答案．【详解】解：由作图可得：BD AC ⊥，∴线段BD 一定是ABC 的高线；故选B6．如图是由11个大小相同的正方体搭成的几何体，它的左视图是（ ）A ．B ．C ．D ．【答案】D【分析】本题考查简单组合体的三视图，左视图每一列的小正方体个数，由该方向上的小正方体个数最多的那个来确定，通过观察即可得出结论．掌握几何体三种视图之间的关系是解题的关键．【详解】解：通过左边看可以确定出左视图一共有3列，每列上小正方体个数从左往右分别为3、1、1．故选：D ．7．节能环保已成为人们的共识．淇淇家计划购买500度电，若平均每天用电x 度，则能使用y 天．下列说法错误的是（ ）A ．若5x =，则100y =B ．若125y =，则4x =C ．若x 减小，则y 也减小D ．若x 减小一半，则y 增大一倍8．若a ，b 是正整数，且满足8282222222a b a a a b b b ++⋅⋅⋅+=⨯⨯⋅⋅⋅⨯ 个相加个相乘，则a 与b 的关系正确的是（ ）A ．38a b+=B ．38a b =C ．83a b +=D ．38a b=+【答案】A 【分析】本题考查了同底数幂的乘法，幂的乘方的运算的应用，熟练掌握知识点是解题的关键．由题意得：()8822a b ⨯=，利用同底数幂的乘法，幂的乘方化简即可．【详解】解：由题意得：()8822a b ⨯=，∴38222a b ⨯=，∴38a b +=，故选：A ．9．淇淇在计算正数a 的平方时，误算成a 与2的积，求得的答案比正确答案小1，则=a （ ）A ．1B 1C 1D ．11【答案】C【分析】本题考查了一元二次方程的应用，解一元二次方程，熟练掌握知识点是解题的关键．由题意得方程221a a +=，利用公式法求解即可．【详解】解：由题意得：221a a +=，10．下面是嘉嘉作业本上的一道习题及解答过程：已知：如图，ABC 中，AB AC =，AE 平分ABC 的外角CAN ∠，点M 是AC 的中点，连接BM 并延长交AE 于点D ，连接CD ．求证：四边形ABCD 是平行四边形．证明：∵AB AC =，∴3ABC ∠=∠．∵3CAN ABC ∠=∠+∠，12CAN ∠=∠+∠，12∠=∠，∴①______．又∵45∠=∠，MA MC =，∴MAD MCB △≌△（②______）．∴MD MB =．∴四边形ABCD 是平行四边形．若以上解答过程正确，①，②应分别为（ ）A ．13∠=∠，AASB ．13∠=∠，ASAC ．23∠∠=，AASD ．23∠∠=，ASA11．直线l 与正六边形ABCDEF 的边,AB EF 分别相交于点M ，N ，如图所示，则a β+=（ ）A ．115︒B ．120︒C ．135︒D ．144︒12．在平面直角坐标系中，我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”．如图，矩形ABCD 位于第一象限，其四条边分别与坐标轴平行，则该矩形四个顶点中“特征值”最小的是（ ）A ．点AB ．点BC ．点CD ．点D13．已知A 为整式，若计算22A y xy y x xy -++的结果为x y xy -，则A =（ ）A ．x B ．y C ．x y +D ．x y -14．扇文化是中华优秀传统文化的组成部分，在我国有着深厚的底蕴．如图，某折扇张开的角度为120︒时，扇面面积为S 、该折扇张开的角度为n ︒时，扇面面积为n S ，若n m SS =，则m 与n 关系的图象大致是（ ）D．15．“铺地锦”是我国古代一种乘法运算方法，可将多位数乘法运算转化为一位数乘法和简单的加法⨯，运算结果为3036．图运算．淇淇受其启发，设计了如图1所示的“表格算法”，图1表示132232表示一个三位数与一个两位数相乘，表格中部分数据被墨迹覆盖，根据图2中现有数据进行推断，正确的是（ ）A ．“20”左边的数是16B ．“20”右边的“□”表示5C ．运算结果小于6000D ．运算结果可以表示为41001025a +则由题意得：20,5,2,mz nz ny nx a ====，∴4mz nz=，即4=m n ，∴当2,1n y ==时， 2.5z =不是正整数，不符合题意，故舍；当1,2n y ==时，则4,5,m z x a ===，如图：，∴A 、“20”左边的数是248⨯=，故本选项不符合题意；B 、“20”右边的“□”表示4，故本选项不符合题意；∴a 上面的数应为4a ，如图：∴运算结果可以表示为：()1000411002541001025a a a +++=+，∴D 选项符合题意，当2a =时，计算的结果大于6000，故C 选项不符合题意，故选：D ．16．平面直角坐标系中，我们把横、纵坐标都是整数，且横、纵坐标之和大于0的点称为“和点”．将某“和点”平移，每次平移的方向取决于该点横、纵坐标之和除以3所得的余数（当余数为0时，向右平移；当余数为1时，向上平移；当余数为2时，向左平移），每次平移1个单位长度．例：“和点”()2,1P 按上述规则连续平移3次后，到达点()32,2P ，其平移过程如下：若“和点”Q 按上述规则连续平移16次后，到达点()161,9Q -，则点Q 的坐标为（ ）A ．()6,1或()7,1B ．()15,7-或()8,0C ．()6,0或()8,0D ．()5,1或()7,1【答案】D【分析】本题考查了坐标内点的平移运动，熟练掌握知识点，利用反向运动理解是解决本题的关键．先找出规律若“和点”横、纵坐标之和除以3所得的余数为0时，先向右平移1个单位，之后按照向上、向左，向上、向左不断重复的规律平移，按照16Q 的反向运动理解去分类讨论：①16Q 先向右1个单位，不符合题意；②16Q 先向下1个单位，再向右平移，当平移到第15次时，共计向下平移了8次，向右平移了7次，此时坐标为()6,1，那么最后一次若向右平移则为()7,1，若向左平移则为()5,1．【详解】解：由点()32,2P 可知横、纵坐标之和除以3所得的余数为1，继而向上平移1个单位得到()42,3P ，此时横、纵坐标之和除以3所得的余数为2，继而向左平移1个单位得到()41,3P ，此时横、纵坐标之和除以3所得的余数为1，又要向上平移1个单位 ，因此发现规律为若“和点”横、纵坐标之和除以3所得的余数为0时，先向右平移1个单位，之后按照向上、向左，向上、向左不断重复的规律平移，若“和点”Q 按上述规则连续平移16次后，到达点()161,9Q -，则按照“和点”16Q 反向运动16次求点Q 坐标理解，可以分为两种情况：①16Q 先向右1个单位得到()150,9Q ，此时横、纵坐标之和除以3所得的余数为0，应该是15Q 向右平移1个单位得到16Q ，故矛盾，不成立；②16Q 先向下1个单位得到()151,8Q -，此时横、纵坐标之和除以3所得的余数为1，则应该向上平移1个单位得到16Q ，故符合题意，那么点16Q 先向下平移，再向右平移，当平移到第15次时，共计向下平移了8次，向右平移了7次，此时坐标为()17,98-+-，即()6,1，那么最后一次若向右平移则为()7,1，若向左平移则为()5,1，故选：D ．二、填空题17．某校生物小组的9名同学各用100粒种子做发芽实验，几天后观察并记录种子的发芽数分别为：89，73，90，86，75，86，89，95，89，以上数据的众数为．【答案】89【分析】本题考查了众数，众数是一组数据中次数出现最多的数．根据众数的定义求解即可判断．【详解】解：几天后观察并记录种子的发芽数分别为：89，73，90，86，75，86，89，95，89，89出现的次数最多，∴以上数据的众数为89．故答案为：89．18．已知a，b，n均为正整数．（1）若1<<+，则n=；n n（2）若1,1-<<<<+，则满足条件的a的个数总比b的个数少个．n n n n2n 与()21n +之间的整数有2n 个，∴满足条件的a 的个数总比b 的个数少()2222222n n n n --=-+=（个），故答案为：2．19．如图，ABC 的面积为2，AD 为BC 边上的中线，点A ，1C ，2C ，3C 是线段4CC 的五等分点，点A ，1D ，2D 是线段3DD 的四等分点，点A 是线段1BB 的中点．（1）11AC D △的面积为 ；（2）143B C D △的面积为 ．【点睛】本题考查三角形中线的性质，全等三角形的判定与性质，相似三角形的判定与性质，等分点的意义，三角形的面积．掌握三角形中线的性质是解题的关键．三、解答题20．如图，有甲、乙两条数轴．甲数轴上的三点A，B，C所对应的数依次为4-，2，32，乙数轴上的三点D，E，F所对应的数依次为0，x，12．(1)计算A ，B ，C 三点所对应的数的和，并求ABAC的值；(2)当点A 与点D 上下对齐时，点B ，C 恰好分别与点E ，F 上下对齐，求x 的值．21．甲、乙、丙三张卡片正面分别写有,2,a b a b a b ++-，除正面的代数式不同外，其余均相同．a b +2a b +a b-a b +22a b+2a2a b+a b-2a(1)将三张卡片背面向上并洗匀，从中随机抽取一张，当1,2a b ==-时，求取出的卡片上代数式的值为负数的概率；(2)将三张卡片背面向上并洗匀，从中随机抽取一张，放回后重新洗匀，再随机抽取一张．请在表格中补全两次取出的卡片上代数式之和的所有可能结果（化为最简），并求出和为单项式的概率．22．中国的探月工程激发了同学们对太空的兴趣．某晚，淇淇在家透过窗户的最高点P 恰好看到一颗星星，此时淇淇距窗户的水平距离4m BQ =，仰角为α；淇淇向前走了3m 后到达点D ，透过点P 恰好看到月亮，仰角为β，如图是示意图．已知，淇淇的眼睛与水平地面BQ 的距离1.6m ==AB CD ，点P 到BQ 的距离2.6m PQ =，AC 的延长线交PQ 于点E ．（注：图中所有点均在同一平面）(1)求β的大小及tanα的值；∠的值．(2)求CP的长及sin APC∵1tan tan 4CH PAE AH α=∠==，设∴()22249x x AC +==，解得：31717x =，∴317CH =m，23．情境 图1是由正方形纸片去掉一个以中心O 为顶点的等腰直角三角形后得到的．该纸片通过裁剪，可拼接为图2所示的钻石型五边形，数据如图所示．（说明：纸片不折叠，拼接不重叠无缝隙无剩余）操作 嘉嘉将图1所示的纸片通过裁剪，拼成了钻石型五边形．如图3，嘉嘉沿虚线EF ，GH 裁剪，将该纸片剪成①，②，③三块，再按照图4所示进行拼接．根据嘉嘉的剪拼过程，解答问题：（1）直接写出线段EF的长；（2）直接写出图3中所有与线段BE相等的线段，并计算BE的长．探究淇淇说：将图1所示纸片沿直线裁剪，剪成两块，就可以拼成钻石型五边形．请你按照淇淇的说法设计一种方案：在图5所示纸片的BC边上找一点P（可以借助刻度尺或圆规），画出裁剪线（线段PQ）的位置，并直接写出BP的长．由拼接可得：HF FO KG '==由正方形的性质可得：45A ∠=∴AHG ，H G D '' ，AFE △为等腰直角三角形，∴G KH '' 为等腰直角三角形，设H K KG x ''==，此时2BP '=，222P Q ''=+=，符合要求，或以C 圆心，CO 为半径画弧，交BC 此时2CP CQ ==，222PQ =+=∴22BP =-，综上：BP 的长为2或22-．24．某公司为提高员工的专业能力，定期对员工进行技能测试，考虑多种因素影响，需将测试的原始成绩x （分）换算为报告成绩y （分）．已知原始成绩满分150分，报告成绩满分100分、换算规则如下：当0x p ≤<时，80x y p=；当150p x ≤≤时，()2080150x p y p -=+-．（其中p 是小于150的常数，是原始成绩的合格分数线，80是报告成绩的合格分数线）公司规定报告成绩为80分及80分以上（即原始成绩为p 及p 以上）为合格．(1)甲、乙的原始成绩分别为95分和130分，若100p =，求甲、乙的报告成绩；(2)丙、丁的报告成绩分别为92分和64分，若丙的原始成绩比丁的原始成绩高40分，请推算p 的值：(3)下表是该公司100名员工某次测试的原始成绩统计表：原始成绩（分）9510010511115120125130135140145150人数1225810716201595①直接写出这100名员工原始成绩的中位数；②若①中的中位数换算成报告成绩为90分，直接写出该公司此次测试的合格率．25．已知O 的半径为3，弦MN =ABC 中，90,3,ABC AB BC ∠=︒==先将ABC 和O 按图1位置摆放（点B 与点N 重合，点A 在O 上，点C 在O 内），随后移动ABC ，使点B 在弦MN 上移动，点A 始终在O 上随之移动，设BN x =．(1)当点B与点N重合时，求劣弧 AN的长；∥时，如图2，求点B到OA的距离，并求此时x的值；(2)当OA MN(3)设点O到BC的距离为d．①当点A在劣弧 MN上，且过点A的切线与AC垂直时，求d的值；②直接写出d的最小值．∵O 的半径为3，3AB =，∴3OA OB AB ===，∴AOB 为等边三角形，∴60AOB ∠=︒，∴ AN 的长为60π3π180´=；∵25MN =，O H M N ⊥，∴5MH NH ==，而OM =∴222OH OM MH =-==∴点B 到OA 的距离为2；⊥于J，过O作过O作OJ BC∴四边形KOJB为矩形，=，∴OJ KB∵3AB=，32BC=，∴2233=+=，AC AB BC⊥于Q 如图，过A作AQ OB⊥∵B为MN中点，则OB MN∵90ABC AQB ∠=︒=∠，∴90OBJ ABO ABO ∠+∠=︒=∠∴OBJ BAQ ∠=∠，∴tan tan OBJ BAQ ∠=∠，∴122OJ BQ BJ AQ ==，26．如图，抛物线21:2C y ax x =-过点(4,0)，顶点为Q ．抛物线22211:()222C y x t t =--+-（其中t 为常数，且2t >），顶点为P ．(1)直接写出a 的值和点Q 的坐标．(2)嘉嘉说：无论t 为何值，将1C 的顶点Q 向左平移2个单位长度后一定落在2C 上．淇淇说：无论t 为何值，2C 总经过一个定点．请选择其中一人的说法进行说理．(3)当4t =时，①求直线PQ 的解析式；②作直线l PQ ∥，当l 与2C 的交点到x 轴的距离恰为6时，求l 与x 轴交点的横坐标．(4)设1C 与2C 的交点A ，B 的横坐标分别为,A B x x ，且A B x x <．点M 在1C 上，横坐标为()2B m m x ≤≤．点N 在2C 上，横坐标为()A n x n t ≤≤．若点M 是到直线PQ 的距离最大的点，最大距离为d ，点N 到直线PQ 的距离恰好也为d ，直接用含t 和m 的式子表示n ．∴交点()426,6J --，交点()426,6K +，由直线l PQ ∥，设直线l 为4y x b =+，∴()44266b -+=-，解得：8622b =-，∴直线l 为：48622y x =+-，∵()2,2P -，21,22Q t t ⎛⎫- ⎪⎝⎭，∴L 的横坐标为2t 2+，∵21,22M m m m ⎛⎫- ⎪⎝⎭，()21,2N n n t ⎡--+⎢⎣∴L 的横坐标为2m n +，。

2011河北省初中毕业生升学文化课考试数 学 试 卷本试卷分卷Ⅰ和卷Ⅱ两部分：卷I 为选择题，卷Ⅱ为非选择题.本试卷满分为120分，考试时间为120分钟.卷Ⅰ（选择题，共30分）注意事项：1．答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡，考试结束，监考人员将试卷和答题卡一并收回.2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，答在试卷上无效.一、选择题（本大题共12个小题.1－6小题，每小题2分，7－12小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的1．计算30的结果是A ．3B ．30C ．1D ．02．如图1，∠1＋∠2等于 A ．60° B ．90° C ．110° D ．180° 3．下列分解因式正确的是 A ．－a ＋a 3=－a (1＋a 2) B ．2a －4b ＋2=2(a －2b )C ．a 2－4=(a －2)2D ．a 2－2a ＋1=(a －1)24．下列运算中，正确的是 A ．2x －x =1 B ．x ＋x 4=x 5 C ．(－2x )3=－6x 3 D ．x 2y ÷y =x 25．一次函数y =6x ＋1的图象不经过．．． A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限6．将图2①围成图2②的正方体，则图②中的红心“”标志所在的正方形是正方体中的A ．面CDHEB ．面BCEFC ．面ABFGD ．面ADHG 7．甲、乙、丙三个旅行团的游客人数都相等，且每团游客的平均年龄都是32岁，这三个团游客年龄的方并有分别是227S =甲，219.6S =乙，2 1.6S =丙，导游小王最喜欢带游客年龄相近的团队，若在这三个团中选择一个，则他应选A ．甲团B ．乙团C ．丙团D ．甲或乙团8．一小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下面的函数关系式：h =－5(t －1)2＋6，则小球距离地面的最大高度是A ．1米B ．5米C ．6米D ．7米9．如图3，在△ABC 中，∠C =90°，BC =6，D ，E 分别在AB ，AC 上，将△ABC 沿DE 折叠，使点A 落在A ′处，若A ′为CE 的中点，则折痕DE 的长为A ．12 B ．5米 C ．6米 D ．7米10．已知三角形三边长分别为2，x ，13，若x 为正整数，则这样的三角形个数为 A ．2 B ．3 C ．5 D ．13图1① ②图211．如图4，在长形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆住的侧面，刚好能组合成圆住.设矩形的长和宽分别为y 和x ，则y 与x 的函数图象大致是12．根据图5中①所示的程序，得到了y 与x 的函数图象，如图5中②，若点M 是y 轴正半轴上任意一点，过点M 作PQ∥x 轴交图象于点P 、Q ，连接OP 、OQ ，则以下结论：①x ＜0时，y =2x②△OPQ 的面积为定值③x ＞0时，y 随x 的增大而增大④MQ =2PM⑤∠POQ 可以等于90°其中正确结论是A ．①②④B ．②④⑤C ．③④⑤D ．②③⑤ 2011年河北省初中毕业生升学文化课考试数 学 试 卷卷Ⅱ（非选择题，共90分）注意事项：1．答卷Ⅱ前，将密封线左侧的项目填写清楚.2．答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题（本大题共6个小是，每小题3分，共18分，把答案写在题中横线上） 13π，－4，0这四个数中，最大的数是___________.14．如图6，已知菱形ABCD ，其顶点A 、B 在数轴上对应的数分别为－4和1，则BC =_____.15．若︱x －3︱＋︱y ＋2︱=0，则x ＋y 的值为_____________.16．如图7，点O 为优弧ACB 所在圆的心，∠AOC =108°，点D 在AB 的延长线上，BD =BC ，则∠D =____________.图6图40 ①②图5 A BC D O 图7 C ① ② 图817．如图8中图①，两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置得到图②，则阴影部分的周长为_________18．如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.如：小宇在编号为3的顶点时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”. 若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是____________.三、解答题（本大题共8个小题，共72分，解答应写出文字说明、证明过程 或演算步骤）19．（本小题满分8分）已知2x y =⎧⎪⎨=⎪⎩x ，yy a =+的解.求(a ＋1)(a －1)＋7的值20．（本小题满分8分）如图10，在6×8的网格图中，每个小正方形边长均为1，点O 和△ABC 的顶点均为小正方形的顶点.⑴以O 为位似中心，在网格图．．．中作△A ′B ′C ′，使△A ′B ′C ′和△ABC 位似，且位似比为1：2⑵连接⑴中的AA ′，求四边形AA ′C ′C 的周长.（结果保留根号）2图9如图11，一转盘被等分成三个扇形，上面分别标有关－1，1，2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，鞭个扇形恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）.⑴若小静转动转盘一次，求得到负数的概率；⑵小宇和小静分别转动一次，若两人得到的数相同，则称两人“不谋而合”，用列表法（或画树形图）求两人“不谋而合”的概率.22．（本小题满分8分）甲、乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工，若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工.⑴问乙单独整理多少分钟完工？⑵若乙因式作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？23．（本小题满分9分）如图12，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE=BK=AG.⑴求证：①DE=DG；②DE⊥DG；⑵尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；⑶连接⑵中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；⑷当1C EC B n时，衣直接写出A B C DD E F GSS正方形正方形的值.小宇小静AB CD图11已知A 、B 两地的路程为240千米，某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地，受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订.现在有货运收费项目及收费标准表，行驶路程S （千米）与行驶时间t （时）的函数图象（如图13中①），上周货运量折线统计图（如图13中②）等信息如下：货运收费项目及收费标准表⑴汽车的速度为__________千米/时，火车的速度为_________千米/时；设每天用汽车和火车运输的总费用分别为y 汽（元）和y 火（元），分别求y 汽、y 火与x 的函数关系式（不必写出x 的取值范围）及x 为何值时y 汽＞y 火；（总费用=运输费＋冷藏费＋固定费用）⑶请你从平均数、折线图走势两个角度分析，建议该经销商应提前下周预定哪种运输工具，才能使每天的运输总费用较省？图13① 图13 ②如图14①至图14④中，两平行线AB、CD音的距离均为6，点M为AB上一定点.思考：如图14①中，圆心为O的半圆形纸片在AB、CD之间（包括AB、CD），其直径MN在AB上，MN=8，点P为半圆上一点，设∠MOP=α，当α=________度时，点P到CD的距离最小，最小值为____________.探究一在图14①的基础上，以点M为旋转中心，在AB、CD之间顺时针旋转该半圆形纸片，直到不能再转动为止.如图14②，得到最大旋转角∠BMO=_______度，此时点N到CD的距离是______________.探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉，使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.⑴如图14③，当α=60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值：⑵如图14④，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的取值范围.（参考数据：sin49°=34，cos41°=34，tan37°=34）BADC图14 ①BADC图14 ③BADC图14 ②BADC图14 ④PM如图15，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P.已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）.⑴求c、b（用含t的代数式表示）；⑵当4＜t＜5时，设抛物线分别与线段AB、CD交于点M、N.①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；②求△MPN的面积S与t的函数关系式，并求t为何值时，S=218；③在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接．．写出t的取值范围.。

2011河北中考数学试题及答案考试是评价学生学习成绩的一种常见方式，而数学试题作为其中的一部分，对于学生的数学水平有着重要的检验作用。

本文将为大家介绍2011年河北中考数学试题及答案，帮助学生们更好地了解考试内容和解题思路。

2011年河北中考数学试题题目一：已知正方形ABCD的边长为4cm，点E是BC延长线上的一点，且BE=2cm，连接AE交对角线BD于F。

求EF的长度。

解析：首先，根据正方形ABCD的性质，可以得知BD是对角线，在点E处交对角线BD得到弦EF。

我们可通过相似三角形的知识来求解。

在△ABF和△DEC中，由于正方形ABCD为等腰直角三角形，故△ABF和△DEC为相似三角形，且由比例关系可得BF/DE=AB/DC=1。

根据已知条件，我们可以得到BE=2cm，BF=BC-FC=4-FC，DE=2cm，代入比例关系可得(4-FC)/2=1，解得FC=2cm。

由△ABF与△CFE的相似关系可知，AB/CF=AF/CE=BF/EF，代入已知数据可得4/(2+EF)=2/EF，解得EF=1cm。

综上所述，EF的长度为1cm。

题目二：甲乙两人进行长跑比赛，已知甲第一圈跑完全程的1/4，第二圈跑完全程的1/2，第三圈跑完全程的1/3，如此往复。

乙第一圈跑完全程的1/5，第二圈跑完全程的1/4，第三圈跑完全程的1/3，如此往复。

如果两人同时开始比赛，两人相遇时甲刚好跑完第n圈，求n 的值。

解析：通过观察题目中给出的比例关系可以得知，甲和乙两人分别每一圈的跑步长度从第一圈开始逐渐递增。

我们可以列出甲乙两人每一圈的跑步长度的等差数列，并找到二者的公共项。

甲的每一圈跑步长度为1/4，1/2，1/3...，是一个等差数列，而乙的每一圈跑步长度为1/5，1/4，1/3...，也是一个等差数列。

根据等差数列的性质，公式为an=a1+(n-1)d，其中an代表第n项，a1代表首项，d代表公差。

设甲第n圈时刚好跑完全程，乙第m圈时刚好跑完全程，则有：1/4+1/2+1/3+...+1/n=11/5+1/4+1/3+...+1/m=1通过计算等差数列的和，我们可以得到甲乙两人各自跑的圈数：n=4m=5综上所述，两人相遇时甲刚好跑完第4圈，即n的值为4。

2011河北省初中毕业生升学文化课考试数 学 试 卷卷Ⅰ（选择题，共30分）一、选择题（本大题共12个小题.1－6小题，每小题2分，7－12小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的 1．计算30的结果是A ．3B ．30C ．1D ．0 2．如图1，∠1＋∠2等于A ．60°B ．90°C ．110°D ．180°3．下列分解因式正确的是A ．－a ＋a 3=－a (1＋a 2)B ．2a －4b ＋2=2(a －2b )C ．a 2－4=(a －2)2D ．a 2－2a ＋1=(a －1)2 4．下列运算中，正确的是A ．2x －x =1B ．x ＋x 4=x 5C ．(－2x )3=－6x 3D ．x 2y ÷y =x 2 5．一次函数y =6x ＋1的图象不经过．．． A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限6．将图2①围成图2②的正方体，则图②中的红心“”标志所在的正方形是正方体中的 A ．面CDHE B ．面BCEFC ．面ABFGD ．面ADHG7．甲、乙、丙三个旅行团的游客人数都相等，且每团游客的平均年龄都是32岁，这三个团游客年龄的方并有分别是227S =甲，219.6S =乙，21.6S =丙，导游小王最喜欢带游客年龄相近的团队，若在这三个团中选择一个，则他应选 A ．甲团 B ．乙团 C ．丙团 D ．甲或乙团8．一小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下面的函数关系式：h =－5(t －1)2＋6，则小球距离地面的最大高度是 A ．1米 B ．5米 C ．6米 D ．7米9．如图3，在△ABC 中，∠C =90°，BC =6，D ，E 分别在AB ，AC 上，将△ABC 沿DE 折叠，使点A 落在A ′处，若A ′为CE 的中点，则折痕DE 的长为A ．12B ．5米C ．6米D ．7米10．已知三角形三边长分别为2，x ，13，若x 为正整数，则这样的三角形个数为A ．2B ．3C ．5D ．1311．如图4，在长形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆住的侧面，刚好能组合成圆住.设矩形的长和宽分别为y 和x ，则y 与x的函数图象大图1图4① ②图2致是12．根据图5中①所示的程序，得到了y 与x 的函数图象，如图5中②，若点M 是y 轴正半轴上任意一点，过点M 作PQ ∥x 轴交图象于点P 、Q ，连接OP 、OQ ，则以下结论：①x ＜0时，y =2x②△OPQ 的面积为定值③x ＞0时，y 随x 的增大而增大 ④MQ =2PM⑤∠POQ 可以等于90° 其中正确结论是 A ．①②④ B ．②④⑤C ．③④⑤D ．②③⑤2011年河北省初中毕业生升学文化课考试数 学 试 卷卷Ⅱ（非选择题，共90分）二、填空题（本大题共6个小是，每小题3分，共18分，把答案写在题中横线上） 13π，－4，0这四个数中，最大的数是___________.14．如图6，已知菱形ABCD ，其顶点A 、B 在数轴上对应的数分别为－4和1，则BC =_____.15．若︱x －3︱＋︱y ＋2︱=0，则x ＋y 的值为_____________. 16．如图7，点O 为优弧ACB 所在圆的心，∠AOC =108°，点D 在AB 的延长线上，BD =BC ，则∠D =____________.17．如图8中图①，两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置得到图②，则阴影部分的周长为_________18．如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.如：小宇在编号为3的顶点时，那么他应走3个边长，即从3→4图6ABCD①②ABC DO 图7C① ②图8 图9→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是____________.三、解答题（本大题共8个小题，共72分，解答应写出文字说明、证明过程 或演算步骤） 19．（本小题满分8分）已知2x y =⎧⎪⎨=⎪⎩x ，yy a =+的解.求(a ＋1)(a －1)＋7的值 20．（本小题满分8分）如图10，在6×8的网格图中，每个小正方形边长均为1，点O 和△ABC 的顶点均为小正方形的顶点.⑴以O 为位似中心，在网格图．．．中作△A ′B ′C ′，使△A ′B ′C ′和△ABC 位似，且位似比为1：2⑵连接⑴中的AA ′，求四边形AA ′C ′C 的周长.（结果保留根号）21．（本小题满分8分）如图11，一转盘被等分成三个扇形，上面分别标有关－1，1，2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，鞭个扇形恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）. ⑴若小静转动转盘一次，求得到负数的概率； ⑵小宇和小静分别转动一次，若两人得到的数相同，则称两人“不谋而合”，用列表法（或画树形图）求两人“不谋图11小宇 小静而合”的概率.22．（本小题满分8分）甲、乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工，若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工.⑴问乙单独整理多少分钟完工？⑵若乙因式作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？23．（本小题满分9分）如图12，四边形ABCD 是正方形，点E ，K 分别在BC ，AB 上，点G 在BA 的延长线上，且CE =BK =AG .⑴求证：①DE =DG ；②DE ⊥DG ；⑵尺规作图：以线段DE ，DG 为边作出正方形DEFG （要求：只保留作图痕迹，不写作法和证明）；⑶连接⑵中的KF ，猜想并写出四边形CEFK 是怎样的特殊四边形，并证明你的猜想；⑷当1CE CB n 时，衣直接写出ABCD DEFGS S 正方形正方形的值.24．（本小题满分9分）已知A 、B 两地的路程为240千米，某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地，受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订.现在有货运收费项目及收费标准表，行驶路程S （千米）与行驶时间t （时）的函数图象（如图13中①），上周货运量折线统计图（如图13中②）等信息如下：A B CD图11 图13①⑴汽车的速度为__________千米/时， 火车的速度为_________千米/时；设每天用汽车和火车运输的总费用分别为y 汽（元）和y 火（元），分别求y 汽、y 火与x 的函数关系式（不必写出x 的取值范围）及x 为何值时y 汽＞y 火；（总费用=运输费＋冷藏费＋固定费用）⑶请你从平均数、折线图走势两个角度分析，建议该经销商应提前下周预定哪种运输工具，才能使每天的运输总费用较省？25．（本小题满分10分） 如图14①至图14④中，两平行线AB 、CD 音的距离均为6，点M 为AB 上一定点.思考：如图14①中，圆心为O 的半圆形纸片在AB 、CD 之间（包括AB 、CD ），其直径MN 在AB 上，MN =8，点P 为半圆上一点，设∠MOP =α， 当α=________度时，点P 到CD 的距离最小，最小值为____________. 图13 ②B A DC图14 ① BA D C 图14 ③B A DC 图14 ② BA DC图14 ④M探究一在图14①的基础上，以点M为旋转中心，在AB、CD之间顺时针旋转该半圆形纸片，直到不能再转动为止.如图14②，得到最大旋转角∠BMO=_______度，此时点N到CD的距离是______________.探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉，使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.⑴如图14③，当α=60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值：⑵如图14④，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的取值范围.（参考数据：sin49°=34，cos41°=34，tan37°=34）26．(本小题满分12分)如图15，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P.已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）.⑴求c、b（用含t的代数式表示）；⑵当4＜t＜5时，设抛物线分别与线段AB、CD交于点M、N.①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；②求△MPN的面积S与t的函数关系式，并求t为何值时，S=218；③在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接．．写出t的取值范围.新课标第一网。

]河北省2002-2021专题04 图形的变换1. （2004年河北省大纲2分）如图，一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔，如果一个球按图中所示的方向被击出（球可以经过多次反射），那么该球最后将落入【】球袋A、1号B、2号C、3号D、4号2. （2004年河北省课标2分）图中几何体的主视图是【】A．B．C．D．3. （2004年河北省课标2分）如图是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔果一个球按图中所示的方向被击出（球可以经过多反射），那么该球最后将落入的球袋是【】4. （2005年河北省大纲2分）一根绳子弯曲成如图1所示的形状．当用剪刀像图2那样沿虚线a把绳子剪断时，绳子被剪为5段；当用剪刀像图3那样沿虚线b（b∥a）把绳子再剪一次时，绳子就被剪为9段．若用剪刀在虚线a，b之间把绳子再剪（n﹣2）次（剪刀的方向与a平行），这样一共剪n次时绳子的段数是【】A．4n+1 B．4n+2 C．4n+3D．4n+55. （2005年河北省课标2分）图中几何体的主视图是【】A．B．C．D．6. （2005年河北省课标2分）将一正方形纸片按图中⑴、⑵的方式依次对折后，再沿⑶中的虚线裁剪，最后将⑷中的纸片打开铺平，所得图案应该是下面图案中的【】A．B．C．D．7. （2006年河北省大纲课标2分）《九章算术》是我国东汉初年编订的一部数学经典著作．在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1、图2．图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是3x2y19x4y23+=⎧⎨+=⎩类似地，图2所示的算筹图我们可以表述为【】A．2x y114x3y27+=⎧⎨+=⎩B．2x y114x3y22+=⎧⎨+=⎩C．3x2y19x4y23+=⎧⎨+=⎩D．2x y64x3y27+=⎧⎨+=⎩8. （2006年河北省大纲2分）观察图给出的四个点阵，s表示每个点阵中的点的个数，按照图形中的点的个数变化规律，猜想第n个点阵中的点的个数s为【】A ．3n 2-B ．3n 1-C ．4n 1+D ．4n 3-9. （2006年河北省大纲2分）小宇同学在一次手工制作活动中，先把一张矩形纸片按图1的方式进行折叠，使折痕的左侧部分比右侧部分短1cm ；展开后按图2的方式再折叠一次，使第二次折痕的左侧部分比右侧部分长1cm ，再展开后，在纸上形成的两条折痕之间的距离是【 】A ．0.5cmB ．1cmC ．1.5cmD ．2cm10. （2006年河北省课标2分）图中几何体的主视图是【 】A ．B ．C ．D ．11. （2006年河北省课标2分）如图，现有一圆心角为90°，半径为8cm 的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为【 】A ．4cmB ．3cmC ．2cmD ．1cm12. （2007年河北省2分）我国古代的“河图”是由3×3的方格构成，每个方格内均有数目不同的点图，每一行、每一列以及每一条对角线上的三个点图的点数之和均相等．图给出了“河图”的部分点图，请你推算出P 处所对应的点图是【 】A．B．C．D．13. （2008年河北省2分）有一个四等分转盘，在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌，如图1．若将位于上下位置的两个字牌对调，同时将位于左右位置的两个字牌对调，再将转盘顺时针旋转90，则完成一次变换．图2，图3分别表示第1次变换和第2次变换．按上述规则完成第9次变换后，“众”字位于转盘的位置是【】A．上B．下C．左D．右14. （2009年河北省2分）从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积是【】A．20 B．22 C．24 D．2615. （2009年河北省2分）古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是【】A．13 = 3+10 B．25 = 9+16 C．36 = 15+21 D．49 = 18+3116. （2010年河北省2分）将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图1．在图2中，将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换．若骰子的初始位置为图1所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是【】A．6 B．5 C．3 D．217. （2011年河北省2分）将图①围成图②的正方体，则图②中的红心“”标志所在的正方形是正方体中的【】A．面CDHE B．面BCEF C．面ABFG D．面ADHG18. （2011年河北省3分）如图，在△ABC中，∠C=90°，BC=6，D，E分别在AB，AC上，将△ABC沿DE折叠，使点A落在A′处，若A′为CE的中点，则折痕DE的长为【】A．12B．5 C．6 D．719. （2012年河北省2分）图中几何体的主视图为【】A．B．C．D．A．70°B．40°C．30°D．20°21. （2012年河北省3分）如图，两个正方形的面积分别为16，9，两阴影部分的面积分别为a，b（a＞b），则（a－b）等于【】A．7 B．6 C．5 D．422.【2014中考河北3分】图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中正方形顶点A，B在围成的正方体的距离是【】A、0B、1C、2D、3对于两人的观点，下列说法正确的是【】A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对24.【2015中考河北3分】一张菱形纸片按图1-1、图1-2依次对折后.再按图l-3打出一个圆形小孔，则展开铺平后的图案是（）A. B. C. D.25.【2015中考河北3分】图中的三视图所对应的几何体是（）A. B.C. D.26. 【2016中考河北3分】下列图形中，既是轴对称图形，又是中心对称图形的是（）A B C D27.【2016中考河北2分】如图，将ABCD沿对角线AC折叠，使点B落在点B’处.若∠1=∠2=44°，则∠B为（）第13题图A．66°B．104°C．114°D．124°1. （2003年河北省2分）如图，是用火柴棍摆出的一系列三角形图案，按这种方式摆下去，当边上摆8（即n=8）根时，需要的火柴总数为▲ 根.2. （2005年河北省大纲2分）如图，已知圆锥的母线长OA=8，底面圆的半径r=2．若一只小虫从A点出发，绕圆锥的侧面爬行一周后又回到了A点，求小虫爬行的最短路线的长▲ ．3. （2006年河北省课标3分）图是由边长为1m的正方形地砖铺设的地面示意图，小明沿图中所示的折线从A→B→C所走的路程为▲ m．（结果保留根号）4. （2006年河北省课标3分）小宇同学在一次手工制作活动中，先把一张矩形纸片按图1的方式进行折叠，使折痕的左侧部分比右侧部分短1cm；展开后按图2的方式再折叠一次，使第二次折痕的左侧部分比右侧部分长1cm，再展开后，在纸上形成的两条折痕之间的距离是▲ cm．5. （2007年河北省3分）如图，在10×6的网格图中（每个小正方形的边长均为1个单位长），⊙A的半径为1，⊙B的半径为2，要使⊙A与静止的⊙B内切，那么⊙A由图示位置需向右平移▲ 个单位长．6. （2009年河北省3分）如图，等边△ABC的边长为1 cm，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为▲ cm．7. （2011年河北省3分）如图中图①，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A′B′D′的位置得到图②，则阴影部分的周长为▲8. （2012年河北省3分）用4个全等的正八边形进行拼接，使相等的两个正八边形有一条公共边，围成一圈后中间形成一个正方形，如图1，用n个全等的正六边形按这种方式进行拼接，如图2，若围成一圈后中间形成一个正多边形，则n的值为▲ 。