Origin 常用小技巧 分段线性拟合

Origin8.0分层拟合问题
1)先输入所有的数据到origin中；再将所有的点作成散点
图，再将作的图缩小。

选择第一组数据，作散点图，可以改变一下图标的颜色，以免和后面的冲突。

再点击“图层1”右击选择隐藏图层。

2)可以直接点击快捷菜单上的“新建图层”(要么在空白处
右击，选择New layer)；再右击图层，选择Layer contents,选择数据。

(如果此时出现的是一条线，而不是散点图，可以右击，选择Change plot to改为散点图)，再改坐标。

注意：不同图层的坐标范围应一致。

3)分层时如果一个散点图的“图标”不见了，可以右击选择
“New Legend”
4)拟合时，选用“Fit Polynomial”拟合。

origin拟合函数Origin是一款功能强大的数据分析软件，它提供了丰富的数据分析工具来处理实验数据，其中包括曲线拟合功能。

本文将着重介绍Origin中的曲线拟合功能，包括常见的拟合函数及其应用。

一、拟合函数在Origin中，可以通过选择不同的拟合函数来拟合所需的曲线。

常见的拟合函数有线性函数、二次函数、三次函数、指数函数、对数函数、幂函数、指数增长函数、正弦函数、余弦函数等。

下面将对这些函数进行详细介绍。

1. 线性函数一元线性函数的表达式为y=a+bx，其中a和b分别为截距和斜率，x为自变量，y为因变量。

线性函数是最简单的拟合函数之一，适用于线性关系较为明显的数据。

例如，当我们在光电效应实验中测量出光电子的动能和光子的频率时，它们之间就存在着线性关系，此时可以使用线性函数来拟合数据。

2. 二次函数三次函数的表达式为y=a+bx+cx^2+dx^3，其中a、b、c和d分别为常数，x为自变量，y为因变量。

三次函数通常用于描述抛物线，这种函数在物理和工程学中经常被应用。

例如，在材料科学中可以使用三次函数来描述一个材料的弹性行为。

4. 指数函数指数函数的表达式为y=ae^(bx)，其中a和b为常数，x为自变量，y为因变量。

指数函数适用于描述随时间或位置而变化的某些现象。

例如，当我们观察放射性衰变时，衰变速率随时间的变化可以使用指数函数来拟合。

8. 正弦函数正弦函数的表达式为y=a sin(bx+c)，其中a、b和c为常数，x为自变量，y为因变量。

正弦函数适用于描述像周期性的变化，例如，天文学中的多个现象，如日、月、星星的运动都是可以用正弦函数表示的。

二、常见应用在实际应用中，我们可以使用Origin中的曲线拟合功能来解决各种问题。

下面列举几种常见的应用。

1. 数据分析在实验数据分析中，使用拟合函数可以帮助我们理解和预测实验数据的变化趋势。

例如，在物理实验中，我们可以使用线性函数来分析位移和时间的关系，使用指数函数来分析辐射物质的衰变过程。

origin线性拟合的斜率和截距
求origin线性拟合的斜率和截距，是求解一元线性回归问题的
基本步骤。

一元线性回归问题的模型可以表示为：y=ax+b，
其中a为斜率，b为截距。

要求求解origin线性拟合的斜率和截距，首先需要准备足够的
数据，即x和y的值，并将其分别放入x和y的数组中。

然后，根据x和y的值，计算出x的平均值和y的平均值，分别记为
x_mean和y_mean。

接下来，根据x和y的值，计算出x和y的方差，分别记为
x_var和y_var，以及x和y的协方差，分别记为x_cov和
y_cov。

最后，根据以上计算出的x_mean、y_mean、x_var、y_var、
x_cov和y_cov，可以计算出origin线性拟合的斜率a和截距b，其计算公式分别为：
a=x_cov/x_var
b=y_mean-a*x_mean
因此，求origin线性拟合的斜率和截距，需要准备足够的数据，并计算出x的平均值、y的平均值、x的方差、y的方差、x的
协方差和y的协方差，最后根据以上计算出的值，可以计算出origin线性拟合的斜率和截距。

origin分段函数拟合
拟合的函数形式为：
\[ f(x) =
\begin{cases}
a_1x + b_1 & \text{if } x < x_1 \\
a_2x + b_2 & \text{if } x_1 \leq x < x_2 \\
\vdots \\
a_{n-1}x + b_{n-1} & \text{if } x_{n-2} \leq x < x_{n-1} \\ a_nx + b_n & \text{if } x \geq x_{n-1} \\
\end{cases}
\]
其中，$a_i$和$b_i$为拟合参数，$x_i$为分段点。

拟合的过程可以分为以下几步：
1. 确定分段点$x_i$的个数和位置。

可以根据数据的分布情况和特点来选择合适的分段点。

2. 对每个区间$(x_{i-1}, x_i)$内的数据进行线性拟合，得到参数$a_i$和$b_i$。

3. 将每个区间的拟合结果拼接起来，得到最终的拟合函数。

具体的拟合算法可以使用最小二乘法来求解，最小化真实数据与拟合函数之间的误差。

可以使用数值优化算法，如梯度下降法或牛顿法来求解最优的参数值。

需要注意的是，拟合的结果可能会受到分段点的选择和初始参数值的影响，因此需要进行多次尝试和调整，以找到最优的拟合结果。

在Origin中拟合曲线时，选取合适的数据点非常重要。

以下是几个建议：
1. 代表性：选择具有代表性的数据点进行拟合。

这些点应该能够反映数据整体的变化规律。

2. 分布均匀：尽量选择分布均匀的数据点，避免在某些区域选择过多的点，而其他区域选择过少的点。

3. 考虑噪声和异常值：在选择数据点时，应考虑噪声和异常值的影响。

对于噪声，可以选择滤波或平滑处理来减少其影响。

对于异常值，可以将其去除或进行特殊处理。

4. 交互式拟合：可以在Origin中采用交互式拟合方式，即手动选择需要拟合的数据点，然后进行拟合。

这样可以更灵活地选择数据点，并获得更好的拟合效果。

5. 分段拟合：对于具有不同变化趋势的数据，可以考虑采用分段拟合方法。

这样可以更好地适应数据的局部变化规律，提高拟合精度。

6. 非线性拟合：如果数据呈现出非线性变化趋势，可以选择合适的非线性拟合函数进行拟合。

在Origin中，可以通过Analysis > Fitting > Nonlinear Curve Fit菜单进行非线性拟合。

7. 拟合曲线类型：根据数据的特征和变化规律，选择合适的拟合曲线类型。

例如，线性拟合、多项式拟合、指数拟合、对数拟合等。

总之，在Origin中拟合曲线时，需要仔细考虑数据点的选择，并根
据实际情况灵活调整拟合策略，以获得最佳的拟合效果。

Origin7.5使用说明--直线拟合我们根据数据作出y=a*x+b的直线拟合，具体使用origin7.5软件的方法如下：1、打开origin，输入数据
2、选中数据，并按图选择菜单。

3、出来如图菜单，点击“ok”。

4、这时会根据数据得出数点，如果不是线性关系，我们也可以在f(x)中选择Categories选中polynomial；Functions中选择Line。

就会得出如图线性关系，并拟合曲线。

下面就是我们想要得出直线的拟合曲线方程。

5、出现Select Function对话框，点击红框所示菜单
6、当出现下图图页时，我们要选择红框所示或者红线所示参数，并按Done确定。

7、我们就可以得出我们想要的直线拟合曲线，并附带方程。

8、经过加班熬夜的研究琢磨，终于得出我想要的结果了，很是高兴，于是写下方法，以备共鉴！谢谢大家@！。

本君使用的是origin8版本，如果版本不一样大家可以按照类似方式摸索一下！首先输入数据如左下图所示：
选择要作图的数据，然后点击左下方按钮如右上图，可作出散点图
然后进行线性拟合。

然后在出现的对话框中选择拟合未知数的次数为1，即线性方程：
如果到时候需要用拟合方程来算具体的值，可以拉动滑动条在下面的对话框中选择：
这个就是看你是用X算Y还是Y算X了~
选择好以后点OK~以下就是算出来的图形。

（自己调整图表大小）
点击左侧菜单中的book1可以看到各种表：
从左至右依次是原始数据表格、拟合报告（可能有的人没有）、数据计算表格（？看起来貌似是根据拟合曲线算的数据）、计算实际数据用的表格（就是刚刚勾选的那个XY神马的~）
点击最后一个表，在左侧输入Y值右侧就可以得到对应的X值啦~
PS：还有一个问题就是如果计算的数据超过了范围的话可能会出现这样的哟~
即如框出来的那样没有数据！
这个时候就要改一下拟合函数的范围！
见下图所示：
点击左侧菜单中的graph重新点出图来。

然后点击上图中蓝框框出的绿色小锁，如图选择就会出现刚刚做拟合时的对话框。

拉动滑动条至下面这一栏：
选择X的范围为自定义，如下图：
出来的最大最小值大家自己填，只要包括自己要算的数据就可以啦~
然后点OK！
再回到刚刚计算XY的地方是不是先前是“---”的地方现在变得有数据啦~！
PS：本君自己也不是专业人士，这个是自己摸索出来的origin小白教程，希望对要使用origin8的各位化学同仁们有点小小帮助啦~。

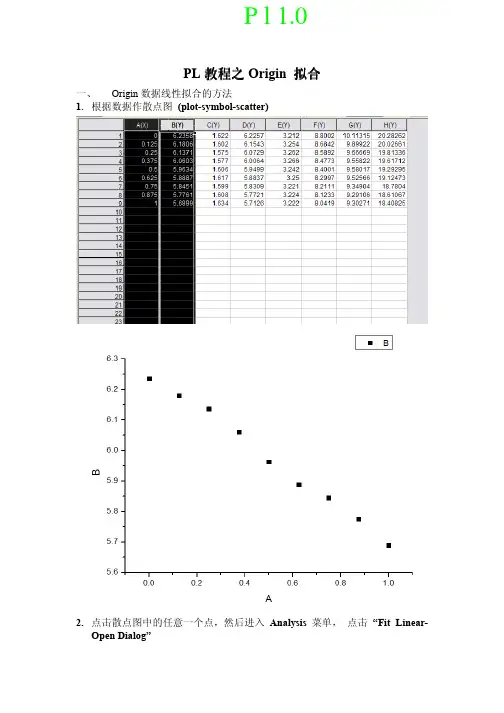
PL教程之Origin 拟合
一、 Origin数据线性拟合的方法
1.根据数据作散点图(plot-symbol-scatter)
2.点击散点图中的任意一个点，然后进入Analysis菜单，点击“Fit Linear-
Open Dialog”
3.设置拟合参数（如无需特殊要求，可以不作任何改变，系统自己会生产参数），
然后点击“OK”。

注意：Input Dat：拟合数据范围
Fit Option：拟合选项（包括是否给出固定的截距或者斜率等）
4.系统会自动给出结果，红色的线即为拟合得到的曲线，并提供了一张数据表。

Equation : 拟合方程
Adjusted R-squared: 调整后的离差平方和 Intercept: 截距
Slope: 斜率
Standard Error: 标准偏差
所以此数据拟合得到的拟合方程为所以此数据拟合得到的拟合方程为：： Y = -0.5536X + 6.2520
5. 拟合的详细情况， 可以通过双击工作表查看。

origin拟合曲线的方程并计算一、Origin软件简介Origin是一款功能强大的数据分析和图形绘制软件，广泛应用于生物学、物理学、化学、工程学等领域。

通过Origin，我们可以进行数据拟合，从而得到曲线的方程，并对其进行计算和分析。

二、拟合曲线的方程拟合曲线通常是指通过给定的数据点，使用数学函数来拟合曲线，从而得到一条最佳拟合曲线。

在Origin中，常用的拟合方法包括线性拟合、多项式拟合、指数拟合、幂函数拟合等。

下面以线性拟合为例，介绍拟合曲线的方程。

线性拟合曲线方程为：y = mx + b，其中m为斜率，b为截距。

在Origin中，可以通过添加两个数据系列（x和y）来创建线性拟合图表，并通过“拟合”功能选择线性模型进行拟合。

三、计算步骤以下是使用Origin进行拟合曲线方程计算的一般步骤：1. 打开Origin软件并导入数据。

你可以将数据导入Origin中的数据表或从文件中导入。

确保数据具有相应的格式和准确性。

2. 创建一个新的图表，并将数据添加到图表中。

确保将正确的x 和y数据系列添加到图表中。

3. 选择“分析”菜单中的“拟合”选项，然后选择“线性”或其他适合的拟合模型。

在弹出的对话框中，输入拟合模型的参数值并进行其他必要的设置。

4. 执行拟合操作并得到拟合曲线和相关参数。

在拟合结果中，你将获得斜率和截距的值，即m和b。

这些值可用于后续的计算和分析。

5. 根据需要使用拟合曲线进行进一步的分析，如绘制其他图表、进行统计分析和建模等。

四、计算实例下面是一个简单的实例，演示如何使用Origin进行拟合曲线的方程计算。

假设我们有一组实验数据（x，y），并希望通过线性拟合得到拟合曲线的方程和相关参数。

1. 导入数据：打开Origin软件，并将实验数据导入数据表中。

确保数据具有相应的格式和准确性。

2. 创建图表：创建一个新的图表，并将x和y数据系列添加到图表中。

3. 进行拟合：选择“分析”菜单中的“拟合”选项，然后选择“线性”。

使用Origin7.5来作演示1. 先随意输入一组数据吧
2. 选中这2列数据，然后点左下角的作scatter图的图标，
3. 然后就生成了散点图
4. 点击Analysis菜单中的Fit Polynomial，在弹出的对话框中，Order处设为1，这样就是作线性拟合，可能有人问，为什么不直接选择Fit Liner呢？因为只有选Fit Polynomial, 才能在图形上显示公式，也就是勾选对话框中的Show Flormula on graph。

（可能Origin的设计者认为线性拟合公式太简单，默认就不用显示了）
5. 点击OK后，就得到了拟合后的图形。

线性方程公式也显示在了图形上。

注意窗口的右下角。

点击那里的小箭头后，我们可以看到完整的拟合统计信息，如相关系数R2=0.9918
6. 好了，标准曲线知道了，现在就来计算IC50。

根据IC50定义，该例子中就是Y取中值时，X对应的数值，这里Y的中值是0.6，那根据线性方程就可以自己算出来对应的X值。

那如果不是线性方程，公式比较复杂手工计算就很麻烦了，所以还是用Origin中的功能吧。

点击Tools，Linear Fit，如果不是线性拟合的，请选择其他拟合方式，如果是S形曲线的，则需要选择Sigmoidal Fit.
7. 在弹出的对话框中，先点击Fit，然后在Find Y处输入0.6，点击Find X按钮，得到的数值就是IC50了。

同样的可以很方便的求得IC90，IC10，IC20 …。

origin 分段函数拟合
分段函数拟合是一种常用的数学方法，用于逼近复杂函数。

它将整个定义域分成多个段落，每个段落内使用简单的函数进行拟合。

这样做的目的是用一组简单的函数来近似整个函数的行为，从而简化计算和分析过程。

在分段函数拟合中，我们首先确定分段点，即将整个定义域划分为不同的段落。

然后，针对每个段落，选择一种适当的函数类型进行拟合。

常用的函数类型包括线性函数、二次函数、指数函数和对数函数等等。

在每个段落内，我们通过调整函数的参数，使得拟合函数与实际函数的取值尽可能接近。

这可以通过最小二乘法等统计方法来实现。

通过不断优化参数，我们可以得到一个在整个定义域上都较好逼近原函数的分段函数。

分段函数拟合可以应用于多个领域，如物理学、经济学和工程学等。

它可以用于描述非线性关系、曲线拟合和数据分析等问题。

通过将问题分解为多个简单的段落，分段函数拟合可以简化复杂问题的处理，并提高计算效率。

总的来说，分段函数拟合是一种有效的数学方法，可以将复杂函数近似为一组简单的函数。

通过合理选择分段点和拟合函数，我们可以得到一个在整个定义域上都较好逼近原函数的分段函数，从而简化计算和分析过程。