excel2007中梯形法计算定积分的算法
- 格式:doc
- 大小:58.50 KB
- 文档页数:2

定积分的近似计算方法定积分近似计算方法指的是利用数值计算方法来估算给定函数在一定区间上的积分值。
这些方法常常用于当函数在该区间内无法求得解析式时,或者解析式难以求得的情况下。
下面将介绍常用的数值积分近似计算方法。
一、矩形法矩形法即将积分区间等分为若干小区间,然后在每个小区间中选择一个代表点,将函数在该点的函数值作为近似积分的值。
具体可以分为左矩形法、右矩形法和中矩形法。
1.左矩形法左矩形法即取每个小区间的左端点作为代表点,近似积分的值为:∫[a, b]f(x)dx ≈ Δx * [f(a) +f(a+Δx) + … + f(a+(n-1)Δx)]其中,Δx=(b-a)/n,n为区间的等分数。
2.右矩形法右矩形法即取每个小区间的右端点作为代表点,近似积分的值为:∫[a, b]f(x)dx ≈ Δx * [f(a+Δx) + f(a+2Δx) + … +f(a+nΔx)]其中,Δx=(b-a)/n,n为区间的等分数。
3.中矩形法中矩形法即取每个小区间的中点作为代表点,近似积分的值为:∫[a, b]f(x)dx ≈ Δx * [f(a+Δx/2) + f(a+3Δx/2) + … +f(a+(2n-1)Δx/2)]其中,Δx=(b-a)/n,n为区间的等分数。
二、梯形法梯形法是通过将积分区间上的曲线拟合为多个梯形来近似计算定积分的方法。
将积分区间[a,b]等分为n个小区间,然后在每个小区间上用两个端点处的函数值拟合成一个梯形,然后将这些梯形的面积加起来即可得到近似的定积分的值。
具体计算公式为:∫[a, b]f(x)dx ≈ Δx/2 * [f(a) + 2f(a+Δx) + 2f(a+2Δx)+ … + 2f(a+(n-1)Δx) + f(b)]其中,Δx=(b-a)/n,n为区间的等分数。
三、辛普森法辛普森法是通过将积分区间上的曲线拟合为多个二次多项式的方法。
将积分区间[a,b]等分为n个小区间,每两个相邻区间拟合成一个二次多项式。

梯形公式和辛普森求解定积分
数学中,定积分是较为常见的运算,既可以通过梯形公式、辛普森公式等方式求解。
梯形公式是用来计算定积分的一种常用方法,主要就是把封闭的积分区间[a,b]分
成若干等分,每一等分长度相等,每一等分的两端点函数值分别用各积分一次积分而得小梯形面积来等价近似。
然后,将所得的小梯形面积加起来,即可求到积分的近似值。
辛普森求解定积分是将积分区间[a,b]表示为一组有限个点,然后利用辛普森公式
来近似计算函数在该组点上的值,最后加起来就可以得到整个积分区间的值。
一般而言,当积分区间越小而越窄,辛普森公式所得的积分结果的接近的越精确,且求解的速度最快。
定积分的求解方法有多种,梯形公式和辛普森求解定积分就是其中的两种求解方式,一般情况下,梯形公式用于在积分区间中间定点数多,但是积分段数相对较少的情况下,而辛普森求解定积分则用于积分区间窄,但是积分段数稍微多的情况下。
由于梯形公式和辛普森求解定积分有其各自的优点,在实际应用中可以根据不同的情况,灵活选用二者的优点,以达到最优的结果。


定积分算法定积分算法定积分是微积分中的一个重要概念,它可以用来求解曲线下方的面积、体积等问题。
在实际应用中,定积分也被广泛应用于物理、经济、工程等领域。
本文将介绍定积分的定义及其算法。
一、定积分的定义定积分是一个数学概念,它描述了一个函数在一段区间上的面积大小。
具体来说,设函数f(x)在区间[a,b]上连续,则[a,b]上f(x)与x轴所围成的曲边梯形面积为:其中a和b是曲边梯形底边两端点的x坐标,f(x)是曲边梯形边界上每个点的纵坐标。
当n趋向于无穷大时,Δx趋向于0,则上式右侧称为函数f(x)在区间[a,b]上的定积分,记作:二、定积分算法1. 矩形法矩形法是最简单易懂的一种求解定积分的方法。
其基本思想是将区间[a,b]等分成n个小区间,并在每个小区间中取一个代表点xi(i=1,2,...,n),然后用xi代替f(xi)计算出每个小区间的面积,最后将这些面积相加即可得到定积分的近似值。
具体来说,设函数f(x)在区间[a,b]上连续,则将区间[a,b]等分成n个小区间,每个小区间的长度为Δx=(b-a)/n。
然后,在每个小区间中取一个代表点xi(i=1,2,...,n),用xi代替f(xi)计算出每个小区间的面积:最终,将这些面积相加即可得到定积分的近似值:其中,Rn表示用矩形法求解定积分时所得到的近似值。
2. 梯形法梯形法是比矩形法更精确的一种求解定积分的方法。
其基本思想是将区间[a,b]等分成n个小区间,并在每个小区间中取两个代表点xi和xi+1(i=0,1,...,n-1),然后用这两个点对应的函数值f(xi)和f(xi+1)计算出每个小梯形的面积,最后将这些面积相加即可得到定积分的近似值。
具体来说,设函数f(x)在区间[a,b]上连续,则将区间[a,b]等分成n个小区间,每个小区间的长度为Δx=(b-a)/n。
然后,在每个小区间中取两个代表点xi和xi+1(i=0,1,...,n-1),用这两个点对应的函数值f(xi)和f(xi+1)计算出每个小梯形的面积:最终,将这些面积相加即可得到定积分的近似值:其中,Tn表示用梯形法求解定积分时所得到的近似值。


复化梯形算法求解数值积分
下面详细介绍复化梯形算法的原理和步骤:
1.原理:
2.步骤:
(1)将区间[a,b]等分成N个小区间,每个小区间的长度为h=(b-a)/N。
(2) 定义x0 = a 和 xn = b,即第一个小区间的左端点和最后一个
小区间的右端点。
(3) 对于每个小区间[i, i+1],计算f(xi)和f(xi+1),然后计算小
区间[i, i+1]上的积分值Ti = h * (f(xi) + f(xi+1)) / 2
(4)将所有小区间上的积分值相加,得到近似的定积分值
I≈T=T1+T2+...+TN。
3.误差分析:
误差E=-(b-a)^3/12N^2*f''(ξ)
其中f''(ξ)是函数f(x)在区间[a,b]上的二阶导数的最大值。
4.示例:
考虑要求解函数f(x)=x^2在区间[0,1]上的定积分,可以使用复化梯
形算法进行计算。
首先将区间[0,1]等分成N个小区间,假设N=4、则每个小区间的长
度为h=(1-0)/4=0.25
然后计算每个小区间上的积分值:
最后将所有小区间上的积分值相加,得到近似的定积分值:
因此,函数f(x)=x^2在区间[0,1]上的定积分的近似值为0.75
以上就是复化梯形算法求解数值积分的原理和步骤,该算法可以通过增加小区间的数量以提高计算的精度。
同时,利用误差公式可以估计计算的误差,有助于选择适当的参数进行数值积分的计算。

excel表格内进行求积的教程
Excel中经常需要使用到求积功能,在表格内具体该如何进行求积呢?下面是由店铺分享的excel表格内进行求积的教程,以供大家阅读和学习。
excel表格内进行求积的教程:
求积步骤1:打开Excel表格,随意点击一个单元格作为最后输出乘积的位置,然后在“f(x)”后面输入“=A1*B1”即A1和B1所在单元格的数据相乘,最后按“Enter”即可输出答案。
求积步骤2:将鼠标放到第一个结果的单元格的右下角出现黑粗体“+”,直接向下拉即可出现其他数据的乘积结果。
求积步骤3:效果(复制单元格就是复制函数公式,其他的数据都是按这个公式计算):。

几种定积分的数值计算方法摘要:本文归纳了定积分近似计算中的几种常用方法,并着重分析了各种数值方法的计算思想,结合实例,对其优劣性作了简要说明.关键词:数值方法;矩形法;梯形法;抛物线法;类矩形;类梯形Several Numerical Methods for Solving Definite Integrals Abstract:Several common methods for solving definite integrals are summarized in this paper. Meantime, the idea for each method is emphatically analyzed. Afterwards, a numerical example is illustrated to show that the advantages and disadvantages of these methods.Keywords:Numerical methods, Rectangle method, Trapezoidal method, Parabolic method, Class rectangle, Class trapezoid1. 引言在科学研究和实际生产中,经常遇到求积分的计算问题,由积分学知识可知,若函数)(x f 在区间],[b a 连续且原函数为)(x F ,则可用牛顿-莱布尼茨公式求得积分.这个公式不论在理论上还是在解决实际问题中都起到了很大的作用. 在科学研究和实际生产中,经常遇到求积分的计算问题,由积分学知识可知,若函数)(x f 在区间],[b a 连续且原函数为)(x F ,则可用牛顿-莱布尼茨公式求得积分.这个公式不论在理论上还是在解决实际问题中都起到了很大的作用.另外,对于求导数也有一系列的求导公式和求导法则.但是,在实际问题中遇到求积分的计算,经常会有这样的情况:(1)函数)(x f 的原函数无法用初等函数给出.例如积分 dx e x ⎰-102, ⎰10sin dx xx等,从而无法用牛顿-莱布尼茨公式计算出积分。

计算定积分的方法定积分是微积分中的一个重要概念,用来描述曲线下方的面积。
计算定积分的方法通常包括几何法、零散法、换元法和分部积分法等。
一、几何法几何法是通过几何图形的性质计算定积分。
常用的几何法计算定积分的方法有:1. 面积法:将曲线下方的区域分割成许多个简单几何形状,如矩形、三角形等,然后计算每个几何形状的面积,并将所有面积相加得到总面积。
2. 折线法:将曲线下方的区域近似地用折线连接起来,然后计算每段折线的长度,并将所有长度相加得到总长度。
二、零散法零散法是将曲线下方的面积进行分割求和的方法。
常用的零散法计算定积分的方法有:1. 矩形法:将曲线下方的区域分割成若干个矩形,然后计算每个矩形的面积,并将所有面积相加得到总面积。
2. 梯形法:将曲线下方的区域分割成若干个梯形,然后计算每个梯形的面积,并将所有面积相加得到总面积。
3. 辛普森法则:将曲线下方的区域分割成若干个小区间,在每个小区间上使用二次多项式逼近曲线,然后使用辛普森公式进行近似计算。
三、换元法换元法是通过变量替换的方式将复杂的积分转化成简单的积分,从而简化计算。
常用的换元法计算定积分的方法有:1. 对换元法:将被积函数中的自变量替换成新的自变量,通过求出新的积分变量和原积分变量的关系,将原来的积分变量带入进行计算。
2. 三角换元法:将被积函数中的自变量表示成三角函数形式,通过选择合适的三角变换,将原函数转化成更简单的形式进行计算。
四、分部积分法分部积分法是微积分中的一个重要定理,可以将一个积分问题转化为另一个积分问题,从而简化计算。
常用的分部积分法计算定积分的方法有:1. 正比换元法:将被积函数中的一项作为导数,另一项作为原函数,通过求出原函数和导数的关系,将积分变换为另一个积分。
2. 对数换元法:将被积函数中的一项取导数,另一项取倒数,通过求出导数和倒数的关系,将积分变换为另一个积分。
以上是计算定积分的常用方法,通过几何法、零散法、换元法和分部积分法可以解决各种类型的定积分计算问题。

数值分析中的梯形法误差估计技巧数值分析中的梯形法是一种常用的数值积分方法,用于近似计算定积分。
在实际应用中,我们往往需要对梯形法的误差进行估计,以确保计算结果的准确性。
本文将介绍数值分析中的梯形法误差估计技巧。
1. 基本原理梯形法是通过将定积分区间分成若干个小区间,并在每个小区间上应用梯形面积公式来逼近定积分的值。
梯形法的基本原理是利用多项式插值的思想,在每个小区间上用一个二次多项式来逼近被积函数。
因此,梯形法的误差与插值误差有密切关系。
2. 误差估计公式梯形法的误差可以通过以下公式进行估计:\[|E| \leq \frac{(b-a)^3}{12n^2} \max_{a \leq x \leq b} |f''(x)|\]其中,\(E\)为误差,\(a\)和\(b\)为积分区间的上限和下限,\(n\)为分割区间的个数,\(f''(x)\)为被积函数的二阶导数。
3. 误差分析从误差估计公式可知,梯形法的误差与积分区间长度的立方和分割区间数的平方成反比。
因此,我们可以通过减小积分区间长度或增加分割区间数来减小误差。
此外,被积函数的二阶导数在整个积分区间上的最大值也会影响误差的大小,因此在实际应用中需要对被积函数进行适当的选择和分析。
4. 数值实例假设要计算定积分\(\int_{0}^{1} e^{-x^2}dx\),我们可以利用梯形法进行近似计算。
将积分区间\[0,1\]分成n个小区间,应用梯形面积公式计算每个小区间上的定积分值,然后将这些值相加即可得到近似结果。
通过误差估计公式,我们可以对近似结果的准确性进行评估。
5. 总结梯形法是数值分析中常用的积分方法,通过对积分区间进行分割,并利用梯形面积公式来逼近定积分的值。
在实际应用中,我们需要对梯形法的误差进行估计,以保证计算结果的准确性。
通过适当选择积分区间长度、分割区间数和被积函数的二阶导数,我们可以有效地控制误差,提高计算的精确度。
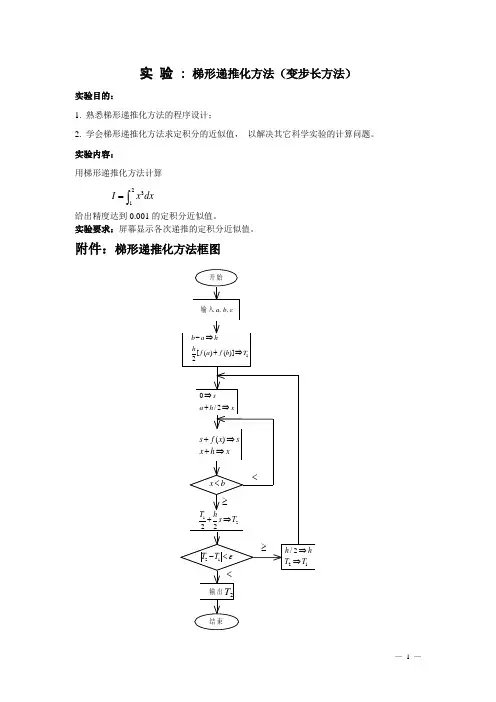
eeeeee计算机软件技术基础(VC)2012年课程设计报告学院 eeeeee 班级 eeeeee 姓名 eeee学号 eeeee 成绩____一、题目:基于梯形法和辛普生法求定积分(36)二、设计思路1、总体设计1)分析程序的功能通过梯形法和辛普生法求定积分,而且可以与理论值进行对比。
2)系统总体结构:该求定积分的程序由两种功能组成,在使用该程序时,必须对功能进行选择(包括功能1和功能2)。
功能1:该功能在每次求定积分时都需要输入下限a和上限b,程序系统默认在该区间[a,b]分成10000份,在进行完计算以后以后,系统会自动提问用户再进行哪何种功能。
该功能共四个步骤。
功能2:该功能在输入一个确定的区间[a,b]时,通过控制分割数n,使分割区间逐渐变小,则两个函数分别通过两种方法的定积分的值逐渐逼近理论值,并且可以与理论值在一定精度内进行比较。
同样,在进行完一次该功能时,系统会自动提问再进行何种功能。
该功能分为三个步骤。
2、各功能模块的设计:说明各功能模块的实现方法1)integralt模块该函数是用梯形法求定积分的通用函数,其参数包括上下限,分割份数,和函数名,其中f为函数指针。
通过主函数传递来的参数,该函数又将这些参数传给f1ti 和f2ti函数,并将f1ti和f2ti函数传来的值再传给主函数。
代码参见integralt函数。
2)integrals模块该函数是用辛普生法求定积分的通用函数,其参数包括上下限,分割份数,和函数名,其中f为函数指针。
通过主函数传递来的参数,该函数又将这些参数传给f1xi和f2xi函数,并将f1xi和f2xi函数传来的值再传给主函数。
代码参见integrals函数。
3)f1ti(其中f2ti,f1xi,f2xi与其类似)模块该函数根据主函数传给integralt函数(或integrals函数)的参数,integralt 函数(或integrals函数)又将参数传给该函数,使该函数获得下限a和上限b和分割数n,再通过梯形法(或辛普生法)计算出定积分的值(该值会随n的逐渐变大而趋近与理论值)。
excel求积函数的使用教程
Excel中的求积函数具体该如何使用呢?接下来是店铺为大家带来的excel 求积函数的使用教程,供大家参考。
excel 求积函数的使用教程:
求积函数使用步骤1:打开Excel表格,随意点击一个单元格作为最后输出乘积的位置,然后在“f(x)”后面输入“=A1*B1”即A1和B1所在单元格的数据相乘,最后按“Enter”即可输出答案。
求积函数使用步骤2:将鼠标放到第一个结果的单元格的右下角出现黑粗体“+”,直接向下拉即可出现其他数据的乘积结果。
求积函数使用步骤3:效果(复制单元格就是复制函数公式,其他的数据都是按这个公式计算):。
变步长梯形求积法计算定积分1.原理:变步长求积法的思想是利用若干小梯形的面积代替原方程的积分,当精度达不到要求时,可以通过增加点数对已有的区间再次划分,达到所需精度时即可;其中由于新的式子中有原来n点中的部分项主要公式:T2n=T n/2+(h/2)*Σf(x k+0.5);2.源程序如下:#include"math.h"#include"iostream.h"double f(double x){double s;s=log(x*x);return(s);}double ffts(double a,double b,double eps){int n,k;double fa,fb,h,t1,p,s,x,t;fa=f(a);fb=f(b);n=1;h=b-a;t1=h*(fa+fb)/2;p=eps+1;while(p>=eps){s=0;for(k=0;k<=n-1;k++){x=a+(k+0.5)*h;s=s+f(x);}t=t1/2+h*s/2;p=fabs(t1-t);cout<<"步长n为:"<<n<<"时的"<<"Tn="<<t1<<'\t'<<"T2n="<<t<<'\t'<<"误差变化:"<<p<<endl;t1=t;n=n*2;h=h/2;}return(t);}void main(){double result,a,b,eps;cout<<"需要求解的积分式为f(x)=log(x^2)"<<endl;cout<<"输入边界值a="<<'\t';cin>>a;cout<<"输入边界值b="<<'\t';cin>>b;cout<<"输入误差限"<<'\t';cin>>eps;result=ffts(a,b,eps);cout<<"经过变步长梯形求积法得方程结果为:"<<result<<endl;}3.运行结果:根据程序提示依次输入积分上限和积分下限,然后输入误差限;本程序需要预先在程序中输入需要积分方程的表达式。
变步长梯形求积法计算定积分1.原理:变步长求积法的思想是利用若干小梯形的面积代替原方程的积分,当精度达不到要求时,可以通过增加点数对已有的区间再次划分,达到所需精度时即可;其中由于新的式子中有原来n点中的部分项主要公式:T2n=T n/2+(h/2)*Σf(x k+0.5);2.源程序如下:#include"math.h"#include"iostream.h"double f(double x){double s;s=log(x*x);return(s);}double ffts(double a,double b,double eps){int n,k;double fa,fb,h,t1,p,s,x,t;fa=f(a);fb=f(b);n=1;h=b-a;t1=h*(fa+fb)/2;p=eps+1;while(p>=eps){s=0;for(k=0;k<=n-1;k++){x=a+(k+0.5)*h;s=s+f(x);}t=t1/2+h*s/2;p=fabs(t1-t);cout<<"步长n为:"<<n<<"时的"<<"Tn="<<t1<<'\t'<<"T2n="<<t<<'\t'<<"误差变化:"<<p<<endl;t1=t;n=n*2;h=h/2;}return(t);}void main(){double result,a,b,eps;cout<<"需要求解的积分式为f(x)=log(x^2)"<<endl;cout<<"输入边界值a="<<'\t';cin>>a;cout<<"输入边界值b="<<'\t';cin>>b;cout<<"输入误差限"<<'\t';cin>>eps;result=ffts(a,b,eps);cout<<"经过变步长梯形求积法得方程结果为:"<<result<<endl;}3.运行结果:根据程序提示依次输入积分上限和积分下限,然后输入误差限;本程序需要预先在程序中输入需要积分方程的表达式。
数值计算方法上机题目3一、计算定积分的近似值:221x e xe dx =⎰ 要求:(1)若用复化梯形公式和复化Simpson 公式计算,要求误差限71021-⨯=ε,分别利用他们的余项估计对每种算法做出步长的事前估计;(2)分别利用复化梯形公式和复化Simpson 公式计算定积分;(3)将计算结果与精确解比较,并比较两种算法的计算量。
1.复化梯形公式程序:程序1(求f (x )的n 阶导数:syms xf=x*exp(x) %定义函数f (x )n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2:clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x),换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))'%因fminbnd()函数求的是表达式的最小值,且要求表达式带引号,故取负号,以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点,也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示:用复化梯形算法计算的结果Tn= 7.3891等分数n=7019已知值与计算值的误差R= 2.8300e-0082. Simpson公式程序:程序1:(求f(x)的n阶导数):syms xf=x*exp(x) %定义函数f(x)n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2:clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x),换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数,输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd()函数求的是表达式的最小值,且要求表达式带引号,故取负号,一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点,也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值,故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示:用Simpson公式计算的结果Sn= 7.3891等分数n=24已知值与计算值的误差R= 2.7284e-008用复化梯形公式计算的结果为:7.3891,与精确解的误差为:2.8300e-008。