第9章 回归方程的函数形式

编号032 §9.1.2 线性回归方程目标要求1、结合具体实例，了解一元线性回归模型的含义．2、结合具体实例，了解模型参数的统计意义．3、结合具体实例，了解最小二乘原理，掌握一元线性回归模型参数的最小二乘估计方法．4、结合具体实例，会使用相关的统计软件．5、针对实际问题，会用一元线性回归模型进行预测．学科素养目标本章内容是在学生已经学习过必修课程中的统计知识和概率知识的基础上，通过对典型案例的研究，了解和使用一些常用统计分析方法，进一步体会运用统计方法解决实际问题的基本思想，认识统计方法在决策中的作用，从而形成运用统计的观点认识客观事物的习惯．在本章教学中，应突出对学生应用意识的培养，不能只限于要求学生会解书本上的习题，还要关注学生应用与解决实际问题的能力．应引导、鼓励学生从现实生活中发现问题，并能自觉地运用所学的统计方法加以理解，应尽量给学生提供一定的实践活动机会，可结合数学建模活动，选择一个案例，要求学生亲自实践．重点难点重点：一元线性回归模型参数的最小二乘估计方法； 难点：用一元线性回归模型进行预测．教学过程基础知识点 1．线性回归模型我们将y ＝___________称为线性回归模型． 2．线性回归方程与最小二乘法(1)线性回归方程：直线＝__________称为线性回归方程．其中__称为回归截距，__称为回归系数，__称为回归值． (2)，的计算公式＝∑i ＝1n（x i －x）（y i －y ）∑i ＝1n（x i －x ）2＝________________ ，＝______________.【课前小题演练】题1．关于回归分析，下列说法错误的是( ) A ．回归分析是研究两个具有相关关系的变量的方法 B ．散点图中，解释变量在x 轴，响应变量在y 轴 C ．回归模型中一定存在随机误差 D ．散点图能明确反映变量间的关系题2．根据如下样本数据：x2 3 4 5 6Y 4 2.5 －0.5 －2 －3得到的经验回归方程为＝x＋，则( )A．＞0，＞0 B．＞0，＜0C．＜0，＞0 D．＜0，＜0题3．已知变量x，Y之间具有线性相关关系，其散点图如图所示，则其经验回归方程可能为( )A．＝1.5x＋2 B．＝－1.5x＋2C．＝1.5x－2 D．＝－1.5x－2题4．若某地财政收入x与支出Y满足经验回归方程＝x＋＋e i(单位：亿元)(i＝1，2，…)，其中＝0.8，＝2，|e i|<0.5，如果今年该地区财政收入10亿元，年支出预计不会超过( )A．10亿元B．9亿元C．10.5亿元D．9.5亿元题5．若施肥量x(kg)与水稻产量Y(kg)的经验回归方程为＝5x＋250，当施肥量为80 kg时，预计水稻产量约为________kg.题6．某种产品的广告费用支出x与销售额Y(单位：百万元)之间有如下的对应数据：x/百万元 2 4 5 6 8Y/百万元30 40 60 50 70(1)画出散点图；(2)求经验回归方程；(3)试预测广告费用支出为10百万元时，销售额多大？【当堂巩固训练】题7．已知x，y的取值如表所示：x234 5y 2.2 3.8 5.5m若y与x线性相关，且回归直线方程为＝1.46x－0.61，则表格中实数m的值为( )A．7.69 B．7.5 C．6.69 D．6.5题8．某药厂为了了解某新药的销售情况，将2019年2至6月份的销售额整理如下：月份 2 3 4 5 6 销售额(万元)1925353742根据2至6月份的数据可求得每月的销售额y 关于月份x 的线性回归方程＝x ＋为( )(参考公式及数据：＝∑i ＝1nx i y i －n x y∑i ＝1n x 2i －n （x ）2，＝y －x ，∑i ＝15x i y i ＝690，∑i ＝15x 2i ＝90)A ．＝5.8x ＋8.4B ．＝8.4x ＋5.8C ．＝6x －9D ．＝4x ＋31.6题9．登山族为了了解某山高y (km )与气温x (℃)之间的关系，随机统计了4次山高与相应的气温，并制作了对照表：气温x (℃) 18 13 10 －1 山高y (km )24343864由表中数据，得到线性回归方程＝－2x ＋()∈R ，由此请估计出山高为72(km )处气温的度数为( )A ．－10B ．－8C ．－4D ．－6题10．根据如下的样本数据：x 1 2 3 y2.133.9得到的回归方程为＝bx ＋a ，则直线ax ＋by －3＝0经过定点( ) A ．(－1，－2) B ．(－1，2) C ．(1，－2)D ．(1，2)题11．某同学在研究学习中，收集到某制药厂今年5个月甲胶囊生产产量(单位：万盒)的数据如表所示：x (月份) 1 2 3 4 5 y (万盒)55668若x ，y 线性相关，线性回归方程为＝0.7x ＋，则以下为真命题的是( ) A ．x 每增加1个单位长度，则y 一定增加0.7个单位长度 B ．x 每增加1个单位长度，则y 必减少0.7个单位长度C．当x＝6时，y的预测值为8.1万盒D．线性回归直线＝0.7x ＋经过点(2，6)题12．下列说法：①设有一个回归方程＝3－5x，变量x增加一个单位时，y平均增加5个单位；②线性回归方程＝x＋必过()x，y；③设某地女儿身高y对母亲身高x的一个回归直线方程是＝34.92＋0.78x，则方程中的＝34.92可以解释为女儿身高不受母亲身高变化影响的部分．其中正确的个数是( )A．0 B．1 C．2 D．3题13．(多选题．．．)两个相关变量x，y的5组对应数据如表：x8.3 8.6 9.9 11.1 12.1y 5.9 7.8 8.1 8.4 9.8根据表格，可得回归直线方程＝x＋，求得＝0.78.据此估计，以下结论正确的是( )A．x＝10 B．y＝9C．＝0.2 D．当x＝15时，＝11.95题14．(多选题．．．)已知x与y之间的几组数据如表：x 1 2 3 4 5 6y0 2 1 3 3 4假设根据表格数据所得线性回归直线方程为＝x＋，若某同学根据上表中的前两组数据()1，0和()2，2求得的直线方程为y＝b′x＋a′，则以下结论正确的是( )参考公式：＝∑i＝1nx i y i－n x y∑i＝1nx2i－n（x）2，＝y－b x .A．a′＝－2 B．b′＝2 C．>b′ D．>a′【综合突破拔高】题15．对于指数曲线y＝ae bx，令U＝ln y，c＝ln a，经过非线性回归分析后，可转化的形式为( ) A．U＝c＋bx B．U＝b＋cxC．y＝c＋bx D．y＝b＋cx题16．若一函数模型为y ＝sin 2α＋2sinα＋1，为将y 转化为t 的经验回归方程，则需作变换t 等于( ) A ．sin 2αB ．(sinα＋1)2C ．⎝ ⎛⎭⎪⎫sin α＋12 2D ．以上都不对题17．在生物学上，有隔代遗传的现象．已知某数学老师的体重为62 kg ，他的曾祖父、祖父、父亲、儿子的体重分别为58 kg 、64 kg 、58 kg 、60 kg .如果体重是隔代遗传，且呈线性相关，根据以上数据可得解释变量x 与预报变量的回归方程为＝x ＋，其中＝0.5，据此模型预测他的孙子的体重约为( ) A ．58 kgB ．61 kgC ．65 kgD ．68 kg题18．(多选题．．．)月亮公转与自转的周期大约为30天，阴历是以月相变化为依据．人们根据长时间的观测，统计了月亮出来的时间y (简称“月出时间”，单位：小时)与天数x (x 为阴历日数，x ∈N *，且0≤x ≤30)的有关数据，如表，并且根据表中数据，求得y 关于x 的线性回归方程为＝0.8x ＋．x 2 4 7 10 15 22 y8.19.41214.418.524其中，阴历22日是分界线，从阴历22日开始月亮就要到第二天(即23日0：00)才升起．则( ) A ．样本点的中心为()10，14.4 B ．＝6.8C ．预报月出时间为16时的那天是阴历13日D ．预报阴历27日的月出时间为阴历28日早上4：00题19．对某台机器购置后的运行年限x (x ＝1，2，3，…)与当年利润Y 的统计分析知x ，Y 具备线性相关关系，经验回归方程为＝10.47－1.3x ，估计该台机器最为划算的使用年限为______年．题20．以模型y ＝ce kx 去拟合一组数据时，为了求出非经验回归方程，设z ＝ln y ，其变换后得到经验回归方程＝0.3x ＋4，则c ＝________.题21．为了响应中央号召，某日深圳环保局随机抽查了本市市区汽车尾气排放污染物x (单位：ppm )与当天私家车路上行驶的时间y (单位：小时)之间的关系，从某主干路随机抽取10辆私家车，已知x 与y 之间具有线性相关关系，其回归直线方程为＝0.3x －0.4，若该10辆车中有一辆私家车的尾气排放污染物为6(单位：ppm )，据此估计该私家车行驶的时间为________小时．题22．某市农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月4日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下数据：日期 12月1日12月2日12月3日12月4日温差 11 13 12 8 发芽数(颗)26322617根据表中12月1日至12月3日的数据，求得线性回归方程＝x ＋中的＝－8，则求得的＝________；若用12月4日的数据进行检验，检验方法如下：先用求得的线性回归方程计算发芽数，再求与实际发芽数的差，若差值的绝对值不超过2颗，则认为得到的线性回归方程是可靠的，则求得的线性回归方程________(填“可靠”或“不可靠”).题23．如表为收集到的一组数据：x 21 23 25 27 29 32 35 Y711212466115325试建立Y 与x 之间的回归方程．题24．宿州市公安局交警支队依据《中华人民共和国道路交通安全法》第90条规定：所有主干道路凡机动车途经十字路口或斑马线，无论转弯或者直行，遇有行人过马路，必须礼让行人，违反者将被处以100元罚款，记3分的行政处罚．如表是本市一主干路段监控设备所抓拍的5个月内，机动车驾驶员“不礼让行人”行为统计数据：月份x 1 2 3 4 5 违章驾驶员人数y1151101009085(1)若x 与y 之间具有很强的线性相关关系，请利用所给数据求违章驾驶员人数y 与月份x 之间的回归直线方程＝x ＋；(2)预测该路段8月份的“不礼让行人”违章驾驶员的人数．参考公式：＝∑i ＝1nx i y i －n x ·y∑i ＝1nx 2i －n （x）2，＝y －x ，参考数据：∑i ＝15x i y i ＝1 420.编号032 §9.1.2 线性回归方程目标要求1、结合具体实例，了解一元线性回归模型的含义．2、结合具体实例，了解模型参数的统计意义．3、结合具体实例，了解最小二乘原理，掌握一元线性回归模型参数的最小二乘估计方法．4、结合具体实例，会使用相关的统计软件．5、针对实际问题，会用一元线性回归模型进行预测．学科素养目标本章内容是在学生已经学习过必修课程中的统计知识和概率知识的基础上，通过对典型案例的研究，了解和使用一些常用统计分析方法，进一步体会运用统计方法解决实际问题的基本思想，认识统计方法在决策中的作用，从而形成运用统计的观点认识客观事物的习惯．在本章教学中，应突出对学生应用意识的培养，不能只限于要求学生会解书本上的习题，还要关注学生应用与解决实际问题的能力．应引导、鼓励学生从现实生活中发现问题，并能自觉地运用所学的统计方法加以理解，应尽量给学生提供一定的实践活动机会，可结合数学建模活动，选择一个案例，要求学生亲自实践．重点难点重点：一元线性回归模型参数的最小二乘估计方法； 难点：用一元线性回归模型进行预测．教学过程基础知识点 1．线性回归模型我们将y ＝a ＋bx ＋ε称为线性回归模型． 2．线性回归方程与最小二乘法(1)线性回归方程：直线＝＋x 称为线性回归方程．其中称为回归截距，称为回归系数，称为回归值．(2)，的计算公式＝∑i ＝1n（x i －x ）（y i －y ）∑i ＝1n（x i －x ）2＝___∑i ＝1nx i y i －n x y∑i ＝1nx 2i －n （x）2___ ，＝__y －x __.【课前小题演练】题1．关于回归分析，下列说法错误的是( ) A ．回归分析是研究两个具有相关关系的变量的方法 B ．散点图中，解释变量在x 轴，响应变量在y 轴 C ．回归模型中一定存在随机误差 D ．散点图能明确反映变量间的关系【解析】选D .用散点图反映两个变量间的关系时，存在误差． 题2．根据如下样本数据：x 2 3 4 5 6Y 4 2.5 －0.5 －2 －3得到的经验回归方程为＝x＋，则( )A．＞0，＞0 B．＞0，＜0C．＜0，＞0 D．＜0，＜0【解析】选B.由题干表中的数据可得，变量Y随着x的增大而减小，则＜0，又回归方程为＝x＋经过(2，4)，(3，2.5)，可得＞0.题3．已知变量x，Y之间具有线性相关关系，其散点图如图所示，则其经验回归方程可能为( )A．＝1.5x＋2 B．＝－1.5x＋2C．＝1.5x－2 D．＝－1.5x－2【解析】选B.设经验回归方程为＝x＋，由题干中散点图可知变量x，Y之间负相关，经验回归直线在Y轴上的截距为正数，所以<0，>0，因此方程可能为＝－1.5x＋2.题4．若某地财政收入x与支出Y满足经验回归方程＝x＋＋e i(单位：亿元)(i＝1，2，…)，其中＝0.8，＝2，|e i|<0.5，如果今年该地区财政收入10亿元，年支出预计不会超过( )A．10亿元B．9亿元C．10.5亿元D．9.5亿元【解析】选C.＝0.8×10＋2＋e i＝10＋e i，因为|e i|<0.5，所以9.5＜<10.5.题5．若施肥量x(kg)与水稻产量Y(kg)的经验回归方程为＝5x＋250，当施肥量为80 kg时，预计水稻产量约为________kg.【解析】把x＝80代入经验回归方程可得其预测值＝5×80＋250＝650(kg).答案：650题6．某种产品的广告费用支出x与销售额Y(单位：百万元)之间有如下的对应数据：x/百万元 2 4 5 6 8Y/百万元30 40 60 50 70(1)画出散点图；(2)求经验回归方程；(3)试预测广告费用支出为10百万元时，销售额多大？【解析】(1)散点图如图所示：(2)列出下表，并用科学计算器进行有关计算：i 1 2 3 4 5 合计 x i 2 4 5 6 8 25 y i 30 40 60 50 70 250 x i y i 60 160 300 300 560 1 380 x 2i416253664145所以x ＝255 ＝5，y ＝2505＝50，∑i ＝15x 2i ＝145，∑i ＝15x i y i ＝1 380.于是可得＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5x 2＝1 380－5×5×50145－52×5＝6.5，＝y －x ＝50－6.5×5＝17.5. 所以所求的经验回归方程为＝6.5x ＋17.5.(3)根据上面求得的经验回归方程，当广告费用支出为 10百万元时，＝6.5×10＋17.5＝82.5(百万元)，即广告费用支出为10百万元时，销售额大约为82.5百万元． 【当堂巩固训练】题7．已知x ，y 的取值如表所示：x 2 3 4 5 y2.23.85.5m若y 与x 线性相关，且回归直线方程为＝1.46x －0.61，则表格中实数m 的值为( ) A ．7.69 B ．7.5 C ．6.69 D ．6.5 【解析】选D .因为x ＝2＋3＋4＋54 ＝72， y ＝2.2＋3.8＋5.5＋m 4 ＝11.5＋m 4，所以11.5＋m 4 ＝1.46×72－0.61，解得m ＝6.5.题8．某药厂为了了解某新药的销售情况，将2019年2至6月份的销售额整理如下：月份 2 3 4 5 6 销售额(万元)1925353742根据2至6月份的数据可求得每月的销售额y 关于月份x 的线性回归方程＝x ＋为( )(参考公式及数据：＝∑i ＝1nx i y i －n x y∑i ＝1n x 2i －n （x ）2，＝y －x ，∑i ＝15x i y i ＝690，∑i ＝15x 2i ＝90)A ．＝5.8x ＋8.4B ．＝8.4x ＋5.8C ．＝6x －9D ．＝4x ＋31.6【解析】选A .由表格中的数据得x ＝2＋3＋4＋5＋65＝4，y ＝19＋25＋35＋37＋425＝31.6，所以＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5（x）2＝690－5×4×31.690－5×42＝5.8， ＝31.6－5.8×4＝8.4，因此，y 关于x 的线性回归方程为＝5.8x ＋8.4.题9．登山族为了了解某山高y (km )与气温x (℃)之间的关系，随机统计了4次山高与相应的气温，并制作了对照表：气温x (℃) 18 13 10 －1 山高y (km )24343864由表中数据，得到线性回归方程＝－2x ＋()∈R ，由此请估计出山高为72(km )处气温的度数为( )A ．－10B ．－8C ．－4D ．－6【解析】选D .由题意可得x ＝10，y ＝40，所以＝y ＋2x ＝40＋2×10＝60.所以＝－2x ＋60，当＝72时，有－2x ＋60＝72，解得x ＝－6. 题10．根据如下的样本数据：x 1 2 3 y2.133.9得到的回归方程为＝bx ＋a ，则直线ax ＋by －3＝0经过定点( ) A ．(－1，－2)B ．(－1，2)C ．(1，－2)D ．(1，2)【解析】选D .由所给数据得x ＝2，y ＝3，3i 1=∑(x i －x )(y i －y )＝1.8，3i 1=∑(x i －x )2＝2，所以b ＝0.9，a ＝3－0.9×2＝1.2，所以直线ax ＋by －3＝0方程为1.2x ＋0.9y －3＝0，过点(1，2). 题11．某同学在研究学习中，收集到某制药厂今年5个月甲胶囊生产产量(单位：万盒)的数据如表所示：x (月份) 1 2 3 4 5 y (万盒)55668若x ，y 线性相关，线性回归方程为＝0.7x ＋，则以下为真命题的是( ) A ．x 每增加1个单位长度，则y 一定增加0.7个单位长度 B ．x 每增加1个单位长度，则y 必减少0.7个单位长度 C ．当x ＝6时，y 的预测值为8.1万盒 D ．线性回归直线＝0.7x ＋经过点(2，6)【解析】选C .由＝0.7x ＋，得x 每增(减)一个单位长度，y 不一定增加(减少)0.7，而是大约增加(减少)0.7个单位长度，故选项A ，B 错误；由已知表中的数据，可知x ＝1＋2＋3＋4＝55 ＝3，y ＝5＋5＋6＋6＋85＝6，则回归直线必过点(3，6)，故D 错误；将(3，6)代入回归直线＝0.7x ＋，解得＝3.9，即＝0.7x ＋3.9，令x ＝6，解得＝0.7×6＋3.9＝8.1万盒． 题12．下列说法：①设有一个回归方程＝3－5x ，变量x 增加一个单位时，y 平均增加5个单位； ②线性回归方程＝x ＋必过()x ，y ；③设某地女儿身高y 对母亲身高x 的一个回归直线方程是＝34.92＋0.78x ，则方程中的＝34.92可以解释为女儿身高不受母亲身高变化影响的部分． 其中正确的个数是( ) A ．0 B ．1 C ．2 D ．3【解析】选C .设有一个回归方程＝3－5x ，变量x 增加一个单位时，y 平均减少5个单位，故①错；线性回归方程＝x ＋必过样本中心点()x ，y ，故②正确；设某地女儿身高y 对母亲身高x 的一个回归直线方程是＝34.92＋0.78x ，当x ＝0时，＝34.92， 方程中的＝34.92可以解释为女儿身高不受母亲身高变化影响的部分，故③正确． 题13．(多选题．．．)两个相关变量x ，y 的5组对应数据如表：x 8.3 8.6 9.9 11.1 12.1 y5.97.88.18.49.8根据表格，可得回归直线方程＝x ＋，求得＝0.78.据此估计，以下结论正确的是( )A ．x ＝10B ．y ＝9C ．＝0.2D ．当x ＝15时，＝11.95【解析】选AC .易求得x ＝10，y ＝8⇒＝y －x ＝8－0.78×10＝0.2，所以＝0.78x ＋0.2. x ＝15⇒＝0.78×15＋0.2＝11.90.题14．(多选题．．．)已知x 与y 之间的几组数据如表：x 1 2 3 4 5 6 y21334假设根据表格数据所得线性回归直线方程为＝x ＋，若某同学根据上表中的前两组数据()1，0 和()2，2 求得的直线方程为y ＝b ′x ＋a ′，则以下结论正确的是()参考公式：＝∑i ＝1nx i y i －n x y∑i ＝1nx 2i －n （x）2，＝y －b x . A ．a ′＝－2 B ．b ′＝2 C ．>b ′ D ．>a ′【解析】选ABD .因为某同学根据前两组数据()1，0 和()2，2 求得的直线方程为y ＝b ′x ＋a ′，所以b ′＝2，a ′＝－2，根据题意得：x ＝3.5，y ＝136，∑i ＝16x i y i ＝0＋4＋3＋12＋15＋24＝58，∑i ＝16x 2i ＝1＋4＋9＋16＋25＋36＝91，所以＝∑i ＝16x i y i －6x y∑i ＝16x 2i －6（x）2＝57 ，＝y －x ＝136 －57 ×72 ＝－13 ，所以<b ′，>a ′. 【综合突破拔高】题15．对于指数曲线y ＝ae bx ，令U ＝ln y ，c ＝ln a ，经过非线性回归分析后，可转化的形式为( ) A ．U ＝c ＋bx B ．U ＝b ＋cx C ．y ＝c ＋bxD ．y ＝b ＋cx【解析】选A .由y ＝ae bx 得ln y ＝ln (ae bx )， 所以ln y ＝ln a ＋ln e bx ，所以ln y ＝ln a ＋bx ，所以U ＝c ＋bx .题16．若一函数模型为y ＝sin 2α＋2sinα＋1，为将y 转化为t 的经验回归方程，则需作变换t 等于( ) A ．sin 2αB ．(sinα＋1)2C ．⎝⎛⎭⎪⎫sin α＋12 2D ．以上都不对 【解析】选B .因为y 是关于t 的经验回归方程，实际上就是y 是关于t 的一次函数，又因为y ＝(sin α＋1)2，若令t ＝(sin α＋1)2，则可得y 与t 的函数关系式为y ＝t ，此时变量y 与变量t 是线性相关关系． 题17．在生物学上，有隔代遗传的现象．已知某数学老师的体重为62 kg ，他的曾祖父、祖父、父亲、儿子的体重分别为58 kg 、64 kg 、58 kg 、60 kg .如果体重是隔代遗传，且呈线性相关，根据以上数据可得解释变量x 与预报变量的回归方程为＝x ＋，其中＝0.5，据此模型预测他的孙子的体重约为( ) A ．58 kgB ．61 kgC ．65 kgD ．68 kg【解析】选B .由于体重是隔代遗传，且呈线性相关， 则取数据(58，58)，(64，62)，(58，60)，得x ＝58＋64＋583 ＝60，y ＝58＋62＋603 ＝60，即样本点的中心为(60，60)，代入＝x ＋， 得＝60－0.5×60＝30，则＝0.5x ＋30， 取x ＝62，可得＝0.5×62＋30＝61 kg . 故预测他的孙子的体重约为61 kg .题18．(多选题．．．)月亮公转与自转的周期大约为30天，阴历是以月相变化为依据．人们根据长时间的观测，统计了月亮出来的时间y (简称“月出时间”，单位：小时)与天数x (x 为阴历日数，x ∈N *，且0≤x ≤30)的有关数据，如表，并且根据表中数据，求得y 关于x 的线性回归方程为＝0.8x ＋．x 2 4 710 15 22 y8.19.41214.418.524其中，阴历22日是分界线，从阴历22日开始月亮就要到第二天(即23日0：00)才升起．则( ) A ．样本点的中心为()10，14.4 B ．＝6.8C ．预报月出时间为16时的那天是阴历13日D ．预报阴历27日的月出时间为阴历28日早上4：00 【解析】选AD .x ＝2＋4＋7＋10＋15＋226＝10，y ＝8.1＋9.4＋12＋14.4＋18.5＋246＝14.4，故样本点的中心为()10，14.4 ，选项A 正确；将样本点的中心()10，14.4 代入＝0.8x ＋得＝6.4，故选项B 错误；因为＝0.8x ＋6.4，当y ＝16时，求得x ＝12，月出时间为阴历12日，选项C 错误；因为阴历27日时，即x ＝27，代入＝0.8×27＋6.4＝28，日出时间应该为28日早上4：00，选项D 正确． 题19．对某台机器购置后的运行年限x (x ＝1，2，3，…)与当年利润Y 的统计分析知x ，Y 具备线性相关关系，经验回归方程为＝10.47－1.3x ，估计该台机器最为划算的使用年限为______年． 【解析】当年利润小于或等于零时应该报废该机器， 当y ＝0时，令10.47－1.3x ＝0，解得x ≈8， 故估计该台机器最为划算的使用年限为8年． 答案：8题20．以模型y ＝ce kx 去拟合一组数据时，为了求出非经验回归方程，设z ＝ln y ，其变换后得到经验回归方程＝0.3x ＋4，则c ＝________. 【解析】由题意，得ln (ce kx )＝0.3x ＋4，所以ln c ＋kx ＝0.3x ＋4，所以ln c ＝4，所以c ＝e 4. 答案：e 4题21．为了响应中央号召，某日深圳环保局随机抽查了本市市区汽车尾气排放污染物x (单位：ppm )与当天私家车路上行驶的时间y (单位：小时)之间的关系，从某主干路随机抽取10辆私家车，已知x 与y 之间具有线性相关关系，其回归直线方程为＝0.3x －0.4，若该10辆车中有一辆私家车的尾气排放污染物为6(单位：ppm )，据此估计该私家车行驶的时间为________小时．【解析】由＝0.3x －0.4，令x ＝6，代入可得＝0.3×6－0.4＝1.4.所以估计该私家车行驶的时间为1.4小时． 答案：1.4题22．某市农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月4日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下数据：日期 12月1日 12月2日12月3日12月4日温差 11 13 12 8 发芽数(颗)26322617根据表中12月1日至12月3日的数据，求得线性回归方程＝x ＋中的＝－8，则求得的＝________；若用12月4日的数据进行检验，检验方法如下：先用求得的线性回归方程计算发芽数，再求与实际发芽数的差，若差值的绝对值不超过2颗，则认为得到的线性回归方程是可靠的，则求得的线性回归方程________(填“可靠”或“不可靠”).【解析】由题得x ＝11＋13＋123 ＝12，y ＝26＋32＋263 ＝28，所以样本中心点为(12，28)，所以28＝×12－8，所以＝3；因为＝3x －8，所以12月4日的估计值为＝3×8－8＝16，又|17－16|＝1，没有超过2，所以求得的线性回归方程可靠． 答案：3 可靠题23．如表为收集到的一组数据：x 21 23 25 27 29 32 35 Y711212466115325试建立Y 与x【解析】作出散点图，如图．从散点图中可以看出x 与Y 不具有线性相关关系，根据已有知识可以发现样本点分布在某一条指数函数曲线的周围．令Z ＝ln Y ，则变换后的样本点分布在直线＝x ＋的周围，这样就可以利用线性经验回归模型来建立非线性经验回归方程了，数据可以转化为：x 21 232527 29 32 35 Z1.9462.3983.0453.1784.1904.7455.784求得经验回归方程为＝0.272x －3.849， 所以＝e0.272x －3.849.题24．宿州市公安局交警支队依据《中华人民共和国道路交通安全法》第90条规定：所有主干道路凡机动车途经十字路口或斑马线，无论转弯或者直行，遇有行人过马路，必须礼让行人，违反者将被处以100元罚款，记3分的行政处罚．如表是本市一主干路段监控设备所抓拍的5个月内，机动车驾驶员“不礼让行人”行为统计数据：月份x 1 2 3 45 违章驾驶员人数y1151101009085(1)若x 与y 之间具有很强的线性相关关系，请利用所给数据求违章驾驶员人数y 与月份x 之间的回归直线方程＝x ＋；(2)预测该路段8月份的“不礼让行人”违章驾驶员的人数．参考公式：＝∑i ＝1nx i y i －n x ·y∑i ＝1nx 2i －n （x）2，＝y －x ，参考数据：∑i ＝15x i y i ＝1 420.【解析】(1)由表中数据得：x ＝15()1＋2＋3＋4＋5 ＝3，y ＝15()115＋110＋100＋90＋85 ＝100，＝∑i ＝15x i y i－5x·y∑i＝15x2i－5（x）2＝1 420－5×3×10055－45＝－8，＝y－x＝100＋8×3＝124.所以y与x之间的回归直线方程为＝－8x＋124；(2)由(1)得，＝－8x＋124，令x＝8，得＝－8×8＋124＝60，预测该路段8月份的“不礼让行人”违章驾驶员人数为60人．。

第9章 非线性回归9.1 在非线性回归线性化时，对因变量作变换应注意什么问题？答：在对非线性回归模型线性化时，对因变量作变换时不仅要注意回归函数的形式， 还要注意误差项的形式。

如：(1) 乘性误差项，模型形式为e y AK L αβε=， (2) 加性误差项，模型形式为y AK L αβε=+。

对乘法误差项模型（1）可通过两边取对数转化成线性模型，（2）不能线性化。

一般总是假定非线性模型误差项的形式就是能够使回归模型线性化的形式，为了方便通常省去误差项，仅考虑回归函数的形式。

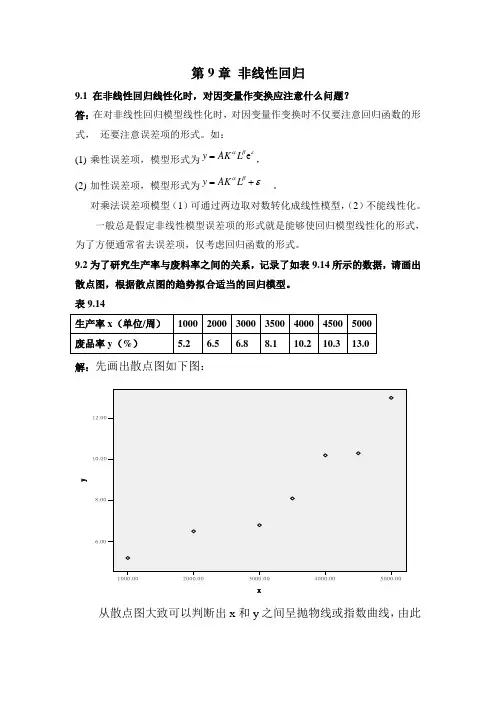
9.2为了研究生产率与废料率之间的关系，记录了如表9.14所示的数据，请画出散点图，根据散点图的趋势拟合适当的回归模型。

表9.14生产率x （单位/周） 1000 2000 3000 3500 4000 4500 5000 废品率y （%）5.26.56.88.110.2 10.3 13.0解：先画出散点图如下图：5000.004000.003000.002000.001000.00x12.0010.008.006.00y从散点图大致可以判断出x 和y 之间呈抛物线或指数曲线，由此采用二次方程式和指数函数进行曲线回归。

（1）二次曲线 SPSS 输出结果如下：Mode l Sum mary.981.962.942.651R R SquareAdjusted R SquareStd. E rror of the E stim ateThe independent variable is x.ANOVA42.571221.28650.160.0011.6974.42444.2696Regression Residual TotalSum of Squares dfMean SquareF Sig.The independent variable is x.Coe fficients-.001.001-.449-.891.4234.47E -007.0001.4172.812.0485.843 1.3244.414.012x x ** 2(Constant)B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.从上表可以得到回归方程为：72ˆ 5.8430.087 4.4710yx x -=-+⨯ 由x 的系数检验P 值大于0.05，得到x 的系数未通过显著性检验。

第九章相关与回归一．判断题部分题目1：负相关指的是因素标志与结果标志的数量变动方向是下降的。

（）答案：×题目2：相关系数为+1时，说明两变量完全相关；相关系数为-1时，说明两个变量不相关。

（）答案：√题目3：只有当相关系数接近+1时，才能说明两变量之间存在高度相关关系。

（）答案：×题目4：若变量x的值增加时，变量y的值也增加，说明x与y之间存在正相关关系；若变量x的值减少时，y变量的值也减少，说明x与y之间存在负相关关系。

（）答案：×题目5：回归系数和相关系数都可以用来判断现象之间相关的密切程度。

（）答案：×题目6：根据建立的直线回归方程，不能判断出两个变量之间相关的密切程度。

（）答案：√题目7：回归系数既可以用来判断两个变量相关的方向，也可以用来说明两个变量相关的密切程度。

（）答案：×题目8：在任何相关条件下，都可以用相关系数说明变量之间相关的密切程度。

（）答案：×题目9：产品产量随生产用固定资产价值的减少而减少，说明两个变量之间存在正相关关系。

（）答案：√题目10：计算相关系数的两个变量，要求一个是随机变量，另一个是可控制的量。

（）答案：×题目11：完全相关即是函数关系，其相关系数为±1。

（）答案：√题目12：估计标准误是说明回归方程代表性大小的统计分析指标，指标数值越大，说明回归方程的代表性越高。

（）答案×二．单项选择题部分题目1：当自变量的数值确定后，因变量的数值也随之完全确定，这种关系属于（）。

A.相关关系B.函数关系C.回归关系D.随机关系答案：B题目2：现象之间的相互关系可以归纳为两种类型，即（）。

A.相关关系和函数关系B.相关关系和因果关系C.相关关系和随机关系D.函数关系和因果关系答案：A题目3：在相关分析中，要求相关的两变量（）。

A.都是随机的B.都不是随机变量C.因变量是随机变量D.自变量是随机变量答案：A题目4：测定变量之间相关密切程度的指标是（）。

第9章相关与回归分析【教学内容】相关分析与回归分析是两种既有区别又有联系的统计分析方法。

本章阐述了相关关系的概念与特点;相关关系与函数关系的区别与联系;相关关系的种类;相关关系的测定方法(直线相关系数的含义、计算方法与运用);回归分析的概念与特点;回归直线方程的求解及其精确度的评价;估计标准误差的计算。

【教学目标】1、了解相关与回归分析的概念、特点和相关分析与回归分析的区别与联系；2、掌握相关分析的定性和定量分析方法；3、掌握回归模型的拟合方法、对回归方程拟合精度的测定和评价的方法。

【教学重、难点】1、相关分析与回归分析的概念、特点、区别与联系；2、相关与回归分析的有关计算公式和应用条件。

第一节相关分析的一般问题一、相关关系的概念与特点（一）相关关系的概念在自然界与人类社会中,许多现象之间是相互联系、相互制约的,表现在数量上也存在着一定的联系。

这种数量上的联系和关系究其实质,可以概括为两种不同类型,即函数关系与相关关系。

相关关系:是指现象之间客观存在的,在数量变化上受随机因素的影响,非确定性的相互依存关系。

例如,商品销售额与流通费用率之间的关系就是一种相关关系。

（二）相关关系的特点1、相关关系表现为数量相互依存关系。

2、相关关系在数量上表现为非确定性的相互依存关系。

二、相关关系的种类1、相关关系按变量的多少,可分为单相关和复相关2、相关关系从表现形态上划分,可分为直线相关和曲线相关3、相关关系从变动方向上划分,可分为正相关和负相关4、按相关的密切程度分,可分为完全相关、不完全相关和不相关三、相关分析的内容相关分析是对客观社会经济现象间存在的相关关系进行分析研究的一种统计方法。

其目的在于对现象间所存在的依存关系及其所表现出的规律性进行数量上的推断和认识,以便为回归分析提供依据。

相关分析的内容和程序是:(1)判别现象间有无相关关系(2)判定相关关系的表现形态和密切程度第二节相关关系的判断与分析一、相关关系的一般判断（一）定性分析对现象进行定性分析,就是根据现象之间的本质联系和质的规定性,运用理论知识、专业知识、实际经验来进行判断和分析。

第九章相关与回归分析习题一、单选题1．下面的函数关系是（）。

A、销售人员测验成绩与销售额大小的关系B、圆周的长度决定于它的半径C、家庭的收入和消费的关系D、数学成绩与统计学成绩的关系2．若要证明两变量之间线性相关程度是高的，则计算出的相关系数应接近于（）。

A、+1B、0C、0.5D、+1或-13．回归系数和相关系数的符号是一致的，其符号均可用来判断现象（）。

A、线性相关还是非线性相关B、正相关还是负相关C、完全相关还是不完全相关D、单相关还是复相关4．在线性相关的条件下，自变量的均方差为2，因变量均方差为5，而相关系数为0.8时，则其回归系数为( )。

A、8B、0.32C、2D、12.55．下面现象间的关系属于相关关系的是（）。

A、圆的周长和它的半径之间的关系B、价格不变条件下,商品销售额与销售量之间的关系C、家庭收入愈多,其消费支出也有增长的趋势D、正方形面积和它的边长之间的关系6．下列关系中，属于正相关关系的是（）。

A、合理限度内，施肥量和平均单产量之间的关系B、产品产量与单位产品成本之间的关系C、商品的流通费用与销售利润之间的关系D、流通费用率与商品销售量之间的关系7．相关分析是研究（）。

A、变量之间的数量关系B、变量之间的变动关系C、变量之间的相互关系的密切程度D、变量之间的因果关系8．在回归直线y=a+bx中，b<0，则x与y之间的相关系数( )。

A、r=0B、r=lC、0<r<1D、-1<r<09．在回归直线y=a+bx中，b表示（）。

A、当x增加一个单位时，y增加a的数量B、当y增加一个单位时，x增加b的数量C、当x增加一个单位时，y的平均增加量D、当y增加一个单位时，x的平均增加量10．当相关系数r=0时，表明（）。

A、现象之间完全无关B、相关程度较小C、现象之间完全相关D、无直线相关关系11．下列现象相关密切程度最高的是（）。

A、某商店的职工人数与商品销售额之间的相关系数0.87B、流通费用水平与利润率之间的相关关系为-0.94C、商品销售额与利润率之间的相关系数为0.51D、商品销售额与流通费用水平的相关系数为-0.8112．估计标准误差是反映（）。

第九章相关与回归一．判断题部分题目1：负相关指的是因素标志与结果标志的数量变动方向是下降的。

（）答案：×题目2：相关系数为+1时，说明两变量完全相关；相关系数为-1时，说明两个变量不相关。

（）答案：√题目3：只有当相关系数接近+1时，才能说明两变量之间存在高度相关关系。

（）答案：×题目4：若变量x的值增加时，变量y的值也增加，说明x与y之间存在正相关关系；若变量x的值减少时，y变量的值也减少，说明x与y之间存在负相关关系。

（）答案：×题目5：回归系数和相关系数都可以用来判断现象之间相关的密切程度。

（）答案：×题目6：根据建立的直线回归方程，不能判断出两个变量之间相关的密切程度。

（）答案：√题目7：回归系数既可以用来判断两个变量相关的方向，也可以用来说明两个变量相关的密切程度。

（）答案：×题目8：在任何相关条件下，都可以用相关系数说明变量之间相关的密切程度。

（）答案：×题目9：产品产量随生产用固定资产价值的减少而减少，说明两个变量之间存在正相关关系。

（）答案：√题目10：计算相关系数的两个变量，要求一个是随机变量，另一个是可控制的量。

（）答案：×题目11：完全相关即是函数关系，其相关系数为±1。

（）答案：√题目12：估计标准误是说明回归方程代表性大小的统计分析指标，指标数值越大，说明回归方程的代表性越高。

（）答案×二．单项选择题部分题目1：当自变量的数值确定后，因变量的数值也随之完全确定，这种关系属于（）。

A.相关关系B.函数关系C.回归关系D.随机关系答案：B题目2：现象之间的相互关系可以归纳为两种类型，即（）。

A.相关关系和函数关系B.相关关系和因果关系C.相关关系和随机关系D.函数关系和因果关系答案：A题目3：在相关分析中，要求相关的两变量（）。

A.都是随机的B.都不是随机变量C.因变量是随机变量D.自变量是随机变量答案：A题目4：测定变量之间相关密切程度的指标是（）。