当前位置：文档之家 › 实数复习资料

实数复习资料

  • 格式：doc
  • 大小：306.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

实数的复习

实数的复习

二、立方根的概念
1、一般地，如果一个数x的立方等于a，即x³=a, 那么这个数x就叫做a的立方根（也叫做三次方 根）．记为：3 a 2、立方根的性质 正数的立方根是正数；负数的 立方根是负数；0的立方根是0．
3、重要公式
( a ) a,
3 3 3
a a,
3
3
a a .
3
三、实数的概念
11．若
(3 x 2) 1
3
，则
1 4
x 等于（
）.
1
A、
2 1 C、 4
B、
D、
9 4
巩固练习
12．计算： （1） 2
5 5 1
（2） 1 0 3
2
10 4
（3）
2
3 2 4
3
（4） 32 2 50
1 4
1 2
1 2

1 8
2
5
x y
2
2
(x y )3
2 2
底数a>0这个条件不可少. 若无此条件会引起混乱，
1
2
(-1) 3 和(-1) 6
这就说明分数指数幂在底数小于0时无意义.
在把根式化成分数指数幂时，要注意使底数大于0，同时，负数开 奇数次方根是有意义的，所以当奇数次根式要化成分数指数幂时， 先要把负号移到根号外面去，然后再按规定化成分数指数幂，例如，
实数复习
一、平方根的概念 1、一般地，如果一个数的平方等于a， 那么这个数叫做a的平方根或二次方根. 而把正的平方根叫算术平方根.
若x2=a，那么x叫做a的平方根.记作： a （ a叫做被开方数） 2、求一个数a的平方根的运算，叫做开平方. 平方与开平方互逆运算. 3、平方根的性质 一个正数有两个平方根,它们互为相反数. 0的平 方根是0.负数没有平方根. 4、重要公式 2 2 ( a ) a (a 0), a a

实数总复习题及答案

实数总复习题及答案

实数总复习题及答案一、选择题1. 下列哪个数不是实数？A. √2B. πC. -3D. 1/02. 实数集R中的元素包括：A. 有理数B. 无理数C. 复数D. A和B3. 以下哪个表达式等于0？A. √4B. 1 - 1C. 2^0D. 1/∞4. 绝对值的定义是什么？A. 一个数的平方B. 一个数的立方C. 一个数的平方根D. 一个数的正数或05. 如果a是一个正实数，那么1/a是一个：A. 正实数B. 负实数C. 零D. 复数二、填空题6. 一个实数的绝对值总是_________或0。

7. 两个相反数的和是_________。

8. 无理数是_________的数。

9. 实数的运算包括加法、减法、乘法、除法以及_________。

10. 一个数的相反数是_________。

三、解答题11. 证明：对于任意实数a和b，如果a > b，则a - b > 0。

12. 解释实数的完备性。

13. 给出一个无理数的例子，并说明为什么它是无理数。

14. 计算下列表达式的值：(-3)^2 + √4 - 2π。

15. 讨论实数集R的性质。

四、应用题16. 一个圆的半径是5，求圆的周长和面积。

17. 如果一个物体从静止开始以恒定加速度运动，经过2秒后，求其位移和速度。

18. 一个水库的水位在24小时内下降了3米，如果下降速率是恒定的，求每小时的平均下降速率。

答案一、选择题1. D2. D3. B4. D5. A二、填空题6. 非负数7. 08. 不能表示为两个整数的比9. 幂运算10. 与原数符号相反的数三、解答题11. 证明：设a和b是任意实数，且a > b。

根据实数的性质，我们可以定义一个数c = a - b。

由于a > b，c是一个正数。

因此，a - b > 0。

12. 实数的完备性指的是，任意实数序列的极限仍然是一个实数。

这意味着实数集没有“漏洞”，即不存在任何“缺失”的数。

实数的复习课件(共38张PPT)

实数的复习课件(共38张PPT)
零
你知道算术平方根、平方根、立方根联系和区别吗？
算术平方根
平方根
立方根
表示方法
a 的取值
性 正数
0
质
负数
a
a
3a
a≥ 0
a≥ 0
a 是任何数
正数（一个） 互为相反数（两个） 正数（一个）
0
0
0
没有
没有
负数（一个）
开方
求一个数的平方根 求一个数的立方根 的运算叫开平方 的运算叫开立方
是本身
0,1
0
律
则3 5250的值是 17.38
1.已知 x 和 a 2 的和为0,则x的范围是为( B )
A.任意实数 B.非正实数 C .非负实数 D. 0
2.若- 3 m
=
7
3
8
,则m的值是
(B )
A 7
7 B
7
C
8
8
8
D
343 512
3. 若 (x 2)2 2 x成立,则x的取值范围是( A )
5.已知满足 3 a a 4 a ,求a的值
6、a、b互为相反数，c与d互为倒数，则a+1+b+
cd= 2
。
8、已知 a - 2 b 3 0,
则（a b)2 25 ;
9、计算： 1- x x 1 x2 1 0 ;
10、计算： 5 5 2 33
二.已知实数a、b、c，在数轴上的位置如下图所示， 试化简：
a
b0 c
（1） a2－ |a－b|+|c－a|+ (b c)2
（2）|a+b－c|+|b－2c|+ (b a)2 －2 a2

实数相关概念的复习

实数相关概念的复习

03
实数的表示方法
十进制表示法
总结词
十进制表示法是最常用和最直观的实 数表示方法，它使用0-9这十个数字 进行数值的表示。
详细描述
在十进制表示法中，每个实数都可以表 示为一个或多个十进制数字的序列。例 如，实数123.45可以表示为1×10^2 + 2×10^1 + 3×10^0 + 4×10^-1 + 5×10^-2。
实数的性质
实数具有完备性，即 实数集具有加法、减 法、乘法和除法运算 的封闭性。
实数具有有序性，即 实数集合中任意两个 数都可以比较大小。
实数具有连续性，即 实数集合中任意两个 不相等的数之间都存 在其他数。
实数的大小关系
实数的大小关系可以通过其数值大小来比较，数值大的实数在数轴上位置更靠右。
对于任意两个实数a和b，如果a>b，则a+c>b+c（c为任意实数）；如果a<b，则 a-c<b-c（c为任意正实数）。
除法运算
总结词
除法运算的基本性质
详细描述
实数的除法运算可以通过乘法转换为乘法运算，即a÷b=a×(1/b)。同时，除法运算也满足结合律和交换 律。
指数运算
总结词
指数运算的基本性质
详细描述
实数的指数运算满足指数的乘法法则、除法法则和幂的运算法 则，即a^m^n=a^(m×n)，(a^m)^n=a^(m×n)，以及 (ab)^n=a^n×b^n。同时，指数运算还满足对数函数的性质， 如log_a(mn)=log_a m + log_a n等。
对数的运算性质
log_a (M/N) = log_a M - log_a N， log_a (MN) = log_a M + log_a N。

实数知识点总复习含答案解析

实数知识点总复习含答案解析
【答案】A
【解析】
【分析】
由于 ，于是 ，10与9的距离小于16与10的距离，可得答案．
【详解】
由于 ，于是 ，10与9的距离小于16与10的距离，可得答案．
解：∵ ，
∴ ，
10与9的距离小于16与10的距离，
∴与 最接近的是3．
故选：A．
【点睛】
本题考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题．
【答案】B
【解析】
分析：直接利用2＜ ＜3，进而得出答案．
详解：∵2＜ ＜3，
∴3＜ +1＜4，
故选B．
点睛：此题主要考查了估算无理数的大小，正确得出 的取值范围是解题关键．
10．若 则 的值是（）
A．2 B、1 C、0 D、
【答案】B
【解析】
试题分析：由题意得，3﹣a=0，2+b=0，解得，a=3，b=﹣2，a+b=1，故选B．
【详解】
，
∴25的算术平方根是：5.
故答案为：5.
【点睛】
本题考查了算术平方根，熟练掌握该知识点是本题解题的关键.
19．估计 的值是在（）
A．5和6之间B．6和7之间C．7和8之间D．8和9之间
【答案】B
【解析】
解：由于16＜19＜25，所以4＜ ＜5，因此6＜ +2＜7．故选B．
点睛：本题主要考查了估算无理数的大小的能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．
4．在－3.5， ，0， ，－ ，－ ，0.161161116…(相邻两个6之间依次多一个1)中，无理数有()
A．1个B．2个C．3个D．4个
【答案】C

复习资料

复习资料

第一章 实数1．1实数的有关概念及实数的分类一、规定了原点．．、正方向．．．和单位长度．．．．的直线叫做数轴。

数轴上所有的点与全体实数是一一对应关系。

二、⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧无限不循环小数负无理数正无理数无理数数有限小数或无限循环小负分数正分数分数负整数零正整数整数有理数实数 三、在数轴上，原点两旁且与原点距离相等的两个点所表示的数是互为相反数。

四、两个互为相反数的和等于零；互为倒数的两个数的积等于1；零没有倒数。

五、任何一个分数都可以化成有限小数或无限循环小数的形式。

六、绝对值⎩⎨⎧<-≥==)0()0(2a a a a a a 七、非负数 像a ，2a ，)0(≥a a 形式的数都表示非负数。

非负数性质 ①最小的非负数是0；②若几个非负数的和是0，则每个非负数都是0。

八、近似数与有效数字 一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位，这时，从左边第一个不是0的数字起到精确的数位止，所有的数字都叫这个数的有效数字。

九．科学记数法 把一个数记成n a 10⨯的形式叫做科学记数法，其中101<≤a ，n 为整数。

第二章 代数式2．1整式 代数式的分类⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧无理式分式多项式单项式整式有理式代数式 二、同类项 所含的字母相同并且相同字母的指数也相同的项叫做同类项，合并同类项时，只把系数相加，所含字母和字母的指数不变。

三、整式的运算（1）整式的加减 先去括号或添括号，再合并同类项。

（2）整式的乘除 幂的运算性质①n m n m a a a +=⋅（m ，n 为整数，0≠a ）；②mn n m a a =)(（m ，n 为整数，0≠a ）；③n n n b a ab ⋅=)(（n 为整数且0≠a ）；④n m n m a a a -=÷（m ，n 为整数，0≠a ）。

乘法公式（1）平方差：22))((b a b a b a -=-+。

实数的复习题及答案

实数的复习题及答案

实数的复习题及答案
1. 判断题：实数包括有理数和无理数。

答案：正确。

2. 选择题：以下哪个数是有理数？
A. π
B. √2
C. 0.33333...
D. 1/3
答案：D。

3. 填空题：实数a和b的和记作______。

答案：a+b。

4. 计算题：计算下列各题。

(1) 3 + 4i - 5i
(2) (2/3) + (-1/2)
答案：
(1) 3 - i
(2) 1/6
5. 应用题：一个数的平方根是它本身的数有几个？
答案：有两个，分别是0和1。

6. 证明题：证明实数集是完备的。

答案：实数集的完备性可以通过戴德金分割来证明。

戴德金分割是将
实数集分为两个非空子集A和B，使得A中的每一个元素都小于B中的每一个元素，且A没有最大元素。

这样的分割可以唯一确定一个实数，
从而证明了实数集的完备性。

7. 简答题：实数和复数的主要区别是什么？
答案：实数是复数的一个子集，复数包括实数和虚数。

实数可以表示为a+0i的形式，其中a是实数，而复数可以表示为a+bi的形式，其中a和b是实数，i是虚数单位。

8. 论述题：试述实数的连续性。

答案：实数的连续性是指在实数线上，任意两个实数之间都存在另一个实数。

这一性质可以通过实数的完备性来证明，即任意两个实数之间都存在一个实数的分割，这个分割可以确定一个唯一的实数，从而保证了实数的连续性。

实数的基本概念 复习课

实数的基本概念 复习课

3 无理数的个数有 ___ 个。
无限不循环小数叫做无理数 ( 强调: 无限 、 不循环.) 无理数常见的4种典型:
2 1、带根号的（指开方开不尽的数）：2，
3 3+1，9
(3)、无限不循环小)
(4)、三角函数型：tan60°，sin45 °．．．
返回
1 4 3+ 2 、含有的数： ，，
二、实数的基本概念
一.负数：在正数前面加“—”的数； 0既不是正数，也不是负数。 1、判断： 1）a一定是正数； （× 2）－a一定是负数； （× 3）－（－a）一定大于0； （ × 4）0是正整数。 （×
） ） ） ）
2、（1）如果零上5℃记作5℃，则零下2℃记作_____ （2） 如果上升10m记作10m，那么-5m表示____
已知 x a(a 0), 求x时，注意x a。 即绝对值的原数是双值性。
1、已知数轴上的Ａ点所表示的数是２，那么在数 B 轴上到Ａ点的距离是３的点所表示的数有（） Ａ．１个 Ｂ．２个 Ｃ．３个 Ｄ．４个 2、若x的相反数是3,∣y∣=5，则x+y的值为 -8或2 . 3、若3，ｍ，5为三角形三边，化简： 2m-10 •绝对值的性质——要注意正确区分数的三种情 况，尤其是负数去掉绝对值应变为其相反数。
１、下列各组数中，互为相反数的是（ c ） 1 2 2 A.2与 B. 1 与1 C. 1与 1 D.2与 2 2
２、若|a-3|-3+a＝０，则a的取值范围是（ ） c A.a≥3 B.a<3 C.a≤3 D.a>3
3、 3 的相反数是 A.－3 B. －1/3 （ A ） C. 3 D. 3 （2004广东）
要点、考点聚焦 一、实数的分类：

第3章实数复习

第3章实数复习
（3） ( 2 1)2 ( 2 3)2
算术平方根的隐含条件应用
（ 1） 若 1 3a | 8b 3 | 0 ,求 3 ab的值
（ 2） 若y
x 2 2 x 3, 求y x的平方根
(3)求 a 4 9 2a a 2的值
(4)已知| 2004- a | a 2005 a，求a 20042的值
2
112 121 2 12 144 132 169 2 14 196 152 225
162 256 2 17 289 182 324 192 361 2 20 400 252 625
121 11 144 12 169 13 196 14 225 15 256 16 289 17 324 18 361 19 400 Biblioteka 0 625 25二.识记
1 1 23 8
3
（立方根）
3 27
3
4 64 3 5 125
3
1 1 3 82 3 27 3 3 64 4
3
63 216
7 3 343 83 512 93 729 103 1000
3 3
216 6
3
125 5
343 7 3 512 8 3 729 9 3 1000 10
已知 128x 是一个正整数，求最小正整数x的值.
2 x 5.设x、y为有理数，且满足等式 2 y y 2 17 4 2，
3
求x+y的值
7.2121121112… (两个“2”之间依次多一个1)
(1)
(2)
9 3
×
× ×

第六章《实数》总复习课件

第六章《实数》总复习课件
2、如果一个正数的平方根是a＋3和2a－15，求这个数的立方 根。
3、计算：
(1) 2 2 2 (2)
3 3
2 2 (1
2)
(3)、 2 9 2

5 2

谢谢指导！ 再见！
(4)、 点A在数轴上表示的数为3 5，
点B在数轴上对应的数为 5， 则A，B两点的距离为
实数与数轴上的点
4 5
是一一对应的
(5)、3
2 （ 2 2 - 3）
5 2 -2 3
在进行实数的运算时，有理数的运算法则及 运算性质同样适用。
三、典例赏析
例1：计算
（1） 1.44 0.16 3 1 3 8


32 2

2 3


2 3

2 2 3
3 2
解原式 2 2 3 2 3 （ 3 2）
2 2 3 2 3 3 2 2 2 2 2 3 3 3
4 2 3ຫໍສະໝຸດ 三、典例赏析1 3 (1).( 2 x 1) 4 0 ( 2). ( x 3) 4 0 2 2
4、 5 的整数部分是 ，则它的小数部分是 ；
5、已知实数a、b在数轴上对应点的位置如图所示。 化简：a b (a b) 2
b
a
o
6、 | x 3 | y 2 0， 则x - y
x
五、达标检测
4、解答题：
1、若M＝a b 2 a＋8是（a＋8）的算术平方根， N＝2 a b 4 b 3是（b 3）的立方根，求： M N的值.
二、诊断回顾
2、填空
几个基本公式：（注意字母的取值范围）

实数复习及习题.docx

实数复习及习题.docx

实数复习及习题.docx知识要点:-。

平⽅根和⽴⽅根类型项⽬7^平⽅根⽴⽅根被开⽅数⾮负数任意实数符号表⽰ ± y[al/a 性质—个正数有两个平⽅根，且互为相反数；零的平⽅根为零；负数没有平⽅根； —个正数有⼀个正的⽴⽅根；⼀个负数有⼀个负的⽴⽅根；零的⽴⽅根是零；重要结论 (亦⼫=a(p. > 0) 圧科如0) ri [- a(a < 0) 阿=a ^ = a= -\[a⼆.实数有理数和⽆理数统称为实数.1. 实数的分类有理数：有限⼩数或⽆限循环⼩数⽆理数：⽆限不循环⼩数正数按与0的⼤⼩关系分：实数＜ 0负数2. 实数与数轴上的点⼀⼀对应.数轴上的任何⼀个点都対应⼀个实数，反之任何⼀个实数都能在数轴上找到⼀个点A/Z 对应.三、实数⼤⼩的⽐较对于数轴上的任意两个点，右边的点所表⽰的实数总是⽐左边的点表⽰的实数⼤.⽌实数⼤于0,负实数⼩于0,两个负数，绝对值⼤的反⽽⼩.四. 实数的运算：数4的相反数是⼀a ； —个正实数的绝对值是它本⾝；⼀个负实数的绝对值是它的相反数；0的绝对值是0.有理数的运算法则和运算律在实数范围内仍然成⽴.实数混合运算的运算顺序：先乘⽅、开⽅、再乘除，最后算加减?同级运算按从左到右顺序进⾏，有括号先算括号⾥.实数复习按定义分: 实数五.实数的⼤⼩的⽐较：有理数⼤⼩的⽐较法则在实数范围内仍然成⽴。

法则1.实数和数轴上的点⼀⼀对应，在数轴上表⽰的两个数，右边的数总⽐左边的数⼤；法则2.正数⼤于0, 0⼤于负数，⽌数⼤于⼀切负数，两个负数⽐较，绝对值⼤的反⽽⼩；法则3.两个数⽐较⼤⼩常见的⽅法有：求差法，求商法，倒数法，估算法，平⽅法。

例题分析J ⽆-3 + ^3 — |x| + 121、x-3求⽦⼙的值.练习1.已知y = &-2 + - x + 3,求严的平⽅根。

练习2?若勿3— 7和哥3⼙+ 4互为相反数,求x+y的值。

2、已知〃是满⾜不等式-巧X < ------2的最⼤整数.求』什"的平⽅根.3、已知a是怖的整数部分，&是它的⼒澈部分，求° f 1 b + 3 f 的值.练习：已知5 + TH的⼒澈部分为a, 5- VH的⼩数部分为b,则⾊+b的值是_______ ； a—b的值是__________4、阅读理解，回答问题.在解决数学问题的过程⼬，有时会遇到⽐较两数⼈⼩的问题，解决这类问题的关键是根据命题的题设和结论特征，采川相应办法，其中巧川“作差法”是解决此类问题的⼀种⾏之有效的⽅法：若 a —b>0,则 a 〉b ；若 a —b=0,则 a = b ；若 a —b<0,则 a 〈b.例如：在⽐较m2 + l 与m2的⼤⼩时,⼩东同学的作法是:T （陀$ +1）⼀（叨⼻）=叨2 * ] _ ⾎2 = 1 >:.m 2+1 > ^2.请你参考⼩东同学的作法，⽐较⼈⼩：4$ ----------- （2 + 练习： a 在数轴上的位置如图所⽰，则丄卫*的⼤⼩关系是：a.----- * ----- ? ------------------- * ---------------------------------- > -1 a 05、L 2? 知 a 、b ['两⾜ +8 + |b — = 0解关于x 的⽅程 @ + 2）兀+沪=么-1练习：设a 、b 、c 都是实数’且满⾜（2_拧+』/+⼼+以+ * +別=0 求代数式 2a-3b-c 的值。

实数知识总复习

实数知识总复习

一、知识结构有理数实数的分类无理数实数→用数轴上的点表示实数运算法则及运算性质实数的运算→↑近似数及近似计算↓数的开方→分数指数幂→有理数指数幂→运算性质二、概念复习1、无理数的定义：叫做无理数。

2、有理数与无理数的区别：有理数总可以用或表示；反过来，任何或也都是有理数。

而无理数是小数，有理数和无理数区别之根本是有限及无限循环和无限不循环。

3、常见的无理数类型：（1）一般的无限不循环小数，如：1.41421356¨···（2）看似循环而实际不循环的小数，如0.1010010001···(相邻两个1之间0的个数逐次加1)。

（3）有特定意义的数，如：π=3.14159265···,3。

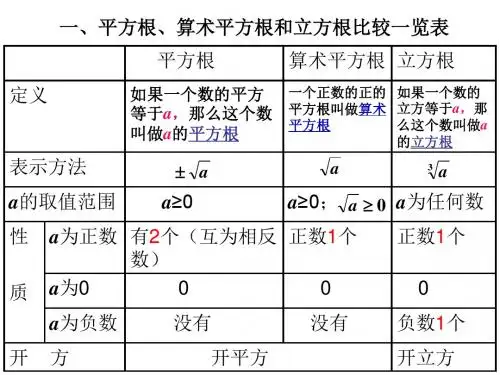
（4）开方开不尽的数，如：354、平方根（1）定义： .（2）非负数a的平方根的表示方法:（3）性质：一个（）有两个平方根，这两个平方根( )。

( )只有一个平方根，它是( )。

( )没有平方根。

5、算术平方根（1）定义： . （2）性质：算术平方根a具有双重非负性：①被开方数a是非负数，即a≥0.②算术平方根a本身是非负数，即a≥0。

也就是说，（）的算术平方根是一个正数，0的算术平方根是（），（）没有算术平方根。

说明：平方根有三种表示形式：±a，a，－a，它们的意义分别是非负数a的平方根、非负数a的算术平方根、非负数a的负平方根。

要特别注意：a≠±a。

6、a 2的算术平方根的性质①当a ≥0时，2a =（ ） ② 当a<0时，2a =（ ）我们还知道，当a ≥0时，│a │=a ；当a<0时，│a │=a.综上所述，有a (a ≥0)2a =│a │=-a (a<0)从算术平方根的定义可得：2)(a =a (a ≥0)7、立方根（1） 定义： .（2） 数a 的立方根的表示方法:_________（3） 互为相反数的两个数的立方根之间的关系：_________（4） 两个重要的公式 为任何数）为任何数）a a a a a (()a (3333==8、实数（1）概念： 和 统称为实数。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数学七年级上总复习之实数一、知识结构知识结构中，平方根与立方根两部分内容是平行的，可对比着进行记忆．二、知识要点要点1 平方根、立方根的定义与性质1、要判断一个对象有无平方根，首先要对这个对象进行转化，直到能看出它的符号，然后依据平方根的性质进行判断。

2、因为正数、0、负数均有立方根，所以所给各数都有立方根。

要点2 实数的分类与性质要正确判断一个数属于哪一类，理解各数的意义是关键。

要点3 二次根式的性质及有关概念二次根式要紧扣两个要素，即：根指数为2；被开方数大于或等于0。

要点4 实数的混合运算在实数范围内进行加、减、乘、除、乘方和开方运算，运算顺序依然是从高级到低级。

值得注意的是，在进行开方运算时，正实数和零可以开任何次方，负实数能开奇次方，但不能开偶次方。

要点5 非负数非负数，即不是负数，也即正数和零，常见的非负数主要有三种：实数的绝对值、实数的算术平方根、实数的偶次方。

它有一个非常重要的性质：若干个非负数的和为0，这几个非负数均为零。

要点6 数形结合题数形结合是解决数学问题常用的思想方法，解题时必须通过所给图形抓住相关数的信息。

要点7 与二次根式有关的探究题这类题目需要我们细心观察及思考，探究其中的规律，寻找解决问题的途径。

三、考查要点1、利用平方根、算术平方根、立方根的定义与性质解题（1）如果某数的一个平方根是-6，那么这个数为________．2、考查实数的有关概念及实数大小的比较（2）比较大小：7 50．（填“＞”、“＝”或“＜”）3、考查二次根式的概念（3）根号x-1 在实数范围内有意义，则x 的取值范围是( )(A)x>1 (B)x≥l (C)x<1 (D)x≤14、考查同类二次根式分析：掌握同类二次根式的概念是解决此类问题的关键。

首先要把能化简的二次根式化成最简二次根式，再分别看被开方数是否相同即可。

5、考查二次根式的化简与运算（4）化简400的结果是（ ）A ．10B ．2C ．4D ．20四、考试易错点1、对平方根、算术平方根、立方根的概念与性质理解不透理解不透平方根、算术平方根、立方根的概念与性质，往往出现以下错误：求一个正数的平方根时，漏掉其中一个，而求立方根时，又多写一个；求算术平方根时前面加上正负号，成了平方根等等。

2、忽略平方根成立的条件只有非负数才能开平方， 成立的条件是a≥0，这一条件解题时往往被我们忽略。

3、实数分类时只看表面形式对实数进行分类不能只看表面形式，应先化简，再根据结果去判断。

4、二次根式的运算错误在进行二次根式的运算时要注意运算法则与公式的正确应用，千万不要忽略公式的应用条件。

五、平方根和立方根考点例析在中考试题中，平方根和立方根的考点有以下几个方面：一、平方根的概念如果一个数的平方等于A ，那么这个数叫做A 的平方根．例1.9的平方根是【 】(A) 3 (B) (C) 81 (D)例2.(-5)2的平方根是【 】 (A)5 (B)-5 (C)±5 (D)±5例3.81的平方根是【 】(A) ±9 (B) ±3(C)9 (D)3二、算术平方根正数A 的正的平方根叫做A 的算术平方根.例4.| -4|的算术平方根是【 】(A)2 (B)±2 (C)4 (D) ±4例5.设x 为正整数，若1+x 是完全平方数，则它前面的一个完全平方数是 【 】(A)x (B)12+-x x (C)112++-x x (D)212++-x x三、立方根如果一个数的立方等于A ，那么这个数叫做A 的立方根．例6.立方根等于3的数是【 】 （A ）9 （B ）9± （C ）27 （D ）27±例7.38-等于 【 】（A ）2 （B ）2- （C ）3 （D ）-3例8.336.28的值为【 】（A ）3.049 (B)3.050 (C)3.051 (D)3.052四、科学计算器的应用例9.用计算器计算2116.0的按键顺序是______,结果等于_____.六、复习时需要强调和注意的问题1．平方根与算术平方根的联系和区别：(1)联系：只有非负数有平方根和算术平方根．0的平方根，算术平方根都为0．(2)区别：正数的平方根有两个，互为相反数，正数的算术平方根只有一个，用a 表示一个正数，其平方根为a ±，其算术平方根为a （a 为正数）（3）当0a ≥时，0a ≥；0a <时，a 无意义2．平方根与立方根的性质：3、无理数是无限不循环小数，一般来说开方开不尽的数，如2,3等都是无理数，但是并不是所有的无理数都可以写成根号的形式，如π就是一个特例．4、在实数范围内，对于非负数是可以开平方的，但负数开平方是没有意义的．5、实数的分类例1判断题：1、 16的平方根是4±2、 25-是425的平方根 3、 25-是425的平方根 4、 425的平方根是25- 5、 425的平方根是25± 6、有算术平方根的数是正数．这六道判断题，主要是考查了学生对平方根和算术平方根这两个概念的掌握．七、例题解析[例1]判断题：(1)绝对值等于它本身的实数只有零． ( )(2)倒数等于它本身的实数只有1． ( )(3)相反数等于它本身的实数只有0． ( )(4)算术平方根等于它本身的实数只有1． ( )(5)有算术平方根的数是有理数． ( )(6)0是最小的实数． ( )(7)无限小数都是无理数． ( )(8)带根号的数都是无理数． ( )(9)不带根号的数都是有理数．( )(10)两个无理数的和为无理数． ( )特别注意1、平方根是其本身的数是0；算术平方根是其本身的数是0和1；立方根是其本身的数是0和±1。

2、每一个正数都有两个互为相反数的平方根，其中正的那个是算术平方根；任何一个数都有唯一一个立方根，这个立方根的符号与原数相同。

3≥0有意义的条件是a ≥0。

4、公式：⑴)2=a （a ≥0a 取任何数）。

5、区分2=a （a ≥0），与 2a =a6.非负数的重要性质：若几个非负数之和等于0，则每一个非负数都为0（此性质应用很广，务必掌握）。

7.易混淆的三个数：（1）2a （2）2)(a （3）33a 补充练习(一)、精心选一选1． 有下列说法：（1）无理数就是开方开不尽的数； （2）无理数包括正无理数、零、负无理数；（3）无理数是无限不循环小数；（4）无理数都可以用数轴上的点来表示。

其中正确的说法的个数是（ ）A ．1B ．2C ．3D ．42．如果一个实数的平方根与它的立方根相等，则这个数是（ ）A ． 0B ． 正整数C ． 0和1D ． 13.能与数轴上的点一一对应的是（ ）A 整数B 有理数C 无理数D 实数4. 下列各数中，不是无理数的是 （ ） A.7 B. 0.5 C. 2π D. 0.151151115…）个之间依次多两个115(5．()20.7-的平方根是（ ）A ．0.7-B ．0.7±C ．0.7D ．0.496. 下列说法正确的是（ ）A ． 0.25是0.5 的一个平方根B ．.正数有两个平方根，且这两个平方根之和等于0C ． 7 2 的平方根是7D ． 负数有一个平方根7.一个数的平方根等于它的立方根，这个数是 （ ）A.0B.－1C.1D.不存在8.下列运算中，错误的是 （ ） ①1251144251=，②4)4(2±=-，③3311-=- ④2095141251161=+=+ A ． 1个 B. 2个 C. 3个 D. 4个9. 若225a =，3b =，则b a +的值为 （ ）A ．-8B ．±8C ．±2D ．±8或±2(二)、细心填一填 (每小题 分，共 分)10．在数轴上表示的点离原点的距离是 。

设面积为5的正方形的边长为x ,那么x = 。

11. 9的算术平方根是 ；94的平方根是 ,271的立方根是 , －125的立方根是 .12. 25-的相反数是 ，32-= ； 13. =-2)4( ； =-33)6( ； 2)196(= . 38-= .14. 比较大小；215- 5.0； (填“>”或“<”) 15. 要使62-x 有意义，x 应满足的条件是 。

16.已知051=-+-b a ，则2)(b a -的平方根是________；17.10.1== ；18. 一个正数x 的平方根是2a -3与5-a ，则a=________；19.一个圆它的面积是半径为3cm 的圆的面积的25倍，则这个圆的半径为_______.(三)、用心做一做20．（6分）将下列各数填入相应的集合内。

－7，0.32, 13，0，3125-，π，0.1010010001… ①有理数集合｛ … ｝ ②无理数集合｛ … ｝ ③负实数集合｛ … ｝21．化简（每小题5分，共20分）① 2+32—52 ② 7(71-7)③ |23- | + |23-|- |12- | ④ 41)2(823--+22．求下列各式中的x （10分,每小题5分）（1）12142=x （2）125)2(3=+x23．比较下列各组数的大少（5分）（1） 4 与 363 （2）24．．．一个正数．．．．．a ．的平方根是．．．．．3．x ．―．4．与．2．―．x ．，则．．a ．是多少？．．．．(6．．分．)．25．已知a 是根号8的整数部分，b 是根号8的小数部分，求（-a ）³+（2+b ）²的值26.求值（1）、已知a 、b 满足0382=-++b a ，解关于x 的方程()122-=++a b x a 。

（2）、已知x 、y 都是实数，且4y ，求x y 的平方根。

27、如果A=323+-+b a b a 为3a b +的算术平方根，B=1221---b a a 为21a -的立方根，求A+B 的平方根。

28、实数a 、b 互为相反数，c 、d 互为倒数，X 的绝对值为7，求代数式2()x a b cd x +++的值。