《系统建模与仿真》作业题

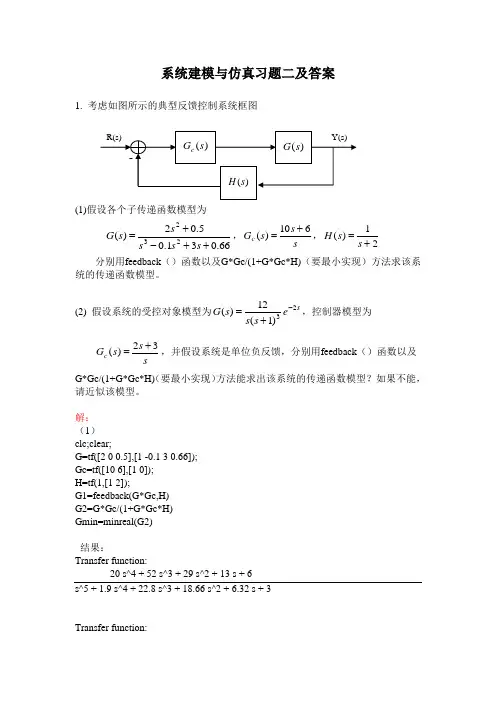
系统建模与仿真习题二及答案1. 考虑如图所示的典型反馈控制系统框图(1)假设各个子传递函数模型为66.031.05.02)(232++-+=s s s s s G ，s s s G c 610)(+=，21)(+=s s H 分别用feedback （）函数以及G*Gc/(1+G*Gc*H)（要最小实现）方法求该系统的传递函数模型。

(2) 假设系统的受控对象模型为s e s s s G 23)1(12)(-+=，控制器模型为 ss s G c 32)(+=，并假设系统是单位负反馈，分别用feedback （）函数以及G*Gc/(1+G*Gc*H)（要最小实现）方法能求出该系统的传递函数模型？如果不能，请近似该模型。

解：（1）clc;clear;G=tf([2 0 0.5],[1 -0.1 3 0.66]);Gc=tf([10 6],[1 0]);H=tf(1,[1 2]);G1=feedback(G*Gc,H)G2=G*Gc/(1+G*Gc*H)Gmin=minreal(G2)结果：Transfer function:20 s^4 + 52 s^3 + 29 s^2 + 13 s + 6s^5 + 1.9 s^4 + 22.8 s^3 + 18.66 s^2 + 6.32 s + 3Transfer function:20 s^8 + 50 s^7 + 83.8 s^6 + 179.3 s^5 + 126 s^4 + 57.54 s^3 + 26.58 s^2 + 3.96 ss^9 + 1.8 s^8 + 25.61 s^7 + 22.74 s^6 + 74.11 s^5 + 73.4 s^4 + 30.98 s^3+ 13.17 s^2 + 1.98 s Transfer function:20 s^4 + 52 s^3 + 29 s^2 + 13 s + 6s^5 + 1.9 s^4 + 22.8 s^3 + 18.66 s^2 + 6.32 s + 3(2)由于s c e s s s s G s G 232)1(3624)(*)(-++= 方法1：将s e 2-转换为近似多项式。

1.信息时代认识世界（科学研究）的三种方法是：理论研究、（_实验研究_）、（__仿真___）。

2.根据系统状态随时间变化是连续性还是间断性的，可将系统划分为（_连续系统_）、（__离散系统__）。

3.系统仿真中的三个基本概念是系统、（__模型_）、仿真。

4.拟对某系统进行研究，首先要对系统作出明确的描述，即确定系统各个要素：实体、属性、活动、（__状态_）、（_事件___）。

•阶段性知识测试5.系统仿真有三个基本的活动，即系统建模、仿真建模和（__仿真实验__），联系这三个活动的是系统仿真的三要素，即系统、模型和计算机（硬件和软件）。

6.系统仿真的一般步骤是：（1）调研系统，明确问题、（2）（___设立目标，收集数据__）、（3）建立仿真模型、（4）编制程序、（5）运行模型，计算结果、（6）（_统计分析，进行决策__）•阶段性知识测试7.仿真软件发展经历了四个阶段（1）高级程序语言阶段；（2）仿真程序包、初级仿真语言阶段；（3）商业化仿真语言阶段；(4)（_一体化建模与仿真环境_）阶段。

8.常用的仿真软件有Arena、Automod、MATLAB、Promodel、（__WITNESS______）、（______FLEXSIM___）。

9.求解简单系统问题的“原始”方法是（___解析解决____），借助（___实验__）可大大提高该方法的效率和精度。

•阶段性知识测试10.排队系统可简化表示为A/B/C/D/E。

其中A为到达模式；B为（服务模式）、C为服务台数量、D为系统容量；E为排队规则。

11.常见的排队规则有：先到先服务、后到后服务、优先级服务、最短处理时间优先服务、随机服务等。

请以连线方式将下列排队规则名称的中英文对照起来。

先进先出FIFO后进先出LIFO随机服务SIRO最短处理时间优先SPT优先级服务PR•阶段性知识测试12.模型中，习惯称实体为成分。

成分可分为主动成分和被动成分。

请问排队系统中的随机到达的顾客属于（主动）成分（主动/被动）。

共10题 每题10分1、什么是数学建模形式化的表示？试列举一例说明形式化表示与非形式化表示的区别；模型的非形式描述是说明实际系统的本质，但不是详尽描述。

是对模型进行深入研究的基础。

主要由模型的实体、包括参变量的描述变量、实体间的相互关系及有必要阐述的假设组成。

模型的非形式描述主要说明实体、描述变量、实体间的相互关系及假设等。

例子：环形罗宾服务模型的非形式描述：实体CPU ，USR1，…，USR5描述变量CPU:Who,Now(现在是谁)----范围{1,2,…,5}; Who.Now=i 表示USRi 由CPU 服务。

USR ：Completion.State （完成情况）----范围[0，1]；它表示USR 完成整个程序任务的比例。

参变量i X -----范围[0，1]；它表示USRi 每次完成程序的比率。

实体相互关系（1）CPU 以固定速度依次为用户服务，即Who.Now 为1，2，3，4，5，1，2…..循环运行。

（2）当Who.Now=I,CPU 完成USRi 余下的i X 工作。

假设：CPU 对USR 的服务时间固定，不依赖于USR 的程序；USRi 的进程是由各自的参变量i X 决定。

2、模型描述变量化简的四种方法比较；建模过程中，在能满足建模的前提下，系统的描述变量应是愈简单愈好。

模型描述变量一般有以下四种方法：（1）、淘汰一个或多个实体、描述变量或相互关系规则；建模者决定淘汰那些次要因素，只要忽略的因素不会显著地改变整个模型行为，相反却使不必要的复杂了。

淘汰一个实体可能要淘汰或修改其他实体：淘汰一个实体，需要淘汰所有涉及这个实体的描述变量；淘汰一个描述变量，需要淘汰或修改涉及该变量的相互关系。

（2）、随机变量取代确定性变量；在一个确定性模型中，相互关系的规则控制着整个描述变量的值。

有些随机值也是由相互关系的规则确定，为了使模型相对简化，可利用概率原理，用随机变量来取代某些变量的相互关系规则，从而将影响变量转换成随机变量。

第一章习题1-1什么是仿真？它所遵循的基本原则是什么？答：仿真是建立在控制理论，相似理论，信息处理技术和计算技术等理论基础之上的,以计算机和其他专用物理效应设备为工具，利用系统模型对真实或假想的系统进行试验，并借助专家经验知识，统计数据和信息资料对试验结果进行分析和研究，进而做出决策的一门综合性的试验性科学。

它所遵循的基本原则是相似原理。

1-2在系统分析与设计中仿真法与解析法有何区别?各有什么特点?答：解析法就是运用已掌握的理论知识对控制系统进行理论上的分析，计算。

它是一种纯物理意义上的实验分析方法,在对系统的认识过程中具有普遍意义。

由于受到理论的不完善性以及对事物认识的不全面性等因素的影响，其应用往往有很大局限性.仿真法基于相似原理，是在模型上所进行的系统性能分析与研究的实验方法.1-3数字仿真包括那几个要素？其关系如何？答: 通常情况下，数字仿真实验包括三个基本要素，即实际系统，数学模型与计算机。

由图可见，将实际系统抽象为数学模型，称之为一次模型化，它还涉及到系统辨识技术问题,统称为建模问题；将数学模型转化为可在计算机上运行的仿真模型，称之为二次模型化，这涉及到仿真技术问题，统称为仿真实验.1—4为什么说模拟仿真较数字仿真精度低？其优点如何?.答：由于受到电路元件精度的制约和容易受到外界的干扰,模拟仿真较数字仿真精度低但模拟仿真具有如下优点：（1）描述连续的物理系统的动态过程比较自然和逼真。

（2）仿真速度极快，失真小，结果可信度高。

（3）能快速求解微分方程.模拟计算机运行时各运算器是并行工作的，模拟机的解题速度与原系统的复杂程度无关.（4）可以灵活设置仿真试验的时间标尺，既可以进行实时仿真，也可以进行非实时仿真.（5）易于和实物相连。

1-5什么是CAD技术？控制系统CAD可解决那些问题？答：CAD技术，即计算机辅助设计（Computer Aided Design)，是将计算机高速而精确的计算能力,大容量存储和处理数据的能力与设计者的综合分析，逻辑判断以及创造性思维结合起来，用以加快设计进程，缩短设计周期，提高设计质量的技术.控制系统CAD可以解决以频域法为主要内容的经典控制理论和以时域法为主要内容的现代控制理论。

《系统建模与仿真》作业第一次（共两次）布置作业时间：“经典建模法”结束后 要求交作业时间：从布置日开始不超过1周 作业量：共3道题第1题——体现电气系统经典建模[题目] 在如图所示的电路中，R 表示一个电阻，L 表示一个电感，C 表示一个电容，i 表示电流强度，u 表示输入电压，c u 表示电容器的输出电压。

试写出一个状态空间数学模型。

u图1 典型的RLC 电路第2题——体现机械系统经典建模[题目]如图2是一个文字处理器打印轮轴控制系统的简化图。

打印轮轴由一个直流电动机通过皮带和滑轮进行控制。

假设皮带是刚性的，电动机与皮带轮之间的连接也是刚性的，并定义如下的参数和变量：m ()T t 是电动机的力矩；m ()t 是电动机的角位移；()y t 是打印轮轴的线性位移；m J 式电动机的惯量；m B 是电动机的粘性摩擦系数；K 是扭转轴的刚性系数；r 是滑轮的半径；M 是打印轮轴的质量。

（1）写出系统的微分方程；（2）写出系统的传递函数模型m ()()Y s T s 。

T打印轮轴图2 打印轮轴控制系统简化图第3题——体现热工过程经典建模汽轮机高压加热器疏水系统的原理框图如图3所示，其中各段抽汽的压力大小关系为321p p p >>，抽汽温度大小关系为321T T T >>。

给水流量w 和给水温度T 一般来说为两个随机变量。

三个疏水管道阀门的开度为归一化量，即]1,0[,,321∈u u u 。

三个高压加热器的疏水水位分别为1y ，2y ，3y 。

它们的关系可描述为),,,(111111T w T p f u k y+-= ),,,(22223122T w T p f u k u k y+-= ),,,(T w T p f u k u k y+-=图3 汽机高加疏水系统原理框图式中的),,,(111T w T p f ，),,,(222T w T p f ，),,,(333T w T p f 表示系统的不确定干扰，1k ，2k ，3k ，4k ，5k 表示适当的正常数。

系统建模与仿真习题一及答案1. 有源网络如图所示（1） 列些输出0u 与输入1u 之间的微分方程。

（2） Ω=101R 、Ω=52R 、Ω=23R 、Ω=34R 、F C 2=，在零初始条件下，将（1）中的微分方程表示为传递函数、状态空间形式、零极点增益形式。

（3）求（2）中方程在输入1u 为单位阶跃响应下的输出曲线。

解：（1） 由运算放大器的基本特点以及电压定理)4()3()(1)2()()1(2132021421320111R i R i u dt i i Cu R i i u R i u R i u c c -=+=+++==⎰（3）式代入（2）式得：42121320)()(1R i i dt i i C R i u ++++=⎰ （5）消去中间变量21,i i 有13142430114131230111120)(1u R R R R R R u u R R dt u R R R R u R u C u R R u ++++++=⎰ 两边求导整理后得（2）代入数据可以得到微分方程为：11007.02.610u u u u--=+ 程序如下：clc;clear;num=[-6.2 -0.7]; den=[10 1]; Gtf=tf(num,den) Gss=ss(Gtf) Gzpk=zpk(Gtf)结果：Transfer function: -6.2 s - 0.7 ------------ 10 s + 1状态空间形式： a =x1 x1 -0.1 b =u1 x1 0.125 c =x1 y1 -0.064 d =u1 y1 -0.62Continuous-time model.Zero/pole/gain: -0.62 (s+0.1129) ---------------- (s+0.1)（3）由（2）知系统的传递函数为-6.2 s - 0.7 ------------ 10 s + 1系统的输入信号为单位阶跃函数，则其Laplace 变换为1/s ，这样系统的输出信号的Laplace 变换为Y(s)=-6.2 s - 0.7 ------------ 10 s^2 + s编写程序，将其表示为（R,P,Q ）形式 clc;clear; s=tf('s')Gtf=(-6.2*s-0.7)/(10*s^2+s) [num,den]=tfdata(Gtf,'v') [R,P,Q]=residue(num,den) R =0.0800 -0.7000 P =-0.1000 0 Q = []于是得到：7.008.0)(1.0-=-t e t y 绘制曲线程序： clc;clear; t=0:0.1:100;y=0.08*exp(-0.1*t)-0.7; plot(t,y)2.已知系统的框图如下：其中：G1=1/(s+1)，G2=s/(s^2+2)，G3=1/s^2，G4=(4*s+2)/(s+1)^2，G5=(s^2+2)/(s^3+14)。

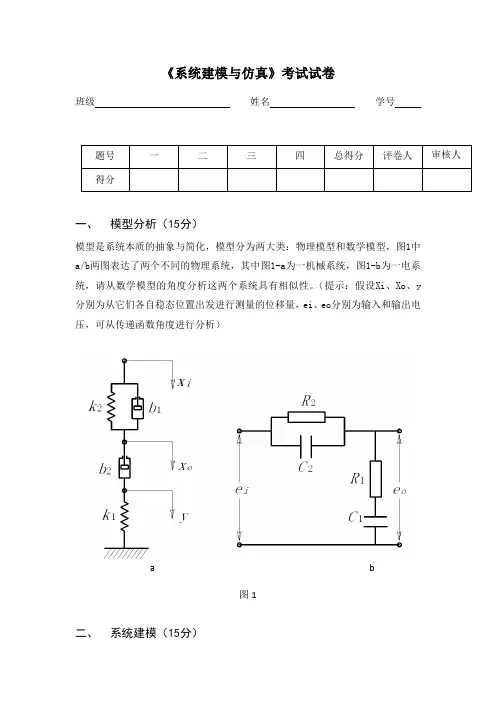
《系统建模与仿真》考试试卷班级姓名学号一、模型分析（15分）模型是系统本质的抽象与简化，模型分为两大类：物理模型和数学模型，图1中a/b两图表达了两个不同的物理系统，其中图1-a为一机械系统，图1-b为一电系统，请从数学模型的角度分析这两个系统具有相似性。

（提示：假设Xi、Xo、y 分别为从它们各自稳态位置出发进行测量的位移量，ei、eo分别为输入和输出电压，可从传递函数角度进行分析）a b图1二、系统建模（15分）图2所示为一种简化的汽车悬架系统模型，其中k1为轮胎的弹性系数，m1为车轮质量，k2为悬架的弹性系数，C为悬架阻尼系数，m2为车体质量，忽略其它参数。

当车辆沿着道路行驶时，由道路凹凸引起的垂直位移作为系统的输入激励u，由此传递到车体，引起车体的垂直位移为y。

(1)试求系统的传递函数Y(S)/U(S);(2)在作用于轮胎上的激励u一定情况下，试分析减小车体响应y的措施（可通过仿真分析）。

图2三、 仿真工具Matlab 应用（20分）（1）设一个双输入双输出系统的状态空间表达式为试用MATLAB 控制系统工具箱提供的相关转换函数，求解上述系统的传递函数。

（2）已知某系统的传递函数为试用MATLAB 控制系统工具箱提供的相关转换函数，求解上述系统的状态空间表达式。

（3）已知某系统的传递函数为试用MATLAB 控制系统工具箱提供的相关转换函数，求解上述系统的零点和极点。

（4）已知某系统的传递函数为试用MATLAB 控制系统工具箱提供的相关函数，绘制上述系统的单位阶跃响应曲线。

四、 建模与仿真分析（50分）倒立摆实际上是一个空间起飞助推器的姿态控制模型，图3所示为一倒立摆简化模型：质量为M 的小车在驱动力u 的作用下可以沿x 轴做直线运动，其位置为x ，摆杆长度为l ，下端通过无摩擦的铰链固定于小车的P 点，摆杆上端固连一个集中质量m ，摆杆质量不计。

摆杆l 和m 可以绕P 点铰链只能在x-y 平面内自由旋转，其u x t x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=202264510623421)( x y ⎥⎦⎤⎢⎣⎡=02010016332)(232+++++=s s s s s s G 13316)(232++++=s s s s s G 15.01)(2++=s s s G它方向受机械约束。

系统建模与仿真习题三及答案1.已知系统)24(32)(21+++=s s s s s G 、2103)(2+-=s s s G 求G 1(s)和G 2(s)分别进行串联、并联和反馈连接后的系统模型。

解：clc;clear;num1=[2 3];den1=[1 4 2 0];num2=[1 -3];den2=[10 2];G1=tf(num1,den1);G2=tf(num2,den2);Gs1=series(G1,G2)Gp1=parallel(G1,G2)Gf=feedback(G1,G2)结果：Transfer function:2 s^2 -3 s - 9------------------------------10 s^4 + 42 s^3 + 28 s^2 + 4 sTransfer function:s^4 + s^3 + 10 s^2 + 28 s + 6------------------------------10 s^4 + 42 s^3 + 28 s^2 + 4 sTransfer function:20 s^2 + 34 s + 6--------------------------------10 s^4 + 42 s^3 + 30 s^2 + s – 92.某双闭环直流电动机控制系统如图所示：利用feedback( )函数求系统的总模型。

解：模型等价为：编写程序：clc;clear;s=tf('s');G1=1/(0.01*s+1);G2=(0.17*s+1)/(0.085*s);G3=G1;G4=(0.15*s+1)/(0.051*s);G5=70/(0.0067*s+1);G6=0.21/(0.15*s+1);G7=(s+2)/s;G8=0.1*G1;G9=0.0044/(0.01*s+1);sys1=feedback(G6*G7,0.212);sys2=feedback(sys1*G4*G5,G8*inv(G7)); sys=G1*feedback(sys2*G2*G3,G9)结果：Transfer function:3.749e-005 s^6 + 0.008117 s^5 + 0.5024 s^4 + 6.911 s^3 + 36.57 s^2 + 78.79 s + 58.8 -------------------------------------------------------------------------------------------------------4.357e-014 s^10 + 2.432e-011 s^9 +5.43e-009 s^8 +6.303e-007 s^7 + 4.145e-005 s^6 + 0.001578 s^5 + 0.03217 s^4 + 0.2098 s^3 + 0.4116 s^2 + 0.3467 s + 0.2587根据需要可忽略高阶项。

西工大2022年4月机考《系统建模与仿真》作业参考答案试卷总分:100 得分:100本科目3次作答机会，每次试题内容相同，只是题目和选项顺序是随机调整的，大家可放心下载使用一、单选题(共20 道试题,共40 分)1.数学模型根据模型的状态变量可以分为（）。

A.连续变化模型和离散变化模型B.连续时间模型和离散时间模型C.确定性模型和随机性模型D.同构模型和同态模型正确答案:A2.在仿真模型一样，所要仿真的时间长度也一样的情况下，采用（）可获得最高的效率。

A.固定步长时间推进机制B.下次事件时间推进机制C.混合时间推进机制D.随机步长时间推进机制正确答案:B3.忽略具体事物的特殊性，着眼于整体和一般规律，这种研究方法是（）。

A.抽象B.归纳C.演绎D.推导正确答案:A4.（）是把过程调用和响应调用执行码结合在一起的过程A.汇编B.联编C.调试D.执行正确答案:B5.在系统与模型之间，如果在行为一级等价，则称之为（）。

A.同构模型B.同态模型C.数学模型D.本构模型正确答案:B6.一种产品进入市场之后，一般会经过销售速度先不断增加然后又逐渐下降的过程，这称为产品的（）。

A.生命周期B.保质期C.生产周期D.销售周期正确答案:A7.由于大多数微分方程是求不出其解析解的，因此研究其（）和数值解法是十分重要的手段。

A.离散性B.连续性C.非稳定性D.稳定性正确答案:D8.根据事件调度法建立的仿真模型称为（）仿真模型。

A.面向事件的B.面向对象的C.面向用户的D.面向系统的正确答案:A9.能够预定事件发生时间的策略方法是（）。

A.事件调度法B.活动扫描法C.进程交互法D.结果预测法正确答案:A10.系统在有确定输入时，得到的输出却不确定，这种事物发展变化没有确定因果关系的模型是（）。

A.连续变化模型B.离散变化模型C.随机性模型D.因果模型正确答案:C11.系统数学模型的建立需要按照模型论对输入、输出状态变量及其间的函数关系进行抽象，这种抽象理论称为（）。

系统建模与仿真习题五及答案1.已知系统的开环传递函数为)62)(5)(33(12)(222++++++=s s s s s s s s G ，根据相角裕度，幅值裕度判断单位负反馈下闭环系统的稳定性，并用时域响应验证结论。

解：clc;clear;num=[2 1];den=conv([1 0 0],conv([1 3 3],conv([1 5],[1 2 6])));G1=tf(num,den); margin(G1)由图知20lgh=24.8dB ，h>1；r=2.67deg 。

因此对应的闭环系统稳定。

下面由负反馈的阶跃响应验证闭环系统的稳定性clc;clear;num=[2 1];den=conv([1 0 0],conv([1 3 3],conv([1 5],[1 2 6])));G1=tf(num,den);step(feedback(G1,1))2. 已知某系统的开环传递函数为)32)(5()5(2)(2++++=s s s s s G （1）绘制系统的奈奎斯特曲线，判断闭环系统的稳定性。

（2）求出系统的单位阶跃响应，证明（1）中稳定性的判断。

解：clc;clear;num=[2 10];den=conv([1 2],[1 2 3]);G=tf(num,den);subplot(2,1,1)Nyquist(G)subplot(2,1,2)step(feedback(G,1))结论：开环传递函数位于s右半平面的极点数p=0。

由Nyquist图知：Nyquist曲线逆时针包围临界点(-1,j0)的圈数R=0。

因此，闭环正实部特征根个数Z=0，说明系统是稳定的。

仿真曲线也表明闭环系统是稳定的。

3. 已知一个离散系统的输入、输出数据如下：u=[0.9103;0.7622;0.2625;0.0475;0.7361;0.3282;0.6326;0.7564;0.9910;0.3653;0.2470 ;0.9826;0.7227;0.7534;0.6515;0.0727;0.6316;0.8847;0.2727;0.4364;0.7665;0.4777;0. 2378;0.2749]y=[0;18.4984;31.4285;32.3228;28.5690;39.1704;39.8825;46.4963;54.5252;65.9972;6 2.9181;57.5592;67.6080;70.7397;73.7718;74.0165;62.1589;63.0000;68.6356;60.8267 ;57.1745;60.5321;57.3803;49.6011]请用最小二乘法辨识出系统的脉冲传递函数模型，要求该模型的分子、分母的阶次分别为2、3次。

系统建模与仿真习题六及答案1.一个离散的系统：-x+-n-+=nnynyyn-xxn2+(()1)3()2)5.0((-()25.0)1分别利用dimpulse（）函数、filter（）函数、impz（）求解系统的脉冲响应。

解：clc;clear;b=[1 2 0 1];a=[1 -0.5 0.25]u=[1,zeros(1,9)]num=[1 2 0 1];den=[1 -0.5 0.25 0]; %补零subplot(311)[y,x]=dimpulse(num,den,10) ;stem(y)title('dimpulse求解')subplot(312)y=filter(b,a,u);stem(y)title('filter求解')subplot(313)y=impz(b,a,10);stem(y)title('impz求解')2. 假设信号：t=)(txπsin()10002分别以采样频率为2000Hz、1500Hz、1200Hz三种情况对该信号进行采样。

然后用理想的低通滤波器恢复该连续信号，观察恢复波形与实际波形的差异，分别计算出最大恢复误差。

解：clear;clc;for k=1:3if k==1Fs=2000;elseif k==2Fs=1500;elseFs=1200;endt1=0:1/Fs:0.002;%采样的时间间隔n=0:0.002*Fs;%采样的点数x=2*sin(1000*pi*t1);T=1/Fs;dt=T/10;%每个采样周期取多个样点，保证g(t)的连续性t=0:dt:0.002;M=ones(length(n),1)*t-n'*T*ones(1,length(t));xa=x*sinc(Fs*M);x0=2*sin(1000*pi*t);%实际函数subplot(3,1,k);stem(t,xa,'.');hold onplot(t,x0,'r','linewidth',1.5)wucha(k)=max(abs(xa-x0));endwuchawucha =0.3993 0.2847 1.52713.系统传递函数为：12312)(2+++=s s s s G 假设系统输入为)2sin(1)(t t u +=，请用卷积、lsim 函数方法求其零状态响应的结果。

1. (单选题) 在仿真模型一样，所要仿真的时间长度也一样的情况下，采用（）可获得最高的效率。

(本题2.0分)A. 固定步长时间推进机制B. 下次事件时间推进机制C. 混合时间推进机制答案: B解析: 无2. (单选题) 能够预定事件发生时间的策略方法是（）。

(本题2.0分)A. 事件调度法B. 活动扫描法C. 进程交互法答案: A解析: 无3. (单选题) 按照下一事件预计将要发生的时刻，以不等距的时间间隔向前推进，这种仿真时钟推进机制是（）。

(本题2.0分)A. 下次事件时间推进机制B. 固定步长时间推进机制C. 混合时间推进机制答案: A解析: 无4. (单选题) 一个实体通过执行（）终结。

(本题2.0分)A. Create短语B. Free短语C. Wait短语答案: B解析: 无5. (单选题) 进程交互法的基本模型单元是（）。

(本题2.0分)A. 事件处理B. 活动处理C. 进程答案: C解析: 无6. (单选题) 如果对一个类的意义进行描述，那么应该采用（）。

(本题2.0分)A. 标记值B. 规格描述C. 注释D. 构造型答案: C解析: 无7. (单选题) 面向对象仿真设计的缩写是（）。

(本题2.0分)A. OOSAB. OOSIC. OOSD答案: C解析: 无8. (单选题) 下列UML图形中，可用来刻画系统实时需求的是（）。

(本题2.0分)A. 交互图B. 用例图C. 类图答案: A解析: 无9. (单选题) 人们对客观对象某一方面认识的形式或非形式化描述是（）。

(本题2.0分)A. 抽象对象B. 计算机对象C. 概念对象答案: C解析: 无10. (单选题) Matlab中，能够绘制二维图形的命令是（）。

(本题2.0分)A. plotB. subplotC. figure答案: A解析: 无11. (单选题) 对于一个电子商务网站而言，（）不是合适的用例。

(本题2.0分)A. 用户登录B. 预订商品C. 邮寄商品D. 结账答案: C解析: 无12. (单选题) 下面不是用例间主要关系的是（）。

、系统、模型和仿真三者之间具有怎样的相互关系答：系统是研究的对象，模型是系统的抽象，仿真通过对模型的实验以达到研究系统的目的。

、通过因特网查阅有关蒲丰投针实验的文献资料，理解蒙特卡罗方法的基本思想及其应用的一般步骤。

答：蒲丰投针实验内容是这样的：在平面上画有一组间距为a的平行线，将一根长度为L（L<a）的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。

”布丰本人证明了，这个概率是：p=2L/（πa) (π为圆周率)利用这个公式可以用概率的方法得到圆周率的近似值。

所以，蒙特卡罗方法的基本思想就是：当试验次数充分多时，某一事件出现的频率近似等于该事件发生的概率。

一般步骤：（1）构造或描述概率过程（2）以已知概率分布进行抽样（3）建立各种估计量、简述离散事件系统仿真的一般步骤。

（1）阐明问题与设定目标（2）仿真建模（3）数据采集（4）仿真模型的验证（5）仿真程序的编制与校核（6）仿真模型的运行（7）仿真输出结果的统计分析、以第二章图2-5所示的并行加工中心系统为对象，试分别画出相应的实体流图和活动循环图，并比较它们两者有何区别和练习。

（1）实体流图(2)活动循环图、以第二章中图2-5所示的并行加工中心系统为对象，建立Petri 网模型。

3214Petri 网模型的运行过程，并将分析结果同例3-5相比较。

、任取一整数作为种子值，采用第三题中得到的随机数发生器生成随机数序列的前200项数据，并对其统计性能进行检验。

解：由第3题可得到一个随机数发生器： a=5 b=9 c=3 m=512取种子值，生成的随机数序列前200项数据如下： nn1500000332326458458t 4t 3 P 1 t 1P 2P 6 P 3 P 5 t 2 P 4(2)t 3发生后 t 4t 3 P 1 t 1P 2P 6 P 3 P 5 t 2P 4(3)t 2发生后 (4)t 1不能发生t 4t 3 P 1t 1 P 2 P 6 P 3 P 5 t 2 P 4 (5)t 4发生后2161882272293245 3413413281228204 4206820291023511 5103103302558510 65186312553505 73333322528480 8168168332403355 9843331341778242 101658122351213189 1161310136948436 12508508372183135 13254349538678166 14247843039833321 15215310540160872 165281641363363 178383421818282 18418418431413389 19209345441948412 2022822845206315 211143119467878 225988647393393 23433433481968432 242168120492163115 25603915057866n n 5133333376828316 52166813277158347 5366315178238238 54758246791193169 55123320980848336 56104824811683147 5712312382738226 58618106831133109 59533218454836 6010810885183183 615433186918406 62158158872033497 63793281882488440 641408384892203155 65192338790778266 661938402911333309 67201347792154812682388340936363 69170316794318318 7083832695159357 7116339796288288 72488488971443419 73244339598209850 74197844299253253 7522131651001268244n n 1011223199126478478 1029984861272393345 10324333851281728192 1041928392129963451 10519634271302258210 106213890131105329 107453453132148148 1082268220133743231 1091103791341158134 110398398135673161 1111993457136808296 11222882401371483459 11312031791382298250 1148983861391253229 11519333971401148124 1161988452141623111 117226321514255846 118107854143233233 1192732731441168144 1201368344145723211 1211723187146105834 122938426147173173 123213385148868356 1244284281491783247 1252143951501238214n n 1511073491764848 152248248177243243 15312432191781218194 154109874179973461 1553733731802308260 1561868332181130327915716631271821398374 1586381261831873337 1596331211841688152 16060896185763251 1614834831861258234 16224183701871173149 1631853317188748236 1641588521891183159 165263263190798286 16613182941911433409 1671473449192204800 168224820019333 16910034911941818 17024584101959393 17120535196468468 17228281972343295 1731431431981478454 1747182061992273225 175103392001128104对上述数据进行参数检验如下：经计算可知，===因此可知统计量=()==()=假定显著性水平，则查表可知故可以认为：在显著性水平时，该随机数序列总体的均值和方差与均匀分布U（0,1）的均值和方差没有显著性的差异。

系统建模与仿真习题四及答案1. 假设函数，通过以下两种方法求该函数的laplace变换。

（1）F= int(f(t)*exp(-s*t),0,inf)计算（2）laplace(f)解：clc;clear;syms a t sf=(2*t^2+a*sin(t));F1=int(f*exp(-s*t),'t',0,inf)F2=laplace(2*t^2+a*sin(t))结果：F1 =limit(-(2*exp(-s*t)*s^4*t^2+2*exp(-s*t)*s^2*t^2+4*exp(-s*t)*s^3*t+4*s*t*exp(-s*t)+4*exp(-s*t)*s^2+4*exp(-s*t)+a*exp(-s*t)*s^3*cos(t)+a*exp(-s*t)*s^4*sin(t)-4-4*s^2-a*s^3)/s^3/(s^2+1),t = Inf) F2 =4/s^3+1/(s^2+1)*a2. 已知系统的传递函数为：求其输入为响应输出的解析解。

解：clc;clear;syms sG=(2*s^2+1)/((s+1)*(s+2));R=1/(s^2+1);y=ilaplace(G*R)结果y = -9/5*exp(-2*t)+3/10*cos(t)-1/10*sin(t)+3/2*exp(-t)3.考虑下面给出的多变量系统：（1）试求出系统的零点与极点；（2）绘制零极点图，判断系统的稳定性及系统是否为最小相位系统。

解：clc;clear;A=[-3 1 2 1;0 -4 -2 -1;1 2 -1 1;-1 -1 1 2]; B=[1 0;0 2;0 3;1 1];C=[1 2 2 -1;2 1 -1 2];D=[0 0;0 0];G=ss(A,B,C,D)[p,z] = pzmap(G)pzmap(G)结果：p =2.2361-2.2361-3.0000 + 0.0000i-3.0000 - 0.0000iz =-3.19830.6427系统不稳定，为非最小相位系统。

《系统建模与仿真》复习题样例一、单项选择题(每题0.5分,共32题) 1、WITNESS 建模过程中，需要修改布局窗口的名称和背景颜色，可以通过下列哪个菜单操作完成（操作完成（）。

----序号473 A 、VIEW->Screen EditorB 、Window->Interact BoxC 、Window->ControlD 、Window->Designer Elements 2、在程序执行时，根据不同的条件，选择执行不同的程序语句，用来解决有选择、有转移的诸多问题的结构是（ ）。

----序号237 A 、顺序结构、顺序结构 B 、循环结构、循环结构 C 、分支结构、分支结构 D 、模块结构、模块结构3、零件（part ）到达系统的时间间隔规律在零件详细设计对话框的（）到达系统的时间间隔规律在零件详细设计对话框的（）中进行设置。

----序号148A 、typeB 、first arrivalC 、inter arrivalD 、to4、机器（machine ）元素的静态显示图标是由（）元素的静态显示图标是由（）显示项目确定的----序号99 A 、name B 、icon C 、style D 、text5、图标代表的是那种类型的元素（代表的是那种类型的元素（）。

----序号461 A 、Fluid B 、Pipe C 、Processor D 、Tank6、在Index 型输送链中对其长度进行设置需要在conveyor 详细设计对话框中的（ ）进行设置。

----序号168A 、length in partsB 、index timeC 、actions on finishD 、from7、如果要对容器的轮廓进行可视化设计以便能看到流体经过该容器，我们需要对容器的（ ）属性进行设置。

----序号309A 、tankB 、contentsC 、mixD 、laborqueue8、一系统中有一流体（fluid ）元素oil ，系统运行100min 后检查该流体在某一处理器Processor 中的在制品库存，所用到的函数是（中的在制品库存，所用到的函数是（）。