2017年四川省泸州市高考数学四诊试卷(理科)及参考答案

2017年四川省高考数学试卷（理科）（全国新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

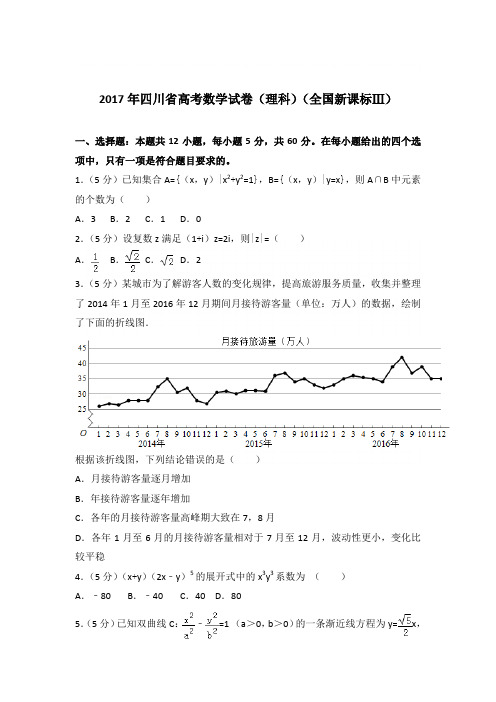
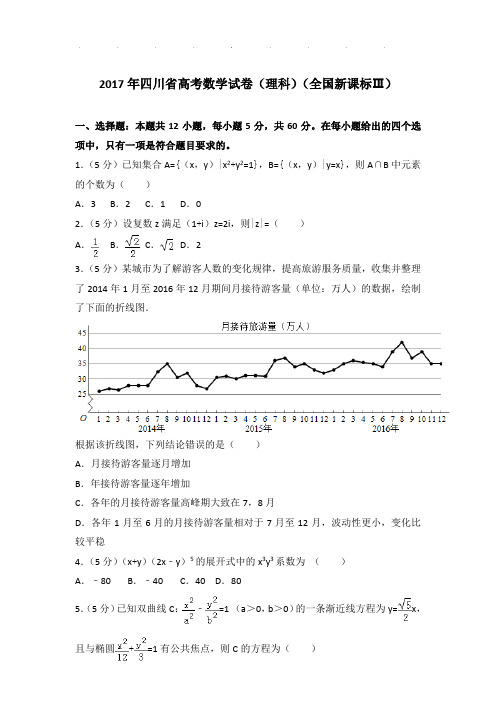
1．（5分）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3 B．2 C．1 D．02．（5分）设复数z满足（1+i）z=2i，则|z|=（）A．B．C．D．23．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80 B．﹣40 C．40 D．805．（5分）已知双曲线C：﹣=1 （a＞0，b＞0）的一条渐近线方程为y=x，且与椭圆+=1有公共焦点，则C的方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=16．（5分）设函数f（x）=cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．（5分）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N 的最小值为（）A．5 B．4 C．3 D．28．（5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB． C．D．9．（5分）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24 B．﹣3 C．3 D．810．（5分）已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切，则C的离心率为（）A．B．C．D．11．（5分）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A．﹣ B．C．D．112．（5分）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2 C．D．2二、填空题:本题共4小题，每小题5分，共20分。

四川省2017年高考理科数学试题及答案四川省2017年高考理科数学试题及答案（考试时间：120分钟试卷满分：150分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A={}22(,)1x y x y+=│，B={}(,)x y y x=│，则A I B中元素的个数为A．3 B．2 C．1 D．02．设复数z满足(1+i)z=2i，则∣z∣=A．12B．22C．2D．23．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是A．月接待游客量逐月增加B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 4．(x +y )(2x -y )5的展开式中x 3y 3的系数为A ．-80B ．-40C ．40D ．80 5． 已知双曲线C ：22221x y a b -= (a ＞0,b ＞0)的一条渐近线方程为52y x =,且与椭圆221123x y += 有公共焦点，则C 的方程为A ．221810x y -= B ．22145x y -= C ．22154x y -=D ．22143x y -=6．设函数f(x)=cos(x+3π)，则下列结论错误的是 A ．f(x)的一个周期为−2π B ．y=f(x)的图像关于直线x=83π对称C ．f(x+π)的一个零点为x=6πD ．f(x)在(2π,π)单调递减 7．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为 A ．5 B ．4 C ．3 D ．28．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．3π4C ．π2D ．π49．等差数列{}na 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}na 前6项的和为A ．-24B ．-3C ．3D ．8 10．已知椭圆C ：22221x y a b+=，（a>b>0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A ．B C ．3 D ．1311．已知函数211()2()x x f x xx a e e --+=-++有唯一零点，则a=A ．12-B ．13C ．12D ．1 12．在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP u u u r=λ ABu u u r +μADu u u r ，则λ+μ的最大值为A ．3B ．CD ．2二、填空题：本题共4小题，每小题5分，共20分。

2017年四川省高考数学试卷（理科）（全国新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3 B．2 C．1 D．02．（5分）设复数z满足（1+i）z=2i，则|z|=（）A．B．C．D．23．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80 B．﹣40 C．40 D．805．（5分）已知双曲线C：﹣=1 （a＞0，b＞0）的一条渐近线方程为y=x，且与椭圆+=1有公共焦点，则C的方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=16．（5分）设函数f（x）=cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．（5分）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N 的最小值为（）A．5 B．4 C．3 D．28．（5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB． C．D．9．（5分）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24 B．﹣3 C．3 D．810．（5分）已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切，则C的离心率为（）A．B．C．D．11．（5分）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A．﹣ B．C．D．112．（5分）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2 C．D．2二、填空题:本题共4小题，每小题5分，共20分。

四川省2017年高考理科数学试题及答案
（考试时间：120分钟试卷满分：150分）
一、选择题：本大题共
12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A=
22(,)1x y x y │，B=(,)x y y x │，则A B 中元素的个数为A ．3 B ．2
C ．1
D ．0 2．设复数z 满足(1+i)z=2i
，则∣z ∣= A ．1
2B ．22C ．2D ．2
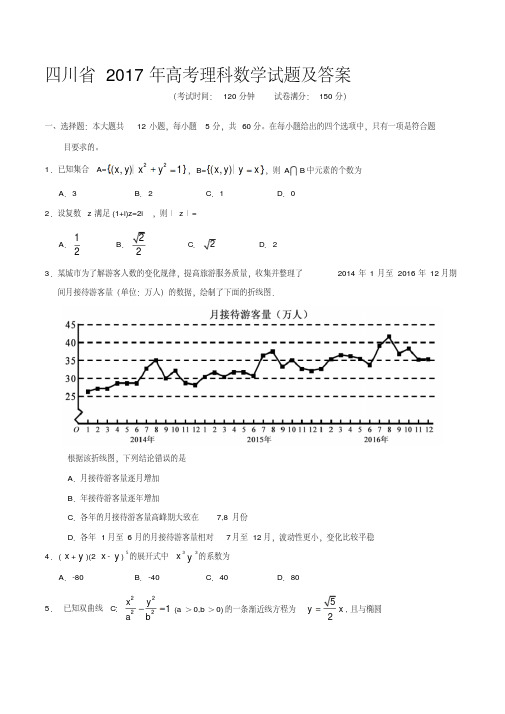
3．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期
间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是
A ．月接待游客量逐月增加
B ．年接待游客量逐年增加
C ．各年的月接待游客量高峰期大致在
7,8月份D ．各年1月至6月的月接待游客量相对
7月至12月，波动性更小，变化比较平稳4．(x +y )(2x -y )5的展开式中x
3y 3的系数为A ．-80
B ．-40
C ．40
D ．80 5．已知双曲线C ：22221x
y a b (a ＞0,b ＞0)的一条渐近线方程为5
2y x ,且与椭圆。

四川省泸州市2017届高三第一次诊断考试数 学 试 题（理）本试卷分第一部分（选择题）和第二部分（非选择题）两部分。

共150分。

考试时间120分钟。

第一部分的答案涂在机读卡上，第二部分的答案写在答题卡上。

参考公式：如果事件A 、B 互斥，那么 P (A +B )=P (A )+P (B )如果事件A 、B 相互独立，那么 P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率k n k k n n P P C k P --=)1()(第一部分（选择题 共60分）注意事项：1．答第一部分前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂、写在机读卡上。

2．每小题选出答案后，用2B 铅笔把机题卡上对应题的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在草稿子、试题卷上。

一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设集合{1,2,3,4},{1,2,3},{2,3,4},()U U M N M N === 则C =（ ） A ．{1，2} B ．{2，3} C ．{2，4}D ．{1，4} 2．23(1)lim 6!x n n n →∞++的值为 （ ） A ．0 B ．1C ．16D ．不存在 3．复数52i +的值为（ ） A ．2i - B ．2i + C ．12i - D ．12i +4．若函数2log (1), 1.()2, 1.x a x x f x x -+>⎧=⎨≤⎩在定义域内连续，则a 的值为（ ）A ．0B ．1C ．2D ．-15．已知函数()x f x e =（e 是自然对数的底数），则函数()f x 的导函数'()f x 的大致图象为（ ）6．设函数()tan()3f x x π=+，则下列结论中正确的是 （ ）A ．函数()f x 的图象关于点(,0)3π对称B ．函数()f x 的图象关于直线3x π=对称C ．把函数()f x 的图象向右平移3π个单位，得到一个奇函数的图象D ．函数()f x 的最小正周期为2π7．设p ，q 是两个命题，121:log (||3)0,:112p x q x -><-，则p 是q 的 （ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件8．经全国人大常委会批准，自2011年9月1日起我国实行新的《中华人民共和国所得税法》，新法规定：个人工资、薪金所得，以每月收入额减除费用3500元后的余额，为全月应纳税所得额，且税率也作了调整，调整后的部分税率见《中华人民共和国个人所得税税率表》。

2017年四川省泸州市高考数学四诊试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合M={x|x2+x﹣2＜0}，N={x|x+1＜0}，则M∩N=（）A．（﹣1，1）B．（﹣2，﹣1）C．（﹣2，1）D．（1，2）2．已知复数z满足（1+i）z=2i（i为虚数单位），则|z|=（）A．B．C．D．23．“”是“log2a＞log2b”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件4．某位股民购进某只股票，在接下来的交易时间内，他的这只股票先经历了3次涨停（每次上涨10%）又经历了3次跌停（每次下降10%），则该股民这只股票的盈亏情况（不考虑其他费用）为（）A．略有盈利 B．无法判断盈亏情况C．没有盈也没有亏损 D．略有亏损5．双曲线=1（a＞0，b＞0）的离心率为，则其渐近线方程为（）A．y=±3x B． C．y=±2x D．6．已知，则=（）A．B．C．D．7．《孙子算经》是我国古代内容极为丰富的数学名著，其中一个问题的解答可以用如图的算法来实现，若输入的S，T的值分别为40，126，则输出a，b的值分别为（）A．17，23 B．21，21 C．19，23 D．20，208．已知函数f（x）=asinx+bcosx（x∈R），若x=x0是函数f（x）的一条对称轴，且tanx0=3，则点（a，b）所在的直线为（）A．x﹣3y=0 B．x+3y=0 C．3x﹣y=0 D．3x+y=09．正四面体ABCD的棱长为4，E为棱AB的中点，过E作此正四面体的外接球的截面，则截面面积的最小值是（）A．4πB．8πC．12π D．16π10．某几何体的正视图和侧视图如图（1）所示，它的俯视图的直观图是A'B'C'，如图（2）所示，其中O'A'=O'B'=2，，则该几何体的表面积为（）A．B．C．D．11．过抛物线C：y2=2px（p＞0）的焦点F作斜率为的直线l与C及其准线分别相交于A、B、D三点，则的值为（）A．2或B．3或C．1 D．4或12．已知函数f（x）=，关于x的不等式f2（x）+af（x）＞0只有两个整数解，则实数a的取值范围是（）A． B．C．D．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．已知向量=（λ，1），=（λ+2，1），若|+|=|﹣|，则实数λ= ．14．若（x2﹣）n展开式的二项式系数之和为128，则展开式中x2的系数为．15．当实数x，y满足不等式组时，ax+y+a+1≥0恒成立，则实数a的取值范围是．16．在等腰△ABC中，AB=AC，AC边上的中线BD长为6，则当△ABC的面积取得最大值时，AB 的长为．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．已知数列{a n}的前n项和S n满足S n=2a n﹣a1，且a1，a2+1，a3成等差数列．（1）求数列{a n}的通项公式；（2）设b n=，求数列{b n}的前n项和T n．18．某市对创“市级示范性学校”的甲、乙两所学校进行复查验收，对办学的社会满意度一项评价随机访问了20位市民，这20位市民对这两所学校的评分（评分越高表明市民的评价越好）的数据如下：甲校：58，66，71，58，67，72，82，92，83，86，67，59，86，72，78，59，68，69，73，81；乙校：90，80，73，65，67，69，81，85，82，88，89，86，86，78，98，95，96，91，76，69，．检查组将成绩分成了四个等级：成绩在区间的为A等，在区间22．在直角坐标系xOy中，圆C的参数方程（ϕ为参数）．以O为极点，x轴的非负半轴为极轴建立坐标系．（1）求圆C的极坐标方程；（2）设直线l的极坐标方程是，射线x ﹣y=0（x≥0）与圆C的交点为O，P，与直线l的交点为Q，求线段PQ的长．23．设函数f（x）=|x﹣|+|x+a|（a＞0）．（1）证明：f（x）≥4；（2）若f（2）＜5，求a的取值范围．2017年四川省泸州市高考数学四诊试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合M={x|x2+x﹣2＜0}，N={x|x+1＜0}，则M∩N=（）A．（﹣1，1）B．（﹣2，﹣1）C．（﹣2，1）D．（1，2）【考点】1E：交集及其运算．【分析】运用二次不等式和一次不等式的解法，化简集合M，N，再由交集的定义，即可得到所求．【解答】解：集合M={x|x2+x﹣2＜0}={x|（x+2）（x﹣1）＜0}={x|﹣2＜x＜1}，N={x|x+1＜0}={x|x＜﹣1}，可得M∩N={x|﹣2＜x＜﹣1}，故选：B．2．已知复数z满足（1+i）z=2i（i为虚数单位），则|z|=（）A．B．C．D．2【考点】A8：复数求模．【分析】直接利用复数两边求模的运算法则求解即可．【解答】解：复数z满足（1+i）z=2i，则：|（1+i）||z|=|2i|，可得|z|=2，∴|z|=．．故选：C3．“”是“log2a＞log2b”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件【考点】2L：必要条件、充分条件与充要条件的判断．【分析】由“”⇔a＞b，“log2a＞log2b”⇔a＞b＞0．即可判断出结论．【解答】解：“”⇔a＞b，“log2a＞log2b”⇔a＞b＞0．∴“”是“log2a＞log2b”的必要不充分条件．故选：B．4．某位股民购进某只股票，在接下来的交易时间内，他的这只股票先经历了3次涨停（每次上涨10%）又经历了3次跌停（每次下降10%），则该股民这只股票的盈亏情况（不考虑其他费用）为（）A．略有盈利 B．无法判断盈亏情况C．没有盈也没有亏损 D．略有亏损【考点】46：有理数指数幂的化简求值．【分析】由题意可得：（1+10%）3（1﹣10%）3=0.993≈0.97．即可判断出结论．【解答】解：由题意可得：（1+10%）3（1﹣10%）3=0.993≈0.97＜1．因此该股民这只股票的盈亏情况为：略有亏损．故选：D．5．双曲线=1（a＞0，b＞0）的离心率为，则其渐近线方程为（）A．y=±3x B． C．y=±2x D．【考点】KC：双曲线的简单性质．【分析】根据题意，由双曲线的离心率公式可得e==，变形可得e2===1+=10，解可得的值，进而由双曲线的方程可得其渐近线方程为y=±x，将的值代入即可得答案．【解答】解：根据题意，双曲线=1（a＞0，b＞0）的离心率为，则有e==，即e2===1+=10，解可得=9，即=3，又由双曲线=1的焦点在x轴上，其渐近线方程为：y=±x，则该双曲线的渐近线方程为y=±3x，故选：A．6．已知，则=（）A．B．C．D．【考点】GI：三角函数的化简求值．【分析】利用诱导公式和二倍角公式即可计算．【解答】解：由，可得：cos（）=sin[﹣（）]=．那么： =cos2（）=2cos2（）﹣1=2×=．故选：B．7．《孙子算经》是我国古代内容极为丰富的数学名著，其中一个问题的解答可以用如图的算法来实现，若输入的S，T的值分别为40，126，则输出a，b的值分别为（）A．17，23 B．21，21 C．19，23 D．20，20【考点】EF：程序框图．【分析】根据程序框图的内容，进行模拟计算即可．【解答】解：若输入的S，T的值分别为40，126，第一次，126≥2×40，满足条件．则T﹣2S=126﹣80=46除以2的余数为0，满足t=0，则b===23，a=S﹣b=40﹣23=17，即a=17，b=23，故选：A8．已知函数f（x）=asinx+bcosx（x∈R），若x=x0是函数f（x）的一条对称轴，且tanx0=3，则点（a，b）所在的直线为（）A．x﹣3y=0 B．x+3y=0 C．3x﹣y=0 D．3x+y=0【考点】H6：正弦函数的对称性．【分析】利用辅助角公式将函数进行化简，求出函数的对称轴即可得到结论．【解答】解：f（x）=asinx+bcosx=（sinx+cosx），令sinα=，则cosα=，即tanα=，则f（x）=cos（x﹣α），由x﹣α=kπ，得x=α+kπ，k∈Z，即函数的对称轴为x=α+kπ，k∈Z，∵x=x0是函数f（x）的一条对称轴，∴x0=α+kπ，则tanx0=tanα==3，即a=3b，即a﹣3b=0，则点（a，b）所在的直线为x﹣3y=0，故选：A9．正四面体ABCD的棱长为4，E为棱AB的中点，过E作此正四面体的外接球的截面，则截面面积的最小值是（）A．4πB．8πC．12π D．16π【考点】LR：球内接多面体．【分析】根据题意，将四面体ABCD放置于如图所示的正方体中，则正方体的外接球就是四面体ABCD的外接球．因此利用题中数据算出外接球半径R，当球心O到截面的距离最大时，截面圆的面积达最小值，再利用球的截面圆性质可算出截面面积的最小值．【解答】解：将四面体ABCD放置于正方体中，如图所示可得正方体的外接球就是四面体ABCD的外接球，∵正四面体ABCD的棱长为4，∴正方体的棱长为2，可得外接球半径R满足2R=2×，R=．E为棱BC的中点，过E作其外接球的截面，当球心O到截面的距离最大时，截面圆的面积达最小值，此时球心O到截面的距离等于正方体棱长的一半，可得截面圆的半径为r=．得到截面圆的面积最小值为S=πr2=4π．故选：A．10．某几何体的正视图和侧视图如图（1）所示，它的俯视图的直观图是A'B'C'，如图（2）所示，其中O'A'=O'B'=2，，则该几何体的表面积为（）A．B．C．D．【考点】L!：由三视图求面积、体积．【分析】由俯视图的直观图可得原图形：为边长为4的等边三角形．可得原几何体为四棱锥P ﹣ABC．其中PC⊥底面ABC．【解答】解：由俯视图的直观图可得原图形：为边长为4的等边三角形．可得原几何体为四棱锥P﹣ABC．其中PC⊥底面ABC．∴该几何体的表面积S=++=24．故选：C．11．过抛物线C：y2=2px（p＞0）的焦点F作斜率为的直线l与C及其准线分别相交于A、B、D三点，则的值为（）A．2或B．3或C．1 D．4或【考点】K8：抛物线的简单性质．【分析】设抛物线方程，代入椭圆方程，设=λ，根据向量数量积的坐标运算，即可求得λ的值，分类讨论，根据抛物线的定义及相似性，即可求得丨BD丨及丨AD丨，即可求得的值．【解答】解：抛物线C：y2=2px（p＞0）的焦点F（，0），过A和B分别做准线的垂线，垂足分别为A′，B′，则直线AB的方程：y=（x﹣）设A（x1，y1），B（x2，y2），，整理得：y2﹣py﹣p2=0，则y1+y2=p，y1y2=﹣p2，设=λ，（﹣x1，﹣y1）=（x2﹣，y2），则﹣y1=λy2，由=++2=﹣，∴﹣λ﹣+2=﹣，整理得：λ2﹣17λ+4=0，解得：λ=4或λ=，当λ=4时，丨AF丨=4丨BF丨，则丨AB丨=5丨BF丨，由抛物线的定义可知：丨BF丨=丨BB′丨，由直线AB的斜率为，则sin∠∠BDB′=，即sin∠BDB′==，∴丨BD丨=丨BB′丨=丨BF丨，丨AD丨=丨AB丨+丨BD丨=，∴的值4，当λ=，4丨AF丨=丨BF丨，则丨AB丨=5丨AF丨，由抛物线的定义可知：丨AF丨=丨AB′丨，由直线AB的斜率为，则sin∠∠AD F′=，即sin∠ADF′==，∴丨AD丨=丨AB′丨=丨AF丨，丨BD丨=丨AB丨+丨AD丨=，∴的值，故选D．12．已知函数f（x）=，关于x的不等式f2（x）+af（x）＞0只有两个整数解，则实数a的取值范围是（）A． B．C．D．【考点】54：根的存在性及根的个数判断．【分析】判断f（x）的单调性，作出f（x）的图象，利用函数图象得出a的范围．【解答】解：f′（x）=，令f′（x）=0得x=，∴当0＜x＜时，f′（x）＞0，f（x）单调递增，当x＞时，f′（x）＜0，f（x）单调递减，由当x时，f（x）＜0，当x时，f（x）＞0，作出f（x）的大致函数图象如图所示：∵f2（x）+af（x）＞0，（1）若a=0，即f2（x）＞0，显然不等式有无穷多整数解，不符合题意；（2）若a＞0，则f（x）＜﹣a或x＞0，由图象可知f（x）＞0有无穷多整数解，不符合题意；（3）若a＜0，则f（x）＜0或f（x）＞﹣a，由图象可知f（x）＜0无整数解，故f（x）＞﹣a有两个整数解，∵f（1）=f（2）=ln2，且f（x）在（，+∞）上单调递减，∴f（x）＞﹣a的两个整数解必为x=1，x=2，又f（3）=，∴≤﹣a＜ln2，解得﹣ln2＜a≤﹣．故选：A．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．已知向量=（λ，1），=（λ+2，1），若|+|=|﹣|，则实数λ= ﹣1 ．【考点】9P：平面向量数量积的坐标表示、模、夹角．【分析】先求得得和的坐标，再根据|+|=|﹣|，求得λ的值．【解答】解：由题意可得=（2λ+2，2），=（﹣2，0），再根据|+|=|﹣|，可得=，解得λ=﹣1，故答案为：﹣1．14．若（x2﹣）n展开式的二项式系数之和为128，则展开式中x2的系数为35 ．【考点】DC：二项式定理的应用．【分析】由条件利用二项式系数的性质求得n=7，再利用二项展开式的通项公式，求得展开式中x2的系数．【解答】解：∵（x2﹣）n展开式的二项式系数之和为2n=128，∴n=7，∴（x2﹣）n=（x2﹣）7展开式的通项公式为T r+1=•（﹣1）r•x14﹣3r，令14﹣3r=2，求得r=4，可得展开式中x2的系数为=35，故答案为：35．15．当实数x，y满足不等式组时，ax+y+a+1≥0恒成立，则实数a的取值范围是．【考点】7C：简单线性规划．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义结合数形结合进行求解即可．【解答】解：作出不等式组对应的平面区域如图：直线ax+y+a﹣1=a（x+1）+（y+1）=0，过定点D（﹣1，﹣1）．ax+y+a+1≥0恒成立等价为可行域都在直线ax+y+a+1=0的上方；则由图象知只要B（1，0）满足ax+y+a+1≥0即可，即2a+1≥0，得a≥，故答案为：；16．在等腰△ABC中，AB=AC，AC边上的中线BD长为6，则当△ABC的面积取得最大值时，AB的长为4．【考点】HT：三角形中的几何计算．【分析】设AB=AC=2x，三角形的顶角θ，则由余弦定理求得cosθ的表达式，进而根据同角三角函数基本关系求得sinθ，最后根据三角形面积公式表示出三角形面积的表达式，根据一元二次函数的性质求得面积的最大值．【解答】解：在等腰△ABC中，设AB=AC=2x，AD=x．设三角形的顶角为θ，则由余弦定理得cosθ=，∴sinθ=，由公式三角形：S=absinθ==得：当 x2=20时，三角形面积有最大值，即AB=2x=4时三角形面积有最大值．所以答案为：4．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．已知数列{a n}的前n项和S n满足S n=2a n﹣a1，且a1，a2+1，a3成等差数列．（1）求数列{a n}的通项公式；（2）设b n=，求数列{b n}的前n项和T n．【考点】8E：数列的求和；8H：数列递推式．【分析】（1）由S n=2a n﹣a1，利用a n=S n﹣S n﹣1（n≥2），可得a n=2a n﹣1（n≥2），数列{a n}是以2为公比的等比数列，又a1，a2+1，a3成等差数列，可得a1+a3=2（a2+1），解得a1，即可得出．（2）由（1）得，可得b n==，利用裂项求和方法即可得出．【解答】解：（1）因为S n=2a n﹣a1，所以a n=S n﹣S n﹣1（n≥2），即a n=2a n﹣1（n≥2），即数列{a n}是以2为公比的等比数列，又a1，a2+1，a3成等差数列，所以a1+a3=2（a2+1），即a1+4a1=2（2a1+1），解得a1=2，所以数列{a n}的通项公式为．（2）由（1）得，所以=，．18．某市对创“市级示范性学校”的甲、乙两所学校进行复查验收，对办学的社会满意度一项评价随机访问了20位市民，这20位市民对这两所学校的评分（评分越高表明市民的评价越好）的数据如下：甲校：58，66，71，58，67，72，82，92，83，86，67，59，86，72，78，59，68，69，73，81；乙校：90，80，73，65，67，69，81，85，82，88，89，86，86，78，98，95，96，91，76，69，．检查组将成绩分成了四个等级：成绩在区间的为A等，在区间．22．在直角坐标系xOy中，圆C的参数方程（ϕ为参数）．以O为极点，x轴的非负半轴为极轴建立坐标系．（1）求圆C的极坐标方程；（2）设直线l的极坐标方程是，射线x ﹣y=0（x≥0）与圆C的交点为O，P，与直线l的交点为Q，求线段PQ的长．【考点】QH：参数方程化成普通方程；Q4：简单曲线的极坐标方程．【分析】（1）因为，利用平方关系消参得：（x﹣1）2+y2=1，把x=ρcosθ，y=ρsinθ代入可得圆C的极坐标方程．（2）射线的极坐标方程是，设点P（ρ1，θ1），则：，解得ρ1，θ1．设点Q（ρ2，θ2），则：，解得ρ2，θ2，根据θ1=θ2，可得|PQ|=|ρ1﹣ρ2|．【解答】解：（1）因为，消参得：（x﹣1）2+y2=1，把x=ρcosθ，y=ρsinθ代入得（ρcosθ﹣1）2+（ρsinθ）2=1，所以圆C的极坐标方程为ρ=2cosθ；（2）射线的极坐标方程是，设点P（ρ1，θ1），则有：，解得，设点Q（ρ2，θ2），则：，解得，由于θ1=θ2，所以|PQ|=|ρ1﹣ρ2|=2，所以线段PQ的长为2．23．设函数f（x）=|x﹣|+|x+a|（a＞0）．（1）证明：f（x）≥4；（2）若f（2）＜5，求a的取值范围．【考点】R6：不等式的证明；R5：绝对值不等式的解法．【分析】（1）利用绝对值三角不等式，化简，然后利用基本不等式证明即可．（2）化简f（2）＜5，通过对a与2的大小比较，讨论求解不等式的解集即可．【解答】证明：（1）；当且仅当a=2时取等号．…解：（2）①当a=2时，显然满足；②当0＜a≤2时，，即a2﹣5a+4＜0⇒1＜a＜4，联立求解得1＜a≤2；③当a＞2时，⇒a2﹣a﹣4＜0，⇒，联立求解得综上，a的取值范围为。

四川省泸州市2017年高考一模试卷（理科数学）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知（a，b∈R），其中i为虚数单位，则a+b=（）A．0 B．1 C．﹣1 D．22．已知集合A={x|x2+3x≤0}，集合B={n|n=2k+1，k∈Z}，则A∩B=（）A．{﹣1，1} B．{1，3} C．{﹣3，﹣1} D．{﹣3，﹣1，1，3}3．“x＜2”是“ln（x﹣1）＜0”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件4．如果a＜b＜0，那么下列不等式成立的是（）A．B．ab＜b2C．﹣ab＜﹣a2D．5．一算法的程序框图如图所示，若输出的，则输入的x可能为（）A．﹣1 B．1 C．1或5 D．﹣1或16．已知向量，向量，则△ABC的形状为（）A．等腰直角三角形B．等边三角形C．直角非等腰三角形D．等腰非直角三角形7．已知a＞0，x，y满足约束条件，z=x+2y的最小值为﹣2，则a=（）A．B．C．1 D．28．《张丘建算经》中女子织布问题为：某女子善于织布，一天比一天织得快，且从第2天开始，每天比前一天多织相同量的布，已知第一天织5尺布，一月（按30天计）共织390尺布，则从第2天起每天比前一天多织（）尺布．A．B．C．D．9．函数的图象与x轴交点的横坐标构成一个公差为的等差数列，要得到函数g（x）=Acosωx的图象，只需将f（x）的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位10．已知函数f（x）=，则y=f（x）的图象大致为（）A．B．C．D．11．如图所示，用一边长为的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋（球体）离蛋巢底面的最短距离为（）A．B．C．D．12．已知函数f（x）=，若存在实数x1，x2，x3，x4，当x1＜x2＜x3＜x4时满足f （x 1）=f （x 2）=f （x 3）=f （x 4），则x 1•x 2•x 3•x 4的取值范围是（ ）A ．（7，）B ．（21，） C ．[27，30） D ．（27，）二、填空题（每题5分，满分20分，将答案填在答题纸上） 13．设函数f （x ）=（x+1）（2x+3a ）为偶函数，则a= ．14．在三角形ABC 中，点E ，F 满足，，若，则x+y= ．15．小王同学骑电动自行车以24km/h 的速度沿着正北方向的公路行驶，在点A 处望见电视塔S 在电动车的北偏东30°方向上，20min 后到点B 处望见电视塔在电动车的北偏东75°方向上，则电动车在点B 时与电视塔S 的距离是 km ．16．已知f （x ）=x+alnx （a ＞0）对于区间[1，3]内的任意两个相异实数x 1，x 2，恒有成立，则实数a 的取值范围是 ．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．已知2sin α•tan α=3，且0＜α＜π． （1）求α的值；（2）求函数f （x ）=4sinxsin （x ﹣α）在上的值域．18．如图，在四棱锥S ﹣ABCD 中，底面ABCD 是菱形，SA ⊥平面ABCD ，M ，N 分别为SA ，CD 的中点．（I ）证明：直线MN ∥平面SBC ； （Ⅱ）证明：平面SBD ⊥平面SAC ．19．某企业拟用10万元投资甲、乙两种商品．已知各投入x 万元，甲、乙两种商品分别可获得y 1，y 2万元的利润，利润曲线，P 2：y 2=bx+c ，如图所示．（1）求函数y 1，y 2的解析式；（2）应怎样分配投资资金，才能使投资获得的利润最大？20．已知数列{a n }的前n 项和s n ，点（n ，s n ）（n ∈N *）在函数y=x 2+x 的图象上 （1）求{a n }的通项公式；（2）设数列{}的前n 项和为T n ，不等式T n ＞log a （1﹣a ）对任意的正整数恒成立，求实数a 的取值范围．21．已知f （x ）=2ln （x+2）﹣（x+1）2，g （x ）=k （x+1）． （Ⅰ）求f （x ）的单调区间；（Ⅱ）当k=2时，求证：对于∀x ＞﹣1，f （x ）＜g （x ）恒成立；（Ⅲ）若存在x 0＞﹣1，使得当x ∈（﹣1，x 0）时，恒有f （x ）＞g （x ）成立，试求k 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22．已知直线l 的参数方程是（t 是参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系．曲线C 的极坐标方程为ρ=4cos （θ+）．（1）判断直线l 与曲线C 的位置关系；（2）过直线l 上的点作曲线C 的切线，求切线长的最小值． 23．已知函数f （x ）=|2x ﹣1|﹣|x+2|． （1）求不等式f （x ）＞0的解集；（2）若存在x 0∈R ，使得f （x 0）+2a 2＜4a ，求实数a 的取值范围．四川省泸州市2017年高考一模试卷（理科数学）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知（a，b∈R），其中i为虚数单位，则a+b=（）A．0 B．1 C．﹣1 D．2【考点】复数代数形式的乘除运算．【分析】直接由复数代数形式的乘除运算化简，再由复数相等的充要条件列出方程组，求解即可得a，b的值，则答案可求．【解答】解：∵=，∴，解得，则a+b=1．故选：B．2．已知集合A={x|x2+3x≤0}，集合B={n|n=2k+1，k∈Z}，则A∩B=（）A．{﹣1，1} B．{1，3} C．{﹣3，﹣1} D．{﹣3，﹣1，1，3}【考点】交集及其运算．【分析】求出集合A中的一元二次不等式的解集确定出集合A，观察发现集合B为所有的奇数集，所以找出集合A解集中的奇数解即为两集合的交集．【解答】解：由集合A中的不等式x2+3x≤0，因式分解得：x（x+3）＜0，解得：﹣3＜x＜0，所以集合A=（﹣3，0）；根据集合B中的关系式n=2k+1，k∈Z，得到集合B为所有的奇数集，则集合A∩B={﹣3，﹣1}．故选：C3．“x＜2”是“ln（x﹣1）＜0”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据对数函数的性质结合集合的包含关系判断即可．【解答】解：由ln（x﹣1）＜0，得：0＜x﹣1＜1，解得：1＜x＜2，故x＜2是1＜x＜2的必要不充分条件，故选：B．4．如果a＜b＜0，那么下列不等式成立的是（）A．B．ab＜b2C．﹣ab＜﹣a2D．【考点】不等关系与不等式．【分析】由于a＜b＜0，不妨令a=﹣2，b=﹣1，代入各个选项检验，只有D正确，从而得出结论．【解答】解：由于a＜b＜0，不妨令a=﹣2，b=﹣1，可得=﹣1，∴，故A不正确．可得ab=2，b2=1，∴ab＞b2，故B不正确．可得﹣ab=﹣2，﹣a2=﹣4，∴﹣ab＞﹣a2，故C不正确．故选D．5．一算法的程序框图如图所示，若输出的，则输入的x可能为（）A．﹣1 B．1 C．1或5 D．﹣1或1【考点】选择结构；程序框图．【分析】根据流程图所示的顺序，逐框分析程序中各变量、各语句的作用可知：该程序的作用是求分段函数的函数值．利用输出的值，求出输入的x的值即可．【解答】解：这是一个用条件分支结构设计的算法，该程序框图所表示的算法的作用是求分段函数y=的函数值，输出的结果为，当x≤2时，sin=，解得x=1+12k，或x=5+12k，k∈Z，即x=1，﹣7，﹣11，…当x＞2时，2x=，解得x=﹣1（不合，舍去），则输入的x可能为1．故选B．6．已知向量，向量，则△ABC的形状为（）A．等腰直角三角形B．等边三角形C．直角非等腰三角形D．等腰非直角三角形【考点】平面向量的坐标运算．【分析】由已知向量的坐标求得的坐标，可得，结合得答案．【解答】解：∵，，∴=（3，1），∴．又．∴△ABC的形状为等腰直角三角形．故选A．7．已知a＞0，x，y满足约束条件，z=x+2y的最小值为﹣2，则a=（）A．B．C．1 D．2【考点】简单线性规划．【分析】由约束条件作出可行域，数形结合得到最优解，联立方程组求得最优解的坐标，代入ax﹣y﹣2a=0得答案．【解答】解：由约束条件，作出可行域如图，联立，解得A（1，﹣），z=x+2y的最小值为﹣2，由图形可知A是目标函数的最优解，A在ax﹣y﹣2a=0上，可得：a+﹣2a=0解得a=．故选：B．8．《张丘建算经》中女子织布问题为：某女子善于织布，一天比一天织得快，且从第2天开始，每天比前一天多织相同量的布，已知第一天织5尺布，一月（按30天计）共织390尺布，则从第2天起每天比前一天多织（）尺布．A．B．C．D．【考点】数列的应用．【分析】利用等差数列的求和公式即可得出．}的公差为d，【解答】解：设此等差数列{an则30×5+d=390，解得d=，故选：D．9．函数的图象与x轴交点的横坐标构成一个公差为的等差数列，要得到函数g（x）=Acosωx的图象，只需将f（x）的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位【考点】函数y=Asin（ωx+φ）的图象变换．【分析】函数的图象与x轴交点的横坐标构成一个公差为的等差数列，可知周期T=，可得ω的值，根据三角函数的平移变换规律可得结论．【解答】解：由题意，函数的图象与x轴交点的横坐标构成一个公差为的等差数列，可知周期T=，那么：ω=．则f（x）=Asin（3x+）=Asin3（x+）要得到g（x）=Acos3x，即Acos3x=Asin（3x+）=Asin3（x+）由题意：可得：f（x）向左平移可得g（x）故选A10．已知函数f（x）=，则y=f（x）的图象大致为（）A．B．C．D．【考点】利用导数研究函数的单调性；函数的图象．【分析】利用函数的定义域与函数的值域排除B，D，通过函数的单调性排除C，推出结果即可．【解答】解：令g（x）=x﹣lnx﹣1，则，由g'（x）＞0，得x＞1，即函数g（x）在（1，+∞）上单调递增，由g'（x）＜0得0＜x＜1，即函数g（x）在（0，1）上单调递减，=g（0）=0，所以当x=1时，函数g（x）有最小值，g（x）min于是对任意的x∈（0，1）∪（1，+∞），有g（x）≥0，故排除B、D，因函数g（x）在（0，1）上单调递减，则函数f（x）在（0，1）上递增，故排除C，故选A．11．如图所示，用一边长为的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋（球体）离蛋巢底面的最短距离为（）A．B．C．D．【考点】球的体积和表面积．【分析】由条件利用球的截面的性质求得球心到截面圆的距离，再求出垂直折起的4个小直角三角形的高，再与球的半径相加即得答案．【解答】解：由题意可得，蛋巢的底面是边长为1的正方形，故经过4个顶点截鸡蛋所得的截面圆的直径为1，由于鸡蛋的体积为π，故鸡蛋（球）的半径为1，故球心到截面圆的距离为=，而垂直折起的4个小直角三角形的高为，故鸡蛋最低点与蛋巢底面的距离为，故选：D．12．已知函数f（x）=，若存在实数x1，x2，x3，x4，当x1＜x2＜x3＜x4时满足f（x1）=f（x2）=f（x3）=f（x4），则x1•x2•x3•x4的取值范围是（）A．（7，）B．（21，）C．[27，30）D．（27，）【考点】函数的值．【分析】画出分段函数的图象，求得（3，1），（9，1），令f（xl ）=f（x2）=f（x3）=f（x4）=a，作出直线y=a，通过图象观察，可得a的范围，运用对数的运算性质和余弦函数的对称性，可得x1x2=1，x3+x4=12，再由二次函数在（3，4.5）递增，即可得到所求范围．【解答】解：画出函数f（x）的图象，令f（xl ）=f（x2）=f（x3）=f（x4）=a，作出直线y=a，由x=3时，f（3）=﹣cosπ=1；x=9时，f（9）=﹣cos3π=1．由图象可得，当0＜a＜1时，直线和曲线y=f（x）有四个交点．由图象可得0＜x1＜1＜x2＜3＜x3＜4.5，7.5＜x4＜9，则|log3x1|=|log3x2|，即为﹣log3x1=log3x2，可得x1x2=1，由y=﹣cos（x）的图象关于直线x=6对称，可得x3+x4=12，则x1•x2•x3•x4=x3（12﹣x3）=﹣（x3﹣6）2+36在（3，4.5）递增，即有x1•x2•x3•x4∈（27，）．故选：D．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．设函数f（x）=（x+1）（2x+3a）为偶函数，则a= ﹣．【考点】函数奇偶性的性质．【分析】根据偶函数的定义，可得一次项系数为0，从而可得结论．【解答】解：函数f（x）=（x+1）（2x+3a）=2x2+（3a+2）x+3a∵函数f（x）=（x+1）（2x+3a）为偶函数，∴2x2﹣（3a+2）x+3a=2x2+（3a+2）x+3a∴3a+2=0∴a=﹣，故答案为：14．在三角形ABC中，点E，F满足，，若，则x+y= ．【考点】平面向量的基本定理及其意义．【分析】首先利用平面向量的三角形法则得到，然后用表示，结合平面向量基本定理得到x，y．【解答】解：在三角形ABC中，点E，F满足，，若==，所以x=﹣，y=，则x+y=；故答案为：15．小王同学骑电动自行车以24km/h的速度沿着正北方向的公路行驶，在点A处望见电视塔S 在电动车的北偏东30°方向上，20min 后到点B 处望见电视塔在电动车的北偏东75°方向上，则电动车在点B 时与电视塔S 的距离是 km ．【考点】解三角形的实际应用．【分析】在△ABS 中，可得∠BAS=30°，AB=8，∠ABS=180°﹣75°=105°则∠ASB=45°，由正弦定理可得BS=．【解答】解：如图，由已知可得，AB=24×=8． 在△ABS 中，∠BAS=30°，AB=8，∠ABS=180°﹣75°=105° ∠ASB=45°由正弦定理可得BS==4，故答案为16．已知f （x ）=x+alnx （a ＞0）对于区间[1，3]内的任意两个相异实数x 1，x 2，恒有成立，则实数a 的取值范围是 （0，） ．【考点】利用导数求闭区间上函数的最值．【分析】问题等价于|1+|＜，（1），由x 1，x 2→时（1）变为|1+3a|＜9，由x 1，x 2→1时（1）变为|1+a|＜1，得到关于a 的不等式，解出即可． 【解答】解：已知a ＞0，f （x ）=x+alnx ，对区间[1，3]内的任意两个相异的实数x 1，x 2，恒有|f （x 1）﹣f （x 2）|＜|﹣|，∴|x 1﹣x 2+a （lnx 1﹣lnx 2）|＜||，两边都除以|x 1﹣x 2|，∵|1+|＜，（1）（lnx ）′=∈[，1]，∴∈[，1]，x 1，x 2→时（1）变为|1+3a|＜9，解得：﹣＜a ＜，x 1，x 2→1时（1）变为|1+a|＜1， 解得：﹣2＜a ＜0， 又∵a ＞0，∴0＜a ＜，故答案为（0，）．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．已知2sin α•tan α=3，且0＜α＜π． （1）求α的值；（2）求函数f （x ）=4sinxsin （x ﹣α）在上的值域．【考点】同角三角函数基本关系的运用；三角函数中的恒等变换应用． 【分析】（1）利用同角三角函数的基本关系，求得sin α的值，可得α的值．（2）利用三角恒等变换化简函数的解析式，再利用正弦函数的定义域和值域求得函数f （x ）=4sinxsin （x ﹣α）在上的值域．【解答】解：（1）∵2sin α•tan α=3，且0＜α＜π．∴2sin 2α=3cos α，∴2﹣2cos 2α=3cos α，∴2cos 2α+3cos α﹣2=0，解得cos α=，或cos α=﹣2（舍），∴α=．（2）∵α=，∴函数f（x）=4sinxsin（x﹣）=4sinx（sinxcos﹣cosxsin）==，∵，∴，∴，则，∴f（x）∈[﹣1，0]．18．如图，在四棱锥S﹣ABCD中，底面ABCD是菱形，SA⊥平面ABCD，M，N分别为SA，CD的中点．（I）证明：直线MN∥平面SBC；（Ⅱ）证明：平面SBD⊥平面SAC．【考点】直线与平面平行的判定；直线与平面垂直的判定．【分析】（Ⅰ）取SB中点E，连接ME、CE，由三角形中位线定理、菱形性质得四边形MECN是平行四边形，由此能证明直线MN∥平面SBC．（Ⅱ）连接AC、BD，交于点O，由线面垂直得SA⊥BD，由菱形性质得AC⊥BD，由此能证明平面SBD⊥平面SAC．【解答】（Ⅰ）证明：如图，取SB中点E，连接ME、CE，因为M为SA的中点，所以ME∥AB，且ME=，…因为N为菱形ABCD边CD的中点，所以CN∥AB，且CN=，…所以ME∥CN，ME=CN，所以四边形MECN是平行四边形，所以MN∥EC，…又因为EC⊂平面SBC，MN⊄平面SBC，所以直线MN ∥平面SBC ．…（Ⅱ）证明：如图，连接AC 、BD ，交于点O ， 因为SA ⊥底面ABCD ，所以SA ⊥BD ．… 因为四边形ABCD 是菱形，所以AC ⊥BD ．… 又SA ∩AC=A ，所以BD ⊥平面SAC ．…又BD ⊂平面SBD ，所以平面SBD ⊥平面SAC ．…19．某企业拟用10万元投资甲、乙两种商品．已知各投入x 万元，甲、乙两种商品分别可获得y 1，y 2万元的利润，利润曲线，P 2：y 2=bx+c ，如图所示．（1）求函数y 1，y 2的解析式；（2）应怎样分配投资资金，才能使投资获得的利润最大？【考点】函数的最值及其几何意义；函数解析式的求解及常用方法．【分析】（1）将（1，1.25），（4，2.5）代入曲线，解方程可得；由P 2：y 2=bx+c过原点，可得c=0，将（4，1）代入，可得b ，即可得到P 2的方程；（2）设甲投资x 万元，则乙投资为（10﹣x ）万元，投资获得的利润为y 万元，则=，令，转化为二次函数的最值求法，即可得到所求最大值．【解答】解：（1）由题知（1，1.25），（4，2.5）在曲线P 1上，则，解得，即．又（4，1）在曲线P 2上，且c=0，则1=4b ，则，所以．（2）设甲投资x 万元，则乙投资为（10﹣x ）万元，投资获得的利润为y 万元，则=，令，则．当，即（万元）时，利润最大为万元，此时10﹣x=3.75（万元），答：当投资甲商品6.25万元，乙商品3.75万元时，所获得的利润最大值为万元．20．已知数列{a n }的前n 项和s n ，点（n ，s n ）（n ∈N *）在函数y=x 2+x 的图象上 （1）求{a n }的通项公式；（2）设数列{}的前n 项和为T n ，不等式T n ＞log a （1﹣a ）对任意的正整数恒成立，求实数a 的取值范围．【考点】等差数列与等比数列的综合．【分析】（1），再写一式，即可求{a n }的通项公式；（2）由（1）知a n =n ，利用裂项法可求=（﹣），从而可求得T n ═ [（1﹣）+（﹣）+（﹣）+…+（﹣）]，由T n+1﹣T n =＞0，可判断数列{T n }单调递增，从而可求得a 的取值范围．【解答】解：（1）∵，∴①当②①﹣②得a n =n当，∴a n =n ；（2）由（1）知a n =n ，则=（﹣）．∴T n ═ [（1﹣）+（﹣）+（﹣）+…+（﹣）]=（1+﹣﹣）=﹣（+）．∵T n+1﹣T n =＞0，∴数列{T n }单调递增，∴（T n ）min =T 1=．要使不等式T n ＞log a （1﹣a ）对任意正整数n 恒成立，只要＞log a （1﹣a ）． ∵1﹣a ＞0， ∴0＜a ＜1．∴1﹣a ＞a ，即0＜a ＜．21．已知f （x ）=2ln （x+2）﹣（x+1）2，g （x ）=k （x+1）． （Ⅰ）求f （x ）的单调区间；（Ⅱ）当k=2时，求证：对于∀x ＞﹣1，f （x ）＜g （x ）恒成立；（Ⅲ）若存在x 0＞﹣1，使得当x ∈（﹣1，x 0）时，恒有f （x ）＞g （x ）成立，试求k 的取值范围．【考点】利用导数研究函数的单调性；函数恒成立问题．【分析】（Ⅰ）求出定义域和导数f′（x ），令f′（x ）＞0，解出增区间，令f′（x ）＜0，解出减区间；（Ⅱ）令H （x ）=f （x ）﹣g （x ），利用导数判断出H （x ）的单调性和单调区间，得出H （x ）的最大值，证明H max （x ）＜0即可．【解答】解：（Ⅰ），当f′（x ）＞0 时，所以 x 2+3x+1＜0，解得﹣2＜x ，当f′（x）＜0时，解得，所以 f（x）单调增区间为，递减区间是（，+∞）；（Ⅱ）当k=2时，g（x）=2（x+1）．令H（x）=f（x）﹣g（x）=2ln（x+2）﹣（x+1）2﹣2（x+1）．H′（x）=，令H′（x）=0，即﹣2x2﹣8x﹣6=0，解得x=﹣1或x=﹣3（舍）．∴当x＞﹣1时，H′（x）＜0，H（x）在（﹣1，+∞）上单调递减．（x）=H（﹣1）=0，∴Hmax∴对于∀x＞﹣1，H（x）＜0，即f（x）＜g（x）．（Ⅲ）由（II）知，当k=2时，f （x）＜g （x）恒成立，即对于“x＞﹣1，2 ln （x+2）﹣（x+1）2＜2 （x+1），不存在满足条件的x；当k＞2时，对于“x＞﹣1，x+1＞0，此时2 （x+1）＜k （x+1）．∴2 ln （x+2）﹣（x+1）2＜2 （x+1）＜k （x+1），即f （x）＜g （x）恒成立，不存在满足条件的x；令h（x）=f（x）﹣g（x）=2ln（x+2）﹣（x+1）2﹣k（x+1），h′（x）=，当k＜2时，令t （x）=﹣2x2﹣（k+6）x﹣（2k+2），可知t （x）与h′（x）符号相同，，+∞）时，t （x）＜0，h′（x）＜0，h （x）单调递减，当x∈（x当x∈（﹣1，x）时，h （x）＞h （﹣1）=0，即f （x）﹣g （x）＞0恒成立，综上，k的取值范围为（﹣∞，2）．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22．已知直线l的参数方程是（t是参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．曲线C的极坐标方程为ρ=4cos（θ+）．（1）判断直线l与曲线C的位置关系；（2）过直线l上的点作曲线C的切线，求切线长的最小值．【考点】简单曲线的极坐标方程；参数方程化成普通方程．【分析】（1）分别求出直线和曲线的普通方程，根据点到直线的距离，求出直线l与曲线C 的位置关系；（2）根据点到直线的距离求出直线l上的点向圆C引的切线长的最小值即可．【解答】解：（1）直线l方程：y=x+4，ρ=4cos（θ+）=2cosθ﹣2sinθ，∴ρ2=2ρcosθ﹣2sinθ，∴圆C的直角坐标方程为x2+y2﹣2x+2y=0，即+=4，∴圆心（，﹣）到直线l的距离为d=6＞2，故直线与圆相离．（2）直线l的参数方程化为普通方程为x﹣y+4=0，则圆心C到直线l的距离为=6，∴直线l上的点向圆C引的切线长的最小值为=4．23．已知函数f（x）=|2x﹣1|﹣|x+2|．（1）求不等式f（x）＞0的解集；（2）若存在x0∈R，使得f（x）+2a2＜4a，求实数a的取值范围．【考点】绝对值三角不等式．【分析】（1）把f（x）用分段函数来表示，令f（x）=0，求得x的值，可得不等式f（x）＞0的解集．（2）由（1）可得f（x）的最小值为f（），再根据f（）＜4a﹣2a2 ，求得a的范围．【解答】解：（1）函数f（x）=|2x﹣1|﹣|x+2|=，令f（x）=0，求得x=﹣，或 x=3，故不等式f（x）＞0的解集为{x|x＜﹣，或x＞3}．（2）若存在x0∈R，使得f（x）+2a2＜4a，即f（x）＜4a﹣2a2 有解，由（1）可得f （x ）的最小值为f （）=﹣3•﹣1=﹣，故﹣＜4a ﹣2a 2 ，求得﹣＜a ＜．。

泸州市2017届高三第一次教学教学质量诊断性考试数学（理工类）一、选择题：本大题共有10个小题，每小题5分，共50分.每小题给出的四个选项中，只有一项是符合要求的． 1．已知全集U ={1，2，3，4，5，6，7，8}，M ={1，3，5，7}，N ={5，6，7}，则()U M N ð=A ．{5，7}B ．{2，4}C ．{1，3，5，6，7}D ．{2，4，8}2. 下列命题中的假命题是A ．x ∀∈R ，120x -> B ．x *∀∈N ，2(1)0x -> C ．x ∃∈R ，lg 1x < D ．x ∃∈R ，tan 2x =3. 12lg 2lg25-的值为 A ．1 B ．2 C ．3 D ．44.函数()211sin f x x x ⎛⎫=- ⎪⎝⎭的图象大致为A ．B ．C ．D ．5．△ABC 中，若 2AD DB = ，13CD CA CB λ=+，则λ=A ．13B ．23C ．23-D ．13-6．将函数()()sin 2f x x θ=+（其中22ππθ-<<）的图象向右平移()0ϕϕ>个单位长度后得到函数()g x 的图象，若函数()(),f x g x 的图象都经过点P ⎛ ⎝⎭，则的值可以是A ．53πB ．6πC ．2πD ．56π7．设数列{}n a 是首项大于零的等比数列，则“12a a <”是“数列{}n a 是递增数列”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 8． 若曲线()12f x x =在点()(),a f a 处的切线与两条坐标轴围成的三角形的面积为18，则a =A. 64B. 32C. 16D. 89．一支人数是5的倍数且不少于1000人的游行队伍，若按每横排4人编队，最后差3人；若按每横排3人编队，最后差2人；若按每横排2人编队，最后差1人．则这只游行队伍的最少人数是 A ．1025 B ．1035 C ．1045 D ．105510．定义在R 上的函数()f x 满足()221,11(4)(),()log 22,1 3.x x f x f x f x x x ⎧-+-⎪+==⎨--+<⎪⎩≤≤≤，若关于x 的方程()0f x ax -=有5个不同实根，则正实数a 的取值范围是A ．11(,)43B ．11(,)64C．1(16)6-D．1(,86-二、填空题：本大题共5小题，每小题5分，共25分．11．复数22(56)(215)i m m m m +++--（i 是虚数单位）是纯虚数，则实数m 的值为 ．12．等比数列{}n a 中，若公比4q =，且前3项之和等于21，则该数列的通项公式n a = ． 13．函数()log a f x x=（其中01a <<），则使314f ⎛⎫< ⎪⎝⎭成立的a 的取值范围是 ．14. 设()f x 是定义在R 上的奇函数，且当0x ≥时，2()f x x =，若对任意[],2x a a ∈+，不等式()()31f x a f x +≥+恒成立，则实数a 的取值范围是 . 15．已知集合()()()()(){}22|,A f x fx f y f x y f x y x y R =-=+-∈，有下列命题；①若()1,01x f x x ≥⎧=⎨-<⎩，则()f x A ∈；②若()f x kx =，则()f x A ∈；③若()f x A ∈，则()y f x =可为奇函数；④若()f x A ∈，则对任意不等实数12,x x ，总有()()1212f x f x x x-<-成立。