托勒密定理塞瓦定理梅涅劳斯定理西姆松定理

《竞赛数学解题研究》之平面几何专题一、平面几何中的一些重要定理：1、梅涅劳斯定理：设D 、E 、F 分别是ABC ∆三边（或其延长线）上的三点，则D 、E 、F 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。

2、塞瓦定理：设D 、E 、F 分别是ABC ∆三边（或其延长线）上的三点，则AF 、BE 、CD 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。

3、托勒密定理：四边形ABCD 内接于圆的充要条件是CD BC CD AB BD AC ⋅+⋅=⋅4、西摩松定理：设P 是ABC ∆外接圆上任一点，过P 向ABC ∆的三边分别作垂线，设垂足为D 、E 、F ，则D 、E 、F 三点共线。

5、斯德瓦特定理：设P 是ABC ∆的边BC 边上的任一点，则BC PC BP AP BC AB PC AC BP ⋅⋅+⋅=⋅+⋅2226、共角定理：设ABC ∆和C B A '''∆中有一个角相等或互补（不妨设A=A '）则 C A B A ACAB S S C B A ABC ''⋅''⋅='''∆∆7、共边定理：设ABC ∆和C B A '''∆中有一个边相等，则CA B A ACAB S S C B A ABC ''⋅''⋅='''∆∆举例说明：1、设M 、N 分别是正六边形ABCDEF 的对角线AC 、CE 上的点，且AM:AC=CN:CE=k,如果BMN 三点共线，试求k 。

（IMO23,1982）2、在四边形ABCD 中，ABD ∆、BCD ∆、ABC ∆的面积之比为3：4：1，点M 、N 分别 是AC 、CD 上的点，且AM:AC=CN:CD, 并且BMN 三点共线，求证：M 、N 分别是AC 、 CD 的中点。

初等几何五大ZB定理某日，燕尾模型讲毕，一六年级学霸级学生说，其可用燕尾模型证梅涅劳斯定理，大惊，问其如何得之，其说：一老师讲的。

六年级学生学梅涅劳斯定理，ZB大于实用。

既然学生感兴趣，咱就一装到底。

一、梅涅劳斯定理梅涅劳斯：古希腊数学家。

梅涅劳斯定理指的是：一条直线（红线）与一个三角形的三边或延长线相交，三角形的三个顶点按顺时针或逆时针方向，三条边顶点到交点的比值的积为1.其证明方法很多，相似三角形即可证明。

下面咱们用小学奥数的“燕尾模型”证明一下。

二、塞瓦定理塞瓦：意大利数学家、水利工程师，该定理于1678年发表于《直线论》一书。

塞瓦定理：可以简单记为三线共点的充要条件是：顺时针或逆时针的分线段的比值积为1.该定理可以用上面的梅涅劳斯定理证明。

三、斯坦纳定理斯坦纳：瑞士几何学家斯坦纳定理：两内角平分线相等的三角形必为等腰三角形。

早在2000多年前，《几何原本》就有定理：等腰三角形的两底角平分线的长相等。

可是它的逆定理书上却只字未提，估计作者也不会，呵呵。

直到1840年，莱默斯请求斯图姆给予纯几何证明，可斯图姆也不会，最后斯坦纳给出了证明，因此该定理也称作：斯坦纳——莱默斯定理。

现在很多高中生也能证明。

大家可以试试有没有难度。

四、托勒密定理托勒密定理:圆内接凸四边形的对边积的和等于对角线的积。

用相似可以证明五、西姆松定理西姆松定理：过三角形外接圆上异于三角形顶点的任意一点作三边所在直线垂线，则三垂足在一点直线上，这条直线我们称作西姆松线。

这些定理一般的中考都不考，一和四和中学的相似联系比较紧密，尽量掌握，培优课上可能会有，感兴趣的同学可以看看。

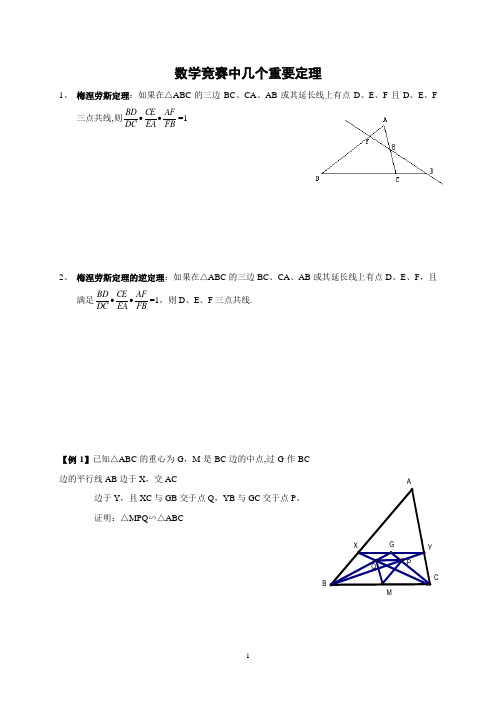
数学竞赛中几个重要定理1、 梅涅劳斯定理：如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理：如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ，且满足FBAFEA CE DC BD ••=1，则D 、E 、F 三点共线.【例1】已知△ABC 的重心为G ，M 是BC 边的中点,过G 作BC 边的平行线AB 边于X ，交AC边于Y ，且XC 与GB 交于点Q ，YB 与GC 交于点P 。

证明：△MPQ ∽△ABCjMQGACBXYP【例2】以△ABC的底边BC为直径作半圆,分别与边AB，AC交于点D和E，分别过点D，E作BC的垂线,垂足依次为F，G，线段DG和EF交于点M.求证：AM⊥BC【例3】四边形ABCD内接于圆，其边AB,DC的延长线交于点P，AD和BC的延长线交于点Q，过Q作该圆的两条切线,切点分别为E,F。

求证:P,E，F三点共线。

【练习1】设凸四边形ABCD 的对角线AC 和BD 交于点M,过M 作AD 的平行线分别交AB ，CD于点E ，F ，交BC 的延长线于点O,P 是以O 为圆心，以OM 为半径的圆上一点。

求证：∠OPF=∠OEP【练习2】 在△ABC 中,∠A=900，点D 在AC 上，点E 在BD 上，AE 的延长线交BC 于F 。

若BE:ED=2AC ：DC ，则∠ADB=∠FDCD塞瓦定理：设O 是△ABC 内任意一点，AO 、BO 、CO 分别交对边于N 、P 、M ，则1=••PACPNCBN MBAM塞瓦定理的逆定理： 设M 、N 、P 分别在△ABC 的边AB 、BC 、CA 上，且满足1=••PACP NCBN MBAM ，则AN 、BP 、CM 相交于一点。

【例1】B E 是△ABC 的中线，G 在BE 上，分别延长AG ,CG 交BC ，AB 于点D,F ， 过D 作DN ∥CG 交BG 于N ，△DGL 及△FGM 是正三角形.求证:△LMN 为正三角形。

几何篇梅涅劳斯定理：当直线交三角形ABC三边所在直线BC、AC、A于点D、E、F时，（AF/FB）×（BD/DC）×（CE/EA）=1以及逆定理：在三角形ABC三边所在直线上有三点D、E、F，且（AF/FB）×（BD/DC）×（CE/EA）=1，那么D、E、F三点共线。

角元形式梅捏劳斯定理：（sin∠BAD/sin∠DAC）×(sin∠ACF/sin∠FCB)×(sin∠CBE/sin∠EBA)=1塞瓦定理：指在△ABC内任取一点O，直线AO、BO、CO分别交对边于D、E、F，则(BD/DC)×(CE/EA)×(AF/FB)=1。

角元塞瓦定理：AD,BE,CF交于一点的充分必要条件是：(sin∠BAD/sin∠DAC)*(sin∠ACF/sin∠FCB)*(sin∠CBE/sin∠EBA)=1逆定理：在△ABC的边BC，CA，AB上分别取点D，E，F，如果(AF/FB)(BD/DC)(CE/EA)=1那么直线AD，BE，CF相交于同一点。

”正弦定理：在△ABC中，角A、B、C所对的边长分别为a、b、c，三角形外接圆的半径为R。

则有：a/sinA=b/sinB=c/sinC=2R余弦定理：，在△ABC中，余弦定理可表示为：c²=a²+b²-2ab cosCa²=b²+c²-2bc cosAb²=a²+c²-2ac cosB托勒密定理：指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。

三弦定理：由圆上一点引出三条弦,中间一弦与最大角正弦的积等于其余每条弦与不相邻角正弦的积之和。

用图表述；圆上一点A,引出三条弦AB(左)、AC(右)、及中间弦AD,BC与AD交于P,根据《三弦定理》,有以下关系, ABsin∠CAP +ACsin∠BAP= ADsin∠BAC。

B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理（梅氏线）△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ，则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。

塞瓦(Ceva)定理（塞瓦点）△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ，则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。

托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。

西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。

例题：1、设AD 是△ABC 的边BC 上的中线，直线CF 交AD 于F 。

求证：FBAF 2ED AE =。

【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅（梅氏定理） 【评注】也可以添加辅助线证明：过A 、B 、D 之一作CF 的平行线。

2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ，交CB 于D 。

求证：1FACFEA BE =+。

【分析】连结并延长AG 交BC 于M ，则M 为BC 的中点。

DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅（梅氏定理）DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅（梅氏定理）∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上，λ===EACEFB AF DC BD ，AD 、BE 、CF 交成△LMN 。

求S △【分析】【评注】梅氏定理4、以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。

求证：AE 、BF 、CG 相交于一点。

【分析】【评注】塞瓦定理5、已知△ABC 中，∠B=2∠C 。

托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。

原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．定理的提出一般几何教科书中的“定理”，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。

证明一、（以下是推论的证明，托勒密定理可视作特殊情况。

）在任意四边形ABCD中，作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE，，∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数，则AB、C D、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。

首先注意到：(a? b)(c? d) + (a? d)(b? c) = (a? c)(b?d) ，两边取，运用得。

等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。

四点不限于同一。

平面上，托勒密不等式是三角不等式的形式。

二、设ABCD是。

在BC上，∠BAC = ∠BDC，而在AB上，∠ADB = ∠ACB。

在AC上取一点K，使得∠ABK = ∠CBD；因为∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD，所以∠CBK = ∠ABD。

平面几何中的几个重要定理一．塞瓦定理塞瓦（G 。

Ceva 1647—1743），意大利著名数学家。

塞瓦定理 设S 为ABC ∆三边所在直线外一点，连接CS BS AS ,,分别和ABC ∆的边或三边的延长线交于R Q P ,,（如图1），则1=⋅⋅RB ARQA CQ PC BP与塞瓦定理同样重要的还有下面的定理。

塞瓦定理逆定理 设R Q P ,,为ABC ∆的边或三边的延长线上的三点（R Q P ,,都在三边上或只有其中之一在边上），如果有1=⋅⋅RBARQA CQ PC BP ，则三直线CR BQ AP ,,交于一点或互相平行。

ABCSPQRABCPQR2图ABCSPQRBACSPQR1 图例1． 如图3，P 是ABC ∆内一点，CP BP AP ,,分别与边AB CA BC ,,交于F E D ,,，过F E D ,,三点作圆，与三边交于F E D ''',,。

求证：F C E B D A ''',,交于一点。

例2．设C B A ''',,分别为ABC ∆三边AB CA BC ,,的中点，P 为C B A '''∆内一点，P C P B P A ''',,分别交B A A C C B '''''',,于N M L ,,（如图4）。

求证：CN BM AL ,,三线共点。

例3． 以ABC ∆各边为底边向外作相似的等腰三角形ABG CAF BCD ,,（如图5）。

求证CG BF AE ,,相交于一点。

3图•B 'ABCA 'L 'M 'N 'C 'MN P K 4图MNLABCFG5图二．梅涅劳斯定理Menelaus （公元98年左右），希腊数学家、天文学家，梅涅劳斯定理包含在其几何著作《球论》里。

数学竞赛中几个重要定理1、 梅涅劳斯定理：如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F 三点共线，则FB AF EA CE DC BD ∙∙=12、 梅涅劳斯定理的逆定理：如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ，且满足FB AF EA CE DC BD ∙∙=1，则D 、E 、F 三点共线。

3、 塞瓦定理：设O 是△ABC 内任意一点，AO 、BO 、CO 分别交对边于N 、P 、M ，则1=∙∙PA CP NC BN MB AM4、 塞瓦定理的逆定理：设M 、N 、P 分别在△ABC 的边AB 、BC 、CA 上，且满足1=∙∙PA CP NC BN MB AM ，则AN 、BP 、CM 相交于一点。

5、 广勾股定理的两个推论：推论1：平行四边形对角线的平方和等于四边平方和。

推论2：设△ABC 三边长分别为a 、b 、c ，对应边上中线长分别为m a 、m b 、m c则：m a =2222221a c b -+；m b =2222221b c a -+；m c =2222221c b a -+6、 三角形内、外角平分线定理：内角平分线定理：如图：如果∠1=∠2，则有AC AB DC BD =外角平分线定理：如图，AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D ，则有AC AB DC BD =7、 托勒密定理：四边形ABCD 是圆内接四边形，则有AB ·CD+AD ·BC=AC ·BD8、 三角形位似心定理：如图，若△ABC 与△DEF 位似，则通过对应点的三直线AD 、BE 、CF 共点于P9、正弦定理、在△ABC中有RCcBbAa2sinsinsin===（R为△ABC外接圆半径）余弦定理：a、b、c为△ABC的边，则有：a2=b2+c2-2bc·cosA; b2=a2+c2-2ac·cosB; c2=a2+b2-2ab·cosC;10、西姆松定理：点P是△ABC外接圆周上任意一点，PD⊥BC，PE⊥AC，PF⊥AB，D、E、F为垂足，则D、E、F三点共线，此直线称为西姆松线。

数学竞赛中几个重要定理1、梅涅劳斯定理：如果在厶ABC 的三边BC 、CA 、AB 或其延长线上有点 D 、E 、F 且D 、E 、F:如果在厶ABC 的三边 BC 、CA 、AB 或其延长线上有点 D 、E 、F ,且满足BC?C A?A F =1，则D 、E 、F 三点共线.【例1】已知△ ABC 的重心为G , M 是BC 边的中点，过 G 作BC 边的平行线 AB 边于X ，交AC边于Y ，且XC 与GB 交于点Q ，YB 与GC 交于点P. 证明：△ MPQ ABC三点共线，则BC?CA?AF=12、梅涅劳斯定理的逆定理AC【例2】以厶ABC的底边BC为直径作半圆，分别与边AB AC交于点D和E,分别过点D, E作BC的垂线，垂足依次为F，G,线段DG和EF交于点M.求证：AML BCH G【例3】四边形ABCD内接于圆，其边AB , DC 的延长线交于点P，AD和BC的延长线交于点过Q作该圆的两条切线，切点分别为E，F.求证: P，E，F三点共线.【练习1】设凸四边形ABCD的对角线AC和BD交于点M ,过M作AD的平行线分别交AB , CD于点E, F,交BC的延长线于点O, P是以0为圆心，以0M为半径的圆上一点.求证：/ 0PF= / 0EP【练习2】在厶ABC中, / A=90°,点D在AC上，点E在BD 上, AE的延长线交BC于F.若BE : ED=2AC : DC，则/ ADB= / FDCN、P、M,则j AM?_BN?Cp i MB NC塞瓦定理：设o是厶ABC内任意一点，AO、BO、CO分别交对边于PA Array塞瓦定理的逆定理：设M、N、P分别在△ ABC的边AB、BC、CA上，且满足空？聖？竺1，MB NC PA则AN、BP、CM相交于一点.【例1】BE是厶ABC的中线，G在BE上，分别延长AG，CG交BC，AB于点D, F,过D作DN // CG交BG于N, △ DGL及厶FGM是正三角形求证：△ LMN为正三角形.BD 1【例2】在厶ABC中，D是BC上的点=— , E是AC中点.AD与BE交于O, CO交AB于FDC 3求四边形BDOF的面积与厶ABC的面积的比【练习1】设P ABC内一点，使/ BPA= / CPA, G是线段AP上的一点，直线BG , CG分别交边AC , AB于E, F.求证：/ BPF= / CPEC【练习2】在厶ABC中，/ ABC和/ACB均为锐角.D是BC边BC上的内点，且AD平分/ BAC ,过点D作垂线DP丄AB于P, DQ丄AC于Q, CP于BQ相交于K.求证：AK丄BC【例1】 已知在△ ABC 中，AB>AC ,/ A 的一个外角的平分线交厶 ABC的外接圆于点 E ,过E 作EF 丄AB ，垂足为F.求证：2AF=AB -AC【例2】经过/ XOY 的平分线上的一点 A ，任作一直线与 0X 及0Y 分别相交于P , Q.求证：+ ^^为定值OP 0Q托勒密定理：四边形ABCD 是圆内接四边形，则有 AB • CD+AD • BC=AC •BDEAFBV【例3】解方程.x24+ ... x21八7X【练习1】设AF为O O1与O O2的公共弦，点B, C分别在O O1 , O O2上，且AB=AC，/ BAF , / CAF的平分线交O 01,0 02于点D , E.求证：DE丄AF【练习2】O 0为正△ ABC的外接圆，AD是O 0的直径，在弧BC上任取一点P （与B , C 不重合）.设E, F分别为△ PAB, △ PAC的内心证明：PD=I PE-PFI西姆松定理：点P 是厶ABC 外接圆周上任意一点, 垂足，则D 、E 、F 三点共线，此直线称为西姆松线 .【例1】过正△ ABC 外接圆的弧 AC 上点P 作P D 丄直线AB 于D,作PE 丄AC 于E,作PF 丄BC 于F.求证：丄+丄二丄PF PD PE【练习1】设P ABC 外接圆周上任一点，P 点关于边BC , AC 所在的直线的对称点分别为 P i , P 2.求证：直线P 1P 2经过△ ABC 的垂心.PD 丄 BC ,D APEB三角形的五心内心【例1】设点M是厶ABC的BC边的中点，I是其内心，AH是BC边上的高，E为直线IM与AH的交点.求证：AE等于内切圆半径rC【例2】在厶ABC中，AB=4 , AC=6 , BC=5 , / A的平分线AD交厶ABC的外接圆于K.O , I分别为△ ABC的外心，内心•求证：01丄AKC【练习】在厶ABC中，/ BAC=30°,/ ABC=7O0, M为形内一点，/ MAB= / MCA=20 0求/ MBA的度数.外心【例1】锐角△ ABC的外心为0,线段0A , BC的中点为M , N，/ ABC=4 / OMN ,/ ACB=6 / 0MN.求/ 0MNC【例2】在等腰△ ABC中，AB=BC , CD是它的角平分线，0是它的外心,过0作CD的垂线交BC于E,再过E作CD的平行线交AB于F，证明:BE=FD.【练习】1、O O i与o 02相交于P, Q,O O1的弦PA与O 02相切，O 02的弦PB与O O i相切.设厶PAB的外心为0,求证：0Q丄PQ重心【例1】在厶ABC中，G为重心，P是形内一点，直线PG交直线BC, CA, AB 于F, E, D.FP EP DP求证：+ + =3FG EG DG【例2】已知△ ABC的重心G和内心I的连线GI // BC,求证：AB+AC=2BCP02 010.BA【练习】1、设M为厶ABC的重心，且AM=3 , BM=4 , CM=5，求△ ABC的面积.2、设0是厶ABC的外心，AB=AC，D是AB的中点，G是厶ACD的重心，求证：0G丄CDA 垂心三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍.【例1】△ ABC的外接圆为O0, / C=6O0, M是弧AB的中点，H是厶ABC的垂心.求证：0M丄0HC【例2】已知AD , BE , CF是锐角△ ABC的三条高，过D作EF的平行线RQ, RQ分别交AB和AC于R, Q, P为EF与CB的延长线的交点证明：△ PQR的外接圆通过BC的中点M.旁心【例1】在锐角/ XAY内部取一点，使得/ ABC= / XBD，/ ACB= / YCD.证明：△ ABC的外心在线段AD上.【例2】AD是直角△ ABC斜边BC上的高（AB<AC ）, I i, I2分别是△ ABD , △ ACD的内心,△ A I i 12的外接圆O O分别交AB , AC于E, F,直线FE与CB的延长线交于点M.证明：I i, 12分别是△ ODM的内心与旁心相交两圆的性质与应用【例1】证明：若凸五边形ABCDE中，/ ABC= / ADE，/ AEC= / ADB.证明：/ BAC= / DAE【例2】已知O O i与O 02相交于A , B,直线MN垂直于AB且分别与O O i与O 02交于M , N , P是线段MN的中点，Q i, Q2分别是O O i与O 02上的点，/ AO i Q i = / AO2Q2求证：PQ i=PQ2【练习】梯形ABCD中，AB // CD , AB>CD, K, M分别是腰AD , CB上的点，/ DAM= / CBK,求证：/ DMA= /CKB其他的一些数学竞赛定理1、广勾股定理的两个推论：推论1：平行四边形对角线的平方和等于四边平方和推论2:设厶ABC 三边长分别为a 、b 、c ，对应边上中线长分别为m a 、m b 、m e贝U ： m a = — \2b 2 2c 2 a 2 ； 册=丄¥‘~2c 2~b 2 ； 咖=丄它 ~2b 2~e 2 2 '2 '2外角平分线定理：如图，AD 是厶ABC 中/ A 的外角平分线交 BC 的延长线与D ,3、三角形位似心定理：如图，若△ ABC 与厶DEF 位似，则通过对应点的三直线 AD 、BE 、CF 共点 2、三角形内、外角平分线定理 ：BD 内角平分线定理：如图：如果/ 1= / 2,则有 丿ABDC AC 则有电 DC AB ACP5、欧拉定理：△ ABC 的外接圆圆心为 O,半径为R ，内切圆圆心为I ，半径为r,记Ol=d,则有：d 2=R 2-2Rr.6、巴斯加线定理：圆内接六边形ABCDEF （不论其六顶点排列次序如何），其三组对边AB 与DE 、 BC 与EF 、CD 与FA 的交点P 、Q 、R 共线.4、 正弦定理、在△ ABC 中有 a sin A bsin B 2R （ R ABC 外接圆半径）sin C 余弦定理：a 、b 、cABC 的边，则有:a=b 2+c 2-2bc • cosA; b 2=a 2+c 2-2ac • cosB; c 2=a 2+b 2-2ab • cosC;。

托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。

原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．定理的提出一般几何教科书中的“托勒密定理”，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。

证明一、（以下是推论的证明，托勒密定理可视作特殊情况。

）在任意四边形ABCD中，作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE，，∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数，则AB、CD、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。

首先注意到复数恒等式：(a − b)(c− d) + (a− d)(b− c) = (a− c)(b− d) ，两边取模，运用三角不等式得。

等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。

四点不限于同一平面。

平面上，托勒密不等式是三角不等式的反演形式。

二、设ABCD是圆内接四边形。

在弦BC上，圆周角∠BAC = ∠BDC，而在AB上，∠ADB = ∠ACB。

在AC上取一点K，使得∠ABK = ∠CBD；因为∠ABK + ∠CBK =∠ABC = ∠CBD + ∠ABD，所以∠CBK = ∠ABD。