快速傅里叶变换及其应用实验文档及程序

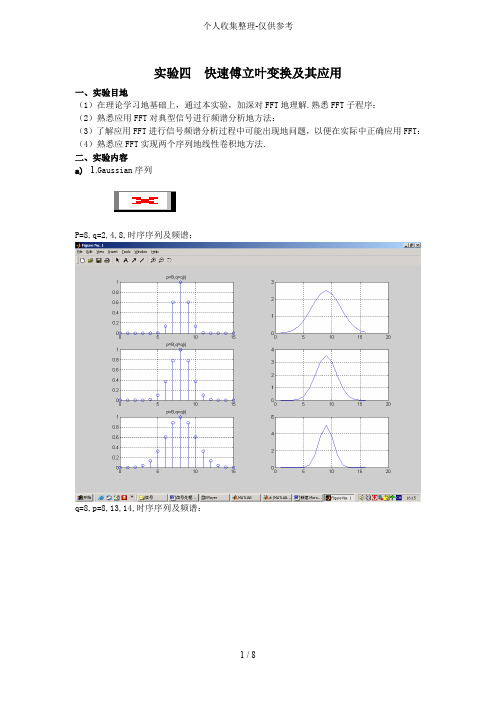
实验四快速傅立叶变换及其应用一、实验目地（1）在理论学习地基础上，通过本实验，加深对FFT地理解.熟悉FFT子程序：（2）熟悉应用FFT对典型信号进行频谱分析地方法：（3）了解应用FFT进行信号频谱分析过程中可能出现地问题，以便在实际中正确应用FFT：（4）熟悉应FFT实现两个序列地线性卷积地方法.二、实验内容a) 1.Gaussian序列P=8,q=2,4,8,时序序列及频谱：q=8,p=8,13,14,时序序列及频谱：b)衰减正弦序列a=0.1,f=0.0625,0.4375,0.5625,时序序列c)三角波序列反三角波序列N=8,未补零地时序序列及频谱：N=16,补零后地时序序列及频谱：(4)一个连续信号含两个频率分量，经采样得已知分别为1/16和1/64，观察其频谱;时不变、其结果有何不同，为什么？（5）用FFT分别实现和地16 点圆周卷积和线性卷积.三、思考题（1）实验中地信号序列和，在单位圆上地Z变换频谱和相同吗，如不同，你能说出哪一个低频分量更多一些吗？为什么？(2)对一个有限长序列进行DFT等价于将该序列周期延拓后进行DFS展开，因为DFS也只是取其中一个周期来运算，所以FFT在一定条件下也可用以分析周期信号序列.对正弦信号什么？版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.DXDiT。

用户可将本文地内容或服务用于个人学习、研究或欣赏，以及其他非商业性或非盈利性用途，但同时应遵守著作权法及其他相关法律地规定，不得侵犯本网站及相关权利人地合法权利.除此以外，将本文任何内容或服务用于其他用途时，须征得本人及相关权利人地书面许可，并支付报酬.RTCrp。

快速傅立叶变换〔FFT〕算法试验一．试验目的1.加深对DFT 算法原理和根本性质的理解；2.生疏FFT 算法原理和FFT 子程序的应用；3.学习用FFT 对连续信号和时域信号进展谱分析的方法，了解可能消灭的分析误差及其缘由，以便在实际中正确应用FFT。

二．试验设备计算机，CCS 3.1 版软件，E300 试验箱，DSP 仿真器，导线三．根本原理1.离散傅立叶变换DFT 的定义：将时域的采样变换成频域的周期性离散函数，频域的采样也可以变换成时域的周期性离散函数，这样的变换称为离散傅立叶变换，简称DFT。

2.FFT 是DFT 的一种快速算法，将DFT 的N2 步运算削减为〔N/2〕logN 步，极大2的提高了运算的速度。

3.旋转因子的变化规律。

4.蝶形运算规律。

5.基2FFT 算法。

四．试验步骤1.E300 底板的开关SW4 的第1 位置ON，其余置OFF。

其余开关不用具体设置。

2.E300 板子上的SW7 开关的第1 位置OFF，其余位置ON3.阅读本试验所供给的样例子程序；4.运行CCS 软件，对样例程序进展跟踪，分析结果；记录必要的参数。

5.填写试验报告。

6.供给样例程序试验操作说明A.试验前预备用导线连接“Signal expansion Unit”中2 号孔接口“SIN”和“A/D 单元”的2 号孔接口“AD_IN0”。

〔试验承受的是外部的AD模块〕B.试验1.正确完成计算机、DSP 仿真器和试验箱的连接后，系统上电。

2.启动CCS3.1，Project/Open 翻开“algorithm\01_fft”子名目下“fft.pjt”工程文件；双击“fft.pjt”及“Source”可查看各源程序；加载“Debug\fft.out”；3.单击“Debug\Go main”进入到主程序，在主程序“flag=0；”处设置断点；4.单击“Debug \ Run”运行程序，或按F5 运行程序；程序将运行至断点处停顿；5.用View / Graph / Time/Frequency 翻开一个图形观看窗口；设置该观看图形窗口变量及参数；承受双踪观看在启始地址分别为px 和pz，长度为128，数值类型为16 位整型，p x：存放经A/D 转换后的输入信号；p z：对该信号进展FFT 变换的结果。

实验四应用快速傅里叶变换对信号进行频谱分析引言：频谱分析是信号处理领域中的重要技术之一，可以用于研究信号的频率特性和频域内的信号成分。

傅里叶变换是一种能将时域信号转换为频域信号的数学工具，通过将信号分解成一系列频率分量来分析信号。

快速傅里叶变换（FFT）是一种高效的计算傅里叶变换的方法，尤其适合实时信号处理。

实验目的：1.理解傅里叶变换在频谱分析中的应用；2.掌握使用FFT对信号进行频谱分析的方法；3.实现频谱分析并得出相应的频谱图。

实验器材和材料：1.信号源（例如信号发生器）；2.电脑或数字信号处理器（DSP）；3.音频线或数据线连接信号源和电脑或DSP。

实验步骤：1.确定实验所需信号源的类型和参数，例如正弦信号、方波信号或任意信号；2.连接信号源和电脑或DSP，确保信号源输出的信号能够被电脑或DSP接收；3. 在电脑或DSP上选择合适的软件或编程语言环境，例如MATLAB、Python或C；4.编写程序或命令以控制信号源产生相应的信号，并将信号输入到电脑或DSP中；5.读取信号，并使用FFT对信号进行傅里叶变换；6.分析得到的频谱数据，绘制频谱图；7.对得到的频谱图进行解读和分析。

实验注意事项：1.在选择信号源和连接电脑或DSP时，注意信号源的输出范围和电脑或DSP的输入范围，避免信号超出范围导致损坏设备；2.根据实际需要选择合适的采样率和采样点数，以保证能够对信号进行充分的频谱分析；3.在进行FFT计算时，注意选择适当的窗函数和重叠率，以克服频谱分析中的泄漏效应。

实验结果与讨论：通过对信号进行频谱分析，我们可以得到信号的频率特性和频域内的成分信息。

根据得到的频谱图，我们可以分析信号的主要频率分量、功率谱密度以及可能存在的干扰或噪声。

通过对频谱图的解读和分析，可以帮助我们理解信号的特征和变化规律，为后续的信号处理和应用提供有价值的信息。

结论：本实验通过应用快速傅里叶变换对信号进行频谱分析，从而得到信号在频域内的成分信息并绘制出频谱图。

实验二快速傅立叶变换（FFT ）及其应用一、实验目的1.在理论学习的基础上，通过本实验，加深对FFT 的理解，熟悉FFT 子程序。

2.熟悉应用FFT 对典型信号进行频谱分析的方法3.了解应用FFT 进行信号频谱分析过程中可能出现的问题以便在实际中正确应用FFT 。

二、实验原理在各种信号序列中，有限长序列信号处理占有很重要地位，对有限长序列，我们可以使用离散Fouier 变换(DFT)。

这一变换不但可以很好的反映序列的频谱特性，而且易于用快速算法在计算机上实现，当序列x(n)的长度为N 时，它的DFT 定义为：1()()N kn Nn X k x n W-==∑，2n jNN W e-=反换为：11()()N kn Nk x n X k WN--==∑有限长序列的DFT 是其Z 变换在单位圆上的等距采样，或者是序列Fourier 变换的等距采样，因此可以用于序列的谱分析。

FFT 并不是与DFT 不同的另一种变换，而是为了减少DFT 运算次数的一种快速算法。

它是对变换式进行一次次分解，使其成为若干小点数的组合，从而减少运算量。

常用的FFT 是以2为基数的，其长度 N=2L ，它的效率高，程序简单使用非常方便，当要变换的序列长度不等于2的整数次方时，为了使用以2为基数的FFT ，可以用末位补零的方法，使其长度延长至2的整数次方。

在运用DFT 进行频谱分析的过程中可能产生几种问题：(1) 混叠序列的频谱时被采样信号的周期延拓，当采样速率不满足Nyquist 定理时，就会发生频谱混叠，使得采样后的信号序列频谱不能真实的反映原信号的频谱。

避免混叠现象的唯一方法是保证采样速率足够高，使频谱混叠现象不致出现，即在确定采样频率之前，必须对频谱的性质有所了解，在一般情况下，为了保证高于折叠频率的分量不会出现，在采样前，先用低通模拟滤波器对信号进行滤波。

(2) 泄漏实际中我们往往用截短的序列来近似很长的甚至是无限长的序列，这样可以使用较短的DFT 来对信号进行频谱分析，这种截短等价于给原信号序列乘以一个矩形窗函数，也相当于在频域将信号的频谱和矩形窗函数的频谱卷积，所得的频谱是原序列频谱的扩展。

试验二快速傅里叶变换及其应用一、试验目的（1）.在理论学习的基础上。

加深对FFT的理解，熟悉matlab中的有关函数。

（2）.应用FFT对典型信号进行频谱分析。

（3）.了解应用FFT进行信号频谱分析过程中可能出现的问题。

（4）.应用FFT实现序列的线性卷积和相关。

二、实验内容1．观察高斯序列的时域和幅频特性，固定信号xa(n)中参数p=8,改变q的值使q分别等于2、4、8，观察他们的时域和幅频特性，了解当q取不同值时，对信号序列的时域和幅频特性的影响；固定q=8，改变p,使p分别等于8、13、14，观察参数p变化对信号序列的时域和幅频特性的影响，注意p等于多少时会发生明显的泄漏现象，混叠是否也随之出现？记录实验中观察到的现象，绘出相应的时域序列和幅频特性曲线。

(1)固定p=8，使q=2和4的时域和频域图n=0:15x=exp((16*n-n.^2-64)./2)subplot(2,2,1);plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))subplot(2,2,2);stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');x=exp((16*n-n.^2-64)./4)subplot(2,2,3);plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))subplot(2,2,4);stem(n,y,'-o');xlabel('k');ylabel('y(k)')title('幅频特性');使q=8的时域和频域图n=0:15x=exp((16*n-n.^2-64)./8)plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');(2)固定q=8，使q=8和13的时域和频域图n=0:15x=exp((16*n-n.^2-64)./8)subplot(2,2,1);plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))subplot(2,2,2);stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');x=exp((26*n-n.^2-169)./8) subplot(2,2,3);plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))subplot(2,2,4);stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');使p=14的时域和频域图x=exp((28*n-n.^2-196)./8)plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');实验结果分析：由图形可知，当固定p,q取不同值时，随着q的增大，其相对应的时域幅值会增大，而且容易看出，它们的时域图关于n=8对称。

附录：实验1 快速傅里叶变换及其应用1、程序一：n=0:1:15;%p=8不变，q变化（2,4,8）; p=8;q=2; %p=8;q=2;xa1=exp(-((n-p).^2)/q); subplot(5,2,1);plot(n,xa1,'-*');xlabel('t/T');ylabel('xa(n)');title('p=8 q=2')xk1=abs(fft(xa1));subplot(5,2,2);stem(n,xk1)xlabel('k');ylabel('Xa(k)');title('p=8 q=2')p=8;q=4; %p=8;q=4;xa1=exp(-((n-p).^2)/q); subplot(5,2,3);plot(n,xa1,'-*');xlabel('t/T');ylabel('xa(n)');title('p=8 q=4')xk1=abs(fft(xa1));subplot(5,2,4);stem(n,xk1)xlabel('k');ylabel('Xa(k)');title('p=8 q=4')p=8;q=8; %p=8;q=8;xa1=exp(-((n-p).^2)/q); subplot(5,2,5);plot(n,xa1,'-*');xlabel('t/T');ylabel('xa(n)');xk1=abs(fft(xa1));title('p=8 q=8')subplot(5,2,6);stem(n,xk1)xlabel('k');ylabel('Xa(k)');title('p=8 q=8') %q=8不变,p变化(8,13,14); p=8;q=8; %p=8;q=8;xa1=exp(-((n-p).^2)/q); subplot(5,2,5);plot(n,xa1,'-*');xlabel('t/T');ylabel('xa(n)');xk1=abs(fft(xa1));title('p=8 q=8')subplot(5,2,6);stem(n,xk1)xlabel('k');ylabel('Xa(k)');title('p=8 q=8')p=13;q=8; %p=13;q=8;xa1=exp(-((n-p).^2)/q); subplot(5,2,7);plot(n,xa1,'-*');xlabel('t/T');ylabel('xa(n)');xk1=abs(fft(xa1));title('p=13 q=8')subplot(5,2,8);stem(n,xk1)xlabel('k');ylabel('Xa(k)');title('p=13 q=8')p=14;q=8; %p=14;q=8;xa1=exp(-((n-p).^2)/q); subplot(5,2,9);plot(n,xa1,'-*');xlabel('t/T');ylabel('xa(n)');title('p=14 q=8')xk1=abs(fft(xa1));subplot(5,2,10);stem(n,xk1)xlabel('k');ylabel('Xa(k)');title('p=14 q=8')图1-1 （a）高斯序列的时域和频域特性（p=8，改变q）图1-1（b）高斯序列的时域和频域特性（q =8，改变p）2、程序二：n1=0:1:15;xb1=exp(-0.1*n1).*sin(2*pi*0.0625*n1);subplot(3,2,1); plot(n1,xb1,'-*'); xlabel('n'); ylabel('x(n)'); title('f=0.0625'); xk1=abs(fft(xb1)); subplot(3,2,2); stem(n1,xk1) xlabel('k'); ylabel('X(k)'); title('f=0.0625'); n2=0:1:15;xb2=exp(-0.1*n2).*sin(2*pi*0.4375*n2);subplot(3,2,3); plot(n2,xb2,'-*'); xlabel('n'); ylabel('x(n)');title('f=0.4375'); xk2=abs(fft(xb2)); subplot(3,2,4); stem(n2,xk2) xlabel('k'); ylabel('X(k)'); title('f=0.4375'); n3=0:1:15;xb3=exp(-0.1*n3).*sin(2*pi*0.5625*n3);subplot(3,2,5); plot(n3,xb3,'-*'); xlabel('n'); ylabel('x(n)'); title('f=0.5625'); xk3=abs(fft(xb3)); subplot(3,2,6); stem(n3,xk3) xlabel('k'); ylabel('X(k)'); title('f=0.5625')图1-2衰减正弦序列的时域波形和幅频特性3、程序三：%N=8程序：n1=0:1:7;xc1=[0 1 2 3 4 3 2 1]; subplot(2,2,1);plot(n1,xc1,'-*'); xlabel('n');ylabel('xc(n)');title('时域特性');xk1=abs(fft(xc1)); subplot(2,2,2);stem(n1,xk1)xlabel('k');ylabel('Xc(k)');title('频域特性');n2=0:1:7;xd1=[4 3 2 1 0 1 2 3]; subplot(2,2,3);plot(n2,xd1,'-*'); xlabel('n');ylabel('xd(n)');title('时域特性');xk2=fft(xd1); subplot(2,2,4);stem(n2,xk2)xlabel('k');ylabel('Xd(k)');title('频域特性'); %N=32程序：n1=0:1:31;xc1=[0 1 2 3 4 3 2 1 zeros(1,24)]; subplot(2,2,1);plot(n1,xc1,'-*');xlabel('n');ylabel('xc(n)');title('时域特性');xk1=abs(fft(xc1));subplot(2,2,2);stem(n1,xk1)xlabel('k');ylabel('Xc(k)');title('频域特性');n2=0:1:31;xd1=[4 3 2 1 0 1 2 3 zeros(1,24)]; subplot(2,2,3);plot(n2,xd1,'-*');xlabel('n');ylabel('xd(n)');title('时域特性');xk2=fft(xd1);subplot(2,2,4);stem(n2,xk2)xlabel('k');ylabel('Xd(k)');title('频域特性')图1-3 三角波和反三角波序列的时域波形和幅频特性n1=0:1:15;x1=sin(2*pi*0.125*n1)+cos(2*pi* (0.125+1/16)*n1);x2=sin(2*pi*0.125*n1)+cos(2*pi* (0.125+1/64)*n1);xk1=abs(fft(x1));subplot(2,2,1);stem(n1,xk1)xlabel('k');ylabel('X(k)');title('N=16,df=1/16频谱图');xk2=abs(fft(x2));subplot(2,2,2);stem(n1,xk2)xlabel('k');ylabel('X(k)');title('N=16,df=1/64频谱图'); n2=0:1:127;x3=sin(2*pi*0.125*n2)+cos(2*pi* (0.125+1/16)*n2);x4=sin(2*pi*0.125*n2)+cos(2*pi* (0.125+1/64)*n2);xk3=abs(fft(x3));subplot(2,2,3);stem(n2,xk3)xlabel('k');ylabel('X(k)');title('N=128,df=1/16频谱图');xk4=abs(fft(x4));subplot(2,2,4);stem(n2,xk4)xlabel('k');ylabel('X(k)');title('N=128,df=1/64频谱图');图1-4 双频信号频谱n1=0:1:15;x=exp(-(n1-8).^2./2);y=exp(-0.1*n1).*sin(2*pi*0.0625*n1); N=length(x); n=0:N-1; n2=0:1:30; X=fft(x); Y=fft(y);x32=[x zeros(1,16)]; y32=[y zeros(1,16)]; X32=fft(x32); Y32=fft(y32); z16=ifft(X.*Y); z32=ifft(X32.*Y32); subplot(2,2,1); plot(n,z16,'-o');xlabel('n');ylabel('z(n)'); title('循环卷积的结果');subplot(2,2,2);plot(n2,z32(1:2*N-1),'-o'); xlabel('n');ylabel('z(n)'); title('线性卷积的结果'); rm16=real(ifft(conj(X).*Y));rm32_0=real(ifft(conj(X32).*Y32)); rm32=[rm32_0(N+2:2*N); rm32_0(1:N)]; m=n;subplot(2,2,3); plot(m,rm16,'-o');xlabel('m');ylabel('rm'); title('循环相关的结果'); m=-(N-1):N-1; subplot(2,2,4); plot(m,rm32,'-o');xlabel('m');ylabel('rm'); title('线性相关的结果');图1-5 16点的循环卷积和线性卷积。

实验五--快速傅里叶变换CENTRAL SOUTH UNIVERSITY数字信号处理实验报告题目快速傅里叶变换学生姓名学院物理与电子学院专业班级电子信息科学与技术1105班学号140411072实验五快速傅里叶变换一、实验仪器PC机一台、JQ-SOPC开发系统实验箱及辅助软件（DSP Builder、Matlab/Simulink、Quartus II、Modelsim）。

二、实验目的1、了解快速傅里叶变换的基本结构组成。

2、学习使用DSP Builder设计FFT。

三、实验原理1、FFT的原理：快速傅里叶变换（FFT）是离散傅里叶变换（DFT）的一种高效运算方法，它大大简化了DFT 的运算过程,使运算时间缩短几个数量级。

FFT 算法可以分为按时间抽取（DIT）和按频率抽取（DIF）两类，输入也可分为实数和复数两种情况。

八点时间抽取基-2FFT算法信号流图如图1示：图1 8点基-2 DIT-FFT信号流图四、实验步骤1、将桌面的my_fft_8.mdl拷贝到“D:\Program Files\MATLAB71\work”(MATLAB安装目录下的work文件夹)处，并双击打开。

图5-1 快速傅里叶变换系统图图5-2 快速傅里叶变换子系统1图图5-3 快速傅里叶变换子系统2图图5-3 快速傅里叶变换子系统3图2、点击工具栏即可开始系统级simulink仿真，以验证该模型的正确性。

在仿真进行过程中分别将三个输入控制开关打到000、001、010、011、100以选择五组输入数据进行FFT运算。

（1）当开关打到000时选择第一组数据{2.0,2.0,4.0,7.0,3.0,5.0,5.0,8.0}，其运算结果应为36、-2.41+3.84i、-4+8i、0.4219+1.844i、-8、0.4102-1.84i、-4-8i、-2.422-3.844i。

（2）当开关打到001时选择第二组数据{1.1,5.0,10.5,15.3,20.2,25.7,30.6,40.1},其运算结果应该为148.5、-16.1+52.35i、-19.8+24.7i、-22.02+12.25i、-23.7、-22.1-12.15i、-19.8-24.7i、-16.9-52.45i。

1.快速傅里叶变换FFT实验.1）快速傅里叶变换FFT源程序：#include"iostream.h"#include"math.h"//using namespace std#define pi 3.1415926536 //定义pai void swap(double &a,double &b) //定义交换函数swap{double t=a;a=b;b=t;}void fft(double A[],double B[],int M) //定义fft快速傅里叶函数{ long int J,I,L,LE,LE1,P,Q,R;double N,K,Wr,Wi,W1r,W1i,WTr,WTi,theta,Tr,Ti;J=0;N=pow(2,M);//雷达算法码位倒置程序for(I=0;I<N-1;I++){if(J>I){swap(A[I],A[J]);swap(B[I],B[J]);}K=N/2;//向低位进位while(K>=2&&J>=K){J-=K;K=K/2;}J+=K;}//蝶形运算程序//最外层循环由蝶形图的级数确定for(L=1;L<=M;L++){LE=pow(2,L); //各级群间隔LE1=LE/2; //输入间隔Wr=1.0; //Wn的实部Wi=0.0; //Wn的虚部theta=(-1)*pi/LE1;W1r=cos(theta);W1i=sin(theta);//中层循环由Wn的个数确定for(R=0;R<LE1;R++){//内层循环由每一级群的个数确定for(P=R;P<N-1;P+=LE){Q=P+LE1;Tr=Wr*A[Q]-Wi*B[Q];Ti=Wr*B[Q]+Wi*A[Q];A[Q]=A[P]-Tr;B[Q]=B[P]-Ti;A[P]+=Tr;B[P]+=Ti;}//计算每一级的Wn的值WTr=Wr;WTi=Wi;Wr=WTr*W1r-WTi*W1i;Wi=WTr*W1i+WTi*W1r;}}}void main(){int M;double N;cout<<"实验人的信息：姓名：张超华学号：200801000728 专业班级：电力电子0801"<<endl;cout<<"输入序列的个数N(N必须为2^M)，N=";cin>>N;//判断输入N的个数是否符合2^M个while(1){double b=log10(N)/log10(2);int a=b/1;if(a-b==0){M=a;break;}else{cout<<"输入序列的个数须为2^M个,重新输入N=";cin>>N;}}double *A=new double[N]; //为序列的实部分配动态空间double *B=new double[N]; //为序列的虚部分配动态空间for(int i=0;i<N;i++){A[i]=0.0;B[i]=0.0;}// 输入序列cout<<"请在下方输入序列的实部："<<endl;for(int j=0;j<N;j++){cin>>A[j];}cout<<"请在下方输入序列的虚部："<<endl;for(j=0;j<N;j++){cin>>B[j];}fft(A,B,M); //调用fft函数 cout<<"经快速傅里叶变换后得到的结果为："<<endl; //输出变换结果 for(int m=0;m<N;m++){cout<<" "<<A[m]<<"+j("<<B[m]<<")"<<endl;}//释放内存空间delete [] A;delete [] B;}2）FFT程序运行结果：（参考课本160页的‘例6-3’运行程序。

[实验2] 快速傅里叶变换 (FFT) 实现一、实验目的1、掌握FFT 算法和卷积运算的基本原理；2、掌握用C 语言编写DSP 程序的方法；3、了解利用FFT 算法在数字信号处理中的应用。

二、实验设备 1. 一台装有CCS 软件的计算机； 2. DSP 实验箱的TMS320C5410主控板； 3. DSP 硬件仿真器。

三、实验原理 （一）快速傅里叶变换傅里叶变换是一种将信号从时域变换到频域的变换形式，是信号处理的重要分析工具。

离散傅里叶变换（DFT ）是傅里叶变换在离散系统中的表示形式。

但是DFT 的计算量非常大， FFT 就是DFT 的一种快速算法, FFT 将DFT 的N 2 步运算减少至 ( N/2 )log 2N 步。

离散信号x(n)的傅里叶变换可以表示为∑=-=10][)(N N nk N W n x k X ， Nj N e W /2π-=式中的W N 称为蝶形因子，利用它的对称性和周期性可以减少运算量。

一般而言，FFT 算法分为时间抽取（DIT ）和频率抽取（DIF ）两大类。

两者的区别是蝶形因子出现的位置不同，前者中蝶形因子出现在输入端，后者中出现在输出端。

本实验以时间抽取方法为例。

时间抽取FFT 是将N 点输入序列x(n) 按照偶数项和奇数项分解为偶序列和奇序列。

偶序列为：x(0), x(2), x(4),…, x(N-2)；奇序列为：x(1), x(3), x(5),…, x(N-1)。

这样x(n) 的N 点DFT 可写成：()()∑++∑=-=+-=12/0)12(12/02122)(N n kn NN n nkNW n x Wn x k X考虑到W N 的性质，即2/)2//(22/)2(2][N N j N j N W e e W ===--ππ因此有：()()∑++∑=-=-=12/02/12/02/122)(N n nkN k NN n nkN W n x WWn x k X或者写成：()()12()kN X k X k W X k =+由于X 1(k) 与X 2(k) 的周期为N/2，并且利用W N 的对称性和周期性，即：k N N k N W W -=+2/可得：()()12(/2)kN X k N X k W X k +=-对X 1(k) 与X 2(k)继续以同样的方式分解下去，就可以使一个N 点的DFT 最终用一组2点的DFT 来计算。