当前位置：文档之家 › 方差分析与正交实验设计初步

方差分析与正交实验设计初步

  • 格式：ppt
  • 大小：429.00 KB
  • 文档页数：72

下载文档原格式

  / 72

合集下载

实验设计的方差分析与正交试验

实验设计的方差分析与正交试验

实验设计的方差分析与正交试验一、实验设计中的方差分析方差分析（analysis of variance，ANOVA）是一种统计方法，用于比较不同组之间的均值差异是否具有统计学上的显著性。

在实验设计中，方差分析主要被用来分析因变量（dependent variable）在不同水平的自变量（independent variable）中的变化情况。

通过比较不同组之间的方差，判断是否存在显著差异，并进一步分析差异的原因。

1. 单因素方差分析单因素方差分析是最简单的方差分析方法，适用于只有一个自变量的实验设计。

该方法通过比较不同组之间的方差来判断各组均值是否有差异。

步骤如下：（1）确定研究目的，选择合适的因变量和自变量。

（2）设计实验，确定各组的样本个数。

（3）进行实验，并收集数据。

（4）计算各组的平均值和总平均值。

（5）计算组内方差和组间方差。

（6）计算F值，通过计算F值来判断各组均值是否有显著差异。

2. 多因素方差分析多因素方差分析是在单因素方差分析的基础上，增加了一个或多个自变量的情况下进行的。

这种方法可以用来分析多个因素对因变量的影响，并判断各因素的主效应和交互效应。

步骤如下：（1）确定研究目的，选择合适的因变量和多个自变量。

（2）设计实验，确定各组的样本个数。

（3）进行实验，并收集数据。

（4）计算各组的平均值和总平均值。

（5）计算组内方差、组间方差和交互方差。

（6）计算F值，通过计算F值来判断各组均值是否有显著差异。

二、正交试验设计正交试验设计是一种设计高效实验的方法，可以同时考虑多个因素和各个因素之间的交互作用，并通过较少的试验次数得到较准确的结果。

1. 正交表的基本原理正交表的设计是基于正交原理，即每个因素和其他所有因素的交互效应都是独立的。

通过正交表设计实验，可以确保各因素和交互作用在样本中能够均匀地出现，从而减少误差来源，提高实验结果的可靠性。

2. 正交试验设计的步骤（1）确定要研究的因素和水平。

正交试验设计及其方差分析

正交试验设计及其方差分析
Lp(nm)中，p=m(n-1)+1. 下面通过实例来说明如何用正交表来 安排试验.
例 9. 8 提高某化工产品转化率的试验 . 某种化工产品的转化率可能与反应温度A，反应时间B，某两 种原料之配比C和真空度D有关.为了寻找最优的生产条件，因此 考虑对 A ， B ，C ， D 这4个因素进行试验.根据以往的经验，确 定各个因素的3个不同水平，如表9-19所示 .分析各因素对产品的 转化率是否产生显著影响，并指出最好生产条件.
3
显然 T Tij ,j =1，2，3，4.此处 i 1
T11 大致反映了A1 对试验结果的影响, T21 大致反映了A2 对试验结果的影响, T31 大致反映了A3 对试验结果的影响, T12 , T22 和 T32 分别反映了B1 , B2 , B3 对试验结果的影响,
T13 , T23 和T33 分别反映了C1, C2 , C3 对试验结果的影响, T14 , T24 和 T34 分别反映了D1, D2 , D3 对试验结果的影响.
Rj 反映了第j列因素的水平改变对试验结果的影响大小, Rj 越大反映第j列因素影响越大.上述结果列表 of range) 由极差大小顺序排出因素的主次顺序:
这里, Rj值相近的两因素间用“、”号隔开,而Rj 值相差较 大的两因素间用“;”号隔开.由此看出,特别要求在生产过程中 控制好因素B，即反应时间.其次是要考虑因素A和D，即要控制 好反应温度和真空度.至于原料配比就不那么重要了.
(2 ) 表中任两列，其横向形成的有序数对出现的次数相同 . 如 表 L4 (23) 中任意两列，数字1 ， 2 间的搭配是均衡的 .
凡满足上述两性质的表都称为正交表(Orthogonal table).
常用的正交表有L9(34)， L8(27)，L16(45)等,见附表7. 用正 交表来安排试验的方法,就叫正交试验设计. 一般正交表)

第4讲5(1) 正交试验设计(方差分析)

第4讲5(1) 正交试验设计(方差分析)

处理号 1 2
第1列（A） 1 1
表 L9(34)正交表
第2列 1 2
第3列 1 2
第4列 1 2
因素A第1 试验结果y水i 平3次
重复测定 y1 值 y2
3
1
3
3
3
y3
单4 因素 2
1
2
3
y4
试5 验数 2
2
3
1
y5
因素A第2
SS据A6＝资13（料y1 y22
格式 78＝13（K12

3 K322
y3）2 （y43y5

K32）-
T2 9
1 2
y6）2 （ 1 y7 3 1
y 82y 9）2 2 3
（y1yy62 ...
9
y7 y8

y水9）平2（修 3次正重项） 复测定值
9
3
3
2
1
y9
分析第1列因素时，其它列暂不考虑，将其看做条件因因素素A。第3
因素 重复1 重复2 重复3
显著影响
（6）列方差分析表
（1）偏差平方和分解：
总偏差平方和＝各列因素偏差平方和+误差偏差平方和
SST SS因素 SS空列（误差）
（2）自由度分解：
dfT df因素 df空列（ 误列（
（3）方差：MS因素＝
SS因素 df因素
，MS误差＝
SS误差 df误差
（4）构造F统计量：
F因素＝
MS因素 MS误差
（5）列方差分析表，作F检验
若计算出的F值F0>Fa，则拒绝原假设，认为 该因素或交互作用对试验结果有显著影响；若 F0≼Fa，则认为该因素或交互作用对试验结果 无显著影响。

5-2正交试验设计(方差分析)

5-2正交试验设计(方差分析)
衡量试验条件好坏的特性（可以是质量特性 也 可以是产量特性或其它）称为指标，用 y表示。 由于y是一个随机变量，因此可以假定它 有如下的结构式：y=μ+ε 其中μ是一个依赖于试验条件的常量，随 试验条件的变化而改变，ε是一个随机变量， 常假定它服从正态分布N（0,σ2）。
正交表
选择部分条件进行试验，再通过数据分析来 寻找好的条件，这便是试验设计问题。通过 少量的试验获得较多的信息，达到试验的目 的：发现那些因子对试验结果确有影响，因 子的什么水平组合是最好的。
第五章 正交试验设计
一、试验设计的基本概念与正交表
多因素试验遇到的最大困难是试验次数太 多，若十个因素对产品质量有影响，每个因素 取两个不同状态进行比较，有210=1024、 如 果每个因素取三个不同状态310=59049个不同 的试验条件
在多因素试验中，有人采用“单因素轮换 法”，但是这种方法不一定能找到好的条件 譬如：考察两个因子，先固定A在A1，发 现B3好，再固定B3，发现A1好，但是实际上好 的条件是A2B2。 B1 B2 B3 A1 50 56 62 A2 56 70 60 A3 54 60 58
利用正交表进行试验设计的方法就是正交试 验设计。
表 4 .1 试验号 1 2 3 4 5 6 7 8 9 列号 1 1 1 1 2 2 2 3 3 3
L 9 (3 ) 2 1 2 3 1 2 3 1 2 3 3 1 2 3 2 3 1 3 1 2 4 1 2 3 3 1 2 2 3 1
4
“L”表示正交表，“9”是行数，在试验中表示试 验的条件数，“4”是列数，在试验中表示可以安排 的因子的最多个数，“3”是表的主体只有三个不同 数字，在试验中表示每一因子可以取的水平数。
二、无交互作用的正交设计与数据分析

正交设计与方差分析

正交设计与方差分析
适用范围
正交设计适用于多因素、多水平的试验安排，而方差分析 适用于检验数据间的差异和因素显著性。
04
正交设计与方差分析的实例
正交设计实例
实验设计
正交设计是一种实验设计方法， 通过选择合适的正交表，安排多 因素多水平的实验，以最小实验 次数获得尽可能多的信息。
特点
正交设计具有均衡分散、整齐可 比的特点，能够快速有效地找到 最优方案。
THANKS
感谢观看
复合正交设计
适用于多个因素，每个因素有多个水平的实验。
混合水平正交设计
适用于某些因素水平较多，而其他因素水平较少 的实验。
02
方差分析简介
方差分析的定义
• 方差分析（ANOVA）是一种统计分析方法，用于比较两 个或多个组之间的平均值差异是否显著。它通过分析数据 的变异来源，将总变异分解为组间变异和组内变异，从而 评估不同组之间的差异是否具有统计意义。
适用范围有限
正交设计主要适用于多因素、多水平的实验设计，对于其他类型 的实验可能不太适用。
对实验条件要求较高
正交设计要求实验条件相同，对于实验条件不易控制的情况可能不 太适用。
对实验结果分析要求较高
正交设计需要对实验结果进行复杂的统计分析，对于数据分析能力 要求较高。
正交设计与方差分析的发展趋势
多元化
正交设计与方差分析在未来的应用前景
科学研究
正交设计与方差分析在科学研究领域的应用将会越来越广泛，特别是在生物、化学、物理 等领域。
工业生产
工业生产中需要进行大量的实验研究和数据分析，正交设计与方差分析可以为工业生产提 供有效的实验设计和数据分析方法。
数据分析
正交设计与方差分析作为一种统计分析方法，在数据分析领域的应用将会越来越广泛。

第十章 方差分析与正交试验设计

第十章 方差分析与正交试验设计

第十章方差分析与正交试验设计方差分析与试验设计是英国统计学家和遗传学家费希尔进行农业试验发展起来的通过试验获取数据并进行分析的统计方法。

方差分析讨论的是生产和科学试验中有哪些因素对试验结果有显著作用，哪些因素没有显著作用。

讨论的是一个因素对试验结果是否有影响称为一元方差分析，讨论的是多个因素对试验结果是否有影响称为多元方差分析．对于因素多于两个的方差分析，公式变得相当复杂，试验次数较多，我们介绍一个试验次数少的试验设计方案，正交试验设计。

10．1 一元方差分析人们常常通过试验来考察了解各种因素对产品或成品的性能，成本、产量等的影响，我们把性能、成本、产量等统称为试验指标。

有些指标可以直接用数量表示，称为定量指标；不能直接用数量表示的，称为定性指标，可按评定结果打出分数或评出等级，这时就能用数量表示了。

在试验中，影响试验指标的原因称为因素。

因素在试验中所处的各种状态称为因素的水平，某个因素在试验中需要考察它的几种状态，就称它为几水平的因素。

在生产实践和科学试验中，人们经常要研究这样的问题：如果改变生产条件是否会对产品（指标）产生显著影响?如果改变试验条件是否会对试验结果（指标）产生显著影响?方差分析的作用就在于通过对试验数据的统计分析，从而推断试验数据间的差异是由于生产条件的改变还是由于随机误差的影响，并分析出最佳的试验条件。

为此弄清楚方差分析处理问题的基本思想，下面举例说明。

例10.1.1 某灯泡厂用四种不同配料方案制成的灯丝生产四批灯泡,在每批，其中下标i表示第i批灯泡中取若干个做寿命试验，它们的寿命分别记为xij灯泡，第二个下标j表示第j次试验。

具体数据如下表10.1.1 四批灯泡的寿命试验表响。

在这里灯泡的寿命就是指标，灯泡品种就是因子，四种不同品种的灯泡就是四个水平,因此这是一个单因子四水平试验。

我们将每一种配料制成的灯泡，其寿命看成同一总体，而不同品种的灯泡就是不同总体，因而出现四个不同总体。

正交试验设计中的方差分析

正交试验设计中的方差分析
方差分析（ANOVA）是一种统计技术， 用于比较三个或更多组数据的平均值 是否存在显著差异。
目的
通过方差分析，可以确定不同组之间 的平均值差异是否由随机误差引起， 还是由处理因素或自变量引起。
方差分析的数学模型
数学模型
方差分析使用数学模型来描述数据之间的关系，特别是不同组之间的平均值差异。模型通常包括组间差异和组内 差异两部分。
医学研究
通过正交试验设计中的方差分析，研究不同治疗方案、药物剂量等因素对疾病治疗效果的影响，为临床 治疗提供科学依据。
方差分析的局限性
04
方差分析对数据的要求
独立性
数据必须是相互独立的，不存 在相互关联或依赖关系。
正态性
数据应符合正态分布，才能保 证统计推断的准确性。
同方差性
各组数据的方差应相等，否则 可能导致误判。
制定试验方案
根据正交表设计试验方案，确定每个因素的每个 水平。
实施试验
按照试验方案进行试验，记录每个试验的结果。
方差分析
利用方差分析法对试验结果进行分析，确定各因 素对试验结果的影响程度和显著性。
优化方案
根据方差分析结果，优化试验方案，进行下一步试验。
方差分析的基本原理
02
方差分析的定义与目的
定义
拉丁方设计方差分
析
适用于需要控制试验条件的试验， 通过拉丁方设计平衡试验条件和 试验误差。
正交试验设计中的方差分析步骤
确定试验因素和水平
根据研究目的和实际情况确定试验因 素和水平。
制定正交表
根据试验因素和水平选择合适的正交 表。
安排试验
按照正交表进行试验，记录试验数据。
方差分析
对试验数据进行方差分析，包括自由 度、离均平方和、均方、F值等计算。

正交试验设计中的方差分析

正交试验设计中的方差分析
个水平，每个水平做p次试验，则n=mp。
那么正交试验的方差分析可以从以下几步进行：
1.计算差方和（离差平方和）： 包括以下几部分：
1)各因素差方和：
正交试验都是多因素多水平的试验，因此有必要对各因素的 差方和进行计算。 各因素差方和等于它的各水平均值k1A,k2A,…,kmA之间偏差平 方和。 以因素A为例，它在正交表中的某列，用xij表示A在第i个水 平的第j次试验结果，则;
即：fA×B=fA×fB 试验误差的自由度fe＝fT－f因 。
3.计算平均差方和（均方）： 在计算各因素的差方和时，按照前面的讲述，它是各水平的 偏差方的和，其大小与水平数有关，故此还不能确切的反映 各因素的情况。为了消除水平数的影响，可以计算其平均差 方和：
因素的平均差方和＝因素差方和 ＝Q因 因素的自由度 f因
试验误差的差方和是所有试验结果在不同水平下的指标值与该 水平下的均值之间的差的平方和。它是由随机误差引起的，故 叫误差的差方和。
Qe QT ( QA QB QN )
2.计算自由度：
试验的总自由度： fT n 1
各因素自由度： f因 m 1
如果有交互作用，则交互作用的自由度为两因素自由度之积:
一．几个数据处理中常用的数理统计名词：
首先对几个数理统计名词进行回顾
1. 平均值 x
就是所有数据的和除以数据的个数。
x
1 n
n i 1
xi
1 n
x1
x2
xn
总体平均值：
1 n
n
xi
i 1
n
总体：数理统计学中指的是研究对象的某一特性值的全体； 样本：从总体中随机抽出的一组测量值。
2.极差 R： 就是一组数据中的最大值减去最小值得到的差值。 3.差方和Q： 测量值对平均值的偏差的平方和，就叫～。也叫离差平方和。

第七章方差分析与正交试验设计初步

第七章方差分析与正交试验设计初步

度的数量指标。

称为组内平方和或误差平方和，是观察值与组
内平均数之差的平方和，它反映了组内（即在同一水
平之下）样本的随机波动。

的自由度
，其组内方差为
。

称为组间平方和，是组内平均数与总平均数之差
的平方和，它反映了因素水平的不同及随机因素引起
的差异。 的自由度
，其组间方差为

。
2019/10/30
版权所有 BY 统计学课程组
(2) 如果还有一个因素B（试验配方，共三种）也对缩 水率产生作用，应该如何选择最优方案？
(3) 如果还有两个或者两个以上的因素也对缩水率产生 作用，应该如何选择最优方案？

为了回答上述问题，本章将介绍单因素方差分析、
双因素方差分析和正交试验设计法的有关概念、分析
思想、数学模型、方差分析表和正交试验设计的基本
2019/10/30
版权所有 BY 统计学课程组
7
一、方差分析的有关概念和基本思想
（一）简单平均数

方差分析（Analysis of Variance，
ANOVA）是一种检验多个总体均值是否相等
的统计方法。

一般将方差分析研究的对象称为因素，而
因素中的内容称为水平。若方差分析同时针对
两个因素进行，则称为双因素方差分析。
版权所有 BY 统计学课程组
17
2．计算有关均值及平方和
2019/10/30
版权所有 BY 统计学课程组
18
在表7.1中增加若干计算栏，计算有关均值，如表 7.3所示。
2019/10/30
版权所有 BY 统计学课程组
19
2019/10/30

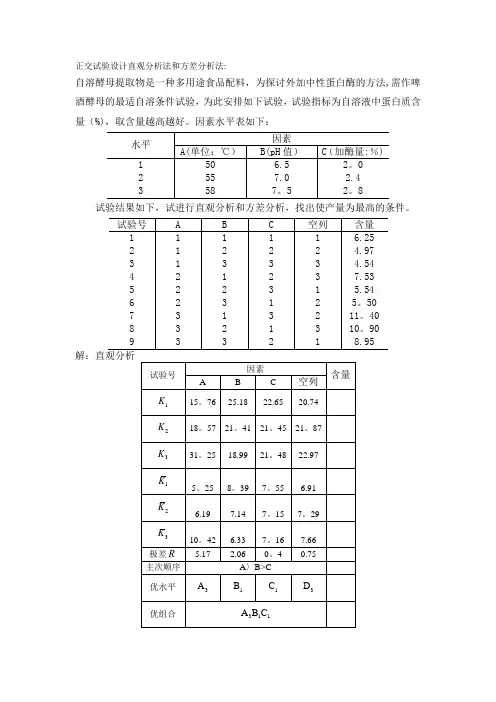
正交试验设计直观分析法和方差分析法

正交试验设计直观分析法和方差分析法

正交试验设计直观分析法和方差分析法:
自溶酵母提取物是一种多用途食品配料，为探讨外加中性蛋白酶的方法,需作啤酒酵母的最适自溶条件试验，为此安排如下试验，试验指标为自溶液中蛋白质含量（%)，取含量越高越好。

因素水平表如下：
试验结果如下，试进行直观分析和方差分析，找出使产量为最高的条件。

A B C e df df df df ====3-1=2
2A A A SS MS df =
=45.422.72=，2B B B SS MS df ==6.49
3.232=, 2C C C SS MS df =
=0.310.1552=,2e e e
SS MS df ==0.83
0.4152= 因为22
2C e MS MS <,所以因素C 的偏差平方和、自由度并入误差的偏差平方和、自由度
因素A 高度显著,因素B 显著，因素C 不显著.本试验指标越大越好.对因素A 、B 分析，确定优水平为3A 、1B ；因素C 的水平改变对试验结果几乎无影响，从经济角度考虑，选1C 。

优水平组合为311A B C 。

即温度为58℃,pH 值为6。

5,加酶量为2。

0％.。

第9章 方差分析与正交试验设计

第9章 方差分析与正交试验设计
SSB ( s 1) FB 在H 0 B为真时 SSE (r 1)( s 1) FB F ( s 1, (r 1)( s 1))
由上面讨论,我们找到了一种检验H0A和H0B方法: 选取统计量 SSA (r 1) SSB (s 1) FA FB SSE (r 1)(s 1) SSE (r 1)(s 1) H0A拒绝域为
i 1 j 1 r ni
记
X ij i ij ij 1 i ni 1 N 1 ij , N j 1
ni
N (0, )
2

i 1 j 1
r
ni
ij
n
i 1 i
r
i
则
X i i i
r ni i 1 j 1
r
X
r ni i 1 j 1
SSE (i ij i i )2 ( ij i )2
SSR ni ( i i )2
SST ( i ij )2
i 1 j 1
i 1 r
ni
并且
E (SSE ) E ( ( ij i )2 ) (ni 1) 2 ( N r ) 2
本例中灯丝的品种, 我们称之为因子,而选取了 四个品种,我们之为因子的四个水平.这种情况,我们 称为单因子四水平试验.对这种试验的分析称为单 因子方差分析.一般单因子r水平试验数据可列表如 下
水平水平 A1 A2
Ar
试验结果
x11 , x12 , , x1n1 x21 , x22 , , x2n2
A A1(不施氮肥) A2(施50公斤氮肥) B B1(不施磷肥) 300kg 400kg B2(施50公斤磷肥) 450kg 700kg

利用SPSS进行方差分析以及正交试验设计

利用SPSS进行方差分析以及正交试验设计

利用SPSS进行方差分析以及正交试验设计方差分析是一种常见的统计方法，用于比较两个或多个组之间的差异。

正交试验设计是一种实验设计方法，能够同时考虑多个因素对结果的影响。

本文将利用SPSS进行方差分析和正交试验设计的步骤介绍，并讨论如何解读分析结果。

首先，我们将介绍方差分析的步骤。

方差分析的基本思想是比较组间和组内的变异程度。

假设我们有一个因变量和一个自变量，自变量有两个或多个水平。

下面是方差分析的步骤：1.导入数据：将数据导入SPSS软件，并确保每个变量都已正确标记。

2.选择统计分析：点击SPSS菜单栏上的"分析"，然后选择"方差"，再选择"单因素"。

3.设置因变量和自变量：在弹出的对话框中，将需要进行方差分析的因变量拖放到因素列表框中，然后将自变量也拖放到因素列表框中。

4.点击"设定"按钮：点击"设定"按钮，设置方差分析的参数，例如是否需要进行正态性检验、多重比较等。

然后点击"确定"。

5.查看结果：SPSS将输出方差分析的结果，包括各组之间的F值、p值等统计指标。

可以根据p值判断各组之间是否存在显著差异。

接下来，我们将介绍正交试验设计的步骤。

正交试验设计是一种多因素独立变量的实验设计方法，可以在较小的实验次数内获得较高的信息量。

下面是正交试验设计的步骤：1.设计矩阵：根据研究目的和独立变量的水平，构建正交试验的设计矩阵。

2.导入数据：将设计矩阵导入SPSS软件，并将每个变量的水平标注为自变量。

3.选择统计分析：点击SPSS菜单栏上的"分析"，然后选择"一般线性模型"，再选择"多元方差分析"。

4.设置因变量和自变量：在弹出的对话框中，将因变量拖放到因子列表框中，然后将自变量也拖放到因子列表框中。

5.点击"设定"按钮：点击"设定"按钮，设置正交试验设计的参数，例如交互作用是否显著、多重比较等。

第4讲5(2) 正交试验设计(方差分析)

第4讲5(2) 正交试验设计(方差分析)

3
4 5 6 7 8 K1j K2j K1j-K2j SSj
1
1 2 2 2 2 9.9 10.31 -0.41 0.021
2
2 1 1 2 2 9.42 10.79 -1.37 0.235
2
2 2 2 1 1 10.21 10 0.21
1
2 1 2 1 2 10.23 9.98 0.25
1
2 2 1 2 1 10.24 9.97 0.27
拟水平列：第2列
表4-36
试验号 试验号 1 2 3 4 5 6 7 8 9 K1j K2j K3j k1j k2j k3j 调整R＇ 优水平 优组合 主次顺序 A 1 1 1 1 2 2 2 3 3 3 275.5 252.0 270.0 91.8 84.0 90.0 7.8 A1
例3 试验结果分析表
水 试 验 1 2 3 4 平 号 列 号 A 1 1 1 1 B 1 1 2 2 A×B 1 1 2 2 C 1 2 1 2 A×C 1 2 1 2 B×C 1 2 2 1 误差列 1 2 2 1 数据 5.26 3.90 6.90 7.03
5
6 7 8
2
2 2 2
1
1 2 2 18.68
2
1 2 1 2 11.4 11.5
2
2 1 2 1 10.2 12.7
1
1 2 2 1 12.1 10.8
1
2 1 1 2 12.5 10.4
129.96 132.25
104.04 161.29
146.41 116.64
156.25 108.16
自由度计算： df B df C 2 - 1 1 dfe df 4 df5 1 1 2 （2）显著性检验

第4章 方差分析、正交试验设计

第4章 方差分析、正交试验设计
i 1 j 1
r r
i 2 ( X ij X i )( X i X ) 2[( X i X ) ( X ij X i )] 其中： 2 ( X ij X i )(X i X ) 21[(X i X )1( X ij X i )] 其中： i 1 j 1 i j
r i 1 j 1
i
j n 1 r ni n i 1 11r X X ij ni X i n i 1 j 1 n i 1
X rX 1 r n X 1 r n X ij i i
i 1
i 1 QT ( jX1ij X ) 2
r
i 1 j 1 r r
ni ni
i 1
j 1
r
i 1
j 1
i 1 i 1
E、
QE
2 [( X i X )(ni X i ni X i )] 0
i 1
i
Ar
QT QE QA
QA
r n r 于是，总离差平方和被分解为组内离差平方和与 ( X ij X i )2 ni ( X i X )2 从而： QT i 1 j 1 i 1 组间离差平方和之和。 QE ——反映了 ij 的作用 ②组内离差平方和 ②组内离差平方和QQE——反映了 的作用 ②组内离差平方和 E ——反映了 ij 的作用 ②组内离差平方和QEEE ——反映了ijij的作用 ②组内离差平方和 Q ——反映了 ij ij 的作用 r ②组内离差平方和 ③分解定理 QA 2 Q E——反映了的作用 QEn、 X ) ②组内离差平方和Q ——反映了 )] n ( ) ij 的作用 QEr ( X ij nn [( ) ( i n r r r rn 2 2 2 i 1 ( jXX X )) 2 ( X 1 n Q r ) QQQ ( X ij X 设 [( Yn ( 立 ( ij) ,ij ) 2 [( ( ( )] , ) ) ) (Q 2 (i ~ ( E 理 ( Q 定 E ((XijX：XiX)))2Y11r,Yn12,i相)互独)])]QiAr( N(( i )i ) 2 4.1.1 X i j [([( QT)ij( E i ， Yjn (0 )1 ， )] )] QE i 11j j11 ij X i i[( i ij ) ( i i )] 1 ij i i i) ③组间离差平方和1Qj 1 ——反映了 i 的作用. ii 1j11j 11 A i 1 j 1 i 2 2 Q A——反映了 Y 2 ~ 2 (n) ， 又 若 ③组间离差平方和 是 r——反映了的作用. i ③组间离差平方和 QQ A——反映了 的作用. 1,2,n,于是，总离差平方和被分解为组内离差平方和 n ， 于 Q ——反映了i 的作用. n ③组间离差平方和 r ③组间离差平方和 A A Q Y1 Y22 ③组间离差平方和 QA ——反映了i iri i的作用. 的作用. 2 rr rr nn Q ni ( X i 2X ) ni的作用.i ( )]2 i [( i ③组间离差平方和rrr A ——反映了 QA r ( X i X ) rn n QQ1 (( Xi i ) 2 i ( X i QiX 2 2, ni 1, n 的线性组合的 X 22 r i i QA rnQ21X X )Q2，nn1 ( X iX )是 Yr2 , Y )])] 2 ( Q A ( X X2) n ( X X ) 2 Y1 n r[([([( ( )] 其中 ) i 1 j Q 组间离差平方和之和。 nn ( ( )] 2 nj j 1 X i X ) i 1 1r ni ( Xi X ) 2 Q A r ii1 1( r [( i 1

方差分析与正交试验设计

方差分析与正交试验设计
方差分析与正交试验设计
第七章 方差分析与正交试验设计
一 基 本 要 求
1．了解单因素试验的方差分析；会利用正交表安排试验设计。 2．了解双因素无重复试验的方差分析及双因素有重复试验的方差分析。
二
重 点 与 难 点
重点：正确理解方差分析的基本思想及解决简单实际问题一般步骤。 难点：因子间有交互作用的正交试验设计及方差分析。
j = 1,2,3,L , r ）。设对每一个水平组合 Ai B j 做了 n 次试验（这里只讨论每个水
平所作试验次数相同的情形），试验结果为 yij1 , yij 2 ,L , yijn （ i = 1,2,3,L , k ；
j = 1,2,3,L , r ）。假定对水平组合 Ai B j 试验结果的理论值为 µ ij ，即 Eyijl = µ ij ，
$ =y −y $ = y ，α $ i = yi⋅ − y ， β µ j ⋅j $ ij = yij − yi⋅ − y⋅ j + y i = 1,2,L , k；j = 1,2,L , r γ
（7-11）
n
其中， y =
1 k r n 1 r n 1 y ， y = yijl ， y⋅ j = ∑ ∑ ∑ ∑ ∑ i⋅ ijl nkr i =1 j =1 l =1 nr j =1 l =1 nk
—151—
方差分析与正交试验设计
差异，这是由随机误差所引起的，因此称为误差平方和，有时也称为组内差。
2 2 一定时，若 而 S 组间 = r ∑ ( y i − y ) 2 则是由 A 的不同水平变化所引起的。所以 S 总 i =1 2 2 A 的不同水平引起的变化非常显著时，则 S 组间 较大，相应地 S 误 就较小；而 2 2 当因子 A 的不同水平引起的变化不显著时，则 S 组间 较小，相应地 S 误 就较大， 2 即数据的差别主要是由随机误差造成的。这样一来我们就可以通过比较 S 组间 2 与 S误 的相对大小，来检验因子水平改变时引起的差异是否显著。记 n = kr , k

正交设计试验资料的方差分析

正交设计试验资料的方差分析

数据整理
将收集到的数据整理成 表格形式，便于后续分 析。
数据筛选
对异常值进行筛选和处 理，确保数据质量。
正交设计试验资料的方差分析过程
确定试验因素和水平
明确试验因素和各因素的水平， 为后续分析提供基础。
计算各因素的效应值
根据试验结果，计算各因素的效 应值。
计算误差平方和
根据效应值和水平，计算误差平 方和。
跨学科融合
标准化与规范化
结合其他学科的理论和方法，拓展正交设 计试验的应用领域，推动多学科交叉融合 发展。
制定和完善正交设计试验的标准和规范， 提高试验的可靠性和可比性。
正交设计试验资料方差分析的实际应用价值
科学研究
在科学研究领域，正交设计 试验资料方差分析可用于探 索和验证科学假设，揭示现 象背后的机制和规律。
正交试验设计的基本原理
1 2
正交性原理
正交试验设计基于正交性原理，即每个因素在试 验中出现的次数相同，且各次出现的概率相等。
均匀分散原理
正交试验设计通过均匀分散原理，确保每个水平 在试验中都有均衡的分布，从而减少结果的偏差。
3
代表性原理
正交试验设计通过代表性原理，选取具有代表性 的样本点进行试验，以反映整体情况。
正交设计试验资料的方差 分析
• 正交设计试验概述 • 方差分析基础 • 正交设计试验资料的方差分析方法 • 实例分析 • 总结与展望
01
正交设计试验概述
正交试验设计的基本概念
正交试验设计是一种统计技术，用于 在多因素、多水平条件下进行试验， 以最小化试验次数，同时最大化信息 收集。
它利用正交表来安排试验，确保每个 因素的每个水平都被等可能地选取， 从而得到全面而均衡的试验结果。

正交实验设计与方差分析2024

正交实验设计与方差分析2024

引言概述正交实验设计与方差分析是一种常用于实验设计和数据分析的统计方法。

这种方法能够帮助研究人员系统地设计实验、收集数据，并通过方差分析对数据进行统计分析。

正交实验设计适用于多因素实验设计，能够探究多个因素对结果变量的影响，并确定各个因素对结果变量的相对重要性。

方差分析则是用来比较不同组别之间的均值差异是否显著，并推断这些差异是否由于随机因素引起。

正文内容1.正交实验设计的基本原理1.1.因素和水平1.2.正交实验设计的完备性和平衡性1.3.主效应和交互效应的概念1.4.正交表和正交实验设计的选择1.5.正交实验设计的优点和局限性2.正交实验设计的建立步骤2.1.确定要研究的因素和水平2.2.选择适当的正交表2.3.构建试验方案2.4.进行实验和数据收集2.5.数据分析和结果解释3.方差分析的基本原理3.1.单因素方差分析3.2.多因素方差分析3.3.方差分析中的假设检验3.4.方差分析的效应量和效应大小3.5.方差分析结果的解释和报告4.正交实验设计与方差分析的应用领域4.1.医学研究4.2.工程设计4.3.农业实验4.4.社会科学研究4.5.生产过程优化5.正交实验设计与方差分析的案例分析5.1.一个药物疗效评价的正交实验设计案例5.2.一个工程设计的正交实验设计案例5.3.一个农业实验的正交实验设计案例5.4.一个社会科学研究的正交实验设计案例5.5.一个生产过程优化的正交实验设计案例总结正交实验设计与方差分析是一种重要的统计方法，在实验设计和数据分析中具有广泛的应用。

通过正交实验设计，研究人员能够系统地探究多个因素对结果变量的影响，并确定各个因素的相对重要性。

方差分析则用于比较不同组别之间的均值差异，并推断这些差异是否显著。

正交实验设计与方差分析能够帮助研究人员有效地设计实验、收集数据并进行统计分析，为科学研究和应用提供有力支持。

在不同领域，如医学研究、工程设计、农业实验、社会科学研究和生产过程优化等方面都有广泛的应用。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1. 随机误差
▪ 因素的同一水平(总体)下，样本各观察值之间的差
异
▪ 比如，同一行业下不同企业被投诉次数是不同的 ▪ 这种差异可以看成是随机因素的影响，称为随机
误差
2. 系统误差
因素的不同水平(不同总体)下，各观察值之间的差异
比如，不同行业之间的被投诉次数之间的差异
这种差异可能是由于抽样的随机性所造成的，也可能
可Байду номын сангаас理ppt
14
方差分析的基本思想和原理
1. 比较两类误差（系统性误差、随机误差）， 以检验均值是否相等； 2. 比较的基础是方差比；
3.如果系统(处理)误差明显地不同于随机误差， 则均值就是不相等的；反之，均值就是相等的；
4. 误差是由各部分的误差占总误差的比例来测 度的。
可整理ppt
15
方差分析的基本思想和原理(两类误差)
行业
观测值
零售业
旅游业
航空公司 家电制造业
1
57
68
31
44
2
66
39
49
51
3
49
29
21
65
4
40
45
34
77
5
34
56
40
58
6
53
51
7
44
可整理ppt
8
什么是方差分析?(例题分析)
1. 分析四个行业之间的服务质量是否有显著差 异，也就是要判断“行业”对“投诉次数” 是否有显著影响
2. 作出这种判断最终被归结为检验这四个行业
被投诉次数的均值是否相等。怎样检验？
3. 若它们的均值相等，则意味着“行业”对投 诉次数是没有影响的，即它们之间的服务质 量没有显著差异；若均值不全相等，则意味 着“行业”对投诉次数是有影响的，它们之 间的服务质量有显著差异。
可整理ppt
9
方差分析中的其他有关概念
1.因素或因子(factor) ▪ 所要检验的对象 ▪ 要分析行业对投诉次数是否有影响，行业是要检验
是由于行业本身所造成的，后者所形成的误差是
由系统性因素造成的可整，理pp称t 为系统误差
16
方差分析的基本思想和原理(两类方差)
1. 数据的误差用平方和(sum of squares)表示，又 构成方差。
可整理ppt
5
7.1.1方差分析的有关概念
可整理ppt
6
什么是方差分析(ANOVA)?
1）检验多个总体均值是否相等
▪ 通过分析数据的误差判断各总体均值是否相
等
2）研究分类型自变量对数值型因变量的影响
一个或多个分类尺度的自变量
两个或多个 (k 个) 处理水平或分类
一个间隔或比率尺度的因变量
3）有单因素方差分析和双因素方差分析
以看作是四个总体
6.样本数据
▪ 被投诉次数可以看作是从这四个总体中抽取的样
本数据
可整理ppt
11
7.1.2方差分析的基本思想和原理
80
60
被投诉次数
40
20
0
0
零1 售业 2旅游业 3航空公司 4 家电制造 5
不同行业被投可整诉理pp次t 数的散点图
行业12
方差分析的基本思想和原理(图形分析)
1. 从散点图上可以看出
采用方差分析方法很容易解决这样的问题，它是同时考 虑所有的样本数据，一次检验即可判断多个总体的均值 是否相同，这不仅排除了犯错误的累积概率，也提高了 检验的效率。
可整理ppt
4
7.1 方差分析的基本思想
7.1.1方差分析的有关概念 7.1.2方差分析的基本思想和原理 7.1.3方差分析中的基本假定 7.1.4假设问题的一般提法
第 7 章 方差分析与正交实验设计初步
7.1 方差分析的基本思想 7.2 单因素方差分析 7.3 双因素方差分析 7.4 正交实验设计初步
可整理ppt
1
学习目标
方差分析的基本思想和原理 单因子方差分析 多重比较 双因子方差分析的方法 实验设计方法与数据分析
可整理ppt
2
不同运动队的平均成绩之间是否有显著差异？
3
不同运动队的平均成绩之间是否有显著差异？
每个队伍的24箭成绩可以看作是该队伍射箭成绩的一个 随机样本。获得金牌、银牌和铜牌的队伍之间的射箭成 绩是否有显著差异呢？
如果采用第5章介绍的假设检验方法，用分布做两两的比 较，则需要做次数比较。这样做不仅繁琐，而且每次检 验犯第Ι类错误的概率都是一样的，作多次检验会使犯第Ι 类错误的概率相应地增加，检验完成时，犯第Ι类错误的 概率将会很大。同时，随着检验的次数的增加，偶然因 素导致差别的可能性也会增加。
这种差异可能是由于抽样的随机性所造成的, 也有可能是系统性影响因素造成的。
4需要有更准确的方法来检验这种差异是否显著，也 就是进行方差分析
所以叫方差分析，因为虽然我们感兴趣的是均 值，但在判断均值之间是否有差异时则需要借 助于方差
这个名字也表示：它是通过对数据误差来源的 分析判断不同总体的均值是否相等。因此，进 行方差分析时，需要考察数据误差的来源
不同行业被投诉的次数是有明显差异的
同一个行业，不同企业被投诉的次数也明显不同
家电制造被投诉的次数较高，航空公司被投诉的次数 较低
2. 行业与被投诉次数之间有一定的关系
如果行业与被投诉次数之间没有关系，那么它们 被投诉的次数应该差不多相同，在散点图上所呈 现的模式也就应该很接近
可整理ppt
13
3仅从散点图上观察还不能提供充分的证据证明不同 行业被投诉的次数之间有显著差异
单因素方差分析：涉及一个分类的自变量 双因素方差分析：涉及两个分类的自变量
可整理ppt
7
什么是方差分析? (例题分析) 一个
分类
【 例 】为了对几个行业的服务质量进行评价，消费者协会 变量 在四个行业分别抽取了不同的企业作为样本。最近一年中消
费者对总共23家企业投诉的次数如下表
消费者对四个行业的投诉次数
奥运会女子团体射箭 比赛，每个队有3名 运动员。进入最后决 赛的运动队需要进行 4组射击，每个队员 进行两次射击。这样， 每个组共射出6箭， 4组共射出24箭
在2008年8月10日进 行 的 第 29 届 北 京 奥 运会女子团体射箭比 赛中，获得前3名的 运动队最后决赛的成 绩如下表所示
可整理ppt
的因素或因子
2.水平或处理(treatment) ▪ 因子的不同表现 ▪ 零售业、旅游业、航空公司、家电制造业就是因子
的水平
3.观察值 ▪ 在每个因素水平下得到的样本数据 ▪ 每个行业被投诉的次数就是观察值
可整理ppt
10
4.试验
▪ 这里只涉及一个因素，因此称为单因素四水平的
试验
5.总体
▪ 因素的每一个水平可以看作是一个总体 ▪ 比如零售业、旅游业、航空公司、家电制造业可