概率论中不同条件下的Jensen不等式及应用
- 格式:doc
- 大小:118.00 KB
- 文档页数:5

Jensen不等式是数学中的一个重要不等式,它描述了凸函数的性质,并应用于众多领域,如概率论、统计学和信息论等。
Jensen不等式在均值不等式中具有重要作用。
本文将从Jensen不等式的数学定义入手,展开对其在均值不等式中的证明,并讨论其在实际问题中的应用。
一、Jensen不等式的定义1.1 凸函数的定义凸函数是指对于定义域内的任意两点,连接这两点的线段位于函数图像的上方。
具体而言,若对于定义域内的任意两点x1和x2,以及任意0≤λ≤1,有f(λx1 + (1-λ)x2) ≤ λf(x1) + (1-λ)f(x2),则函数f(x)为凸函数。
1.2 Jensen不等式的表述设f(x)为凸函数,X为随机变量,则有E[f(X)] ≥ f(E[X]),其中E[·]表示随机变量的期望值。
此即Jensen不等式的常见表述形式。
二、Jensen不等式在均值不等式中的应用2.1 均值不等式的概念均值不等式是指描述一组数的平均值与其它某些特定数之间的大小关系的不等式。
常见的均值不等式包括算术平均数-几何平均数不等式、柯西-施瓦兹不等式等。
2.2 Jensen不等式与均值不等式的关系通过Jensen不等式,我们可以推导出许多均值不等式。
具体而言,对于凸函数f(x)和非负权重λi(∑λi=1),有f(∑λiXi) ≤ ∑λif(Xi),其中Xi为实数。
这一不等式即表明了均值不等式的一种形式。
三、Jensen不等式在实际问题中的应用3.1 概率论中的应用在概率论中,Jensen不等式常常用于证明随机变量的期望值与函数的值之间的大小关系。
对于凸函数f(x)和随机变量X,有E[f(X)] ≥f(E[X])。
这一性质在风险管理、金融工程等领域有重要应用。
3.2 统计学中的应用在统计学中,Jensen不等式被广泛应用于证明估计量的不偏性、有效性等性质。
通过Jensen不等式,可以建立统计量与其期望值之间的关系,从而为统计推断提供理论基础。

1. Jensen不等式回忆优化理论中的一些概念。
设f是定义域为实数的函数,如果对于所有的实数x,,那么f是凸函数。
当x是向量时,如果其hessian矩阵H是半正定的〔〕,那么f是凸函数。
如果或者,那么称f是严格凸函数。
Jensen不等式表述如下:如果f是凸函数,X是随机变量,那么特别地,如果f是严格凸函数,那么当且仅当,也就是说X是常量。
这里我们将简写为。
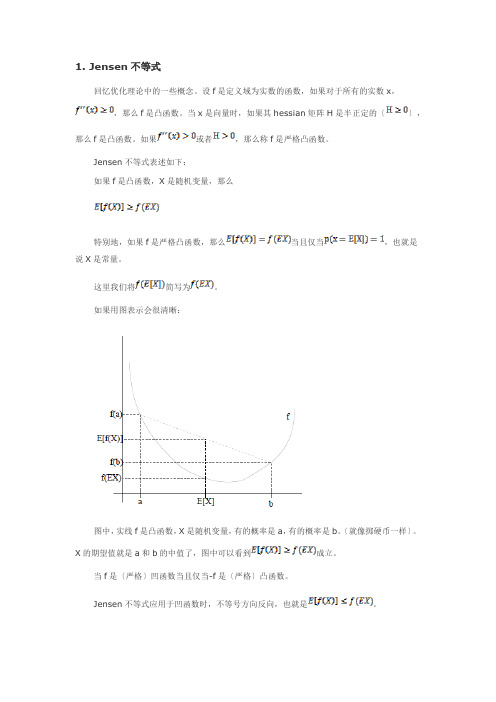
如果用图表示会很清晰:图中,实线f是凸函数,X是随机变量,有的概率是a,有的概率是b。
〔就像掷硬币一样〕。
X的期望值就是a和b的中值了,图中可以看到成立。
当f是〔严格〕凹函数当且仅当-f是〔严格〕凸函数。
Jensen不等式应用于凹函数时,不等号方向反向,也就是。
先验概率与后验概率事情还没有发生,要求这件事情发生的可能性的大小,是先验概率. 事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率.一、先验概率是指根据以往经历和分析得到的概率,如全概率公式,它往往作为“由因求果〞问题中的“因〞出现。
后验概率是指在得到“结果〞的信息后重新修正的概率,如贝叶斯公式中的,是“执果寻因〞问题中的“因〞。
先验概率与后验概率有不可分割的联系,后验概率的计算要以先验概率为根底。
二、A prior probability is a marginal probability, interpreted as a description of what is known about a variable in the absence of some evidence. The posterior probability is then the conditional probability of the variable taking the evidence into account. The posterior probability is computed from the prior and the likelihood function via Bayes' theorem.三、先验概率与后验概率通俗释义事情有N种发生的可能,我们不能控制结果的发生,或者影响结果的机理是我们不知道或是太复杂超过我们的运算能力。

概率论中不同条件下的jensen不等式及应用
概率论中的Jensen不等式是由匈牙利数学家Johannes Jensen在1906
年提出的重要理论,它告诉我们,同一场景下,熵增大时,贝叶斯风险最小。
目前,该不等式在概率论中广泛应用,有许多与之相关的推论。
这里提出的Jensen不等式定义如下:在给定的条件下,当一个熵函数是凸函数时,它的期望值不大于其期望的加性函数的期望值。
该不等式的应用很广泛,它可以应用于随机变量X的均值和方差的关系,其中X服从二项分布。
根据舍加瓦定理和Jensen不等式,P(X>=k)的期望
值不大于2^(k-μ)μ。
这一不等式也可以应用于优化和搜索问题。
例如,机器学习中的最小负梯度算法可以被用来求解复杂的最优解,该算法通过利
用Jensen不等式来实现。
此外,Jensen不等式也被用于统计学中的准则函数优化,比如假设函数
中的参数估计。
给定的准则函数,他可以求解参数μ的最佳估计值,然后
根据Jensen不等式求得参数期望。
它也可以用来设计一种新的分布,以便
使估计更加准确。
总之,Jensen不等式是概率论中一个重要的不等式,它可以有效地解决
很多问题,并且可以广泛应用于机器学习、统计学和优化问题中。

jensen不等式的条件证明logistic regression 损失函数凸函数摘要:一、引言二、Jensen不等式的概念和条件1.Jensen不等式的定义2.Jensen不等式成立的条件三、Jensen不等式在Logistic Regression中的应用1.Logistic Regression的基本概念2.Logistic Regression的损失函数3.Jensen不等式在优化损失函数中的应用四、凸函数与Jensen不等式1.凸函数的定义和性质2.凸函数与Jensen不等式的关系3.在凸函数中应用Jensen不等式的方法正文:一、引言Jensen不等式是一种在凸函数中具有重要作用的不等式,它可以帮助我们更好地理解和优化损失函数。
本文将详细介绍Jensen不等式的条件,以及如何在Logistic Regression中应用Jensen不等式来优化损失函数。
二、Jensen不等式的概念和条件1.Jensen不等式的定义Jensen不等式是由丹麦数学家Jensen提出的,它描述了在凸函数中,平均值大于等于最小值,即:`frac{1}{n}sum_{i=1}^{n}f(x_i) geq f(frac{1}{n}sum_{i=1}^{n}x_i)`其中,f(x)是一个凸函数,x_i是函数的自变量,n是样本数量。
2.Jensen不等式成立的条件Jensen不等式成立的条件是:- 函数f(x)是凸函数;- 自变量x_i满足平均值不等式,即$frac{1}{n}sum_{i=1}^{n}x_i leq max_{i=1}^{n}x_i$。
当这两个条件都满足时,Jensen不等式才能成立。
三、Jensen不等式在Logistic Regression中的应用1.Logistic Regression的基本概念Logistic Regression是一种常见的二分类算法,它的目的是找到一个最佳的超平面,使得两类数据在此超平面上被正确地分开。

概率论中几个不等式的推广及应用
1. 闵可夫斯基不等式:它是概率论中最重要的不等式,它的推广及应用包括:
(1)贝叶斯不等式:它是闵可夫斯基不等式的一种推广,它可以用来证明贝叶斯定理,以及证明条件概率的关系。
(2)拉普拉斯不等式:它是闵可夫斯基不等式的另一种推广,它可以用来证明拉普拉斯定理,以及证明条件概率的关系。
(3)抽样不等式:它是闵可夫斯基不等式的另一种推广,它可以用来证明抽样定理,以及证明条件概率的关系。
(4)泰勒不等式:它是闵可夫斯基不等式的一种推广,它可以用来证明泰勒定理,以及证明条件概率的关系。
(5)大数定律:它是闵可夫斯基不等式的一种推广,它可以用来证明大数定律,以及证明条件概率的关系。
2. 黎曼不等式:它是概率论中另一个重要的不等式,它的推广及应用包括:
(1)熵不等式:它是黎曼不等式的一种推广,它可以用来证明熵定理,以及证明条件概率的关系。
(2)马尔可夫不等式:它是黎曼不等式的一种推广,它可以用来证明马尔可夫定理,以及证明条件概率的关系。
(3)惩罚不等式:它是黎曼不等式的一种推广,它可以用来证明惩罚定理,以及证明条件概率的关系。
(4)贝尔不等式:它是黎曼不等式的一种推广,它可以用来证明贝尔定理,以及证明条件概率的关系。
(5)贝尔-黎曼不等式:它是黎曼不等式的一种推广,它可以用来证明贝尔-黎曼定理,以及证明条件概率的关系。
凸函数的Jensen不等式的矩阵形式及应用97,/to)丫/第16卷第3期成都大学(自然科学版)V o1.16No.31997年9月AcatScientiarumNaturaliumUniversitatisChengduens~Sep.1997凸函数的Jensen不等式的矩阵形式及应用摘要关键词分类号罗睾f】0I7(成都大学成都610081)导出Je嗍手式的矩阵形式.由此简坼地证明几个着名不午点的矩阵形式.矩阵不等式Hermite矩阵凸函矗AMS(1991)26D15/CCLO178.1了机等文1前言Bellman在1978年国际第二次一般不等式会议上提出,对于几何一算术平均不等式在矩阵中是否有类似的结论?[1]证明了(叫~≤≤击(客A】这里A是同阶正定矩阵,AA尸Ai,i,j—l,2...?,m.[2]证明了三mm,Bi≤《∑酬(∑酬这里A,B是同阶半正定矩阵(i—l,2,…,m)?p>llq_l_1.A..'Am.B..,Bm两两可交换.[2]还证明了[妻(A+Bi)p]{≤《)}+(妻J}这里Ai,BI是同阶正定阵,i=l?2??lrn,p>l,A1..A,Bl?,Bm两两可交换.本文给凸函数的Jeasen不等式的Hermite矩阵形式,并由此导出几个着名不等式的正定(半正定)的Hermite矩阵形式.收稿日期1997—03—112?成都大学(自然科学版)2几个引理设A和B为两个n阶Hermite阵,A>B(A≥B)是指A—B是正定(半正定)的Hermite阵[".显然,当A>B(A~-B)时有一B>一A(一B≥一A).设A是n阶Hermite阵,f是复函数,那么存在酉矩阵u[|]使得A=U.diag(~I,…,)U这里u是u的共辊转置,'..?,∈R是A的特征值,若f()是定义在区问I(ICR)上复函数,当∈I,i=1,2,…,n,鄢么f(A)可以定义为"】.f(A)一U.diag(f(~),f(k),…,f())U显见.若所有f()∈R,那么f(A)是Hermite阵,如果的有的f()≥0(>0),那么f(A)是半正定(正定)的Hermite阵.引理l设A,B为两个n阶Hermite阵,则存在酉阵u即满足UU=I使U'AU,U. BU同时为对角阵当且仅当AB=BA.一见[3,PP.18]引理2设A和B是q阶正定的Hermite阵.且AB=BA,财(1)In(AB)~lnA+lnB;(2)In(AB-.)=InA—lnB;(3)A>B(A~B当且仅当lnA>lnB(InA≥InB);(4)当k为实数时,lnA=klnA.证(1),由引理1,有酉阵u,使A—U.diag(X,,…,)UB—U.diagCm,…,)U再设f(x)一1nxt故In(AB)=lnl'U'dhgCXl,…,)u?U'dhgCUit..?,)u]=lnEU'dhg(it…,)u]=U'diag(InO,I脚),…,In())U—Udiag(1n~+1"'..?,In+ln)U=Udhg(1n~,…,In)U+Udiag(In~I,…,)U=InA—LInB(2)一(4)类似可证.3主要结果定理1(凸函数的3ensen不等式的Hermite矩阵形式)设f是区问I(ICR)的一个凸函数,,i=1'.'-m是Hermite阵,它们的特征值垒在I里, 且A.,,….A.两两可交换,)【i>0,i=1,…,m,上xj=1,鄢么m三f(A)≤xi)(1)凸函数的Jensen不等式的矩阵形式及应JII?3?证由引理1知有酉矩阵u,使得A,i=1,2'.-?m同时对角化AI=U'dhg(~,'..',)u这里,…,.是A的全部特征值,从而mⅢ∑f(A)一f(∑Ai)j-lI-l一u协g[....()]U—f{diag(.,…,)U)池g[(...,()]u—Ig[f{x^)....'f{xAj.)]u—u'diag[∑】【If(.{∑i-1)--fx),….∑xLf(~.i)一f{∑x-)]u≥o●?1i-1t--1●-1这里最后一式用到了熟知的分析中凸函数的Jenen不等式,由此即得(1)式.下面利用定理导出几个着名不等式的Hermite矩阵形式.推论1(调和.几何一算术平均不等式Hermite阵形式)若Ai,i=l,2,….m是正定的Hermite阵,且AIAj—AA,i,j:l,2,…,m,那么有()~≤≤()㈣证取(0,+..)内的凸函数f(x)=一lnx,定理1中令x一…xm一吉,并利用引理2 得一f砉mA.1t≤i-~吉c一_..一(∑A-)~<--ln(IT)(3)(客A)≥显见,A_.,._1,2...?,m也是正定的Hermite阵,且AiAj-1=AjAI_.,i,j=1,2,…,m,利用(3)式有In击{Ai)≤In(gJ=In{gA.)(4)这正是要证的结果.定理1中,若取f(x)一.Inx,m=2,x=吉,一百1,且1p+1q一1,可得AB÷≤+B(5)这里A,B为同阶正定的Hermite阵,且AB=BA.推论2(Ho~er不等式的Hermite矩阵形式)若AI,l3i均为正定的Hermite阵(j1,2,…,m),p>l,言+言hA1..-',A匝,Bl,…,Bm 两两可交换,则.-4?成都大学(自然科学版)宝A.B≤(妻Aij(宝j证:令C一∑A.D:∑A=APC~B一珏D一由(5)式得AiBjc≤+(i.1.2..r…)将上面m个不等式相加后稍加整理即可得所证的不等式利用推论2可得.推论3(Mimkowski不等式的Hermlte形式)设A.B均为正定的Hermite阵,i一1,2,m, p>l,A..'A.B_..两两可交换,则有[∑(A1-Bi)]≤(∑Ai)÷+(∑)}参考文献1王炜籽,几个矩阵不等式,广西师范太学,1981年第1期.2罗钊,Holder不等式及Minkowski不等式的矩阵形式,成都太学,]990.4+.3王公挂,贾忠,矩阵论中不等式,安微教育出版社.19944B.Mond.JE+Peearic,GeneralizationofaMatrixInequalityofKyFan.JMath.AnalAppl 19O,244—247(1995) AMatrixFormofJenenInequalityandItsApplicationsLUOZhao(ChertgduUniverity610081)Inthispaperwegiveamatrixanalogue0fthe2eneninequality,andderiveSomewell—knowninequalitiesfromthisenequalityforHermitianmatrices KeywordsMatrixinequality,Hermitianmatrix,Convexfunction。
代数函数的jensen不等式的加细与推广Jensen不等式是数学和统计学中发挥重要作用的数学定理,它以一个有限个变量构成的累积函数形式,对这些变量的累积函数的期望进行有限的界定及求解。
下面就Jensen不等式的加细与推广作一进一步的讨论:一、 Jensen不等式的加细1、基本的Jensen不等式:即假设函数f(x)是连续可微函数,而X是一个有限个变量构成的随机变量,那么对任意可行赋值θ,有:E(f(X))≥f(E(X)),这就是基本的Jensen不等式。
2、海森堡不等式:假设fx(x1, x2, ..., xn)在[αi, βi]下是一个凸函数,Then, for any arbitrary set of values θ1, θ2, ..., θn, there is:E[f(X)]≥f[E(X1), E(X2), ..., E(Xn)],这就是海森堡不等式。
3、勒贝格不等式:前提条件是函数f(x)是可微的,对任意可行赋值θ,有:E[f(X)]≥E(g(X)),其中g(X)=E{f(X′) |X=θ} ,这就是提出了勒贝格不等式。
4、贝叶斯不等式:前提条件是f(x)是可微的,对任意可行赋值θ,有:E[f(X)]≥E{g(X)|X=θ},其中g(x)是贝叶斯可合并的,这就是贝叶斯不等式。
二、Jensen不等式的推广1、统计不等式:假设f(x)是连续可微函数,而X是一个有限个变量构成的随机变量,那么对任意可行赋值θ,有:E[f(X)]≤f[E(X1), E(X2), ..., E(Xn)],这称为统计不等式。
2、博弈论不等式:博弈论中,假设f(x)是一个单局博弈积分函数,X是一个等概率随机策略,则Frame‐Stewart不等式规定:E[f(X)]≤f[E(X1), E(X2), ..., E(Xn)],这称为博弈论不等式。
3、期望函数不等式:期望函数不等式指的是在一个期望函数的类中,存在某种非负函数f,有:E[f(X)]≤f(E(X)),这就是期望函数不等式。
探讨凸函数的Jensen不等式的应用不等式在数学中的地位相当高,而Jensen不等式这样的一类基本不等式,在凸函数理论中占据着重要位置,一般而言对凸函数的研究均是对Jensen不等式着手,而且随着其发展而不断发展完善,且在数学很多分支中有深入的应用。
关于凸函数的Jensen不等式的改进、扩展、推广及应用仍是现阶段数学家门所关注的热点话题。
本文拟从凸函数和Jensen不等式的基本知识出发,探讨一类凸函数Jensen不等式的加细及其应用,再对其进行展望。
1 预备知识Jensen不等式是描述刻画凸函数的一个最基本的不等式。
在凸函数相关理论中往往是通过Jensen不等式来定义凸函数:若,,有≤(1)则是定义在上的凸函数。
若(1)式等号成立当且仅当,此时称之为在上的一个严格凸函数。
还有一般的叙述:,,有≤ (2)则是定义在E上的凸函数。
若(2)式等号成立当且仅当,此时称之为在E上的一个严格凸函数。
同时还可以将上式推广为更为一般的情形,鉴于本文所讨论的Jensen不等式一个加细内容,只对以上两种情形的Jensen不等式形式进行展开论述。
凸函数的性质[1]:性质1:设是定义在的凸函数,,,则存在,且:≥性质2:设是定义在的连续凸函数,则有:性质3:设是定义在的凸函数,则,、均存在,且,,当<,有如下式子:≤≤≤2 Jensen不等式的加细继(1)式进行讨论,引入插值问题,即:当是是定义在上的凸函数,则有:≤≤ (3)从(3)来看,此式是在(1)式中插入了一个函数平均值,是对(1)的一个加细。
我国王成良教授在这方面的理论研究比较深,且他通过文献[2]、[3]中将(3)进行了推广:≤≤ (4)上式中,是定义上的凸函数,。
同时可以看出(4)式是对(2)式进行了加细,即在(2)式Jensen不等式中插入了两个函数平均加权平均。
3 加细Jensen不等式的性质研究3.1 定义新函数假设在上可积,且,,定义两个新函数:(5)(6)由以上定义的两个新函数,再结合连续凸函数的Jensen不等式相关性质和其加细不等式,能够得到如下较为严谨的连续型变量不等式。
本科毕业论文题目: 概率论中不同条件下的Jensen不等式及应用学院:数学学院专业:信息与计算科学年级:2007级本科(汉班)姓名:魏永健指导教师:白根柱完成日期:2010年10月10日概率论中不同条件下的Jensen 不等式及应用作者 魏永健(数学学院信息与计算科学2007级汉班)指导教师 白根柱摘 要:介绍了概率论中离散型、连续型和条件期望型的Jensen 不等式,利用凸函数的性质、期望和条件期望的性质来证明;并应用于证明和式不等式、最小风险估计和条件期望收敛等一些问题.关键词;概率论;不等式;凸函数;证明概率不等式是概率论和数理统计的理论研究中的重要工具.对于概率极限理论和统计大样本理论,几乎所有重要结果的论证都是借助于概率不等式的巧妙应用]1[, Jensen 不等式就是其中著名的一个.接下来将给出不同条件下的Jensen 不等式和证明,并应用其来解决一些相关问题.1 不同条件下的Jensen 不等式Jensen 不等式的形式有多种,经典的如下:如果f(x)为连续实值凸函数,且x1≤x2≤…≤xn,∑=ni i 1λ=1,1≥i λ,i=1,2,…,n ,则有∑=n i i 1λf(xi) ≥ f(∑=ni i 1λxi)]2[.在概率论中Jensen 不等式有:离散型、连续型、条件期望型和中位数型等形式.下面将给出最常用的前三种形式.不等式1]3[ 设f(x)是[a, b]上的凸函数,X 是取值于[a, b]上子集A 的离散型随机变量,E 表示期望,则(1)E(f(X)) ≥f(E(X));(2)如果f(x)是严格凸的,则不等式中等号当且仅当P(X=E(X))=1时成立.证明 (1)对X 取值的个数归纳证明.首先对两点分布:X~{p(x1),p(x2)},简记p1=p(x1),p2=p(x2).注意到p1=1-p2,则f(X))=p1f(x1)+p2f(x2) ≥f(p1x1+p2x2)=f(E(X)).其中≥成立应用了f(x)的凸函数性质,现假设X 的值域A 中元素个数为n-1(n ≥2),A={x1,x2,…,xn-1}时,不等式1中的(1)成立.则对A 中元素个数为n(n ≥2),A=(x1,x2,…,xn)时,简记pi=p(xi),p ′i=pi1-pn, i=1,2,…, n,则有{p ′1, p ′2,…,p ′n-1}是一个概率分布,从而有E(f(X)) =p1f(x1) +p1f (x2)+…+pnf(x n)=(1-pn)∑-='11)(n i xi f i p +pnf(xn) ≥pnf(xn)+(1-pn)f(∑-='11)(n i xi f i p )≥pnf(xn) +(1-pn)f(∑-='11)(n i xi f i p ) =f(∑-='11)(n i xi f i p ) =f(E(X)).(2)若f(x)是严格凸的,则总有E(f(X)) ≥f(E(X))成立,除非当且仅当P (X=E (X))=1时,E(f(X))=f(E(X))成立.不等式2]1[ 设X 是m 维随机向量,f(x)为定义在Rm 上的凸函数(m=1,2,…),其中E(X)<∞,则(1) E(f(X)) ≥f(E(X));(2)如果f(x)是严格凸的,则不等式中等号当且仅当P(X=E(X))=1时成立. 证明 (1)由于y=f(x)是Rm+1中的一个凸曲面,而点(E(X),f(E(X)))在次曲面上.由凸集 概率论中不同条件下的Jensen 不等式及应用论中周知的事实,存在一个过此点的平面,使得上述曲面全在此平面的上方.若以y=f(E(X))+c ′(x-E(X))记此平面的方程,则有f(x) ≥f(E(X))+c ′(x-E(X)).因而E(f(X)) ≥f(E(X))+c ′E(X-E(X))=f(E(X)).(2)若f(x)是严格凸的,则除非x=E(X),总有f(x)>f(E(X))+c ′(x-E(X))成立,因而当且仅当P(X=E(X))=1时E(f(X))=f(E(X))成立.不等式3]4[ 设f(x)是连续凸函数,X 为关于g 为σ可积的随机变量,则f(X)关于g 的条件期望存在,且有f(E[X|g]) ≤E[f(X)|g]几乎必然成立.证明 令f ′(x)为f(x)的右导数,则对任意实数x 与y 有f ′(x)(y-x) ≥f(y)-f(x),以E[X|g]及X 代替上式中的x 与y 得f ′(E[X|g])(X-E[X|g])+f(E[X|g]) ≤f(X),记上式左边的随机变量为Y ,则Y 关于g 的条件期望存在,且E[Y|g]=f(E[X|g]).特别地,由于f(X-)≤Y-,故E[f(X)-|g] ≤E[Y-|g]<∞几乎必然成立.因此,f(X)关于g 的条件期望存在,且有f(E[X|g]) ≤E[f(X)|g]几乎必然成立. 2 应用举例例1 设a1,a2,…,an 和b1, b2,…, bn 为两组非负实数,则有∑=n i ai 1logbi ai ≥(∑=n i ai 1)log (∑∑==n i n i biai 11) ,其中等号成立的充要条件是ai/bi 为常数,i=1,2,…,n.证明 不失一般性,可设所有ai>0,bi>0, i=1,2,…,n.函数f(t)=tlogt 是严格凸函数,因f ″(t)=t1loge>0(t>0), 由Jensen 不等式1可得()∑=n i i i t f a 1)(1in i i t a f ∑=≥,对≥i α0,∑=ni i 1α=1成立. 取i α=i b /∑=n j j b 1,ti=ai/bi,i=1,2,…,n 得∑∑==n i n j j ib a 11log j i b a ≥∑∑==n i n j j i b a 11log ∑∑==n i n j j i b a 11, 两边除去∑=nj j b 1即得∑=n i ai 1log bi ai ≥(∑=n i ai 1)log (∑∑==n i n i biai 11)成立,其中等号成立的充要条件是ai/bi 为常数,i=1,2,…,n.例2每有一个无偏的随机化估计g^,则必可找到一个非随机化估计g^1,其风险总不比g^的风险大,其中损失函数L(θ,a)为凸的.证明 现设随机化估计g^ (x,da)是g(θ)的一个无偏估计.基于g^,作一个非随机化估计g^1:g^1(x) =∫Rmag^ (x,da)则由g^的无偏估计推出g1的无偏性.由Jensen 不等式2,有L(θ,g^1(x)) ≤∫RmL(θ,a)g^ (x,da),因此R(θ,g^1) =E(L(θ,g^1(X))) ≤∫RmL(θ,a)g^ (X,da). =R(θ,g^ ).即每有一个无偏的随机化估计g^,则必可找到一个非随机化估计g^1,其风险总不比g^的风险大.例3设T 为g(θ)的一个充分统计量,若损失函数L(θ,a)为凸的,则基于T 的无偏估计h(t)即为g(θ)的无偏一致最小风险估计.证明 设g^ (x)为g(θ)任意无偏估计,考虑条件期望h(t)=Eθ(g^ (X)|T=t),由T 的充分性,知此条件期望与θ无关,因而h(t)=h(t(x))可作为g(θ)的一个估计.由于Eθ(h(T(X)))=Eθ(Eθ(g^ (X)|T))=Eθ(g^ (X))=g(θ),则h(t)=h(t(x))为g(θ)的一个无偏估计.由L(θ,a)的凸性,用Jensen 不等式2,易得R(θ,g^ )≥R(θ,h),故基于T 的无偏估计h(t)即为g(θ)的无偏一致最小风险估计.例4 设Xn →X,a. s. (a. s.表示几乎必然,下同)且E(X-1|g)<∞a. s.,则X 关于g 的条件期望存在(实际有E(X-|g)<∞a. s.),且有E(Xn|g)→E(X|g)a. s..证明 令Y 为一g 可测实值的随机变量,使YX-1为可积,则YXn 的期望存在,且YXn →YXa. s.,故由Jensen 不等式3得E(YXn|g)→E(YX|g)a. s.,但有E(YXn|g)=YE(Xn|g)E(YX|g)=YE(X|g),从而有E(Xn|g)→E(X|g)a. s..参考文献[1]林正炎,陆传荣,苏中根.概率极限理论基础[M].北京:高等教育出版社, 1999.[2]Jensen J L W V. Sur les fonctions convexes et lesinégalités entre les valeurs moyennes[ J]. ActaMath.,1906, 30: 175-193.[3]李贤平.概率论基础[M]. 2版.北京:高等教育出版社, 1997.[4]严加安.测度论讲义[M]. 2版.北京:科学出版社, 2004.The Jensen inequalities of different conditions in probabilitytheory and their applicationsWeiYong-jian(Class (1) 2007 Mathematics and Applied Mathematics,College of Mathematics )Directed by:BaiGen-zhuAbstract:The proofand applications are given, these are Jensen inequalities of different conditions in probability theory: discrete and continuous and conditional expectation. And the inequalities are used to solve some relatedproblems.Key words:probability; inequality; convex function; proof。