下载文档原格式
应用全站仪进行三角高程测量
1三角高程测量的传统方法
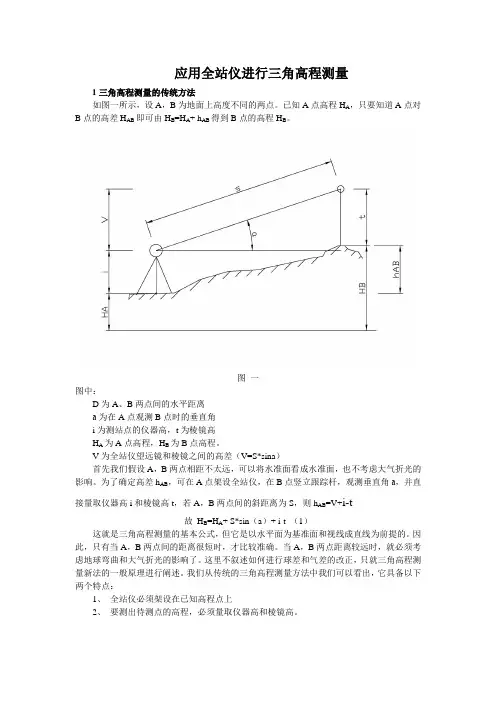
如图一所示，设A，B为地面上高度不同的两点。
已知A点高程H A，只要知道A点对B点的高差H AB即可由H B=H A+ h AB得到B点的高程H B。
图一
图中：
D为A、B两点间的水平距离
а为在A点观测B点时的垂直角
i为测站点的仪器高，t为棱镜高
H A为A点高程，H B为B点高程。
V为全站仪望远镜和棱镜之间的高差（V=S*sina）
首先我们假设A，B两点相距不太远，可以将水准面看成水准面，也不考虑大气折光的影响。
为了确定高差h AB，可在A点架设全站仪，在B点竖立跟踪杆，观测垂直角а，并直
接量取仪器高i和棱镜高t，若A，B两点间的斜距离为S，则h AB=V+i-t
故H B=H A+ S*sin（a）+ i-t （1）
这就是三角高程测量的基本公式，但它是以水平面为基准面和视线成直线为前提的。
因此，只有当A，B两点间的距离很短时，才比较准确。
当A，B两点距离较远时，就必须考虑地球弯曲和大气折光的影响了。
这里不叙述如何进行球差和气差的改正，只就三角高程测量新法的一般原理进行阐述。
我们从传统的三角高程测量方法中我们可以看出，它具备以下两个特点：
1、全站仪必须架设在已知高程点上
2、要测出待测点的高程，必须量取仪器高和棱镜高。
随着全站仪在工程测量中的普及，使用既可任意置站，又可减少误差来源，同时还无需每次量取仪器高及棱镜高度的棱镜跟踪杆配合全站仪测量高程方法，已愈发受到广大测量人员青睐。
通过已有工程实例证明，无量高全站仪三角高程测量法可使测量精度进一步提高、施测速度更快，特别适合于复杂环境下工程的应用。
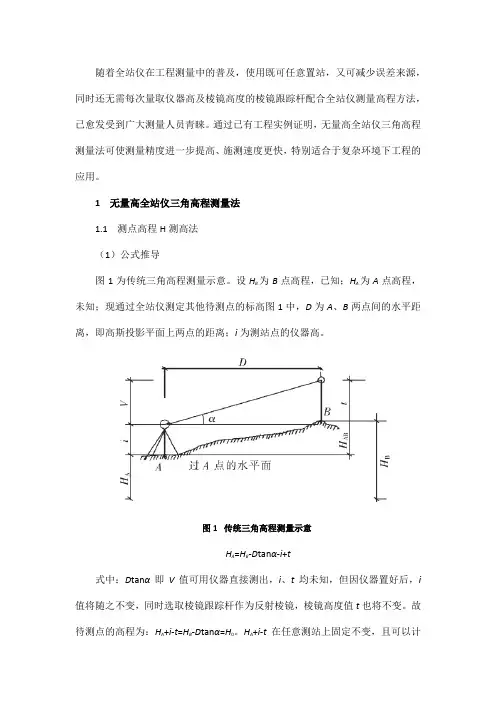
1 无量高全站仪三角高程测量法1.1 测点高程H测高法（1）公式推导图1为传统三角高程测量示意。
设HB为B点高程，已知；H A为A点高程，未知；现通过全站仪测定其他待测点的标高图1中，D为A、B两点间的水平距离，即高斯投影平面上两点的距离；i为测站点的仪器高。
图1 传统三角高程测量示意H A=H B-D tanα-i+t式中：D tanα即V值可用仪器直接测出，i、t均未知，但因仪器置好后，i 值将随之不变，同时选取棱镜跟踪杆作为反射棱镜，棱镜高度值t也将不变。
故待测点的高程为：HA+i-t=H B-D tanα=H0。
H A+i-t在任意测站上固定不变，且可以计算出其测站点高程H0。
故有H求= H0+D'tanα'+i-t。
式中：H求为待测点高程；D'为测站点到待测点的水平距离；α'为测站点到待测点的观测垂直角。
当i=0、t=0时，H求= H0+D'tanα'。
（2）操作过程1）选择与已知高程点通视的位置将仪器任意置点。
2）测出V值，计算出H0。
3）重新设定仪器测站点高程为H0，且设置仪器高及棱镜高为0。
4）照准待测点，测出其高程。
1.2 借高三维Z坐标测高法（1）公式推导借高三维Z坐标值测高法测量如图2所示，B=BM为后视点B的高程代号。
假设B点的高程H；已知，C点的高程HC未知，A点为任意置站点，通过全站仪测定C点的高程HC。
图2 借高三维Z坐标值测高法测量示意由Z坐标测量原理可知：Z B=Z A+D tanα+i-t式中：D tanα即V值可以用仪器直接测出，测出V值后将仪器中仪高值i改设为（t-D tanα）值、将测站点ZA坐标设置为基准点高点H B。
三角高程测量的计算公式-CAL-FENGHAI.-(YICAI)-Company One1三角高程测量的计算公式如图所示，已知A点的高程H A，要测定B点的高程 H B，可安置经纬仪于A点，量取仪器高i A；在B点竖立标杆，量取其高度称为觇 B 标高v B；用经纬仪中丝瞄准其顶端，测定竖直角α。
如果已知AB两点间的水平距离D （如全站仪可直接测量平距），则AB两点间的高差计算式为：如果当场用电磁波测距仪测定两点间的斜距D′，则AB两点间的高差计算式为：以上两式中，α为仰角时tanα或sinα为正，俯角时为负。
求得高差h AB以后，按下式计算B点的高程：以上三角高程测量公式、中，设大地水准面和通过A、B点的水平面为相互平行的平面，在较近的距离(例如200米)内可以认为是这样的。
但事实上高程的起算面——大地水准面是一曲面，在第一章中已介绍了水准面曲率对高差测量的影响，因此由三角高程测量公式、计算的高差应进行地球曲率影响的改正，称为球差改正f1，如图(见课本）所示。
按式：式中:R为地球平均曲率半径，一般取R=6371km。
另外，由于视线受大气垂直折光影响而成为一条向上凸的曲线，使视线的切线方向向上抬高，测得竖直角偏大，如图所示。
因此还应进行大气折光影响的改正，称为气差改正f2，f2恒为负值。
图三角高程测量图地球曲率及大气折光影响设大气垂直折光使视线形成曲率大约为地球表面曲率K倍的圆曲线(K称为大气垂直折光系数)，因此仿照式，气差改正计算公式为：球差改正和气差改正合在一起称为球气差改正f，则f应为：大气垂直折光系数K随气温、气压、日照、时间、地面情况和视线高度等因素而改变，一般取其平均值，令K=。
在表中列出水平距离D=100m-200m的球气差改正值f，由于f1>f2，故f恒为正值。
考虑球气差改正时，三角高程测量的高差计算公式为：或由于折光系数的不定性，使球气差改正中的气差改正具有较大的误差。
但是如果在两点间进行对向观测，即测定h AB及h BA而取其平均值，则由于f2在短时间内不会改变，而高差h BA必须反其符号与h AB取平均，因此f2可以抵消，f1同样可以抵消，故f的误差也就不起作用，所以作为高程控制点进行三角高程测量时必须进行对向观测。
全站仪三角高程测量流程一、引言全站仪是一种高精度的测量仪器，广泛应用于土木工程、建筑工程和测量工程等领域。
在实际测量中，三角高程测量是全站仪的常用功能之一。
本文将介绍全站仪三角高程测量的流程，包括准备工作、测量操作和数据处理等内容。
二、准备工作1. 确定测量范围：根据实际需要，确定测量的区域范围，并进行必要的勘测和标志设置。
2. 设置全站仪：将全站仪安装在稳固的三脚架上，并进行水平调平和垂直调准。
3. 设置参考点：选择一个稳定的点作为基准点，并进行标志和记录。
三、测量操作1. 设置测站：选择一个适合的测站点，将全站仪准确对准目标点。
2. 观测目标点：使用全站仪的望远镜对目标点进行观测，并记录观测数据，包括水平角和垂直角。
3. 移至下一个测站点：根据需要，移动全站仪至下一个测站点，并重复步骤2，将所有目标点都进行观测。
四、数据处理1. 计算水平角：根据观测数据，使用全站仪的内置程序或专业测量软件，计算各个目标点的水平角。
2. 计算垂直角：根据观测数据，计算各个目标点的垂直角。
3. 计算高程差：根据测站点的基准点和各个目标点的观测数据，计算各个目标点的高程差。
4. 计算三角高程：根据测站点的高程和各个目标点的高程差，计算各个目标点的三角高程。
5. 数据校正：对测量数据进行校正，包括仪器误差的校正和大气条件的校正等。
6. 数据输出：将测量结果输出为报告或数据文件，以便后续的分析和应用。
五、注意事项1. 在测量过程中，要注意仪器的精度和稳定性，保证测量结果的准确性。
2. 测量时要避免遮挡物，确保目标点的清晰可见。
3. 在计算过程中，要仔细检查和核对数据，避免计算错误。
4. 在数据处理过程中，要注意单位的一致性，避免单位转换带来的误差。
5. 在数据输出时，要按照规范的格式和要求进行，确保结果的可读性和可用性。
六、总结全站仪三角高程测量是一种常用的测量方法，通过全站仪的精确观测和数据处理，可以获得目标点的高程信息。
如何使用全站仪进行三角高程测定
全站仪是用来测量地面上各个点的三维坐标和高程的仪器。
在
进行三角高程测量时，我们需要准备好以下工具：
- 全站仪
- 一架三脚架
- 一个反光棒
- 一张三角高程测量表
具体操作步骤如下：
1. 将全站仪放在需要测量的点上，将三脚架张开并调整好高度，将全站仪放在三脚架上并固定。
2. 打开全站仪并对准带反光棒的目标点。
3. 在全站仪上选择三角高程测量功能，并输入目标点与全站仪
之间的距离。
4. 移动全站仪并对准另一个目标点，重复步骤3直到测量完所
有需要测量的点为止。
5. 将测量结果填入三角高程测量表中，并根据表格计算出每个
点的高程。
需要注意的事项：
- 在进行测量前应先校准全站仪，以确保测量结果的准确性。
- 在对准目标点时要注意不要对着阳光测量，避免阳光反射影
响测量结果。
- 在存储数据时要注意标注清楚每个点的具体位置，避免混淆。
以上就是使用全站仪进行三角高程测量的方法及注意事项。
希
望对你有所帮助！。
三角高程单向高差计算公式在测量领域中，三角高程单向高差计算公式可是个相当重要的家伙。
咱们先来说说这个公式到底是啥。
三角高程单向高差计算公式是：$h = D \tan\alpha + i - v + f$ 。
这里的“$h$”代表高差，“$D$”是两点间的水平距离，“$\alpha$”是观测的竖直角，“$i$”是仪器高，“$v$”是目标高，“$f$”是球气差改正数。
要说这个公式的应用，我想起之前参与的一个测量项目。
那是在一个山区，要为新建的一条公路做前期的地形测量。
山区的地形复杂得就像个迷宫，高低起伏，陡峭难行。
我们带着仪器，沿着预定的路线一步步推进。
那天阳光特别强烈，晒得人头皮发烫。
我负责操作全站仪，眼睛紧紧盯着目镜，认真读取每一个数据。
当测到一个山坡的时候，竖直角特别大，我心里直犯嘀咕，这可不好测啊。
但没办法，工作还得继续。
按照三角高程单向高差计算公式，仔细地记录下水平距离、竖直角、仪器高和目标高。
这时候，旁边的同事小李满头大汗，一边擦汗一边说：“这鬼天气，真要命！”我笑着回他：“别抱怨啦，赶紧把数据弄准确，早点完成任务。
”计算高差的时候，可不能有一点马虎。
每一个数字都关系到最终的测量结果是否准确。
如果算错了，那后续的设计和施工可就全乱套了。
就拿这个公式里的球气差改正数“$f$”来说，它虽然看起来不起眼，但要是忽略了，误差可就大了去了。
这就好比做菜的时候，少放了一味调料，味道就全变了。
在实际操作中，水平距离的测量也不容易。
有时候地形复杂，视线受阻，得想办法找合适的测量点，保证测量的精度。
仪器高和目标高的测量同样要精确，哪怕是一点点的误差，都可能在最后的高差计算中被放大。
还记得有一次，因为仪器高测量的时候有点偏差，导致计算出的高差出现了明显的错误。
后来经过反复检查，才发现是这个小细节出了问题。
当时真的是懊悔不已，从那以后，每一个测量步骤都更加小心谨慎。
总之，三角高程单向高差计算公式在测量工作中起着至关重要的作用。
全站仪水平测量及计算公式因为用全站仪（附加棱镜）、经纬仪（附加塔尺）测量高程，是根据两点间的距离和竖直角，应用三角公式计算两点的高差，用全站仪测定高程的方法通常称为三角高程测量（或称测距高程）。
用全站仪测量高程的特点是，精度比用水准仪测量低，但是这种方法简便、灵活，受地形的限制小。
因此通常用于山区的高程测量和地形测量。
三角高程测量，一般应在一定密度的水准测量控制之下。
通常三角高程测量是高程控制测量的一种补充手段，其精度应同同等级的水准测量相同。
当我们采用全站仪（光电测距仪）进行高程测量放样时，如图2-2所示，由于全站仪的视线不都在一个水平面上，而全站仪所读读数由正负之分，在进行高程测量放样计算时，我们输入的数据必须以全站仪所读读数实际输入，设后视点BM的高程为H0，在同一测站下（全站仪的仪器高恒等），放样点的实测高程的计算公式（以下为棱镜高度保持不变的放样点高程推导公式）如下：视线高程H视线 = H0－h0 + v放样点高程H n = H视线－hn－v =（H0－h0 + v）+ hn－v= H0－h0 + hn当棱镜高度改变时，设棱镜改变后的高度相对与后视时的高度改变值为w（改变后的高度减去棱镜初始高度），则放样点的的实测高程为：Hn = H0－h0 + hn－w。
为避免误差因距离的传递，各等级的三角高程测量必须限制一次传递高程的距离。
三角高程测量路线的总长原则上可参考同等级的水准路线的长度，路线尽可能组成闭合多边形，以便对高差闭合差进行校核。
除以上介绍的基本方法外，采用全站仪测量高程中，视线高程有两种计算方法：一、若已知置站点地面高程，则视线高程为“置站点地面高程与全站仪仪器高之和”。
二、若已知后视点地面高程，则视线高程为“后视点地面高程减去后视高差读数加上棱镜高度”。
三角高程测量是一种常用的测量方法，它可以用来测量地面上点的准确高程。
在这篇文章中，我们将着重介绍三角高程测量中的往返观测计算公式。
一、三角高程测量原理三角高程测量是利用三角形的相似性原理，通过已知两点的高程和这两点到待测点的水平距离，来计算待测点的高程。
三角高程测量的基本原理如下：1. 在地面上选择一个已知高程的点A，以及要测量高程的点P。
2. 通过测量仪器测量点A和点P之间的水平距离d和两点的高程差h。
3. 通过三角函数计算出点P的高程。
二、三角高程测量的往返观测在实际测量中，为了提高精度，常常采用往返观测的方法进行测量。
往返观测的原理是利用观测仪器来回测量两点之间的距离和高程差，然后取平均值作为最终结果，以减小由于观测仪器误差、大气温度、大气压力等因素造成的误差。
三、三角高程测量往返观测计算公式往返观测的三角高程测量计算公式如下：1. 求点P的高程差首先需要计算出点P的高程差，使用以下公式：\[ \Delta h = h_1 - h_2 \]其中，\(h_1\) 为第一次测量的高程，\(h_2\) 为第二次测量的高程。
2. 求两次测量的平均距离将两次测量的距离\(d_1\)和\(d_2\)求均值，得到平均距离：\[ \bar{d} = \frac{d_1 + d_2}{2} \]3. 计算点P的高程利用三角函数计算出点P的高程：\[ H = h_2 + \frac{\Delta h \times \bar{d}}{d_2} \]其中，\(H\)为最终计算出的点P的高程。
四、注意事项在进行三角高程测量的往返观测时，需要注意以下几点：1. 观测仪器的选择和校准非常重要，需要保证其精度和稳定性。
2. 大气温度和大气压力对测量结果有较大影响，需要进行相应的修正。
3. 观测时需要注意周围环境的影响，避免受到建筑物、树木、地形等因素干扰。
4. 测量终点的选取应当避免大坡度地形，以减小误差。
通过以上介绍，我们了解了三角高程测量中的往返观测计算公式及其应用注意事项。
