七年级试卷-2013年“华杯赛”冬令营深圳营数学测试初一试题(一)
- 格式:doc
- 大小:254.00 KB
- 文档页数:2

深圳市初一数学竞赛试题时间:120分钟一. 选择题(每小题5分,共50分)以下每题的四个结论中,仅有一个是正确的,请将表示正确答案的英文字母填在每题后面的圆括号内。
1. 数a的任意正奇数次幂都等于a的相反数,则()A. ;B. ;C. ;D. 不存在这样的a值,则与点C所表示的2. 如图所示,在数轴上有六个点,且A. B. 0 C. 1 D. 2(根据深圳市南山区蛇口中学王远征供题改编)3. 我国古代伟大的数学家祖冲之在1500年以前就已经相当精确地算出圆周率是在3.1415926和3.1415927之间,并取为密率、为约率,则()A. B.C. D.4. 已知x和y满足,则当时,代数式的值是()A. 4B. 3C.2 D. 15. 两个正整数的和是60,它们的最小公倍数是273,则它们的乘积是()A. 273B.819 C. 1911 D. 35496. 用一根长为a米的线围成一个等边三角形,测知这个等边三角形的面积为b平方米。
现在这个等边三角形内任取一点P,则点P到等边三角形三边距离之和为()米A. B. C. D.7. If we let <a> be the greatest prime number not more than a ,then the resultof the expression <<3>×<25>×<30>> is ()A. 1333B. 1999C.2001 D. 2249(英汉词典:greatest prime number 最大的质数;result 结果;expression 表达式)8. 古人用天干和地支记次序,其中天干有10个:甲乙丙丁戊己庚辛壬癸。
地支也有12个:子丑寅卯辰巳午未申酉戌亥,将天干的10个汉字和地支的12个汉字分别循环排列成如下两行:甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸……子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥……从左向右数,第1列是甲子,第2列是乙丑,第3列是丙寅……,则当第2次甲和子在同一列时,该列的序号是( )A. 31B. 61C. 91D. 121 9. 满足的有理数a 和b ,一定不满足的关系是( ) A. B.C.D.10. 已知有如下一组x ,y 和z 的单项式: 7x 3z 2,8x 3y ,12x 2yz ,-3xy 2z,9x 4z y,zy 2,-15xyz,9y 3z,xz 2y,0.3z 3,我们用下面的方法确定它们的先后次序;对任两个单项式,先看x 的幂次,规定x 幂次高的单项式排在x 幂次低的单项式的前面;再看y 的幂次,规定y 的幂次高的排在y 的幂次低的前面;再看的z 幂次,规定的z 幂次高的排在z 的幂次低的前面。



第十三届华罗庚杯数学竞赛初一试题1、一个小数的小数点分别向右,左边移动一位所得两数之差为2.2,则这个小数用分数表示为。
2、某种皮衣标价为1650元,若以8折降价出售仍可盈利10%(相对于进价)那么若以标价1650元出售,可盈利元。
3、求多位数111……11(2000个)222……22(2000个)333……33(2000个)被多位数333……33(2000个)除所得商的各个数上的数字的和为。
4、计算(1/(1×2)+2/(1×2×3)+3/(1×2×3×4)+......+9/(1×2×3× (10)的值为。
5、一只船顺流而行的航速为30千米/小时,已知顺水航行3小时和逆水航行5小时的航程相等,则此船顺水漂流1小时的航程为()千米。
6、某电视机厂计划15天生产1500台,结果生产5天后,由于引进新的生产线生产效率提高25%,则这个电视机厂会提前()天完成计划。
7、从1,2,3,4,5,6,7,8,9中任意选出三个数,使它们的和为偶数,则共有()种不同的选法。
8、某书的页码是连续的自然数1,2,3,4,…9,10…当将这些页码相加时,某人把其中一个页码错加了两次,结果和为2001,则这书共有()页。
9、现有21朵鲜花分给5人,若每个人分得的鲜花数各不相同,则分得鲜花最多的人至少分得()朵鲜花。
10、三名工人师傅张强、李辉和王充分别加工200个零件。
他们同时开始工作,当李辉加工200个零件的任务全部完成时,张强才加工了160个,王充还有48个没有加工。
当张强加工200个零件的任务全部完成时,王充还有__个零件没有加工。
11、有一块表在10月29日零点比标准时间慢4分半,一直到11月5日上午7时,这块表比标准时间快了3分钟,那么这块表正好指向正确的时间是在11月日时。
12、一个水箱中的水以等速流出箱外,观察到上午9:00时,水箱中的水是2/3满,到11点,水箱中只剩下1/6的水,那么到什么时间水箱中的水刚好流完?()13、清华大学附中共有学生1800名,若每个学生每天要上8节课,每位教师每天要上4节课,每节课有45名学生和1位教师,据此请推出清华大学附中共有教师名?14、某班45人参加一次数学比赛,结果有35人答对了第一题,有27人答对了第二题,有41人答对了第三题,有38人答对了第四题,则这个班四道题都对的同学至少有人?15、一个数先加3,再除以3,然后减去5,再乘以4,结果是56,这个数是_______。

第八届“华杯赛”初一年级组复赛试题一、填空题:1、计算:41112111111+++++2、某种零件的合格品规格为Фmm 4.02.050+-,其中有一个不合格零件与合格品的要求相差0.02mm .这个不合格的零件的直径,其最大的可能值与最小的可能值的差是______mm .3、令 ||||||ab ab b b a a x ++=,则x 的最大值与最小值的和是___________. 4、已知 c a c b a +=+=321,则有 ba c += ____________. 5、1998年火车第一次提速30%,1999年第二提速25%,2000年第三次提速20%.经过这三次提速后,从北京到G 城的特快列车只需运行10小时,提速前则需要运行___________小时.6、有很多方法能将2001写成25个自然数(可以相同,也可以不相同)的和,对于每一种分法,这25个自然数均有相应的最大公约数,那么这些最大公约数中的最大值是__________.二、解答下列各题7、已知如图两个同心圆的半径为R 和r ,均为自然数,圆环(阴影部分)面积是713π,问:这两个同心圆的半径R 和r 各多少?8、已知m 是整数,方程组⎩⎨⎧=+=-,266,634my x y x 有整数解,求出m 的值.9、已知 AC DC 31=,DOC ∆是等边三角形,OB 和OC 都垂直于BC (如图),阴影部分面积的2倍与扇形DMC 的面积相比,哪个面积大?10、10个人围成一圈,每人心里想一个数,并把这个数告诉左右相邻的两个人,然后每个人把左右两个相邻人告诉自己的数的平均数亮出来,如图所示,问亮5的人心中想的数是多少?三、解答下列各题11、电子跳蚤游戏盘(如图所示)为ABC ∆,AB =8,AC =9,BC =10,如果电子跳蚤开始时在BC 边上0P 点,40=BP .第一步跳蚤跳到AC 边上1P 点,且01CP CP =;第二步跳蚤从1P 跳到AB 边上2P 点,且12AP AP =;第三步跳蚤从2P 跳回到BC 边3P 点,且23BP BP =;……跳蚤按上述规则跳下去,第2001次落点为2001P ,请计算0P 与2001P 之间的距离.12、某工厂每天用于生产玩具小狗和小猫的全部劳动力为90个工时,原料为80个单位.生产一个小狗要用2个工时和4个单位的原料;生产一个小猫要用3个工时和1个单位的原料.问:每天生产玩具小狗和小猫的总数最多是多少?第八届“华杯赛”初一年级组复赛试题答案一、填空题1、223242 解:原式=5421111111++++=1+14511111++=19141111++=1+22324222319=. 2、0.64解:既然合格品规格为Фmm 4.02.050+-,这个不合格零件的直径,可能在(50-0.22)mm 到(50+0.42)mm 之间.所以,这个不合格的零件的直径最大的可能值与最小的可能值的差是0.64mm .3、2解:既然 ⎩⎨⎧<->=时当时当0,10,1||y y y y , x 有三项类似于||y y 的式子,x 的最大值是3,x 的最小值是-1.所以,x 的最大值与最小值的和是2.4、2解:⎩⎨⎧=+=+,3,2a c a a c b ⎩⎨⎧==+⇒,2,2a c a c b ⎩⎨⎧==⇒.2,0a c b 所以, 202=+=+a a b a c . 5、19.5解:设3次提速前的速度是v ,3次提速后的速度是v (1+30%)(1+25%)(1+20%),设北京到G 城的路程是s , 则有10%)201%)(251%)(301(=+++v s (小时), 所以,提速前则需要运行的时间=5.19%)201%)(251%)(301(10=+++⨯=vs (小时).6、3,23,29,69解:首先需要说明,本题中的自然数是指正整数,即不包括0.分解因子2001=3×23×29.设d 是这25个正整数的最大公约数,则这25个正整数为=⨯k a d k (1,2, (25), 29233)(2521⨯⨯=+++a a a dda a a 292332521⨯⨯=+++ d 整除2001,并且 1(=k a k ,2,…,25)是正整数,25≤da a a 292332521⨯⨯=+++ . 所以,d 可能的取值是3,23,29和69.答:是69.二、解答下列各题7、27,4解:由圆的面积公式: ππ713)(22=⨯-r R ,已知 713=23×31,只能有 R+r=31, R -r=23,解上面二元一次方程组,得到R =27,r =4.8、-4,-5,-13解:首先将m 看作已知量,解二元一次方程组⎩⎨⎧=+=-)2(,266)1(,634my x y x第(2)个方程乘2减第(1)个方程乘3,得到(2m +9)y=34=1×2×17.即然y 是整数, (2m +9)|1×2×17.因为m 是整数,所以,m 可能的取值是:-4、-5、4和-13.第(2)个方程乘3加第(1)个方程乘m ,得到 92393++=m m x ,(3) 将m 可能的取值代入(3),为使x 是整数,m 只能是-4,-5和-13.9、2解:因为DOC ∆是等边三角形,︒=∠60DCO ,OC 都垂直于BC ,︒=∠30DCB ,DCB∆是直角三角形,所以,DCB ∆的面积=DCO ∆21的面积,又因为已知AC DC 31=,ACB ∆的面积=DCB ∆3的面积=DCO ∆23的面积.所以, 阴影部分面积的2倍=DCO ∆5的面积.既然扇形DMC 的面积>5DCO ∆的面积,所以,扇形DMC 的面积大于图中阴影部分面积的2倍.10、10解:设亮5的人心中想的数是5x ,设亮7的人心中想的数是7x ,设亮9的人心中想的数是9x ,设亮11的人心中想的数是11x ,设亮13的人心中想的数是13x ,可列出方程:1275=+x x ,1697=+x x ,241311=+x x ,28513=+x x ,直接解这组5元一次方程,就可以得到解答,但比较烦琐.可以用尝法,5个方程相加,得到501311975=++++x x x x x .五个方程两两相减,可以得到7x ,11x ,5x ,9x ,13x 是公差为4的等差数列.所以, 27=x ,611=x ,105=x ,149=x ,1813=x .三、解答下列各题11、1解:电子跳蚤跳3步回到BC 边,所以,既然2001能被3整除,第2001步落在BC 边上.因40=BP ,BC =10,故 61=CP .因AC =9,故 32=AP .因AB =8, 故 53=BP .因BC =10,故 54=CP .因AC =9,故 45=AP .因AB =8,故46=BP ,……电子跳蚤跳6步后回到原来位置,2001被6除余3,故52001=BP ,所以,1450200120010=-=-=BP BP P P .答:0P 与2001P 之是的距离是1.12、35解:设生产玩具小狗和小猫的数量分别是x 和y ,由已知条件,可以得到两个不等式:⎩⎨⎧≤+≤+,804,9032y x y x (1)将(1)的第1个不等式方程乘2加第2个不等式相加,得到8x +7y ≤260.即有不等式7(x+y )≤260-x ,x+y ≤713777137--=-+x x . (2) 解二元一次方程组 ⎩⎨⎧=+=+,804,9032y x y x 得到x =15,y =20是满足(1)的一组解,即,可以有x+y ≥35. (3)从(1)的第一个方程y ≤3230x - (4) (4)说明y 最大是30,结合(3),所以 x ≥5.再次利用(4)y ≤3230x -≤31030-≤3226. 因为y 必须是整数,所以 y ≤26.再次利用(3)不等式,得到 x ≥9.利用(2)不等式,得到x+y ≤7137--x ≤76357837=-. 上式说明x+y 最大不超过35,(3)说明x+y 可以达到35.所以答案是:每天生产玩具小狗和小猫的总数最多可以是35个.。

全国初一初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.船在江中顺水航行与逆水航行的速度之比为7:2,那么它在两港间往返一次的平均速度与顺水速度之比为( )。
A.B.C.D.。
2.如右图所示,三角形ABC的面积为1cm2。
AP垂直ÐB的平分线BP于P。
则与三角形PBC的面积相等的长方形是( )。
3.设a,B是常数,不等式+>0的解集为x<,则关于x的不等式bx-a>0的解集是( )。
A.x>B.x<-C.x> -D.x<。
4.下图所示的五角星是用螺栓将两端打有孔的5根木条连接构成的图形,它的形状不稳定。
如果在木条交叉点打孔加装螺栓的办法使其形状稳定,那么至少需要添加( )个螺栓。
A.1B.2C.3D.4 。
5.对四堆石子进行如下“操作”:每次允许从每堆中各拿掉相同个数的石子,或从任一堆中取出一些石子放入另一堆中。
若四堆石子的个数分别为2011,2010,2009,2008,则按上述方式进行若干次“操作”后,四堆石子的个数可能是( )。
A.0, 0, 0, 1B.0, 0, 0, 2C.0, 0, 0, 3D.0, 0, 0, 4 。
二、填空题1.对整数按以下方法进行加密;每个数字的数字变为与7乘积的个位数字,再把每个数位上的数字a变为10-a。
如果一个数按照上面的方法加密后为473392,则该数为。
2.老师问A、B、C、D、E五位学生:“昨天你们有几个人玩过游戏?”他们的回答分别为A:没有人;B:一个人;C:二个人;D;三个人;E:四个人。
老师知道:他们之中有人玩过游戏,也有人没有玩过游戏。
若没有玩过游戏的人说的是真话,那么他们5个人中有个人玩过游戏。
3.公交车的线路号是由数字显示器显示的三位数,其中每个数字是由横竖放置的七支荧光管显示,如下图所示:由于坏了一支荧光管,某公交线路号变成“351”。

第十三届华罗庚杯数学竞赛初一试题1、一个小数的小数点分别向右,左边移动一位所得两数之差为2.2,则这个小数用分数表示为。
2、某种皮衣标价为1650元,若以8折降价出售仍可盈利10%(相对于进价)那么若以标价1650元出售,可盈利元。
3、求多位数111……11(2000个)222……22(2000个)333……33(2000个)被多位数333……33(2000个)除所得商的各个数上的数字的和为。
4、计算(1/(1×2)+2/(1×2×3)+3/(1×2×3×4)+......+9/(1×2×3× (10)的值为。
5、一只船顺流而行的航速为30千米/小时,已知顺水航行3小时和逆水航行5小时的航程相等,则此船顺水漂流1小时的航程为()千米。
6、某电视机厂计划15天生产1500台,结果生产5天后,由于引进新的生产线生产效率提高25%,则这个电视机厂会提前()天完成计划。
7、从1,2,3,4,5,6,7,8,9中任意选出三个数,使它们的和为偶数,则共有()种不同的选法。
8、某书的页码是连续的自然数1,2,3,4,…9,10…当将这些页码相加时,某人把其中一个页码错加了两次,结果和为2001,则这书共有()页。
9、现有21朵鲜花分给5人,若每个人分得的鲜花数各不相同,则分得鲜花最多的人至少分得()朵鲜花。
10、三名工人师傅张强、李辉和王充分别加工200个零件。
他们同时开始工作,当李辉加工200个零件的任务全部完成时,张强才加工了160个,王充还有48个没有加工。
当张强加工200个零件的任务全部完成时,王充还有__个零件没有加工。
11、有一块表在10月29日零点比标准时间慢4分半,一直到11月5日上午7时,这块表比标准时间快了3分钟,那么这块表正好指向正确的时间是在11月日时。
12、一个水箱中的水以等速流出箱外,观察到上午9:00时,水箱中的水是2/3满,到11点,水箱中只剩下1/6的水,那么到什么时间水箱中的水刚好流完?()13、清华大学附中共有学生1800名,若每个学生每天要上8节课,每位教师每天要上4节课,每节课有45名学生和1位教师,据此请推出清华大学附中共有教师名?14、某班45人参加一次数学比赛,结果有35人答对了第一题,有27人答对了第二题,有41人答对了第三题,有38人答对了第四题,则这个班四道题都对的同学至少有人?15、一个数先加3,再除以3,然后减去5,再乘以4,结果是56,这个数是_______。


第七届“华杯赛”初一复赛试题一、直接写出答案: 1.=-÷---)65()]2478(125.26.1[ . 2.52||31y x m +和3||33+n y x 是同类项,问:22n m +的值是多少?3.a -2b 的相反数数是0.685, 3b+c 的倒数是25,问:a+b+c 减-0.125的负数是多少?4.04)(=++x m k 和01)2(=--x m k 是关于x 的同解方程,问:2-nk的值是多少?5.小明在假期里打工挣了abc 元,已知a bcb =+,a +1=b ,c =2d .问:小明假期打问工挣了多少?6.将糖果300粒,饼干210块和苹果163个平均分给某班同学,余下的糖果、饼干和苹果的数量之比是1∶3∶2,问:该班有多少名同学?7.一串数1,1,1,2,2,3,4,5,7,9,12,16,21,……称为帕多瓦数列,请陈述这个数列的一个规律,并且写出其中的第14个数和第18个数.8.某商贸服务公司,为客户出售货物,收取3%的服务费;代客户购置物品,收取2%的服务费,今有一客户委托该公司出售自产的某种物品并代为购置新设备.已知该公司共收取了客户服务费264元,客户恰好收到平衡,问:所购置的新设备花费了多少元?9.由甲地到乙地前三分之二的路是高速公路,后三分之一的路是普通公路,高速公路和普通公路的交界处是丙地.A 车在高速公路上的行驶速度是100千米/时,在普通公路上的行驶速度是60千米/时.B 车在高速公路上的行驶速度是110千米/时,在普通公路上的行驶速度是70千米/时.A 、B 两车分别从甲乙二地相向行驶,在距离丙地20千米处相遇,求:甲乙两地之间距离是多少?10.如右图,在一个边长为a 厘米的正方体的两对侧面的中心各打通一个长方体的洞,在上下侧面的中心打通一个圆柱形的洞.已知侧耳面上的洞口是边长为a 52厘米的正方形,上下底面的口是直径为a 52厘米的圆,求右图立体的表面积的体积.(取14.3=π)11.AOMEN和MACAO分别是澳门的汉语拼音和英文名字,如果它们分别代表两个5位数,其中不同的字母代表从1到9不同的数字,相同的字母代表相同的数字,而且它们的和仍是一个5位数,求这个和可能的最大值是多少?12.用10个边长分别为3,5,6,11,17,19,22,23,24,25的正方形,可以拼接一个长方形,(1)求:这个长方形的长和宽各是多少?(2)请画出拼接图.第七届“华杯赛”初一组复赛试题答案1.解:这是一道有理数的混合运算试题,且含有小数和分数,其中有一个小数还是循环小数.根据题意,这道运算题最后求的是商,所以,先将题中的小数转化为分数,然后再根据有理数的运算运法则进行计算. 812125.2-=-3219616.1== (纯循环小数化成分数,分子是一个循环节表示的数,分母的各位数都是9,而9的个数与循环节的位数相同,最后能约分的再约分). 所以 原式=)65()]2478(812321[-÷--- 根据有理数减去法则,“减去一个数,等于加上这个数的相反数”;有理数乘法法则,“两数相乘,同号得正,异号得负,并把绝对值相乘”;还根据有理数除法法则,“除以一个数等于乘上这个数的倒数”,就可以得到结果原式=)56(]2478812321[-⨯+-=)56(657-⨯529)56647(-=⨯-=有关有理数的运算,掌握有理数运算法则是关键,而在掌握有理数运算法则的过程中,要特别注意符号问题,然后才是绝对值的计算.为了突出确定符号的训练,在进行有理数的运算时,绝对值就不必选择过大. 2.5解:根据题意,52||31y x m +和3||33+n y x 是同类项,就是说它们不仅所含字母相同,并且相同字母的次数也相同,即|m |+2=3, 也就是|m |=1, |n |+3=5,也就是|n |=2 又根据题意,一个数的平方等于这个数的绝对值的平方,所以 22||m m =, 22||n n =.因此,521||||222222=+=+=+n m n m . 答:22n m +的值是5. 3.a+b+c 减-0.125的负倒数是132552100=解:根据题意,a -2b 的相反数是0.685,而根据数a 的相反数是-a ,那么,a -2b 就是200137685.0-=-.又根据题意,3b+c 的倒数是25,而根据乘积是1的两个数互为倒数,那么20082513==+c b . 所以,a+b+c 减-0.125的负倒数是)125.0()(--++c b a 的负倒数,根据去括号法则,也就是125.0)(+++c b a 的负倒数.又因为c b a c b b a ++=++-)3()2(,所以, c b a ++减-0.125的负倒数,即200252008700137++-的负倒数,即200104-的负倒数, 也就是13251042002001041==--. 答:a+b+c 减-0.125的负倒数是132552100=. 4.321-解:根据题意,04)(=++x m k 和01)2(=--x m k 是关于x 的同解方程,那么,4)(-=+x m k 和1)2(=-x m k 同样是关于x 的同解方程.根据等式性质“等式两边都乘以(或除以,除数不能是0)的数,所得结果仍是等式.所以14)2()(-=-+x m k x m k 142-=-+m k m k m k m k +=+-48 k m 93= m k =93 31=m k 因此,3212312-=-=-m k答:3212--的值是m k .5.348解:根据题意,abc 为三位数,且a bcb =+, a +1=b ,那么, 0≠b (零不能作分母), a=b -1,所以 a b cb =+,也就是12-=+b bb b 则 b b b -=23即0)4(=-b b ,4=b 将b =4代入c =2b , 则c =2×4=8 4=b , 8=c 代入a b c b =+,则3484=+=a . 这样abc =348答:小明假期打工挣了348元. 6.23解:根据题意,糖果、饼干和苹果是平均分给全班同学的,所以,糖果、饼干和苹果减去余下的数量,也就是被平均分给全班同学的糖果、饼干和苹果的数量,一定是全班学生人数的整数倍.又根据题意,将糖果、饼干和苹果平均分给全班同学后,余下的糖果、饼干和苹果数量比是1∶3∶2,如果假设余下的糖果、饼干和苹查果的数为1份、3份、2份,甚至更直接的设余下的糖果、饼干和苹果的数量,分别是1粒、3块、2个,那么,被平均分给全班的糖果、饼干和苹果的数量,分别为300-1=299(粒),210-3=207(块),163-2=161(个).因为,299=23×13; 207=23×9; 161=23×7. 所以,该班有23名同学. 答:该班有23名同学. 7.86解:根据题意,要求陈述数列的一个规律,而帕多瓦数列蕴含有若干规律,可以通过该数列前后项之间的和、差、积、商,各自所具有的特征,归纳出规律,如: (1) 从第4项开始,每一项均是前面第2项和第3项的和.如(2) 从第6项开始,第一项均是前面第1项与第5项的和.如(3)以5项为一组,从第二组开始,每一组的5项,均是前一组的末项依次加上前一组各项的和.如……根据规律(1)可知:这串数的第14个数是第11个数与第12个数的和,即12+16=28;第18个数是第15个数与第16数的和,而第15个数是第12个数与第13个数的和,即16+21=37,第16个数是13个数与第14个数的和,即21+28=49,所以,第18个数即37+49=86. 8.5121.6解:根据题意,下列等量关系很明显:(1)出售物品的收入-服务费=购置设备费用+服务费(出售物品) (购置设备)即:出售物品收入-购置设备费用=总服务费(出售物品、购置设备) (2)服务费出售物品的 + 服务费购置设备的=总服务费即:收入出售物品 ×30%+费用购置设备 ×2%=264 (元)所以,本题如果设出售物品的收入用x 元,购置设备的费用用y 元表示,那么,用二元一次方程组来分析解答就比较容易了.⎩⎨⎧=+=-264%2%3264y x y x )2()1(将(2)化简,得3x +2y =26400 (3)由(1)得 y=x -264 (4) 用(4)代入(3),得3x +2(x -264)=26400 (5) 化简(5),得 5x -528=26400 5x =26928 x =5385.6将x =5385.6代入(1),得y =5121.6 答:购置的新设备花费了5121.6元. 9.1152000解:根据题意,结合如图所示可知,A 车的速度虽然是B 车的速度的73170100=(倍),但A 车在高速公路上行驶的路程却是B 车在普通公路上行驶路程的23132=÷(倍),所以,当A 、B 两车分别从甲乙两地相向行驶,B 车已经行驶完普通公路的路程时,A 车还在高速公路上行驶,因此,A 、B 两车在高速公路上距丙地20千米处相遇.又根据相向运动的主要特征——运动的时间相等,可知:A 车所用时间=B 车所用时间因为,A 车从出发到相遇,全都在高速公路上行驶,而B 车除了行驶完普通公路外,还在高速公路上行驶了20千米,因此:高速路上时间车行驶在A = 普通公路上时间车行驶在B + 高速公路的时间千米车行驶20B千米千米高速公路路程10020- 千米普通公路路程70 千米千米11020也就是1102070311002032+⨯=-⨯甲乙全程甲乙全程 因此,只要设甲乙两地之间的路程为x 千米,那么本题就可以用方程解答.1102070311002032+=-x x 1102010020703110032+=-xx 11251)21011501(+=-x 271505521⨯⨯=x 115200=x 答:甲乙两地之间距离是115200千米.10.28512.7a ,366864.0a解:根据题意,所求图形的总表面积包括外侧表面积和内侧表面积;所求图形的体积是由原正方体积减去被挖去部分的体积.那么,外侧表面积、内侧表面积和被挖去部分的体积分别指哪些部分呢?如果将被挖去的部分完整地表示出来,就比较容易理解了. 结合图示可右,外侧表面积是原正方体的表面积减去前后左右4个边长为a 52厘米的正形面积和两个直径为a 52厘米的圆面积,即 外侧表面积=表面积原正方体 -洞口面积挖去的正方形 -洞口面积挖去的圆62⨯a 4)52(2⨯a 2)2152(2⨯⨯a π22221088.525225166a a a a S =--=π外侧表 结合图示可知,内侧表面积是由16个长a 52厘米,宽a ]21)521[(⨯-厘米的长方形面积,加上2个边长为a 52厘米的正方形减去直径为a 52厘米的圆形后的环形面积,再加上2个底面直径为a 52厘米的圆柱侧面积,即])2152()52[(16]21)521[(52222⨯-+⨯⎭⎬⎫⎩⎨⎧⨯-⨯=a a a S π内侧表]21)521)[(52(22a a ⨯⨯-⨯+⨯π =2222562]25254[1610352a a a ⨯+⨯⨯-+⨯⨯⨯ππ=22225625)4(22548a a a ππ+-⨯+227424.225456a a =+=π所以,所求图形的立体表面积为:内侧表外侧表总表S S S +=2228512.77424.21088.5a a a =+=根据题意,所求图形的立体的体积是原正方体体积减去挖去部分的体积,而挖去部分的体积如图,可以看作两底面为正方形,边长为a 52厘米,高a 厘米的长方体,减去中间交叉部分的体积,交叉部分恰好是棱长为a 52厘米的正方体,再加上2个同样的圆柱体的体积,这个圆柱的底面直径为a 52厘米,高为a a 5321)521(=⨯-厘米,即a a 5321)521(=⨯-即交叉圆柱长方体挖V V V V -⨯+⨯=22a a ⋅2)52( a a 53)2152(2⨯⨯π 3)52(a33312581253258a a a -+=π3125842.940a -+=333136.0a =(立方厘米) 所以,所求立体的体积为:挖原V V V -=33366864.033136.0a a a =-=答:所以图形的立体的表面积是28512.7a 平方厘米,体积是366864.0a 立方厘米. 11.99782解:根据题意,设这两个五位数的和为WUVXY ,则 WUVXYMACAO AOMEN虽然最大的五位数为99999,但W U V X Y 不可能为99999.如果A+M =9, O+A =9, 那么M -O =0, 则M 与O 所代表的数字相同,与题意矛盾.但是当A+M =9, O+A =8时,只要M+C 能够进位,O+A 的和仍可能为9,所以,为了使和的值尽可能大,那么,M+C =17时最好,故必须取如下和式:甲: ⎝⎛=+=+=+,17,8,9C M A O M A此时, W =9, U =9, V =7.如果A+M =8,那么O+A 必须是17,那么W =9,但这样 U ≤8,因此,A+M =8时,和的最大值不是最大,而依甲式取值所得的和最大。
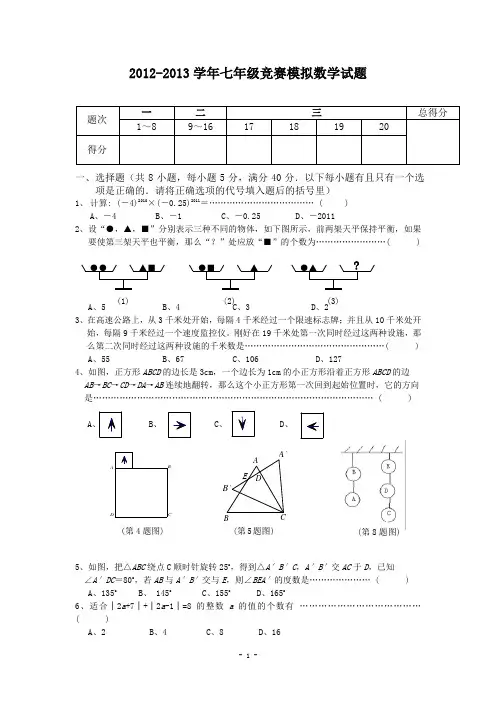
2012-2013学年七年级竞赛模拟数学试题一、选择题(共8小题,每小题5分,满分40分.以下每小题有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里)1、 计算: (-4)2010×(-0.25)2011=……………………………… ( )A 、-4B 、-1C 、-0.25D 、-20112、设“●,▲,■”分别表示三种不同的物体,如下图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么“?”处应放“■”的个数为……………………( )A 、5B 、4C 、3D 、23、在高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌;并且从10千米处开始,每隔9千米经过一个速度监控仪。
刚好在19千米处第一次同时经过这两种设施,那么第二次同时经过这两种设施的千米数是…………………………………………( ) A 、55 B 、67 C 、106 D 、1274、如图,正方形ABCD 的边长是3cm ,一个边长为1cm 的小正方形沿着正方形ABCD 的边AB →BC →CD →DA →AB 连续地翻转,那么这个小正方形第一次回到起始位置时,它的方向是…………………………………………………………………………………… ( )A、、、5、如图,把△ABC 绕点C 顺时针旋转25o,得到△A ′B ′C ,A ′B ′交AC 于D ,已知 ∠A ′DC =80o ,若AB 与A ′B ′交与E ,则∠BEA ′的度数是………………… ( )A 、135oB 、 145oC 、155oD 、165o6、适合│2a +7│+│2a -1│=8的整数a 的值的个数有 ………………………………… ( )A 、2B 、4C 、8D 、16●●▲■ ●■ ▲ ●▲ ? (1) (2) (3)(第4题图) D A A 'B ' E (第8题图)7座的人数是听数学的6倍,还剩下一个小组在教室里讨论问题,这一小组是… ( ) A 、第4组 B.、第6组 C 、第7组 D 、第11组8、甲、乙、丙、丁、戊五位同学参加一次节日活动,很幸运的是他们都得到了一件精美的礼品(如图),他们每人只能从其中一串的最下端取一件礼品,直到礼物取完为止,甲第一个取得礼物,然后乙、丙、丁、戊依次取得第2到第5件礼物,他们的取法各种各样.,发现礼物D 最精美,那么取得礼物D 可能性最大的是同学是 ………………… ( )A 、乙B 、丙C 、丁D 、戊二、填空题(每小题5分,共40分)9、定义a*b=ab+a+b,若3*x=27,则x 的值是_____。
第十八届华罗庚金杯少年邀请赛初赛试题A (初一组)(时间2013年3月23日10:00~11:00)一、选择题(每题10分,满分60分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1. 下列的结论中, 正确的有( )个:① 两个正数的和一定是正数; ② 两个正数的差可以是正数;③ 两个负数的和一定是负数; ④ 两个负数的差可以是负数。
A .1B .2C .3D .42. 从—6,—4,—3,—2,—1,3,6中任取两个数相乘, 所得积中的最大值记为a , 最小值记为b , 那么ba 的值为( )。
A .32- B .43- C .-1 D .323.将∙∙∙∙⨯352323.0342.0乘积化为小数, 小数点后第2014位数字是( )。
A .0B .7C .9D .14.如果a 、b 、c 都是大于21-的负数, 那么下列式子成立的是( )。
A .a+c-b<0B .a 2-b 2-c 2>0C .abc>81-D .∣abc ∣81>5.在方格的每个格中填上数字1,2,3,4中的一个, 要求每行、每列和每条对角线上所填的数字各不相同。
右图中已经填好了3个数字,请完成填数, 那么两个阴影方格中所填数的乘积最小值为( )。
A .5B .4C .3D .26.满足不等式 m3n 532<<的有序整数对(m ,n )的个数是( ) A .12 B .13 C .14 D .15二、填空题(每小题 10 分, 满分40分)7. 如果x=3,y=1时, 代数式ax+by 的值等于9, 那么x=-3,y=-1时代数式ax+by+9的值等于________.8.一个水池有甲、乙、丙三个进水口和一个出水口。
同时打开出水口和其中的两个进水口, 注满整个水池分别需要6小时、5小时和4小时;同时打开出水口和三个进水口, 注满整个水池需要3小时。
2013初一第一学期数学竞赛试卷一、选择题(每小题4分,共24分)1、设a是最小的自然数,b是最大的负整数,c是绝对值最小的整数,则cba++的值为()A.-1 B.0 C.1 D.32、已知|x|=3,|y|=2,x、y异号,则x+y的值是( )A.5或1 B.-1或1 C.5或-5 D.-5或-13、某商品提价100%后要恢复原价,则应降价()A、30%B、50%C、75%D、100%4、客运列车在哈尔滨与A站之间运行,沿途要停靠5个车站,那么哈尔滨与A站之间需要安排( )种不同的车票。
A、6B、7C、21D、425、如图,在ABC∆中,ECBDCEACDEBCDBEABD∠=∠=∠∠=∠=∠,,若=∠BEC145°,则BDC∠等于()A.100°B.105°C.110°D.115°6、现有3×3的方格,每个小方格内均有数目不同的点图,要求方格内每一行、每一列以及每一条对角线上的三个点图的点数之和....均相等.图中给出了部分点图,则P()二、填空题(每小题4分,共32分)1、3点分时,时针和分针重合.2、观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128……用你发现的规律写出22013的末位数字是_______。
3、一位同学在斜坡上练习骑自行车,上坡速度为m km/h,下坡速度为n km/h,则上下坡的平均速度为()km/h4、自然数n被3除余2,被4除余3,被5除余4,则n的最小值是A.B.C D5、若a 是有理数,则|)|(||||)(a a a a -+-++-的最小值是___. 6. 如图,∠AOB 是直角,i OP (i =1,2,3,4,5,6)是射线, 则图中共有锐角 个.7、整片牧场上的草长得一样密,一样地快。
已知70头牛在24天里把草吃完,而30头牛就得60天。
如果要在96天内把牧场的草吃完,那么有 头牛。
2013华杯赛冬令营深圳营应用题21、一个小数的小数点分别向右,左边移动一位所得两数之差为2.2,则这个小数用分数表示为________。
[2/9]2、某种皮衣标价为1650元,若以8折降价出售仍可盈利10%(相对于进价)那么若以标价1650元出售,可盈利________元。
[450]3、求多位数111……11(2000个)222……22(2000个)333……33(2000个)被多位数333……33(2000个)除所得商的各个数上的数字的和为________。
[6002]4、三名工人师傅张强、李辉和王充分别加工200个零件。
他们同时开始工作,当李辉加工200个零件的任务全部完成时,张强才加工了160个,王充还有48个没有加工。
当张强加工200个零件的任务全部完成时,王充还有___个零件没有加工。
[10]5、一个人从县城骑车去乡办厂。
他从县城骑车出发,用30分钟时间行完了一半路程,这时,他加快了速度,每分钟比原来多行50米。
又骑了20分钟后,他从路旁的里程标志牌上知道,必须再骑2千米才能赶到乡办厂,求县城到乡办厂之间的总路程。
[18000]6、某电视机厂计划15天生产1500台,生产5天后,引进新的生产线生产效率提高25%,则这个电视机厂会提前( )天完成计划。
[2]7、从1,2,3,4,5,6,7,8,9中任意选出三个数,使它们的和为偶数,则共有( )种不同的选法。
[44]8、有一块表在10月29日零点比标准时间慢4分半,一直到11月5日上午7时,这块表比标准时间快了3分钟,那么这块表正好指向正确的时间是在11月____日____时。
[2\ 9]9、有一块边长24厘米的正方形厚纸,如果在它的四个角各剪去一个小正方形,就可以做成一个无盖的纸盒。
现在要使做成的纸盒容积最大,剪去的小正方形的边长应为几厘米?[4]10、六年级某班学生中有161的学生为13岁,有43的学生为12岁,其余学生为11岁,这个班学生的平均年龄是________岁。
数学集训试题(1)学校:姓名:成绩:一.解答题1.幼儿园大班和中班共有32个男生,18个女生。
已知大班中男生数与女生数的比为5:3,中班中男生数与女生数的比为2:1,那么大班的女生数等于多少?2.如图所示,A、B、C分别代表面积为8、9、11的三张不同形状的纸片,它们重叠放在一起盖住的面积是18,且A与B,B与C,C与A公共部分的面积分别是5、3、4,求A、B、C三个图形公共面积部分(阴影部分)的面积。
3.分母是385的最简真分数有多少个,并求这些真分数的和。
4.某人从住地外出有两种方案:一种是骑自行车去;另一种是乘公共汽车去。
显然公共汽车的速度比自行车的速度快,但乘公共汽车有一个等候时间(候车时间可看作是固定不变的,且不考虑到站停车时间)。
在任何情况下,他总是采用花时间最少的最佳方案。
下表表示他到达A,B,C三地采用最佳方案所需要的时间。
目的地目的地离住地的距离最佳方案所需的时间A 2千米12分钟B 3千米15.5分钟C 4千米18分钟为了到达离住地8千米的地方,他需要花多少分钟?并简述理由。
5.某城市的街道非常整齐(如图),从西南角A处走到对角线DB上任何一个交叉点处,只许向东或者向北走,共有多少种不同的走法?6.一段路程分成上坡、平坡、下坡三段,各段路程之比依次是1:2:3.某人走各段路所用时间之比依次是4:5:6,已知他上坡时速度为每小时3千米,路程全长50千米。
问此人走完全程用了多少时间?二、填空题1.有人沿公路前进,对面来了一辆汽车,他问司机:“后面有自行车吗?”司机回答:“十分钟前我超过一辆自行车”,这人继续走了10分钟,遇到自行车。
已知自行车速度是人步行速度的三倍,汽车的速度是步行速度的倍。
2.某车间有28名工人,生产一种螺栓和螺帽,平均每人每时能生产螺栓12个或螺帽18个,应分配人生产螺栓、人生产螺帽,才能使生产出的螺栓和螺帽刚好配套(每一个螺栓要配两个螺帽)。
3.有一满池水,池底有泉水总能均匀地向外涌流,已知用24部A型抽水机6天可抽干池水,若用21部A型抽水机8天也可抽干池水,设每部抽水机单位时间的抽水量相同,要使这一池水永抽不干,则至多只能用部A型抽水机抽水。
第八届“华杯赛”初一组第二试决赛试题1、 设 2001200020022001200120002001200010++⨯=N ,求N 的整数部分.2、周长为100,边长为整数的等腰三角形共有多少种?3、已知01=a ,|1|||12+=a a ,|1|||23+=a a ,…,|1||||99100+=a a .求 10021a a a +++ 的最小值.4、2n名棋手参加象棋循环赛,胜者得2分,负者得0分,平局各得1分.赛后各棋手得分互不相同,且第二名得分恰好等于后n名得分总和.求n的最大值,并给出n取最大值时各位选手的一种得分表.5、n张卡片,每张上写一个正整数,彼此不同,小李和另外(n-1)个小朋友做游戏,同一局游戏取走的卡片不放回来,每人任意取一张,共取n次,每次各人记下自己取得的数字,最后各人计算自己取得的数字和作为得分,并按得分多少排名.已知小李n次取得的数字各不相同,其余的小朋友的得分彼此不相同,他们(不包括小李)得分之和为2001.问n等于多少?小李最高能是第几名?6、用1×2的“日形块”共18块,以任何方式完全覆盖6×6的棋盘那么沿任意一条棋盘线一定切割偶数块“日形块”,请说明理由.第八届华杯赛初一组第二试决赛试题答案1、 20009解: 2000200120002001200020012000(2000102001200020012000>+⨯+=N , 200010-N =20002001200020012000201200020022001-++ =2001200020012001200220012001200020012000200020012000+⨯--+ =200120002001200120002001+, 而 20002001200020012001200020011112001200020011⎪⎭⎫ ⎝⎛⨯+=+>9.02001111>+> 所以, 9.2000102001>>N 答:N 的整数部分为20009.2、 24解:设a ,b ,c 为三角形的三边长.第一种情况:a=b<c =100-2a , a <34三角形两边和大于第三边.2a >100-2a .4a >100,所以a>25.共有8种.第二种情况:a<b=c , a =100-2c<c , 所以33<c .又 100=a+b+c >1+2c , 所以50>c .答:共有24种.3、-50解:令 |1|||100101+=a a所有的等式都平方,得到021=a1212122++=a a a1222223++=a a a12992992100++=a a a 1210021002101++=a a a上面101个等式相加,得到,0≤21012100232221a a a a a +++++ =100)(21002121002322++++++++a a a a a a所以 0≤100)(210021210121++++=+a a a a a10021a a a +++ ≥-50当 0101=a 时,等号成立,此时013959799======a a a a a1249698100-======a a a a a答:最小值是-50.4、解:每一棋手比赛2n -1场,第二名选手不可能全胜(否则是第一名),也不可能胜2n -2场,平1场(否则是第一或并列第一).因此,他最多胜2n -2场,他的得分不会超过2(2n -2)=4n -4分.后n 名棋手彼此之间要赛)1(21-n n 场,每场的分数都被他们自己得去,共计n (n -1)分,因此,他们得分和不会少于n (n -1)分.所以 4n -4≥n n n n -=-2)1(所以 0≤4)5(452--=--n n n n显然,n ≤4上式才能成立,当n =4时,上式的等号成立,所以最多8人参赛. 当85、2解:设n 张卡片写的数字为1a ,2a ,…,n a ,每次都取完,共取n 次,所有小朋友得分之和为)(21n a a a n +++ ,小李的得分为 )(21n a a a +++ ,除小李外其他小朋友的得分和为))(1(21n a a a n +++- =2001=3×23×29.若(n -1)>3, 则(n -1)≥232001≥23)(2421a a a +++ ≥23×(1+2+…24)=23×12×25=6900这是不可能的.所以,n =4. 667)(21=+++n a a a ,即小李得分为667.若小李是第一名,其他三人得分都少于667,那么他们得分之和就小于2001.因此,小李最高是第二名.答:n =667,小李最高是和二名.6、解:设L 是一条棋盘线,在它的上(左)方有偶数个方格(6的倍数个),记为6n 个;设它切割x 个“日形块”,而没有被它切割的“日形块”有m 块.由于被切割的“日形块恰有一半(即一个方格)在L 上(左),因此, x +2m =6n所以,x 必为偶数.若没有一条棋盘线不切割“日形块”,由前面说明,每条棋盘线至少切割2块“日形块”,共有10条棋盘线,所以至少有20个“形块”,但是,18块“日形块”就完全覆盖了棋盘,矛盾.。
初一数学竞赛测试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 如果一个数的平方等于这个数本身,那么这个数可能是:A. 0B. 1C. -1D. 2答案:A、B3. 一个数的绝对值是它本身,这个数是:A. 正数B. 负数C. 零D. 正数或零答案:D4. 下列哪个分数是最简分数?A. 4/8B. 5/10C. 3/4D. 6/9答案:C5. 如果一个三角形的三个内角分别为x°,y°和z°,那么x+y+z的值是:A. 180°B. 360°C. 90°D. 270°答案:A二、填空题(每题3分,共15分)6. 一个数的平方根是它本身,这个数可以是______。
答案:0或17. 如果a和b是两个连续的自然数,且a>b,那么a-b的值是______。
答案:18. 一个数的立方等于它本身,这个数可能是______。
答案:1或-1或09. 如果一个数的相反数是它本身,那么这个数是______。
答案:010. 一个数的绝对值等于它本身,这个数是非负数,即这个数是______。
答案:正数或零三、计算题(每题5分,共20分)11. 计算下列各题:(1) (-3) × (-4) = ______。
答案:12(2) 5 - (-3) = ______。
答案:8(3) (-2)² = ______。
答案:4(4) √16 = ______。
答案:4四、解答题(每题10分,共30分)12. 一个直角三角形的两条直角边分别为3厘米和4厘米,求斜边的长度。
答案:根据勾股定理,斜边长度为√(3² + 4²) = √(9 + 16) = √25 = 5厘米。
13. 一个数列的前三项为1, 1, 2,从第四项开始,每一项都是前三项的和。
求第10项的值。
2013年“华杯赛”冬令营深圳营数学测试(一)
初一试题
一、填空题。
1、设2m +m —1=0,求3m +22m +2012的值为________.
2、设E ,F 分别是△ABC 的边AC 、AB 上的一点,线段BE 、CF 交于点D 。
已知△BDF,△BCD,△CDE 的面积分别为3,6,6。
问:四边形AEDF 的面积是________.
3、对自然数n 规定一种“G ”运算:
① 当n 是奇数时,G (n )=3n+1;
② 当n 是偶数时,G (n )等于n 持续被2整除,直到是奇数的商; 将k 次“G ”运算记作k G ,请计算)
(13G 2013=________. 4、已知,y=|x+3|+|x —2|,则y 的最小值是________.
5、单项式
41b x c y 和单项式-1.1251x -m 12y -n 是同类项,且它们的和为161a n x m y ,那么b (-a)—b c =________.
6、黑板上写着一个形如777…77的数,每次擦掉一个末位数,将前面的数乘以3,然后再加上刚才擦掉的数字,所得新数继续这样操作下去,则最后必获得的数为________.
7、如图,已知平行四边形ABCD 的面积为12,E 为BC 边中点,求图中阴影部分面积是________.
8、一个29位数,如果把这个整数的每相邻的两个数字组成的整数作为两位数来考虑,任何一个这样的两位数都可以被17或43整除。
另外,这个29位数的数字钟只有1个7.则这个29位数的所有数字之和为________。
二、解答题
9、有一位精明的老板对某商品用下列办法确定售价:设商品件数是N,那么N 尖商品售价(单位:元)按每件成本×(1—20%)×N算出后,凑成5的整数倍(只增不减)。
按这一定价方法得到:1件50元;2件95元;3件140元;4件185元;……。
如果每件成本是整元,那么这一商品每件成本是多少元?
10、已知连续2008个正整数的和是一个完全平方数,问:其中最大的数的最小值是多少?。