面板数据模型panel data model分析

面板数据模型的检验方法研究一、本文概述在统计学和经济学的实证研究中，面板数据模型已经成为了一种非常重要的工具。

由于其能够同时考虑时间序列和横截面数据的信息，使得模型设定更加丰富，能够更好地刻画现实世界的复杂性。

然而，随着面板数据模型应用的广泛，如何对其进行准确且有效的检验，确保模型的适用性和预测准确性，成为了亟待解决的问题。

本文旨在探讨面板数据模型的检验方法，以期为相关领域的实证研究提供有益的参考。

具体而言，本文首先将对面板数据模型的基本理论进行梳理，明确其特点和适用场景。

然后，将详细介绍面板数据模型的常见检验方法，包括但不限于单位根检验、协整检验、模型设定检验等。

这些检验方法不仅能够检验模型的内在稳定性和一致性，还能为模型参数的估计和预测提供重要依据。

本文还将对面板数据模型检验方法的最新研究进展进行综述，以期为读者提供全面的视角。

本文将通过实际案例分析，演示面板数据模型检验方法的应用，从而增强文章的实用性和操作性。

总体而言，本文期望通过对面板数据模型检验方法的深入研究，为相关领域的研究者提供一套系统、完整的检验方法体系，以推动面板数据模型在实证研究中的应用和发展。

二、面板数据模型理论基础面板数据模型（Panel Data Model）是计量经济学中一个重要的分析工具，它能够同时处理横截面和时间序列两个维度的数据。

面板数据模型不仅能够控制不可观测的异质性，提高估计效率，还能更好地捕捉数据的动态特征。

因此，面板数据模型在经济、金融、社会学等领域得到了广泛的应用。

面板数据模型的理论基础主要建立在三大类别之上：固定效应模型、随机效应模型和混合效应模型。

固定效应模型假设每个个体的截距项是固定的，不同个体之间的截距项存在差异，但不随时间变化。

随机效应模型则假设截距项是随机的，并且与解释变量不相关。

混合效应模型则假设所有个体的截距项都相同，没有考虑个体差异。

在实际应用中，研究者通常需要根据样本数据和研究目的选择合适的模型。

1960年代有微观经济学、发展经济学和劳动经济学开始， 收入动态行为、劳动力市场、家庭状况、社会经济等 2000年代以来金融学、宏观经济学深入， 失业问题、国际资本流向、汇率、经济增长、购买力平价等☆Panel Data （面板、平行数据）分析有 4类模型1.经典模型，2.变截踞模型：固定影响、随机影响3.变系数模型：固定影响、随机影响，4.动态模型：固定影响、随机影响 研究重点： 检验方法和估计方法 前沿：Panel Data 单位根检验和协整分析; 模型的非参数方法Panel Data面板数据模型分类用面板数据建立的模型通常有3种，即混合模型、固定效应模型和随机效应模型。

1.混合模型（Pooled model ）如果一个面板数据模型定义为，it it it y X αβε'=++ 1,2,...,;1,2,...,i N t T ==其中it y 为被回归变量（标量）， α表示截距项，it X 为1k ⨯阶回归变量列向量（包括k 个回归量）， β为1k ⨯阶回归系数列向量， it ε为误差项（标量）。

则称此模型为混合回归模型。

混合回归模型的特点是无论对任何个体和截面，回归系数α和β都相同。

如果模型是正确设定的，解释变量与误差项不相关，即(,)0it it Cov X ε=。

那么无论是N →∞，还是T →∞ ，模型参数的混合最小二乘估计量（Pooled OLS ）都是一致估计量。

2固定效应模型（fixed effects model ）固定效应模型分为3种类型，即个体固定效应模型、时点固定效应模型和个体时点双固定效应模型。

下面分别介绍。

2.1个体固定效应模型（entity fixed effects model ） 如果一个面板数据模型定义为，it i it it y X αβε'=++ 1,2,...,;1,2,...,i N t T ==其中i α是随机变量，表示对于i 个个体有i 个不同的截距项，且其变化与it X 有关系；it X 为1k ⨯阶回归变量列向量（包括k 个回归量）， 为1k ⨯阶回归系数列向量，对于不同个体回归系数相同，it y 为被回归变量（标量），为误差项（标量），则称此模型为个体固定效应模型。

面板数据模型1. 引言面板数据模型（Panel Data Model）是一种针对面板数据分析的统计模型。

面板数据也称为纵向数据或者长期追踪数据，在经济学和社会科学领域广泛应用。

面板数据由包含多个个体和多个时间点的观测数据组成，可以提供比截面数据（cross-sectional data）更多的信息。

本文将介绍面板数据模型的基本概念、应用领域、建模方法和相关统计分析技术。

2. 面板数据模型的基本概念2.1 面板数据的构成面板数据由个体维度和时间维度两个维度构成。

个体维度指的是一组被观察的个体，可以是人、公司、地区等；时间维度指的是一段时间内的观测点，可以是年、月、季度等。

面板数据是在个体和时间维度上的交叉观测数据。

2.2 面板数据的类型面板数据分为平衡面板数据和非平衡面板数据。

平衡面板数据指的是所有个体在每个时间点上都有观测值；非平衡面板数据指的是个体在某些时间点上缺少观测值。

2.3 面板数据模型的优势相比于截面数据和时间序列数据，面板数据有以下几个优势：•能够控制个体固定效应：面板数据模型可以减少个体固定效应的干扰，提高模型的解释能力；•能够捕捉个体间的异质性：面板数据模型可以捕捉个体之间的差异和变动，提供更全面的分析结果；•提供更多的信息和数据点：面板数据相对于时间序列数据，提供了更多的观测点，可以提高统计分析的准确性。

3. 面板数据模型的应用领域面板数据模型在经济学、金融学、社会学等领域广泛应用，具体领域包括但不限于：•劳动经济学：分析个体的劳动供给行为和工资决定因素；•金融学：评估公司和证券的风险和收益；•医学研究：研究药物治疗的效果和副作用；•教育经济学：评估教育政策的效果和影响；•发展经济学：分析发展中国家的经济增长和贫困问题。

4. 面板数据模型的建模方法面板数据模型的建模方法主要包括固定效应模型（Fixed Effects Model）和随机效应模型（Random Effects Model）。

面板数据模型面板数据模型（Panel Data Model）是一种经济学和统计学中常用的数据分析方法，它允许研究人员在时间和个体维度上分析数据。

该模型结合了截面数据（Cross-sectional Data）和时间序列数据（Time Series Data），能够捕捉到个体间的异质性和时间的动态变化。

面板数据模型的基本假设是个体间存在固定效应（Fixed Effects）和时间效应（Time Effects），即个体特定的不变因素和时间特定的不变因素会对观测数据产生影响。

通过控制这些效应，面板数据模型可以更准确地估计变量之间的关系。

面板数据模型的普通形式可以表示为：Yit = α + βXit + εit其中，Yit表示第i个个体在第t个时间点的观测值，α是截距项，β是自变量Xit的系数，εit是误差项。

面板数据模型可以通过固定效应模型（Fixed Effects Model）和随机效应模型（Random Effects Model）来估计参数。

固定效应模型假设个体间的差异是固定的，即个体特定的不变因素对观测数据产生影响。

该模型通过引入个体固定效应来控制个体间的差异，估计其他变量对因变量的影响。

随机效应模型假设个体间的差异是随机的，即个体特定的不变因素对观测数据不产生影响。

该模型通过引入个体随机效应来控制个体间的差异，估计其他变量对因变量的影响。

面板数据模型的估计方法包括最小二乘法（Ordinary Least Squares, OLS）、固定效应估计法（Fixed Effects Estimation）和随机效应估计法（Random Effects Estimation）。

最小二乘法是一种常用的估计方法，但在面板数据模型中存在一致性问题。

固定效应估计法通过个体间的差异来估计参数，可以解决一致性问题。

随机效应估计法则通过个体间和时间间的差异来估计参数，可以更全面地捕捉到数据的变化。

面板数据模型在经济学和社会科学研究中具有广泛的应用。

第7章面板数据模型分析面板数据模型（Panel Data Model）是一种多变量时间序列数据模型，常用于经济学、金融学和社会科学等领域的研究。

该模型可以同时考虑个体差异、时间效应以及个体和时间的交互作用，具有较高的灵活性和效率。

面板数据可以分为平衡面板数据（Balanced Panel Data）和非平衡面板数据（Unbalanced Panel Data）。

平衡面板数据指各个时间点上个体数目稳定、缺失数据较少的数据集，而非平衡面板数据则相反。

根据数据的特征和研究问题的需要，可以选择适合的模型进行分析。

面板数据模型通常可以分为固定效应模型（Fixed Effects Model）和随机效应模型（Random Effects Model）两类。

固定效应模型假设个体异质性对因变量的影响恒定不变，主要通过个体间的差异来解释变量的变化；而随机效应模型则将个体异质性视为随机变量，并通过估计随机误差项的协方差矩阵来解释因变量的变化。

在面板数据模型分析中，常用的方法包括固定效应模型的最小二乘法（Least Squares Dummy Variable Estimation）和随机效应模型的广义最小二乘法（Generalized Least Squares）。

此外，基于面板数据的研究还可以通过引入仪器变量（Instrumental Variables）来处理内生性问题，或者利用面板数据的特点进行因果推断。

面板数据模型的分析结果可以提供更准确和全面的推断，相比于传统的截面数据或时间序列数据分析方法，更能反映出个体和时间的异质性和相关性。

此外，面板数据模型还可以帮助解决共线性等常见问题，提高模型的解释能力和预测精度。

然而，面板数据模型也存在一些限制和挑战。

首先，面板数据的收集和整理相对复杂，需要耗费较多的时间和精力。

其次，面板数据模型假设个体和时间上的相关性，但在实际研究中，个体和时间的交互作用可能没有那么显著。

面板数据模型和双向固定效应模型
面板数据模型和双向固定效应模型是两种在经济学和其他社会科学领域常用的统计模型。

面板数据模型（Panel Data Model）主要用于分析一段时间内多个对象的动态变化。

这种模型不仅考虑了对象的特性，还考虑了这些特性随时间的变化。

这种模型也被称为混合效应模型，因为它将固定效应和随机效应结合在一个模型中。

双向固定效应模型（Two-way Fixed Effects Model）是一种更复杂的模型，它同时控制了个体和时间两个维度的固定效应。

这种模型主要用于分析面板数据，特别是当研究者关注某一特定个体在一段时间内的变化时。

在双向固定效应模型中，个体和时间层面的效应都是固定的，这意味着它们不会随着其他变量的变化而变化。

在解释这两种模型时，需要注意一些关键点。

例如，面板数据模型的系数可以解释为自变量对因变量的影响，其正负号和大小可以用来判断变量之间的关系。

而双向固定效应模型的系数虽然不能直接观察到个体固定效应和时间固定效应，但可以通过检查残差项的平均值和方差来进行间接验证。

此外，这两种模型在使用时也有一些注意事项。

例如，在解读双向固定效应模型时需要关注共线性问题，如果两个或多个自变量高度相关，则它们的系数可能会失真。

另外，模型的选择也需要基于特定的研究背景和问题。

总的来说，面板数据模型和双向固定效应模型都是用于处理和分析复杂数据的强大工具，但它们在应用和解释上存在一定的差异。

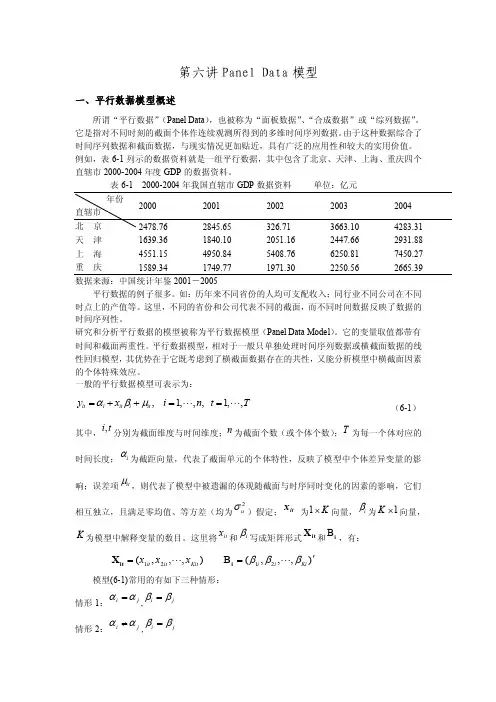
第六讲Panel Data 模型一、平行数据模型概述所谓“平行数据”（Panel Data ），也被称为“面板数据”、“合成数据”或“综列数据”。

它是指对不同时刻的截面个体作连续观测所得到的多维时间序列数据。

由于这种数据综合了时间序列数据和截面数据，与现实情况更加贴近，具有广泛的应用性和较大的实用价值。

例如，表6-1列示的数据资料就是一组平行数据，其中包含了北京、天津、上海、重庆四个直辖市2000-2004年度GDP 的数据资料。

表6-1 2000-2004年我国直辖市GDP 数据资料 单位：亿元天 津 1639.36 1840.10 2051.16 2447.66 2931.88 上 海 4551.154950.845408.76 6250.81 7450.27 重 庆1589.34 1749.771971.302250.562665.39数据来源：中国统计年鉴2001－2005平行数据的例子很多。

如：历年来不同省份的人均可支配收入；同行业不同公司在不同时点上的产值等。

这里，不同的省份和公司代表不同的截面，而不同时间数据反映了数据的时间序列性。

研究和分析平行数据的模型被称为平行数据模型（Panel Data Model ）。

它的变量取值都带有时间和截面两重性。

平行数据模型，相对于一般只单独处理时间序列数据或横截面数据的线性回归模型，其优势在于它既考虑到了横截面数据存在的共性，又能分析模型中横截面因素的个体特殊效应。

一般的平行数据模型可表示为：,1,,,1,, it i it i it y x i n t T αβμ=++== （6-1）其中，,i t 分别为截面维度与时间维度；n 为截面个数（或个体个数）；T 为每一个体对应的时间长度；i α为截距向量，代表了截面单元的个体特性，反映了模型中个体差异变量的影响；误差项it μ，则代表了模型中被遗漏的体现随截面与时序同时变化的因素的影响，它们相互独立，且满足零均值、等方差（均为2u σ）假定；it x 为K ⨯1向量，i β为1⨯K 向量，K 为模型中解释变量的数目。

面板数据的模型(panel data model)王志刚 2004年11月11日一． 混合数据模型和面板数据模型如果扰动项it ε服从独立同分布假定，而且和解释变量不相关，那么就可以采用混合最小二乘法估计（Pooled OLS ），但是这里要注意POLS 暗含着一个假定就是，截距项和解释变量的系数是相同的，不随着个体和时间而变化。

我们一般采用单因子（one-way effects ）模型，假定截距项具有个体异质性，也就是：这种模型是最常见的面板模型（又称为纵列数据longitudinal data ），因为面板数据往往要求个体纬度 N>>T(时间纬度)，下面我们基本上以这种模型为例。

it u 是独立同分布，而且均值为0，方差为2u σ。

如对截距项和解释变量系数均有个体的异质性，那么要采用随机系数模型（Random coefficient model ），stata 的xtrchh 过程提供了相应的估计。

双因子模型（two-way ）：it t i it u ++=γαε二． 固定效应（Fixed effects ） vs 随机效应(Random effects)如果个体效应i α是一个均值为0，方差为2ασ的独立同分布的随机变量，也就是()0,cov =it i x α，该模型就称为随机效应模型（又称为error component model ）；如果相关，则称为固定效应模型。

1．在随机效应模型中，it ε在每个个体内部存在着一阶自相关，因为他们都包含着相同的个体效应；此时OLS 无效，而且标准差也失真，应该采用广义最小二乘估计(GLS)其中：是个体按时间的均值；有待估计；我们可以通过对组内和组间估计得到相应的残差，从而可以计算出方差；T k n e e e e nnk nT ubetween between between between within within u 22222,,ˆˆ1σσσσσα-=-'='--=；组间估计：εβ+=..i i x y ；组内估计如下；2．如果个体效应和解释变量相关，OLS 和GLS 都将失效，此时要采用固定效应模型。