掌门人一对一全套资料高一数学1-5指数与指数函数

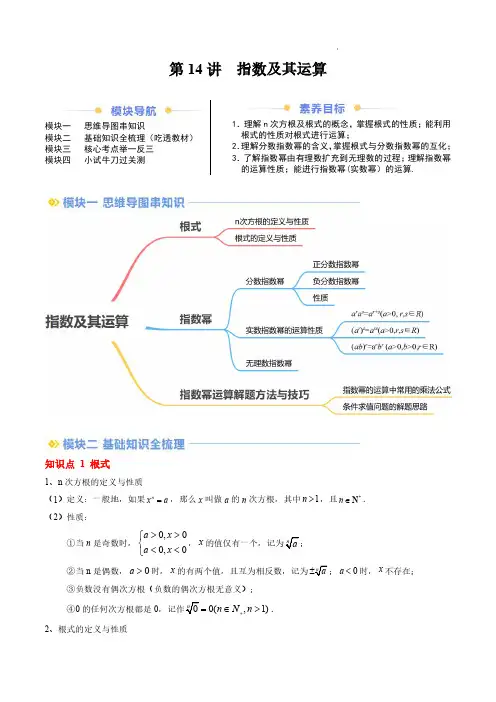
第14讲指数及其运算模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．理解n 次方根及根式的概念，掌握根式的性质；能利用根式的性质对根式进行运算；2．理解分数指数幂的含义，掌握根式与分数指数幂的互化；3．了解指数幂由有理数扩充到无理数的过程；理解指数幂的运算性质；能进行指数幂(实数幂）的运算.知识点1根式1、n 次方根的定义与性质（1）定义：一般地，如果n x a =，那么x 叫做a 的n 次方根，其中1n >，且*n ∈N ．（2）性质：①当n 是奇数时，0,00,0>>⎧⎨<<⎩a x a x ，x；②当n 是偶数，0>a 时，x的有两个值，且互为相反数，记为；0<a 时，x 不存在；③负数没有偶次方根（负数的偶次方根无意义）；④0的任何次方根都是00(,1)n N n +=∈>．2、根式的定义与性质（1n 叫做根指数，a 叫做被开方数．（2）性质：（1n >，且n *∈N）n =a；,,,.⎧⎪=⎨⎪⎩为奇数为偶数n a n a n 知识点2指数幂1、分数指数幂（1）正分数指数幂：规定：mn a=()0,,,1a m n n *>∈>N （2）负分数指数幂：规定：1mn m naa-==()0,,,1a m n n *>∈>N （3）性质：0的正分数指数幂等于0，0的负分数指数幂没有意义．【要点辨析】分数指数幂的注意事项：①分数指数幂是指数概念的又一推广，分数指数幂mna 不可理解为mn个a 相乘，它是根式的一种新的写法．在这样的规定下，根式与分数指数幂是表示相同意义的量，只是形式不同而已．化成分数指数幂的形式时，不要轻易对mn进行约分．③在保证相应的根式有意义的前提下，负数也存在分数指数幂，如()235-=()345-=就没有意义．2、实数指数幂的运算性质①(0,,)+=>∈r s r s a a a a r s R ．②()=sra rs a (0,,)a r s >∈R ．③()=r ab r r a b (0,0,)a b r >>∈R ．3、无理数指数幂一般地，无理数指数幂a α（0a >，α为无理数）是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．【注意】（1）对于无理数指数幂，我们只需要了解两点：①它是一个确定的实数；②它是有理数指数幂无限逼近的结果．（2）定义了无理数指数幂之后，幂的指数就由原来的有理数范围扩充到了实数范围．知识点3指数幂运算解题方法与技巧1、指数幂的运算中常用的乘法公式（1）完全平方公式：222()2a b a ab b -=-+；222()2a b a ab b +=++；（2）平方差公式：22()()a b a b a b -=-+；（3）立方差公式：3322()()a b a b a ab b -=-++；（4）立方和公式：3322()()a b a b a ab b +=+-+；（5）完全立方公式：33223()33a b a a b ab b -=-+-；33223()33a b a a b ab b +=+++．2、条件求值问题的解题思路（1）将条件中的式子用待求式表示出来，进而代入化简得出结论；（2）当直接代入不易时，可以从总体上把握已知式和所求式的特点，从而巧妙求解，一般先利用平方差、立方和（差）以及完全平方公式对其进行化简，再用整体代入法来求值；（3）适当应用换元法，能使公式的使用更加清晰，过程更简洁．考点一：根式的概念及辨析例1．（23-24高一上·全国·专题练习）若a 是实数，则下列式子中可能没有意义的是（）AB C D 【答案】D【解析】A.R a ∈有意义；B.R a ∈有意义；C.R a ∈有意义；D.a<0无意义；故选：D【变式1-1】（23-24高一上·全国·课后作业）R a ∈，下列各式一定有意义的是（）A ．2a -B ．14a C ．23a D ．0a【答案】C【解析】对于A ，当0a =时，2a -无意义，A 不是；对于B ，当a<0时，14a 无意义，B 不是；对于C ，23a =C 是；对于D ，当0a =时，0a 无意义，D 不是.故选：C【变式1-2】（2023高一·江苏·a 的取值范围是（）A ．0a ≥B ．1a ≥C ．2a ≥D ．Ra ∈【答案】B有意义，得102R a a -≥⎧⎨-∈⎩，解得1a ≥，所以a 的取值范围是1a ≥.故选：B【变式1-3】（223-24高一下·贵州遵义·月考）若34(12)x --有意义，则实数x 的取值范围为【答案】1(,)2-∞【解析】由34(12)x --120x ->，解得12x <，故答案为：1(,2-∞．考点二：利用根式的性质化简求值例2.（23-24高一上·北京·期中）下列各式正确的是（）A 3=-Bx=C 2=D ．01a =【答案】C【解析】A 3=，故A 错误；B x =，故B 错误；C2=，故C 正确；D ：01a =，当0a ≠时成立，故D 错误；故选：C.【变式2-1】（23-24高一上·贵州贵阳·月考）若0ab <，则化简）A ．-1B ．0C ．1D ．2【答案】B【解析】=a b a b ⎛=+ ⎝因为0ab <，所以,a b 异号，0a b a b +=，所以0a b a b a b a b a b++==，所以，0=.故选：B.【变式2-2】（23-24高一上·全国·+【答案】6-6(446-+=-．【变式2-3】（23-24高一上·甘肃兰州·期中）（多选）若412x<-3的结果可能为（）A ．210x -B ．46x -C ．24x -+D ．410x --【答案】AC 【解析】由题意知412x <-，即4102x-<-，即202x x +>-，故(2)(2)0,2x x x +->∴<-或2x >，3|2|3x =+-3523210,23523352324,2x x x x x x x x x x ----=->⎧=--+-=⎨-+++-=-+<-⎩，故选：AC考点三：根式与分数指数幂互化例3.（23-24高一上·湖南株洲·月考）下列关于nm a -(),m n *∈N 的形式的运算正确的是（）A．538-=B．538-=C．538-=D ．()328--【答案】A【解析】由于5353818-==A 正确，B ，C 错误；()328--=D 错误，故选：A【变式3-1】（23-24高一上·浙江杭州·期中）（多选）下列各式正确的是（）A ．46a=B 5=-C．(36=D ．23a -=【答案】AC【解析】对于A ：4263a a ==A正确；对于B 5=，故B 错误；对于C：(2636===，故C 正确；对于D：23231aa-==D 错误.故选：AC【变式3-2】（23-24高一上·江西新余·期中）（多选）下列根式与分数指数幂的互化中正确的有（）A ．)130xx -=≠B()120a a =≥C．21320,0)x y x y -=>>D ．3142(0)x x ⎤=->【答案】BC【解析】对选项A ：)130xx -=≠，错误；对选项B()1313220a a a ⎛⎫==≥ ⎪⎝⎭，正确；对选项C22133212(0,0)y x y x y x-==>>，正确；对选项D：33214432(0)x x x⎛⎫==>⎪⎝⎭，错误；故选：BC【变式3-3】（23-24高一上·广东广州·期中）用分数指数幂表示并计算下列各式（式中字母均正数），写出化简步骤.154m⋅【答案】(1)14b；(2)1【解析】（1=111224b b⎛⎫===⎪⎝⎭.（2）154m⋅11111532423651641m m m m mm m+-⋅⋅====⋅.考点四：利用指数幂运算性质化简例4.（23-24高一上·全国专题练习）下列等式一定成立的是（）A．1332a a a⋅=B．11220⋅=a a C．329()a a=D．111362a a a÷=【答案】D【解析】对于A：11311333262a a a a+⋅==，故A错误；对于B：11212221⋅==a a a a，故B错误；对于C：326()a a=，故C错误；对于D：1111132362a a a a÷==，故D正确；故选：D【变式4-1】（23-24高一上·广东江门·期中）102x=，103y=，则10x y+=．【答案】6【解析】102x=Q，103y=，101010236x y x y+∴=⋅=⨯=，故答案为：6．【变式4-2】（23-24高一上·河南·期中）若a b =，则()2312222a b ab ---⎡⎤=⎢⎥⎣⎦.【答案】1【解析】由题意，0,0a b >>，所以()()231222232246a b ab a b a b -----⎡==⎤⎢⎥⎣⎦，又11322,2a b --===，所以原式6411223222221----⎛⎫⎛⎫=⋅=⋅= ⎪ ⎪⎝⎭⎝⎭.故答案为：1.【变式4-3】（23-24高一上·江西九江·期中）化简或计算下列各式．(1)121121332a b a b ---⎛⎫ ⎪；(2)()10.52332770.02721259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭．【答案】(1)1a；(2)0.09【解析】（1）原式2111111111532322132623615661ab a baba aa b⎛⎫⨯--⎪⎝⎭---+--⋅====.（2）原式22333273550.0910001033⨯⎛⎫⎛⎫==+-= ⎪⎪⎝⎭⎝⎭.考点五：解简单的指数方程例5.（23-24高一·全国·专题练习）方程11416x -=的解为（）A ．2B ．﹣2C ．﹣1D ．1【答案】C 【解析】∵1214416x --==，∴x ﹣1＝﹣2，∴x ＝﹣1．故选：C ．【变式5-1】（22-23高一上·河北沧州·期中）关于x 的方程112250x x +--+=的解的个数为（）A ．0B ．1C ．2D ．4【答案】B【解析】解：原方程即222502xx ⨯-+=，化简可得()2225220x x ⨯+⨯-=，令2(0)x t t =>，可得22520t t +-=，该方程有且只有一个正根，由于2x t =单调递增，所以t 与x 一一对应，即原方程只有一个解.故选：B .【变式5-2】（23-24高一上·北京顺义·期中）关于x 的方程422x x -=的解为．【答案】1x =【解析】由422x x -=可得()22220x x --=，即()()21220x x+-=，因为20x >，可得22x =，故1x =.所以，方程关于x 的方程422x x -=的解为1x =.故答案为：1x =.【变式5-3】（22-23高三·全国·对口高考）方程(2522xx x -+=的解为．【答案】5x =或12x =【解析】由题意可得(2599222222xxx x x -+⎛⎫=== ⎪⎝⎭，所以25922x x x -+=，即221150x x -+=，解得5x =或12x =，故答案为：5x =或12x =考点六：整体换元法解决条件求值例6.（23-24高一下·辽宁抚顺·开学考试）已知12a a+=，则1122a a -+等于（）A ．2B ．4C ．2±D ．4±【答案】A【解析】112221()2224a a a a-+=++=+=，所以11222a a -+=.故选：A.【变式6-1】（23-24高一上·全国·专题练习）已知11223a a -+=，则33221122a a a a--++的值为．【答案】6【解析】因为11223a a-+=，所以2112223a a -⎛⎫+= ⎪⎝⎭，即129a a -++=，所以17a a -+=，所以3333112222a aa a --⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭22111111222222a a a a a a ---⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=+-⋅+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()()11122371181a a a a --⎛⎫=++=⨯- ⎝-=⎪⎭，所以332211221863a a a a--+==+．【变式6-2】（23-24高一上·全国·专题练习）已知11223x x -+=，计算：22111227x x x x x x---+-+++.【答案】4【解析】因为11223x x-+=，所以211229x x -⎛⎫+= ⎪⎝⎭，所以129x x -++=，所以17x x -+=，所以()2127x x -+=，即22249x x -++=，所以2247x x -+=，所以22111227477473x x x x x x---+--==++++.【变式6-3】（23-24高一上·湖南娄底·期末）已知11223a a -+=，求下列各式的值：(1)1a a -+；(2)33222232a a a a --+-+-．【答案】(1)7；(2)13【解析】（1）由题意11223a a-+=，所以21112222327a a a a --⎛⎫+=+-=-= ⎪⎝⎭.（2）由题意11223a a -+=，所以()()1111212233222222213371331512744534a a a a a a a a a a a a ------⎛⎫⎛⎫- ⎪⎪⨯--+-⎝⎭⋅⎝⎭==-==+--+++-.一、单选题1．（23-24高一上·青海海南·期中）已知R a ∈，则下列各式一定有意义的是（）A ．2a -B ．13a C ．12a D ．0a 【答案】B【解析】对于A ，由221aa -=可知，0a =时表达式无意义；对于B ，根据幂函数性质可知，R a ∈时，表达式13a 恒有意义；对于C，易知12a =a<0时，表达式无意义；对于D ，当0a =时，0a 无意义；故选：B2．（23-24高一上·陕西咸阳·期末）化简32的结果为（）A ．5BC ．5-D．【答案】A【解析】332232232332555⨯⎛⎫=== ⎪⎝⎭=，故选：A3．（23-24高一上·北京大兴·月考）已知0a >=（）A ．12a B ．32a C ．2a D ．3a 【答案】A12a ==，故选：A4．（23-24高一上·安徽淮南·月考改编）下列根式与分数指数幂的互化错误的是（）A()120a a =>B．)340xx -=>C．)21320,0x y x y -=>>D ．()32140x x =>【答案】B【解析】对于A()1313220a a a ⎛⎫==> ⎪⎝⎭，故A 正确；对于B选项，)334410xx x -⎛⎫=> ⎪⎝⎭，故B 错误；对于C，)21321210,0x y x y x-=>>，故C 正确；对于D ，)()33321444320x x x ⎛⎫===> ⎪⎝⎭，故D 正确．故选：B ．5．（23-24高一上·江苏泰州·期中）已知14x x -+=，则22x x -+等于（）A ．6B ．12C ．14D ．16【答案】C【解析】由14x x -+=可得：()2122216x x x x --+=++=，则2214x x -+=.故选：C.6．（23-24高一上·四川德阳·月考）010.256371.586-⎛⎫⨯-++= ⎪⎝⎭（）A ．110B ．109C ．108D ．100【答案】A【解析】原式()11133333112344131442222223221083331210810231-⎛⎫=+=+= ⎪⎝⎭⎛⎫⎛⎫⎛⎫⨯+⨯+⨯-=⨯+-⎪ ⎪⎝⎭⎝⎭⎝⎭.故选：A.二、多选题7．（23-24高一上·四川成都·期中）以下运算结果等于2的是（）AB ．C ．D【答案】BCD 【解析】对于Aπ44π=-=-，不合题意；对于B ，2=，符合题意；对于C ，()22=--=，符合题意；对于D 22=-=，符合题意.故选：BCD8．（23-24高一上·浙江·月考）已知0a >，0b >，则下列各式正确的是（）A π3=-B 1=C ．m na-=D ．121133332463b ab a b ---⎛⎫÷-=- ⎪⎝⎭【答案】ABD【解析】A 选项：由π30->π3=-，A 选项正确；B ()11111123612312600222221a b b a ab a b ⎛⎫⎛⎫-⨯-+⨯ ⎪ ⎪--⎝⎭⎝⎭⎡⎤====⎢⎥⎣⎦，B 选项正确；C 选项：m na-=C 选项错误；D 选项：112121101333333331246663b ab a a b a b b ⎛⎫⎛⎫------- ⎪ ⎪⎝⎭⎝⎭⎛⎫÷-=-=-=- ⎪⎝⎭，D 选项正确；故选：ABD.三、填空题9．（22-23高一上·上海奉贤·期末）化简()222a b ⋅=（其中0a >，0b >）．【答案】4ab【解析】()((42222222a b ab ab ⨯⋅=⋅=.故答案为：4ab .10．（23-24高一上·全国·单元测试）方程2129240x x +-⋅+=的解集是．【答案】{1,2}-【解析】令2x t =，则0t >，方程可化为22940t t -+=，解得12t =或4t =，所以，122x=或24x =，解得=1x -或2x =.所以，方程的解集为{1,2}-.故答案为：{1,2}-.11．（23-24高一上·重庆沙坪坝·期中）已知12102α-=，131032β=，则314210βα+=（填数值）【答案】2【解析】()()31131113113142513422342242101010=322222βαβα⎛⎫⎛⎫⨯⨯+-⨯+- ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫=⨯⨯=== ⎪ ⎪⎝⎭⎝⎭.故答案为：2四、解答题12．（23-24高一上·安徽马鞍山·期中）化简求值：(1)()12120.344⎛⎫+ ⎪⎝⎭(2)20.5231103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭；【答案】(1)52；(2)0【解析】（1）()120120.344⎛⎫+ ⎪⎝⎭1293511422⎛⎫=+=+= ⎪⎝⎭.（2）20.5231103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222364493322220273444-⎛⎫⎛⎫⎛⎫⎛⎫⨯-÷=-⨯-⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭13．（23-24高一上·辽宁丹东·期中）已知正实数a 满足11221a a --=.(1)求1a a -+的值；(2)求33221122a a a a---+的值.【答案】(1)3；(2)5【解析】（1）将11221a a --=两边平方得121a a -+-=，所以13a a -+=.（2）因为a 是正实数，令1122(0)a a x x -+=>，则2125x a a -=++=，所以x =可得()33111222214a aa a a a ---⎛⎫-=-++= ⎪⎝⎭，所以33221122a a a a---==+。

高中数学知识点完整结构图-掌门1对 1高中数学知识点1 集合函数附：一、函数的定义域的常用求法：1、分式的分母不等于零；2、偶次方根的被开方数大于等于零；3、对数的真数大于零；4、指数函数和对数函数的底数大于零且不等于1；5、三角函数正切函数tan y x =中()2x k k Z ππ≠+∈；余切函数cot y x =中；6、如果函数是由实际意义确定的解析式，应依据自变量的实际意义确定其取值范围。

二、函数的解析式的常用求法：1、定义法；2、换元法；3、待定系数法；4、函数方程法；5、参数法；6、配方法三、函数的值域的常用求法：1、换元法；2、配方法；3、判别式法；4、几何法；5、不等式法；6、单调性法；7、直接法四、函数的最值的常用求法：1、配方法；2、换元法；3、不等式法；4、几何法；5、单调性法五、函数单调性的常用结论： 1、若(),()f xg x 均为某区间上的增（减）函数，则()()f x g x +在这个区间上也为增（减）函数 2、若()f x 为增（减）函数，则()f x -为减（增）函数3、若()f x 与()g x 的单调性相同，则[()]y f g x =是增函数；若()f x 与()g x 的单调性不同，则[()]y f g x =是减函数。

4、奇函数在对称区间上的单调性相同，偶函数在对称区间上的单调性相反。

5、常用函数的单调性解答：比较大小、求值域、求最值、解不等式、证不等式、作函数图象。

六、函数奇偶性的常用结论：1、如果一个奇函数在0x =处有定义，则(0)0f =，如果一个函数()y f x =既是奇函数又是偶函数，则()0f x =（反之不成立）2、两个奇（偶）函数之和（差）为奇（偶）函数；之积（商）为偶函数。

3、一个奇函数与一个偶函数的积（商）为奇函数。

4、两个函数()y f u =和()u g x =复合而成的函数，只要其中有一个是偶函数，那么该复合函数就是偶函数；当两个函数都是奇函数时，该复合函数是奇函数。

高一数学1到5章知识点高中数学是学生们面临的一门必修课程。

从高一开始，学生将逐步接触到数学的不同领域和知识点。

本文将讨论高一数学的1到5章知识点，包括函数、三角函数、数列与数学归纳法、排列与组合以及概率等内容。

1. 函数在高中数学的1章中，学生首先学习了函数的概念和表示方法。

函数是一种对应关系，将自变量的取值映射到因变量的取值。

函数的表示方法有多种形式，如函数表、函数图像和函数式。

在学习函数的过程中，学生将接触到函数的定义域、值域和奇偶性等概念。

2. 三角函数在高一数学的2章中，学生开始学习三角函数的知识。

三角函数是与角度相关的一类函数，包括正弦函数、余弦函数和正切函数等。

学生需要掌握三角函数的定义、性质和图像等内容。

此外，学生还需要学习三角函数的基本关系式和解三角方程的方法。

3. 数列与数学归纳法在高一数学的3章中，学生将学习数列与数学归纳法的知识。

数列是一系列有序的数按照一定规律排列而成的。

学生需要掌握常见数列的定义、性质和求和公式等内容。

同时，数学归纳法是一种证明方法，通过证明某个命题在满足初始条件的情况下对所有自然数成立，从而得出结论。

4. 排列与组合在高一数学的4章中，学生开始学习排列与组合的知识。

排列与组合是数学中的一类问题，涉及到从一组元素中选择若干个进行排列或组合的方式。

学生需要了解排列与组合的定义、计算公式和应用等内容。

此外，学生还需要掌握排列与组合之间的互相转化关系。

5. 概率在高一数学的5章中，学生将学习概率的知识。

概率是研究随机事件发生的可能性的数学方法。

学生需要了解概率的定义、性质和计算方法等内容。

在学习概率的过程中，学生还将接触到事件的互斥与独立性、条件概率和贝叶斯定理等概念。

通过学习这些知识点，学生将逐渐建立起数学的基础，为后续的学习打下坚实的基础。

高中数学不仅仅是考试的内容，更是培养学生思维能力和解决问题的能力的重要工具。

因此，学生需要通过不断的练习和思考来巩固和应用所学知识，才能真正理解数学的魅力和应用的价值。

高一数学指数及指数函数1•根式的性质(3)负数没有偶次方根 (4)零的任何正次方根都是零2•幕的有关概念 (1)正整数指数幕：naa a a ..… n...... a (n N )(2)零指数幕a 01(a 0)1⑶负整数指数幕 a p-(a 0.p N )a pm(4)正分数指数幕a nnma (a0, m, n N ,且 n 1) (5)负分数指数幕a m1 nm(a0, m, n N ,且 n 1)a 石(6)0的正分数指数幕等于0，0的负分数指数幕无意义3•有理指数幕的运算性质rr s⑶(ab) a a ,(a0,b 0, r Q)4、指数函数的定义：函数y a% 0且a °叫做指数函数，其中x 是自变量，函数定义域是R 。

① 若a 0，则当x 0时，『0；当x 0时，a x 无意义.1 1② 若a 0，则对于X 的某些数值，可使a 无意义•如(2)，这时对于 4，2，等等，在实数范围内函数值不存在•③ 若a 1，则对于任何x R ，a x 1，是一个常量，没有研究的必要性• 对于任何x R ，「都有意义，且『0.因此指数函数的定义域是R ，值域是(°)有些函数貌似指数函数，实际上却不是，如y 『k (a 0且 a 1，k Z )；x有些函数看起来不像指数函数，实际上却是，如y a (a 0且a 1)，因为它可 x1 1 1 0 1 a ，其中a ，且a(1)当n 为奇数时，有n a na(2)当n 为偶数时，有；a" a a, (a 0) a, (a 0)r sr s .八 亠、(1) a a a ,(a 0, r, s Q)/ r、srs , -亠、⑵(a )a ,(a 0,r,s Q)以化为y5、函数的图象(1)①特征点：指数函数y = a x (a > 0且a ^ 1) 的图象经过两点(0 , 1)和(1,a).②指数函数y = a x (a > 0且a 工1)的图象中，y = 1 反映了它的分布特征；而直线x = 1 与指数函数图象的交点(1,a)的纵坐 标则直观反映了指数函数的底数特 征，称直线x = 1和y = 1为指数函 数的两条特征线•(2)、函数的图象单调性当a > 1时，函数在定义域范围内 呈单调递增； 当0v a v 1时，函数在定义域范围 内呈单调递减； 推论：(1)底互为倒数的两个函数图像关于y 轴对称(2)当a > 1时，底数越大，函数图象越靠近丫轴；当0v a v 1时，底数越小， 函数图象越靠近丫轴。

高一数学上册第三单元指数与指数函数知识点
高一数学上册第三单元指数与指数函数知识点
以指数为自变量，底数为大于0且不等于1的常量的函数称为指数函数，它是初等函数中的一种。

以下是高一数学上册第三单元指数与指数函数知识点，希望能帮助大家学习!
一、指数函数的定义
指数函数的一般形式为y=a^x(a>0且≠1) (x∈R).
二、指数函数的性质
1.曲线沿x轴方向向左无限延展〈=〉函数的定义域为(-∞，+∞)
2.曲线在x轴上方，而且向左或向右随着x值的减小或增大无限靠近X轴(x轴是曲线的'渐近线)〈=〉函数的值域为(0，+∞)
三、指数函数的一般形式
(1)指数函数的定义域为所有实数的集合，这里的前提是a大于0，对于a不大于0的情况，则必然使得函数的定义域不存在连续的区间，因此我们不予考虑。

(2)指数函数的值域为大于0的实数集合。

(3)函数图形都是下凹的。

(4)a大于1，则指数函数单调递增;a小于1大于0，则为单调递减的。

(5)可以看到一个显然的规律，就是当a从0趋向于无穷大的过程中(当然不能等于0)，函数的曲线从分别接近于Y轴与X轴的正半轴的单调递减函数的位置，趋向分别接近于Y轴的正半轴与X轴的负半轴的单调递增函数的位置。

其中水平直线y=1是从递减到递增的一个过渡位置。

(6)函数总是在某一个方向上无限趋向于X轴，永不相交。

(7)函数总是通过(0，1)这点。

(8)显然指数函数无界。

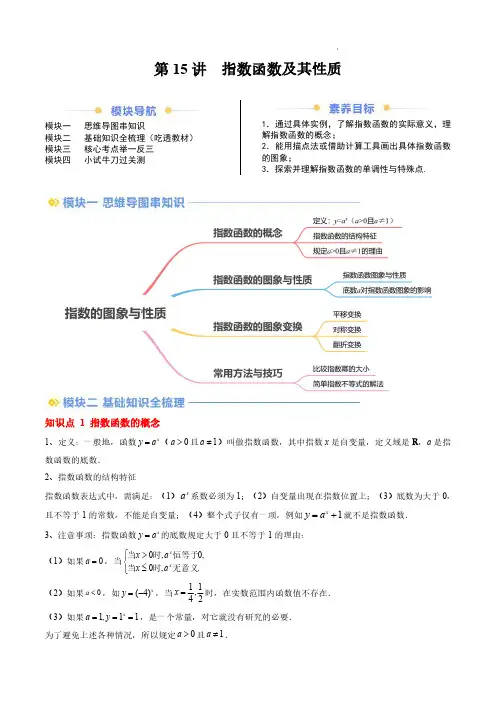
第15讲指数函数及其性质模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．通过具体实例，了解指数函数的实际意义，理解指数函数的概念；2．能用描点法或借助计算工具画出具体指数函数的图象；3．探索并理解指数函数的单调性与特殊点.知识点1指数函数的概念1、定义：一般地，函数x y a =（0a >且1a ≠）叫做指数函数，其中指数x 是自变量，定义域是R ，a 是指数函数的底数．2、指数函数的结构特征指数函数表达式中，需满足：（1）xa 系数必须为1；（2）自变量出现在指数位置上；（3）底数为大于0，且不等于1的常数，不能是自变量；（4）整个式子仅有一项，例如1xy a =+就不是指数函数．3、注意事项：指数函数x y a =的底数规定大于0且不等于1的理由：（1）如果0a =，当0,0,0,.x xx a x a ⎧>⎨≤⎩当时恒等于当时无意义（2）如果0a <，如(4)x y =-，当11,42x =时，在实数范围内函数值不存在．（3）如果1,11x a y ===，是一个常量，对它就没有研究的必要．为了避免上述各种情况，所以规定0a >且1a ≠．知识点2指数函数的图象与性质1、指数函数的图象与性质1>a10<<a图象性质定义域R值域),0(+∞过定点)1,0(单调性在R上是增函数在R上是减函数奇偶性非奇非偶函数2、底数a对指数函数图象的影响函数2xy=，3xy=，4xy=和1(2xy=，1(3xy=，1()4xy=的图象如图所示．（1）当1a>且0x>时，底数越大，图象越“陡”；当01a<<且0x<时，底数越小，图象越“陡”．（2）在y轴右侧，图象从上到下相应的底数由大变小，即“底数大图象高”；在y轴左侧，图象从上到下相应的底数由小变大，即“底数大图象低”．知识点3指数函数的图象变换已知指数函数xy a=（0a>且1a≠）1、平移变换k kx xy a y a k>=−−−−−−−−→=+向上平移个单位长度()；k kx xy a y a k>=−−−−−−−−→=-向下平移个单位长度()；h hx x hy a y a>+=−−−−−−−−→=向左平移个单位长度()；0h h x x h y a y a >-=−−−−−−−−→=向右平移个单位长度()．规律总结：上加下减（针对函数值y ），左加右减（针对自变量x ）．2、对称变换y x x y a y a -=−−−−−→=关于轴对称；x x x y a y a =−−−−−→=-关于轴对称；x x y a y a -=−−−−−→=-关于原点对称．3、翻折变换x y x y y a y a =−−−−−−−−→=保留轴右侧图象并作其关于轴的对称图形；||x x x x x y a y a =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折到轴上方．知识点4常用方法与技巧1、比较指数幂的大小（1）对于底数相同，指数不同的两个幂的大小比较，可以利用指数函数的单调性来判断；（2）对于底数不同，指数相同的两个幂的大小比较，可以利用指数函数图象的变化规律来判断；（3）对于底数不同，且指数也不同的幂的大小比较，可先化为同底的两个幂，或者通过中间值来比较．2、简单指数不等式的解法（1）形如()()>f x g x a a 的不等式，可借助=x y a 的单调性求解；（2）形如()>f x ab 的不等式，可将b 化为a 为底数的指数幂的形式，再借助=x y a 的单调性求解；（3）形如>xxa b 的不等式，可借助两函数=x y a ，=xy b 的图象求解。

高中数学知识点完整结构图-掌门1对1
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学知识点完整结构图-掌门1对1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学知识点完整结构图-掌门1对1的全部内容。

403 Forbidden
JSP3/2。

0.14
Z。

指数函数和对数函数专题指数函数及其性质：要点一、指数函数的概念：函数y=a x(a>0且1)叫做指数函数，其中x是自变量, 要点二、指数函数的图象及性质：xy=a0<a<1时图象a>1时图象图象N1a卜升a1/I11 ■1 ”01划性质①定义域R,值域 (0, +g)②a0=1,即x=0时，y=1，图象都经过(0 , 1)点③a =a，即x=1时，y等于底数a④在定义域上是单调减函数④在定义域上是单调增函数⑤ x<0 时，a x>1 x>0 时，0<a x<1⑤x<0 时，0<a x<1 x>0 时，a x>1⑥既不是奇函数，也不是偶函数要点诠释:1x指数函数y a x与y 的图象关于y轴对称。

a要点三、指数函数底数变化与图像分布规律a为常数，函数定义域为R.④y d x又即：x € (0,+ g)时，x € ( —g ,0)时, (2 )特殊函数d xd1 x 1 x(—)x, y (—)x的图像:2 3要点四、指数式大小比较方法化为同底数指数式，利用指数函数的单调性进行比较y 2x, y 3x, yc x(底大幕大)x xc比较法有作差比较与作商比较两种，其原理分别为:① 若 ABO AB ; ABO AB ; ABO AB ;A A ② 当两个式子均为正值的情况下，可用作商法，判断 -1，或-1即可.B B【典型例题】类型一、函数的定义域、值域例1 •求下列函数的定义域、值域【总结升华】(1) 研究y a f(x)型的复合函数的单调性用复合法， 比用定义法要简便些, 即当a > 1时，y a f(x)的单调性与y f (x)的单调性相同；当 0 v a v 1时, 单调与y f (x)的单调性相反.(2)研究y f(a x )型的复合函数的单调性，一般用复合法，即设 t a x数t a x 与外函数y f(t)的单调性来确定 yf(a x )的单调性.- 11例 4.比较大小(1) (―)3,34,( —)-2(2)22.5, (2.5) 0, ( - )2.5332(1) y 丄^; (2)y=4 x -2x +i ；1 332x1a (a 为大于1 的常数)举一反三：【变式1】求下列函数的定义域:(1) y 2%2-1(2) y 3曲⑶y 2x -1(4)y . 1-a x (a 0,a 1)X 22x的单调性, 例2.讨论函数f(x)1例3 •讨论函数y -4举一反三：2【变式1】求函数y 3 x 3x 2的单调区间及值域.2【变式2】求函数f(x) a x-2x (其中a 0,且a 1)的单调区间 并求其值域.2的单调性.一般地有：y a f(x)的，再由内函举一反三:1 1 1【变式1】比较大小：22 , 33 , 66 ；1【变式2】 比较1.5-0.2 , 1.3 0.7,(|)3的大小.【变式3】如果a 2x 1 a x 5 ( a 0，且a 1)，求x 的取值范围.【总结升华】=偶，偶•偶=偶，奇•偶=奇，得出f(x)的奇偶性.类型四：指数函数的图象问题X例 6 •如图的曲线C 1、C l 、C 3、C 4是指数函数y a 的图象，而a 转巫2 2、,,则图象C 1、C 2、C 3、C 4对应的函数的底数依次是、 •、3C 2rX【总结升华】:在y 轴的右边“底大图高，在y 轴的左边“底大图低”例7•若直线y 2a 与函数 a 的取值范围是【变式1】如图是指数函数①a ,b ,c ,d 与1的大小关系为(A • a v b v 1 v c v dB .C . 1 v a v b v c v dD . y | a x 1| 1 ( a 0,且 a 1)x x xy a ，② y b ，③ y c ,)b v a v 1 v d vc a v b v 1 vd v c例&确定方程2x2x 2的根的个数.类型三、判断函数的奇偶性 例5•判断下列函数的奇偶性:f(x)(x)((x)为奇函数)求 f (x) g(x)(x)的奇偶性，可以先判断g(x)与(x)的奇偶性，然后在根据奇•奇的图象有两个公共点，则对数函数及其性质1.对数函数的概念(1) 定义：一般地，我们把函数Y.三」Og a x(a>0,且1)叫做对数函数，其中x是自变量，函数的定义域是(0 ,+^ ).(2) 对数函数的特征：log a x的系数：1特征log a x的底数：常数，且是不等于1的正实数log a x的真数：仅是自变量x【例1 - 1】函数f(x)= (a2-a+ 1)log(a+ 1)x是对数函数，则实数 a = ______________ .2.对数函数y= log a x(a>0，且a^ 1)的图象与性质(1)［例2】如图所示的曲线是对数函数y= log a x的图象.已知a从，，，中取值,3 5 10则相应曲线C1，C2,C3, C4的a值依次为(1010C.10D.10点技巧根据图象判断对数函数的底数大小的方法作直线尸1,它与各曲线的交点的横坐标就是各对数的底数，由此判断各底数的大小.3. 反函数(1)对数函数的反函数指数函数y = a x(a> 0,且a^ 1)与对数函数y= log a x(a>0,且1)互为反函数.⑵互为反函数的两个函数之间的关系①原函数的定义域、值域是其反函数的值域、定义域；②互为反函数的两个函数的图象关于直线y = x对称.⑶求已知函数的反函数一般步骤如下：①由y= f(x)解岀x，即用y表示岀x；②把x替换为y, y替换为x;③根据y = f(x)的值域，写岀其反函数的定义域.【例3—1】若函数y= f(x)是函数y= a x(a > 0,且a工1)的反函数，且f(2) = 1，则f(x)=( )1A. log 2x B . r2xC. log1x D . 2x 22【例3—2】函数f(x)= 3x(0v x< 2)的反函数的定义域为()A. (0 ,+^ ) B . (1,9]C. (0,1) D . [9 ,+^ )【例3—3】若函数y= f(x)的反函数图象过点(1,5)，则函数y = f(x)的图象必过点()4. 利用待定系数法求对数函数的解析式及函数值【例4- 1】已知f(e x ) = x ,则f(5)=( ) A . e 5B . 5eC . In 5D . ge1【例4- 2】已知对数函数f(x)的图象经过点，2 ，试求f(3)的值.91【例4-3】已知对数函数f(x)的反函数的图象过点(2,9)，且f(b)= ，试求b 的值.25 .对数型函数的定义域的求解 (1)对数函数的定义域为 (0 ,+^ ).⑵在求对数型函数的定义域时，要考虑到真数大于0,底数大于0，且不等于1 .若底数和真数中都含有变量，或式子中含有分式、根式等，在解答问题时需要保证各个方面都有意义.一般地，判断类似于 y = log a f(x)的定义域时，应首先保证 f(x)> 0 .(3)求函数的定义域应满足以下原则：① 分式中分母不等于零；② 偶次根式中被开方数大于或等于零； ③ 指数为零的幕的底数不等于零； ④ 对数的底数大于零且不等于 1;⑤ 对数的真数大于零，如果在一个函数中数条并存，求交集• 【例5】求下列函数的定义域.(1)y = log 5(1 -x); (2)y = log (2x - 1)(5x — 4);⑶ y ,log °.5(4x 3).6.对数型函数的值域的求解【例6- 1】求下列函数的值域： 2 2(1)y = log 2(x + 4);(2)y= log 1 (3 + 2x — x ).2【例6- 2】已知f(x)= 2 + log 3x , x [1,3]，求y =[f(x)]2 + f(x 2)的最大值及相应的 x 的值.7. 对数函数的图象变换及定点问题对数函数y = log a x(a > 0，且1)过定点(1,0)，即对任意的a > 0，且1都有log a 1 = 0.这 是解决与对数函数有关的函数图象问题的关键.【例7- 1】若函数y = log a (x +b)+ c(a > 0,且a ^ 1)的图象恒过定点(3,2)，则实数b ，c 的值 分另V 为 ________________ .A • (5,1)B • (1,5)C • (1,1)D • (5,5)【例7- 2】作岀函数y= |log2(x+ 1)| + 2的图象.8 .禾U用对数函数的单调性比较大小两个对数式的大小比较有以下几种情况： 【例8- 1】比较下列各组中两个值的大小.(1)log 3l.9， Iog 32； (2)log 23， log o.32； (3)log a n Iog a 3.141 .9 •对数型函数单调性的讨论(1)解决与对数函数有关的函数的单调性问题的关键： 一是看底数是否大于 1,当底数未明确 给岀时，则应对底数a 是否大于1进行讨论；二是运用复合法来判断其单调性； 三是注意其定义 域.⑵关于形如y = log a f(x)一类函数的单调性，有以下结论：函数y = log a f(x)的单调性与函数 u = f(x)(f(x) > 0)的单调性，当a > 1时相同，当0 v a v 1时相 反. 例如：求函数 y = log 2(3 — 2x)的单调区间.【例10— 1】求函数y = log a (a — a x )的单调区间.析规律 判断函数y = log a f(x)的单调性的方法 函数y = log a f(x)可看成是y = log a u 与u = f(x) 两个简单函数复合而成的，由复合函数单调性 “同增异减”的规律即可判断•需特别注意的是， 在求复合函数的单调性时，首先要考虑函数的定义域，即 “定义域优先”.【例 10— 2】已知 f(x) = log 1 (x 2 — ax — a)在211.对数型函数的奇偶性问题判断与对数函数有关的函数奇偶性的步骤是：(1)求函数的定义域，当定义域关于原点不对称时，则此函数既不是奇函数也不是偶函数, 当定义域关于原点对称时，判断 f(— X )与f(x)或—f(x)是否相等；⑵当f( — x) = f(x)时，此函数是偶函数；当 f(— x) = — f(x)时，此函数是奇函数；(3)当f( — x) = f(x)且f( — x) = — f(x)时，此函数既是奇函数又是偶函数； ⑷当f( — x)工f(x)且f( — x)工—f(x)时，此函数既不是奇函数也不是偶函数. 例如，判断函数f(x)= log a ( x 2 1+ x) (x R ，a > 0,且1)的奇偶性.1 x【例11】已知函数f(x)= log a ---------- (a > 0,且1).1 x(1)求函数f(x)的定义域； ⑵判断函数f(x)的奇偶性； ⑶求使f(x) > 0的x 的取值范围.1上是增函数，求 a 的取值范围.2。

第03讲指数与指数函数（5类核心考点精讲精练）1.5年真题考点分布2.命题规律及备考策略【命题规律】本节内容是新高考卷的命题载体内容，通常会结合其他知识点考查，需要掌握指数的运算及指数函数的基本性质，难度中等偏下，分值为5-6分【备考策略】1.了解有理数指数幂、实数指数幂含义，掌握指数幂的运算性质.2.了解指数函数的实际意义，理解指数函数的概念3.能画出具体指数函数的图象探索并理解指数函数的单调性与特殊点4.能结合指数函数比较指数式大小【命题预测】本节内容会结合其他函数内容综合考查，需综合性学习备考1.指数的基本知识（1）根式的基本性质①x 的定义域为0≥x ,3x 的定义域为R x ∈②⎩⎨⎧<-≥==0,0,2x x x x x x ，定义域为()R x ∈③()x x =2，定义域为()0≥x ④x x =33，定义域为()R x ∈⑤()x x =33，定义域为()R x ∈（2）指数的基本性质①零指数幂:01(0)a a =≠;②负整数指数幂:1(0,);pp a a p N a-*=≠∈③正分数指数幂:0,,1)m naa m n N n *=>∈>、且;④负分数指数幂:10,,1)m nm naa m n N n a-*==>∈>、且（3）指数的基本计算①同底数幂的乘法运算nm nma a a +=⋅②同底数幂的除法运算nm n ma aa -=③幂的乘方运算()mnnma a =④积的乘方运算()mm mb a ab =2.指数函数（1）指数函数的定义及一般形式一般地，函数()R x a a a y x∈≠>=,10且，叫做指数函数（2）指数函数的图象和性质x a y =1>a 10<<a 图象定义域R值域()+∞,0性质过定点()1,0当0>x 时，1>y ；0<x 时,10<<y 当0>x 时，10<<y ；<x 时,1>y 在()+∞∞-,上是增函数在()+∞∞-,上是减函数1．（2023·全国·模拟预测）29⎛⎫=⎪ ⎪⎝⎭（）A ．13B．3C D ．3【答案】A【分析】利用指数幂的运算性质化简计算即可.【详解】()222341393-⎛⎫===⎪ ⎪⎝⎭．故选：A ．2．（2024·广东·模拟预测）若3xy =，则．【答案】±【分析】分0,0x y >>和0,0x y <<两种情况分类计算.【详解】当0,0x y >>时，==当0,0x y <<时，+-故答案为：±3．（2022·北京·高考真题）已知函数1()12xf x =+，则对任意实数x ，有（）A ．()()0f x f x -+=B ．()()0f x f x --=C ．()()1f x f x -+=D ．1()()3f x f x --=【答案】C【分析】直接代入计算，注意通分不要计算错误．【详解】()()1121112121212x x x x xf x f x --+=+=+=++++，故A 错误，C 正确；()()11212121121212122121x x x x x x x x f x f x ----=-=-==-++++++，不是常数，故BD 错误；故选：C ．1．（2024·上海宝山·二模）（其中0a >）化为有理数指数幂的形式为.【答案】54a 【分析】直接利用根式与分数指数幂的运算法则化简求解即可54a ===故答案为：54a 2．（2023·山东·模拟预测）若114a a --=，则22a a -+的值为（）A ．8B ．16C ．2D ．18【答案】D【分析】利用完全平方公式结合指数幂的运算性质计算即可.【详解】解：因为114a a --=，所以221122()24218a a a a --+=-+=+=.故选：D ．3．（2023·四川宜宾·一模）计算()12410.25lg10-⨯+=.【答案】-【分析】根据根式、指数幂运算以及对数的定义运算求解.()()121422110.25lg 21102-⎡⎤⎛⎫⨯+=-+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦1242=-⨯--()12410.25lg10--⨯⨯=-故答案为：-.1．（2024·四川成都·模拟预测）函数3x y =与13xy =-的图象（）A ．关于x 轴对称B ．关于y 轴对称C ．关于原点对称D ．关于y x =对称【答案】C【分析】根据函数图象的对称性即可判断，对于两个函数()f x 与()g x ，如果它们的图象关于原点对称，即()()g x f x -=-在定义域内恒成立，则称()f x 与()g x 为中心对称，利用指数函数的图象的对称性，得出结论.【详解】令函数()()13,3xxy f x y g x ====-，所以()()133x x g x f x --=-=-=-即()()g x f x -=-，所以函数()f x 与()g x 的的图象关于原点对称，即函数3x y =与13xy =-的图象的的图象关于原点对称，故选：C.2．（23-24高三上·河北衡水·开学考试）已知0a >，则函数()2x f x a a =-的图象可能是（）A．B ．C．D．【答案】AD【分析】通过特值法，排除错误选项，通过a 的取值，判断函数的图象的形状，推出结果即可.【详解】由于当1x =时，(1)20f a a a =-=-<，排除B ，C ，当2a =时，()24x f x =-，此时函数图象对应的图形可能为A ，当12a =时，1()()12xf x =-，此时函数图象对应的的图形可能为D.故选：AD.3．（2024·甘肃张掖·模拟预测）函数()()e 11xf x x x =---的所有零点之和为（）A ．0B ．-1CD ．2【答案】A【分析】令()0f x =，即()e 110xx x ---=，构造函数e x y =与函数11x y x +=-，画出函数图象，可知两个函数图象相交于两点，设为12,x x ，得()()110f x f x =-=，进而得到21x x =-，即120x x +=【详解】由零点定义可知，函数的零点，就是方程()0f x =的实数根，令()0f x =，则()e 110x x x ---=，显然1x ≠，所以1e 1x x x +=-，构造函数e x y =与函数11x y x +=-，则方程1e 1xx x +=-的根，可转化为两个函数图象的交点问题，根据图象可知，两个函数图象相交于两点，所以此方程有两个实数根，即函数()()e 11xf x x x =---有两个零点，设为12,x x ，所以1111e 1xx x +=-，2221e 1x x x +=-，即()()()()12111222e 110,e 110x xf x x x f x x x =---==---=，另外发现，将1x -代入，可得()()()()()11111111111111e 1110e e ex x x x x x x f x x x x --+-++-=-----=+-=+=，所以1x -也是函数()f x 的零点，说明21x x =-，即120x x +=.故选:A.1．（22-23高二下·四川绵阳·期末）要得到函数212x y -=的图象，只需将指数函数4x y =的图象（）A ．向左平移1个单位B ．向右平移1个单位C ．向左平移12个单位D ．向右平移12个单位【答案】D【分析】利用函数图象的平移变换可得出结论.【详解】因为242x x y ==，1221222x x ⎛⎫- ⎪-⎝⎭=，所以，为了得到函数212x y -=的图象，只需将指数函数4x y =的图象向右平移12个单位，故选：D.2．（23-24高三上·山西晋中·阶段练习）（多选）在同一直角坐标系中，函数21y x ax a =++-与x y a =的图象可能是（）A ．B ．C ．D ．【答案】AC【分析】根据二次函数的图象与指数函数的图象判断，注意分类讨论．【详解】当1a >时，对应的图象可能为选项A ；当01a <<时，对应的图象可能为选项C.故选：AC.3．（2024·黑龙江·二模）已知函数||12x y a b ⎛⎫=+ ⎪⎝⎭的图象经过原点，且无限接近直线2y =，但又不与该直线相交，则ab =（）A ．1-B ．2-C ．4-D ．9-【答案】C【分析】由题意可得0a b +=且2b =，求出a ，即可求解.【详解】因为函数1()()2xy f x a b ==+图象过原点，所以01()02a b +=，得0a b +=，又该函数图象无限接近直线2y =，且不与该直线相交，所以2b =，则2a =-，所以4ab =-.故选：C1．（2023·全国·高考真题）设函数()()2x x a f x -=在区间()0,1上单调递减，则a 的取值范围是（）A ．(],2-∞-B ．[)2,0-C ．(]0,2D ．[)2,+∞【答案】D【分析】利用指数型复合函数单调性，判断列式计算作答.【详解】函数2x y =在R 上单调递增，而函数()()2x x a f x -=在区间()0,1上单调递减，则有函数22()()24a a y x x a x =-=--在区间()0,1上单调递减，因此12a ≥，解得2a ≥，所以a 的取值范围是[)2,+∞.故选：D2．（2024·宁夏银川·三模）已知函数()1221xx f x -=+，则下列说法不正确的是（）A ．函数()f x 单调递增B ．函数()f x 值域为()0,2C ．函数()f x 的图象关于()0,1对称D ．函数()f x 的图象关于()1,1对称【答案】C【分析】分离常数，再根据复合函数单调性的判断方法，即可判断A ；根据函数形式的变形，根据指数函数的值域，求解函数的值域，即可判断B ；根据对称性的定义，()2f x -与()f x 的关系，即可判断CD.【详解】()111222222212121x x x x x f x ---+-===-+++，函数22y t=-，121x t -=+，则1t >，又内层函数121x t -=+在R 上单调递增，外层函数22y t=-在()1,+∞上单调递增，所以根据复合函数单调性的法则可知，函数()f x 单调递增，故A 正确；因为1211x -+>，所以120221x -<<+，则1202221x -<-<+，所以函数()f x 的值域为()0,2，故B 正确；()2112422212221x x xx f x ----===+++，()()22f x f x -+=，所以函数()f x 关于点()1,1对称，故C 错误，D 正确.故选：C.3．（2024·全国·模拟预测）已知函数()2233x xf x --=-，则满足()()830f x f x +->的x 的取值范围是（）A ．(),4-∞B ．(),2-∞C ．()2,+∞D ．()2,2-【答案】B【分析】设()33x x g x -=-，即可判断()g x 为奇函数，又()()2f x g x =-，可得()f x 图象的对称中心为()2,0，则()()40f x f x +-=，再判断()f x 的单调性，不等式()()830f x f x +->，即()()834f x f x ->-，结合单调性转化为自变量的不等式，解得即可.【详解】设()33x x g x -=-，x ∈R ，则()()33x xg x g x --=-=-，所以()g x 为奇函数．又()()()222233332x x x x f x g x -----=-=-=-，则()f x 的图象是由()g x 的图象向右平移2个单位长度得到的，所以()f x 图象的对称中心为()2,0，所以()()40f x f x +-=．因为3x y =在R 上单调递增，3x y -=在R 上单调递减，所以()g x 在R 上单调递增，则()f x 在R 上单调递增，因为()()()()8304f x f x f x f x +->=+-，所以()()834f x f x ->-，所以834x x ->-，解得2x <，故满足()()830f x f x +->的x 的取值范围为(),2∞-．故选：B4．（2024·全国·模拟预测）已知0,1a a >≠，函数()()251,11,1xx a x x f x a x ⎧+-+≤=⎨->⎩是R 上的减函数，则a 的取值范围是（）A ．(]1,3B ．[]2,3C ．[)2,+∞D ．[)3,+∞【答案】B【分析】根据分段函数的单调性和指数函数的单调性列出不等式组，解之即可直接得出结果.【详解】因为函数1(0,1)x y a a a =->≠是减函数，所以1a >．又因为函数2(y x a =+-5）1x +图像的对称轴是直线52ax -=，所以函数()251y x a x =+-+在5,2a -⎛⎫-∞ ⎪⎝⎭上单调递减，在5,2a -⎛⎫+∞ ⎪⎝⎭上单调递增．又函数()f x 是R 上的减函数，所以151231a a a a>⎧⎪-⎪≥⎨⎪-≥-⎪⎩，解得23a ≤≤，所以a 的取值范围是[]2,3．故选:B．1．（2024·江西·模拟预测）函数()223x xf x -=的一个单调递减区间为（）A ．(),0∞-B ．()1,0-C ．()0,1D ．()1,+∞【答案】C【分析】利用指数型复合函数的单调性即可得出答案.【详解】令22t x x =-，则3t y =，由复合函数的单调性可知：()f x 的单调递减区间为函数22t x x =-的单调递减区间，又函数2()()2()t x x x t x -=---=，即函数()t x 为偶函数，结合图象，如图所示，可知函数22t x x =-的单调递减区间为(),1∞--和()0,1，即()f x 的单调递减区间为(),1∞--和()0,1．故选：C．2．（2024·福建福州·模拟预测）设函数()23a xf x -=在区间()1,2上单调递减，则a 的取值范围是（）A ．(],2-∞B ．(],4∞-C ．[)2,+∞D ．[)4,+∞【答案】D【分析】根据题意，由复合函数的单调性，列出不等式，代入计算，即可得到结果.【详解】函数3x y =在R 上单调递增，而函数()23a xf x -=在区间()1,2上单调递减，所以2y x a =-在区间()1,2单调递减，所以22a≥，解得4a ≥．故选：D ．3．（2024·吉林长春·模拟预测）（多选）已知函数()1221xx f x -=+，则下列说法正确的是（）A ．函数()f x 单调递增B ．函数()f x 值域为()0,2C ．函数()f x 的图象关于()0,1对称D ．函数()f x 的图象关于()1,1对称【答案】ABD【分析】根据复合函数单调性的判断方法，即可判断A ，根据函数形式的变形，根据指数函数的值域，求解函数的值域，即可判断B ，根据对称性的定义，()2f x -与()f x 的关系，即可判断CD.【详解】()111222222212121x x x x x f x ---+-===-+++，函数22y t=-，121x t -=+，则1t >，又内层函数121x t -=+在R 上单调递增，外层函数22y t=-在()1,∞+上单调递增，所以根据复合函数单调性的法则可知，函数()f x 单调递增，故A 正确；因为1211x -+>，所以120221x -<<+，则1202221x -<-<+，所以函数()f x 的值域为()0,2，故B 正确；()2112422212221x x x x f x ----===+++，()()22f x f x -+=，所以函数()f x 关于点()1,1对称，故C 错误，D 正确.故选：ABD4．（2024·陕西西安·模拟预测）已知函数()11,021,02x x f x x x +⎧<⎪⎪=⎨⎪≥⎪+⎩，则不等式()()213f a f ->的解集为（）A ．()2,2-B ．()0,∞+C ．(),0∞-D ．()(),22,∞∞--⋃+【答案】A【分析】判断函数()f x 的单调性，再利用单调性解不等式即可.【详解】()11,021,02x x f x x x +⎧<⎪⎪=⎨⎪≥⎪+⎩，易知112x y +=在(),0∞-单调递减，12y x =+在()0,∞+单调递减，且()f x 在0x =处连续，故()f x 在R 上单调递减，由()()213f a f ->，则213a -<，解得22a -<<,故不等式()()213f a f ->的解集为()2,2-.故选：A1．（23-24高三·阶段练习）已知函数()112⎛= ⎪⎝⎭f x ，则()f x 的单调递增区间为，值域为．【答案】(,0]-∞(0,2]【分析】根据同增异减法则求出函数的单调区间；通过指数函数的单调性求出函数值域.【详解】令220x x ≥－，解得2x ≥或0x ≤，∴()f x 的定义域为(][),02,∞+∞ -，令1t =，则其在(,0]-∞上递减，在[2,)+∞上递增，又12ty ⎛⎫= ⎪⎝⎭为减函数，故()f x 的增区间为(,0]-∞．∵11t =≥-，∴(]10,22t⎛⎫∈ ⎪⎝⎭，故()f x 的值域为(0,2]．故答案为：(,0]-∞，(0,2].2．（2024·上海松江·二模）已知02a <<，函数()1241,22,2x a x a x y a x -⎧-++≤=⎨>⎩，若该函数存在最小值，则实数a 的取值范围是.【答案】1{|02a a <≤或1}a =【分析】令()(2)41g x a x a =-++，(],2x ∞∈-，1()2x h x a -=，(2,)x ∈+∞，分类讨论a 的取值范围，判断()g x ，()h x 的单调性，结合()f x 存在最小值，列出相应不等式，综合可得答案．【详解】由题意，令()(2)41g x a x a =-++，(],2x ∞∈-，1()2x h x a -=，(2,)x ∈+∞，当01a <<时，()g x 在(],2-∞上单调递减，()h x 在(2,)+∞上单调递减，则()h x 在(2,)+∞上的值域为(0,2)a ，因为()f x 存在最小值，故需()2(2)2410g a a =-⨯++≤，解得12a ≤，结合01a <<，此时102a <≤；当12a <<时，()g x 在(],2-∞上单调递减，()h x 在(2,)+∞上单调递增，则()h x 在(2,)+∞上的值域为(2,)a +∞，因为()f x 存在最小值，故需()22g a ≤，即(2)2412a a a -⨯++≤，解得34a ≤，这与12a <<矛盾；当1a =时，()5g x x =-+在(],2-∞上单调递减，且在(],2-∞上的值域为[)3,+∞，()2h x =，此时存在最小值2；则实数a 的取值范围为1{|02a a <≤或1}a =．故答案为：1{|02a a <≤或1}a =．3．（2024·四川成都·二模）已知函数()212axx f x -+=的值域为M ．若()1,M ∞+⊆，则实数a 的取值范围是（）A ．1,4⎛⎤-∞ ⎥⎝⎦B ．10,4⎡⎤⎢⎥⎣⎦C ．11,,44⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭D ．1,4⎡⎫+∞⎪⎢⎣⎭【答案】B 【分析】对实数a 分类讨论，根据二次函数的性质及指数函数的值域可得结果.【详解】当0a =时，()()120,x f x ∞-+=∈+，符合题意；当0a ≠时，因为函数()212axx f x -+=的值域为M 满足()1,M ∞+⊆，由指数函数的单调性可知，即二次函数21y ax x =-+的最小值小于或等于零；若0a >时，依题意有21y ax x =-+的最小值4104a a-≤，即104a <≤，若0a <时，不符合题意；综上：104a ≤≤，故选：B.1．（2024·贵州·模拟预测）已知函数223()2x x f x -++=，则()f x 的最大值是.【答案】16【分析】求出223t x x =-++的范围，根据复合函数的单调性求解.【详解】由()2232xx f x -++=，而2223(1)44t x x x =-++=--+≤，因为2t y =单调递增，所以422t y =≤，则()f x 的最大值是16.故答案为：162．（2024·山东菏泽·模拟预测）若函数1()1lg ([,100])10f x x x =+∈，则函数22[)()](()2f x f x F x -=的值域为（）A ．1[,16]2B ．[]1,8C ．[]2,16D ．[]1,16【答案】D【分析】根据给定条件，利用对数函数单调性求出()f x 的值域，再借助二次函数求出22[()]()f x f x -的值域，最后利用指数函数单调性求解即得.【详解】函数()1lg f x x =+在1[,100]10上单调递增，()[0,3]f x ∈，令22222[()]()[()]12lg [()]2()1[()1][0,4]t f x f x f x x f x f x f x =-=--=-+=-∈，而函数2t y =在[0,4]上单调递增，则1216t ≤≤，所以函数22[)()](()2f x f x F x -=的值域为[]1,16.故选：D3．（2024·河北保定·三模）已知()11,14()1,1x a x f x a x x x ⎧--≤⎪⎪=⎨⎪+->⎪⎩()1a >的值域为D ，1[,)2D ⊆+∞，则a 的取值范围是（）A ．3[,2]2B ．55[,)43C ．3[,2)2D ．7[,2]4【答案】D【分析】分段函数在两段上分别根据自变量范围求函数值的范围，跟值域对比求实数a 的取值范围.【详解】①若12a <<，当1x ≤时，()()114xf x a =--在(,1]-∞上单调递减，此时5()[,)4f x a ∈-+∞，当1x >时，()11af x x x=+-≥，当且仅当1x =>时，等号成立，又函数()f x 的值域D 满足1[,)2D ⊆+∞，则51,4211,212,a a ⎧-≥⎪⎪⎪≥⎨⎪<<⎪⎪⎩解得724a ≤<；②若2a >，当1x ≤时，()()114xf x a =--在(,1]-∞上单调递增，此时15()(]44f x a ∈--，当1x >时，()11af x x x=+-≥，当且仅当1x =>时，等号成立，又函数()f x 的值域D 满足1[,)2D ⊆+∞，不合题意；③当2a =时，3,1,4()21,1,x f x x x x ⎧≤⎪⎪=⎨⎪+->⎪⎩，若1x >，有21112x x +-->≥（当且仅当x =综上所述：724a ≤≤.故选：D.1．（2024·云南·二模）若12132,6,2a b c π--===，则（）A ．b a c >>B ．c a b>>C ．a b c>>D ．a c b>>【答案】D【分析】根据中间数2比较a 与c ，根据中间数1比较b 与c .【详解】因为21222a π-=>=，1322c =<，所以a c >，因为11616b -==<，103221c =>=，所以c b >，所以a c b >>.故选：D.2．（2024·天津·一模）已知实数a ，b ，c 满足5312a ⎛⎫= ⎪⎝⎭，12e b =，1123c⎛⎫= ⎪⎝⎭，则（）A ．a b c <<B ．b a c<<C ．<<c a bD ．c b a<<【答案】A【分析】根据条件，得到1e 1()2b =，利用函数1(2x y =的单调性，即可得到1a b <<，而1c >，即可求出结果.【详解】因为12eb =，得到1e 1()2b =，又5312a ⎛⎫= ⎪⎝⎭，函数1()2x y =是减函数，所以51311()122a b ⎛⎫=<=< ⎪⎝⎭e ，又1123c⎛⎫= ⎪⎝⎭，得到1221log log 313c ==>，所以a b c <<，故选：A.3．（2024·宁夏银川·三模）设0.29a =，0.313b =，ln1.33c =，则（）A ．c b a <<B ．b c a <<C ．a c b <<D ．a b c<<【答案】A【分析】构造函数()1ln f x x x =--，应用导数得其单调性，可判断0.3ln1.3>，再结合指数函数3x y =的单调性即可判断.【详解】根据题意，构造函数()1ln f x x x =--，则()1x f x x'-=，当1x ≥时，()0f x '≥，所以()f x 在区间[)1,+∞上单调递增，因此可得()()1.310f f >=，即()1.3 1.31ln1.30.3ln1.30f =--=->，所以0.3ln1.3>，又指数函数3x y =为单调递增，可得0.310.3ln1.3333>>，即b c >，因为0.20.40.31933a b ==>=，所以c b a <<.故选：A.1．（2024·四川·模拟预测）设0.40.5a =， 1.10.4b =，0.51.1c =，则（）A ．a c b <<B ．c<a<bC ．a b c<<D ．b a c<<【答案】D【分析】根据指数函数、幂函数的单调性，结合与特殊值1的比较，即可得到答案.【详解】因为指数函数0.5x y =是单调减函数，所以 1.10.400.50.50.51<<=，又由幂函数 1.1y x =在()0,∞+上单调增函数，所以 1.1 1.1 1.1110.50.4=>>，又因为指数函数 1.1x y =是单调增函数，所以0.501.1 1.11>=，综上可得：b a c <<，故选：D.2．（2023·天津·高考真题）设0.50.60.51.01, 1.01,0.6a b c ===，则,,a b c 的大小关系为（）A ．a b c <<B ．b a c <<C ．c b a <<D ．c a b<<【答案】D【分析】根据对应幂、指数函数的单调性判断大小关系即可.【详解】由 1.01x y =在R 上递增，则0.50.61.01 1.01a b =<=，由0.5y x =在[0,)+∞上递增，则0.50.51.010.6a c =>=.所以b a c >>.故选：D3．（2024·辽宁·一模）设123322e 1e 3a b c -==-=-，，则（）A ．a b c <<B ．c b a <<C ．b c a <<D ．a c b<<【答案】B【分析】利用导数证明不等式e 1x x ≥+，可得,b a c a <<；根据不等式的性质可证得21331e e -+>，则c b <，即可求解.【详解】对于函数()e 1x f x x =--，()e 1x f x '=-，令()00,()00f x x f x x ''<⇒<>⇒>，所以函数()f x 在(,0)-∞上单调递减，在(0,)+∞上单调递增，所以min ()(0)0f x f ==，则()0f x ≥，即e 1x x ≥+.所以13122e 2(1)33b =-≤-+=，23221e 1(1)33c -=-≤--+=.由2e 8<，得2133e 82<=，所以13132e e<，则21332133121e1e ee-+=+>=>，所以21331e 2e --<-，即c b <.所以c b a <<.故选：B【点睛】方法点睛：对于比较实数大小方法：（1）利用基本函数的单调性，根据函数的单调性判断，（2）利用中间值“1”或“0”进行比较，（3）构造函数利用函数导数及函数单调性进行判断.一、单选题1．（2024·陕西渭南·二模）设集合{}11M x x =-≤≤，{}e ,0xN y y x ==≤，则M N ⋃=（）A ．()0,1B ．(]0,1C ．[]1,1-D ．[]0,1【答案】C【分析】求出函数值域化简集合N ，再利用并集的定义求解即得.【详解】当0x ≤时，0e 1x <≤，则(0,1]N =，而[1,1]M =-，所以[1,1]M N =-U .故选：C2．（2024·河南·模拟预测）若,a b ∈R ，则“a b >”是“3322a b b a ->-”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】C【分析】构造函数()32x xf x =+，根据函数单调性得到3232a a b b +>+，故a b >.【详解】构造函数()32x xf x =+，则()f x 在R 上单调递增，所以()()33223232a b b a a a b bf a f b a b ->-⇔+>+⇔>⇔>．故选：C ．3．（2024·湖南邵阳·三模）“01a <<”是“函数()xf x a a =-（0a >且1a ≠）在R 上单调递减”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】C【分析】分1a >和01a <<两种情况讨论()f x 的单调性，结合充分、必要条件分析判断.【详解】若1a >，则()f x 的图象为：可知()f x 在R 上单调递增；若01a <<，则()f x 的图象为：可知()f x 在R 上单调递减；综上所述：“01a <<”是“函数()xf x a a =-（0a >且1a ≠）在R 上单调递减”的充要条件.故选：C ．4．（2024·全国·模拟预测）已知函数()()2x af x a +=∈R 为偶函数，则函数()y f x =的增区间为（）A ．()1,-+∞B ．()0,∞+C ．(),1-∞-D ．(),0∞-【答案】B【分析】由偶函数求得参数值，进而得表达式，结合指数函数单调性即可得解.【详解】因为函数()()2x af x a +=∈R 为偶函数，所以22x ax a-++=，解得0a =，所以函数()2,022,0x xx x f x x -⎧≤==⎨>⎩，其增区间为()0,∞+.故选：B ．5．（2024·辽宁·一模）若函数()223xaxf x -+=在区间()1,4内单调递减，则a 的取值范围是（）A ．(],4∞-B ．[]4,16C ．()16,+∞D ．[)16,+∞【答案】A【分析】利用“同增异减”判断复合函数的单调性，从而求参数的取值范围.【详解】设()3u f u =，22u x ax =-+，则()3uf u =在(),-∞+∞上单调递增.因为()223xaxf x -+=在区间(1,4)内单调递减，所以函数22u x ax =-+在区间()1,4内单调递减，结合二次函数的图象和性质，可得：14a≤，解得a ≤4.故选：A6．（2024·江西景德镇·三模）已知函数()()1,02,0xx f x g x x ⎧⎛⎫<⎪ ⎪=⎨⎝⎭⎪>⎩是奇函数，则0x >时，()g x 的解析式为（）A ．12x⎛⎫- ⎪⎝⎭B ．12x⎛⎫ ⎪⎝⎭C ．2x -D ．2x【答案】C【分析】设0x >，利用0x <时，()12xf x ⎛⎫= ⎪⎝⎭和()()f x f x -=-可求得()g x 的解析式.【详解】设0x >，则0x -<，所以()122xx f x -⎛⎫-== ⎪⎝⎭，又函数()f x 是奇函数，所以()()f x f x -=-，即()2xf x -=⇒()2x f x =-，0x >.即()2xg x =-.故选：C7．（2024·浙江绍兴·三模）已知函数()21f x +为偶函数，若函数()()11225--=++-x x g x f x 的零点个数为奇数个，则()1f =（）A ．1B ．2C ．3D ．0【答案】D【分析】由函数()g x 的图象关于1x =对称得零点关于1x =对称，但()g x 的零点个数为奇数个可得答案.【详解】因为函数()21f x +为偶函数，所以()()2+1=2+1f x f x -，所以()y f x =的图象关于1x =对称，令()11225--=+-xx h x ，则()()112225---=+-=x x h x h x ，可得函数()11225--=+-xx h x 的图象关于1x =对称，所以函数()()11225--=++-x x g x f x 的图象关于1x =对称，则函数()g x 的零点关于1x =对称，但()g x 的零点个数为奇数个，则()10f =.故选：D.二、填空题8．（2024·山东济宁·三模）已知函数410()2log 0xx f x x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩，，，则12f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭.【分析】利用已知的分段函数，可先求11()22f =-，再求1122f f f ⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.【详解】因为410()2log 0xx f x x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩，，，，所以44111log =log 2222f ⎛⎫=-=- ⎪⎝⎭.所以11221112222f f f -⎛⎫⎛⎫⎛⎫⎛⎫=-===⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭.9．（2024·全国·模拟预测）写出一个同时满足下面条件①②的函数解析式()f x =．①()()()1212f x x f x f x +=；②()f x 的值域为(0,)+∞．【答案】2x （答案不唯一）【分析】根据指数函数的值域和指数运算即可得到答案.【详解】对于任意指数函数函数()(0xf x a a =>且1)a ≠,条件①，对于任意12,x x ∈R ，都有()()()12121212x x x xf x f x a a a f x x +=⋅==+，条件②，()f x 是指数函数，所以()f x 的值域为(0,)+∞，例如：函数()2xf x =为指数函数，满足条件①②.故答案为：2x （答案不唯一）.10．（23-24高一上·四川攀枝花·阶段练习）若命题“R x ∃∈，20x a -=”为假命题，则实数a 的取值范围为．【答案】{|0}a a ≤【分析】根据已知条件，推得R x ∀∈，20x a -≠为真命题，再结合指数函数值域的范围，即可求解．【详解】命题“R x ∃∈，20x a -=”为假命题，则R x ∀∈，20x a -≠为真命题，又20x >则0a ≤，故实数a 的取值范围为{|0}a a ≤．故答案为：{|0}a a ≤．一、单选题1．（2024·全国·模拟预测）已知函数()1e xf x a=+的图象关于点()()1,1f 对称，则=a （）A ．1B ．2C ．eD ．2e 【答案】C【分析】利用函数中心对称的性质，代入化简解方程即可求得e a =.【详解】由对称中心性质可知函数()f x 满足()()()221f x f x f +-=，即2112e e e x x a a a-+=+++，整理可得3122e e 2e e 2e e x x x x a a a -+-+=+++，即()()22e e e e e e e 22x x x xa --++--=，解得e a =.故选：C2．（2024·贵州毕节·三模）已知函数e ()e x x af x a-=+是奇函数，若(2023)(2024)f f >，则实数a 的值为（）A ．1B ．1-C ．1±D ．0【答案】B【分析】根据函数奇偶性的定义，即函数的单调性解即可.【详解】因为函数e ()e x x af x a-=+是奇函数，所以e 1e ()()e 1e e e e e x x x xx xx xa a a aa a f x f x a a --+--=---===-=-+++，解得1a =±，又e e 22()1e e e x x x x x a a a af x a a a-+-===-+++，所以当0a >时，函数为增函数，当a<0时，函数为减函数，因为(2023)(2024)f f >，所以a<0，故1a =-.故选：B3．（2024·北京西城·三模）已知函数()2x f x =，若12,R x x ∀∈，且12x x <，则下面结论错误的是（）A ．12()()f x f x <B ．1212()()22x x f x f x f ++⎛⎫<⎪⎝⎭C ．1212()()()f x x f x f x =+D ．1212()()()f x x f x f x +=【答案】C【分析】根据指数函数的单调性判断A ，根据基本不等式判断B ，根据指数的运算判断C D .【详解】由指数函数的单调性可知()f x 在R 上单调递增，又12x x <，所以12()()f x f x <，故A 正确；因为120x >，220x >，所以121212122222()()222x x x x f x f x x x f +++⎛⎫=≥= ⎪⎝+=⎭，又12x x <，所以上式取不到等号，所以1212()()22f x f x x x f ++⎛⎫> ⎝⎭，故B 正确；1212()2x x f x x =，1212()()22x x f x f x +=+，12,R x x ∀∈，12x x <，1212()()()f x x f x f x ≠+，故C 错误；1212()2x x f x x ++=，12121212()()222()xx x x f x f x f x x +=⋅==+，故D 正确.故选：C.4．（2024·四川绵阳·模拟预测）已知函数()e ,0,ln ,0,x x f x x x ⎧≤=⎨>⎩()3,g x x =-方程()()()3f g x g x =--有两个不同的根，分别是12,,x x 则12x x +=（）A ．0B ．3C ．6D ．9【答案】B【分析】方程()()()3f g x g x =--有两个不同的根等价于函数()()y f g x =与y x =-的图象有两个交点，作出函数()()f g x 与y x =-的图象，根据数形结合计算即可得出结果.【详解】由题意得：()3g x x =-为R 上的增函数，且()30,g =当3x ≤时，()0g x ≤，()()3e xfg x -=，当3x >时，()0g x >，()()()ln 3f g x x =-，方程()()()3f g x g x x =--=-有两个不同的根等价于函数()()y f g x =与y x =-的图象有两个交点，作出函数()()f g x 与y x =-的图象如下图所示：由图可知3e x y -=与()ln 3y x =-图象关于3y x =-对称，则,A B 两点关于3y x =-对称，中点C 在3y x =-图象上，由3y x y x =-⎧⎨=-⎩，解得：33,22C ⎛⎫- ⎪⎝⎭.所以123232x x =⨯+=.5．（23-24高三下·河南周口·开学考试）若1235111e ,e ,563a b c ===，则（）A ．b c a >>B ．c a b >>C ．a b c >>D ．a c b>>【答案】B【分析】利用构造函数法，结合导数的性质判断函数的单调性，利用单调性进行判断即可.【详解】由题意知1235212e ,2e 53a b ==，令()e (01)xf x x x =<<，则()()2e 10x xf x x '-=<，所以()f x 在()0,1上单调递减，又120135<<<，所以1235f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，即1235e e 1235>，所以123521e e 53>，即22a b >，所以a b >，又1355e 3a c ===，又53=>>55c a >，所以c a >，所以c a b >>．故选：B ．【点睛】关键点睛：本题的关键是对已知实数进行变形，然后构造函数，利用函数的单调性进行判断.6．（2022·全国·模拟预测）已知124e a =，139e b =，6c =，则a ，b ，c （）A ．a b c <<B ．a c b <<C ．c b a <<D ．c a b<<【答案】D【分析】根据给定条件，构造函数，利用导数探讨单调性即可比较大小.【详解】令2e (),01x f x x x =<<，求导得3(2)e ()xx f x x -'=，当01x <<时，()0f x '<，则()f x 在(0,1)上单调递减，则11()3(2f f >，即11324e 9e <，而9e 4>，于是112294e 4()64>⨯=，所以c a b <<.二、多选题7．（2024·山东临沂·一模）已知函数()()221x f x a a =+∈-R ，则（）A ．()f x 的定义域为()(),00,∞-+∞UB ．()f x 的值域为RC ．当1a =时，()f x 为奇函数D ．当2a =时，()()2f x f x -+=【答案】ACD【分析】由分母不为零求出函数的定义域，即可判断A ，再分210x ->、1210x -<-<分别求出函数值的取值范围，即可得到函数的值域，从而判断B ，根据奇偶性判断C ，根据指数幂的运算判断D.【详解】对于函数()()221xf x a a =+∈-R ，令210x -≠，解得0x ≠，所以()f x 的定义域为()(),00,∞-+∞U ，故A 正确；因为20x >，当210x ->时2021>-x，所以221x a a +>-，当1210x -<-<时2221x<--，所以2221xa a +<-+-，综上可得()f x 的值域为()(),2,a a -∞-++∞ ，故B 错误；当1a =时()22112121x x x f x +=+=--，则()()21212121x x x x f x f x --++-==-=---，所以()2121x f x =+-为奇函数，故C 正确；当2a =时()221212121x x x f x +=+=+--，则()()21211122121x x x x f x f x ---+=++-+++=-，故D 正确.故选：ACD三、填空题8．（2024·辽宁·模拟预测）命题“任意[]1,3x ∈，22x x a -≤+”为假命题，则实数a 的取值范围是.【答案】52a >【分析】根据题意，问题转化为存在[]1,3x ∈，22x x a ->+为真命题，即()min 22x xa ->+，求出22x x y -=+的最小值得解.【详解】若命题任意“[]1,3x ∈，22x x a -≤+”为假命题，则命题存在[]1,3x ∈，22x x a ->+为真命题，因为13x ≤≤时，228x ≤≤，令2x t =，则28t ≤≤，则1y t t=+在[]28,上单调递增，所以56528y ≤≤，所以52a >.故答案为：52a >.9．（2024·上海·三模）若m ∈R ，()2,0,1,02x x x f x x ⎧≥⎪=⎨<⎪⎩，则满足()()23f m f m -≥+的m 的最大值为．【答案】12-/0.5-【分析】先判断函数()f x 的奇偶性与单调性，然后利用偶函数的单调性列不等式，最后解不等式即可得到m 的最大值.【详解】当0x >时，0x -<，即()()122x x f x f x -===-，当0x <时，0x ->，即()()122x xx f x f --===，于是，在(),-∞+∞上，()()f x f x -=都成立，即()f x 为偶函数.由指数函数的单调性可知，()f x 在()0,∞+上单调递增，因此，不等式()()23f m f m -≥+等价于23m m -≥+，即()()2223m m -≥+，解得12m ≤-.故m 的最大值为12-.故答案为：12-.10．（2024·广东广州·三模）函数()2,21331,2x a x f x ax x x ⎧≤=⎨-+>⎩，其中0a >且1a ≠，若函数是单调函数，则a的一个可能取值为．【答案】4（答案不唯一）【分析】根据题意，()f x 在R 上单调递增，根据分段函数单调性列式求解.【详解】因为0a >且1a ≠，若函数是单调函数，结合二次函数可知：()f x 在R 上单调递增，21132245a a a a >⎧⎪⎪≤⎨⎪≤+⎪⎩，解得1354a ≤≤.故答案为：4（答案不唯一）.1．（2024·全国·高考真题）已知函数22,0()e ln(1),0x x ax a x f x x x ⎧---<=⎨++≥⎩在R 上单调递增，则a 的取值范围是（）A ．(,0]-∞B ．[1,0]-C ．[1,1]-D ．[0,)+∞【答案】B【分析】根据二次函数的性质和分界点的大小关系即可得到不等式组，解出即可.【详解】因为()f x 在R 上单调递增，且0x ≥时，()()e ln 1xf x x =++单调递增，则需满足()02021e ln1aa -⎧-≥⎪⨯-⎨⎪-≤+⎩，解得10a -≤≤，即a 的范围是[1,0]-.故选：B.2．（2024·天津·高考真题）若0.30.34.24.2 4.2log 0.2a b c -===，，，则a b c ，，的大小关系为（）A ．a b c >>B ．b a c >>C ．c a b >>D ．b c a>>【答案】B【分析】利用指数函数和对数函数的单调性分析判断即可.【详解】因为 4.2x y =在R 上递增，且0.300.3-<<，所以0.300.30 4.2 4.2 4.2-<<<，所以0.30.30 4.21 4.2-<<<，即01a b <<<，因为 4.2log y x =在(0,)+∞上递增，且00.21<<，所以 4.2 4.2log 0.2log 10<=，即0c <，所以b a c >>，故选：B3．（2023·全国·高考真题）已知函数()2(1)e x f x --=．记,,222a f b f c f ⎫⎛⎛⎫===⎪ ⎪⎝⎭⎝⎭⎝⎭，则（）A ．b c a >>B ．b a c>>C ．c b a>>D ．c a b>>【答案】A【分析】利用作差法比较自变量的大小，再根据指数函数的单调性及二次函数的性质判断即可.【详解】令2()(1)g x x =--，则()g x 开口向下，对称轴为1x =，4112⎛--= ⎝⎭，而22491670-=+=>，所以41102222⎛---=-> ⎝⎭11>-由二次函数性质知g g <，4112⎛-= ⎝⎭，而22481682)0-=+-=-=-<，即1122-<-，所以(()22g g >，综上，(((222g g g <<，又e x y =为增函数，故a c b <<，即b c a >>.故选：A.4．（2023·全国·高考真题）已知e ()e 1xax x f x =-是偶函数，则=a （）A ．2-B ．1-C ．1D ．2【答案】D【分析】根据偶函数的定义运算求解.【详解】因为()e e 1x ax x f x =-为偶函数，则()()()()1e e e e 0e 1e 1e 1a x x x x ax ax axx x x f x f x ---⎡⎤--⎣⎦--=-==---，又因为x 不恒为0，可得()1e e 0a x x --=，即()1e e a x x -=，则()1x a x =-，即11a =-，解得2a =.故选：D.5．（2021·全国·高考真题）下列函数中最小值为4的是（）A ．224y x x =++B ．4sin sin y x x=+C ．2y 22x x -=+D ．4ln ln y x x=+【答案】C【分析】根据二次函数的性质可判断A 选项不符合题意，再根据基本不等式“一正二定三相等”，即可得出,B D 不符合题意，C 符合题意．【详解】对于A ，()2224133y x x x =++=++≥，当且仅当=1x -时取等号，所以其最小值为3，A 不符合题意；对于B ，因为0sin 1x <≤，4sin 4sin y x x=+≥=，当且仅当sin 2x =时取等号，等号取不到，所以其最小值不为4，B 不符合题意；对于C ，因为函数定义域为R ，而20x >，2422242x x xx y -=+=+≥，当且仅当22x =，即1x =时取等号，所以其最小值为4，C 符合题意；对于D ，4ln ln y x x=+，函数定义域为()()0,11,+∞ ，而ln x R ∈且ln 0x ≠，如当ln 1x =-，5y =-，D 不符合题意．故选：C ．【点睛】本题解题关键是理解基本不等式的使用条件，明确“一正二定三相等”的意义，再结合有关函数的性质即可解出．6．（上海·高考真题）方程1139x -=的解为.【答案】1-【分析】根据指数幂的运算性质，化简得到121339x --==，得出方程，即可求解.【详解】由121339x --==，可得12x -=-，解得=1x -.故答案为:1-.【点睛】本题主要考查了实数指数幂的运算性质及其应用，其中解答中熟记实数指数幂的运算性质是解答的关键，着重考查运算与求解能力.7．（福建·高考真题）函数()x b f x a -=的图象如图所示，其中a ，b 为常数，则下列结论正确的是（）A ．1,0a b ><B ．1,0a b >>C ．01,0a b <<>D ．01,0a b <<<【答案】D【分析】由函数单调性判断a 与1的大小，再由图象与y 轴的交点位置判断b 的正负.【详解】由图象可知，函数()f x 为减函数，从而有01a <<；法一：由()x b f x a -=图象，函数与y 轴的交点纵坐标(0,1)y ∈，令0x =，得b y a -=，由01b a -<<，即00b a a -<<，解得0b <.法二：函数()f x 图象可看作是由(01)x y a a =<<向左平移得到的，则0b ->，即0b <.故选：D.8．（山东·高考真题）已知函数()y f x =是偶函数，当(0,)x ∈+∞时，()01xy a a =<<，则该函数在(,0)-∞上的图像大致是（）A ．B ．C ．D ．【答案】B【分析】根据偶函数，指数函数的知识确定正确选项.【详解】当(0,)x ∈+∞时，()01xy a a =<<，所以()f x 在()0,∞+上递减，()f x 是偶函数，所以()f x 在(),0∞-上递增.注意到01a =，所以B 选项符合.故选：B。

高中数学知识点完整结构图-掌门1对1 高中数学知识点1集合 函数附：一、函数的定义域的常用求法：1、分式的分母不等于零；2、偶次方根的被开方数大于等于零；3、对数的真数大于零；4、指数函数和对数函数的底数大于零且不等于1；5、三角函数正切函数tan y x =中()2x k k Z ππ≠+∈；余切函数cot y x =中；6、如果函数是由实际意义确定的解析式，应依据自变量的实际意义确定其取值范围。

二、函数的解析式的常用求法：1、定义法；2、换元法；3、待定系数法；4、函数方程法；5、参数法；6、配方法 三、函数的值域的常用求法：1、换元法；2、配方法；3、判别式法；4、几何法；5、不等式法；6、单调性法；7、直接法 四、函数的最值的常用求法：1、配方法；2、换元法；3、不等式法；4、几何法；5、单调性法 五、函数单调性的常用结论：1、若(),()f x g x 均为某区间上的增（减）函数，则()()f x g x +在这个区间上也为增（减）函数2、若()f x 为增（减）函数，则()f x -为减（增）函数3、若()f x 与()g x 的单调性相同，则[()]y f g x =是增函数；若()f x 与()g x 的单调性不同，则[()]y f g x =是减函数。

4、奇函数在对称区间上的单调性相同，偶函数在对称区间上的单调性相反。

5、常用函数的单调性解答：比较大小、求值域、求最值、解不等式、证不等式、作函数图象。

六、函数奇偶性的常用结论：1、如果一个奇函数在0x =处有定义，则(0)0f =，如果一个函数()y f x =既是奇函数又是偶函数，则()0f x =（反之不成立）2、两个奇（偶）函数之和（差）为奇（偶）函数；之积（商）为偶函数。

3、一个奇函数与一个偶函数的积（商）为奇函数。

4、两个函数()y f u =和()u g x =复合而成的函数，只要其中有一个是偶函数，那么该复合函数就是偶函数；当两个函数都是奇函数时，该复合函数是奇函数。

高一数学前五章知识点总结一、函数与方程1. 函数的概念函数是一种特殊的关系，每一个自变量对应一个唯一的因变量。

2. 一次函数与二次函数一次函数的数学表示形式为y = kx + b，其中k为斜率，b为截距。

二次函数的数学表示形式为y = ax² + bx + c，其中a、b、c为常数，a ≠ 0。

3. 指数函数与对数函数指数函数的数学表示形式为y = aˣ，其中a为底数，x为指数。

对数函数是指数函数的逆运算，数学表示形式为y = logₐx，其中a为底数，x为真数。

4. 不等式不等式是数学中用来表达大小关系的符号，常见的不等式符号有大于(>)、小于(<)、大于等于(≥)、小于等于(≤)。

5. 一元二次方程一元二次方程的一般形式为ax² + bx + c = 0，其中a、b、c为已知常数，a ≠ 0。

二、平面几何1. 三角形的性质三角形是由三条边和三个内角组成的图形，根据边长和角度的不同，可以分为等边三角形、等腰三角形、直角三角形等。

2. 相似三角形相似三角形是指对应角相等，对应边成比例的三角形。

3. 圆的性质圆是由一个固定点（圆心）和到该固定点距离相等的所有点组成的图形。

4. 平行线与垂直线平行线是在同一个平面上且不相交的两条直线，垂直线是与平行线相交且互相垂直的直线。

5. 三角函数三角函数包括正弦函数、余弦函数和正切函数等，可用于计算三角形内角的关系。

三、概率论与统计1. 事件与概率事件是指在一次试验中可能发生的结果，概率是指事件发生的可能性大小。

2. 组合与排列组合是指从n个不同元素中取出r个元素进行组合的方法数，排列是指将n个不同元素进行全排列的方法数。

3. 抽样与抽样分布抽样是指从总体中选取一部分样本进行调查，抽样分布是指在同样的条件下重复抽取样本，所得到的统计量的分布。

四、空间几何与立体几何1. 空间几何空间几何是研究三维空间内点、直线、平面、角等几何元素的性质和关系。