Gauss-Seidel迭代法求解线性方程组
- 格式:docx
- 大小:139.44 KB
- 文档页数:6

线性方程组的迭代解法(Jacobi迭代法Gauss-Seidel迭按照算法(Jacobi迭代法)编写Matlab程序(Jacobi.m) function [x, k, index]=Jacobi(A, b, ep, it_max)% 求解线性方程组的Jacobi迭代法,其中% A --- 方程组的系数矩阵% b --- 方程组的右端项% ep --- 精度要求。
省缺为1e-5% it_max --- 最大迭代次数,省缺为100% x --- 方程组的解% k --- 迭代次数% index --- index=1表示迭代收敛到指定要求;% index=0表示迭代失败if nargin <4 it_max=100; endif nargin <3 ep=1e-5; endn=length(A); k=0;x=zeros(n,1); y=zeros(n,1); index=1;while 1for i=1:ny(i)=b(i);for j=1:nif j~=iy(i)=y(i)-A(i,j)*x(j);endendif abs(A(i,i))<1e-10 | k==it_maxindex=0; return;endy(i)=y(i)/A(i,i);endif norm(y-x,inf)<epbreak;endx=y; k=k+1;end用Jacobi迭代法求方程组的解。
输入:A=[4 3 0;3 3 -1;0 -1 4];b=[24;30;-24];[x, k, index]=Jacobi(A, b, 1e-5, 100)输出:x =-2.999811.9987-3.0001k =100index =2. 熟悉Gauss-Seidel迭代法,并编写Matlab程序function[v,sN,vChain]=gaussSeidel(A,b,x0,errorBound,maxSp) %Gauss-Seidel迭代法求解线性方程组%A-系数矩阵 b-右端向量 x0-初始迭代点 errorBound-近似精度maxSp-最大迭代次数%v-近似解 sN-迭代次数 vChain-迭代过程的所有值step=0;error=inf;s=size(A);D=zeros(s(1));vChain=zeros(15,3);%最多能记录15次迭代次数k=1;fx0=x0;for i=1:s(1)D(i,i)=A(i,i);end;L=-tril(A,-1);U=-triu(A,1);while error>=errorBound & step<maxspx0=inv(D)*(L+U)*x0+inv(D)*b;vChain(k,:)=x0';k=k+1;error=norm(x0-fx0);fx0=x0;step=step+1;endv=x0;sN=step;用Gauss-Seidel迭代法求解上题的线性方程组,取。

Gauss-Seidel迭代法是一种用于求解线性方程组的迭代算法,该算法在科学计算和工程领域被广泛应用。
在使用该算法时,我们需要考虑其收敛性,以确保结果的准确性和可靠性。
下面我们将介绍Gauss-Seidel迭代法收敛判断的相关内容。
1. 收敛性定义在使用迭代法求解线性方程组时,迭代算法的收敛性是一个非常重要的问题。
一个迭代算法如果能够在有限步内得到一个接近于真实解的近似解,就称为收敛。
否则,如果迭代算法无法收敛或者收敛速度非常慢,就需要考虑改进算法或者选择其他更适合的算法。
2. Gauss-Seidel迭代法Gauss-Seidel迭代法是一种逐次逼近法,它通过不断地逼近线性方程组的解来求得近似解。
这种迭代算法的优点是简单易行,适用于各种情况。
然而,它的收敛性需要进行严格的判断。
3. 收敛条件对于Gauss-Seidel迭代法,我们可以使用以下收敛条件来进行判断:a) 对角占优条件:如果线性方程组的系数矩阵是严格对角占优的,那么Gauss-Seidel迭代法一定收敛。
b) 正定条件:如果线性方程组的系数矩阵是正定的,即所有的特征值都是正的,那么Gauss-Seidel迭代法也一定收敛。
c) 非奇异条件:如果线性方程组的系数矩阵是非奇异的,即行列式不为0,那么Gauss-Seidel迭代法也一定收敛。
4. 不收敛的情况尽管Gauss-Seidel迭代法在很多情况下能够收敛,但也存在一些情况下它不收敛的情况。
当线性方程组的系数矩阵不满足对角占优条件、正定条件或者非奇异条件时,Gauss-Seidel迭代法就可能不收敛。
此时,我们需要考虑改进算法或者选择其他更适合的迭代算法。
5. 收敛速度除了考虑Gauss-Seidel迭代法的收敛性外,还需要关注其收敛速度。
一般来说,Gauss-Seidel迭代法的收敛速度相对较快,特别是在满足对角占优条件、正定条件或非奇异条件的情况下。
然而,如果在实际使用中发现收敛速度较慢,也可以考虑使用加速方法如SOR方法等来提高收敛速度。

G a u s s-S e i d e l迭代法-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN数值分析课程论文姓名:学号:Gauss-Seidel迭代法求解线性方程组摘要线性方程组的求解在许多的工程技术中是一个极为常见的问题,对于线性方程组的求解无论从理论上还是实践应用上都已经成熟.对于一般线性方程组的求解有Gauss消元法为基础的直接法,也有迭代法.其中Gauss-Seidel是一个重要的组成部分.鉴于此,本论文细致地研究了用Gauss-Seidel迭代法求解线性方程组.论文的第一部分先介绍了迭代法求解线性方程组的一般模式,并给出这种迭代法的收敛性条件,Gauss-Seidel迭代法求解线性方程组的基本原理.这一部分是Gauss-Seidel迭代法的理论基础.论文的第二部分给出了Gauss-Seidel迭代法的具体操作步骤,以伪代码的形式细致的描绘如何使用Gauss-Seidel迭代法的求解方程组.同时,为了验证算法的有效性,在这一部分,还引入一个简单的算例,用于MATLAB编程发现计算结果完全正确.论文的第三部分给出了关于Gauss-Seidel迭代法的MATLAB程序,用于计算线性方程组.关键词:Gauss-Seidel迭代法,基本原理,算例,MATLAB程序目录1 Gauss-Seidel迭代法的基本理论 (1)1.1线性方程组的迭代法求解 (1)1.2Gauss-Seidel迭代法的原理 (2)2.具体的算例和操作步骤 (3)2.1. Gauss-Seidel迭代法的伪代码 (3)2.2.具体的算例验证算法的有效性 (3)3.MATLAB程序 (4)参考文献 (6)Gauss-Seidel 迭代法求解线性方程组一. Gauss-Seidel 迭代法的基本理论1.1线性方程组的迭代法求解在考虑求解线性方程组Ax=b 时,其中A 为非奇异矩阵.尽管Guass 消元法通过有限次运算可以求解此问题,其对应的计算复杂度为3O(n ).但是对于工程技术中和某些偏微分方程过程中出现的大型稀疏型矩阵利用迭代法可以更快的收敛,找到解.另外一方面,由于迭代法占用的计算机内存少,且便于计算.这两方面的优势促成了迭代法求解线性方程组的研究.关于迭代法的收敛的几个判定条件 1(迭代法基本原理)设有方程组f Bx x +=,对于任意初始向量()0x 及任意f ,解此方程组的迭代法(即()()f Bx x k k +=+1)收敛的充要条件是()1<B ρ.2(迭代法收敛的充分条件)如果方程组f Bx x +=的迭代公式为()()f Bx x k k +=+1(()0x 为任意初始向量),且迭代矩阵的某一种范数1<=q B v ,则:︒1迭代法收敛;︒2()()()v k k vk x x q qx x 11-*--≤-;︒3()()()v kvk x x q q xx 011--≤-*.定理3 如果mn RA ⨯∈为严格对角占优阵或为不可约弱对角占优阵,则对于任意的()0x ,解方程组b Ax =的Jacobi 迭代法,Gauss-Seidel 迭代法均收敛.定理4如果A 为对称正定矩阵,且20<<ω,则解式b Ax =的SOR 方法收敛.1.2Gauss-Seidel 迭代法的原理由Jacobi方法迭代公式()()()()010k k xx B x f +⎧⎪⎨=+⎪⎩初始向量,可知,迭代的每一步计算过程,都是用()k x 的全部分量来计算()1+k x 的所有分量,显然在计算第i 个分量()1+k ix时,已经计算出的最新分量()11+k x ,()12+k x ,…,()11+-k i x 没有被利用.从直观上看,最新计算出的分量可能比旧的分量要好些.因此,对这些最新计算出来的第1+k 次近似()1+k x 的分量()1+k jx 加以利用,就得到所谓解方程组的Gauss-Seidel 迭代法(简称G-S 方法):()()()()()T=002010n x x x x ,,, (初始向量),()()()()n i k x a x a b a x i j n i j k j ij k j ij i iik i,,2,1;,2,1,0111111 ==⎪⎪⎭⎫ ⎝⎛--=∑∑-=+=++或写为()()()()()⎪⎩⎪⎨⎧⎪⎪⎭⎫ ⎝⎛--=∆==∆+=∑∑-==++.1,,,2,1;,2,1,01111i j ni j k j ij k iij i ii i i k i k i x a x a b a x n i k x x x上面第2个式子利用了最新计算出的分量()11+k x ,第i 个式子利用了计算出的最新分量()()1,,2,11-=+i j x k j .还可写成矩阵形式()()()()()()k k k k k Ux b x L D Ux Lx b Dx+=-++=+++111,,若设()1--L D 存在,则()()()()b L D Ux L D x k k 111--+-+-=, 于是Gauss-Seidel 迭代公式的矩阵形式为()()f Gx x k k +=+1,()6.2.8 其中 ()U L D G 1--=,()b L D f 1--=.由此可以看出,应用Gauss-Seidel 迭代法解式b Ax =,就是对方程组f Gx x +=应用迭代法.G 称为解式的Gauss-Seidel 迭代法的迭代矩阵.Gauss-Seidel 迭代法的一个明显优点是,在用计算机计算时,只需一组工作单元,以便存放近似解.由式可以看出,每迭代一步只需计算一次矩阵与向量的乘法.二.具体的算例和操作步骤2.1. Gauss-Seidel 迭代法的伪代码 1.输入问题的参数A,b 2.分解A 为D,L,U.3.计算迭代方程G ,f.4.开始迭代,随机设定一个初值.5.以迭代方程更新x 的值.6.如果到达迭代次数,则进入步骤7;否则,回到步骤5.7.输出x ,结束.2.2.具体的算例验证算法的有效性 求解如下的线性方程组1231231238-3+2=204+11-=336+3+12=36x x x x x x x x x ⎧⎪⎨⎪⎩ 这个方程的真实解为(3,2,1). 程序运行结果: 情况1:输入GS (A,b ) GS(A,b)xhis =0 0 0 2.5000 2.0909 1.2273 2.9773 2.0289 1.0041 3.0098 1.9968 0.9959 2.9998 1.9997 1.0002 2.9998 2.0001 1.0001 3.0000 2.0000 1.0000 3.0000 2.0000 1.0000 3.0000 2.0000 1.0000 3.0000 2.0000 1.0000 3.0000 2.0000 1.0000 ans = 3.0000 2.00001.00000.51.5解的迭代情况图一。
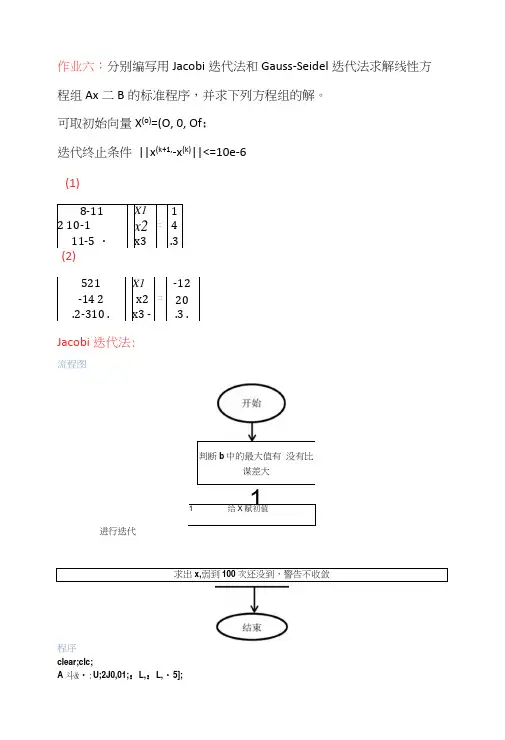
作业六:分别编写用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组Ax二B的标准程序,并求下列方程组的解。
可取初始向量X(o)=(O, 0, Of;迭代终止条件||x(k+1,-x(k)||<=10e-6(1)」521X1-12-14 2x2二20.2-310 .x3 -.3 .Jacobi迭代法:流程图进行迭代程序clear;clc;A 斗&•:U;2J0,01;:L,:L,・5];e=le-6;x0=[0;0;0]1; n=length(A); x=zeros(n/l);k=0;r=max(abs(b));while r>efor i=l:nd=A(iJ);if abs(d)<ewaming('矩阵A输入有误'); return; endsum=0;forj=l:nif j"=isum=sum+A(iJ)*xO(j);endendxl(i)=(b(i)-sum)/A(iJ);endk=k+l;r=max(abs(xl-xO));xO=xl;fprintff第%(1 次迭代:fprintf('\n与上次计算结果的距离56f \n',r) disp(xl); if k>100warningf 不收敛,);endendx=xO;程序结果(1)第1次迭代;与上次计算结果的3^:0.6000000. 1250 0.4000 -0. 6000第2次迭代;与上次计算结果的距誇:0. 1250000.2500 0.4350 -0. 4950第3次迭代;与上次计茸结果的距^:0. 0355000.2412 0.3995 -0. 4630与上次计算结果的距S:0. 0088500.2328 0. 3981 -0. 4718第5次迭代;与上次计算结果的3^:0.0025720.2337 0.4006 -0. 4738策6次迭代:与上次计算结果的距^:0. 0006990.2343 0.4006 -0.4731第:次迭代:与上次计算结果的距离;0. 00Q1840.2342 0.4005 -0.4730第8次迭代;勻上次计算结果的距离:0. 0000540.2342 0.4005 -0.4731第9次迭代:与上次计算结果的距离:0. 0000130.2342 0.4005 -0.4731第10次迭代:与上次计算结果的距离:0. 0000040.2342 0.4005 -0. 4731第11次迭代;与上次计算结果的距离;0・0000010.2342 0.4005 -0.4731(2)第i次迭代:与上次计算结果的距离:5. 000000 -2.4000 5.0000 0.3000第2次迭代:与上次计尊结果的3^:2. 060000 一4・4600 4.2500 2.2800第3次迭代:与上次计算结果的距离:1・505000 -4.5560 2.7450 2.4670第4次迭代:与上次计算结累的距离;0.564600 -3.9914 2.6275 2.0347第5次迭代;与上次计算结果的距离:0・357300 -3. 8579 2.9848 1.8865第6次迭代:与上次计算结果的距高:0・1 13286 -3.9712 3.0922 1.9670第13次迭代:与上次计算结果的距^:0. 001023 -4.0002 2.99922.0002第14次迭代:与上次计算结果的距离;0・000626 -3.9997 2.99981.9998第15次迭代:与上次计算结果的距离:0. 000341 -3.9999 3.00021.9999第16次迭代:与上次计茸结果的距离:0. 000155 -4.0000 3.00012.0000第订次迭代;与上次计算结果的距离:o. 000106 ・4.0000 3.00002.0000第18次迭代:与上次计算结果的距离:0. 000041 -4.0000 3.00032.0000第;次迭代:与上次计算结果的距离:0. 068570 -4. 0303 3.0237 2.0219第8次迭代:与上次计算结果的匪离;0. 042216 -4.0139 2.9815 2.0132第9次迭代:与上次计算结果的距离:0. 018637 -3.9952 2.9900 1.9972第10次迭代:与上次计算结果的范离:0. 0L2637 -3. 9954 3.0026 1.9960第口次迭代:与上次计算结果的徒离:0. 004819 -4.0002 3. 0031 1.9999第12次迭代;与上次计聲结果的施禹:0. 003121 -£ 0012 3.0000 2.0010第19次迭代:与上次计算结果的昵离:3. 000027 -4.0000 3.0000 2.0000第如次迭代;与上次i+算结果的柜胡:3. 000009 -4.0000 3.0000 2.0000第21次迭代:与上次i+算结果的距韶:1 000006 -4.0000 3.0000 2.0000錮22次送代:与上次计算结果的捱离:1 000003 ・4.0000 3.0000 2.0000第23次迭代:与上次计算结果的距离:3. OOOOOL-4.0000 3.0000 2.0000籠加次逑代:与上次计算结果的拒离:3. OOOOOL -4.0000 3.0000 2.0000Gauss-Seidel 迭代法:SJ?clear;clc;%A=[8r14;240,01;14z-5];%b=[l;4;3];A=[5,24;-l/4,2;2,-340];b=[-12;20;3];m=size(A);if m(l)r'=m(2) errorC矩阵A不是方阵J;endn=length(b);%初始化N=0,%迭代次数L=zeros(n)^6分解A=D+L+U,D是对角阵,L是下三角阵,U是上三角阵U=zeros(n);D=zeros(n);G=zeros(n)^6G=-inv(D+L)*Ud=zeros(n/l)56d=inv(D+L)w,bx=zeros(n4);for i=l:n%初始化L和Uforj=l:nif i<jL(iJ)=A(iJ);endif i>jU(iJ)=A(iJ);endendendfori=l:n%初始化 DD(iJ)=A(iJ);endG=-inv(D+L)*U^6初始化Gd=(D+L)\b56初始化 d%迭代开始xl=x;x2=G*x+d;while norm(x2-xljnf)>10A(-6)xl=x2; x2=G*x2+d;N=NU; end x=x2; 程序结果(1) (2)0. 23420. 4005-0.4731-4.00003.00002.0000。

一. 问题描述用Gauss-Seidel 迭代法求解线性方程组由Jacobi 迭代法中,每一次的迭代只用到前一次的迭代值。
使用了两倍的存储空间,浪费了存储空间。
若每一次迭代充分利用当前最新的迭代值,即在计算第i 个分量)1(+k ix 时,用最新分量)1(1+k x ,⋅⋅⋅+)1(2k x )1(1-+k i x 代替旧分量)(1k x ,⋅⋅⋅)(2k x )(1-k i x ,可以起到节省存储空间的作用。
这样就得到所谓解方程组的Gauss-Seidel 迭代法。
二. 算法设计将A 分解成U D L A --=,则b x =A 等价于b x =--U)D (L 则Gauss-Seidel 迭代过程)()1()1(k k k Ux Lx b Dx ++=++故)()1()(k k Ux b x L D +=-+若设1)(--L D 存在,则b L D Ux L D x k k 1)(1)1()()(--+-+-=令b L D f U L D G 11)()(---=-=,则Gauss-Seidel 迭代公式的矩阵形式为f Gx x k k +=+)()1(其迭代格式为Tn x x x x )()0()0(2)0(1)0(,,,⋅⋅⋅= (初始向量),)(11111)()1()1(∑∑-=-+=++--=i j i i j k j ijk j ij i ii i ix ax a b a x)210i 210(n k ⋅⋅⋅=⋅⋅⋅=,,,;,,,或者⎪⎩⎪⎨⎧--=⋅⋅⋅=⋅⋅⋅==∆+=∑∑-=-+=+++)(1)210i 210(1111)()1()1()()1(i j i i j k j ij k j ij i ii i i i k i k i x a x a b a x n k k x x x ,,,;,,,三. 程序框图四. 结果显示TestBench利用Gauss-Seidel 迭代法求解下列方程组⎪⎩⎪⎨⎧=+-=++--=++3103220241225321321321x x x x x x x x x , 其中取→=1)0(x 。

用高斯赛德尔迭代法解方程组
高斯-赛德尔迭代(gauss–seidel method)是数值线性代数中的一个迭代法,可用
来求出线性方程组解的近似值。
该方法以卡尔·弗里德里希·高斯和路德维希·赛德尔命名。
同雅可比法一样,高斯-赛德尔迭代是基于矩阵分解原理。
在数值线性代数中,gauss-seidel方法也称作liebmann方法或已连续加速度方法,
就是用作解线性方程组的运算方法。
它以德国数学家卡尔·弗里德里希·高斯(carl friedrich gauss)和菲利普·路德维希·冯·塞德尔(philipp ludwig von seidel)命名,与雅基数排序方法相近。
高斯-赛德尔迭代法是解线性方程组的常用迭代法之一,设线性方程组为a1x1 +a2x2 +..+ cintn =b.s
(i= 1,2,,n),
高斯赛德尔迭代法的迭代公式,虽然它可以应用于对角线上具有非零元素的任何矩阵,但只能在矩阵是对角线主导的或对称的和正定的情况下,保证收敛。
在年,只在高斯给
他的学生gerling的私人信中提到。
年之前由塞德尔自行出版。

【题目】:Gauss-Seidel迭代法及Matlab代码实例【内容】:1. Gauss-Seidel迭代法介绍Gauss-Seidel迭代法是一种用于解线性方程组的数值方法,基于逐次逼近的思想,通过不断迭代逼近线性方程组的解。
该方法通常用于求解大型稀疏线性方程组,其收敛速度相对较快。
2. 迭代公式推导假设有如下线性方程组:$$Ax=b$$其中A为系数矩阵,b为常数向量,x为未知向量。
Gauss-Seidel迭代法的迭代公式为:$$x^{(k+1)}=(D+L)^{-1}(b- Ux^{(k)})$$其中,D为A的对角矩阵,L为A的严格下三角矩阵,U为A的严格上三角矩阵,k为迭代次数。
3. Matlab代码实现下面给出Gauss-Seidel迭代法的Matlab代码实例:```matlabfunction [x, k] = gaussSeidel(A, b, x0, tol, maxIter)A: 系数矩阵b: 常数向量x0: 初始解向量tol: 容差maxIter: 最大迭代次数x: 解向量k: 迭代次数n = length(b);x = x0;k = 0;while k < maxIterx_old = x;for i = 1:nx(i) = (b(i) - A(i,1:i-1)*x(1:i-1) - A(i,i+1:n)*x_old(i+1:n)) / A(i,i); endif norm(x - x_old, inf) < tolreturnendk = k + 1;enddisp('迭代次数达到最大值,未达到容差要求'); end```4. 应用实例假设有如下线性方程组:$$\begin{cases}2x_1 - x_2 + x_3 = 5\\-x_1 + 2x_2 - x_3 = -2\\x_1 - x_2 + 2x_3 = 6\end{cases}$$系数矩阵A为:$$\begin{bmatrix}2 -1 1\\-1 2 -1\\1 -1 2\end{bmatrix}$$常数向量b为:$$\begin{bmatrix}5\\-2\\6\end{bmatrix}$$取初始解向量x0为:$$\begin{bmatrix}0\\0\\\end{bmatrix}$$容差tol为1e-6,最大迭代次数maxIter为100。

分别用 jacobi 迭代法和 gauss-seidel 迭代法,求解方程组【jacobi 迭代法和 gauss-seidel 迭代法分别应用于方程组的求解】1. 引言在数学领域中,方程组的求解一直是一个重要的课题。
为了解决复杂的线性方程组,人们提出了各种迭代方法,其中 jacobi 迭代法和gauss-seidel 迭代法是两种常见的方法。
本文将探讨这两种迭代方法在求解方程组中的应用。
2. jacobi 迭代法的原理和应用jacobi 迭代法是一种基于逐次逼近的迭代方法。
对于线性方程组AX=B,其中 A 是系数矩阵,X 是未知数向量,B 是已知向量。
我们可以通过以下公式进行逐次逼近:X(k+1) = D^(-1)*(B - (L+U)X(k))其中,D、L、U 分别是 A 的对角线、下三角和上三角矩阵。
jacobi 迭代法的优点在于易于理解和实现,但在收敛速度上较慢,需要进行多次迭代才能得到精确解。
在实际应用中,需要根据实际情况选择合适的迭代次数。
3. gauss-seidel 迭代法的原理和应用与 jacobi 迭代法类似,gauss-seidel 迭代法也是一种基于逐次逼近的迭代方法。
不同之处在于,gauss-seidel 迭代法在计算 X(k+1) 时利用了已经得到的 X(k) 的信息,即:X(k+1)_i = (B_i - Σ(A_ij*X(k+1)_j,j≠i))/A_ii这种方式使得 gauss-seidel 迭代法的收敛速度较快,通常比 jacobi 迭代法更快,尤其是对于对角占优的方程组。
4. 分别用 jacobi 迭代法和 gauss-seidel 迭代法求解方程组为了更具体地说明 jacobi 迭代法和 gauss-seidel 迭代法的应用,我们分别用这两种方法来求解以下方程组:2x1 + x2 = 9x1 + 3x2 = 11我们将该方程组写成矩阵形式 AX=B:|2 1| |x1| |9||1 3| * |x2| = |11|我们根据 jacobi 迭代法和 gauss-seidel 迭代法的原理,依次进行迭代计算,直到满足收敛条件。

Gauss-Seidel 迭代法求解方程组设方程组Ax=b 中的A 是n n ⨯阶矩阵,x 和b 都是n 维列向量。
若系数矩阵A 为非奇异的且0,1,2,ii a i n ≠= ,将A 分解为:A=D+L+U其中1122(,,,)nn D diag a a a =21120000000n n a L a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ , 1212000000n n a a a U ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦将方程组1,1,2,,nij ji j a xb i n ===∑分析雅克比方法的迭代过程我们发现,在计算(1)k i x +时,虽然(1)(1)(1)121,,k k k i x x x +++- 已经全部计算出来,但是(1)k i x +计算还是用()()()121,,k k k i x x x - 而未用(1)(1,2,,1)k j x j i +=- 有理由认为(1)k jx +比()k jx 个接近精确值的相应分量,因此我们计算(1)k i x +时,用(1)k jx +代替()(1,2,,1)k j x j i =- ,即1(1)(1)()111(),1,2,,i nk k k ii ij j ij j j j i ii x b a x a x i n a -++==+=--=∑∑ 简记为:(1)()k k x Bx f +=+其中 B =- (D +L)1-U, f= (D +L)1-b我们称()x Bx f ϕ=+为迭代函数,任取初始向量(0)x x =,按照(1)()k k xBx f +=+即1(1)(1)()111(),1,2,,i nk k k ii ij j ij j j j i ii x b a x a x i n a -++==+=--=∑∑ 形式,称这种迭代方法为 Gauss -Seidel 迭代法。
Gauss -Seidel 迭代法算法简单描述:(0)(0)(0)(0)12(,,,),T n x x x x = ( 向量初始)For 0,1,2,k =For 1,2,,k n =1(1)(1)()111(),1,2,,i nk k k ii ij j ij j j j i ii x b a x a x i n a -++==+=--=∑∑ 如果()(1)k k x xε--≤ 停止,否则Next k 用Gauss -Seidel 迭代法求解方程组实例为:1231212978798x x x x x x x --=⎧⎪-+=⎨⎪-+=⎩,的解,初始向量(0)(0,0,0),T x = 解 由公式知,Gauss -Seidel 迭代法为:(1)()()123(1)(1)21(1)(1)311(7)91(7)81(8)9k k k k k k k x x x x x x x +++++⎧=++⎪⎪⎪=+⎨⎪⎪=+⎪⎩由初始向量(0)(0,0,0),T x =迭代可得(1)(0.7778,0.9722,0.9753),T x =(2)(0.9942,0.9993,0.9994),T x =(3)(0.9999,0.9999,0.9999),T x =(4)(1,1,1),T x =(5)(1,1,1),T x =所以方程组的解为(1,1,1)T x =。

Gauss-Seidel迭代法是解线性方程组的一种常用方法,它通过不断迭代更新解向量,逐步逼近方程组的精确解。
在实际应用中,我们往往需要判断迭代法是否收敛,以保证计算结果的准确性和可靠性。
本文将以matlab为例,介绍如何利用数值计算软件对Gauss-Seidel迭代法的收敛性进行判断,并对其进行详细分析和讨论。
一、Gauss-Seidel迭代法简介Gauss-Seidel迭代法是一种逐次迭代的线性代数方法,用于求解线性方程组Ax=b的解向量x。
它的迭代更新公式为:xn+1i=1/aii(bi-∑(j=1,j≠i)n aijxj)其中,i=1,2,...,n;n为方程组的阶数;aii为系数矩阵A的第i行第i 列元素;bi是方程组右端的常数;xj为解向量x的第j个分量;∑(j=1,j≠i)n aijxj为除去第i个分量的求和。
通过不断迭代更新解向量的各个分量,最终可以逼近线性方程组的解。
二、Gauss-Seidel迭代法的收敛性判断针对Gauss-Seidel迭代法的收敛性判断,我们可以利用数值计算软件matlab进行分析。
在matlab中,可以使用以下命令进行Gauss-Seidel迭代法的计算:function[x,k]=GaussSeidel(A,b,x0,tol,maxk)n=length(b);x=x0;for k=1:maxkx0=x;for i=1:nx(i)=1/A(i,i)*(b(i)-A(i,:)*x+x(i));endif norm(x-x0,inf)<tolreturn;endenderror('达到最大迭代次数,方法未收敛');end在上述matlab代码中,A为系数矩阵,b为右端常数向量,x0为初始解向量,tol为迭代精度,maxk为最大迭代次数。
在函数中,我们设定了最大迭代次数以及迭代精度的条件,当满足这些条件时,算法将停止迭代。
三、Gauss-Seidel迭代法的收敛性分析Gauss-Seidel迭代法的收敛性与系数矩阵A的性质有关。

浅析Gauss-Seidel 迭代在方程迭代计算中的应用摘要:科学研究与生产实践中许多问题都可归结为方程组的求解,对于方程组的求解,主要有直接法求解和迭代法求解,我们通常用的迭代法有Jacobi,Gauss-Seidel 迭代法。
本文主要针对Gauss-Seidel 迭代法在三类方程组迭代计算中的应用进行研究。
一、Gauss-Seidel 迭代法在求解大型稀疏线性方程组中的应用。
Gauss-Seidel 迭代法充分利用矩阵的稀疏性去解大型稀疏线性代数方程组。
本文通过实际算例验证并分析了它的计算速度和效率。
二、Gauss-Seidel 迭代法在求解H-矩阵线性方程组中的应用。
本文针对系数矩阵 A 为H -矩阵, 为线性方程组 Ax =b 引入了两种形式的预处理矩阵 I +S 和 I +S , 给出了相应的预处理 Gauss-Seidel 方法。
三、异步并行非线性对称Gauss-Seidel 迭代法在求解特殊非线性方程组的应用。
利用非线性方程组的特殊结构,建立了一类并行非线性 Gauss-Siedel 型迭代算法。
关键词:Gauss-Seidel 迭代法,线性方程组,H -矩阵,非线性方程组科学研究与生产实践中许多问题都可归结为线性方程组的求解,高效求解线性方程组成为许多科学与工程计算的核心。
解线性方程组的传统方法是利用高斯消元法或矩阵的三角分解法等直接求解,虽然传统方法具有理论上直接得到真解的优点,但当系数矩阵条件数很大时,存在严重的稳定性问题。
同时,当系数矩阵的非零元结构不规则或带宽较大时,其计算量与存储量也十分地大。
与直接法相比,迭代法只需存储原系数矩阵,对应于预处理的几个辅助矩阵和少量的几个向量,且迭代法中除求解辅助线性方程组外,其余的计算主要是系数矩阵与向量的乘积,从而能充分利用系数矩阵的特性来减少计算量。
而且随着计算机技术的发展,计算机的存储量日益增大,计算速度也迅速提高,线性方程组的迭代求解在科学与工程计算中也起着越来越重要的作用。
Gauss Seidel 迭代法:Gauss Seidel 迭代法是逐个分量进行计算的一种方法,考虑线性代数方程组Ax=b 的分量法表示i j j ij b x a==∑n 1 , i=1,2,···,n对于给定的初值)0(x ,Ga迭代法如下: Gauss Seidel 迭代算法:· k=0· 11)(11)1(1/)2(x a x a b n j k j j k ∑=-==+ ·22)(2)1(1212)1(2/)3(x a x a x a b n j k j j k k ∑=--==++· …·1,1)(,12)1(,11)1(1-n /)1(x ----+--+-=-=∑=n n k n n n n j k j j n n k a x a x a b ·nn n j k j nj n k a x a b /)(x 11)1()1(n ∑-++-=== ·2)0()1(2)()1(x x x x k k k -<-++ε停止,否则k=k+1从Gauss Seidel 迭代算法的计算过程可以发现,每计算一个新的分量都需要前面所有新计算出来的分量的结果,这是一个严格的串行过程。
那么,如何设计一个并行计算的方法呢?记)0(1s j n i j ij i x a ∑+== ,i=1,2, …,n-1,s n =0。
并行计算方法如下:并行Gauss Seidel 迭代算法:k=0for i=1,n do0,/)(x )1(=-=+i ii i i k i s a s bfor j=1,n,j ≠i do)1(s ++=k i ji j j x a send{for} end{for}2)0()1(2)()1(x x x x k k k -<-++ε停止,否则k=k+1在并行Gauss Seidel 迭代算法中,每次并行计算j s ,之后可以并行计算截止条件是否满足。
Gauss—Seidel迭代法求解线性方程组的并行化研究作者:米瑞琪于朋来源:《科技视界》2016年第25期【摘要】Gauss-Seidel迭代法在工程计算中具有广泛应用。
高维矩阵对线性方程组的求解效率提出了新的要求。
本文提出了两种模式下的Gauss-Seidel并行计算方法,并对比了在不同矩阵维数下的加速效率,得到了具有较高加速比的并行迭代方法。
【关键词】Gauss-Seidel;迭代法;并行;MPI;矩阵运算1 问题背景与提出在实际工程应用中经常需要用到求解维数较高的线性代数方程组,对于线性代数方程组的求解方法可以分成两类:直接法和迭代法,其中直接法得到的是方程组的真解,其求解过程为通过有限步四则运算,常用的实现方式是Gauss消去方法和矩阵的三角分解方法,这种计算方式在求解过程中会产生大量的非零元素,存储量和计算量均比较大,因此常用于求解低阶、稠密线性方程组。
对于高维线性方程组,可以采用并行运算的方式进一步提高计算效率,Gauss-Seidel迭代法具有收敛速度快、计算稳定性好等优点,是求解高维线性方程组的常用方法,因此本文将对Gauss-Seidel迭代法的并行化进行研究,期望获取较高的运行效率和加速比。
2 Gauss-Seidel迭代法的并行算法描述任务分配模式一:连续等分矩阵法在《并行算法的设计与分析》一书中给出了一种矩阵分配的算法,设矩阵的阶为N,采用m个线程进行计算,则将矩阵等分成m块,每一块分到的任务量为N/m,每一个线程计算完自己的分量之后立刻向其他的线程进行广播。
由于Gauss-Seidel迭代法中,对于右端项的计算和中间项的计算是不需要用到下一次迭代值的,因此在这一阶段各个线程工作量相同,同时完成,问题的关键在于首项的计算,顺序等分矩阵时,以四个线程为例,在计算左端项的时候,各个线程的工作次序如下图所示。
其中不同的颜色代表不同线程的任务,每个线程依次计算分给自己的一个子块,每计算完一个分量后立刻沿上方箭头所指方向进行广播。
数值分析5-⽤Jacobi迭代法和Gauss-Seidel迭代法求解线性⽅程组作业六:分别编写⽤Jacobi迭代法和Gauss-Seidel迭代法求解线性⽅程组Ax⼆B的标准程序,并求下列⽅程组的解。
可取初始向量X(o)=(O, 0, Of;迭代终⽌条件||x(k+1,-x(k)||<=10e-6(1)」521X1-12-14 2x2⼆20.2-310 .x3 -.3 .Jacobi迭代法:流程图进⾏迭代程序clear;clc;A ⽃&?:U;2J0,01;:L,:L,?5];e=le-6;x0=[0;0;0]1; n=length(A); x=zeros(n/l);k=0;r=max(abs(b));while r>efor i=l:nd=A(iJ);if abs(d)waming('矩阵A输⼊有误'); return; endsum=0;forj=l:nif j"=isum=sum+A(iJ)*xO(j);endendxl(i)=(b(i)-sum)/A(iJ);endk=k+l;r=max(abs(xl-xO));xO=xl;fprintff第%(1 次迭代:fprintf('\n与上次计算结果的距离56f \n',r) disp(xl); if k>100warningf 不收敛,);endendx=xO;程序结果(1)第1次迭代;与上次计算结果的3^:0.6000000. 1250 0.4000 -0. 6000第2次迭代;与上次计算结果的距誇:0. 1250000.2500 0.4350 -0. 4950第3次迭代;与上次计茸结果的距^:0. 0355000.2412 0.3995 -0. 4630与上次计算结果的距S:0. 0088500.2328 0. 3981 -0. 4718第5次迭代;与上次计算结果的3^:0.0025720.2337 0.4006 -0. 4738策6次迭代:与上次计算结果的距^:0. 0006990.2343 0.4006 -0.4731第:次迭代:与上次计算结果的距离;0. 00Q1840.2342 0.4005 -0.4730第8次迭代;勻上次计算结果的距离:0. 0000540.2342 0.4005 -0.4731第9次迭代:与上次计算结果的距离:0. 0000130.2342 0.4005 -0.4731第10次迭代:与上次计算结果的距离:0. 0000040.2342 0.4005 -0. 4731第11次迭代;与上次计算结果的距离;0?0000010.2342 0.4005 -0.4731(2)第i次迭代:与上次计算结果的距离:5. 000000 -2.4000 5.0000 0.3000第2次迭代:与上次计尊结果的3^:2. 060000 ⼀4?4600 4.2500 2.2800第3次迭代:与上次计算结果的距离:1?505000 -4.5560 2.7450 2.4670第4次迭代:与上次计算结累的距离;0.564600 -3.9914 2.6275 2.0347第5次迭代;与上次计算结果的距离:0?357300 -3. 8579 2.9848 1.8865与上次计算结果的距⾼:0?1 13286 -3.9712 3.0922 1.9670第13次迭代:与上次计算结果的距^:0. 001023 -4.0002 2.99922.0002第14次迭代:与上次计算结果的距离;0?000626 -3.9997 2.99981.9998第15次迭代:与上次计算结果的距离:0. 000341 -3.9999 3.00021.9999第16次迭代:与上次计茸结果的距离:0. 000155 -4.0000 3.00012.0000第订次迭代;与上次计算结果的距离:o. 000106 ?4.0000 3.00002.0000第18次迭代:与上次计算结果的距离:0. 000041 -4.0000 3.00032.0000第;次迭代:与上次计算结果的距离:0. 068570 -4. 0303 3.0237 2.0219第8次迭代:与上次计算结果的匪离;0. 042216 -4.0139 2.9815 2.0132第9次迭代:与上次计算结果的距离:0. 018637 -3.9952 2.9900 1.9972第10次迭代:与上次计算结果的范离:0. 0L2637 -3. 9954 3.0026 1.9960第⼝次迭代:与上次计算结果的徒离:0. 004819 -4.0002 3. 0031 1.9999第12次迭代;与上次计聲结果的施禹:0. 003121 -£ 0012 3.0000 2.0010第19次迭代:与上次计算结果的昵离:3. 000027 -4.0000 3.0000 2.0000第如次迭代;与上次i+算结果的柜胡:3. 000009 -4.0000 3.0000 2.0000第21次迭代:与上次i+算结果的距韶:1 000006 -4.0000 3.0000 2.0000錮22次送代:与上次计算结果的捱离:1 000003 ?4.0000 3.0000 2.0000第23次迭代:与上次计算结果的距离:3. OOOOOL-4.0000 3.0000 2.0000籠加次逑代:与上次计算结果的拒离:3. OOOOOL -4.0000 3.0000 2.0000 Gauss-Seidel 迭代法:SJ?%A=[8r14;240,01;14z-5];%b=[l;4;3];A=[5,24;-l/4,2;2,-340];b=[-12;20;3];m=size(A);if m(l)r'=m(2) errorC矩阵A不是⽅阵J;endn=length(b);%初始化N=0,%迭代次数L=zeros(n)^6分解A=D+L+U,D是对⾓阵,L是下三⾓阵,U是上三⾓阵U=zeros(n); D=zeros(n);G=zeros(n)^6G=-inv(D+L)*Ud=zeros(n/l)56d=inv(D+L)w,bx=zeros(n4);for i=l:n%初始化L和Uforj=l:nif iL(iJ)=A(iJ);endif i>jU(iJ)=A(iJ);endendendfori=l:n%初始化 DD(iJ)=A(iJ);endG=-inv(D+L)*U^6初始化Gd=(D+L)\b56初始化 d%迭代开始xl=x;x2=G*x+d;while norm(x2-xljnf)>10A(-6)。
数值分析5-用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组————————————————————————————————作者:————————————————————————————————日期:作业六:分别编写用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组Ax=B的标准程序,并求下列方程组的解。
可取初始向量X(0) =(0,0,0)’;迭代终止条件||x(k+1)-x(k)||<=10e-6(1)[8 −1 12 10 −11 1 −5][x1x2x3]=[143](2)[5 2 1−1 4 22 −3 10][x1x2x3]=[−12203]Jacobi迭代法:流程图开判断b中的最大值有没给x赋初值进行迭代结求出x,弱到100次还程序clear;clc;A=[8,-1,1;2,10,01;1,1,-5];b=[1;4;3];e=1e-6;x0=[0;0;0]';n=length(A);x=zeros(n,1);k=0;r=max(abs(b));while r>efor i=1:nd=A(i,i);if abs(d)<ewarning('矩阵A输入有误');return;endsum=0;for j=1:nif j~=isum=sum+A(i,j)*x0(j);endendx1(i)=(b(i)-sum)/A(i,i);endk=k+1;r=max(abs(x1-x0));x0=x1;fprintf('第%d次迭代:',k)fprintf('\n与上次计算结果的距离:%f \n',r)disp(x1);if k>100warning('不收敛');endendx=x0;程序结果(1)(2)Gauss-Seidel迭代法:程序clear;clc;%A=[8,-1,1;2,10,01;1,1,-5];%b=[1;4;3];A=[5,2,1;-1,4,2;2,-3,10];b=[-12;20;3];m=size(A);if m(1)~=m(2)error('矩阵A不是方阵');endn=length(b);%初始化N=0;%迭代次数L=zeros(n);%分解A=D+L+U,D是对角阵,L是下三角阵,U是上三角阵U=zeros(n);D=zeros(n);G=zeros(n);%G=-inv(D+L)*Ud=zeros(n,1);%d=inv(D+L)*bx=zeros(n,1);for i=1:n%初始化L和Ufor j=1:nif i<jL(i,j)=A(i,j);endif i>jU(i,j)=A(i,j);endendendfor i=1:n%初始化DD(i,i)=A(i,i);endG=-inv(D+L)*U;%初始化Gd=(D+L)\b;%初始化d%迭代开始x1=x;x2=G*x+d;while norm(x2-x1,inf)>10^(-6)x1=x2;x2=G*x2+d;N=N+1;endx=x2;程序结果(1)(2)。
gauss-seidel 迭代法
Gauss-Seidel迭代法是一种基于线性代数的数值计算方法,用于求解线性方程组。
该方法是Jacobi迭代法的改进,其主要思想是根据已知的初始解逐步逼近方程组的解,直到达到所需的精度要求。
具体来说,Gauss-Seidel迭代法将线性方程组的每个未知数的近似值逐个更新,每次更新都使用当前解中已经求出的未知数的最新值。
这种迭代方式可以加速求解过程,特别是对于稀疏的线性方程组,其求解效率更高。
Gauss-Seidel迭代法的收敛性与矩阵的特征值有关,当矩阵的特征值都小于1时,该方法一定收敛。
当矩阵不对称时,我们可以将其转化为对称矩阵再进行迭代,这可以提高方法的稳定性和精度。
总之,Gauss-Seidel迭代法是一种有效的求解线性方程组的方法,其方法简单易懂、易于实现,并且可以应用于各种不同类型的线性方程组。
一. 问题描述
用Gauss-Seidel 迭代法求解线性方程组
由Jacobi 迭代法中,每一次的迭代只用到前一次的迭代值。
使用了两倍的存储空间,浪
费了存储空间。
若每一次迭代充分利用当前最新的迭代值,即在计算第i 个分量)
1(+k i
x 时,
用最新分量)
1(1
+k x ,⋅⋅⋅+)
1(2
k x )
1(1
-+k i x 代替旧分量)
(1
k x ,⋅⋅⋅)
(2
k x )
(1
-k i x ,可以起到节省存储
空间的作用。
这样就得到所谓解方程组的Gauss-Seidel 迭代法。
二. 算法设计
将A 分解成U D L A --=,则b x =A 等价于b x =--U)D (L 则Gauss-Seidel 迭代过程
)
()1()1(k k k Ux Lx b Dx ++=++
故
)()1()(k k Ux b x L D +=-+
若设1
)(--L D 存在,则
b L D Ux L D x k k 1)(1)1()()(--+-+-=
令
b L D f U L D G 11)()(---=-=,
则Gauss-Seidel 迭代公式的矩阵形式为
f Gx x k k +=+)()1(
其迭代格式为
T
n x x x x )
()0()0(2)0(1)0(,,,⋅⋅⋅= (初始向量),
)(1
1
1
1
1
)()1()1(∑∑-=-+=++--=i j i i j k j ij
k j ij i ii i i
x a
x a b a x
)210i 210(n k ⋅⋅⋅=⋅⋅⋅=,,,;,,,
或者
⎪⎩
⎪⎨⎧--=⋅⋅⋅=⋅⋅⋅==∆+=∑∑-=-+=+++)
(1)210i 210(111
1)()
1()1()()1(i j i i j k j ij k j ij i ii i i i k i k i x a x a b a x n k k x x x ,,,;,,,
三. 程序框图
四. 结果显示
TestBench
利用Gauss-Seidel 迭代法求解下列方程组
⎪⎩⎪⎨⎧=+-=++--=++3
1032202412
25321
321321x x x x x x x x x , 其中取→
=1)
0(x 。
运行程序
依次输入:
1.方阵维数2.增广矩阵系数3.初始向量
得到:
迭代12次后算出
x[1] = -4.0
x[2] = 3.0
x[3] = 2.0
五.程序
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#include<math.h>
#define MAX_n 100
#define PRECISION 0.0000001
#define MAX_Number 1000
void VectorInput(float x[],int n) //输入初始向量
{
int i;
for(i=1;i<=n;++i)
{
printf("x[%d]=",i);
scanf("%f",&x[i]);
}
}
void MatrixInput(float A[][MAX_n],int m,int n) //输入增广矩阵
{
int i, j;
printf("\n输入系数矩阵:\n");
for(i=1;i<=m;++i)
{
printf("增广矩阵行数%d : ",i);
for(j=1;j<=n;++j)
scanf("%f",&A[i][j]);
}
}
void VectorOutput(float x[],int n) //输出向量
{
int i;
for(i=1;i<=n;++i)
printf("\nx[%d]=%f",i,x[i]);
}
int IsSatisfyPricision(float x1[],float x2[],int n) //判断是否在规定精度内{
int i;
for(i=1;i<=n;++i)
if(fabs(x1[i]-x2[i])>PRECISION) return 1;
return 0;
}
int Jacobi_(float A[][MAX_n],float x[],int n) //具体计算
{
float x_former[MAX_n];
int i,j,k;
printf("\n初始向量x0:\n");
VectorInput(x,n);
k=0;
do{
for(i=1;i<=n;++i)
{
printf("\nx[%d]=%f",i,x[i]);
x_former[i]=x[i];
}
printf("\n");
for(i=1;i<=n;++i)
{
x[i]=A[i][n+1];
for(j=1;j<=n;++j)
if(j!=i) x[i]-=A[i][j]*x[j]; if(fabs(A[i][i])>PRECISION)
x[i]/=A[i][i];
else
return 1;
}
++k;
}while(IsSatisfyPricision(x,x_former,n) && k<MAX_Number);
if(k>=MAX_Number)
return 1;
else
{
printf("\nGauss-Seidel迭代次数为%d 次",k);
return 0;
}
}
int main() //主函数
{
int n;
float A[MAX_n][MAX_n],x[MAX_n];
printf("\n方阵维数n=");
scanf("%d",&n);
if(n>=MAX_n-1)
{
printf("\n\007n must <%d!",MAX_n);
exit(0);
}
MatrixInput(A,n,n+1);
if(Jacobi_(A,x,n))
printf("\nGauss-Seidel迭代失败!");
else
{
printf("\n结果:");
VectorOutput(x,n);
}
printf("\n\n\007Press any key to quit!\n");
getch();
}。