圆周运动高考题含答案推荐文档

微专题—圆周运动习题选编一、单项选择题1．如图所示，B和C是一组塔轮，即B和C半径不同，但固定在同一转动轴上，其半径之比为R B∶R C＝3∶2．A 轮的半径大小与C轮相同，它与B轮紧靠在一起，当A轮绕其中心的竖直轴转动时，由于摩擦作用，B轮也随之无滑动地转动起来，a、b、c分别为三轮边缘的三个点，则a、b、c三点在运动过程中（）A．线速度大小之比为3∶2∶2B．角速度之比为3∶3∶2C．转速之比为2∶3∶2D．向心加速度大小之比为9∶6∶42．A、B两艘快艇在湖面上做匀速圆周运动（如图），在相同时间内，它们通过的路程之比是4：3，运动方向改变的角度之比是3：2，则它们（）A．线速度大小之比为4：3B．角速度大小之比为3：4C．圆周运动的半径之比为2：1D．向心加速度大小之比为1：23．如图所示，一位同学玩飞镖游戏．圆盘最上端有一P点，飞镖抛出时与P等高，且距离P点为L.当飞镖以初速度v0垂直盘面瞄准P点抛出的同时，圆盘以经过盘心O点的水平轴在竖直平面内匀速转动．忽略空气阻力，重力加速度为g，若飞镖恰好击中P点，则（）A ．飞镖击中P 点所需的时间为0LvB ．圆盘的半径可能为2202gL vC ．圆盘转动角速度的最小值为2v Lπ D ．P 点随圆盘转动的线速度不可能为54gLv π 4．如图，有一倾斜的匀质圆盘(半径足够大)，盘面与水平面的夹角为θ，绕过圆心并垂直于盘面的转轴以角速度ω匀速转动，有一物体(可视为质点)与盘面间的动摩擦因数为(μ设最大静摩擦力等手滑动摩擦力)，重力加速度为g ．要使物体能与圆盘始终保持相对静止，则物体与转轴间最大距离为（ ）A ．2cos g μθωB ．2sin g θω C ．2cos sin g μθθω- D ．2cos sin g μθθω+ 5．未来的星际航行中，宇航员长期处于完全失重状态，为缓解这种状态带来的不适，有人设想在未来的航天器上加装一段圆柱形“旋转舱”，如图所示．当旋转舱绕其轴线匀速旋转时，宇航员站在旋转舱内圆柱形侧壁上，可以受到与他站在地球表面时相同大小的支持力．为达到上述目的，下列说法正确的是（ ）A ．旋转舱的半径越大，转动的角速度就应越大B ．旋转舱的半径越大，转动的角速度就应越小C ．宇航员质量越大，旋转舱的角速度就应越大D ．宇航员质量越大，旋转舱的角速度就应越小6．在G20峰会“最忆是杭州”的文化文艺演出中，芭蕾舞演员保持如图所示姿势原地旋转，此时手臂上A、B 两点角速度大小分别为1ω、2ω，线速度大小分别为A v 、B v ，则（ ）A ．12ωω<B ．12ωω>C ．A B v v <D ．A B v v >7．一质量为2.0×103kg 的汽车在水平公路上行驶，路面对轮胎的径向最大静摩擦力为1.4×104N ，当汽车经过半径为80m 的弯道时，下列判断正确的是（ ）A ．汽车转弯时所受的力有重力、弹力、摩擦力和向心力B ．汽车转弯的速度为20m/s 时所需的向心力为1.4×104NC ．汽车转弯的速度为20m/s 时汽车会发生侧滑D ．汽车能安全转弯的向心加速度不超过7.0m/s 28．滑雪运动深受人民群众喜爱，某滑雪运动员（可视为质点）由坡道进入竖直面内的圆弧形滑道AB ，从滑道的A 点滑行到最低点B 的过程中，由于摩擦力的存在，运动员的速率不变，则运动员沿AB 下滑过程中（ ）A ．合外力做功一定大于零B ．所受摩擦力大小不变C ．合外力始终与速度垂直D ．机械能始终保持不变9．如图所示，照片中的汽车在水平路面上做匀速圆周运动，已知图中双向四车道的总宽度约为15m ，内径75m，假设汽车受到的最大静摩擦力等于车重的0.7倍，则运动的汽车（）A．所受的合力可能为零B．只受重力和地面的支持力作用C．最大速度不能超过25m/sD．所需的向心力由重力和支持力的合力提供10．小球P和Q用不可伸长的轻绳悬挂在天花板上，P球的质量大于Q球的质量，悬挂P球的绳比悬挂Q 球的绳短．将两球拉起，使两绳均被水平拉直，如图所示，将两球由静止释放，在各自轨迹的最低点（）A．P球的速度一定大于Q球的速度B．P球的动能一定小于Q球的动能C．P球所受绳的拉力一定大于Q球所受绳的拉力D．P球的向心加速度一定小于Q球的向心加速度11．如图所示，旋转秋千中的两个座椅A、B质量相等，通过相同长度的缆绳悬挂在旋转圆盘上．不考虑空气阻力的影响，当旋转圆盘绕竖直的中心轴匀速转动时，下列说法正确的是（）A．A的速度比B的大B．A与B的向心加速度大小相等C．悬挂A、B的缆绳与竖直方向的夹角相等D．悬挂A的缆绳所受的拉力比悬挂B的小12．如图所示，转动轴垂直于光滑水平面，交点O的上方h处固定细绳的一端，细绳的另一端栓接一质量为m的小球B，绳长l＞h，转动轴带动小球在光滑水平面上做圆周运动，当转动的角速度ω逐渐增大时，下列说法正确的是（）A ．小球始终受三个力的作用B ．细绳上的拉力始终保持不变C ．要使球离开水平面角速度至少为√gℎD ．若小球飞离了水平面则线速度为√gl13．“太极球”运动是一项较流行的健身运动。

第3讲 圆周运动一、非选择题1．(2022·河北高三月考)国家雪车雪橇中心位于北京延庆区西北部，赛道全长1 975 m ，垂直落差121 m ，由16个角度、倾斜度都不同的弯道组成，其中全长179 m 的回旋弯赛道是全球首个360°回旋弯道。

2022年北京冬奥会期间，国家雪车雪橇中心将承担雪车、钢架雪车、雪橇三个项目的全部比赛，其中钢架雪车比赛惊险刺激，深受观众喜爱。

测试赛上，一钢架雪车选手单手扶车，助跑加速30 m 之后，迅速跳跃车上，以俯卧姿态滑行。

该选手推车助跑时间为4.98 s ，运动员质量为80 kg ，通过回旋弯道某点时的速度为108 km/h ，到达终点时的速度为124 km/h 。

该选手推车助跑过程视为匀加速直线运动，回旋弯道可近似看作水平面，重力加速度g 取10 m/s 2，结果保留两位有效数字。

求该选手：(1)助跑加速的末速度；(2)以108 km/h 的速度通过回旋弯道某点时钢架雪车对运动员作用力的大小。

[答案] (1)12 m/s (2)2.6×103 N[解析] (1)运动员助跑加速的末速度为v 1，可知s ＝12v 1t 代入数据，解得v 1＝12 m/s 。

(2)回旋弯道全长179 m ，L ＝2πr ，运动员通过回旋弯道某点时，钢架雪车对运动员作用力设为F ，F y ＝mg ，F x ＝m v 2r，代入数据，解得F ＝F 2x ＋F 2y ＝2.6×103N 。

2．(2022·山东新泰月考)如图所示，水平传送带与水平轨道在B 点平滑连接，传送带AB 长度L 0＝2.0 m ，一半径R ＝0.2 m 的竖直圆形光滑轨道与水平轨道相切于C 点，水平轨道CD 长度L ＝1.0 m ，在D 点固定一竖直挡板。

小物块与传送带AB 间的动摩擦因数μ1＝0.9，BC 段光滑，CD 段动摩擦因数为μ2。

当传送带以v 0＝6 m/s 沿顺时针方向匀速转动时，将质量m ＝1 kg 的可视为质点的小物块轻放在传送带左端A 点，小物块通过传送带、水平轨道、圆形轨道、水平轨道后与挡板碰撞，并以原速率弹回，经水平轨道CD 返回圆形轨道。

1 f; T匀速圆周运动二、匀速圆周运动的描述1．线速度、角速度、周期和频率的概念(1)线速度v 是描述质点沿圆周运动快慢的物理量，是矢量，其大小为v =s=2r t T其方向沿轨迹切线，国际单位制中单位符号是m/s；（2）角速度ω是描述质点绕圆心转动快慢的物理量，是矢量，其大小为==2t T在国际单位制中单位符号是rad／s；(3）周期T 是质点沿圆周运动一周所用时间，在国际单位制中单位符号是s；（4）频率f 是质点在单位时间内完成一个完整圆运动的次数，在国际单位制中单位符号是Hz；（5）转速n 是质点在单位时间内转过的圈数，单位符号为r ／s ，以及r／min．2、速度、角速度、周期和频率之间的关系线速度、角速度、周期和频率各量从不同角度描述质点运动的快慢，它们之间有关系v＝rω．T =，v =2，= 2 f 。

由上可知，在角速度一定时，线速度大小与半径成正比；在线速度一定时，角速度大小与半径成反比．三、向心力和向心加速度1.向心力（1）向心力是改变物体运动方向，产生向心加速度的原因．（2）向心力的方向指向圆心，总与物体运动方向垂直，所以向心力只改变速度的方向．2.向心加速度（1）向心加速度由向心力产生，描述线速度方向变化的快慢，是矢量．（2）向心加速度方向与向心力方向恒一致，总沿半径指向圆心；向心加速度的大小为v 2 a n=r 公式：=2r 42rT 21. 线速度V＝s/t＝2πr/T ；== v 2. 角速度 ω＝Φ/t ＝2π/T ＝2πf 3. 向心加速度 a ＝V 2/r ＝ω2r ＝(2π/T)2r4. 向心力 F 心＝mV 2/r ＝m ω2r ＝mr(2π/T)2＝m ωv=F 合5. 周期与频率：T ＝1/f6. 角速度与线速度的关系：V ＝ωr7. 角速度与转速的关系 ω＝2πn (此处频率与转速意义相同)8. 主要物理量及单位：弧长 s:米(m)；角度 Φ：弧度（rad ）；频率 f ：赫（Hz ）；周期 T ：秒（s ）；转速n ：r/s ；半径 r ：米（m ）；线速度 V ：（m/s ）；角速度 ω：（rad/s ）；向心加速度：（m/s 2）。

高考物理生活中的圆周运动题20套(带答案)及解析一、高中物理精讲专题测试生活中的圆周运动1．已知某半径与地球相等的星球的第一宇宙速度是地球的12倍．地球表面的重力加速度为g ．在这个星球上用细线把小球悬挂在墙壁上的钉子O 上，小球绕悬点O 在竖直平面内做圆周运动．小球质量为m ，绳长为L ，悬点距地面高度为H ．小球运动至最低点时，绳恰被拉断，小球着地时水平位移为S 求：(1)星球表面的重力加速度？(2)细线刚被拉断时，小球抛出的速度多大？(3)细线所能承受的最大拉力？【答案】(1)01=4g g 星 (2)0024g s v H L=-201[1]42()s T mg H L L =+- 【解析】【分析】【详解】 （1）由万有引力等于向心力可知22Mm v G m R R= 2Mm G mg R= 可得2v g R= 则014g g 星＝（2）由平抛运动的规律：212H L g t -=星 0s v t = 解得0024g sv H L=- （3）由牛顿定律，在最低点时：2v T mg m L-星＝解得：20 1142()sT mgH L L⎡⎤=+⎢⎥-⎣⎦【点睛】本题考查了万有引力定律、圆周运动和平抛运动的综合，联系三个问题的物理量是重力加速度g0；知道平抛运动在水平方向和竖直方向上的运动规律和圆周运动向心力的来源是解决本题的关键．2．如图所示,半径R=2.5m的竖直半圆光滑轨道在B点与水平面平滑连接,一个质量m=0.50kg 的小滑块(可视为质点)静止在A点.一瞬时冲量使滑块以一定的初速度从A点开始运动,经B点进入圆轨道,沿圆轨道运动到最高点C,并从C点水平飞出,落在水平面上的D点.经测量,D、B间的距离s1=10m,A、B间的距离s2=15m,滑块与水平面的动摩擦因数 ,重力加速度.求:(1)滑块通过C点时的速度大小;(2)滑块刚进入圆轨道时,在B点轨道对滑块的弹力;(3)滑块在A点受到的瞬时冲量的大小.【答案】（1）（2）45N（3）【解析】【详解】（1）设滑块从C点飞出时的速度为v c，从C点运动到D点时间为t滑块从C点飞出后，做平抛运动，竖直方向：2R=gt2水平方向：s1=v c t解得：v c=10m/s（2）设滑块通过B点时的速度为v B，根据机械能守恒定律mv B2=mv c2+2mgR解得：v B=10m/s设在B点滑块受轨道的压力为N，根据牛顿第二定律：N-mg=m解得：N=45N（3）设滑块从A点开始运动时的速度为v A，根据动能定理；-μmgs2=mv B2-mv A2解得：v A =16.1m/s设滑块在A 点受到的冲量大小为I ，根据动量定理I=mv A解得：I=8.1kg•m/s ；【点睛】本题综合考查动能定理、机械能守恒及牛顿第二定律，在解决此类问题时，要注意分析物体运动的过程，选择正确的物理规律求解．3．如图所示，带有14光滑圆弧的小车A 的半径为R ，静止在光滑水平面上．滑块C 置于木板B 的右端，A 、B 、C 的质量均为m ，A 、B 底面厚度相同．现B 、C 以相同的速度向右匀速运动，B 与A 碰后即粘连在一起，C 恰好能沿A 的圆弧轨道滑到与圆心等高处．则：(已知重力加速度为g )(1)B 、C 一起匀速运动的速度为多少？(2)滑块C 返回到A 的底端时AB 整体和C 的速度为多少？【答案】（1）023v gR =（2）123gR v =253gR v =【解析】本题考查动量守恒与机械能相结合的问题．(1)设B 、C 的初速度为v 0，AB 相碰过程中动量守恒，设碰后AB 总体速度u ，由02mv mu =，解得02v u = C 滑到最高点的过程： 023mv mu mu +='222011123222mv mu mu mgR +⋅=+'⋅ 解得023v gR =(2)C 从底端滑到顶端再从顶端滑到底部的过程中，满足水平方向动量守恒、机械能守恒，有01222mv mu mv mv +=+22220121111222222mv mu mv mv +⋅=+⋅ 解得：123gR v =253gR v =4．如图所示，一轨道由半径2R m =的四分之一竖直圆弧轨道AB 和水平直轨道BC 在B 点平滑连接而成．现有一质量为1m Kg =的小球从A 点正上方2R 处的O '点由静止释放，小球经过圆弧上的B 点时，轨道对小球的支持力大小18N F N =，最后从C 点水平飞离轨道，落到水平地面上的P 点.已知B 点与地面间的高度 3.2h m =，小球与BC 段轨道间的动摩擦因数0.2μ=，小球运动过程中可视为质点. (不计空气阻力，g 取10 m/s 2). 求：（1）小球运动至B 点时的速度大小B v（2）小球在圆弧轨道AB 上运动过程中克服摩擦力所做的功f W（3）水平轨道BC 的长度L 多大时，小球落点P 与B 点的水平距最大．【答案】（1）4?/B v m s ＝ （2）22?f W J ＝ （3） 3.36L m = 【解析】试题分析：（1）小球在B 点受到的重力与支持力的合力提供向心力，由此即可求出B 点的速度；（2）根据动能定理即可求出小球在圆弧轨道上克服摩擦力所做的功；（3）结合平抛运动的公式，即可求出为使小球落点P 与B 点的水平距离最大时BC 段的长度．（1）小球在B 点受到的重力与支持力的合力提供向心力，则有：2B N v F mg m R-= 解得：4/B v m s =（2）从O '到B 的过程中重力和阻力做功，由动能定理可得：21022f B R mg R W mv ⎛⎫+-=- ⎪⎝⎭ 解得：22f W J =（3）由B 到C 的过程中，由动能定理得：221122BC C B mgL mv mv μ-=- 解得：222B C BC v v L g μ-= 从C 点到落地的时间：020.8h t s g== B 到P 的水平距离：2202B C C v v L v t gμ-=+代入数据，联立并整理可得：214445C C L v v =-+ 由数学知识可知，当 1.6/C v m s =时，P 到B 的水平距离最大，为：L=3.36m【点睛】该题结合机械能守恒考查平抛运动以及竖直平面内的圆周运动，解题的关键就是对每一个过程进行受力分析，根据运动性质确定运动的方程，再根据几何关系求出最大值．5．如图所示,半径为4l ,质量为m 的小球与两根不可伸长的轻绳a ,b 连接,两轻绳的另一端分别固定在一根竖直光滑杆的A ,B 两点上.已知A ,B 两点相距为l ,当两轻绳伸直后A 、B 两点到球心的距离均为l ,重力加速度为g ．（1）装置静止时,求小球受到的绳子的拉力大小T ；（2）现以竖直杆为轴转动并达到稳定（轻绳a ,b 与杆在同一竖直平面内）．①小球恰好离开竖直杆时,竖直杆的角速度0ω多大?②轻绳b 伸直时,竖直杆的角速度ω多大？【答案】(1)415T =(2)①ω0=15215g l②2g l ω≥【解析】【详解】 (1)设轻绳a 与竖直杆的夹角为α15cos α=对小球进行受力分析得 cos mg T α=解得： 415T mg = (2)①小球恰好离开竖直杆时，小球与竖直杆间的作用力为零。

基础课时10 圆周运动一、单项选择题1.电风扇的扇叶的重心假如不在转轴上，转动时会使风扇抖动，并加快转轴磨损。

调整时，可在扇叶的一区域通过固定小金属块的方法转变其重心位置。

如图1所示，A、B是两调整重心的金属块(可视为质点)，其质量相等，它们到转轴O的距离r A＜r B。

扇叶转动后，它们的( )图1A.向心加速度相等B.线速度大小相等C.向心力F A＜F BD.角速度ωA＜ωB解析由于两调整重心的金属块A、B固定在风扇上，因此两者绕轴O一起转动，具有相同的角速度，故D错误；依据向心加速度公式a＝ω2r，得a A＜a B，由线速度与角速度的关系v＝ωr，得v A＜v B，由向心力公式F＝mω2r，得F A＜F B，故C正确，A、B错误。

答案 C2.甲、乙两个物体都做匀速圆周运动，其质量之比为1∶2，转动半径之比为1∶2，在相同的时间里甲转过60°，乙转过45°，则它们的向心力大小之比为( )A.1∶4B.2∶3C.4∶9D.9∶16解析m1∶m2＝1∶2，r1∶r2＝1∶2，ω1∶ω2＝θ1∶θ2＝4∶3，向心力F＝mω2r，故F1∶F2＝4∶9，故C 正确。

答案 C3.光盘驱动器读取数据的某种方式可简化为以下模式，在读取内环数据时，以恒定角速度方式读取，而在读取外环数据时，以恒定线速度的方式读取。

如图2所示，设内环内边缘的半径为R1，内环外边缘半径为R2，外环外边缘半径为R3。

A、B、C分别为各边缘线上的点。

则读取内环上A点时的向心加速度大小和读取外环上C点时的向心加速度大小之比为( ) 图2A.R21R2R3B.R22R1R3C.R2R3R21D.R1R3R22解析内环外边缘和外环内边缘为同一圆。

A与B角速度相等，向心加速度之比为a Aa B＝R1R2。

B与C线速度相等，向心加速度之比为a Ba C＝R3R2；读取内环上A点时的向心加速度大小和读取外环上C 点时的向心加速度大小之比为a Aa C＝R1R3R22，选项D正确。

2024全国高考真题物理汇编生活中的圆周运动一、单选题1．（2024江苏高考真题）陶瓷是以粘土为主要原料以及各种天然矿物经过粉碎混炼、成型和煅烧制得的材料以及各种制品。

如图所示是生产陶磁的简化工作台，当陶瓷匀速转动时，台面面上掉有陶屑，陶屑与桌面间的动摩因数处处相同（台面够大），则（ ）A ．离轴OO´越远的陶屑质量越大B ． 离轴OO´越近的陶屑质量越小C ． 只有平台边缘有陶屑D ．离轴最远的陶屑距离不会超过某一值2．（2024广东高考真题）如图所示，在细绳的拉动下，半径为r 的卷轴可绕其固定的中心点O 在水平面内转动。

卷轴上沿半径方向固定着长度为l 的细管，管底在O 点。

细管内有一根原长为2l 、劲度系数为k 的轻质弹簧，弹簧底端固定在管底，顶端连接质量为m 、可视为质点的插销。

当以速度v 匀速拉动细绳时，插销做匀速圆周运动。

若v 过大，插销会卡进固定的端盖。

使卷轴转动停止。

忽略摩擦力，弹簧在弹性限度内。

要使卷轴转动不停止，v 的最大值为（ ）A ．B ．C ．D ．二、多选题3．（2024江苏高考真题）如图所示，细绳穿过竖直的管子拴住一个小球，让小球在A 高度处作水平面内的匀速圆周运动，现用力将细绳缓慢下拉，使小球在B 高度处作水平面内的匀速圆周运动，不计一切摩擦，则（ ）A．线速度vA > vB B．角速度ωA < ωBC．向心加速度aA < aB D．向心力F A > FB三、实验题4．（2024海南高考真题）水平圆盘上紧贴边缘放置一密度均匀的小圆柱体，如图（a）所示，图（b）为俯视图，测得圆盘直径D = 42.02cm，圆柱体质量m = 30.0g，圆盘绕过盘心O1的竖直轴匀速转动，转动时小圆柱体相对圆盘静止。

为了研究小圆柱体做匀速圆周运动时所需要的向心力情况，某同学设计了如下实验步骤：(1)用秒表测圆盘转动10周所用的时间t = 62.8s，则圆盘转动的角速度ω = rad/s（π取3.14）(2)用游标卡尺测量小圆柱体不同位置的直径，某次测量的示数如图（c）所示，该读数d = mm，多次测量后，得到平均值恰好与d相等。

圆周运动水平圆周运动【例题】如图所示，在匀速转动的圆筒内壁上，有一物体随圆筒一起转动而未滑动。

当圆筒的角速度增大以后，下列说法正确的是（ D ）A 、物体所受弹力增大，摩擦力也增大了B 、物体所受弹力增大，摩擦力减小了C 、物体所受弹力和摩擦力都减小了D 、物体所受弹力增大，摩擦力不变【例题】如图为表演杂技“飞车走壁”的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a 、b 两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的侧向摩擦,下列说法中正确的是（ B ）A ．在a 轨道上运动时角速度较大B ．在a 轨道上运动时线速度较大C ．在a 轨道上运动时摩托车对侧壁的压力较大D ．在a 轨道上运动时摩托车和运动员所受的向心力较大【例题】长为L 的细线，拴一质量为m 的小球，一端固定于O 点，让其在水平面内做匀速圆周运动（这种运动通常称为圆锥摆运动），如图所示，当摆线L 与竖直方向的夹角是α时，求：（1）线的拉力F ；（2）小球运动的线速度的大小； （3）小球运动的角速度及周期。

★解析：做匀速圆周运动的小球受力如图所示，小球受重力mg 和绳子的拉力F 。

因为小球在水平面内做匀速圆周运动，所以小球受到的合力指向圆心O １，且是水平方向。

由平行四边形法则得小球受到的合力大小为mgtanα，线对小球的拉力大小为F=mg/cosα由牛顿第二定律得mgtanα=mv 2/r 由几何关系得r=Lsinα 所以，小球做匀速圆周运动线速度的大小为an sin v gLt αα=a bLα O小球运动的角速度小球运动的周期2cos 2L T gπαπ==ω点评：在解决匀速圆周运动的过程中，弄清物体圆形轨道所在的平面，明确圆心和半径是一个关键环节，同时不可忽视对解题结果进行动态分析，明确各变量之间的制约关系、变化趋势以及结果涉及物理量的决定因素。

1、竖直平面内：（1）、如图所示，没有物体支撑的小球，在竖直平面内做圆周运动过最高点的情况：①临界条件：小球达最高点时绳子的拉力（或轨道的弹力）刚好等于零，小球的重力提供其做圆周运动的向心力，即rmv mg 2临界=⇒rg =临界υ（临界υ是小球通过最高点的最小速度，即临界速度）。

[课时作业] 单独成册 方便使用[基础题组]一、单项选择题1.在冬奥会短道速滑项目中，运动员绕周长仅111 m 的短道竞赛．运动员比赛过程中在通过弯道时如果不能很好地控制速度，将发生侧滑而摔离正常比赛路线．图中圆弧虚线Ob 代表弯道，即正常运动路线，Oa 为运动员在O 点时的速度方向(研究时可将运动员看成质点)．下列论述正确的是( ) A ．发生侧滑是因为运动员受到的合力方向背离圆心 B ．发生侧滑是因为运动员受到的合力大于所需要的向心力 C ．若在O 点发生侧滑，则滑动的方向在Oa 左侧D ．若在O 点发生侧滑，则滑动的方向在Oa 右侧与Ob 之间解析：运动员发生侧滑是因为运动员受到指向圆心的合力小于所需要的向心力，A 、B 错误．若在O 点发生侧滑，如果向心力突然消失，则沿切线Oa 运动，而现在是由于所提供的向心力小于所需要的向心力，因此滑动的方向在Oa 与Ob 之间，D 正确． 答案：D2．如图是自行车传动结构的示意图，其中Ⅰ是半径为r 1的大齿轮，Ⅱ是半径为r 2的小齿轮，Ⅲ是半径为r 3的后轮．假设脚踏板的转速为n ，则自行车前进的速度为( )A.2πnr 1r 3r 2B.πnr 2r 3r 1C.πnr 1r 3r 2D ．2πnr 2r 3r 1解析：前进速度即为Ⅲ轮的线速度，由同一个轮上的点角速度相等，同一链条上的点线速度大小相等可得：ω1r 1＝ω2r 2，ω3＝ω2，又有ω1＝2πn ，v ＝ω3r 3，所以v ＝2πnr 1r 3r 2，A 正确．答案：A3.如图所示，圆弧形凹槽固定在水平地面上，其中ABC 是以O 为圆心的一段圆弧，位于竖直平面内．现有一小球从一水平桌面的边缘P 点向右水平飞出，该小球恰好能从A 点沿圆弧的切线方向进入圆轨道．OA 与竖直方向的夹角为θ1，P A 与竖直方向的夹角为θ2.下列关系式正确的是( ) A ．tan θ1tan θ2＝2 B ．cot θ1tan θ2＝2 C ．cot θ1cot θ2＝2D ．tan θ1cot θ2＝2解析：小球在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，小球在A 点时速度与水平方向的夹角为θ1，tan θ1＝v y v 0＝gt v 0，位移与竖直方向的夹角为θ2，tan θ2＝x y ＝v 0t 12gt 2＝2v 0gt ，则tan θ1tan θ2＝2.故A 正确，B 、C 、D 错误． 答案：A4.(2018·安徽合肥高三模拟)如图所示，在粗糙水平木板上放一个物块，使木板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动，ab 为水平直径，cd 为竖直直径，在运动过程中木板始终保持水平，物块相对木板始终静止，则( )A ．物块始终受到三个力作用B ．只有在a 、b 、c 、d 四点，物块受到合外力才指向圆心C ．从a 到b ，物块所受的摩擦力先增大后减小D ．从b 到a ，物块处于超重状态解析：在c 点处，物块可能只受重力作用，在d 点处，物块只受重力和支持力作用，在其他位置处，物块受到重力、支持力、静摩擦力作用，选项A 错误；物块做匀速圆周运动，合外力提供向心力，且始终指向圆心，选项B 错误；从a 运动到b ，向心力的水平分量先减小后增大，所以摩擦力先减小后增大，选项C 错误；从b 运动到a ，向心加速度有向上的分量，所以物块处于超重状态，选项D 正确． 答案：D5.如图所示，长为L 的细绳一端固定在O 点，另一端拴住一个小球．在O 点的正下方与O 点相距2L3的地方有一枚与竖直平面垂直的钉子A .把球拉起使细绳在水平方向伸直，由静止开始释放，当细绳碰到钉子后的瞬间(细绳没有断)，下列说法中正确的是( )A ．小球的向心加速度突然增大到原来的3倍B ．小球的线速度突然增大到原来的3倍C ．小球的角速度突然增大到原来的1.5倍D ．细绳对小球的拉力突然增大到原来的1.5倍解析：细绳碰到钉子的瞬间，线速度不变，B 错误．圆周运动的半径由L 变为L3，由a ＝v 2r 知，a 增大到原来的3倍，A 正确．根据v ＝rω知，角速度ω增大到原来的3倍，C 错误．细绳碰到钉子前瞬间T －mg ＝m v 2L ，碰后瞬间T ′－mg ＝m v 2L 3，再根据机械能守恒有mgL ＝12m v 2，由此可得T ′＝73T ，D 错误． 答案：A 二、多项选择题6.(2018·安徽皖江名校高三模拟)摩擦传动是传动装置中的一个重要模型，如图所示的两个水平放置的轮盘靠摩擦力传动，其中O 、O ′分别为两轮盘的轴心，已知两个轮盘的半径之比r 甲∶r 乙＝3∶1，且在正常工作时两轮盘不打滑．今在两轮盘上分别放置两个同种材料制成的滑块A 、B ，两滑块与轮盘间的动摩擦因数相同，两滑块距离轴心O 、O ′的间距R A ＝2R B .若轮盘乙由静止开始缓慢地转动起来，且转速逐渐增加，则下列叙述正确的是( )A ．滑块A 和B 在与轮盘相对静止时，角速度之比为ω甲∶ω乙＝1∶3 B ．滑块A 和B 在与轮盘相对静止时，向心加速度的比值为a A ∶a B ＝2∶9C ．转速增加后滑块B 先发生滑动D ．转速增加后两滑块一起发生滑动解析：假设轮盘乙的半径为R ，由题意可知两轮盘边缘的线速度大小相等，有ω甲(3R )＝ω乙R ，得ω甲∶ω乙＝1∶3，所以滑块相对轮盘滑动前，A 、B 的角速度之比为1∶3，A 正确；滑块相对轮盘滑动前，根据a ＝ω2r 得A 、B 的向心加速度之比为a A ∶a B ＝2∶9，B 正确；据题意可得滑块的最大静摩擦力分别为f a ＝μm A g ，f b ＝μm B g ，最大静摩擦力之比为f a ∶f b ＝m A ∶m B ，滑块相对轮盘滑动前所受的静摩擦力之比为f a ′∶f b ′＝(m A a A )∶(m B a B )＝m A ∶(4.5 m B )，综上分析可得滑块B 先达到最大静摩擦力，先开始滑动，C 正确，D 错误． 答案：ABC7.(2018·江苏如皋质检)质量为m 的小球由轻绳a 和b 分别系于一轻质细杆的A 点和B 点，如图所示，绳a 与水平方向成θ角，绳b 在水平方向且长为l ，当轻杆绕轴AB 以角速度ω匀速转动时，小球在水平面内做匀速圆周运动，则下列说法正确的是( )A ．a 绳的张力不可能为零B ．a 绳的张力随角速度的增大而增大C ．当角速度ω2＞gl tan θ，b 绳将出现弹力D ．若b 绳突然被剪断，则a 绳的弹力一定发生变化解析：对小球受力分析可得a 绳的弹力在竖直方向的分力平衡了小球的重力，解得T a ＝mgsin θ，为定值，A 正确，B 错误．当T a cos θ＝mω2l ，即ω＝gl tan θ时，b 绳的弹力为零，若角速度大于该值，则b绳将出现弹力，C 正确．由于b 绳可能没有弹力，故b 绳突然被剪断，a 绳的弹力可能不变，D 错误． 答案：AC8.如图所示，竖直放置的光滑圆轨道被固定在水平地面上，半径r ＝0.4 m ，最低点处有一小球(半径比r 小很多)，现给小球一水平向右的初速度v 0，要使小球不脱离圆轨道运动，v 0应当满足(g 取10 m/s 2)( ) A ．v 0≥0 B ．v 0≥4 m/s C ．v 0≥2 5 m/sD ．v 0≤2 2 m/s解析：要使小球不脱离轨道运动，则需越过最高点或不越过四分之一圆周．越过最高点的临界情况：mg ＝m v 2r ，得v ＝gr ＝2 m/s ，由动能定理得－mg ·2r ＝12m v 2－12m v 20，解得v 0＝2 5 m/s ；若不通过四分之一圆周，根据机械能守恒定律有mgr ＝12m v 20，解得v 0＝2 2 m/s.所以v ≥2 5 m/s 或v ≤2 2 m/s 均符合要求，C 、D 正确，A 、B 错误． 答案：CD[能力题组]一、选择题9.如图所示，竖直面内的光滑圆轨道处于固定状态，一轻弹簧一端连接在圆轨道圆心的光滑转轴上，另一端与圆轨道上的小球相连，小球的质量为1 kg ，当小球以2 m/s 的速度通过圆轨道的最低点时，球对轨道的压力为20 N ，轨道的半径r ＝0.5 m ，重力加速度g 取10 m/s 2，则小球要能通过圆轨道的最高点，小球在最高点的速度至少为( ) A ．1 m/s B ．2 m/s C ．3 m/sD ．4 m/s解析：设小球在轨道最低点时所受轨道支持力为F 1、弹簧弹力大小为N ，则F 1－mg －N ＝m v 21r ，求得N ＝2 N ，可判断出弹簧处于压缩状态．小球以最小速度通过最高点时，球对轨道的压力刚好为零，则mg －N ＝m v 22r ，求得v 2＝2 m/s ，B 项正确． 答案：B10.如图所示，细绳长为L ，挂一个质量为m 的小球，小球离地面的高度h ＝2L ，当绳受到大小为2mg 的拉力时就会断裂，绳的上端系一质量不计的环，环套在光滑水平杆上．现让环与小球一起以速度v ＝gL 向右运动，在A 处环被挡住而立即停止，A 离墙的水平距离也为L ，小球在以后的运动过程中，小球第一次碰撞点离墙角B 点的距离是ΔH (不计空气阻力)，则( ) A ．ΔH ＝12L B ．ΔH ＝53L C ．ΔH ＝23LD ．ΔH ＝32L解析：环被A 挡住时，小球做圆周运动，受到重力和绳子的拉力作用，两者的合力充当向心力，故有T －mg ＝m v 2L ，因为v ＝gL ，代入解得T ＝2mg ，故绳子会断开，断开之后小球做平抛运动，设小球直接落地，则h ＝12gt 2，小球的水平位移x ＝v t ＝2L ＞L ，所以小球先与墙壁碰撞．设小球平抛后经时间t ′与墙壁碰撞，则t ′＝L v ＝L g ，小球下落高度h ′＝12gt ′2＝L 2，碰撞点距B 的距离ΔH ＝2L －L 2＝32L ，故D 正确． 答案：D11.(多选)(2018·湖南长沙高三联考)如图所示，质量为m 的小球在竖直放置的光滑圆形管道内做圆周运动，下列说法正确的有( ) A ．小球通过最高点的速度可能小于gRB ．小球通过最低点时对轨道的压力大小等于小球的重力C ．小球在水平线ab 以下管道中运动时，外侧管壁对小球一定有作用力D ．小球在水平线ab 以上管道中运动时，内侧管壁对小球一定有作用力解析：小球在光滑圆形管道内做圆周运动，只受重力和弹力，两者的合力提供向心力．小球通过最高点时，速度可以无限接近于零，选项A 正确；小球通过最低点时，受到重力和弹力，两者合力提供向心力，有N －mg ＝m v 2R ，选项B 错误；小球在水平线ab 以下管道中运动时，受到重力和弹力，合力沿半径方向的分力提供向心力，由于重力有背离圆心的分量，所以弹力一定指向圆心，因此外侧管壁必然对小球有作用力，选项C 正确；同理，小球在水平线ab 以上管道中运动时，由于重力有指向圆心的分量，所以弹力可以背离圆心，也可以指向圆心，选项D 错误．答案：AC二、非选择题12.(2018·陕西西安质检)某工厂生产流水线示意图如图所示，半径R ＝1 m 的水平圆盘边缘E 点固定一小桶，在圆盘直径DE 正上方平行放置的水平传送带沿顺时针方向匀速转动，传送带右端C 点与圆盘圆心O 在同一竖直线上，竖直高度h ＝1.25 m ．AB 为一个与CO 在同一竖直平面内的四分之一光滑圆轨道，半径r ＝0.45 m ，且与水平传送带相切于B 点．一质量m ＝0.2 kg 的滑块(可视为质点)从A 点由静止释放，滑块与传送带间的动摩擦因数μ＝0.2，当滑块到达B 点时，圆盘从图示位置以一定的角速度ω绕通过圆心O 的竖直轴匀速转动，滑块到达C 点时恰与传送带同速并水平抛出，刚好落入圆盘边缘的小桶内．取g ＝10 m/s 2，求：(1)滑块到达圆弧轨道B 点时对轨道的压力N B ； (2)传送带BC 部分的长度L ；(3)圆盘转动的角速度ω应满足的条件． 解析：(1)滑块从A 到B 过程中，由动能定理有 mgr ＝12m v 2B解得v B ＝2gr ＝3 m/s滑块到达B 点时，由牛顿第二定律有 N B ′－mg ＝m v 2B r 解得N B ′＝6 N根据牛顿第三定律，滑块到达B 点时对轨道的压力大小为6 N ，方向竖直向下． (2)滑块离开C 点后做平抛运动，h ＝12gt 21 解得t 1＝2hg ＝0.5 sv C ＝Rt 1＝2 m/s滑块由B 到C 过程中，根据动能定理，有 －μmgL ＝12m v 2C －12m v 2B解得L ＝v 2B －v 2C2μg ＝1.25 m(3)滑块由B 到C 过程中，根据运动学公式，有 L ＝v B ＋v C 2t 2解得t 2＝2Lv B ＋v C ＝0.5 s则t ＝t 1＋t 2＝1 s圆盘转动的角速度ω应满足条件 t ＝n ·2πω(n ＝1,2,3，…)解得ω＝2n π rad/s(n ＝1,2,3，…)． 答案：(1)6 N ，方向竖直向下 (2)1.25 m (3)ω＝2n π rad/s(n ＝1,2,3，…)13．(2018·湖南六校联考)如图所示为水上乐园的设施，由弯曲滑道、竖直平面内的圆形滑道、水平滑道及水池组成，圆形滑道外侧半径R ＝2 m ，圆形滑道的最低点的水平入口B 和水平出口B ′相互错开，为保证安全，在圆形滑道内运动时，要求紧贴内侧滑行．水面离水平滑道高度h ＝5 m ．现游客从滑道A 点由静止滑下，游客可视为质点，不计一切阻力，重力加速度g 取10 m/s 2，求：(1)起滑点A 至少离水平滑道多高？(2)为了保证游客安全，在水池中放有长度L ＝5 m 的安全气垫MN ，其厚度不计，满足(1)的游客恰落在M 端，要使游客能安全落在气垫上，安全滑下点A 距水平滑道的高度取值范围为多少？ 解析：(1)游客在圆形滑道内侧恰好滑过最高点时，有 mg ＝m v 2R ①从A 到圆形滑道最高点，由机械能守恒，有 mgH 1＝12m v 2＋mg ×2R ② 解得H 1＝52R ＝5 m ③(2)落在M 点时抛出速度最小，从A 到C 由机械能守恒 mgH 1＝12m v 21④ v 1＝2gH 1＝10 m/s ⑤水平抛出，由平抛运动规律可知 h ＝12gt 2⑥ 得t ＝1 s 则s 1＝v 1t ＝10 m落在N 点时s 2＝s 1＋L ＝15 m 则对应的抛出速度v 2＝s 2t ＝15 m/s ⑧ 由mgH 2＝12m v 22 得H 2＝v 222g ＝11.25 m安全滑下点A 距水平滑道高度范围为5 m ≤H ≤11.25 m ⑨ 答案：(1)5 m (2)见解析。

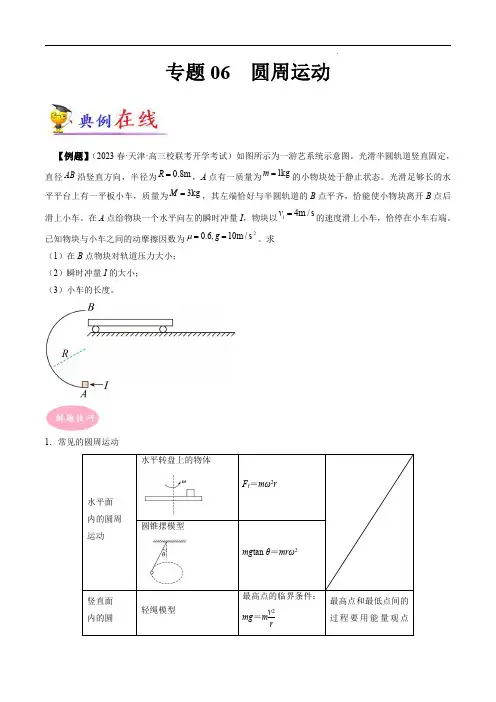
专题06圆周运动【例题】（2023春·天津·高三校联考开学考试）如图所示为一游艺系统示意图。

光滑半圆轨道竖直固定，直径AB 沿竖直方向，半径为0.8m R =，A 点有一质量为1kg m =的小物块处于静止状态。

光滑足够长的水平平台上有一平板小车，质量为3kg M =，其左端恰好与半圆轨道的B 点平齐，恰能使小物块离开B 点后滑上小车。

在A 点给物块一个水平向左的瞬时冲量I ，物块以14m /s v =的速度滑上小车，恰停在小车右端。

已知物块与小车之间的动摩擦因数为20.6,10m /s g μ==。

求（1）在B 点物块对轨道压力大小；（2）瞬时冲量I 的大小；（3）小车的长度。

1．常见的圆周运动水平面内的圆周运动水平转盘上的物体F f ＝mω2r圆锥摆模型mg tan θ＝mrω2竖直面内的圆轻绳模型最高点的临界条件：mg ＝m v2r 最高点和最低点间的过程要用能量观点（动能定理）倾斜转盘上的物体带电小球在叠加场中的圆周运动等效法带电粒子在匀强磁场中做匀速圆周运动2．圆周运动的三种临界情况（1）接触面滑动临界：摩擦力达到最大值．（2）接触面分离临界：F N＝0.（3）绳恰好绷紧：F T＝0；绳恰好断裂：F T达到绳子最大承受拉力．（4）竖直面内的圆周运动两种模型①绳球模型：小球能通过最高点的条件是v≥gR。

②杆球模型：小球能到达最高点的条件是v≥0。

【变式训练】（2023·山东济宁·济宁市育才中学统考一模）火星的半径是地球半径的二分之一，质量为地球质量的十分之一，忽略星球自转影响，地球表面重力加速度g=10m/s²。

假定航天员在火星表面利用如图所示的装置研究小球的运动。

竖直平面放置的光滑半圆形管道固定在水平面上，一直径略小于管道内径的小球（可视为质点）沿水平面从管道最低点A 进入管道，从最高点B 脱离管道后做平抛运动，1s 后与倾角为37°的斜面垂直相碰于C 点。

第六单元圆周运动测试时间：90分钟满分：110分第Ⅰ卷(选择题，共48分)一、选择题(本题共12小题，共48分。

在每小题给出的四个选项中，第1～8小题只有一个选项正确，第9～12小题有多个选项正确，全部选对的得4分，选对但不全的得2分，有选错或不答的得0分)1．[2022·衡水中学周测]关于匀速圆周运动，下列说法正确的是()A．匀速圆周运动是匀速运动B．匀速圆周运动是匀变速运动C．匀速圆周运动是线速度不变的运动D．匀速圆周运动是线速度大小不变的运动，属于变速运动答案 D解析匀速圆周运动速度大小不变，方向时刻变化，故速度是变化的，是变速运动，故A、B、C错误，D正确。

2．[2021·枣庄检测]如图所示，内部为竖直光滑圆轨道的铁块静置在粗糙的水平地面上，其质量为M。

有一质量为m的小球以水平速度v0从圆轨道最低点A 开头向左运动，小球沿圆轨道运动且始终不脱离圆轨道，在此过程中，铁块始终保持静止，重力加速度大小为g，则下列说法正确的是()A．地面受到的压力肯定大于MgB．小球到达B点时与铁块间可能无作用力C．经过最低点A时小球处于失重状态D．小球在圆轨道左侧运动的过程中，地面受到的摩擦力方向可能向右答案 B解析若小球恰好通过C点，重力供应其做圆周运动的向心力，则小球与铁块间无作用力，地面受到的压力为Mg，A错误；若小球恰好到达B点时速度为零，则小球与铁块间无作用力，B正确；小球经过最低点A时具有竖直向上的加速度，则此时小球处于超重状态，C错误；小球在圆轨道左侧运动的过程中，地面可能不受摩擦力，也可能受到水平向左的摩擦力，故D错误。

3．[2021·湖南浏阳模拟]如图所示，半径为R的圆轮在竖直面内绕O轴匀速转动，轮上A、B两点均粘有一小物体，当B点转至最低位置时，A、B两点处的小物体同时脱落，最终落到水平地面上同一点。

此时O、A、B、P四点在同一竖直线上，已知：OA＝AB，P是地面上一点。

高考物理生活中的圆周运动解题技巧及练习题(含答案)含解析一、高中物理精讲专题测试生活中的圆周运动1．如图所示，竖直圆形轨道固定在木板B 上，木板B 固定在水平地面上，一个质量为3m 小球A 静止在木板B 上圆形轨道的左侧．一质量为m 的子弹以速度v 0水平射入小球并停留在其中，小球向右运动进入圆形轨道后，会在圆形轨道内侧做圆周运动．圆形轨道半径为R ，木板B 和圆形轨道总质量为12m ，重力加速度为g ，不计小球与圆形轨道和木板间的摩擦阻力．求：(1)子弹射入小球的过程中产生的内能；(2)当小球运动到圆形轨道的最低点时，木板对水平面的压力；(3)为保证小球不脱离圆形轨道，且木板不会在竖直方向上跳起，求子弹速度的范围．【答案】(1)2038mv (2) 20164mv mg R+ (3)042v gR ≤或04582gR v gR ≤≤【解析】本题考察完全非弹性碰撞、机械能与曲线运动相结合的问题．(1)子弹射入小球的过程，由动量守恒定律得：01(3)mv m m v =+ 由能量守恒定律得：220111422Q mv mv =-⨯ 代入数值解得：2038Q mv = (2)当小球运动到圆形轨道的最低点时，以小球为研究对象，由牛顿第二定律和向心力公式得211(3)(3)m m v F m m g R+-+= 以木板为对象受力分析得2112F mg F =+根据牛顿第三定律得木板对水平的压力大小为F 2 木板对水平面的压力的大小202164mv F mg R=+ (3)小球不脱离圆形轨有两种可能性：①若小球滑行的高度不超过圆形轨道半径R 由机械能守恒定律得：()()211332m m v m m gR +≤+解得：042v gR ≤ ②若小球能通过圆形轨道的最高点 小球能通过最高点有：22(3)(3)m m v m m g R++≤ 由机械能守恒定律得：221211(3)2(3)(3)22m m v m m gR m m v +=+++ 代入数值解得：045v gR ≥要使木板不会在竖直方向上跳起，木板对球的压力：312F mg ≤在最高点有：233(3)(3)m m v F m m g R+++= 由机械能守恒定律得：221311(3)2(3)(3)22m m v m m gR m m v +=+++ 解得：082v gR ≤ 综上所述为保证小球不脱离圆形轨道，且木板不会在竖直方向上跳起，子弹速度的范围是042v gR ≤或04582gR v gR ≤≤2．如图所示，水平长直轨道AB 与半径为R =0.8m 的光滑14竖直圆轨道BC 相切于B ，BC 与半径为r =0.4m 的光滑14竖直圆轨道CD 相切于C ，质量m =1kg 的小球静止在A 点，现用F =18N 的水平恒力向右拉小球，在到达AB 中点时撤去拉力，小球恰能通过D 点．已知小球与水平面的动摩擦因数μ=0.2，取g =10m/s 2．求：（1）小球在D 点的速度v D 大小；（2）小球在B 点对圆轨道的压力N B 大小；（3）A 、B 两点间的距离x ．【答案】(1)2/D v m s = （2）45N (3)2m【解析】【分析】【详解】（1）小球恰好过最高点D ，有：2D v mg m r = 解得：2m/s D v =（2）从B 到D ，由动能定理：2211()22D B mg R r mv mv -+=- 设小球在B 点受到轨道支持力为N ，由牛顿定律有：2B v N mg m R-= N B =N联解③④⑤得：N =45N（3）小球从A 到B ，由动能定理：2122B x F mgx mv μ-= 解得：2m x =故本题答案是：(1)2/D v m s = （2）45N (3)2m【点睛】利用牛顿第二定律求出速度，在利用动能定理求出加速阶段的位移，3．水平面上有一竖直放置长H ＝1.3m 的杆PO ，一长L ＝0.9m 的轻细绳两端系在杆上P 、Q 两点，PQ 间距离为d ＝0.3m ，一质量为m ＝1.0kg 的小环套在绳上。

圆周运动一、选择题1.如图所示，在杂技表演中，杂技演员表演了“球内飞车”的杂技。

一个由钢骨架和铁丝网构成的球壳固定在水平地面上，杂技演员骑摩托车在球壳内飞速旋转，惊险而刺激。

甲演员骑摩托车在球壳内“赤道”平面做匀速圆周运动而不跌落下来；乙演员在“赤道”平面下方某一位置沿水平面做匀速圆周运动。

下列说法正确的是（ ）A ．甲、乙两演员做圆周运动的半径相同B ．甲、乙两演员做圆周运动的角速度一定相同C ．乙演员的速率增大时，其竖直面内的摩擦力可能减小D ．乙演员的速率增大时，其圆周运动的半径一定增大2．如图甲所示，被称为“魔力陀螺”玩具的陀螺能在圆轨道外侧旋转不脱落，其原理可等效为如图乙所示的模型：半径为R 的磁性圆轨道竖直固定，质量为m 的铁球（视为质点）沿轨道外侧运动，A 、B 分别为轨道的最高点和最低点，轨道对铁球的磁性引力始终指向圆心且大小不变，不计摩擦和空气阻力，重力加速度为g ，则（ ）A.铁球绕轨道可能做匀速圆周运动B.由于磁力的作用，铁球绕轨道运动过程中机械能不守恒C ．铁球在A ．轨道对铁球的磁性引力至少为5mg ，才能使铁球不脱轨3．（2022·全国·统考高考真题）北京2022年冬奥会首钢滑雪大跳台局部示意图如图所示。

运动员从a 处由静止自由滑下，到b 处起跳，c 点为a 、b 之间的最低点，a 、c 两处的高度差为h 。

要求运动员经过c 点时对滑雪板的压力不大于自身所受重力的k 倍，运动过程中将运动员视为质点并忽略所有阻力，则c 点处这一段圆弧雪道的半径不应小于（ ）A ．1h k +B ．h kC ．2h kD ．21h k - 4．（2022·北京·高考真题）我国航天员在“天宫课堂”中演示了多种有趣的实验，提高了青少年科学探索的兴趣。

某同学设计了如下实验：细绳一端固定，另一端系一小球，给小球一初速度使其在竖直平面内做圆周运动。

无论在“天宫”还是在地面做此实验（ ）A．小球的速度大小均发生变化B．小球的向心加速度大小均发生变化C．细绳的拉力对小球均不做功D．细绳的拉力大小均发生变化5. （2022·全国乙卷）固定于竖直平面内的光滑大圆环上套有一个小环，小环从大圆环顶端P点由静止开始自由下滑，在下滑过程中，小环的速率正比于（）A. 它滑过的弧长B. 它下降的高度C. 它到P点的距离D. 它与P点的连线扫过的面积6．（2022·河北邯郸·二模）某小组设计一个离心调速装置如图所示，质量为m的滑块Q可沿竖直轴无摩擦地滑动，并用原长为l的轻弹簧与O点相连，两质量均为m的小球1P和2P对称地安装在轴的两边，1P和2P与O、1P和2P与Q间用四根长度均为l的轻杆通过光滑铰链连接起来。

高中物理高考物理生活中的圆周运动解题技巧分析及练习题(含答案)一、高中物理精讲专题测试生活中的圆周运动1．有一水平放置的圆盘，上面放一劲度系数为k的弹簧，如图所示，弹簧的一端固定于轴O上，另一端系一质量为m的物体A，物体与盘面间的动摩擦因数为μ，开始时弹簧未发生形变，长度为l．设最大静摩擦力大小等于滑动摩擦力．求：（1）盘的转速ω0多大时，物体A开始滑动？（2）当转速缓慢增大到2ω0时，A仍随圆盘做匀速圆周运动，弹簧的伸长量△x是多少？【答案】（1）glμ（2）34mglkl mgμμ-【解析】【分析】（1）物体A随圆盘转动的过程中，若圆盘转速较小，由静摩擦力提供向心力；当圆盘转速较大时，弹力与摩擦力的合力提供向心力．物体A刚开始滑动时，弹簧的弹力为零，静摩擦力达到最大值，由静摩擦力提供向心力，根据牛顿第二定律求解角速度ω0．（2）当角速度达到2ω0时，由弹力与摩擦力的合力提供向心力，由牛顿第二定律和胡克定律求解弹簧的伸长量△x．【详解】若圆盘转速较小，则静摩擦力提供向心力，当圆盘转速较大时，弹力与静摩擦力的合力提供向心力．（1）当圆盘转速为n0时，A即将开始滑动，此时它所受的最大静摩擦力提供向心力，则有：μmg＝mlω02，解得：ω0=g l μ即当ω0＝glμA开始滑动．（2）当圆盘转速达到2ω0时，物体受到的最大静摩擦力已不足以提供向心力，需要弹簧的弹力来补充，即：μmg+k△x＝mrω12，r=l+△x解得：34mgl xkl mgμμ-V＝【点睛】当物体相对于接触物体刚要滑动时，静摩擦力达到最大，这是经常用到的临界条件．本题关键是分析物体的受力情况．2．如图所示，竖直圆形轨道固定在木板B 上，木板B 固定在水平地面上，一个质量为3m 小球A 静止在木板B 上圆形轨道的左侧．一质量为m 的子弹以速度v 0水平射入小球并停留在其中，小球向右运动进入圆形轨道后，会在圆形轨道内侧做圆周运动．圆形轨道半径为R ，木板B 和圆形轨道总质量为12m ，重力加速度为g ，不计小球与圆形轨道和木板间的摩擦阻力．求：(1)子弹射入小球的过程中产生的内能；(2)当小球运动到圆形轨道的最低点时，木板对水平面的压力；(3)为保证小球不脱离圆形轨道，且木板不会在竖直方向上跳起，求子弹速度的范围．【答案】(1)2038mv (2) 2164mv mg R+(3)042v gR ≤或04582gR v gR ≤≤【解析】本题考察完全非弹性碰撞、机械能与曲线运动相结合的问题． (1)子弹射入小球的过程，由动量守恒定律得：01(3)mv m m v =+ 由能量守恒定律得：220111422Q mv mv =-⨯ 代入数值解得：2038Q mv =(2)当小球运动到圆形轨道的最低点时，以小球为研究对象，由牛顿第二定律和向心力公式得211(3)(3)m m v F m m g R+-+=以木板为对象受力分析得2112F mg F =+ 根据牛顿第三定律得木板对水平的压力大小为F 2木板对水平面的压力的大小202164mv F mg R=+(3)小球不脱离圆形轨有两种可能性：①若小球滑行的高度不超过圆形轨道半径R由机械能守恒定律得：()()211332m m v m m gR +≤+ 解得：042v gR ≤②若小球能通过圆形轨道的最高点小球能通过最高点有：22(3)(3)m m v m m g R++≤由机械能守恒定律得：221211(3)2(3)(3)22m m v m m gR m m v +=+++ 代入数值解得：045v gR ≥要使木板不会在竖直方向上跳起，木板对球的压力：312F mg ≤在最高点有：233(3)(3)m m v F m m g R+++=由机械能守恒定律得：221311(3)2(3)(3)22m m v m m gR m m v +=+++ 解得：082v gR ≤综上所述为保证小球不脱离圆形轨道，且木板不会在竖直方向上跳起，子弹速度的范围是042v gR ≤或04582gR v gR ≤≤3．如图所示，在光滑的圆锥体顶部用长为的细线悬挂一质量为的小球，因锥体固定在水平面上，其轴线沿竖直方向，母线与轴线之间的夹角为，物体绕轴线在水平面内做匀速圆周运动，小球静止时细线与母线给好平行，已知，重力加速度g 取若北小球运动的角速度，求此时细线对小球的拉力大小。

2022年高考物理热点考点专题09 圆周运动一、单选题1．秋千是朝鲜妇女最喜欢的活动之一，小华荡秋千时，秋千摆起的最大角度为60°，小华的重心到悬点的距离恒定为L，小华受到的重力大小为G，重力加速度大小为g，忽略绳的质量和空气阻力，下列关于小华在最低点时的说法正确的是（）A．处于失重状态B．速度等于√2gLC．向心力大小为2G D．受到秋千的作用力大小为2G2．如图所示，在匀强电场中，一长为L的绝缘细线一端固定于O点，另一端系一个质量为m、电荷量为q的带正电小球。

现使其在竖直平面内绕O点做完整的圆周运动。

AB、CD分别为圆的水平和竖直直径。

已知电场方向斜向右上方且与水平方向夹角为45°（图中未画出），场强大小为√2mgq，重力加速度为g。

则下列说法正确的是（）A．小球运动的最小速度为√2gLB．小球运动到A点时的机械能最小C．小球运动到B点时的动能最大D．小球从C运动到D的过程中合力做功不为零3．如图所示，甲、乙两人分别站在圆周上两个位置，两位置的连线为圆的一条直径。

他们同时按顺时针方向沿圆周运动。

甲、乙做匀速圆周运动的速度大小分别为v1、v2，经时间t后，甲第一次追上乙。

则该圆的直径为（）A．2t(v1+v2)πB．2t(v2−v1)πC．2t(v1−v2)πD．t(v1−v2)π4．如图所示，在水平圆盘同一直径圆心两侧放着两可视为质点的物体A和B，A的质量是B质量的3倍，B到圆心的距离是A到圆心距离的3倍，B与圆盘间的动摩擦因数是A与圆盘间动摩擦因数的3倍，若圆盘从静止开始绕转轴00′缓慢地加速转动。

则下列判断正确的是（）A．A物体将先滑动B．B物体将先滑动C．若两物体之间用细线连接且细线刚好伸直，则在细线断前，整体会向B端移动D．若两物体之间用细线连接且细线刚好伸直，则在细线断前，整体不会移动5．如图所示，a、b、c、d为四个质量均为m的带电小球，恰好构成“三星拱月”之形。

高考必备物理生活中的圆周运动技巧全解及练习题(含答案)含解析一、高中物理精讲专题测试生活中的圆周运动1．如图所示，带有14光滑圆弧的小车A 的半径为R ，静止在光滑水平面上．滑块C 置于木板B 的右端，A 、B 、C 的质量均为m ，A 、B 底面厚度相同．现B 、C 以相同的速度向右匀速运动，B 与A 碰后即粘连在一起，C 恰好能沿A 的圆弧轨道滑到与圆心等高处．则：(已知重力加速度为g ) (1)B 、C 一起匀速运动的速度为多少？(2)滑块C 返回到A 的底端时AB 整体和C 的速度为多少？【答案】（1）023v gR =（2）123gRv =253gR v =【解析】本题考查动量守恒与机械能相结合的问题．(1)设B 、C 的初速度为v 0，AB 相碰过程中动量守恒，设碰后AB 总体速度u ，由02mv mu =，解得02v u =C 滑到最高点的过程： 023mv mu mu +='222011123222mv mu mu mgR +⋅=+'⋅ 解得023v gR =(2)C 从底端滑到顶端再从顶端滑到底部的过程中，满足水平方向动量守恒、机械能守恒，有01222mv mu mv mv +=+22220121111222222mv mu mv mv +⋅=+⋅ 解得：123gRv =253gR v =2．如图所示，半径为R 的四分之三圆周轨道固定在竖直平面内，O 为圆轨道的圆心，D 为圆轨道的最高点，圆轨道内壁光滑，圆轨道右侧的水平面BC 与圆心等高．质量为m 的小球从离B 点高度为h 处（332R h R ≤≤）的A 点由静止开始下落，从B 点进入圆轨道，重力加速度为g ）．（1）小球能否到达D 点？试通过计算说明； （2）求小球在最高点对轨道的压力范围；（3）通过计算说明小球从D 点飞出后能否落在水平面BC 上，若能，求落点与B 点水平距离d 的范围．【答案】（1）小球能到达D 点；（2）03F mg ≤'≤；（3）()()21221R d R ≤≤【解析】 【分析】 【详解】（1）当小球刚好通过最高点时应有：2Dmv mg R =由机械能守恒可得：()22Dmv mg h R -=联立解得32h R =，因为h 的取值范围为332R h R ≤≤，小球能到达D 点； （2）设小球在D 点受到的压力为F ，则2Dmv F mg R ='+ ()22Dmv mg h R ='- 联立并结合h 的取值范围332R h R ≤≤解得：03F mg ≤≤ 据牛顿第三定律得小球在最高点对轨道的压力范围为：03F mg ≤'≤（3）由（1）知在最高点D 速度至少为min D v gR =此时小球飞离D 后平抛，有：212R gt =min min D x v t =联立解得min 2x R R =>，故能落在水平面BC 上，当小球在最高点对轨道的压力为3mg 时，有：2max 3Dv mg mg m R+=解得max 2D v gR = 小球飞离D 后平抛212R gt ='， max max D x v t ='联立解得max 22x R =故落点与B 点水平距离d 的范围为：()()21221R d R -≤≤-3．如图所示，在竖直平面内有一半径为R 的14光滑圆弧轨道AB ，与水平地面相切于B 点。

【例1】 如图所示的装置是在竖直平面内放置光滑的绝缘轨道，处于水平向右的匀强电场中，以带负电荷的小球从高h 的A 处静止开始下滑，沿轨道ABC 运动后进入圆环内作圆周运动。

已知小球所受到电场力是其重力的3／4，圆滑半径为R ，斜面倾角为θ，s BC =2R 。

若使小球在圆环内能作完整的圆周运动，h 至少为多少？【例2】如图所示，用细绳一端系着的质量为M =0.6kg 的物体A 静止在水平转盘上，细绳另一端通过转盘中心的光滑小孔O 吊着质量为m =0.3kg 的小球B ，A 的重心到O 点的距离为0.2m ．若A 与转盘间的最大静摩擦力为f =2N ，为使小球B 保持静止，求转盘绕中心O 旋转的角速度ω的取值范围．【例3】一内壁光滑的环形细圆管，位于竖直平面内，环的半径为R （比细管的半径大得多）．在圆管中有两个直径与细管内径相同的小球（可视为质点）．A 球的质量为m 1，B 球的质量为m 2．它们沿环形圆管顺时针运动，经过最低点时的速度都为v 0．设A 球运动到最低点时，B 球恰好运动到最高点，若要此时两球作用于圆管的合力为零，那么m 1、m 2、R 与v 0应满足的关系式是______．【例4】如图所示，滑块在恒定外力作用下从水平轨道上的A 点由静止出发到B 点时撤去外力，又沿竖直面内的光滑半圆形轨道运动，且恰好通过轨道最高点C ，滑块脱离半圆形轨道后又刚好落到原出发点A ，试求滑块在AB 段运动过程中的加速度.例5、如图所示，M 为悬挂在竖直平面内某一点的木质小球，悬线长为L ，质量为m 的子弹以水平速度V 0射入球中而未射出，要使小球能在竖直平面内运动，且悬线不发生松驰，求子弹初速度V 0应满足的条件。

分两种情况：【例6】火车转弯：设火车弯道处内外轨高度差为h ，内外轨间距L ，转弯半径R 。

由于外轨略高于内轨，使得火车所受重力和支持力的合力F 合提供向心力。

①当火车行驶速率V 等于V 0时，F 合=F 向，内外轨道对轮缘都没有侧压力 ②当火车行驶V 大于V 0时，F 合<F 向，外轨道对轮缘有侧压力，F 合+N=mv 2/R ③当火车行驶速率V 小于V 0时，F 合>F 向，内轨道对轮缘有侧压力，F 合-N'=mv 2/R即当火车转弯时行驶速率不等于V 0时，其向心力的变化可由内外轨道对轮缘侧压力自行调节，但调节程度不宜过大，以免损坏轨道。

高考物理生活中的圆周运动试题(有答案和解析)一、高中物理精讲专题测试生活中的圆周运动1．如图所示，粗糙水平地面与半径为R =0.4m 的粗糙半圆轨道BCD 相连接，且在同一竖直平面内，O 是BCD 的圆心，BOD 在同一竖直线上．质量为m =1kg 的小物块在水平恒力F =15N 的作用下，从A 点由静止开始做匀加速直线运动，当小物块运动到B 点时撤去F ，小物块沿半圆轨道运动恰好能通过D 点，已知A 、B 间的距离为3m ，小物块与地面间的动摩擦因数为0.5，重力加速度g 取10m/s 2．求： （1）小物块运动到B 点时对圆轨道B 点的压力大小． （2）小物块离开D 点后落到地面上的点与D 点之间的距离【答案】（1）160N （2）2 【解析】 【详解】（1）小物块在水平面上从A 运动到B 过程中，根据动能定理，有： （F -μmg ）x AB =12mv B 2-0 在B 点，以物块为研究对象，根据牛顿第二定律得：2Bv N mg m R-=联立解得小物块运动到B 点时轨道对物块的支持力为：N =160N由牛顿第三定律可得，小物块运动到B 点时对圆轨道B 点的压力大小为：N ′=N =160N （2）因为小物块恰能通过D 点，所以在D 点小物块所受的重力等于向心力，即：2Dv mg m R=可得：v D =2m/s设小物块落地点距B 点之间的距离为x ，下落时间为t ，根据平抛运动的规律有： x =v D t ，2R =12gt 2解得：x =0.8m则小物块离开D 点后落到地面上的点与D 点之间的距离20.82m l x ==2．如图所示，在竖直平面内固定有两个很靠近的同心圆形轨道，外圆ABCD 光滑，内圆的上半部分B′C′D′粗糙，下半部分B′A′D′光滑．一质量m=0.2kg 的小球从轨道的最低点A 处以初速度v 0向右运动，球的直径略小于两圆间距，球运动的轨道半径R=0.2m ，取g=10m/s 2．（1）若要使小球始终紧贴着外圆做完整的圆周运动，初速度v 0至少为多少？ （2）若v 0=3m/s ，经过一段时间小球到达最高点，内轨道对小球的支持力F C =2N ，则小球在这段时间内克服摩擦力做的功是多少？（3）若v 0=3.1m/s ，经过足够长的时间后，小球经过最低点A 时受到的支持力为多少？小球在整个运动过程中减少的机械能是多少？（保留三位有效数字） 【答案】（1）0v 10m/s （2）0.1J （3）6N ；0.56J 【解析】 【详解】（1）在最高点重力恰好充当向心力2Cmv mg R= 从到机械能守恒220112-22C mgR mv mv =解得010m/s v =（2）最高点'2-CC mv mg F R= 从A 到C 用动能定理'22011-2--22f C mgR W mv mv =得=0.1J f W（3）由0=3.1m/s<10m/s v 于，在上半圆周运动过程的某阶段，小球将对内圆轨道间有弹力，由于摩擦作用，机械能将减小．经足够长时间后，小球将仅在半圆轨道内做往复运动．设此时小球经过最低点的速度为A v ，受到的支持力为A F212A mgR mv =2-AA mv F mg R= 得=6N A F整个运动过程中小球减小的机械能201-2E mv mgR ∆=得=0.56J E ∆3．如图所示，水平转台上有一个质量为m 的物块，用长为2L 的轻质细绳将物块连接在转轴上，细绳与竖直转轴的夹角θ＝30°，此时细绳伸直但无张力，物块与转台间动摩擦因数为μ，设最大静摩擦力等于滑动摩擦力．物块随转台由静止开始缓慢加速转动，重力加速度为g ，求：（1）当转台角速度ω1为多大时，细绳开始有张力出现； （2）当转台角速度ω2为多大时，转台对物块支持力为零； （3）转台从静止开始加速到角速度3gLω=的过程中，转台对物块做的功．【答案】（1）1g Lμω=（2）233g Lω=（3）132mgL⎛ ⎝ 【解析】 【分析】 【详解】（1）当最大静摩擦力不能满足所需要向心力时，细绳上开始有张力：212sin mg m L μωθ=⋅代入数据得1g Lμω=（2）当支持力为零时，物块所需要的向心力由重力和细绳拉力的合力提供22tan 2sin mg m L θωθ=⋅代入数据得233g Lω=（3）∵32ωω>，∴物块已经离开转台在空中做圆周运动．设细绳与竖直方向夹角为α，有23tan 2sin mg m L αωα=⋅代入数据得60α=︒转台对物块做的功等于物块动能增加量与重力势能增加量的总和即231(2sin 60)(2cos302cos60)2W m L mg L L ω=⋅+-o o o 代入数据得：1(3)2W mgL =+【点睛】本题考查牛顿运动定律和功能关系在圆周运动中的应用，注意临界条件的分析，至绳中出现拉力时，摩擦力为最大静摩擦力；转台对物块支持力为零时，N=0，f=0．根据能量守恒定律求转台对物块所做的功．4．如图甲所示，轻质弹簧原长为2L ，将弹簧竖直放置在水平地面上，在其顶端将一质量为5m 的物体由静止释放，当弹簧被压缩到最短时，弹簧长度为L ．现将该弹簧水平放置，如图乙所示．一端固定在A 点，另一端与物块P 接触但不连接．AB 是长度为5L 的水平轨道，B 端与半径为L 的光滑半圆轨道BCD 相切，半圆的直径BD 在竖直方向上．物块P 与AB 间的动摩擦因数0.5μ=，用外力推动物块P ，将弹簧压缩至长度为L 处，然后释放P ，P 开始沿轨道运动，重力加速度为g ．（1）求当弹簧压缩至长度为L 时的弹性势能p E ；（2）若P 的质量为m ，求物块离开圆轨道后落至AB 上的位置与B 点之间的距离； （3）为使物块P 滑上圆轨道后又能沿圆轨道滑回，求物块P 的质量取值范围．【答案】(1)5P E mgL = (2) 22S L = (3)5532m M m ＃ 【解析】【详解】（1）由机械能守恒定律可知：弹簧长度为L 时的弹性势能为（2）设P 到达B 点时的速度大小为，由能量守恒定律得：设P 到达D 点时的速度大小为，由机械能守恒定律得：物体从D 点水平射出，设P 落回到轨道AB 所需的时间为θ θ 22S L =（3）设P 的质量为M ，为使P 能滑上圆轨道，它到达B 点的速度不能小于零 得54mgL MgL μ> 52M m <要使P 仍能沿圆轨道滑回，P 在圆轨道的上升高度不能超过半圆轨道的中点C ，得212BMv MgL '≤ 2142p BE Mv MgL μ='+5．如图为某种鱼饵自动投放器中的投饵管装置示意图，其下半部AB 是一长为2R 的竖直细管，上半部BC 是半径为R 的四分之一圆弧弯管，管口沿水平方向，AB 管内有一原长为R 、下端固定的轻质弹簧．投饵时，每次总将弹簧长度压缩到0.5R 后锁定，在弹簧上段放置一粒鱼饵，解除锁定，弹簧可将鱼饵弹射出去．设质量为m 的鱼饵到达管口C 时，对管壁的作用力恰好为零．不计鱼饵在运动过程中的机械能损失，且锁定和解除锁定时，均不改变弹簧的弹性势能．已知重力加速度为g ．求： (1)质量为m 的鱼饵到达管口C 时的速度大小v 1; (2)弹簧压缩到0.5R 时的弹性势能E p ;(3)已知地面欲睡面相距1.5R ，若使该投饵管绕AB 管的中轴线OO ' 。

2024高考物理高频考点重点新题精选专题15圆周运动1、（2024上海市崇明县期末）荡秋千是儿童宠爱旳一项体育运动，当秋千荡到最高点时，小孩旳加速度方向是图中旳………………（ ） A ．a 方向 B ．b 方向 C ．c 方向D ．d 方向答案：B解析：当秋千荡到最高点时，小孩旳加速度方向是图中旳b 方向，选项B 正确.2. （2024福建省二校联考）质量为60 kg 旳体操运动员做“单臂大回环”，用一只手抓住单杠，伸展身体，以单杠为轴做圆周运动．如图所示，此过程中，运动员到达最低点时手臂受旳拉力至少约为(忽视空气阻力，g ＝10 m/s 2) ( )A ．600 NB ．2400 NC ．3000 ND ．3600 N3．（2024年浙江省宁波市期末）如图所示，一偏心轮绕垂直纸面旳轴O 匀速转动，a 和b 是轮上质量相等旳两个质点，则偏心轮转动过程中a 、b 两质点 A ．角速度大小相同 B ．向心力大小相同ab第13题cdC．线速度大小相同D．向心加速度大小相同答案：A解析：在同一偏心轮上，偏心轮转动过程中a、b两质点角速度大小相同，选项A正确.4．（2024江苏盐城明达中学测试）无极变速可以在变速范围内随意连续地变换速度，性能优于传统旳档位变速器，许多种高档汽车都应用无极变速.如图所示是截锥式无极变速模型示意图，两个锥轮之间有一个滚动轮，主动轮、滚动轮、从动轮之间靠着彼此之间旳摩擦力带动.当位于主动轮和从动轮之间旳滚动轮从左向右移动时，从动轮转速增加.当滚动轮位于主动轮直径D1、从动轮直径D2旳位置时，主动轮转速n1、从动轮转速n2旳关系是A． B．C． D．答案：B解析：主动轮、滚动轮、从动轮之间靠着彼此之间旳摩擦力带动，接触处线速度大小相等.由ω1r1=ω2r2，ω=2πn，可得，选项B正确.5．（2024重庆一中）两个质量相同旳小球a、b用长度不等旳细线拴在天花板上旳同一点并在空中同一水平面内做匀速圆周运动，如题图所示，则a、b两小球具有相同旳A.角速度B.线速度C.向心力D.向心加速度6．（2024四川资阳诊断）如图所示，水平放置旳两个用相同材料制成旳轮P和Q 靠摩擦传动，两轮旳半径R∶r =2∶1.当主动轮Q匀速转动时，在Q轮边缘上放置旳小木块恰能相对静止在Q轮边缘上，此时Q轮转动旳角速度为ω1，木块旳向心加速度为a1；若变更转速，把小木块放在P轮边缘也恰能静止，此时Q轮转动旳角速度为ω2，木块旳向心加速度为a 2，则A ．B ．C ．121=1aaD ．7（2024温州八校联考）如图2所示，汽车车厢顶部悬挂一个轻质弹簧，弹簧下端拴一个质量为m 旳小球，当汽车以某一速度在水平地面上匀速行驶时弹簧长度为L 1；当汽车以同一速度匀速率通过一个桥面为圆弧形凸形桥旳最高点时，弹簧长度为L 2，下列答案中正确旳是（ ）A ．21L L >B ．21L L =C ．21L L < D ．前三种状况均有可能 答案：A解析：当汽车以同一速度匀速率通过一个桥面为圆弧形凸形桥旳最高点时，加速度向下，处于失重状态，21L L >，选项A 正确.8. （2024广西三校联考）如图所示，一圆盘可绕通过其中心且垂直于盘面旳竖直轴转动，盘上距中心r 处放置一个质量为m 旳物体，物体及盘面间滑动摩擦因数为μ，重力加速度为g.一段时间内视察到圆盘以角速度ω做匀速转动，物体随圆盘一起（相对静止）运动.这段时间内图2A ．物体受到圆盘对它旳摩擦力，大小肯定为μmg ，方向及物体线速度方向相同 B ．物体受到圆盘对它旳摩擦力，大小肯定为mω2r ，方向指向圆盘中心 C ．物体受到圆盘对它旳摩擦力，大小可能小于μmg ，方向指向圆盘中心D.物体受到圆盘对它旳摩擦力，大小可能小于m ω2r ，方向背离圆盘中心9．（2024广州调研）如图所示，当正方形薄板围着过其中心O 并及板垂直旳转动轴转动时，板上A 、B 两点旳 A ．角速度之比ωA ∶ωB =1∶1 B ．角速度之比ωA ∶ωB =1∶2 C ．线速度之比v A ∶v B =2∶1 D ．线速度之比v A ∶v B =1∶2 答案：AD解析：板上A 、B 两点旳角速度相等，角速度之比ωA ∶ωB =1∶1，选项A 正确B 错误；线速度v=ωr ，线速度之比v A ∶v B =1∶2，选项C 错误D 正确.10．（2024山东济南期中检测）如图所示，细绳旳一端悬于O 点，另一端系一小球；在O 点正下方有一钉子.现使小球由高处摆下，当绳摆到竖直位置时及钉子相碰，则绳碰钉子前、后瞬间相比（不计空气阻力）（ ）A ．小球旳线速度变大B ．小球旳角速度变大OA A BOC ．小球旳向心加速度减小D ．绳子旳拉力变大11. （2024山东济南测试）游乐场中有一种叫“空中飞椅”旳设施，其基本装置是将绳子上端固定在转盘旳边缘上，绳子下端连接座椅，人坐在座椅上随转回旋转而在空中飞旋，若将人和座椅看成质点，简化为如图所示旳模型，其中P 为处于水平面内旳转盘，可绕竖直转轴OO ′转动，已知绳长为l ，质点旳质量为m ，转盘静止时悬绳及转轴间旳距离为d ．让转盘由静止渐渐加速转动，经过一段时间后质点及转盘一起做匀速圆周运动，此时绳及竖直方向旳夹角为θ，不计空气阻力及绳重，绳子不行伸长，则质点从静止到做匀速圆周运动旳过程中，绳子对质点做旳功为 （ ） A ．)cos 1(tan )sin (21θθθ-++mgl l d mgB ．)cos 1(tan 21θθ-+mgl mgdC .D ．12．（2024四川资阳诊断）如图所示，水平放置旳两个用相同材料制成旳轮P和Q靠摩擦传动，两轮旳半径R∶r =2∶1.当主动轮Q匀速转动时，在Q轮边缘上放置旳小木块恰能相对静止在Q轮边缘上，此时Q轮转动旳角速度为ω1，木块旳向心加速度为a1；若变更转速，把小木块放在P轮边缘也恰能静止，此时Q 轮转动旳角速度为ω2，木块旳向心加速度为a2，则A．B．C．121 = 1aaD．答案：AC解析：依据题述，a1=ω12 r，ma1=μmg；联立解得μg =ω12 r.小木块放在P轮边缘也恰能静止，μg =ω2R=2ω2r.ωR=ω2 r，联立解得，选项A正确B 错误；a2=μg =ω2R，选项C正确D错误.13．（2024北京四中摸底）如图，两个半径均为R旳1/4光滑圆弧对接于O 点，有物体从上面圆弧旳某点C以上随意位置由静止下滑（C点未标出），都能从O点平抛出去，则（）A．∠COO＝60°1B．∠COO＝45°1C．落地点距O最远为2R2最近为RD．落地点距O214（2024四川绵阳一诊）如图所示，半径为R、圆心角为600旳光滑圆弧槽，固定在高为h旳平台上，小物块从圆弧槽旳最高点A静止起先滑下，滑出槽口点为圆心旳圆弧B时速度水平向左，小物块落在地面上C点， B、C两点在以O2在B点正下方地面上，则上，O2A. 4R=hB.2R=hC.R=hD. R=2h15（2024中原名校联考）如图所示，一根不行伸长旳轻绳一端拴着一个小球，另一端固定在竖直杆上，当竖直杆以角速度ω转动时，小球跟着杆一起做匀速圆周运动，此时绳及竖直方向旳夹角为θ，下列关于ω及θ关系旳图象正确旳是（）16．（2024山西忻州一中检测）如图两段长均为L旳轻质线共同系住一个质量为m 旳小球，另一端分别固定在等高旳A、B两点，A、B两点间距也为L，今使小球在竖直平面内做圆周运动，当小球到达最高点时速率为v，两段线中张力恰好均为零，若小球到达最高点时速率为2v，则此时每段线中张力大小为A3mg B．2mgC．3mg D．4mg答案：A17. （2024安徽皖南八校联考）2024年奥运会在英国伦敦实行，已知伦敦旳地理位里是北纬52°，经度0°；而北京旳地理位里是北纬40°，东经116°，则下列推断正确旳是A．.随地球自转运动旳线速度大小，伦教奥运竞赛场馆及北京奥运竞赛场馆相同B．.随地球自转运动旳线速度大小，伦敦奥运竞赛场馆比北京奥运竞赛场馆大C．.随地球自转运动旳向心加速度大小，伦教奥运竞赛场馆比北京奥运竞赛场馆小D．站立在领奖台上旳运动员，其随地球自转旳向心加速度就是重力加速度18、(2024洛阳期中)如图11所示，具有圆锥形态旳回转器（陀螺）绕它旳轴线在光滑旳桌面上以角速度ω快速旋转，同时以速度v向右运动，若回转器旳轴线始终保持竖直，为使回转器从桌子旳边沿滑出时不会及桌子边缘发生碰撞，速度v至少应等于（设回转器旳高为H，底面半径为R，不计空气对回转器旳作用）A.ωRB. ωHC.D. 答案：D解析：依据平抛运动规律，R=vt ，H=12gt 2，联立解得v=.19．(2024洛阳期中)如图4所示，长为L 旳轻杆，一端固定一个质量为m 旳小球，另一端固定在水平转轴O 上，杆随转轴O 在竖直平面内匀速转动，角速度为ω，某时刻杆对球旳作用力恰好及杆垂直，则此时杆及水平面旳夹角θ是 A ．sin θ=2L gω B ．tan θ=2L gωC ．sin θ=2g Lω D ．tan θ=2g Lω20．（2024深圳市南山区期末）四个质量相同旳物体a 、b 、c 、d ，a 做匀速直线运动、b 做匀速圆周运动，c 做匀减速直线运动，d 做平抛运动，其中 Ａ．速度保持不变旳仅是物体a Ｂ．加速度保持不变旳仅是物体b Ｃ．动能保持不变旳仅是物体a 、b Ｄ．动量保持不变旳仅是物体b 、c 、dO╮θ图4答案：AC解析：速度保持不变旳仅是物体a，加速度保持不变旳仅是物体a、c、d，动能保持不变旳仅是物体a b，、动量保持不变旳仅是物体a，选项AC正确.21．（湖北省荆门市2024-2025学年度高三元月调考）如图所示，地球可以看成一个巨大旳拱形桥，桥面半径R=6400km，地面上．．．行驶旳汽车重力G=3×104N，在汽车旳速度可以达到须要旳随意值，且汽车不离开地面旳前提下，下列分析中正确旳是A．汽车旳速度越大，则汽车对地面旳压力也越大B．不论汽车旳行驶速度如何，驾驶员对座椅压力大小都等于3×104NC．不论汽车旳行驶速度如何，驾驶员对座椅压力大小都小于他自身旳重力D．假如某时刻速度增大到使汽车对地面压力为零，则此时驾驶员会有超重旳感觉22．（12分）（2024山东省临沂市质检）游乐园旳小型“摩天轮”上对称站着质量均为m旳8位同学，如图所示，“摩天轮”在竖直平面内逆时针匀速转动，若某时刻转到顶点a上旳甲同学让一小重物做自由落体运动，并马上通知下面旳同学接住，结果重物掉落时正处在c处（如图）旳乙同学恰好在第一次到达最低点b处接到，己知“摩天轮”半径为R，重力加速度为g，（不计人和吊篮旳大小及重物旳质量）．问：（1）接住前重物下落运动旳时间t=?（2）人和吊篮随“摩天轮”运动旳线速度大小v=?=?（3）乙同学在最低点处对地板旳压力FN23.（8分）（2024浙江金华月考）如图为某工厂生产流水线上水平传输装置旳俯视图，它由传送带和转盘组成.物品从A处无初速放到传送带上，运动到B处后进入匀速转动旳水平转盘，设物品进入转盘时速度大小不发生变更，此后随转盘一起运动(无相对滑动)到C处被取走装箱.已知A、B两处旳距离L=10m，传送带旳传输速度v=2m/s，物品在转盘上及轴O旳距离R=4m，物品及传送带间旳动摩擦因数μ=0.25.取g=10m/s2.（1）物品从A处运动到B处旳时间t；（2）质量为2kg旳物品随转盘一起运动旳静摩擦力为多大？解析．（8分） (1)物品先在传送带上做初速为零旳匀加速直线运动: a=μg=2.5m/s2.24、（16分）（16分）（2024福建惠安月考）地面上有一个半径为R旳圆形跑道，高为h旳平台边缘上旳P点在地面上P′点旳正上方，P′及跑道圆心O旳距离为L（L>R），如图所示.跑道上停有一辆小车，现从P点水平抛出小沙袋，使其落入小车中（沙袋所受空气阻力不计）.问：（1）当小车分别位于A点和B点时（∠AOB＝90°），沙袋被抛出时旳初速度各为多大？（2）若小车在跑道上运动，则沙袋被抛出时旳初速度在什么范围内？（3）若小车沿跑道顺时针运动，当小车恰好经过A点时，将沙袋抛出，为使沙袋能在B处落入小车中，小车旳速率v应满意什么条件？解析:（1）沙袋从P点被抛出后做平抛运动，设它旳落地时间为t，25.(2024洛阳期中)如图18所示，装置BO′O可绕竖直轴O′O转动，可视为质点旳小球A及两细线连接后分别系于B、C两点，装置静止时细线AB水平，细线AC 及竖直方向旳夹角︒=37θ.已知小球旳质量m=1kg ，细线AC 长l ＝1m ，B 点距C 点旳水平和竖直距离相等.（重力加速度g 取10m/s 2,5437cos ,5337sin =︒=︒）（1）若装置匀速转动旳角速度为1ω时，细线AB 上旳张力为0而细线AC 及竖直方向旳夹角仍为37°，求角速度1ω旳大小； （2）若装置匀速转动旳角速度，求细线AC 及竖直方向旳夹角（3）装置可以以不同旳角速度匀速转动，试通过计算在坐标图19中画出细线AC 上张力T 随角速度旳平方2ω变更旳关系图像解：（1）当细线AB 上旳张力为0时，小球旳重力和细线AC 张力旳合力供应小球圆周运动旳向心力，有：l m T 2ω= 2分○3ωω<2时，细线在竖直方向绷直，仍旧由细线AC 上张力旳水平重量供应小球做圆周运动须要旳向心力：26．（10分）（2024安徽江南十校摸底）如图所示，水平放置旳圆筒绕其中心对称轴'OO 匀速转动，转动旳角速度 2.5ωπ= rad/s ，桶壁上P 处有一小圆孔，桶壁很薄，桶旳半径R=2m ，当圆孔正上方h=3.2m 处有一小球由静止起先下落，已知圆孔旳半径略大于小球旳半径，试通过计算推断小球是否会和圆筒碰撞（空气阻力不计，g 取210/m s ）.。