下载文档原格式
GRIDDI NG OF DISCRETE POTENTI AL FIE LD DATAFANG Y ang(School of G eodesy and G eomatics ,Wuhan University ,129Luoyu Road ,Wuhan 430079,China )ABS TRACT The methods of continuous curvature splines in tension ,minimum curvature andShepard ’s method were compared and analyzed using isostatic anomaly data.The results show that continuous curvature splines in tension method has better global properties ,higher preci 2sion and good result of interpolation or extrapolation in poorly constrained regions.KEYWORDS gridding ;continuous curvature splines in tension ;minimum curvature ;shepard项目来源:极地测绘科学国家测绘局重点实验室基金资助项目(200802);地球空间环境与大地测量教育部重点实验室开放基金资助项目(080201)。
文章编号:100723817(2009)0620048202中图分类号:P223 文献标志码:B局部地区布格重力异常的计算王 伟1,2(1武汉大学测绘学院;2极地测绘科学国家测绘局重点实验室,武汉市珞喻路129号,430079)摘 要 概括了空间重力异常和布格重力异常的计算方法,计算了中安第斯山局部地区的空间重力异常、地形改正和布格重力异常,发现了其在海拔较高地区多为负值。
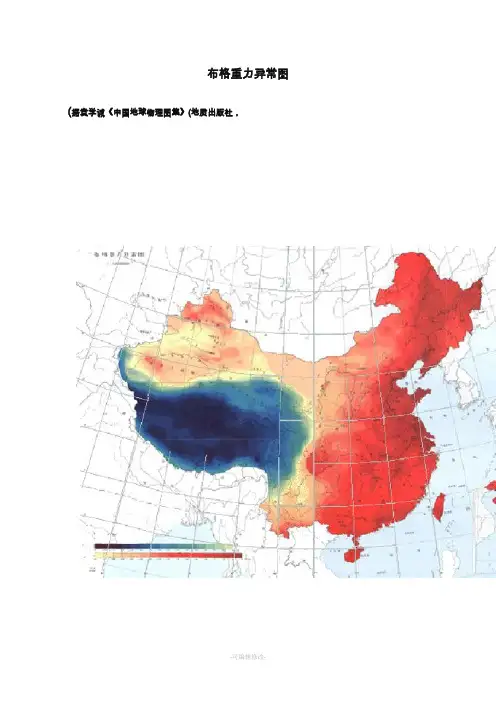
布格重力异常图(据袁学诚《中国地球物理图集》(地质出版社，本图使用了我国80年代以来区域重力调查的最新成果。
东部地区布格重力均方误差小于±2×10－5m/s2，一般为±0.6×10－5m/s2～±1.5×10－5m/s2；西部地区的青藏、内蒙古西部、川滇甘西部及南疆，布格重力均方误差小于±3×10－5m/s2，一般为±1×10－5m/s2～±2×10－5m/s2。
全部资料整理和改算，统一采用波茨坦重力系统；统一采用赫尔默特（1901～1909年）正常重力公式；统一采用重力高度改正系数和中间层密度值（2.67g/cm3）以及统一采用166.7km 的地形改正半径。
我国的布格重力异常是以青藏高原为低值中心（约－550×10－5m/s2），向北向东逐渐升高，形成东高西低、北高南低的总趋势，并被纵、横贯于全国的两大梯级带分割成台阶状的三级区域场，在此背景上叠加有多个形态各异的局部异常和规模较小的梯级带，构成我国复杂而独特的布格重力异常场。
1．重力梯级带（1）大兴安岭－太行山－武陵山大型重力梯级带。
（2）青藏高原周边大型重力梯级带。
2．区域重力场我国大陆区域重力场呈现三级台阶状，由东向西逐次降低，它们被两大梯级带分隔和连接。
1）东部区域重力高，即第一台阶。
2）中部弧形区域重力场，即第二台阶。
3）青藏区域重力低，即第三台阶。
3．局部重力异常1）走向基本为东西向的布格重力异常带。
有天山－阴山－燕山重力低异常带、秦岭－大巴山－大别山重力低异常带，苗岭－南岭－武夷山重力低异常带、唐古拉山重力低异常带及冈底斯重力低异常等。
2）等轴状或团块状布格重力异常。
准噶尔、塔里木、四川等盆地中多出现这类重力高或重力低异常。
3）走向为北东的布格重力异常带。
多呈线状或串珠状出现在东部地区，如长白山重力低、郯－庐－辽－吉重力高异常带等。
关于布格重力异常计算及资料处理与反演和解释的报告姓名：***班级：061084-27学号：**********指导老师：***日期：2011.4.14目录前言 (2)目的 (2)任务要求 (2)工作过程 (2)成果 (2)工作内容及步骤 (3)§1-布格重力异常计算 (3)§2-布格重力异常处理 (3)1.绘制平面等值线图 (3)2.异常处理（分离区域异常和局部异常） (6)§3-布格重力异常反演——特征点法反演 (11)§4-布格重力异常的解释 (13)评述与结论 (13)评述 (13)结论 (14)关于布格重力异常计算及资料处理与反演和解释的报告 前言目的：熟悉并掌握布格重力异常计算及资料处理与反演和解释 任务要求：根据在一个地区重力测量的结果，计算出布格重力异常，并根据异常进行资料处理和解释，并完成一份工作报告。
工作过程：(1)利用实测的相对重力值、相对高程值和X,Y 坐标值，计算各种校正（地形校正除外），纬度校正用 计算，自由空间（或高度）校正用计算，中间层校正用 计算，已知地表物质密度为2.50g/cm 3，起算点纬度为45°；(2)获得各点处的布格重力异常值后，绘出平面等值线图，等值线距为0.5mGal ；(3)根据异常（平面或剖面）特征，选用适当的方法进行处理（如压制干扰、消除区域场等）进行处理，并对处理效果进行描述； (4)将处理后的异常进行反演；(5)写出全部过程和所采用的处理与反演方法之应用理由。
成果：根据布格重力异常数据计算及资料处理与反演初步结果判断，该异常应由地区下一球体引起，球体埋深98.8m ，剩余质量t 6103.07⨯，球体中心在地面的投影点坐标为（248.8,248.8）m 。
):,()2sin(814.0mkX mGal X g ∆⋅-=ϕδϕ):,(3086.0m h mGal h g f ∆⋅=δ):/:,(0419.03m h cm g mGal h g ρρδσ∆⋅-=工作内容及步骤§1-布格重力异常计算用excel先算出各项校正（除地形校正外），需要注意的是在纬度校正中为测点到总基点间纬向距离，由于测点都位于总基点以北，故取正值；为总基点纬度即45°; 单位要划为km。
布格重力异常的地质地球物理意义-概述说明以及解释1.引言1.1 概述概述部分主要介绍本篇长文的主题——布格重力异常的地质地球物理意义。
布格重力异常是指在地球表面上的某个区域内，由于地下构造、地质体或其他因素的影响，引起地球重力场的异常变化。
它可以用来揭示地壳下的岩石结构、地壳变形以及岩石密度分布等信息。
本篇长文将从三个方面对布格重力异常的地质地球物理意义进行详细探讨。
首先，我们将对布格重力异常的概念进行解释，并阐述其产生的原因。
其次，我们将介绍布格重力异常的测量方法和数据分析，以及相关的技术工具和仪器。
最后，我们将重点讨论布格重力异常在地质地球物理领域的意义和应用。
通过对布格重力异常的研究，我们可以深入理解地球的内部结构和过程，探究地球演化的规律。
同时，布格重力异常还可以为矿产资源勘探和地下水资源的开发提供重要的信息和指导。
此外，布格重力异常的研究还对于地震活动的监测和地质灾害的预测具有重要意义。
本篇长文旨在全面系统地阐述布格重力异常的地质地球物理意义，并展望其在未来的应用前景。
通过本文的阅读，读者将对布格重力异常有更加深入的理解，并能够了解布格重力异常在地质地球物理领域的重要作用。
1.2 文章结构文章结构部分的内容如下：文章结构本篇长文将从引言、正文和结论三个部分来论述布格重力异常的地质地球物理意义。
具体结构如下：引言引言部分将首先概述布格重力异常的背景和基本概念，包括对布格重力异常产生原因的简要介绍。
随后，文章将介绍本篇长文的结构和目的，以引导读者了解本篇文章的内容框架。
正文正文部分将分为三个子节：布格重力异常的概念及产生原因、布格重力异常的测量方法和数据分析以及布格重力异常的地质地球物理意义。
首先，在2.1节中，将详细介绍布格重力异常的概念和其产生原因，包括重力异常的基本定义和重力场的变化机制。
接下来，在2.2节中，将介绍布格重力异常的测量方法，包括重力测量仪器和数据处理技术，并说明如何从测量数据中分析和解释布格重力异常。
尼日利亚南部大陆边缘重力场特征及解释尹君【摘要】Variable characteristics of the free air gravity anomaly and Bouguer gravity anomaly were analyzed by using the ship gravity data obtained from international cooperative survey between China and Nigeria . Through analyzing two gravity profiles that start from continental shelf ,slope and extend to the deep sea basin ,we can get the density structure of the crust .The results of research imply that the crustal thickness has been cascade thinning from continental shelf ,slope to deep sea plain .The thinned range on the east side is greater than that on the west side ,it decreases from 24 km to 10 km on the east side and 21 km to 14 km on the west side .%利用中国-尼日利亚国际合作航次获得的船载重力数据,分析了尼日利亚南部大陆边缘的自由空间重力异常和布格重力异常特征,并通过两条从陆架—陆坡—陆隆一直延伸到深海盆地的重力剖面拟合出地壳密度结构.研究结果表明,地壳厚度总体上从陆架、陆坡至深海平原呈现阶梯状减薄的趋势,东侧的减薄幅度大于西侧,东侧从24 km减小到10 km,西侧从21 km减小到14 km.【期刊名称】《海洋学研究》【年(卷),期】2017(035)004【总页数】7页(P87-93)【关键词】尼日利亚;重力异常;地壳结构;莫霍面;重力反演【作者】尹君【作者单位】国家海洋局第二海洋研究所 ,浙江杭州310012【正文语种】中文【中图分类】P7380 引言尼日利亚南部大陆边缘地壳结构一直是许多地球物理研究者所探讨的热点问题。
布格重力异常和自由空气重力异常下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。
文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!布格重力异常和自由空气重力异常引言地球重力场的变化对地球物理学研究至关重要。
关于布格重力异常计算及资料处理与反演和解释的报告姓名：***班级：061084-27学号：**********指导老师：***日期：2011.4.14目录前言 (2)目的 (2)任务要求 (2)工作过程 (2)成果 (2)工作内容及步骤 (3)§1-布格重力异常计算 (3)§2-布格重力异常处理 (3)1.绘制平面等值线图 (3)2.异常处理（分离区域异常和局部异常） (6)§3-布格重力异常反演——特征点法反演 (11)§4-布格重力异常的解释 (13)评述与结论 (13)评述 (13)结论 (14)关于布格重力异常计算及资料处理与反演和解释的报告 前言目的：熟悉并掌握布格重力异常计算及资料处理与反演和解释 任务要求：根据在一个地区重力测量的结果，计算出布格重力异常，并根据异常进行资料处理和解释，并完成一份工作报告。
工作过程：(1)利用实测的相对重力值、相对高程值和X,Y 坐标值，计算各种校正（地形校正除外），纬度校正用 计算，自由空间（或高度）校正用计算，中间层校正用 计算，已知地表物质密度为2.50g/cm 3，起算点纬度为45°；(2)获得各点处的布格重力异常值后，绘出平面等值线图，等值线距为0.5mGal ；(3)根据异常（平面或剖面）特征，选用适当的方法进行处理（如压制干扰、消除区域场等）进行处理，并对处理效果进行描述； (4)将处理后的异常进行反演；(5)写出全部过程和所采用的处理与反演方法之应用理由。
成果：根据布格重力异常数据计算及资料处理与反演初步结果判断，该异常应由地区下一球体引起，球体埋深98.8m ，剩余质量t 6103.07⨯，球体中心在地面的投影点坐标为（248.8,248.8）m 。
):,()2sin(814.0mkX mGal X g ∆⋅-=ϕδϕ):,(3086.0m h mGal h g f ∆⋅=δ):/:,(0419.03m h cm g mGal h g ρρδσ∆⋅-=工作内容及步骤§1-布格重力异常计算用excel先算出各项校正（除地形校正外），需要注意的是在纬度校正中为测点到总基点间纬向距离，由于测点都位于总基点以北，故取正值；为总基点纬度即45°; 单位要划为km。
中间层校正中取值为2.50 。
§2-布格重力异常处理1.绘制平面等值线图获得各点处的布格重力异常值后，用surfer绘图软件中的自然邻点网格法绘出平面等值线图，等值线距为0.5mGal，旁边为经过九点平滑法处理后的等值线图如下：图例：等值线图例：等值线X∆ϕX∆ρ3/cmg—5mGal——5mGal—可以看到经过平滑后的等值线光滑了很多，相当于虑去了高频成分。
平滑处理的目的是消除异常数据中由观测引起的偶然误差以及由地表附近密度分布不均匀引起的杂乱无章的重力效应，以得到有意义的地质体引起的异常。
为了更好的了解该区域重力异常特性，再用surfer 做出其一阶导平面等值线图和二阶导平面等值线图：一阶导在（y=250）线上的剖面图 二阶导在（y=250）线上的剖面图100200300400500-0.04-0.020.020.040.06V xz (mGal/m)X(m)100200300400500-0.10.10.20.30.4V zzz (mGal/m 2)X(m)xz V zzzV由上两图跟以下球形正演得出的平面等值线图和剖面图相比较，可以基本判定地下引起重力异常的物体形态似球，且根据二阶导平面等值线图还可以推断下面可能是由一个大球和四个小球叠加而产生的重力异常。
这为后面的反演过程选用什么模型提供了依据。
下面是球体重力异常一阶及二阶导正演剖面图：2.异常处理（分离区域异常和局部异常）根据异常特征，我们知道该地区异常比较稳定，高频成分较少，在前面已摆出经过九点二次平滑法压制干扰后的等值线图，前后基本上变化不大，只是等值线更加光滑滑而已；而我们看到异常的导数等值线图把局部异常突出的比较好，因此我们可以用高阶导数法来提取局部重力异常。
又我们很容易看出该地区区域重力异常呈线性递增，因此我们还可选用趋势分析（最小二乘多项式拟合）的方法进行处理消除区域场等，最后对处理效果进行描述。
鉴于对编程能力的需要，高阶导数法难度较大，短期内无法实现，借助软件的话，我们不知道其演算过程，反演引起的误差也无法估计，因此我暂时选用趋势分析法（最小二乘多项式拟合法）。
趋势分析法是用多项式拟合区域性背景场。
其原理如下：选用一个曲面函数n阶多项式，用于拟合一个区域内的异常；通过若干点上异常值代入多项式可以得到一个方程组，求解方程组可得到多项式的系数，即得到描述区域异常的多项式函数；由于多项式的阶次一般视情况取1~4阶，去拟合相对简单的异常背景，以实现区域异常与局部异常的分离。
eg.下面我先尝试着用matlab针对NE剖面（y=x）编了一个函数来做最小二乘多项式拟合法进行实验，下面是源代码：clear,clf,clcx=[0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20];y=[0.125527 0.7676005 1.2901735 1.789785 2.529205 3.127242 4.11251 5.200932 6.7870845 8.761621 9.9646955 9.618232 8.793035 8.1096465 8.027642 8.1744065 8.4864405 8.804667 9.265239 9.661196 10.209];cc=polyfit(x,y,1) %求出多项式前的各项系数，改变数字分别xx=0:1:20; 代表做不同次数拟合，此处是1为线性拟合yy=polyval(cc,xx);plot(xx,yy,'--') xy=y-yy;hold on plot(x,xy,'-')plot(x,y,'x') axis([0,20,-2,11])hold on xlabel('x') ylabel('y')实验结果如下：一次线性拟合二次曲线（抛物线）拟合五次多项式拟合十次多项式拟合二十次多项式拟合用多项式拟合进行异常区分，存在两个方面的问题，一是选用多项式阶次问题，二是选择多少点参加拟合，不同的阶次和不同的拟合点数，其结果差异很大。
（实验结果证实了不同的阶次对结果的影响）1）多项式阶次越高，对原始异常拟合越好，异常区分效果往往不好。
阶次太高，会造成趋势值包含过多的局部异常成分，因而计算出局部异常会偏小。
此处明显线性拟合最好，得到了较好的局部异常值。
2）计算点数量越多，趋势异常越平缓简单，会造成对复杂背景拟合不到位的情况。
此处剖面只用21个数据点，效果还好。
3）虚假异常问题及其消除的措施用趋势分析方法区分异常，会产生局部虚假异常。
此处两端出现负值就是最好的证明，我打算重新做一个线性变化的区域异常，即取两端点的连线。
或用迭代计算法消除虚假异常。
下面是处理结果：y=x向剖面图可以看到分离出来的局部异常曲线并不光滑，是因为没做平滑处理和点数太少的关系，接下来再对其剖面数据进行三点平均法并对分离出的局部异常数据进行三次样条插值：三点平均公式：)]1()0()1([31)0(g g g g ++-=∆ 三次样条插值matlab 源代码：csfit.m 文件：function s=csfit(x,y,dx0,dxn) n=length(x)-1; h=diff(x); d=diff(y)./h; a=h(2:n-1);b=2*(h(1:n-1)+h(2:n)); c=h(2:n); u=6*diff(d); b(1)=b(1)-h(1)/2; u(1)=u(1)-3*(d(1)); b(n-1)=b(n-1)-h(n)/2; u(n-1)=u(n-1)-3*(-d(n)); for k=2:n-1temp=a(k-1)/b(k-1); b(k)=b(k)-temp*c(k-1); u(k)=u(k)-temp*u(k-1); endm(n)=u(n-1)/b(n-1); for k=n-2:-1:1m(k+1)=(u(k)-c(k)*m(k+2))/b(k); endm(1)=3*(d(1)-dx0)/h(1)-m(2)/2; m(n+1)=3*(dxn-d(n))/h(n)-m(n)/2; for k=0:n-1s(k+1,1)=(m(k+2)-m(k+1))/(6*h(k+1)); s(k+1,2)=m(k+1)/2;s(k+1,3)=d(k+1)-h(k+1)*(2*m(k+1)+m(k+2))/6; s(k+1,4)=y(k+1); end主函数：clear,clf,clcx=[0*25*2^(1/2) 1*25*2^(1/2) 2*25*2^(1/2) 3*25*2^(1/2) 4*25*2^(1/2) 5*25*2^(1/2) 6*25*2^(1/2) 7*25*2^(1/2) 8*25*2^(1/2) 9*25*2^(1/2) 10*25*2^(1/2) 11*25*2^(1/2) 12*25*2^(1/2) 13*25*2^(1/2) 14*25*2^(1/2) 15*25*2^(1/2) 16*25*2^(1/2) 17*25*2^(1/2) 18*25*2^(1/2) 19*25*2^(1/2) 20*25*2^(1/2)];y=[0.125527 0.727767 1.2825196667 1.8697211667 2.4820773333 3.256319 4.1468946667 5.200932 6.7870845 8.761621 9.9646955 9.618231 8.793035 8.1096465 8.1038983333 8.2294963333 8.4885046667 8.8521155 9.2437006667 9.7118116667 10.209];plot(x,y,'x')hold oncc=[(10.209-0.125527)/(20*25*2^(1/2)) 0.125527];xx=0:25*2^(1/2):20*25*2^(1/2);yy=polyval(cc,xx);plot(xx,yy,'--')hold onxy=y-yy;dx0=0;dxn=0;s=csfit(x,xy,dx0,dxn)x1=0:0.01:1*25*2^(1/2);y1=polyval(s(1,:),x1-x(1));x2=1*25*2^(1/2):0.01:2*25*2^(1/2);y2=polyval(s(2,:),x2-x(2));x3=2*25*2^(1/2):0.01:3*25*2^(1/2);y3=polyval(s(3,:),x3-x(3));x4=3*25*2^(1/2):0.01:4*25*2^(1/2);y4=polyval(s(4,:),x4-x(4));x5=4*25*2^(1/2):0.01:5*25*2^(1/2);y5=polyval(s(5,:),x5-x(5));x6=5*25*2^(1/2):0.01:6*25*2^(1/2);y6=polyval(s(6,:),x6-x(6));x7=6*25*2^(1/2):0.01:7*25*2^(1/2);y7=polyval(s(7,:),x7-x(7));x8=7*25*2^(1/2):0.01:8*25*2^(1/2);y8=polyval(s(8,:),x8-x(8));x9=8*25*2^(1/2):0.01:9*25*2^(1/2);y9=polyval(s(9,:),x9-x(9));x10=9*25*2^(1/2):0.01:10*25*2^(1/2);y10=polyval(s(10,:),x10-x(10));x11=10*25*2^(1/2):0.01:11*25*2^(1/2);y11=polyval(s(11,:),x11-x(11));x12=11*25*2^(1/2):0.01:12*25*2^(1/2);y12=polyval(s(12,:),x12-x(12));x13=12*25*2^(1/2):0.01:13*25*2^(1/2);y13=polyval(s(13,:),x13-x(13));x14=13*25*2^(1/2):0.01:14*25*2^(1/2);y14=polyval(s(14,:),x14-x(14));x15=14*25*2^(1/2):0.01:15*25*2^(1/2);y15=polyval(s(15,:),x15-x(15));x16=15*25*2^(1/2):0.01:16*25*2^(1/2);y16=polyval(s(16,:),x16-x(16));x17=16*25*2^(1/2):0.01:17*25*2^(1/2);y17=polyval(s(17,:),x17-x(17));x18=17*25*2^(1/2):0.01:18*25*2^(1/2);y18=polyval(s(18,:),x18-x(18));x19=18*25*2^(1/2):0.01:19*25*2^(1/2);y19=polyval(s(19,:),x19-x(19));x20=19*25*2^(1/2):0.01:20*25*2^(1/2);y20=polyval(s(20,:),x20-x(20));plot(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,x7,y7,x8,y8,x9,y9,x10,y10,x11,y11,x12,y12,x13,y13,x14,y14,x1 5,y15,x16,y16,x17,y17,x18,y18,x19,y19,x20,y20,x,xy,'.')grid onxlabel('x')ylabel('y')处理结果如下：y=x向剖面图§3-布格重力异常反演根据重力异常的平面和剖面特征，初步选用球体模型做反演：——特征点法反演Δg(Vz):()[]11305.112,232322132232123112122222-±=-±=±≈-±==++=∆nxDnDxxDDxDGMDxGMDxGMDgnn，，)'(6524.0305.12/12/12/1xxxD-==)'(4811.09622.03/13/13/1xxxD-==)'(4056.08111.04/14/14/1xxxD-==当x=351.8m 时， 有mGal g 801.4max =∆当时取max 21g g ∆∆，即mGal g 4.2=∆时，m x .942921=，m x 76.82'21=当时取max 31g g ∆∆，即mGal g 6.1=∆ 时，m x 453.131=，m x 249.9'31= 当时取max 41g g ∆∆，即mGal g 2.1=∆时， m x 471.431=，m x 227.9'31=球体中心点地面投影坐标：()2.8351,2351.8，即（248.8,248.8）mm D .8983/).898.897.999(=++= t D g D G g M 62max 2max 103.07150⨯=∆≈∆=由于求出的几个D 值比较接近，说明场源体确实近于球形，因此埋深D 取其平均值。
