数字电子技术(第三版)第11章时序逻辑电路分析

时序逻辑电路实验报告一、实验目的1．掌握同步计数器设计方法与测试方法。

2．掌握常用中规模集成计数器的逻辑功能和使用方法。

二、实验设备设备：THHD-2型数字电子计数实验箱、示波器、信号源器件：74LS163、74LS00、74LS20等。

三、实验原理和实验电路1．计数器计数器不仅可用来计数，也可用于分频、定时和数字运算。

在实际工程应用中，一般很少使用小规模的触发器组成计数器，而是直接选用中规模集成计数器。

2．(1) 四位二进制（十六进制）计数器74LS161（74LS163）74LSl61是同步置数、异步清零的4位二进制加法计数器，其功能表见表5.1。

74LSl63是同步置数、同步清零的4位二进制加法计数器。

除清零为同步外，其他功能与74LSl61相同。

二者的外部引脚图也相同，如图5.1所示。

表5.1 74LSl61（74LS163）的功能表3．集成计数器的应用——实现任意M进制计数器一般情况任意M进制计数器的结构分为3类，第一类是由触发器构成的简单计数器。

第二类是由集成二进制计数器构成计数器。

第三类是由移位寄存器构成的移位寄存型计数器。

第一类，可利用时序逻辑电路的设计方法步骤进行设计。

第二类，当计数器的模M较小时用一片集成计数器即可以实现，当M较大时，可通过多片计数器级联实现。

两种实现方法：反馈置数法和反馈清零法。

第三类,是由移位寄存器构成的移位寄存型计数器。

4．实验电路：十进制计数器同步清零法同步置数法六进制扭环计数器具有方波输出的六分频电路四、实验内容及步骤1．集成计数器实验（1）按电路原理图使用中规模集成计数器74LS163和与非门74LS00，连接成一个同步置数或同步清零十进制计数器，并将输出连接至数码管或发光二极管。

然后使用单次脉冲作为触发输入，观察数码管或发光二极管的变化，记录得到电路计数过程和状态的转换规律。

（2）根据电路图，首先用D触发器74LS7474构成一个不能自启的六进制扭环形计数器，同样将输出连接至数码管或发光二极管。

"数字电子技术"重要知识点汇总一、主要知识点总结和要求1．数制、编码其及转换：要求：能熟练在10进制、2进制、8进制、16进制、8421BCD、格雷码之间进展相互转换。

举例1：〔37.25〕10= ( )2= ( )16= ( )8421BCD解：〔37.25〕10= ( 100101.01 )2= ( 25.4 )16= ( 00110111.00100101 )8421BCD 2．逻辑门电路：(1)根本概念1〕数字电路中晶体管作为开关使用时，是指它的工作状态处于饱和状态和截止状态。

2〕TTL门电路典型高电平为3.6 V，典型低电平为0.3 V。

3〕OC门和OD门具有线与功能。

4〕三态门电路的特点、逻辑功能和应用。

高阻态、高电平、低电平。

5〕门电路参数：噪声容限V NH或V NL、扇出系数N o、平均传输时间t pd。

要求：掌握八种逻辑门电路的逻辑功能；掌握OC门和OD门，三态门电路的逻辑功能；能根据输入信号画出各种逻辑门电路的输出波形。

举例2：画出以下电路的输出波形。

解：由逻辑图写出表达式为：C+==，则输出Y见上。

+Y+AABBC3．根本逻辑运算的特点：与运算：见零为零，全1为1；或运算：见1为1，全零为零；与非运算：见零为1，全1为零；或非运算：见1为零，全零为1；异或运算：相异为1，一样为零；同或运算：一样为1，相异为零；非运算：零变 1， 1 变零；要求：熟练应用上述逻辑运算。

4. 数字电路逻辑功能的几种表示方法及相互转换。

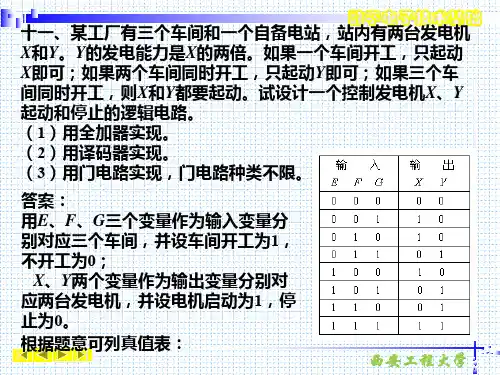
①真值表〔组合逻辑电路〕或状态转换真值表〔时序逻辑电路〕：是由变量的所有可能取值组合及其对应的函数值所构成的表格。

②逻辑表达式：是由逻辑变量和与、或、非3种运算符连接起来所构成的式子。

③卡诺图：是由表示变量的所有可能取值组合的小方格所构成的图形。

④逻辑图：是由表示逻辑运算的逻辑符号所构成的图形。

⑤波形图或时序图：是由输入变量的所有可能取值组合的高、低电平及其对应的输出函数值的高、低电平所构成的图形。

数字电路设计中的时序分析方法
在数字电路设计中，时序分析方法是非常重要的一环。

时序分析涉及到时钟频率、输入和输出延迟等关键参数，对于确保电路的稳定性和正确性至关重要。

在进行时序分析时，需要考虑以下几个关键点：
首先，时钟频率是指时钟信号的周期，是数字电路中的重要参数。

在时序分析中，需要确保所有的信号都能在一个时钟周期内被正确处理。

如果电路中的某些信号延迟时间超过了一个时钟周期，就可能导致数据丢失或不稳定的情况发生。

因此，时钟频率的选择和设计是至关重要的。

其次，输入延迟和输出延迟是时序分析中需要重点关注的另外两个参数。

输入
延迟是指输入信号到达电路内部后需要多长时间才能被正确识别和处理；而输出延迟则是指电路内部的处理结果需要多长时间才能输出。

在设计数字电路时，需要对输入和输出延迟进行准确的测量和分析，以确保信号的稳定性和准确性。

此外，时序分析还需要考虑信号的传播延迟。

信号在电路中传播的时间取决于
电路中的布线长度、逻辑门的延迟等因素。

在进行时序分析时，需要对信号的传播路径进行详细的分析，找出潜在的延迟问题并对其进行优化。

总的来说，时序分析方法是确保数字电路稳定性和正确性的重要手段。

通过对
时钟频率、输入和输出延迟以及信号传播延迟等关键参数进行准确分析和优化，可以有效地提高数字电路的性能和可靠性。

在实际的数字电路设计过程中，时序分析是必不可少的一步，需要认真对待并进行细致的分析和验证。

只有这样，才能保证设计出高质量的数字电路产品。

《数字电子技术》知识点第1章 数字逻辑基础1．数字信号、模拟信号的定义2．数字电路的分类3．数制、编码其及转换要求：能熟练在10进制、2进制、8进制、16进制、8421BCD 之间进行相互转换。

举例1：（37.25）10= ( )2= ( )16= ( )8421BCD 解：（37.25）10= (100101.01)2= ( 25.4)16= (00110111.00100101)8421BCD 4．基本逻辑运算的特点与运算：见零为零，全1为1；或运算：见1为1，全零为零；与非运算：见零为1，全1为零；或非运算：见1为零，全零为1；异或运算：相异为1，相同为零；同或运算：相同为1，相异为零；非运算：零变 1， 1变零；要求：熟练应用上述逻辑运算。

5．数字电路逻辑功能的几种表示方法及相互转换。

①真值表（组合逻辑电路）或状态转换真值表（时序逻辑电路）：是由变量的所有可能取值组合及其对应的函数值所构成的表格。

②逻辑表达式：是由逻辑变量和与、或、非3种运算符连接起来所构成的式子。

③卡诺图：是由表示变量的所有可能取值组合的小方格所构成的图形。

④逻辑图：是由表示逻辑运算的逻辑符号所构成的图形。

⑤波形图或时序图：是由输入变量的所有可能取值组合的高、低电平及其对应的输出函数值的高、低电平所构成的图形。

⑥状态图（只有时序电路才有）：描述时序逻辑电路的状态转换关系及转换条件的图形称为状态图。

要求：掌握这五种（对组合逻辑电路）或六种（对时序逻辑电路）方法之间的相互转换。

6．逻辑代数运算的基本规则①反演规则：对于任何一个逻辑表达式Y ，如果将表达式中的所有“·”换成“＋”，“＋”换成“·”，“0”换成“1”，“1”换成“0”，原变量换成反变量，反变量换成原变量，那么所得到的表达式就是函数Y 的反函数Y （或称补函数）。

这个规则称为反演规则。

②对偶规则：对于任何一个逻辑表达式Y ，如果将表达式中的所有“·”换成“＋”，“＋”换成“·”，“0”换成“1”，“1”换成“0”，而变量保持不变，则可得到的一个新的函数表达式Y ＇，Y ＇称为函Y 的对偶函数。

《数字电子技术》知识点第1章数字逻辑基础1．数字信号、模拟信号的定义2．数字电路的分类3．数制、编码其及转换要求：能熟练在10进制、2进制、8进制、16进制、8421BCD之间进行相互转换。

举例1：（）10= ( )2= ( )16= ( )8421BCD解：（）10= 2= ( 16= 8421BCD4．基本逻辑运算的特点与运算：见零为零，全1为1；或运算：见1为1，全零为零；与非运算：见零为1，全1为零；或非运算：见1为零，全零为1；异或运算：相异为1，相同为零；同或运算：相同为1，相异为零；非运算：零变1，1变零；要求：熟练应用上述逻辑运算。

5．数字电路逻辑功能的几种表示方法及相互转换。

①真值表（组合逻辑电路）或状态转换真值表（时序逻辑电路）：是由变量的所有可能取值组合及其对应的函数值所构成的表格。

②逻辑表达式：是由逻辑变量和与、或、非3种运算符连接起来所构成的式子。

③卡诺图：是由表示变量的所有可能取值组合的小方格所构成的图形。

④逻辑图：是由表示逻辑运算的逻辑符号所构成的图形。

⑤波形图或时序图：是由输入变量的所有可能取值组合的高、低电平及其对应的输出函数值的高、低电平所构成的图形。

⑥状态图（只有时序电路才有）：描述时序逻辑电路的状态转换关系及转换条件的图形称为状态图。

要求：掌握这五种（对组合逻辑电路）或六种（对时序逻辑电路）方法之间的相互转换。

6．逻辑代数运算的基本规则①反演规则：对于任何一个逻辑表达式Y，如果将表达式中的所有“·”换成“＋”，“＋”换成“·”，“0”换成“1”，“1”换成“0”，原变量换成反变量，反变量换成原变量，那么所得到的表达式就是函数Y的反函数Y（或称补函数）。

这个规则称为反演规则。

②对偶规则：对于任何一个逻辑表达式Y，如果将表达式中的所有“·”换成“＋”，“＋”换成“·”，“0”换成“1”，“1”换成“0”，而变量保持不变，则可得到的一个新的函数表达式Y＇，Y＇称为函Y 的对偶函数。

时序逻辑电路的卡诺图分析法赵兴强;金洪颖【摘要】提出了一种分析时序逻辑电路功能的新方法:利用分项满足法和时钟方程来填写状态方程的卡诺图,并由卡诺图直接画出状态转换图【期刊名称】《通化师范学院学报》【年(卷),期】2005(026)004【总页数】4页(P33-36)【关键词】时序逻辑电路;卡诺图;状态转换图;时钟方程【作者】赵兴强;金洪颖【作者单位】西华师范大学计算机学院,四川,南充,637002;西华师范大学计算机学院,四川,南充,637002【正文语种】中文【中图分类】TP3311 引言现有文献对时序逻辑电路的分析采用的是计算法，将各触发器的原态代入状态方程，计算出各个触发器对应的次态，依次列出状态转换表，再画状态转换图，最后得出电路功能结论.此方法的计算工作量太大，一个由n个触发器组成的时序电路，在计算次态时，需进行n×2n 次计算，且容易出错.为此，本文提出了一种分析时序电路的简捷方法——卡诺图分析法：将各触发器的状态方程在卡诺图上表示出来，就可直接找出各现态的次态，而用分项满足法非常容易填写卡诺图.该方法简单易行，计算量少，不易出错.2 分项满足法简介将逻辑函数绘制在卡诺图上，需将表达式化成标准与或式，但变换过程显得冗杂.使用分项满足法只需将表达式化成与或式，找出使每个与项等于1的取值组合，最后将卡诺图中对应这些组合的方格标为1即可.例1：画出逻辑函数Y=AC++ABD的卡诺图解：Y=AC++ABD=AC++ABD当A﹑C同时为1时,第一个与项AC为1.A=1对应卡诺图的第三和第四行，C=1对应卡诺图的第三和第四列，因此将第三﹑第四行和第三﹑第四列公共的四个方格标为1.当A﹑B﹑D同时为0时，第二个与项等于1.A﹑B同时为0对应卡诺图的第一行，D为0对应卡诺图的第一列和第四列,因此，将第一行和第一、四列公共的两个方格标为1.当ABCD为1101时,第三个与项ABD的值为1.AB为11对应卡诺图的第三行，CD为01对应卡诺图的第二列，因此将第三行和第二列公共的一个方格标为1.结果得到图1所示的卡诺图.例2：由卡诺图求触发器的次态：若各触发器的状态方程分别为图1 函数Y的卡诺图图2 Q3n+1的卡诺图图3 Q2n+1的卡诺图图4 Q1n+1的卡诺图图5 Q0n+1的卡诺图图6 Q3n+1Q2n+1Q1n+1Q0n+1的综合卡诺图照例1的方法，可分别得到Q3n+1,Q2n+1,Q1n+1,Q0n+1的卡诺图(图2——图5)，实际运用时可在一个卡诺图上表示出来，形成Q3n+1Q2n+1Q1n+1Q0n+1的综合卡诺图(图6).3 时序电路的卡诺图分析法3．1同步时序电路的卡诺图分析法3.1.1 分析步骤1)由已给定的逻辑图写出驱动方程，输出方程.2)根据触发器的特性方程写出各个触发器的状态方程.3)由状态方程直接画出各变量的综合次态卡诺图.4)由卡诺图直接画出状态转换图并得出逻辑功能.3.1.2例证分析如图(7)所示同步时序电路的逻辑功能.图7 同步十一进制加法计数器驱动方程为：状态方程为：Q1n+1=+ …CP↓Q2n+1=Q1n+Q2nQ1n …CP↓Q3n+1=Q2nQ1n+Q3n+Q3n …CP↓Q4n+1=Q4nQ3nQ2nQ1n …CP↓画Q4n+1Q3n+1Q2n+1Q1n+1的综合卡诺图(图8)图8 Q4n+1Q3n+1Q2n+1Q1n+1的综合卡诺图图9 同步十一进制加法计数器状态转换图由Q4n+1Q3n+1Q2n+1Q1n+1的综合卡诺图可直接画出状态转换图(图9)逻辑功能结论：该电路为一个可自启动的同步十一进制加法计数器.3.2异步时序电路的分析方法3.2.1 分析步骤1)﹑2)步同同步电路3)画卡诺图求次态.对以CP为时钟信号的触发器按同步电路的方法填写卡诺图，对以其它信号为时钟方程的触发器，先把时钟信号在卡诺图的小方格内以↑(上升沿)或↓(下降沿)标示出来，满足时钟信号的则在相应的小方格内按状态方程填写其次态，不满足者则保持原态.4)状态转换图并得出逻辑功能3.2.2分析举例分析如图10所示的时序电路的逻辑功能图10 异步十进制加法计数器时钟方程CP0=CP↓ CP1=Q0n↓CP2=Q1n↓ CP3=Q0n↓输出方程C=Q3nQ0n驱动方程状态方程Q0n+1= …CP↓Q1n+1= …Q0n↓Q2n+1= …Q1n↓Q3n+1=Q2nQ1n …Q0n↓画Q3n+1Q2n+1Q1n+1Q0n+1/C的综合卡诺图为便于说明本文将各变量的次态卡诺图单独画出.对触发器F0,以CP为时钟信号，其次态Q0n+1的卡诺图按同步电路填写(如图11).对触发器F1，以Q0n↓为时钟信号，先在Q0n+1卡诺图中找到满足Q0n=1而Q0n+1=0的小方格并以符号↓表示.则Q1n+1的卡诺图分两步填写，在标有Q0n↓的小方格内，其次态由状态方程按分项满足法填写，没有标有Q0n↓的小方格内保持原态(如图12)图11 Q0n+1的综合卡诺图图12 Q1n+1的卡诺图对触发器F2，以Q1n↓为时钟信号，先在Q1n+1卡诺图中找到满足Q1n=1而Q1n+1=0的小方格并以符号↓表示.则Q2n+1的卡诺图分两步填写，在标有Q1n↓的小方格内，其次态由状态方程按分项满足法填写，没有标有Q1n↓的小方格内保持原态(如图13)对触发器F3，以Q0n↓为时钟信号，其次态Q3n+1的卡诺图的填写步骤同Q1n+1的填写，结果如图14.输出方程的卡诺图按分项满足法填写如图15图13 Q2n+1卡诺图图14 Q3n+1的卡诺图图15 C的卡诺图图16 Q3n+1Q2n+1Q1n+1Q0n+1/C的综合卡诺图将上述5个分卡诺图合并在一起得到Q3n+1Q2n+1Q1n+1Q0n+1/C的综合卡诺图(如图16).实际应用时可直接填写出Q3n+1Q2n+1Q1n+1Q0n+1/C的综合卡诺图由综合卡诺图直接得到状态转换图(图17)图17 异步十进制加法计数器的状态转换图由状态转换图得该电路为异步十进制加法计数器4 结论时序电路的分析，计算次态是关键，由前面分析可知，用卡诺图来分析，可大大提高速度，节省大量时间和提高准确性.这一方法在近几年的教学和科研中收到了良好的效果.参考文献：[1]蔡良伟. 数字电路与逻辑设计[M]. 西安：西安电子科技大学出版社，2003.[2]余孟尝. 数字电子技术基础简明教程(第二版)[M]. 北京：高等教育出版社，2002.[3]清华大学电子学教研组编. 数字电子技术基础(第三版)[M]. 北京：高等教育出版社，1995.。

3 现计算、列状态表态次态注时钟条件 CP0 CP1 CP2 CP0 CP0 CP1 CP0
0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 不变不变
不变不变不变
4 画状态图、时序图 CP Q0 Q1 Q2 (b 时序图 n n n 排列顺序： Q2 Q1 Q0
000←001←010←011 ↓ ↑ 111→110→101→100 (a 状态图 5 电路功能由状态图可以看出，在时钟脉冲CP的作用下，电路的8个状态按递减规律循环变化，即：000→111→110→101→100→011→010→001→000→… 电路具有递减计数功能，是一个3位二进制异步减法计数器。

本节小结：时序电路的特点是：在任何时刻的输出不仅和输入有关，而且还决定于电路原来的状态。

为了记忆电路的状态，时序电路必须包含有存储电路。

存储电路通常以触发器为基本单元电路构成。

时序电路可分为同步时序电路和异
步时序电路两类。

它们的主要区别是，前者的所有触发器受同一时钟脉冲控制，而后者的各触发器则受不同的脉冲源控制。

时序电路的逻辑功能可用逻辑图、状态方程、状态表、卡诺图、状态图和时序图等6种方法来描述，它们在本质上是相通的，可以互相转换。

时序电路的分析，就是由逻辑图到状态图的转换。