某渠道水面线计算

水面线计算
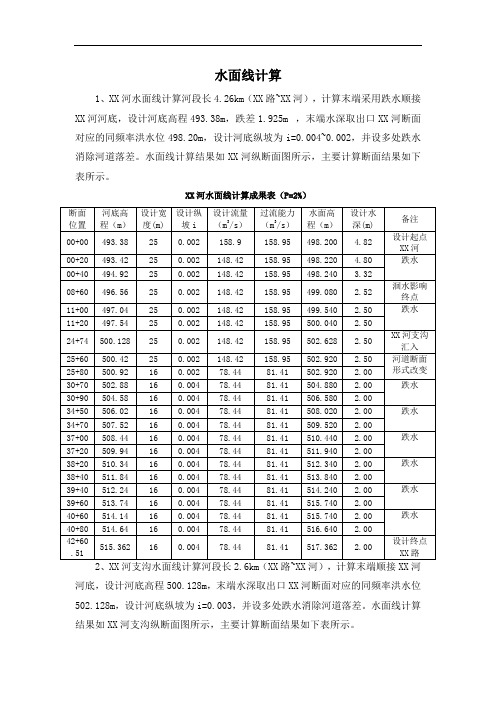
1、XX河水面线计算河段长4.26km（XX路~XX河），计算末端采用跌水顺接XX河河底，设计河底高程493.38m，跌差1.925m ，末端水深取出口XX河断面对应的同频率洪水位498.20m，设计河底纵坡为i=0.004~0.002，并设多处跌水消除河道落差。

水面线计算结果如XX河纵断面图所示，主要计算断面结果如下表所示。

XX河水面线计算成果表（P=2%）
河底，设计河底高程500.128m，末端水深取出口XX河断面对应的同频率洪水位502.128m，设计河底纵坡为i=0.003，并设多处跌水消除河道落差。

水面线计算结果如XX河支沟纵断面图所示，主要计算断面结果如下表所示。

XX河支沟水面线计算成果表（P=2%）
河底高程，设计河底高程491.000m，保证下游顺利接入XX河，设计河底纵坡为i=0.003，并设多处跌水消除河道落差。

水面线计算结果如XX河纵断面图所示，主要计算断面结果如下表所示。

XX河水面线计算成果表（P=2%）
路纵坡分为5段分别排入XX河、XX河支沟、XX河等3条主要河道。

各分段计算末端设计沟底高程应分别按3条主要河道起点位置河底高程确定，各分段末端水深应取3条主要河道起点位置对应的同频率洪水位及相应水深，设计沟底纵坡随道路或地形坡度控制。

但是，受截洪沟位置及高程关系影响，在各段截洪沟末端位置均以跌水方式分别排入三条主要河道，故出口端为自由出流，截洪沟水位不受三条主要河道洄水影响，末端水深可按明渠恒定均匀流考虑，以此推求截洪沟设计洪水线，水面线计算结果如XX路截洪沟纵断面图所示。

XX路截洪沟水位计算参数表。

4.6洪水水面线4.6.1计算公式⑴计算原理天然河道的洪水大多属于不稳定流，水面线的计算可以近似地视为稳定流量以简化计算。

稳定非均匀流按伯努利能量方程进行计算，即：式中：乙、Z i 为计算段上、下游断面水位；V 2、V 为计算段上、下游断面平 均流速，2、 i 为计算段上、下游断面的动能修正系数； h f 为沿程水头损失； h j 为局部水头损失。

在流量、控制断面水位和河段糙率确定后，即可由该式算出河道断面的水力 要素。

⑵主要参数的确定根据一维水面线的计算公式，其关键在于沿程水头损失和局部水头损失的确^定。

① 动能修正系数aa 是以总流的断面平均流速 V 代替过水断面上各点的点流速 V 来计算断面 的平均单位动能，为校正误差而引入的修正系数，理论上可按下式计算：3 A V dA式中：V 为断面单元流速（m/s ）; V 为断面平均流速（m/s ）; A 为过水面积。

是个大于1.0的数值，其值取决于断面上流速分布不均匀的程度，流速分布越不均匀， 值越大。

② 沿程水头损失水流在流动过程中，由于克服河床的阻滞作用，边壁的低流速层对高流速层 Z 2M 22g h f h j扩散段取=-0.5〜-1.0 ;对于收缩段 =0产生的阻力而消耗的能量，就是沿程阻力损失损失h f ，主要决定于均匀流的坡降, 可表示为：式中：L 为计算段上下游断面间距（m ，K 为流量模数，K CAJR ，—般采用扛 K7是上下两断面的流量模数；C 为谢才系数，C 朴， n 为糙率，y 可取1/4〜1/6。

由上式可知，欲求h f ，主要是确定糙率n 值，工程河段天然河道糙率根据河 道形态，河床组成及两岸植被情况结合， 采用历史洪水反推糙率，未进行历史洪 水调查段结合《天然河道糙率表》选定。

③ 局部水头损失局部水头损失即为河道的河床断面沿程不均匀引起的水头损失。

局部阻力系 数与河槽形态、收缩或放宽的比例以及水流情况有关， 特别是在跨河桥梁河段特 别明显，局部水头损失h f 可按下式计算:2 2 准 V 2_） （2g 2g ）式中： 为局部阻力系数。

沙河水面线推求过程1.1 水面线计算理论基础根据沿程比降、流量、建筑物及支流汇入情况，水面线分段进行推算。

（1）水面线推算的基本公式水面线计算按明渠恒定非均匀渐变流能量方程，在相邻断面之间建立方程，采用逐段试算法从下游往上游进行推算。

具体如下：2g2g 21w 2221V h V Z Z αα-++= （1-1）式中： 1Z 、1V ——上游断面的水位和平均流速； 2Z 、2V ——下游断面的水位和平均流速；j f w h h h +=——上、下游断面之间的能量损失； l RC Vh f 22=——上、下游断面之间的沿程水头损失；)22(2122gVg V h j -=ζ——上、下游断面之间的局部水头损失；ζ——局部水头损失系数，根据《水力计算手册》，在收缩河段，一般局部水头损失系数ζ=0；在扩散<段，由于2V <1V ，所以ζ<0，其中在渐扩段，ζ取值-0.333，急扩段、桥渡处ζ取值-0.05~-0. 1。

C ——谢才系数； R ——水力半径；α——动能修正系数。

分段求和法计算时，应注意以下及点：第一，把已知水深的断面作为起始断面。

第二，明渠中水流必须是恒定流，并且流量沿程不变。

第三，渠道糙率系数n 沿程不变。

（2）河道糙率沙河河道与滩地糙率虽然有所不同，但相差较小，沙河主槽0.027，滩地0.03对水位影响较小，这里统一按0.027取值计算。

推求中一律按河道糙率计算。

1.2 计算过程本次计算从K0+000断面到K14+400断面，河道纵断面变化如图1-1，图1-2。

图1-1 河道纵断面图图1-2 沙河河道图图1-3 河道局部横断面图、地形图K1+600断面到K0+000断面为收缩段，局部水头损失系数ζ=0。

K3+200断面到K1+600断面为渐扩段，局部水头损失系数ζ=-0.333。

K4+800断面到K3+200断面为收缩段，局部水头损失系数ζ=0。

K4+800断面到K5+600断面为渐扩段，局部水头损失系数ζ=-0.333。

设计洪水水面线推算根据沿程比降、流量、建筑物及支流汇入情况，水面线分段进行推算。

(1）水面线推算的基本公式水面线计算按明渠恒定非均匀渐变流能量方程，在相邻断面之间建立方程，采用逐段试算法从下游往上游进行推算。

具体如下：2g2g 21w 2221V h V Z Z αα-++= 式中： 1Z 、1V —-上游断面的水位和平均流速；2Z 、2V ——下游断面的水位和平均流速；j f w h h h +=——上、下游断面之间的能量损失；l RC Vh f 22=-—上、下游断面之间的沿程水头损失； )22(2221gV g V h j -=ζ—-上、下游断面之间的局部水头损失; ζ——局部水头损失系数，根据《水力计算手册》，由于断面逐渐扩大的ζ取值0.333，桥渡处ζ取值0。

05～0。

1。

C —-谢才系数；R ——水力半径；α——动能修正系数。

（2）河道糙率河道的粗糙系数受到河床组成床面特性、平面形态及水流流态、植物、岸壁特性等影响，情况复杂,不易估计,本工程河道基本顺直,床面平整，经过整治的河床粗糙系数可以采用《水工设计手册》第一卷P1—404介绍的当量粗糙系数x Nxnn ∑=1当 ；设总湿周x 的各组成部分1x ，2x ，……N x 及所对应的粗糙系数分别为n 1，n 2……n N 。

1糙率的选取河道糙率影响因素有河槽方面也有水流方面。

河槽边壁及河床粗糙程度，滩地植被，河槽纵横形态的变化是主要因素。

大洪水糙率小于小洪水糙率，若附近有大洪水资料时可采用河段附近现状河道纵横断面资料反推综合糙率；若河道纵横断面于大洪水有较大变化时应在河道原貌的基础上反推糙率;反推糙率实际上小于实际糙率.无资料时可根据经验参照水力计算手册确定，偏重于安全考虑，在河道整治工作中糙率适当选小些，在防洪规划中适当大一些。

2起推断面与起推水位的确定水流为缓流时起推断面一般选在推算河段下游，急流时选在上游，附近下游有水文站时以水文站为起推断面,依据实测水位资料分析不同标准洪水位,当缺乏高标准的水位流量关系时可适当将水位流量关系外延。

5.5.3设计洪水水面线推算根据防洪设计标准及洪水分析，设计流量采用P=10%设计洪峰流量确定整治河道的治导岸线。

根据沿程比降、流量、建筑物及支流汇入情况，水面线分段进行推算。

（1）水面线推算的基本公式水面线计算按明渠恒定非均匀渐变流能量方程，在相邻断面之间建立方程，采用逐段试算法从下游往上游进行推算。

具体如下：Z] = Z +式中：Z]、V]——上游断面的水位和平均流速;Z2、V2 ——下游断面的水位和平均流速;"广七+h——上、下游断面之间的能量损失;七=三l——上、下游断面之间的沿程水头损失;h =Z（匕2 - M）——上、下游断面之间的局部水头损失；j 2 g 2 gZ——局部水头损失系数，根据《水力计算手册》，由于断面逐渐扩大的Z取值0.333，桥渡处Z取值0.05〜0. 1。

c——谢才系数；R --- 水力半径；a ——动能修正系数。

（2）河道糙率河道的粗糙系数受到河床组成床面特性、平面形态及水流流态、植物、岸壁特性等影响，情况复杂，不易估计，本工程河道基本顺直，床面平整，经过整治的河床粗糙系数可以采用《水工设计手册》第一卷P1-404介绍的当量粗糙系数%xnn当=十；设总湿周X的各组成部分x1 ,x2,……x»及所对应的粗糙系数分别为n1，n2 n N。

选用砂土及淤泥渠道n=0.030；砌石护面n = 0.030；草皮n = 0.030。

本工程护坡基本为干砌块石及草皮，护底采用天然地层。

根据水位情况可以计算出不同水位下的综合糙率为0.030。

（3）水面线计算成果根据城市发展规划和河段所处的地理位置条件，确定河道横断面采用梯形断面型式。

护坡类型共有草土体结合柳桩护坡、干砌石结合格栅石笼护脚护坡两种，护坡边坡均为1:2。

结合上下游河床实际宽度和河道比降合理拟定断面底宽和纵向比降。

为了不改变现有河势和水沙冲淤平衡，河道设计底坡尽量与天然河道底坡一致。

表5-1治理段设计底宽及纵向比降分段统计表根据清水沟的地形条件，按照控制断面侯汉公路断面（桩号4+365）、尹桥大沟（7+219）、清二沟（14+848）、新华桥水文站（24+400）、新渠渡槽（24+400）处的设计流量，从下游往上游逐段推算水面线。

专题4. 棱柱体渠道水面线计算在工程中，仅对明渠恒定非均匀渐变流的水面曲线进行定性分析是不能满足要求的，还需要知道沿程各断面水力要素的改变情况，即要对水面曲线进行定量的计算和绘制。

水面曲线的计算结果可以预测水位的变化对两岸的影响，确定淹没范围，估算淹没损失等。

在工程中，最常用的方法是分段求和法。

基本公式如下：21s s s E E E l i J i J∆-∆==-- （4-1） 式中：1s E 、2s E 分别表示流段上、下游断面的断面比能；J 表示流段内的平均水力坡度；i 表示渠道的底坡；l ∆为流段长度。

流段的平均水力坡度J 一般采用以下方法计算：)(2121J J J +=（4-2） 22KQ J =（4-3）流量模数平均值K 或2K 可用以下三种方法之一计算：（1） R C A K = （4-4）式中：)(2121A A A +=， )(2121C C C +=，)(2121R R R +=（2）)(2122212K K K +=（4-5）（3）)1(21122212K K K+=（4-6） 用分段求和法计算水面曲线的基本方法，是先把渠道按水深划分为几个流段，然后计算每个流段的长度，逐段推算。

具体步骤如下：（1）分析判别水面曲线的类型；（2）确定控制断面，以控制断面的水深作为流段的第一已知水深1h ； （3）假设流段另一断面水深为h h h ∆±=12，进行分段； （4）根据水深1h 和2h ，应用公式（4-1）求出第一流段长1l ∆；（5）将2h 作为下一流段的控制水深，重复以上计算，求出第二流段长2l ∆；依次类推，可求出3l ∆、4l ∆……，最后求得水面曲线全长∑=∆=ni il l 1（4-7）（6）根据计算结果，按比例绘出水面曲线。

需要注意的是，分段越多，计算量越大，精度也越高。

【工程任务】有一长直的梯形断面棱柱体渠道，底宽20=b m ，边坡系数5.2=m ，糙率0225.0=n ，底坡0001.0=i 。

水面线计算简介水面线计算是指在地理信息系统（GIS）领域中，根据地形和水文条件，通过模拟算法计算出水体在不同液态水位下所形成的水面轮廓线。

水面线计算在水利工程、河流管理、环境保护和城市规划等领域具有重要的应用价值。

算法原理水面线计算的核心算法是基于地理信息系统中的高程数据和水文条件模型。

下面是水面线计算的基本原理：1.高程数据获取：首先，需要获取地理信息系统中的高程数据。

高程数据可以是数字高程模型（DEM）或其他形式的地形数据。

2.确定起始点：根据水位的高低，选择一个起始点作为计算的初始点。

通常情况下，选择地理信息系统中的一个合适的点作为起始点。

3.计算相邻点：根据起始点，计算其相邻点的高程数据，并判断相邻点是否在水位以下。

如果相邻点在水位以下，则将其加入到水面线计算的点集中。

4.递归计算：根据已有的点集，继续计算相邻点的高程数据，并判断相邻点是否在水位以下。

如果相邻点在水位以下，则将其加入到水面线计算的点集中，直到没有新的相邻点在水位以下为止。

5.生成水面线：根据计算得到的点集，生成水面线。

通常情况下，水面线是由一系列离散点组成的多边形。

算法实现水面线计算可以使用各种编程语言和地理信息系统软件实现。

下面以Python语言为例，介绍一种基于DEM的水面线计算方法。

import numpy as npdef waterline_calculation(dem, water_level): # 获取DEM数据的行数和列数rows, cols = dem.shape# 初始化水面线点集waterline_points = []# 遍历DEM数据的每一个像元for i in range(rows):for j in range(cols):# 判断像元的高程是否在水位以下if dem[i, j] < water_level:# 将水位以下的像元加入到水面线点集中 waterline_points.append((j, i)) return waterline_points使用上述代码可以实现根据给定的DEM数据和水位高度，计算出水面线的功能。