【精品】2015年浙江省温州市瑞安中学高二上学期期中数学试卷带解析答案

浙江省瑞安中学高二上学期期中考试（数学理）考试时间100分钟，不能使用计算器）一、选择题（本大题共10个小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）. 1．要得到函数)42sin(π+=x y 的图象，可以把函数x y 2sin =的图象（ ）A ．向右平移8π个单位 B ．向左平移8π个单位 C ．向左平移4π个单位 D ．向右平移4π个单位 2．下列正确的是（ ）A ．平行于同一个平面的两条直线平行B ．垂直于同一条直线的两条直线平行C ．若直线a 与平面α内的无数条直线平行，则a ∥αD ．若一条直线平行于两个平面的交线，则这条直线至少平行于两个平面中的一个 3．根据表格中的数据，可以判定方程062=-+x e x的一个根所在的区间为（ ）A ．(1,0)- B.(0,1)C ．(1,2)D.(2,3)4． 已知a 、b 是平面内两个不共线的向量，,5+=b a BC 82-=，b a CD -=，则（ ）A. ,,A B D 三点共线B. ,,A C D 三点共线C. ,,B C D 三点共线D. ,,A B C 三点共线5．函数xxay x=)1(>a 的图象的大致形状是( )6．如下图是一个算法的程序框图，当输入的x 值为3时，输出y的结果恰好是31，则空白 处的关系式可以是（ ） A ．3x y = B ．xy -=3C ．xy 3= D ． 31x y =7．通过下面程序：若输入a=333，k=5，则输出的b 为（ ）A ．(5)2313 B. (5)3132 C. (5)93 D. (10)938．已知βα,都是锐角，ββααcos ,21)cos(,21sin 则=+=等于 （ ）A ．231- B ．213- C ．21 D ．23 9．设等差数列{a n }的前7项1a ，2a ， 3a ，4a ，5a ，6a ，7a 的方差．．为1，则{a n }的公差d 等于( ) A ．1± B ．21±C . 2±D ．.147±10．设函数)(x f 的定义域为R ，且)(x f 是以．．3．为周期的奇函数．．．．．．．，4log )2(,2|)1(|a f f => （10≠>a a ，且），则实数a 的取值范围是 （ ）A ．2>a 或210<<a B ．210<<a 或12>>a C ． 121<<a 或2>a D ． 121<<a 或12>>a二、填空题：本大题共5小题，每小题4分，共把答案填在题中横线上。

浙江省温州市十校联合体联考2014-2015学年高二上学期期中数学试卷（文理同卷）一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．1．（4分）直线的倾斜角的大小是（）A．30°B．60°C．120°D．150°2．（4分）已知m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（）A．若m∥α，n∥α，则m∥n B．若m∥n，m⊥α，则n⊥αC．若m∥α，m∥β，则α∥βD．若m∥α，α⊥β，则m⊥β3．（4分）直线mx+（2m﹣1）y+1=0与直线3x+my+3=0垂直，则m为（）A．﹣1 B．1 C．2 D．﹣1或04．（4分）P、Q分别为3x+4y﹣10=0与6x+8y+5=0上任意一点，则|PQ|的最小值为（）A．B．C．3 D．65．（4分）若圆x2+y2﹣2ax+3by=0的圆心位于第三象限，那么直线x+ay+b=0一定不经过（）A．第一象限B．第二象限C．第三象限D．第四象限6．（4分）将棱长为1的正方体木块切削成一个体积最大的球，则该球的体积为（）A．B．C．D．7．（4分）如图，三棱锥V﹣ABC底面为正三角形，侧面VAC与底面垂直且VA=VC，已知其主视图的面积为，则其左视图的面积为（）A．B．C．D．8．（4分）如图是正方体的平面展开图，则在这个正方体中的AB与CD的位置关系为（）A．平行B．相交成60°角C．异面成60°角D．异面且垂直9．（4分）将边长为a的正方形沿对角线AC折起，使得BD=a，则三棱锥D﹣ABC的体积为（）A．B．C．D．10．（4分）设集合，，且A∩B≠∅，则实数a的取值范围是（）A．B．C．D．二、填空题（本大题共7小题，每小题4分，共28分）11．（4分）空间直角坐标系中，点（3，2，﹣5）到xoy平面的距离为．12．（4分）直线kx+3y+k﹣9=0过定点．13．（4分）轴截面是边长等于2的等边三角形的圆锥，它的表面积等于．14．（4分）若在平面直角坐标系内过点且与原点的距离为d的直线有两条，则d的取值范围是．15．（4分）过P（2，0）的直线l1截圆C：x2+y2﹣6x+4y+4=0所得的弦长为，则直线l1的方程为．16．（4分）已知点A（2，0），B是圆x2+y2=4上的定点，经过点B的直线与该圆交于另一点C，当△ABC面积最大时，直线BC的方程为．17．（4分）如图，直线l⊥平面α，垂足为O，已知在直角三角形ABC中，BC=1，AC=2，AB=．该直角三角形在空间做符合以下条件的自由运动：（1）A∈l，（2）C∈α．则B、O两点间的最大距离为．三、解答题（本大题共4小题，共52分，解答应写出文字说明、证明过程或演算步骤）．18．（12分）△ABC的三个顶点为A（﹣3，0），B（2，1），C（﹣2，3），求：（1）AC所在直线的方程；（2）BC边的垂直平分线的方程．19．（12分）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，O为AC的中点，PO⊥平面ABCD，PO=2，M为PD的中点．（1）证明：PB∥平面ACM；（2）求直线AM与平面ABCD所成角的正切值．20．（14分）如图，在四面体A﹣BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2．M是AD的中点．（1）证明：平面ABC⊥平面ADC；（2）若∠BDC=60°，求二面角C﹣BM﹣D的大小．21．（14分）已知圆M过定点D（0，2），圆心M在二次曲线上运动．（1）若圆M与y轴相切，求圆M方程；（2）已知圆M的圆心M在第一象限，半径为，动点Q（x，y）是圆M外一点，过点Q与圆M相切的切线的长为3，求动点Q（x，y）的轨迹方程；（3）若圆M与x轴交于A，B两点，设|AD|=a，|BD|=b，求的取值范围？浙江省温州市十校联合体联考2014-2015学年高二上学期期中数学试卷（文理同卷）参考答案与试题解析一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．1．（4分）直线的倾斜角的大小是（）A．30°B．60°C．120°D．150°考点：直线的倾斜角．专题：计算题．分析：设出直线的倾斜角，求出斜率，就是倾斜角的正切值，然后求出倾斜角．解答：解：设直线的倾斜角为α，由题意直线的斜率为，即tanα=所以α=150°故选D．点评：本题考查直线的倾斜角、直线的斜率，考查计算能力，是基础题．2．（4分）已知m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（）A．若m∥α，n∥α，则m∥n B．若m∥n，m⊥α，则n⊥αC．若m∥α，m∥β，则α∥βD．若m∥α，α⊥β，则m⊥β考点：空间中直线与平面之间的位置关系．专题：综合题；空间位置关系与距离．分析：A，以正方体的上底面为α，可得下底面内的直线m、n均与α平行，但不一定有m∥n，因此是假命题；B，根据线面垂直的性质，可以得到n⊥α；C，D列举所有可能，即可得出结论．解答：解：对于A，设正方体的上底面为α，则在下底面内任意取两条直线m、n，有m∥α且n∥α，但不一定有m∥n成立，故是假命题；对于B，m∥n，m⊥α，根据线面垂直的性质，可以得到n⊥α，故正确；对于C，m∥α，m∥β，则α∥β或α、β相交，故是假命题；对于D，m∥α，α⊥β，则m与β平行、相交、m在β内都有可能，故不正确．故选：B．点评：本题考查学生对空间中点、线、面的位置关系的理解与掌握．重点考查学生的空间想象能力．3．（4分）直线mx+（2m﹣1）y+1=0与直线3x+my+3=0垂直，则m为（）A．﹣1 B．1 C．2 D．﹣1或0考点：直线的一般式方程与直线的垂直关系．专题：直线与圆．分析：由两条直线垂直可得 3m+（2m﹣1）m=0，解方程求得m的值．解答： 解：若直线mx+（2m ﹣1）y+1=0与直线3x+my+3=0垂直，则 3m+（2m ﹣1）m=0， 解得m=﹣1，或m=0． 故选：D点评： 本题主要考查两条直线垂直的条件，属于基础题． 4．（4分）P 、Q 分别为3x+4y ﹣10=0与6x+8y+5=0上任意一点，则|PQ|的最小值为（）A ．B ．C ． 3D ． 6考点： 两条平行直线间的距离． 专题： 计算题．分析： 由题意可知两条直线平行，直接利用平行线的距离公式求解即可．解答： 解：因为3x+4y ﹣10=0与6x+8y+5=0是平行线，即3x+4y ﹣10=0与3x+4y+=0所以|PQ|的最小值d=='故选B ．点评： 本题考查两条平行线间的距离公式，注意平行线的系数对应相等是易错点．5．（4分）若圆x 2+y 2﹣2ax+3by=0的圆心位于第三象限，那么直线x+ay+b=0一定不经过（） A ． 第一象限 B ． 第二象限 C ． 第三象限 D ． 第四象限考点： 圆的标准方程；直线的图象特征与倾斜角、斜率的关系． 专题： 计算题；直线与圆．分析： 由已知圆的圆心在第三象限，建立关于a 、b 的不等式组解出a ＜0且b ＞0，由此算出直线x+ay+b=0经过x 轴负半轴一点和y 轴正半轴一点，可得它不经过第四象限． 解答： 解：∵圆x 2+y 2﹣2ax+3by=0的圆心为（a ，﹣）∴圆心位于第三象限，得a ＜0且﹣＜0，解得a ＜0且b ＞0又∵直线x+ay+b=0，在x 轴的截距为﹣b ＜0，在y 轴的截距为﹣＞0∴直线x+ay+b=0经过x 轴负半轴一点和y 轴正半轴一点 由此可得直线经过一、二、三象限，不经过第四象限 故选：D点评： 本题给出含有参数a 、b 的圆的圆心在第三象限，求直线x+ay+b=0经过的象限．着重考查了直线的方程、圆的方程等知识，属于基础题． 6．（4分）将棱长为1的正方体木块切削成一个体积最大的球，则该球的体积为（）A ．B ．C ．D ．考点： 棱柱、棱锥、棱台的体积．专题：转化思想；空间位置关系与距离．分析：将棱长为1的正方体木块切削成一个体积最大的球，结合正方体和球的结构特征，可以求出球的半径，代入球的体积公式即可求出答案．解答：解：将棱长为1的正方体木块切削成一个体积最大的球时，球的直径等于正方体的棱长1，则球的半径R=则球的体积V=•π•R3=故选：A．点评：本题考查的知识点是球的体积，其中根据正方体和圆的结构特征，求出球的半径，是解答本题的关键．7．（4分）如图，三棱锥V﹣ABC底面为正三角形，侧面VAC与底面垂直且VA=VC，已知其主视图的面积为，则其左视图的面积为（）A．B．C．D．考点：简单空间图形的三视图．专题：计算题．分析：由三视图的画图要求“长对正，高平齐，宽相等”可以找出左视图的宽、高与俯视图的宽、主视图的高的相等关系，进而求出答案．解答：解：设底面正△ABC的边长为a，侧面VAC的底边AC上的高为h，可知底面正△ABC 的高为，∵其主视图为△VAC，∴；∵左视图的高与主视图的高相等，∴左视图的高是h，又左视图的宽是底面△ABC的边AC上的高，∴S侧视图===．故选B．点评：本题考查了三视图的有关计算，正确理解三视图的画图要求是解决问题的关键．8．（4分）如图是正方体的平面展开图，则在这个正方体中的AB与CD的位置关系为（）A．平行B．相交成60°角C．异面成60°角D．异面且垂直考点：空间中直线与直线之间的位置关系．专题：空间位置关系与距离．分析：以CD所在平面为底面，将正方体的平面展开图还原成直观图，因为CE∥AB，所以∠DCE 即为直线AB，CD所成的角，在△CDE中求解即可．解答：解：如图，直线AB，CD异面．因为CE∥AB，所以∠DCE即为直线AB，CD所成的角，因为△CDE为等边三角形，故∠DCE=60°故选C点评：本题以图形的折叠为载体，考查平面图形向空间图形的转化，考查折叠问题、异面直线的判断及异面直线所成的角，考查空间想象能力和运算能力．9．（4分）将边长为a的正方形沿对角线AC折起，使得BD=a，则三棱锥D﹣ABC的体积为（）A．B．C．D．考点：棱柱、棱锥、棱台的体积．专题：空间位置关系与距离．分析：如图，由正方形的性质可以求得其对角线长度是，折起后的图形中，DE=BE=a，又知BD=a，由此三角形BDE三边已知，求出∠BED，解出三角形BDE的面积，又可证得三棱锥D﹣ABC的体积可看作面BDE为底，高分别为AE，AC的两个棱锥的体积和．解答：解：如图，由题意知DE=BE=a，BD=a由勾股定理可证得∠BED=90°故三角形BDE面积是a2又正方形的对角线互相垂直，且翻折后，AC与DE，BE仍然垂直，故AE，CE分别是以面BDE 为底的两个三角形的高故三棱锥D﹣ABC的体积为×a×a2=a3故选：A．点评：本题考查棱柱、棱锥、棱台的体积，解题的关键是正确理解图形，将求几何体体积变为求两个几何体的体积，换一个角度求解，使得解题过程变得容易．10．（4分）设集合，，且A∩B≠∅，则实数a的取值范围是（）A．B．C．D．考点：集合的包含关系判断及应用．专题：计算题．分析：由，我们易得A集合表示以原点为圆心，以为半径的圆在X轴上方的部分，，B集合表示以（1，）为原点以a为半径的圆，根据A∩B≠∅，我们对a进行分析讨论，我们易得到结论．解答：解：∵∴A集合表示以原点为圆心，以为半径的圆在X轴上方的部分，又∵，∴B集合表示以（1，）为原点以a为半径的圆若A∩B≠∅，则两个圆相切或相交故a﹣a≤2≤a+a解得a∈故选D．点评：本题考查的知识点是两个集合的交集运算及圆与圆之间的位置关系，根据A∩B≠∅，准确判断两个圆的位置关系，并根据圆的位置关系列出两圆半径与圆心距的关系，是解答的关键．二、填空题（本大题共7小题，每小题4分，共28分）11．（4分）空间直角坐标系中，点（3，2，﹣5）到xoy平面的距离为5．考点：空间两点间的距离公式．专题：空间位置关系与距离．分析：根据点P关于平面xOy的对称点的坐标横标和纵标不变，竖标变成0，即可求出距离．解答：解：∵点（3，2，﹣5），在平面xOy的射影点的坐标横标和纵标不变，竖标变成0，即得到（3，2.0）∴空间直角坐标系中，点（3，2，﹣5）到xoy平面的距离为5．故答案为：5．点评：本题考查图形的对称性和空间中点的坐标，本题解题的关键是了解关于坐标轴和坐标平面射影点的坐标的特点．12．（4分）直线kx+3y+k﹣9=0过定点（﹣1，3）．考点：恒过定点的直线．专题：直线与圆．分析：将kx+3y+k﹣9=0转化为k（x+1）+3y﹣9=0，依题意，，解之即可．解答：解：∵kx+3y+k﹣9=0，∴k（x+1）+3y﹣9=0，∴，解得，∴直线kx+3y+k﹣9=0过定点（﹣1，3）．故答案为：（﹣1，3）．点评：本题考查恒过定点的直线，考查等价转化思想与方程思想的应用，属于中档题．13．（4分）轴截面是边长等于2的等边三角形的圆锥，它的表面积等于3π．考点：棱柱、棱锥、棱台的侧面积和表面积．专题：空间位置关系与距离．分析：由轴截面是边长等于2的等边三角形，求出圆锥的底面半径，母线长，进而求出圆锥的底面周长，代入圆锥表面积公式，即可求出圆锥的表面积．解答：解：一个圆锥的轴截面（过旋转轴的截面）是边长为2的等边三角形，所以圆锥的母线为l=2；底面半径为r=1；圆锥的底面周长为C=2πr=2π．所以圆锥的表面积为：×2π×2+π•12=3π故答案为：3π点评：本题是基础题，考查圆锥的轴截面知识，圆锥的表面积的求法，实际上这个圆锥又叫等边圆锥，需要同学注意它的边角关系，常考题目．14．（4分）若在平面直角坐标系内过点且与原点的距离为d的直线有两条，则d的取值范围是（0，2）．考点：点到直线的距离公式．专题：直线与圆．分析：由两点间的距离公式求得原点到过点的直线的距离的最大值，又原点到过原点与P点的直线的距离为0，则满足条件的答案可求．解答：解：∵过点的直线与原点的距离最大为．此时直线与PO垂直，有且只有一条．当直线过原点的时候，距离d=0．此时也只有一条．如图，∴当0＜d＜2时，直线有两条．∴在平面直角坐标系内过点且与原点的距离为d的直线有两条，则d的取值范围是（0，2）．故答案为：（0，2）．点评：本题考查两点间的距离公式，训练了数形结合的解题思想方法，是基础题．15．（4分）过P（2，0）的直线l1截圆C：x2+y2﹣6x+4y+4=0所得的弦长为，则直线l1的方程为x=2或3x+4y﹣6=0．考点：直线与圆的位置关系．专题：直线与圆．分析：当直线l1的斜率不存在时，直线x=2满足题意；当斜率存在时，设为k，表示出直线方程，利用垂径定理及勾股定理求出k的值，即可确定出满足题意的直线l1方程．解答：解：当直线l1的斜率不存在时，直线x=2满足题意；当直线l1的斜率存在时，设为k，直线方程为y=k（x﹣2），即kx﹣y﹣2k=0，∵直线l1截圆C：x2+y2﹣6x+4y+4=0，即（x﹣3）2+（y+2）2=9，所得的弦长为4，∴圆心（3，﹣2）到直线的距离d==1，即=1，解得：k=﹣，此时直线l1的方程为3x+4y﹣6=0，综上，直线l1的方程为x=2或3x+4y﹣6=0．故答案为：x=2或3x+4y﹣6=0点评：此题考查了直线与圆的位置关系，涉及的知识有：圆的标准方程，垂径定理，勾股定理，直线的点斜式方程，学生做题时容易忽略直线斜率不存在的情况．16．（4分）已知点A（2，0），B是圆x2+y2=4上的定点，经过点B的直线与该圆交于另一点C，当△ABC面积最大时，直线BC的方程为x=﹣1．考点：圆的参数方程；直线与圆的位置关系．专题：直线与圆．分析：由题意，当△ABC面积最大时，C到AB的距离最大，设C的坐标，求出直线AB的方程，可得C到AB的距离，利用三角函数的值域即可得出结论．解答：解：由题意，当△ABC面积最大时，C到AB的距离最大，设C（2cosα，2sinα），则∵点A（2，0），B，∴直线AB的方程为，∴C到AB的距离为=|2cos（α+）﹣1|，∴cos（α+）=﹣1时，C到AB的距离最大为3，此时α可取，∴C（﹣1，﹣），∵B，直线BC的方程为x=﹣1．故答案为：x=﹣1．点评：本题考查直线与圆的位置关系，考查学生分析解决问题的能力，属于中档题．17．（4分）如图，直线l⊥平面α，垂足为O，已知在直角三角形ABC中，BC=1，AC=2，AB=．该直角三角形在空间做符合以下条件的自由运动：（1）A∈l，（2）C∈α．则B、O两点间的最大距离为1+．考点：点、线、面间的距离计算．专题：转化思想．分析：先将原问题转化为平面内的最大距离问题解决，以O为原点，OA为y轴，OC为x轴建立直角坐标系，B、O两点间的距离表示处理，结合三角函数的性质求出其最大值即可．解答：解：将原问题转化为平面内的最大距离问题解决，以O为原点，OA为y轴，OC为x轴建立直角坐标系，如图．设∠ACO=θ，B（x，y），则有：x=ACcosθ+BCsinθ=2cosθ+sinθ，y=BCcosθ=cosθ．∴x2+y2=4cos2θ+4sinθcosθ+1=2cos2θ+2sin2θ+3=2sin（2θ+）+3，当sin（2θ+）=1时，x2+y2最大，为2+3，则B、O两点间的最大距离为1+故答案为：1+．点评：本题考查了点、线、面间的距离计算，解答关键是将空间几何问题转化为平面几何问题解决，利用三角函数的知识求最大值．三、解答题（本大题共4小题，共52分，解答应写出文字说明、证明过程或演算步骤）．18．（12分）△ABC的三个顶点为A（﹣3，0），B（2，1），C（﹣2，3），求：（1）AC所在直线的方程；（2）BC边的垂直平分线的方程．考点：直线的一般式方程与直线的垂直关系；直线的一般式方程．专题：计算题．分析：（1）因为点A和点B的坐标已知，所以直接利用直线的两点式得到方程即可；（2）由中点坐标公式可得BC中点以及BC所在的直线方程的斜率，根据两直线垂直求出垂直平分线的方程的斜率，进而可得方程．解答：解：（1）由直线方程的两点式得，所以AC所在直线的方程3x﹣y+9=0；（2）∵B（2，1），C（﹣2，3），∴kAB==﹣中点坐标M（0，2）k AM=2∴B C边的垂直平分线的方程为：y﹣0=2（x﹣2）故所求的直线方程为：2x﹣y+4=0点评：本题考查直线方程的两点式、中点公式，以及两直线垂直的性质，属于中档题．19．（12分）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，O为AC的中点，PO⊥平面ABCD，PO=2，M为PD的中点．（1）证明：PB∥平面ACM；（2）求直线AM与平面ABCD所成角的正切值．考点：直线与平面平行的判定；直线与平面所成的角．专题：综合题；空间位置关系与距离．分析：（1）连接BD，MO，在平行四边形ABCD中，由O为AC的中点，知O为BD的中点，再由M为PD的中点，知PB∥MO，由此能够证明PB∥平面ACM．（2）取DO中点N，连接MN，AN，由M为PD的中点，知MN∥PO，且MN=PO=1，由PO⊥平面ABCD，得MN⊥平面ABCD，故∠MAN是直线AM与平面ABCD所成的角，由此能求出直线AM与平面ABCD所成角的正切值．解答：（1）证明：连接BD，MO，在平行四边形ABCD中，∵O为AC的中点，∴O为BD的中点，又∵M为PD的中点，∴PB∥MO，∵PB⊄平面ACM，MO⊂平面ACM，∴PB∥平面ACM．（2）解：取DO中点N，连接MN，AN，∵M为PD的中点，∴MN∥PO，且MN=PO=1，由PO⊥平面ABCD，得MN⊥平面ABCD，∴∠MAN是直线AM与平面ABCD所成的角，在Rt△DAO中，∵AD=1，AO=，∠DAO=90°，∴DO=，∴AN=，在Rt△ANM中，tan∠MAN===，即直线AM与平面ABCD所成角的正切值为．点评：本题考查直线与平面平行的证明，考查直线与平面所成角的正切值的求法．解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题．20．（14分）如图，在四面体A﹣BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2．M是AD的中点．（1）证明：平面ABC⊥平面ADC；（2）若∠BDC=60°，求二面角C﹣BM﹣D的大小．考点：与二面角有关的立体几何综合题；平面与平面垂直的判定．专题：综合题；空间位置关系与距离；空间角．分析：（1）先证明BC⊥AD，结合BC⊥CD，AD∩CD=D，可得BC⊥平面ACD，利用面面垂直的判定定理，可得平面ABC⊥平面ADC；（2）作CG⊥BD于点G，作GH⊥BM于点HG，连接CH，证明∠CHG为二面角的平面角，结合∠BDC=60°，即可求二面角C﹣BM﹣D的大小．解答：（1）证明：∵AD⊥平面BCD，BC⊂平面BCD，∴BC⊥AD．又∵BC⊥CD，AD∩CD=D，∴BC⊥平面ACD，又∵BC⊂平面ABC，∴平面ABC⊥平面ADC；（2）解：作CG⊥BD于点G，作GH⊥BM于点HG，连接CH．∵AD⊥平面BCD，CG⊂平面BCD，∴CG⊥AD又∵CG⊥BD，AD∩BD=D，∴CG⊥平面ABD，又∵BM⊂平面ABD，∴BM⊥CG又∵BM⊥GH，CG∩GH=G，∴BM⊥平面CGH，∵CH⊂平面CGH，∴BM⊥CH∴∠CHG为二面角的平面角．在Rt△BCD中，CD=BDcos60°=，CG=CD，BG=BC．在Rt△BDM中，HG==在Rt△CHG中，tan∠CHG=，∴∠CHG=60°，即二面角C﹣BM﹣D的大小为60°．点评：本题考查面面垂直的判定，考查线面垂直，考查面面角，考查学生分析解决问题的能力，考查学生的计算能力，属于中档题．21．（14分）已知圆M过定点D（0，2），圆心M在二次曲线上运动．（1）若圆M与y轴相切，求圆M方程；（2）已知圆M的圆心M在第一象限，半径为，动点Q（x，y）是圆M外一点，过点Q与圆M相切的切线的长为3，求动点Q（x，y）的轨迹方程；（3）若圆M与x轴交于A，B两点，设|AD|=a，|BD|=b，求的取值范围？考点：圆方程的综合应用．专题：综合题．分析：（1）圆心M，半径，由此能求出圆M方程．（2）设圆心，则．由此得到圆M的方程为：（x﹣2）2+（y﹣1）2=5．设QP于圆M相切，切点为P，则|QM|2=|QP|2+|MP|2=14，由此能求出动点Q的轨迹方程．（3）设圆心M（2m，m2），可知圆M方程为：（x﹣2m）2+（y﹣m2）2=4m2+（m2﹣2）2，取y=0，得x=2m±2，取A（2m+2，0），B（2m﹣2，0），则，由此能求出的取值范围．解答：解：（1）设圆心M（x，y），∵圆M过定点D（0，2），且圆M与y轴相切，∴直线MD⊥y轴，∴，∴y=2，∵圆心M在二次曲线上运动，∴M（x，2）在上，∴2=，解得x=，∴圆心M，半径=2，∴圆M方程为：．…（4分）（2）设圆心，则解得m=1，所以圆M的方程为：（x﹣2）2+（y﹣1）2=5设QP于圆M相切，切点为P，则|QM|2=|QP|2+|MP|2=14所以动点Q的轨迹方程是（x﹣2）2+（y﹣1）2=14…．（9分）（3）设圆心M（2m，m2），可知圆M方程为：（x﹣2m）2+（y﹣m2）2=4m2+（m2﹣2）2取y=0得x=2m±2，不妨取A（2m+2，0），B（2m﹣2，0），则若m≠0，有，则，故所求的取值范围为点评：本题考查圆的方程的综合应用，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是2015届高考的重点．解题时要认真审题，仔细解答．。

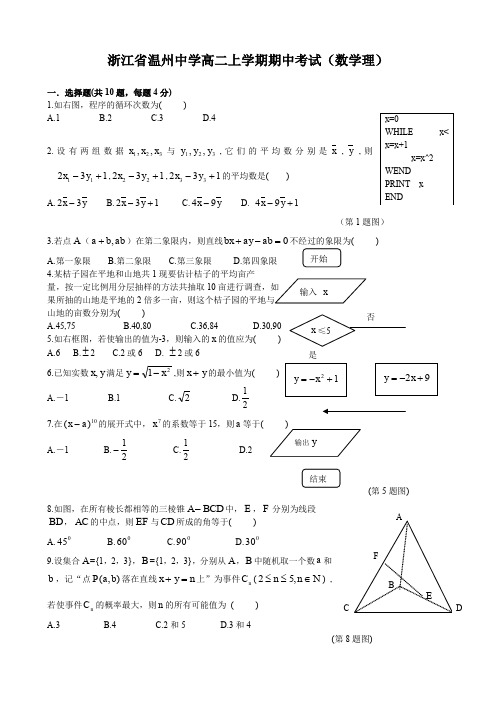
浙江省温州中学高二上学期期中考试（数学理）一．选择题(共10题，每题4分) 1.如右图，程序的循环次数为( )A.1B.2C.3D.42.设有两组数据321,,x x x 与321,,y y y ,它们的平均数分别是x ,y ,则13211+-y x ,13222+-y x ,13233+-y x 的平均数是( )A.y x 32-B.132+-y xC.y x 94-D. 194+-y x（第1题图）3.若点A （ab b a ,+）在第二象限内，则直线0=-+ab ay bx 不经过的象限为( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限4.某桔子园在平地和山地共1现要估计桔子的平均亩产量，按一定比例用分层抽样的方法共抽取10果所抽的山地是平地的2山地的亩数分别为( )A.45,75B.40,80C.36,84D.30,90 5.如右框图，若使输出的值为-3，则输入的x 的值应为( ) A.6 B.±2 C.2或6 D.±2或66.已知实数y x ,满足21x y -=,则y x +的最小值为( ) A.－1 B.1 C.2 D.21 7.在10)(a x -的展开式中，7x 的系数等于15，则a 等于( A.－1 B.21- C.21D.28.如图，在所有棱长都相等的三棱锥BCD A -中，E ，F 分别为线段BD ，AC 的中点，则EF 与CD 所成的角等于( ) A.045 B.060 C.090 D.0309.设集合A ={1，2，3}，B ={1，2，3}，分别从A ，B 中随机取一个数a 和b ，记“点),(b a P 落在直线n y x =+上”为事件n C (N n n ∈≤≤,52) ,若使事件n C 的概率最大，则n 的所有可能值为 ( )A.3B.4C.2和5D.3和4(第8题图)是C(第5题图)10.以正方体1111D C B A ABCD -的8个顶点及6个表面的中心点共14个点中的某些点为顶点的正棱锥共有( )个.A.38B.32C.28D.．填空题(共6题，每题4分)11.甲乙两人在相同的条件下各射击3次，命中的环数如下：甲： 7， 8，9；乙：6，8，10。

瑞安中学2014学年第一学期高二期中考试数学试卷一、选择题：本大题共 10小题，每小题3分，共30分.在每小题给出的四个选项中，只有 一项符合题目要求.1直线・、3x-y / =0的倾斜角的大小是（）B . 120C . 60D . 302•直线2x y ^0与圆（x 1）2 （y-1）2 =1的位置关系是（）4.设I , m 是两条不同的直线， 二是一个平面，则下列命题正确的是（）A .若 l 」二,l// m ，则 m 」二B .若 l — m , m :，贝y l -:C .若 l // :- , m 二：J 则 l 〃 mD .若 l // :- , m 〃 ［，则 l 〃 m5.若直线l 1 :ax 3y 0与l 2: 2x （a 1）y • 1 = 0互相平行，则a 的值是（ ）A. -3或2B. 3或-2C. -3D. 22 2 2 26•已知圆x y =4与圆x y -2y -6=0，则两圆的公共弦长为 （ ）A .、、3B . 2.3C . 2D . 17.在正方体ABCD - A 1B 1C 1D 1中，0是底面ABCD 的中心，E 为CC 1的中点，那么直线OE 与AD 1所成角的余弦值为（）A. &若圆x 2 y 2 -4x • 2my m 0与y 轴的两交点 A, B 位于原点的同侧，贝U 实数m 的 取值范围是（）A . m ：： -6B . m -6C . -6 ：： m ：： -2D . -6 ：： m ：： -2或 m 39.若直线y = x ■ b 与曲线x = 3 - 4y - y 2有公共点，贝U b 的取值范围是（）A.相交B .相切C .相离D .不确定3.如图，Rt 「：QAB •是一平面图形的直观图， 斜边OB'2，则这个平面图形 的面积是（）A'2C . 、、2D . 2、、2D.A.[T-2.2 , -1 2\ 2]B.[-3, -1 2,2]C.[ -1-2,2 , 1]D. [ -3 , -1^2]10•如图，在矩形 ABCD 中，AB 八3, BC =1 , E 为线段CD 上一动点，现将 AED 沿AE 折起，使点D 在面ABC 上的射影K 在直线AE 上，当E 从D 运动到C ，则K 所形成 轨迹的长度为()兀C.—211.已知直线ax y ^0恒过一定点，则此定点的坐标是 _______________ ▲ 12.直线 l 1 :x y ^0与l 2 :2x 2y 3=0 的距离是 ▲13.一长方体的各顶点均在同一个球面上，且一个顶点上的三条棱长分别为 1, 6,3，则这个球的表面积为▲.14. 已知点E(2,1)和圆O ： x 2 y 2 =16,过点E 的直线l 被圆O 所截得的弦长为 4 3，则 直线l 的方程为▲.15. 已知正方体 ABCD -A 1B 1C 1D 1的棱长为1,E,F 分别为线段AA 1P1C 上的点，则三棱 锥D^ EDF 的体积为▲.16. 在直角坐标系xOy 中，设A(3,2), B( -2, -3),沿y 轴把坐标平面折成120的二面角后,AB 的长为 ▲.17. 已知圆 0:x 2 • y 2 =4，圆内有定点P(1,1),圆周上有两个动点分别记为 A , B ,使PA _ PB ，则矩形APBQ 的顶点Q 的轨迹方程为▲.、填空题：本大题共7小题，每小题3分，共21分.D .3D兀三、解答题：本大题共5小题，共49分，解答应写出文字说明、证明过程或演算步骤18.(本小题8分)若空间某几何体的三视图如图所示，求该几何体的表面积和体积.佃.(本小题9 分)已知直线I : y二4x和点P(6,4)，点A为第一象限内的点且在直线I上,K—6 ―>1側视图直线PA交X轴正半轴于点B ,(1)当OP _ AB时，求AB所在直线的直线方程；(2)求A OAB面积的最小值，并求当A OAB面积取最小值时的B的坐标.20.(本小题10分)如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD丄底面ABCD , PD二DC , E是PC的中点，作EF丄PB交PB于点F .(1)证明：PA//平面EDB ;(2)证明：DE _ BC ；(3)求BD和平面EFD所成角的余弦值.f21. （本小题10分）已知圆C经过原点O,与x轴另一交点的横坐标为4,与y轴另一交点的纵坐标为2，（1）求圆C的方程；（2）已知点B的坐标为（0,2），设P,Q分别是直线l :x y ^0和圆C上的动点，求PB + PQ的最小值及此时点P的坐标.22. （本小题12分）如图，在三棱锥D - ABC中，已知A BCD是正三角形，AB _平面BCD , AB = BC , E 为BC 的中点，F 在棱AC 上，且AF =3FC ,（1）求证：AC _平面DEF ；（2）若M为BD的中点，问AC上是否存在一点N，使MN //平面DEF ?若存在，说明点N的位置；若不存在，试说明理由；（3）求平面DEF与平面ABD所成的锐二面角的余弦值.瑞安中学2014学年第一学期高二期中考试数学答案题号 1 2 3 45 6 7 8 9 10 答案CADACBBDBD14._X =2 或 3x 4y-10=0_15.17. ______ X 2 y 2 =6 _________ 三、解答题 (8+9+10+10+12=49 分) 18. V =57；S =54 二 19.解：(1) 3X 2y -26 =05a(2)设A(a,4a),B(b,0),则由A, B,P 三点共线可得 b 二旦 ,a 1 a —11当且仅当 a -1 = —— 即a = 2时，取到最小值，此时 B 的坐标为（10,0）。

浙江省温州市瑞安中学2014-2015学年高二上学期期中数学试卷（实验班）一、选择题：（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．（5分）若直线l1：ax+3y+1=0与l2：2x+（a+1）y+1=0互相平行，则a的值是（）A．﹣3 B．2 C．﹣3或2 D．3或﹣22．（5分）已知复数z=，则复数z在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．（5分）设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：①若m⊥α，n∥α，则m⊥n；②若m∥α，n∥α，则m∥n；③若α∥β，β∥γ，m⊥α，则m⊥γ；④若α⊥γ，β⊥γ，则α∥β；其中正确命题的序号是（）A．①和③B．②和③C．②和④D．①和④4．（5分）已知a＞0，x，y满足约束条件，若z=2x+y的最小值为1，则a=（）A．B．C．1 D．25．（5分）已知函数f（x）=log a x（0＜a＜1）的导函数f′（x），A=f′（a），B=f（a+1）﹣f（a），C=f′（a+1），D=f（a+2）﹣f（a+1），则A，B，C，D，中最大的数是（）A．A B．B C．C D．D6．（5分）如图，P是正方体ABCD﹣A1B1C1D1对角线AC1上一动点，设AP的长度为x，若△PBD 的面积为f（x），则f（x）的图象大致是（）A．B． C． D．7．（5分）若直线y=x+b与曲线x=3﹣有公共点，则b的取值范围是（）A．[﹣1﹣2，﹣1+2] B．[﹣3，﹣1+2] C．[﹣1﹣2，1] D．[﹣3，﹣1+]8．（5分）一多面体的三视图如图所示，则该多面体的体积是（）A．B．C．6 D．79．（5分）在《爸爸去哪儿》第二季第四期中，村长给6位“萌娃”布置一项搜寻空投食物的任务．已知：①食物投掷地点有远、近两处；②由于Grace年纪尚小，所以要么不参与该项任务，但此时另需一位小孩在大本营陪同，要么参与搜寻近处投掷点的食物；③所有参与搜寻任务的小孩须被均分成两组，一组去远处，一组去近处．则不同的搜寻方案有（）A．40种B．70种C．80种D．100种10．（5分）如图为函数f（x）=的部分图象，ABCD是矩形，A，B在图象上，将此矩形绕x轴旋转得到的旋转体的体积的最大值为（）A．πB．2πC．3πD．4π二、填空题：（本大题共7小题，每小题4分，共28分）11．（4分）（x2﹣）5展开式中的常数项为．12．（4分）已知点E（2，1）和圆O：x2+y2=16，过点E的直线l被圆O所截得的弦长为2，则直线l的方程为．13．（4分）有两排座位，前排11个座位，后排12个座位．现在安排甲、乙2人就座，规定前排中间的3个座位不能坐，并且甲、乙不能左右相邻，则一共有不同安排方法多少种？（用数字作答）．14．（4分）在直角坐标系xOy中，设A（3，2），B（﹣2，﹣3），沿y轴把坐标平面折成120°的二面角后，AB的长为．15．（4分）函数y=2sinx（x∈[0，π]）在点P处的切线与函数y=lnx+x2在点Q处切线平行，则直线PQ的斜率是．16．（4分）如图，四面体OABC的三条棱OA、OB、OC两两垂直，OA=OB=2，OC=3，D为四面体OABC外一点．给出下列命题．①不存在点D，使四面体ABCD有三个面是直角三角形②不存在点D，使四面体ABCD是正三棱锥③存在点D，使CD与AB垂直并且相等④存在无数个点D，使点O在四面体ABCD的外接球面上其中真命题的序号是．17．（4分）设函数y=f（x）在（﹣∞，+∞）内有定义，对于给定的正数K，定义函数f K （x）=，取函数f（x）=2﹣x﹣e﹣x，若对任意的x∈（﹣∞，+∞），恒有f K（x）=f（x），则K的最小值为．三、解答题（本大题共5小题，共70分.）18．（14分）底面半径为2，高为4的圆锥有一个内接的正四棱柱（底面是正方形，侧棱与底面垂直的四棱柱）．（1）设正四棱柱的底面边长为x，试将棱柱的高h表示成x的函数；（2）当x取何值时，此正四棱柱的表面积最大，并求出最大值．19．（14分）已知直线l：y=4x和点P（6，4），点A为第一象限内的点且在直线l上，直线PA交x轴正半轴于点B，（1）当OP⊥AB时，求AB所在直线的直线方程；（2）求△OAB面积的最小值，并求当△OAB面积取最小值时的B的坐标．20．（14分）已知函数f（x）=a（x﹣1）2+lnx+1．（Ⅰ）当a=﹣时，求函数f（x）的极值；（Ⅱ）若函数f（x）在区间[2，4]上是减函数，求实数a的取值范围．21．（15分）如图，在三棱锥D﹣ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC，E 为BC的中点，F在棱AC上，且AF=3FC，（1）求证：AC⊥平面DEF；（2）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由；（3）求平面DEF与平面ABD所成的锐二面角的余弦值．22．（15分）设函数f（x）=2ax﹣+lnx．（Ⅰ）当b=a时，若f（x）在（0，+∞）上是单调函数，求a的取值范围．（Ⅱ）若f（x）在x=m，x=n（m＜n）处取得极值，若方程f（x）=c在（0，2n]上有唯一解，则c的取值范围为 {x|x＜x0或s≤x＜t}，求t﹣s的最大值．浙江省温州市瑞安中学2014-2015学年高二上学期期中数学试卷（实验班）参考答案与试题解析一、选择题：（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．（5分）若直线l1：ax+3y+1=0与l2：2x+（a+1）y+1=0互相平行，则a的值是（）A．﹣3 B．2 C．﹣3或2 D．3或﹣2考点：直线的一般式方程与直线的平行关系．专题：直线与圆．分析：利用两条直线平行，斜率相等，建立等式即可求a的值．解答：解：直线l1：ax+3y+1=0，的斜率存在，斜率为﹣，l2：2x+（a+1）y+1=0，斜率为﹣∵直线l1：ax+3y+1=0与l2：2x+（a+1）y+1=0互相平行∴﹣=﹣解得：a=﹣3或2当a=2时，两直线重合，∴a=﹣3故选：A．点评：本题考查直线的一般式方程与直线的平行关系，属基础题．2．（5分）已知复数z=，则复数z在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限考点：复数代数形式的混合运算；复数的基本概念．专题：数系的扩充和复数．分析：根据复数的几何意义，先将复数进行化简，即可得到结论．解答：解：∵z====，∴复数z在复平面内对应的点（）位于第一象限．故选：A．点评：本题主要考查复数的几何意义，根据复数的四则运算是解决本题的关键，比较基础．3．（5分）设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：①若m⊥α，n∥α，则m⊥n；②若m∥α，n∥α，则m∥n；③若α∥β，β∥γ，m⊥α，则m⊥γ；④若α⊥γ，β⊥γ，则α∥β；其中正确命题的序号是（）A．①和③B．②和③C．②和④D．①和④考点：空间中直线与直线之间的位置关系．专题：证明题；空间位置关系与距离．分析：对四个命题分别进行判断，即可得出结论．解答：解：若m⊥α，n∥α，则m⊥n，正确若m∥α，n∥α，则m与n可能平行、相交也可能异面，故②错误；α∥β，β∥γ，则α∥γ，因为m⊥α，所以m⊥γ，故③正确；若α⊥γ，β⊥γ，则α∥β，此命题不正确，因为垂直于同一平面的两个平面可能平行、相交，不能确定两平面之间是平行关系，故④错误，故选：A点评：本题考查平面的基本性质及推论，解题的关键是有着较强的空间感知能力及对空间中线面，面面，线线位置关系的理解与掌握，此类题是训练空间想像能力的题，属于基本能力训练题．4．（5分）已知a＞0，x，y满足约束条件，若z=2x+y的最小值为1，则a=（）A．B．C．1 D．2考点：简单线性规划．专题：不等式的解法及应用．分析：先根据约束条件画出可行域，设z=2x+y，再利用z的几何意义求最值，只需求出直线z=2x+y过可行域内的点B时，从而得到a值即可．解答：解：先根据约束条件画出可行域，设z=2x+y，将最大值转化为y轴上的截距，当直线z=2x+y经过点B时，z最小，由得：，代入直线y=a（x﹣3）得，a=故选：B．点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．线性规划中的最优解，通常是利用平移直线法确定．5．（5分）已知函数f（x）=log a x（0＜a＜1）的导函数f′（x），A=f′（a），B=f（a+1）﹣f（a），C=f′（a+1），D=f（a+2）﹣f（a+1），则A，B，C，D，中最大的数是（）A．A B．B C．C D．D考点：导数的运算．专题：计算题；作图题；导数的概念及应用．分析：作函数f（x）=log a x（0＜a＜1）的图象，A，B，C，D分别表示了直线l4，l3，l2，l1的斜率，从而求解．解答：解：作函数f（x）=log a x（0＜a＜1）的图象如下：A=f′（a），B=f（a+1）﹣f（a），C=f′（a+1），D=f（a+2）﹣f（a+1）分别表示了直线l4，l3，l2，l1的斜率；故A，B，C，D，中最大的数是D，故选D．点评：本题考查了导数的几何意义，属于基础题．6．（5分）如图，P是正方体ABCD﹣A1B1C1D1对角线AC1上一动点，设AP的长度为x，若△PBD 的面积为f（x），则f（x）的图象大致是（）A．B． C． D．考点：棱柱的结构特征；函数的图象．专题：图表型．分析：先设正方体的棱长为1，连接AC交BD于O，连PO，则PO是等腰△PBD的高，从而△PBD的面积为f（x）=BD×PO，再在△PAO中，利用余弦定理得出PO，最后得出f（x）的解析式，画出其图象，对照选项即可解决问题．解答：解：设正方体的棱长为1，连接AC交BD于O，连PO，则PO是等腰△PBD的高，故△PBD的面积为f（x）=BD×PO，在三角形PAO中，PO==，∴f（x）=××=，画出其图象，如图所示，对照选项，A正确．故选A．点评：本小题主要考查棱柱的结构特征、函数的图象等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．7．（5分）若直线y=x+b与曲线x=3﹣有公共点，则b的取值范围是（）A．[﹣1﹣2，﹣1+2] B．[﹣3，﹣1+2] C．[﹣1﹣2，1] D．[﹣3，﹣1+]考点：直线和圆的方程的应用．专题：计算题；直线与圆．分析：曲线即（x﹣3）2+（y﹣2）2=4（1≤x≤3，0≤y≤4），表示以A（3，2）为圆心，以2为半径的一个半圆，由圆心到直线y=x+b的距离等于半径2，解得b，可得b的范围．解答：解：曲线x=3﹣，即（x﹣3）2+（y﹣2）2=4（1≤x≤3，0≤y≤4），表示以A（3，2）为圆心，以2为半径的一个半圆．由圆心到直线y=x+b的距离等于半径2，可得=2，∴b=﹣1+2，或b=﹣1﹣2．∴﹣3≤b≤﹣1+2，故选：B．点评：本题主要考查直线和圆的位置关系，点到直线的距离公式，体现了数形结合的数学思想，属于中档题．8．（5分）一多面体的三视图如图所示，则该多面体的体积是（）A．B．C．6 D．7考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：判断几何体的形状，结合三视图的数据，求出几何体的体积．解答：解：由三视图可知，该多面体是由正方体截去两个正三棱锥所成的几何体，如图，正方体棱长为2，正三棱锥侧棱互相垂直，侧棱长为1，故几何体的体积为：V正方体﹣2V棱锥侧==．故选：B．点评：本题考查三视图求解几何体的体积，解题的关键是判断几何体的形状．9．（5分）在《爸爸去哪儿》第二季第四期中，村长给6位“萌娃”布置一项搜寻空投食物的任务．已知：①食物投掷地点有远、近两处；②由于Grace年纪尚小，所以要么不参与该项任务，但此时另需一位小孩在大本营陪同，要么参与搜寻近处投掷点的食物；③所有参与搜寻任务的小孩须被均分成两组，一组去远处，一组去近处．则不同的搜寻方案有（）A．40种B．70种C．80种D．100种考点：进行简单的合情推理．专题：计算题；推理和证明．分析：Grace不参与该项任务，需一位小孩在大本营陪同，则其余4人被均分成两组，一组去远处，一组去近处；Grace参与该项任务，则从其余5人中选2人去近处，即可得出结论．解答：解：Grace不参与该项任务，则有=30种；Grace参与该项任务，则有=10种，故共有30+10=40种故选：A．点评：本题考查进行简单的合情推理，考查分类讨论的数学思想，考查学生分析解决问题的能力，比较基础．10．（5分）如图为函数f（x）=的部分图象，ABCD是矩形，A，B在图象上，将此矩形绕x轴旋转得到的旋转体的体积的最大值为（）A．πB．2πC．3πD．4π考点：函数的图象．专题：函数的性质及应用；不等式的解法及应用．分析：先求出y的范围，再设出点AB的坐标，根据AB两点的纵坐标相等得到x2•x1=1，再求出高h，根据圆柱体的体积公式得到关于y的代数式，最后根据基本不等式求出体积的最大值．解答：解：∵f（x）===y≤1当且仅当x=1时取等号，∴x+=∵矩形绕x轴旋转得到的旋转体一个圆柱，设A点的坐标为（x1，y），B点的坐标为（x2，y），则圆柱的底面圆的半径为y，高位h=x2﹣x1，∵f（x1）=，f（x2）=，∴=，即（x2﹣x1）（x2•x1﹣1）=0，∴x2•x1=1，∴h2=（x2+x1）2﹣4x2•x1=﹣4=﹣4，∴h=2•，∴V圆柱=πy2•h=2π≤2π•=π，当且仅当y=时取等号，故此矩形绕x轴旋转得到的旋转体的体积的最大值为π，故选：A点评：本题主要考查空间几何体的体积计算，基本的不等式的应用，本题求出x2•x1=1是关键，属于中档题．二、填空题：（本大题共7小题，每小题4分，共28分）11．（4分）（x2﹣）5展开式中的常数项为40．考点：二项式定理．专题：计算题．分析：先求得二项式展开式的通项公式，再令x的幂指数等于0，求得r的值，即可求得常数项．解答：解：（x2﹣）5展开式中的通项公式为 T r+1=•x10﹣2r•（﹣2）r•x﹣3r=（﹣2）r••x10﹣5r，令10﹣5r=0，r=2，故展开式的常数项为4•=40，故答案为 40．点评：本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．12．（4分）已知点E（2，1）和圆O：x2+y2=16，过点E的直线l被圆O所截得的弦长为2，则直线l的方程为y=1，或4x﹣3y﹣5=0．考点：直线与圆的位置关系．专题：直线与圆．分析：由题意利用弦长公式可得弦心距d=1，用点斜式设除直线l的方程，根据圆心到直线的距离等于1，求得斜率k的值，可得要求直线的方程．解答：解由于圆的半径为r=4，弦长2，故弦心距d==1．由题意可得，所求直线的斜率存在，设为k，可得直线l的方程为y﹣1=k（x﹣2），即 kx﹣y+1﹣2k=0，由弦心距d==1，求得k=0，或k=，故要求的直线l的方程为y=1，或4x﹣3y﹣5=0，故答案为：y=1，或4x﹣3y﹣5=0．点评：本题主要考查直线和圆的位置关系，点到直线的距离公式，弦长公式的应用，属于基础题．13．（4分）有两排座位，前排11个座位，后排12个座位．现在安排甲、乙2人就座，规定前排中间的3个座位不能坐，并且甲、乙不能左右相邻，则一共有不同安排方法多少种？346（用数字作答）．考点：计数原理的应用．专题：概率与统计．分析：利用间接法，先求出2个人坐的方法数为，再排除两左右相邻的情况，即可得到结论．解答：解：由题意，一共可坐的位子有20个，2个人坐的方法数为，还需排除两左右相邻的情况；把可坐的20个座位排成连续一行（甲与乙相接），任两个座位看成一个整体，即相邻的坐法有，但这其中包括甲、乙不在同一排情形，还应再加上2．∴不同排法的种数为=346．故答案为：346．点评：本题考查计数原理的运用，考查学生分析解决问题的能力，属于中档题．14．（4分）在直角坐标系xOy中，设A（3，2），B（﹣2，﹣3），沿y轴把坐标平面折成120°的二面角后，AB的长为2．考点：用空间向量求平面间的夹角．专题：空间位置关系与距离．分析：作AC⊥y轴，BD⊥y轴，AM平行等于CD，连接AB，MD，根据二面角的平面角的定义可知∠BDM就是二面角的平面角，则∠BDM=120°，最后根据余弦定理可知AB的长．解答：解：作AC垂直y轴，BD垂直y轴，AM平行等于CD，连接AB，MD，CD=5，BD=2，AC=3=MD，BD=2，AC=MD=3，而BD⊥y轴，MD⊥y轴（MD∥AC），∠BDM就是二面角的平面角，∴∠BDM=120°，∴由余弦定理得：BM=，AM=5，∴由勾股定理得AB=2，故答案为：2点评：本题主要考查了空间两点的距离，以及二面角平面角的应用，同时考查了空间想象能力，计算能力，属于基础题．15．（4分）函数y=2sinx（x∈[0，π]）在点P处的切线与函数y=lnx+x2在点Q处切线平行，则直线PQ的斜率是．考点：利用导数研究曲线上某点切线方程．专题：计算题；压轴题．分析：函数y=2sinx （x∈[0，π]）在点P处的切线与函数y=lnx+x2在点Q处切线平行，对两个函数分别求导，根据导数与斜率的关系，进行求解；解答：解：函数y=2sinx （x∈[0，π]），∴y′=2cosx，﹣2≤y′≤2，对函数y=lnx+x2，（x＞0）y′=+x≥2（x=1时等号成立），∵函数y=2sinx （x∈[0，π]）在点P处的切线与函数y=lnx+x2在点Q处切线平行，∴2cosx=+x=2，可得P（0，0），Q（1，），∴直线PQ的斜率k PQ==，故答案为：；点评：此题主要考查利用导数研究曲线上某点的切线方程，注意导数与斜率的关系，本题是一道基础题；16．（4分）如图，四面体OABC的三条棱OA、OB、OC两两垂直，OA=OB=2，OC=3，D为四面体OABC外一点．给出下列命题．①不存在点D，使四面体ABCD有三个面是直角三角形②不存在点D，使四面体ABCD是正三棱锥③存在点D，使CD与AB垂直并且相等④存在无数个点D，使点O在四面体ABCD的外接球面上其中真命题的序号是③④．考点：球内接多面体；棱锥的结构特征．专题：计算题．分析：对于①可构造四棱锥CABD与四面体OABC一样进行判定；对于②，使AB=AD=BD，此时存在点D，使四面体ABCD是正三棱锥；对于③取CD=AB，AD=BD，此时CD垂直面ABD，即存在点D，使CD与AB垂直并且相等；对于④先找到四面体OABC的内接球的球心P，使半径为r，只需PD=r，可判定④的真假．解答：解：对于①，∵四面体OABC的三条棱OA，OB，OC两两垂直，OA=OB=2，OC=3，∴AC=BC=，AB=当四棱锥CABD与四面体OABC一样时，即取CD=3，AD=BD=2，四面体ABCD的三条棱DA、DB、DC两两垂直，此时点D，使四面体ABCD有三个面是直角三角形，故①不正确；对于②，由①知AC=BC=，AB=，使AB=AD=BD，此时存在点D，CD=，使四面体C﹣ABD是正三棱锥，故②不正确；对于③，取CD=AB，AD=BD，此时CD垂直面ABD，即存在点D，使CD与AB垂直并且相等，故③正确；对于④，先找到四面体OABC的内接球的球心P，使半径为r，只需PD=r即可∴存在无数个点D，使点O在四面体ABCD的外接球面上，故④正确故答案为：③④．点评：本题主要考查了棱锥的结构特征，同时考查了空间想象能力，转化与划归的思想，以及构造法的运用，属于中档题．17．（4分）设函数y=f（x）在（﹣∞，+∞）内有定义，对于给定的正数K，定义函数f K （x）=，取函数f（x）=2﹣x﹣e﹣x，若对任意的x∈（﹣∞，+∞），恒有f K（x）=f（x），则K的最小值为1．考点：函数的零点；函数的值域；分段函数的解析式求法及其图象的作法．专题：函数的性质及应用．分析：利用导数研究函数f（x）的单调性极值与最值，和函数f K（x）的定义即可得出．解答：解：f′（x）=﹣1+e﹣x=，当x＞0时，f′（x）＜0，函数f（x）单调递减；当x＜0时，f′（x）＞0，函数f（x）单调递增．因此当x=0时，函数f（x）取得最大值f（0）=1．∵对任意的x∈（﹣∞，+∞），恒有f K（x）=f（x）≤1，又对任意的x∈（﹣∞，+∞），恒有f K（x）=f（x），∴故K的最小值为1．故答案为：1．点评：本题考查了导数研究函数f（x）的单调性极值与最值和新定义，属于难题．三、解答题（本大题共5小题，共70分.）18．（14分）底面半径为2，高为4的圆锥有一个内接的正四棱柱（底面是正方形，侧棱与底面垂直的四棱柱）．（1）设正四棱柱的底面边长为x，试将棱柱的高h表示成x的函数；（2）当x取何值时，此正四棱柱的表面积最大，并求出最大值．考点：函数的最值及其几何意义；函数解析式的求解及常用方法．专题：计算题；函数的性质及应用；空间位置关系与距离．分析：（1）由相似性可得=，从而化出h=4﹣2x，（其中0＜x＜2）；（2）设该正四棱柱的表面积为y，则y=2x2+4xh=2x2+4x（4﹣2x）=﹣6x2+16，利用配方法求函数的最大值．解答：解：（1）根据相似性可得：=，解得：h=4﹣2x，（其中0＜x＜2）．（2）解：设该正四棱柱的表面积为y．则有关系式：y=2x2+4xh=2x2+4x（4﹣2x）=﹣6x2+16=﹣6（x﹣）2+，因为0＜x＜2，所以当x=时，y max=，故当正四棱柱的底面边长为时，此正四棱柱的表面积最大，为．点评：本题考查了空间几何体的结构特征及函数的最值问题，属于中档题．19．（14分）已知直线l：y=4x和点P（6，4），点A为第一象限内的点且在直线l上，直线PA交x轴正半轴于点B，（1）当OP⊥AB时，求AB所在直线的直线方程；（2）求△OAB面积的最小值，并求当△OA B面积取最小值时的B的坐标．考点：直线的一般式方程．专题：直线与圆．分析：（1）由垂直关系可得k AB=，由AB过点P（6，4）可得点斜式方程，化为一般式可得；（2）设点A（a 4a），a＞0，点B坐标为（b，0），b＞0，可得△OAB面积为S=××4a=，即10a2﹣Sa+S=0，由判别式△=S2﹣40S≥0可得S≥40，即S的最小值等于40，代入解此时的方程可得B坐标．解答：解：（1）∵点P（6，4），∴k OP=，∵OP⊥AB，∴k AB=，∵AB过点P（6，4），∴AB的方程为y﹣4=（x﹣6）化为一般式可得：3x+2y﹣26=0（2）设点A（a 4a），a＞0，点B坐标为（b，0），b＞0，则直线PA的斜率为=，解得b=，故B的坐标为（，0），故△OAB面积为S=××4a=，即10a2﹣Sa+S=0．由题意可得方程10a2﹣Sa+S=0有解，故判别式△=S2﹣40S≥0，S≥40，故S的最小值等于40，此时方程为a2﹣4a=4=0，解得a=2．综上可得，△OAB面积的最小值为40，当△OAB面积取最小值时点B的坐标为（10，0）．点评：本题考查直线的一般式方程的应用，直线的斜率公式，一元二次方程有解的条件，属基础题．20．（14分）已知函数f（x）=a（x﹣1）2+lnx+1．（Ⅰ）当a=﹣时，求函数f（x）的极值；（Ⅱ）若函数f（x）在区间[2，4]上是减函数，求实数a的取值范围．考点：利用导数研究函数的单调性；利用导数研究函数的极值．专题：导数的综合应用．分析：（Ⅰ）通过a=﹣，求出函数的导数，利用导数为0，然后求出极值点，然后求函数f（x）的极值；（Ⅱ）利用函数f（x）在区间[2，4]上是减函数，导数小于0恒成立，然后求实数a的取值范围．解答：（本题满分14分）解：（I）当时，…（2分）则当0＜x＜2时f'（x）＞0，故函数f（x）在（0，2）上为增函数；当x＞2时f'（x）＜0，故函数f（x）在（2，+∞）上为减函数，…（5分）故当x=2时函数f（x）有极大值…（7分）（Ⅱ），因函数f（x）在区间[2，4]上单调递减，则在区间[2，4]上恒成立，…（9分）即在[2，4]上恒成立，而当2≤x≤4时，，…（12分），即，故实数a的取值范围是．…（14分）点评：本题考查考查函数的导数的应用，函数的极值，函数的单调性的应用，考查分析问题解决问题的能力．21．（15分）如图，在三棱锥D﹣ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC，E 为BC的中点，F在棱AC上，且AF=3FC，（1）求证：AC⊥平面DEF；（2）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由；（3）求平面DEF与平面ABD所成的锐二面角的余弦值．考点：二面角的平面角及求法；直线与平面垂直的判定．专题：综合题；空间位置关系与距离；空间角．分析：（1）要证AC⊥平面DEF，先证AC⊥DE，再证AC⊥EF，即可；（2）M为BD的中点，连CM，设CM∩DE=O，连OF，只要MN∥OF即可，求出CN；（3）分别计算面积，利用面积比，即可求平面DEF与平面ABD所成的锐二面角的余弦值．解答：（1）证明：取AC的中点H，连接BH，∵AB=BC，∴BH⊥AC．∵AF=3FC，∴F为CH的中点．∵E为BC的中点，∴EF∥BH．则EF⊥AC．∵△BCD是正三角形，∴DE⊥BC．∵AB⊥平面BCD，∴AB⊥DE．∵AB∩BC=B，∴DE⊥平面ABC，∴DE⊥AC．∵DE∩EF=E，∴AC⊥平面DEF；（2）存在这样的点N，当CN=CA时，MN∥平面DEF．连CM，设CM∩DE=O，连OF．由条件知，O为△BCD的重心，CO=CM．所以当CF=CN时，MN∥OF．所以CN=CA=CA（3）解：设AB=BC=2a，则DE=a，EF=a，∴S△DEF==，∵S△ABD=∴平面DEF与平面ABD所成的锐二面角的余弦值为．点评：本题考查线面垂直，线面平行，考查面面角，考查逻辑思维能力，属于中档题．22．（15分）设函数f（x）=2ax﹣+lnx．（Ⅰ）当b=a时，若f（x）在（0，+∞）上是单调函数，求a的取值范围．（Ⅱ）若f（x）在x=m，x=n（m＜n）处取得极值，若方程f（x）=c在（0，2n]上有唯一解，则c的取值范围为 {x|x＜x0或s≤x＜t}，求t﹣s的最大值．考点：利用导数研究函数的极值；函数的单调性与导数的关系．专题：计算题；分类讨论；导数的综合应用．分析：（Ⅰ）当a=b，f（x）=2ax﹣+lnx，对a讨论，分①当a=0时，②当a＞0时，③当a＜0时，通过导数判断即可得到a的取值范围；（Ⅱ）由于f（x）=2ax﹣+lnx，定义域为（0，+∞）求出导数，又f（x）在x=m，x=n处取得极值，则f′（m）=f′（n）=0．求得a，b，得到f′（x），为使方程f（x）=c只有唯一解的c的取值范围为{x|x＜x0或s≤x＜t}，只有可能s=f（2n），t=f（2m），f（m）＞f（2n），故只要求f（m）﹣f（2n）的最大值，记m=kn（0＜k＜1），对k讨论，当0＜k＜时，当＜k≤1时，通过导数的符号，即单调性即可得到．解答：解：（Ⅰ）当a=b，f（x）=2ax﹣+lnx，①当a=0时，f（x）=lnx，则f（x）在（0，+∞）上单调递增；②当a＞0时，又x＞0，∴2ax2+x+a＞0，∴f′（x）＞0，则f（x）在（0，+∞）上单调递增．③当a＜0时，设g（x）=2ax2+x+a，令△≤0解得a≤﹣．f（x）在（0，+∞）上单调递减．综上得，a的取值范围是（﹣∞，﹣]∪[0，+∞）．（Ⅱ）由于f（x）=2ax﹣+lnx，定义域为（0，+∞）∴f′（x）=2a++．又f（x）在x=m，x=n处取得极值，f′（m）=f′（n）=0．即所以故f′（x）=﹣=﹣，故f（x）在（0，m）上单调递减，在[m，n]上单调递增，在[n，2m]上单调递减．所以f（m）是f（x）在（0，2n）上的极小值，f（n）是f（x）在（0，2n]上的极大值．为使方程f（x）=c只有唯一解的c的取值范围为{x|x＜x0或s≤x＜t}，只有可能s=f（2n），t=f（2m），f（m）＞f（2n），故只要求f（m）﹣f（2n）的最大值．f（m）=lnm+，f（2n）=+ln2n．f（m）﹣f（2n）=+ln．记m=kn（0＜k＜1），则f（m）﹣f（2n）=+ln．令g（k）=）=+ln．则g′（k）=当0＜k＜时，f′（x）＞0，故f（x）在[m，n]上单调递增；当＜k≤1时，f′（x）＜0，故f（x）在[n，2n]上单调递减．所以g（k）的最大值为g（）=﹣ln4．所以t﹣s的最大值为﹣ln4．点评：本题考查导数的运用：求单调区间和求极值，考查分类讨论的思想方法和函数方程的思想方法，考查运算能力，属于中档题．。

2014-2015学年浙江省瑞安四校联考高二（上）期中数学试卷（文科）一、选择题：本大题共10小题，每小题4分，共40分.1．（4分）直线2x+3y+1=0的斜率为（）A．B．C．D．2．（4分）下列命题正确的是（）A．三点可以确定一个平面B．一条直线和一个点可以确定一个平面C．四边形是平面图形D．两条相交直线可以确定一个平面3．（4分）若一个正方体截去一个三棱锥后所得的几何体如图所示，则该几何体的正视图是（）A．B．C．D．4．（4分）一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底边均为1的等腰梯形，则这个平面图形的面积是（）A．B．C．D．5．（4分）如图，E、F分别是三棱锥P﹣ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为（）A．30°B．60°C．0°D．120°6．（4分）已知底面边长为1，侧棱长为的正四棱柱的各顶点均在同一球面上，则该球的体积为（）A．B．4πC．2πD．7．（4分）设α，β，γ是三个互不重合的平面，m，n是两条不重合的直线，则下列命题中正确的是（）A．若m∥α，n∥β，α⊥β，则m⊥n B．若α∥β，m⊄β，m∥α，则m∥βC．若α⊥β，m⊥α，则m∥βD．若α⊥β，β⊥γ，则α⊥γ8．（4分）如图，在正方体ABCD﹣A1B1C1D1中，E为BC1的中点，则DE与面BCC1B1所成角的正切值为（）A．B．C．D．9．（4分）直线l过P（1，2），且A（2，3），B（4，﹣5）到l的距离相等，则直线l的方程是（）A．4x+y﹣6=0 B．x+4y﹣6=0C．3x+2y﹣7=0或4x+y﹣6=0 D．2x+3y﹣7=0或x+4y﹣6=010．（4分）如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，则下列四个结论中错误的是（）A．BD⊥AC B．△ABC是等边三角形C．平面ADC⊥平面ABC D．二面角A﹣BC﹣D的正切值为二、填空题：本大题共6小题，每小题4分，共24分.11．（4分）过点A（a，4）和B（﹣2，a）的直线的倾斜角等于45°，则a的值是．12．（4分）已知两条相交直线a，b，a∥平面α，则b与α的位置关系是．13．（4分）已知直线的斜率为4，且在x轴上的截距为2，此直线方程为．14．（4分）圆柱的底面积为S，侧面展开图为一个正方形，那么这个圆柱的侧面积是．15．（4分）一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形，则其体积是．16．（4分）如图，正三棱柱ABC﹣A1B1C1的各棱长都等于2，D在AC1上，F为BB1中点，且FD⊥AC1，有下述结论（1）AC1⊥BC；（2）=1；（3）二面角F﹣AC1﹣C的大小为90°；（4）三棱锥D﹣ACF的体积为．正确的有．三、解答题（本题共4小题，总分为56分．解题必须有文字说明、解题过程和演算步骤．）17．（13分）已知直线l1：ax+2y+1=0，直线l2：x﹣y+a=0．（1）若直线l1⊥l2，求a的值及垂足P的坐标；（2）若直线l1∥l2，求a的值及直线l1与l2的距离．18．（14分）如图，在直三棱柱ABC﹣A1B1C1（侧棱与底面垂直的棱柱称为直棱柱）中，AC=CC1=3，BC=4，AB=5，点D是AB的中点．（1）求证：AC 1∥平面CDB1；（2）求异面直线AC1与CB1所成的角的余弦值．19．（14分）已知ABCD是矩形，PA⊥平面ABCD，AB=2，PA=AD=4，E为BC的中点．（1）求证：DE⊥平面PAE；（2）求直线DP与平面PAE所成的角．20．（15分）如图，已知直二面角α﹣PQ﹣β，A∈PQ，B∈α，C∈β，∠BAP=45°，CA=CB，直线CA和平面α所成的角为30°．（Ⅰ）证明BC⊥PQ；（Ⅱ）求二面角B﹣AC﹣P的大小．2014-2015学年浙江省瑞安四校联考高二（上）期中数学试卷（文科）参考答案与试题解析一、选择题：本大题共10小题，每小题4分，共40分.1．（4分）直线2x+3y+1=0的斜率为（）A．B．C．D．【解答】解：化直线2x+3y+1=0的方程为斜截式可得：y=x﹣，由斜截式的特点可知已知直线的斜率为：故选：A．2．（4分）下列命题正确的是（）A．三点可以确定一个平面B．一条直线和一个点可以确定一个平面C．四边形是平面图形D．两条相交直线可以确定一个平面【解答】解：由平面的公理2及推论可知：不共线的三点可以确定一个平面，故A不正确；直线和直线外的一点可以确定一个平面，故B不正确；四边形可以为空间四边形，故C不正确；两条相交直线可以确定一个平面，故D正确．故选：D．3．（4分）若一个正方体截去一个三棱锥后所得的几何体如图所示，则该几何体的正视图是（）A．B．C．D．【解答】解：所给图形的正视图是A选项所给的图形，满足题意．故选：A．4．（4分）一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底边均为1的等腰梯形，则这个平面图形的面积是（）A．B．C．D．【解答】解：水平放置的图形为一直角梯形，由题意可知上底为1，高为2，下底为1+，S=（1++1）×2=2+．故选：B．5．（4分）如图，E、F分别是三棱锥P﹣ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为（）A．30°B．60°C．0°D．120°【解答】解：取AC的中点G，连接EG，GF，由中位线定理可得：GE∥PC，GF∥AB且GE=5，GF=3，∴∠EGF或补角是异面直线PC，AB所成的角．在△GEF中由余弦定理可得：cos∠EGF===﹣∴∠EGF=120°，则异面直线PC，AB所成的角为60°．故选：B．6．（4分）已知底面边长为1，侧棱长为的正四棱柱的各顶点均在同一球面上，则该球的体积为（）A．B．4πC．2πD．【解答】解：∵正四棱柱的底面边长为1，侧棱长为，∴正四棱柱体对角线的长为=2又∵正四棱柱的顶点在同一球面上，∴正四棱柱体对角线恰好是球的一条直径，得球半径R=1根据球的体积公式，得此球的体积为V=πR3=π．故选：D．7．（4分）设α，β，γ是三个互不重合的平面，m，n是两条不重合的直线，则下列命题中正确的是（）A．若m∥α，n∥β，α⊥β，则m⊥n B．若α∥β，m⊄β，m∥α，则m∥βC．若α⊥β，m⊥α，则m∥βD．若α⊥β，β⊥γ，则α⊥γ【解答】解：若m∥α，n∥β，α⊥β，则m与n相交、平行或异面，故A错误；若α∥β，m⊄β，m∥α，则由直线与平面平行的判定定理得m∥β，故B正确；若α⊥β，m⊥α，则m∥β或m⊂β，故C错误；若α⊥β，β⊥γ，则α与γ相交或平行．故D错误．故选：B．8．（4分）如图，在正方体ABCD﹣A1B1C1D1中，E为BC1的中点，则DE与面BCC1B1所成角的正切值为（）A．B．C．D．【解答】解：设正方体ABCD﹣A1B1C1D1的棱长为2，以D为原点，以DA为x轴，以DC为y轴，以DD1为z轴，建立空直角坐标系，∵E为BC1的中点，∴D（0，0，0），E（1，2，1），∴=（1，2，1），设DE与面BCC1B1所成角的平面角为θ，∵面BCC1B1的法向量=（0，1，0），∴sinθ=|cos＜，＞|=||=，∴cosθ=，∴tanθ==．故选：C．9．（4分）直线l过P（1，2），且A（2，3），B（4，﹣5）到l的距离相等，则直线l的方程是（）A．4x+y﹣6=0 B．x+4y﹣6=0C．3x+2y﹣7=0或4x+y﹣6=0 D．2x+3y﹣7=0或x+4y﹣6=0【解答】解设所求直线为l，由条件可知直线l平行于直线AB或过线段AB的中点，…（2分）（1）AB的斜率为=﹣4，当直线l∥AB时，l的方程是y﹣2=﹣4（x﹣1），即4x+y﹣6=0．…（6分）（2）当直线l经过线段AB的中点（3，﹣1）时，l的斜率为=，l的方程是y﹣2=（x﹣1），即3x+2y﹣7=0．…（10分）故所求直线的方程为3x+2y﹣7=0或4x+y﹣6=0．…（12分）故选：C．10．（4分）如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，则下列四个结论中错误的是（）A．BD⊥AC B．△ABC是等边三角形C．平面ADC⊥平面ABC D．二面角A﹣BC﹣D的正切值为【解答】解：设等腰直角三角形△ABC的腰为a，则斜边BC=a，对于A，∵D为BC的中点，∴AD⊥BC，又平面ABD⊥平面ACD，平面ABD∩平面ACD=AD，BD⊥AD，BD⊂平面ABD，∴BD⊥平面ADC，又AC⊂平面ADC，∴BD⊥AC，故A正确；对于B，由A知，BD⊥平面ADC，CD⊂平面ADC，∴BD⊥CD，又BD=CD=a，∴由勾股定理得：BC=•a=a，又AB=AC=a，∴△ABC是等边三角形，故B正确；对于C，∵△ADC为等腰直角三角形，取斜边AC的中点F，则DF⊥AC，又△ABC 为等边三角形，连接BF，则BF⊥AC，∴∠BFD为平面ADC与平面ABC的二面角的平面角，由BD⊥平面ADC可知，∠BDF为直角，∠BFD不是直角，故平面ADC与平面ABC 不垂直，故C错误；对于D，依题意知，AD⊥底面BDC，过点D作DE⊥BC于点E，连接AE，则AE⊥BC，∴∠AED为二面角A﹣BC﹣D的平面角，设为θ，则tanθ====，故D正确；故选：C．二、填空题：本大题共6小题，每小题4分，共24分.11．（4分）过点A（a，4）和B（﹣2，a）的直线的倾斜角等于45°，则a的值是1．【解答】解：∵过点A（a，4）和B（﹣2，a）的直线的倾斜角等于45°，∴tan45°==1，解得a=1．故答案为：1．12．（4分）已知两条相交直线a，b，a∥平面α，则b与α的位置关系是平行或相交（直线b在平面α外）．【解答】解：由题意画出图形，当a，b所在平面与平面α，平行时b与平面α平行，当a，b，所在平面与平面α相交时，b与平面α相交，故答案为：平行或相交（直线b在平面α外）．13．（4分）已知直线的斜率为4，且在x轴上的截距为2，此直线方程为4x﹣y﹣8=0．【解答】解：直线的斜率为4，且在x轴上的截距为2，所以所求直线方程为：y=4（x﹣2），即4x﹣y﹣8=0．故答案为：4x﹣y﹣8=0．14．（4分）圆柱的底面积为S，侧面展开图为一个正方形，那么这个圆柱的侧面积是4πs．【解答】解：圆柱的底面积为S，所以底面半径为：，底面周长为：；侧面展开图为一个正方形，所以圆柱的高为：，所以圆柱的侧面积为：=4πS故答案为：4πs15．（4分）一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形，则其体积是．【解答】解：如图据条件可得几何体为底面边长为2的正方形，侧面是等腰三角形，其底边上的高也为2的正四棱锥，故其体积V==．故答案为：．16．（4分）如图，正三棱柱ABC﹣A1B1C1的各棱长都等于2，D在AC1上，F为BB1中点，且FD⊥AC1，有下述结论（1）AC1⊥BC；（2）=1；（3）二面角F﹣AC1﹣C的大小为90°；（4）三棱锥D﹣ACF的体积为．正确的有（2）（3）（4）．【解答】解：（1）连接AB 1，则∠B1C1A即为BC和AC1所成的角，在三角形AB1C1中，B1C1=2，AB1=2，AC1=2，cos∠B1C1A==，故（1）错；（2）连接AF，C1F，则易得AF=FC1=，又FD⊥AC1，则AD=DC1，故（2）正确；（3）连接CD，则CD⊥AC1，且FD⊥AC1，则∠CDF为二面角F﹣AC1﹣C的平面角，CD=，CF=，DF===，即CD2+DF2=CF2，故二面角F﹣AC1﹣C的大小为90°，故（3）正确；（4）由于CD⊥AC1，且FD⊥AC1，则AD⊥平面CDF，=V A﹣DCF=•AD•S△DCF=×××=．故（4）正确．则V D﹣ACF故答案为：（2）（3）（4）三、解答题（本题共4小题，总分为56分．解题必须有文字说明、解题过程和演算步骤．）17．（13分）已知直线l1：ax+2y+1=0，直线l2：x﹣y+a=0．（1）若直线l1⊥l2，求a的值及垂足P的坐标；（2）若直线l1∥l2，求a的值及直线l1与l2的距离．【解答】解：（1）∵直线l1：ax+2y+1=0，直线l2：x﹣y+a=0，当直线l1⊥l2时，a×1+2×（﹣1）=0，解得a=2，∴l1：2x+2y+1=0，直线l2：x﹣y+2=0，联立解得∴a的值为2，垂足P的坐标为（，）；（2）当直线l1∥l2时，，解得a=﹣2，∴l1：﹣2x+2y+1=0，直线l2：﹣2x+2y+4=0，由平行线间的距离公式可得d==∴a的值为﹣2，直线l1与l2的距离为18．（14分）如图，在直三棱柱ABC﹣A1B1C1（侧棱与底面垂直的棱柱称为直棱柱）中，AC=CC1=3，BC=4，AB=5，点D是AB的中点．（1）求证：AC1∥平面CDB1；（2）求异面直线AC1与CB1所成的角的余弦值．【解答】（1）证明：连接BC1，交CB1于E，连接DE，由于D为中点，E为中点，则DE∥AC1，DE⊂平面CDB1，AC1⊄平面CDB1，则有AC1∥平面CDB1；（2）解：由（1）可得DE∥AC1，DE=AC1，则DE和CB1所成的角或补角即为异面直线AC1与CB1所成的角．在三角形ABC中，AC=3，BC=4，AB=5，则△ABC为直角三角形，AB为斜边，即有CD=，AC1==3，DE=，CE==，在三角形CDE中，cos∠CED==．故异面直线AC1与CB1所成的角的余弦值为．19．（14分）已知ABCD是矩形，PA⊥平面ABCD，AB=2，PA=AD=4，E为BC的中点．（1）求证：DE⊥平面PAE；（2）求直线DP与平面PAE所成的角．【解答】解：在△ADE中，AD2=AE2+DE2，∴AE⊥DE∵PA⊥平面ABCD，DE⊂平面ABCD，∴PA⊥DE又PA∩AE=A，∴DE⊥平面PAE（2）∠DPE为DP与平面PAE所成的角在Rt△PAD，，在Rt△DCE中，（12分）在Rt△DEP中，PD=2DE，∴∠DPE=30°20．（15分）如图，已知直二面角α﹣PQ﹣β，A∈PQ，B∈α，C∈β，∠BAP=45°，CA=CB，直线CA和平面α所成的角为30°．（Ⅰ）证明BC⊥PQ；（Ⅱ）求二面角B﹣AC﹣P的大小．【解答】解：（I）在平面β内过点C作CO⊥PQ于点O，连接OB．因为α⊥β，α∩β=PQ，所以CO⊥α，又因为CA=CB，所以OA=OB．而∠BAO=45°，所以∠ABO=45°，∠AOB=90°．从而BO⊥PQ．又CO⊥PQ，所以PQ⊥平面OBC．因为BC⊂平面OBC，故PQ⊥BC．（II）由（I）知，BO⊥PQ，又α⊥β，α∩β=PQ，BO⊂α，所以BO⊥β．过点O作OH⊥AC于点H，连接BH，由三垂线定理知，BH⊥AC．故∠BHO是二面角B﹣AC﹣P的平面角．由（I）知，CO⊥α，所以∠CAO是CA和平面α所成的角，则∠CAO=30°，不妨设AC=2，则，．在Rt△OAB中，∠ABO=∠BAO=45°，所以，于是在Rt△BOH中，．故二面角B﹣AC﹣P的大小为arctan2．赠送初中数学几何模型【模型五】垂直弦模型：图形特征：运用举例：1.已知A、B、C、D是⊙O上的四个点.(1)如图1，若∠ADC＝∠BCD＝90°，AD＝CD，求证AC⊥BD；(2)如图2，若AC⊥BD，垂足为E，AB＝2，DC＝4，求⊙O的半径.O DAB CEAOD CB2.如图，已知四边形ABCD 内接于⊙O ，对角线AC ⊥BD 于P ，设⊙O 的半径是2。

1a = 3b = a a b =+ b a b =- PRINT a ，b浙江省瑞安中学高二上学期期中考试（数学文）考试时间100分钟，不能使用计算器）一、选择题（本大题共10个小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）.1.从一副标准的52张（不含大小王）扑克牌中任意抽一张，抽到方片K 的概率为 ( )A ．152B ．113C. 126D ．142．已知{a n }是等比数列，2512,4a a ==,则公比q= ( ) A.21-B.-2C.2D.213．下列正确的是（ ）A ．平行于同一个平面的两条直线平行B ．垂直于同一条直线的两条直线平行C ．若直线a 与平面α内的无数条直线平行，则a ∥αD ．若一条直线垂直于平面内两条相交直线，则这条直线垂直这个平面。

4．要得到函数)42sin(π+=x y 的图象，可以把函数x y 2sin =的图象（ ）A ．向右平移8π个单位 B ．向左平移8π个单位 C ．向左平移4π个单位 D ．向右平移4π个单位5．计算机执行下面的程序段后，输出的结果是（ ）A ．1,3B ．4,1C ．0,0D ．6,06．已知向量),2(),1,1(x b a == 若b a +与a b24-平行，则实数x 的值是（ ）A ．-2B ．0C ．1D ．27．根据表格中的数据，可以判定方程062=-+x e x 的一个根所在的区间为（ ）A ．(1,0)- B.(0,1)C ．(1,2)D.(2,3)8.如下图是一个算法的程序框图，当输入的x 值为3时，输出y 的结果恰好是31，则空白处的关系式可以是（ ）A ．3x y =B ．xy -=3C ．xy 3= D ． 31x y =9．如下图，在半径为1的半圆内，放置一个边长为21的正方形ABCD ，向半圆内任投一点，该点落在正方形内的概率是（ ）．A ．πB ．1πC ．12πD ． 2π10．已知函数()f x 是(,)-∞+∞上的偶函数，若对于0x ≥，都有(2()f x f x +=），且当[0,2)x ∈时，2()log (1f x x =+），则(2008)(2009)f f -+的值为A ．2-B ．1-C ．1D ．2二、填空题：本大题共5小题，每小题4分，共把答案填在题中横线上。

2014-2015学年浙江省温州市瑞安市八校联考高二（上）期中数学试卷一、选择题（本大题共10小题，每小题5分，共50分）1．（5分）直线x=﹣1的倾斜角为（）A．0°B．45°C．90°D．135°2．（5分）已知a＞b，则下列不等式正确的是（）A．ac＞bc B．a﹣c＜b﹣c C．a3＞b3D．＜3．（5分）已知直线l1：3x+4y﹣3=0，l2：3x+4y+7=0，则这两条直线间的距离为（）A．B．1 C．2 D．44．（5分）方程x2+y2﹣2x+6y+m=0表示圆，则实数m的取值范围（）A．m＞10 B．m≥10 C．m≤10 D．m＜105．（5分）三条直线x=2，x﹣y﹣1=0，x+ky=0相交于一点，则实数k=（）A．2 B．C．﹣2 D．﹣6．（5分）已知点（1，1）、（0，﹣2）在直线x+ay+1=0的两侧，则实数a的取值范围（）A．（﹣2，﹣）B．（﹣∞，﹣2）∪（﹣，+∞）C．（﹣2，）D．（﹣∞，﹣2）∪（，+∞）7．（5分）已知点M与两个定点（1，0），（﹣2，0）的距离的比为，则点M 的轨迹所包含的图形面积等于（）A．9πB．8πC．4πD．π8．（5分）直线l：ax﹣y+b=0与圆M：x2+y2﹣2ax+2by=0，则l与M在同一坐标系内的图形可能是（）A．B． C．D．9．（5分）已知三角形的三边长分别为3，4，5，则它的边与半径为1的圆的公共点的个数最多为（）A．3 B．4 C．5 D．610．（5分）在R上定义运算：x*y=x（1﹣y），若不等式（x﹣y）*（x+y）＜1对一切实数x恒成立，则实数y的取值范围是（）A．B．C．﹣1＜y＜1 D．0＜y＜2二、填空题（本大题共7题，每小题4，共28分）11．（4分）已知点A（1，0，2），B（1，﹣3，1），则|AB|=．12．（4分）若x＞1，则的取值范围．13．（4分）点A（2，3）关于直线x+y=0的对称点A′的坐标是．14．（4分）直线y=x+1被圆x2+y2﹣2x﹣2y=0截得弦长为．15．（4分）若实数x，y满足，则x+y的最大值为．16．（4分）已知点A（1，2）在直线mx+ny﹣1=0（mn＞0）上，则+的最小值为．17．（4分）若直线l1：x+ay+a=0与2x+3y﹣6=0的交点M在第一象限，则l1的倾斜角的取值范围．三、简答题（本大题共4题，共42分，解答应写出文字符号说明，证明过程或演算步骤）18．（8分）三角形的三个顶点是A（4，0）、B（6，8）、C（9，3）．（1）求AB边所在的直线方程．（2）求AB边上高的长度．19．（10分）已知圆x2+y2+x﹣6y+m=0和直线x+2y﹣3=0交于P、Q两点，且OP ⊥OQ（O为坐标原点），求该圆的圆心坐标及半径．20．（12分）已知关于x的不等式kx2﹣2x+6k＞0．（1）若不等式的解集是{x|﹣3＜x＜﹣2}，求实数k的值．（2）若不等式对一切x∈（0，3）恒成立，求实数k的取值范围．21．（12分）已知点P（1，a）和圆x2+y2=4．（1）若过点P的圆的切线只有一条，求a的值及切线方程；（2）若a=，过点P的圆的两条弦AC、BD互相垂直，求四边形ABCD面积的最大值．2014-2015学年浙江省温州市瑞安市八校联考高二（上）期中数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题5分，共50分）1．（5分）直线x=﹣1的倾斜角为（）A．0°B．45°C．90°D．135°【解答】解：因为直线的方程为x=﹣1，为垂直于x轴的直线，故直线无斜率，故直线x=﹣1的倾斜角为90°，故选：C．2．（5分）已知a＞b，则下列不等式正确的是（）A．ac＞bc B．a﹣c＜b﹣c C．a3＞b3D．＜【解答】解：A．若c=0，则不等式ac＞bc不成立，B．∵a＞b，∴a﹣c＞b﹣c，故B不成立，C．函数y=x3是增函数，则a3＞b3成立，D．当a＞0＞b时，＜不成立，故选：C．3．（5分）已知直线l1：3x+4y﹣3=0，l2：3x+4y+7=0，则这两条直线间的距离为（）A．B．1 C．2 D．4【解答】解：直线l1：3x+4y﹣3=0，l2：3x+4y+7=0，则这两条直线间的距离为：=2．故选：C．4．（5分）方程x2+y2﹣2x+6y+m=0表示圆，则实数m的取值范围（）A．m＞10 B．m≥10 C．m≤10 D．m＜10【解答】解：由圆的一般式方程可得D2+E2﹣4F＞0，即4+36﹣4m＞0，求得m ＜10，故选：D．5．（5分）三条直线x=2，x﹣y﹣1=0，x+ky=0相交于一点，则实数k=（）A．2 B．C．﹣2 D．﹣【解答】解：∵三条直线相交于一点P，∴直线x=2，x﹣y﹣1=0，相交于一点P则，解得：，∴P（2，1）；∴直线x+ky=0过点P，即2+k=0，∴k=﹣2；故选：C．6．（5分）已知点（1，1）、（0，﹣2）在直线x+ay+1=0的两侧，则实数a的取值范围（）A．（﹣2，﹣）B．（﹣∞，﹣2）∪（﹣，+∞）C．（﹣2，）D．（﹣∞，﹣2）∪（，+∞）【解答】解：∵点A（1，1）与B（0，﹣2），在直线x+ay+1=0的两侧，∴A，B两点对应式子x+ay+1的符号相反，即（1+a+1）（0﹣2a+1）＜0，即（a+2）（1﹣2a）＜0，∴（a+2）（2a﹣1）＞0，解得a＞或a＜﹣2，即实数a的取值范围是（﹣∞，﹣2）∪（，+∞），故选：D．7．（5分）已知点M与两个定点（1，0），（﹣2，0）的距离的比为，则点M 的轨迹所包含的图形面积等于（）A．9πB．8πC．4πD．π【解答】解：设M（x，y），由点M与两个定点（1，0），（﹣2，0）的距离的比为，得=整理得：（x﹣2）2+y2=4．∴点M的轨迹所包含的图形面积为4π．故选：C．8．（5分）直线l：ax﹣y+b=0与圆M：x2+y2﹣2ax+2by=0，则l与M在同一坐标系内的图形可能是（）A．B． C．D．【解答】解：圆M：x2+y2﹣2ax+2by=0的标准方程为：（x﹣a）2+（y+b）2=a2+b2，圆心M（a，﹣b），半径直线l：ax﹣y+b=0的斜率为：a，y轴上的截距为：b，对于A，由直线方程可知：a＞0，b＞0，圆心M（a，﹣b），满足题意，但是圆与y轴不相交，图形不满足题意，A不正确；对于B，由直线方程可知：a＞0，b＜0，圆心M（a，﹣b），满足题意，但是圆与x，y轴相交，图形满足题意，所以B正确；对于C，由直线方程可知：a＜0，b＞0，圆心M（a，﹣b），不满足题意，图形不满足题意，所以C不正确；对于D，由直线方程可知：a＜0，b＜0，圆心M（a，﹣b），不满足题意，图形不满足题意，所以D不正确；故选：B．9．（5分）已知三角形的三边长分别为3，4，5，则它的边与半径为1的圆的公共点的个数最多为（）A．3 B．4 C．5 D．6【解答】解：对于半径为1的圆有一个位置是正好是三角形的内切圆，此时只有三个交点，对于圆的位置稍一右移或其他的变化，能实现4个交点的情况，但5个以上的交点不能实现．故选：B．10．（5分）在R上定义运算：x*y=x（1﹣y），若不等式（x﹣y）*（x+y）＜1对一切实数x恒成立，则实数y的取值范围是（）A．B．C．﹣1＜y＜1 D．0＜y＜2【解答】解：由题意可得，（x﹣y）*（x+y）=（x﹣y）（1﹣x﹣y）＜1对于任意的x都成立即y2﹣y＜x2﹣x+1对于任意的x都成立设g（x）=x2﹣x+1=所以，所以解可得，故选：A．二、填空题（本大题共7题，每小题4，共28分）11．（4分）已知点A（1，0，2），B（1，﹣3，1），则|AB|=．【解答】解：点A（1，0，2），B（1，﹣3，1），则|AB|==．故答案为：．12．（4分）若x＞1，则的取值范围（0，1）．【解答】解：∵函数y=在x＞1上是减函数，∴此时0＜＜1，故答案为：（0，1）13．（4分）点A（2，3）关于直线x+y=0的对称点A′的坐标是（﹣3，﹣2）．【解答】解：设点A（2，3）关于直线x+y=0的对称点A′的坐标为（m，n），则由求得，故A′（﹣3，﹣2），故答案为：（﹣3，﹣2）．14．（4分）直线y=x+1被圆x2+y2﹣2x﹣2y=0截得弦长为．【解答】解：圆x2+y2﹣2x﹣2y=0即（x﹣1）2+（y﹣1）2=2，表示以C（1，1）为圆心，半径等于的圆．由于圆心到直线y=x+1的距离为d==，故弦长为2=2=，15．（4分）若实数x，y满足，则x+y的最大值为 2.5．【解答】解：由题意作出其平面区域，令z=x+y，可化为y=﹣x+z，z相当于直线y=﹣x+z的纵截距，故过点A（1，1.5）时有最大值，最大值为1+1.5=2.5，故答案为：2.5．16．（4分）已知点A（1，2）在直线mx+ny﹣1=0（mn＞0）上，则+的最小值为9．【解答】解：∵点A（1，2）在直线mx+ny﹣1=0（mn＞0）上，∴m+2n=1．则+=（m+2n）=5+≥5+2×2=9，当且仅当n=m=取等号，∴+的最小值为9．17．（4分）若直线l1：x+ay+a=0与2x+3y﹣6=0的交点M在第一象限，则l1的倾斜角的取值范围（，）．【解答】解：联立两直线方程得：，解得：所以两直线的交点坐标为（，），因为两直线的交点在第一象限，所以得到，解得：﹣，设直线l的倾斜角为θ，则ta nθ＞，所以θ∈（，）．故答案为：（，）．三、简答题（本大题共4题，共42分，解答应写出文字符号说明，证明过程或演算步骤）18．（8分）三角形的三个顶点是A（4，0）、B（6，8）、C（9，3）．（1）求AB边所在的直线方程．（2）求AB边上高的长度．【解答】解：（1）∵k AB==4，则AB的直线方程：y=4（x﹣4），即：4x﹣y﹣16=0．（2）AB边的高的长度为点C到直线AB的距离，则=．则AB边上的高的长度为．19．（10分）已知圆x2+y2+x﹣6y+m=0和直线x+2y﹣3=0交于P、Q两点，且OP⊥OQ（O为坐标原点），求该圆的圆心坐标及半径．【解答】解：将x=3﹣2y代入方程x2+y2+x﹣6y+m=0，得5y2﹣20y+12+m=0．设P（x1，y1）、Q（x2，y2），则y1、y2满足条件y1+y2=4，y1y2=．∵OP⊥OQ，∴x1x2+y1y2=0．而x1=3﹣2y1，x2=3﹣2y2，∴x1x2=9﹣6（y1+y2）+4y1y2．9﹣6×4+5×=0∴m=3，此时△＞0，圆心坐标为（﹣，3），半径r=．20．（12分）已知关于x的不等式kx2﹣2x+6k＞0．（1）若不等式的解集是{x|﹣3＜x＜﹣2}，求实数k的值．（2）若不等式对一切x∈（0，3）恒成立，求实数k的取值范围．【解答】解：（1）∵不等式kx2﹣2x+6k＞0的解集是{x|﹣3＜x＜﹣2}，∴k＜0，且﹣3和﹣2是方程kx2﹣2x+6k=0的实数根，由根与系数的关系，得；（﹣3）+（﹣2）=，∴k=﹣；（6分）（2）根据题意kx2﹣2x+6k＞0，得：k＞在（0，3）上恒成立；设y==，x∈（0，3），∵x+≥2，即=2，当且仅当x=时取“=”；∴==，∴k的取值范围为（，+∞）．（12分）21．（12分）已知点P（1，a）和圆x2+y2=4．（1）若过点P的圆的切线只有一条，求a的值及切线方程；（2）若a=，过点P的圆的两条弦AC、BD互相垂直，求四边形ABCD面积的最大值．【解答】解：（1）若过点P的圆的切线只有一条，则知点P圆上，则1+a2=4，解得a=±；当a=时，点P（1，），切线方程为x+y﹣4=0，当a=﹣时，点P（1，﹣），切线方程为x﹣y﹣4=0，（2）设原点O到AC、BD的距离为d 1，d2，（d1≥0，d2≥0）则，于是|AC|=，|BD|=，由AC、BD相互垂直，则四边形ABCD的面积S====2，∵d12+d22≥2d1d2，则d1d2，当且仅当d1=d2=时取“=”则d12d22，从而S=2≤5，即：四边形ABCD的面积最大值为5．赠送初中数学几何模型【模型三】双垂型：图形特征：运用举例：1.在Rt△ABC中，∠ACB＝90°，以斜边AB为底边向外作等腰三角形PAB，连接PC. （1）如图，当∠APB＝90°时，若AC=5，PC＝62，求BC的长；（2）当∠APB＝90°时，若AB=45APBC的面积是36，求△ACB的周长.P2.已知：如图，B、C、E三点在一条直线上，AB＝AD，BC＝CD.（1）若∠B＝90°，AB＝6，BC＝23，求∠A的值；（2）若∠BAD＋∠BCD＝180°，cos∠DCE＝35，求ABBC的值.3.如图，在四边形ABCD中，AB=AD，∠DAB=∠BCD=90°，（1）若AB=3，BC+CD=5，求四边形ABCD的面积（2）若p= BC+CD，四边形ABCD的面积为S，试探究S与p之间的关系。

绝密★启用前【百强校】2015-2016学年浙江温州中学高二上期中试卷（学考班）（带解析）试卷副标题考试范围：xxx ；考试时间：46分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）1、小鼠中有一对控制灰砂色的基因（T ）和正常灰色的基因（t ），位于X 染色体上。

正常灰色但性染色体组成为XO 的雌鼠与灰砂色雄鼠交配，预期后代表现型之比为（胚胎的存活至少要有一条X 染色体）A ．灰砂♀∶灰色♂=2∶1B ．灰砂♀∶灰色♂=1∶2C ．灰砂♀∶灰色♂=1∶1D ．灰砂♀∶灰色♂=3∶12、人类的正常色觉与红绿色盲由一对等位基因（B 、b ）控制，红细胞形态由常染色体上的一对等位基因（H 、h ）控制。

镰刀形细胞贫血症有关的基因型和表现型如下表：现有一对色觉正常且有部分镰刀形红细胞的夫妇，生了一个男孩——李某。

这对夫妇的父母色觉均正常，妻子的弟弟是红绿色盲症患者。

下列有关判断错误的是 A ．性状的显隐性关系不是绝对的※※线※※内※※答※※………订………B．色觉和红细胞形态的遗传遵循自由组合定律C．妻子的基因型是HhX B X B或HhX B X bD．李某不患镰刀形细胞贫血症的概率是1/43、下图能正确表示基因分离定律实质的是4、下列表示高茎豌豆（Dd）自交产生子代的遗传图解中，正确的是5、小麦的高茎（T）对矮茎（t）为显性，无芒（B）对有芒（b）为显性，这两对等位基因符合自由组合定律。

高茎无芒和矮茎有芒的小麦杂交，后代表现型为高茎无芒、高茎有芒、矮茎无芒、矮茎有芒，且比例是l：l：l：1 ，则两个亲本的基因型为A．TtBb 和ttbb B．TtBb 和TtbbC．Ttbb 和ttbb D．TtBb 和ttBB6、将基因型为AABbCc和aabbcc的植株杂交（遗传遵循自由组合规律），后代表现型比为A．9:3:3:1 B．4:4:2:2 C．1:1:1:1 D．3:17、抗螟非糯性水稻（GGHH）与不抗螟糯性水稻（gghh）为亲本杂交得F1，F1自交得F2，F2的性状分离比为9∶3∶3∶1。

中学部2015-2016学年第一学期高二年级期中测试数 学 学 科 试 题 参 考 答 案（第一部分 满分100分） 一、填空题 (本大题共8小题，每小题5分，共40分)1. 10x y --=2.2y x =3.28y x = 4.相离5.2e +6.47. 55(2,)(,3)228.{0}二、解答题 (本大题共4小题，共计60分) 9. （本小题满分14分）解（1）53BC k =-，BC 边所在直线在y 轴上的截距为2， BC 边所在直线方程为52,53603y x x y =-++-=（2）25AC k =，AC 边上的高的斜率为52k =-，AC 边上的高的直线的方程为53(3)2y x +=--，即5290x y +-=10. （本小题满分14分）解（1）右焦点2(3,0)F ，对应右准线253x =.右焦点到对应准线的距离为163. （2）椭圆的离心率为35e =,根据第二定义, 231616535PF ed ==⋅=, 根据第一定义12163421055PF a PF =-=-=,点P 到左焦点1F 的距离为345. 11. （本小题满分16分）解（1）17 (2)能切点坐标(2(2,)33k k k Z ππππ+-∈或 12. （本小题满分16分）解：（1）设圆C 方程为,022=++++F Ey Dx y x则0443206480F D E F D F ⎧=⎪+++=⎨⎪+++=⎩ 解得D= —8，E=F=0.所以圆C ：2280.x y x +-= （2）圆C ：22(4)16.x y -+=圆心C(4,0),半径4当斜率不存在时，:0l x =符合题意；当斜率存在时，设直线:0,l y kx kx y =+-+=即因为直线l 与圆C 相切，所以圆心到直线距离为4，4,k ==解得所以直线:120.l y x x =++-=即故所求直线0,120.l x x =-=为或（第二部分满分60分）三、填空题 (本大题共6小题，每小题5分，共30分)13.20x y -= 14. 22(1)(3)25x y -+-= 15.4259()122f x x x =-+ 16. 25/2. 17.011x -≤≤ 18．.6 四、解答题 (本大题共2小题，共计30分) 19. (本题满分14分)解：（1）由抛物线2:C y x =得x y 2='，02|0x y x x ='∴= 切线l 的方程为)(2000x x x y y -=- 其中200x y = 令,0=x 得20x y -=；令,0=y 得20x x =；所以)0,2(0x A ，),0(20x B - 22400174x AB x =+=得到2004,2x x ==±,点P 的坐标为(2,4)±（2）设圆心E 的坐标为),0(b ，由题知1-=⋅l PE k k ，即12000-=⋅-x x by ，所以210-=-b y ；由||||PA PE =得20202020)2()(y x b y x +=-+整理得0134020=--y y解得10=y 或410-=y （舍去） 所以23=b ，圆E 的圆心E 的坐标为)23,0(，半径=r =||PE 25)(2020=-+b y x 圆E 的方程为45)23(22=-+y x20. (本题满分16分)解(1)①由已知得c a =，22411a b +=，222a b c =+，联立解得228,2a b ==. 椭圆M 的方程为22182x y +=. ②直线AB 的斜率为定值12由已知直线1:1(2)PA y k x -=-代入椭圆M 的方程消去y 并整理得22111(2)[(14)(288)]0x k x k k -+++-=所以2112188214A k k x k --=+,从而2112144114A k k y k --+=+同理2222288214B k k x k --=+,2222244114B k k y k --+=+因为120k k +=所以121222124()(41)(14)(14)A B k k k k y y k k ---==++121222128()(41)(14)(14)A B k k k k x x k k ---=++12A B ABA B y y k x x -==-为定值 (2) 解法一：12TBC S BC t =⋅=△直线TB 方程为：11y x t =+，联立221411x y y x t ⎧+=⎪⎪⎨⎪=+⎪⎩，得E x 22284,44t t E t t ⎛⎫-- ⎪++⎝⎭到:TC 30x ty t --=的距离d ==直线TC 方程为：31y x t =-，联立221431x y y x t ⎧+=⎪⎪⎨⎪=-⎪⎩，得22436F t x t =+，所以=所以S 所以k 令21212t m +=>，则2213k m m m ==+-≤，当且仅当24m =，即t =±=”， 所以k 的最大值为43．解法二：直线TB 方程为11y x t =+，联立221411x y y x t ⎧+=⎪⎪⎨⎪=+⎪⎩，得E x直线TC 方程为：31y x t =-，联立221431x y y x t ⎧+=⎪⎪⎨⎪=-⎪⎩，得F x =1sin 21sin 2TBC TEFTB TC BTCS TB TC k S TE TF TE TF ETF ⋅⋅∠⋅===⋅⋅⋅∠△△T CT B T E T F x x x x TB TC TE TF x x x x --=⋅=⋅-- 22824436t tt t t t t t =⋅=+-++令21212t m +=>，则22192413k m m ==+-≤，当且仅当24m =，即t =±=”，所以k 的最大值为43．18解。