广东省佛山市2012届高三4月教学文科数学质量检测

2012佛山一中高考文科数学模拟试卷(含答案)广东省佛山市第一中学2012届高考模拟(文科数学)试题审题人：高三备课组2012.5一．选择题(每小题5分，共60分)1.设集合，，则CR（A∩B）等于A．RB．C．{0}D．2.函数的定义域为A．B．C．D．3.现要完成3项抽样调查：①从10盒酸奶中抽取3盒进行卫生检查；②科技报告厅有座椅32排，每排40个座位，有一次报告会恰好坐满了观众，抽取32位进行座谈；③某中学共有160名教职工，其中教师120名，行政人员16名，后勤人员24名，为了解教职工对校务公开方面的意见，抽取一个容量为20的样本进行调查A．①简单随机抽样②系统抽样③分层抽样B．①简单随机抽样②分层抽样③系统抽样C．①系统抽样②简单随机抽样③分层抽样D．①分层抽样②系统抽样③简单随机抽样4.曲线在横坐标为的点处的切线为L，则点（3,2）到L的距离是A．B．C．D．5.在平行四边形ABCD中，E、F分别是CD和BC的中点，若，其中，则的值是A．B．1C．D.6.一个空间几何体的三视图如下，则它的体积是A．B．C．D．7.设椭圆的两个焦点分别为F1，F2，过F2作椭圆长轴的垂线交椭圆于点P，若三角形F1PF2为等腰直角三角形，则椭圆的离心率为A．B．C．D．8.三角形ABC中，角A、B、C所对的边分别是，则的值是A．B．C．D．9.下列四个命题中真命题是P1：P2：P3：P4：A．P1，P3B．P1，P4C．P2，P3D．P2，P410.当x>0时，下列函数中最小值为2的是A．B．C．D．二．填空题(每小题5分，共20分)(必做题11----13，选做题14----15考生只能从中选做一题)11.过原点且倾斜角为60度的直线被圆所截得的弦长为12.设复数满足，且，则13.设满足，则的取值范围是14.极坐标方程为与的两个圆的圆心距为15.如图所示，圆O上一点C在直径AB上的射影为D，CD=4，BD=8，则圆O的半径等于三．解答题16.(12分)掷两枚骰子，记事件A为“向上的点数之和为n”.（1）求所有n值组成的集合；（2）n为何值时事件A的概率P(A)最大？最大值是多少？（3）设计一个概率为0.5的事件（不用证明）17.(12分)如图，有三个并排放在一起的正方形，.（1）求的度数；（2）求函数的最大值及取得最大值时候的x值。

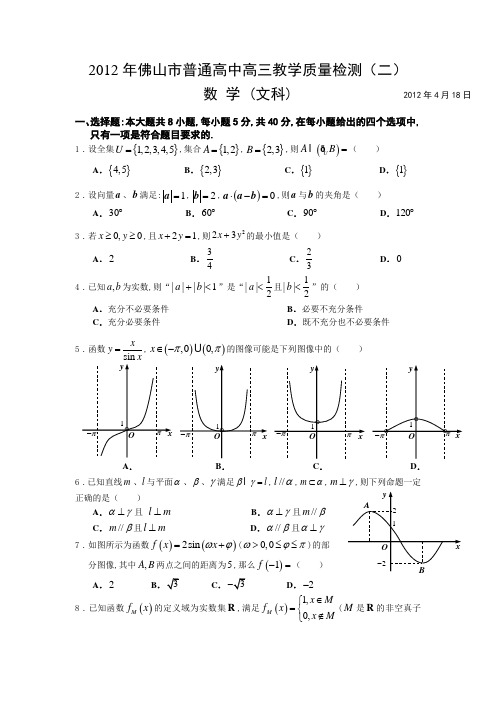
2012年佛山市普通高中高三教学质量检测（二）数 学 (文科)一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1．设全集{}1,2,3,4,5U =,集合{}1,2A =,{}2,3B =,则()U A B =ð（ ）A ．{}4,5B ．{}2,3C ．{}1D ．{}1 2．设向量a 、b 满足:1=a ,2=b ,()0⋅-=a a b ,则a 与b 的夹角是（ ）A ．30︒B ．60︒C ．90︒D ．120︒ 3．若0,0x y ≥≥,且21x y +=,则223x y +的最小值是（ ）A ．2B ．34 C ．23D ．0 4．已知,a b 为实数,则“||||1a b +<”是“1||2a <且1||2b <”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 5．函数xy =,()(),00,x ππ∈-的图像可能是下列图像中的（ ）A ．B ．C ．D ．6．已知直线m 、l 与平面α、β、γ满足l βγ=,//l α,m α⊂,m γ⊥,则下列命题一定正确的是（ ）A ．αγ⊥且 l m ⊥B ．αγ⊥且//m βC ．//m β且l m ⊥D ．//αβ且αγ⊥ 7．如图所示为函数()()2sin f x x ωϕ=+(0,0ωϕπ>≤≤)的部 分图像,其中,A B 两点之间的距离为5,那么()1f -=（ ） A ．2 B C ． D ．2- 8．已知函数()M f x 的定义域为实数集R ,满足()1,0,M x Mf x x M ∈⎧=⎨∉⎩(M 是R 的非空真子2012年4月18日FAEDBC集),在R 上有两个非空真子集,A B ,且A B =∅,则()()()()11A B A B f x F x f x f x +=++的值域为（ ）A ．20,3⎛⎤ ⎥⎝⎦ B ．{}1 C ．12,,123⎧⎫⎨⎬⎩⎭D ．1,13⎡⎤⎢⎥⎣⎦二、填空题：本题共7小题，考生作答6小题，每小题5分，共30分 (一)必做题(9～13题)9. 设i 为虚数单位,则()51i +的虚部为 ．10. 设,x y 满足约束条件0201x x y x y ≥⎧⎪-≥⎨⎪-≤⎩,则2z x y =+的最大值是 ．11. 抛掷一枚质地均匀的骰子,所得点数的样本空间为{}1,2,3,4,5,6S =,令事件{}2,3,5A =,事件{}1,2,4,5,6B =,则()|P A B 的值为 ．12. 直线2y x =和圆221x y +=交于,A B 两点,以Ox 为始边,OA ,OB 为终边的角分别为,αβ,则()sin αβ+的值为 ． 13. 已知等比数列{}n a 的首项为2,公比为2,则1123n na a a a a a a a a a +=⋅⋅⋅⋅ ．（二）选做题（14、15题,考生只能从中选做一题,两题全答的,只计前一题的得分）14.(坐标系与参数方程选做题)在极坐标系中,射线()03πθρ=≥与曲线1C :4sin ρθ=的异于极点的交点为A ,与曲线2C :8sin ρθ=的异于极点的交点为B ,则||AB =________.15.(几何证明选做题)如图,已知圆中两条弦AB 与CD 相交于点F ,E 是AB 延长线上一点,且DF CF ==:::4:2:1AF FB BE ,若CE与圆相切,则线段CE 的长为 ．三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤.16．（本题满分12分）在四边形ABCD 中,2AB =,4BC CD ==,6AD =,A C π∠+∠=.PEFA（Ⅰ）求AC 的长； （Ⅱ）求四边形ABCD 的面积.17．（本题满分12分）空气质量指数PM2.5(单位:3/g m μ)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:35 3575 75115 115150 150250 一级 二级 三级四级五级 优良轻度污染 中度污染重度污染严重污染后得到如下条形图:（Ⅰ）估计该城市一个月内空气质量类别为良的概率；（Ⅱ）在上述30个监测数据中任取2个,设X 为空气 质量类别为优的天数,求X 的分布列.18．（本题满分14分）如图所示四棱锥P ABCD -中,PA ⊥底面ABCD ,四边形ABCD 中,AB AD ⊥,//BC AD ,2PA AB BC ===,4AD =,E 为PD 的中 点,F 为PC 中点.（Ⅰ）求证:CD ⊥平面PAC ； （Ⅱ）求证://BF 平面ACE ；（Ⅲ）求直线PD 与平面PAC 所成的角的正弦值；19．（本题满分14分）已知椭圆E :()222210x y a b a b+=>>的一个交点为()1F ,而且过点12H ⎫⎪⎭.（Ⅰ）求椭圆E 的方程；（Ⅱ）设椭圆E 的上下顶点分别为12,A A ,P 是椭圆上异于 12,A A 的任一点,直线12,PA PA 分别交x 轴于点,N M ,若直线OT 与过点,M N 的圆G 相切,切点为T .证明：线段OT 的长为定值,并求出该定值.20．（本题满分14分）记函数()()()*112,nn f x x n n =+-≥∈N的导函数为()nf x ',函数()()n g x f x nx =-.（Ⅰ）讨论函数()g x 的单调区间和极值； （Ⅱ）若实数0x 和正数k 满足：()()()()0101n nn n f x f k f x f k ++'='，求证：00x k <<.ABCD21．（本题满分14分）设曲线C ：221x y -=上的点P 到点()0,n n A a 的距离的最小值为n d ,若00a =,1n n a -,*n ∈N（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）求证:321212435214622n nn n a a a a a a a a a a a a -+++++<+++； （Ⅲ）是否存在常数M ,使得对*n ∀∈N ,都有不等式:33312111nM a a a +++<成立?请说明理由.2012年佛山市普通高中高三教学质量检测（二）参考答案数 学 (理科)二、填空题：本题共7小题，考生作答6小题，每小题5分，共30分9．4-； 10．5； 11．25； 12．45-； 13.4；三、解答题：本大题共6小题,满分80分.解答应写出文字说明、证明过程和演算步骤16．【解析】（Ⅰ）如图,连结AC ,依题意可知,B D π+=, 在ABC ∆中,由余弦定理得22224224cos AC B =+-⨯⨯ 2016cos B =-在ACD ∆中,由余弦定理得22264264cos AC D =+-⨯⨯ 5248cos 5248cos D B =-=+由2016cos 5248cos B B -=+,解得1cos 2B =-从而22016cos 28AC B =-=,即AC =6分2012年4月18日PCDEFBAOG PC DEF B A O GH（Ⅱ）由（Ⅰ）可知sin sin B D==, 所以11sinsin 22ABCD ABC ACD S S S AB BC B AD CD D ∆∆=+=⋅+⋅==.………12分17．【解析】（Ⅰ）由条形统计图可知,空气质量类别为良的天数为16天, 所以此次监测结果中空气质量类别为良的概率为 1683015=.…………………4分 （Ⅱ）随机变量X 的可能取值为0,1,2,则()2222302310435C P X C ===,()118222301761435C C P X C ===,()28230282435C P X C === 所以X 的分布列为:18．【解析】（Ⅰ）因为PA ⊥底面ABCD ,CD ⊂面ABCD ,所以PA CD ⊥,又因为直角梯形面ABCD 中,AC CD == 所以222AC CD AD +=,即AC CD ⊥,又PAAC A =,所以CD ⊥平面PAC ；………4分（Ⅱ）解法一:如图,连接BD ,交AC 于O ,取PE 中点G , 连接,,BG FG EO ,则在PCE ∆中,//FG CE ,又EC ⊂平面ACE ,FG ⊄平面ACE ,所以//FG 平面ACE ,因为//BC AD ,所以BO GEOD ED=,则//OE BG , 又OE ⊂平面ACE ,BG ⊄平面ACE ,所以//BG 平面ACE , 又BG FG G =,所以平面//BFG 平面ACE ,因为BF ⊂平面BFG ,所以//BF 平面ACE .………10分解法二:如图,连接BD ,交AC 于O ,取PE 中点G , 连接FD 交CE 于H ,连接OH ,则//FG CE ,在DFG ∆中,//HE FG ,则12GE FH ED HD ==,在底面ABCD 中,//BC AD ,所以12BO BC OD AD ==, 所以12FH BO HD OD ==,故//BF OH ,又OH ⊂平面ACE ,BF ⊄平面ACE , 所以//BF 平面ACE .………10分（Ⅲ）由（Ⅰ）可知,CD ⊥平面PAC ,所以DPC ∠为直线PD 与平面PAC 所成的角,……12分在Rt PCD ∆中,CD PD ===所以sin 5CD DPC PD ∠===, 所以直线PD 与平面PAC所成的角的正弦值为5.………14分 19．【解析】（Ⅰ）解法一:由题意得223a b -=,223114a b+=,解得224,1a b ==,所以椭圆E 的方程为2214x y +=.………………………………………………4分 解法二:椭圆的两个交点分别为())12,F F ,由椭圆的定义可得12712||||422a PF PF =+=+=,所以2a =,21b =, 所以椭圆E 的方程为2214x y +=.………………………………………………4分 （Ⅱ）解法一:由（Ⅰ）可知()()120,1,0,1A A -,设()00,P x y , 直线1PA :0011y y x x --=,令0y =,得001N x x y -=-; 直线2PA :0011y y x x ++=,令0y =,得001M xx y =+; 设圆G 的圆心为00001,211x x h y y ⎛⎫⎛⎫- ⎪ ⎪ ⎪+-⎝⎭⎝⎭,则2r =22220000000000112111411x x x xx h h y y y y y ⎡⎤⎛⎫⎛⎫--+=++⎢⎥ ⎪ ⎪+-++-⎝⎭⎝⎭⎣⎦,22200001411xx OG h y y ⎛⎫=-+ ⎪+-⎝⎭2222222200000200000114114111x x x x x OT OG r h h y y y y y ⎛⎫⎛⎫=-=++---=⎪ ⎪+-+--⎝⎭⎝⎭ 而220014x y +=,所以()220041x y =-,所以()202204141y OT y -==-, 所以||2OT =,即线段OT 的长度为定值2.…………………………………………14分 解法二:由（Ⅰ）可知()()120,1,0,1A A -,设()00,P x y , 直线1PA :0011y y x x --=,令0y =,得001N x x y -=-;直线2PA :0011y y x x ++=,令0y =,得001M xx y =+; 则20002000||||111x x x OM ON y y y -⋅=⋅=-+-,而220014x y +=,所以()220041x y =-,所以2020||||41x OM ON y ⋅==-,由切割线定理得2||||4OT OM ON =⋅= 所以||2OT =,即线段OT 的长度为定值2.…………………………………………14分 20．【解析】（Ⅰ）由已知得()()11ng x x nx =+--,所以()()111n g x n x -⎡⎤'=+-⎣⎦.………………2分① 当2n ≥且n 为偶数时,1n -是奇数,由()0g x '>得0x >;由()0g x '<得0x <. 所以()g x 的递减区间为(),0-∞,递增区间为()0,+∞,极小值为()00g =.……………5分② 当2n ≥且n 为奇数时,1n -是偶数,由()0g x '>得2x <-或0x >;由()0g x '<得20x -<<. 所以()g x 的递减区间为()2,0-,递增区间为(),2-∞-和()0,+∞,此时()g x 的极大值为()222g n -=-,极小值为()00g =.……………8分（Ⅱ）由()()()()0101n n n n f x f k f x f k ++'='得()()()()()10101111111n nn n n x k n x k -+++-=+++-, 所以()()()10111111n n n k x n k +⎡⎤+-⎣⎦+=⎡⎤++-⎣⎦,()()()()0111111nnnk k x n k -++=⎡⎤++-⎣⎦……………10分 显然分母()()1110n n k ⎡⎤++->⎣⎦,设分子为()()()()1110nh k nk k k =-++>则()()()()()()11111110n n n h k n k n k nk n n k k --'=+++-=++>所以()h k 是()0,+∞上的增函数,所以()()00h k h >=,故00x >……………12分 又()()()()10111111n nk n k x k n k +++-+-=⎡⎤++-⎣⎦,由（Ⅰ）知,()()11ng x x nx =+-- 是()0,+∞上的增函数,故当0x >时,()()00g x g >=,即()11nx nx +>+,所以()()1111n k n k +++>+所以00x k -<,从而0x k <. 综上,可知00x k <<.……………14分 21．【解析】（Ⅰ）设点(),P x y ,则221x y -=,所以||n PA ==因为y R ∈,所以当2n a y =时,||n PA 取得最小值n d ,且n d =又1n n a -=,所以1n n a +,即1n n d +=将1n n d +=代入n d =1n +=两边平方得2212n n a a +-=,又00a =,212a =故数列{}2n a 是首项212a =,公差为2的等差数列,所以22n a n =,因为1n n a -0>,所以n a ………………………………………6分（Ⅱ）因为()()()222122120n n n n +--+=-<,所以()()()2221221n n n n +-<+所以2221212n n n n a a a a +-+<所以2122122n n n n a a a a -++<,所以321212434562122,,,n n n n a a aa a aa a a a a a -++<<< 以上n 个不等式相加得321212435214622n nn n a a a aa a a a a a a a -+++++<+++.…………………10分（Ⅲ）因为31k a=,当2k≥时,<==,=<=<=<2211nnk k==<=<∑所以31211142nn i k ia ===<+=+∑. 故存在常数14M =+对*n ∀∈N ,都有不等式:33312111nM a a a +++<成立. …………14分。

佛山市20XX 届高三教学质量检测(一)文科数学参考公式: 棱锥的体积公式：13V Sh =. 一、选择题:本大题共10小题,每小题5分,满分50分,1． 已知全集U =R ，集合{10}A x x =+<，{30}B x x =-<，则集合()U A B =ðA ．{13}x x -≤<B ．{13}x x -<<C ．{1}x x <-D ．{3}x x >2．等差数列{}n a 中，2=d ，且431,,a a a 成等比数列，则=2a A ．4- B ．6-C ．8-D ．10-3．下列函数中既是奇函数，又在区间()1,1-上是增函数的为A ．y x =B ．sin y x =C ．x x y e e -=+D ．3y x =-4．已知i 是虚数单位，m 、n ∈R ，且(1i)1i m n +=+，则2i i m n m n +⎛⎫= ⎪-⎝⎭A ．iB ．i -C ．1D ．1-5．已知椭圆2215x y m +=的离心率e =，则m 的值为A ．3BCD ．253或36．“关于x 的不等式220x ax a -+>的解集为R ”是“01a ≤≤”A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件7．把函数sin ()y x x =∈R 的图象上所有的点向左平移6π个单位长度，再把所得图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到的图象所表示的函数为 A ．sin(2),3y x x π=-∈R B ．sin(2),3y x x π=+∈RC ．1sin(),26y x x π=+∈R D ．1sin(),26y x x π=-∈R8．①长方形；②正方形；③圆；④椭圆.其中正确的是 A ．①② B ． ②③ C ．③④ D ． ①④9. 某市要对两千多名出租车司机的年龄进行调查，现从中随机抽出100名司机，已知抽到的司机年龄都在[)20,45岁之间，根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数．．．大约是 A ．31.6岁 B ．32.6岁 C ．33.6岁 D ．36.6岁10. 已知向量=a (,2)x ，=b (1,)y ，其中0,0x y >>.若4=a b ，则12x y+的最小值为 A ．32B ．2C ．94D ．二、填空题:本大共5小题,考生作答4小题,每小题5分，满分20分） (一)必做题(11～13题)11. 某学校三个社团的人员分布如下表（每名同学只参加一个社团）学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果合唱社被抽出12人，则这三个社团人数共有_______________.12. 已知不等式组⎪⎩⎪⎨⎧≤-≥≤a x x y x y ， 表示的平面区域的面积为4，点),(y x P 在所给平面区域内，则y x z +=2的最大值为 .13. 对任意实数b a ,，函数()1(,)||2F a b a b a b =+--，如果函数2()23,f x x x =-++ ()1g x x =+，那么函数()()(),()G x F f x g x =的最大值等于 .(二)选做题(14～15题,考生只能从中选做一题)14．（坐标系与参数方程）在极坐标系下，已知直线l 的方程为21)3cos(=-πθρ，则点)2,1(πM 到直线l 的距离为__________.15.（几何证明选讲）如图，P 为圆O 外一点，由P 引圆O 的 切线PA 与圆O 切于A 点，引圆O 的割线PB 与圆O 交于C 点.已知AC AB ⊥， 1,2==PC PA .则圆O 的面积为 .三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16．（本题满分12分）在△ABC 中，角A 、B 、C 的对边分别为a b c 、、，若60B =， 且1411)cos(-=+C B . （1）求C cos 的值； （2）若5=a ，求△ABC 的面积.17．（本题满分12分）文科班某同学参加广东省学业水平测试，物理、化学、生物获得等级A 和获得等级不是A 的机会相等，物理、化学、生物获得等级A 的事件分别记为1W 、2W 、3W ，物理、化学、生物获得等级不是A 的事件分别记为1W 、2W 、3W .（1）试列举该同学这次水平测试中物理、化学、生物成绩是否为A 的所有可能结果（如三科成绩均为A 记为()123,,W W W ）；（2）求该同学参加这次水平测试获得两个A 的概率；（3）试设计一个关于该同学参加这次水平测试物理、化学、生物成绩情况的事件，使该事件的概率大于85%，并说明理由. 18．（本题满分14分）如图，三棱锥ABC P -中，PB ⊥底面ABC ，90BCA ∠=， 4===CA BC PB ，E 为PC 的中点， M 为AB 的中点，点F 在PA 上，且2AF FP =. （1）求证：BE ⊥平面PAC ； （2）求证：//CM 平面BEF ； （3）求三棱锥ABE F -的体积.19．（本题满分14分）已知圆221:(4)1C x y -+=，圆222:(2)1C x y +-=，圆1C ,2C 关于直线l 对称. （1）求直线l 的方程；（2）直线l 上是否存在点Q ，使Q点到(A -点的距离减去Q点到B 点的距离的差AP4，如果存在求出Q 点坐标，如果不存在说明理由.20．（本题满分14分）设a R ∈,函数()ln f x x ax =-. （1）讨论函数()f x 的单调区间和极值;（2）已知1 2.71828)x e =L 和2x 是函数()f x 的两个不同的零点, 求a 的值并证明:322x e >.21．（本题满分14分）设*n N ∈，圆n C ：222(0)n n x y R R +=>与y 轴正半轴的交点为M ，与曲线y =(,)n n N x y ，直线MN 与x 轴的交点为(,0)n A a .（1）用n x 表示n R 和n a ；（2）若数列{}n x 满足：1143,3n n x x x +=+=. ①求常数p 的值使数列{}1n n a p a +-⋅成等比数列； ②比较n a 与23n⋅的大小.20XX 年佛山市普通高中高三教学质量检测（一）参考答案一、 1-5、ABBDD 6-10、ACBCC二、 二、11．150 12．6 13． 3 14．213- 15．π4916．（本题满分12分） 解：（1）∵1411)cos(-=+C B , ∴ 1435)(cos 1)sin(2=+-=+C B C B …………………3分 ∴()cos cos cos()cos sin()sin C B C B B C B B C B =+-=+++⎡⎤⎣⎦7123143521411=⨯+⨯-= ………6分 （2）由（1）可得734cos 1sin 2=-=C C …………………8分 在△ABC 中，由正弦定理AaB bC c sin sin sin == ∴8sin sin ==A C a c , 5sin ==aAb b (10)分∴310238521sin 21S =⨯⨯⨯==B ac . …………………12分 17．（本题满分12分）解：（1）该同学这次水平测试中物理、化学、生物成绩是否为A 的可能结果有8种，分别为123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）； …………………4分 （2）由（1）可知，有两个A 的情况为123,,W W W （）、123,,W W W （）、123,,W W W （）三个， 从而其概率为38P =…………………8分 （3）方案一、该同学参加这次水平测试中物理、化学、生物成绩不全为A 的事件概率大于85%， …………………10分 理由如下：该同学参加这次水平测试中物理、化学、生物成绩不全为A 的事件有如下七种情况：123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （），概率是70.87585%8P ==>. .....................12分 方案二、该同学参加这次水平测试中物理、化学、生物成绩至少一个A 的事件概率大于85%， (10)分理由如下：该同学参加这次水平测试中物理、化学、生物成绩不全为A 的事件有如下七种情况：123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）、123,,W W W （）， 概率是70.87585%8P ==>. ……………………12分 18．（本题满分14分）（1）证明：∵⊥PB 底面ABC ，且⊂AC 底面ABC ， ∴AC PB ⊥ …………………1分由90BCA ∠=，可得CB AC ⊥ ………2分又 PBCB B = ，∴AC ⊥平面PBC ……………3分注意到⊂BE 平面PBC ， ∴AC BE ⊥ …………4分BC PB = ,E 为PC 中点，∴BE PC ⊥ ………5分PCAC C =， ∴BE ⊥平面PAC …………6分（2）取AF 的中点G ，AB 的中点M ，连接,,CG CM GM ， ∵E 为PC 中点，2FA FP =，∴//EF CG . ………7分∵CG ⊄平面,BEF EF ⊂平面BEF ， ∴//CG 平面BEF . ......8分 同理可证：//GM 平面BEF . 又CG GM G =， ∴平面//CMG 平面BEF . (9)分∵CD ⊂平面CDG ，∴//CD 平面BEF . …………10分（3）由（1）可知BE ⊥平面PAC又由已知可得22=BE .238213131=⋅⨯==∆∆PC AC S S PAC AEF …………12分 ∴93231=⋅==∆--BE S V V AEF AEF B ABE F所以三棱锥ABE F -的体积为932. …………14分19．（本题满分14分）解：（1）因为圆1C ,2C 关于直线l 对称，圆1C 的圆心1C 坐标为(4,0)，圆2C 的圆心2C 坐标为(0,2)， ……………………2分 显然直线l 是线段12C C 的中垂线， ……………………3分 线段12C C 中点坐标是(2,1)，12C C 的斜率是1212021402y y k x x --===---， ……………………5分所以直线l 的方程是11(2)y x k-=--，即23y x =-. ……………………6分（2）假设这样的Q 点存在，因为Q点到(A -点的距离减去Q点到B 点的距离的差为4， 所以Q点在以(A -和B 为焦点，实轴长为4的双曲线的右支上，即Q 点在曲线221(2)44x y x -=≥上， ……………………10分又Q 点在直线l 上， Q 点的坐标是方程组2223144y x x y =-⎧⎪⎨-=⎪⎩的解， (12)分消元得2312130x x -+=，21243130∆=-⨯⨯<，方程组无解，所以点P 的轨迹上是不存在满足条件的点Q . ……………………14分20．（本题满分14分） 解：在区间()0,+∞上,11()axf x a x x-'=-=. ……………………2分①若0a ≤,则()0f x '>,()f x 是区间()0,+∞上的增函数,无极值； ……………………4分②若0a >,令()0f x '=得: 1x a=.在区间1(0,)a上, ()0f x '>,函数()f x 是增函数; 在区间1(,)a+∞上, ()0f x '<,函数()f x 是减函数; 在区间()0,+∞上, ()f x 的极大值为11()ln1ln 1f a a a=-=--. 综上所述，①当0a ≤时,()f x 的递增区间()0,+∞,无极值； ……………………7分③当0a >时，()f x 的是递增区间1(0,)a ，递减区间是1(,)a+∞，函数()f x 的极大值为1()ln 1f a a=--. ……………………9分(2) 0,f =∴102-=，解得:a =……………………10分∴()ln f x x x =. (11)分又323()022e f e =->Q ,5325()022e f e =-<,3522()()0f e f e ∴⋅< ……………………13分由(1)函数()f x在)+∞递减,故函数()f x 在区间3522(,)e e 有唯一零点,因此322x e >. ……………………14分21．（本题满分14分） 解：(1)y =n C 交于点N ,则2222,nn n n n n R x y x x R =+=+= ……………………2分 由题可知，点M 的坐标为()0,n R ，从而直线MN 的方程为1n nx y a R +=, ……………………3分 由点(,)n n N x y 在直线MN 上得:1n nn nx y a R +=, ……………………4分将n R =n y =: 1n n a x =+ ……………………6分(2)由143n n x x +=+得：114(1)n n x x ++=+， ……………………7分又114x +=，故11444n n n x -+=⋅=，442n n nn a ∴=+=+ ……………………8分 ①11142(42)(4)4(2)2n n n n n n n n a p a p p p +++-⋅=+-⋅+=-⋅+-⋅，22112142(42)(164)4(42)2n n n n n n n n a p a p p p ++++++-⋅=+-⋅+=-⋅+-⋅令211()n n n n a p a q a p a +++-⋅=-⋅得：(164)4(42)2(4)4(2)2n n n n p p q p q p -⋅+-⋅=-⋅+-⋅ (9)分由等式(164)2(42)(4)2(2)n n p p q p q p -⋅+-=-⋅+-对任意*n N ∈成立得：164(4)842(2)6p q p pq p q p p q -=-=⎧⎧⇔⎨⎨-=-+=⎩⎩，解得：24p q =⎧⎨=⎩或42p q =⎧⎨=⎩ 故当2p =时，数列{}1n n a p a +-⋅成公比为4的等比数列；当4p =时，数列{}1n n a p a +-⋅成公比为2的等比数列。

4．“关于x 的不等式220x ax a -+>的解集为R ”是“01a ≤≤”A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件6．已知点P 是抛物线24x y =上的一个动点，则点P 到点(2,0)M 的距离与点P 到该抛物线准线的距离之和的最小值为A ．172B ．5C ．22D ．92 8．对于非空集合,A B ，定义运算：{|,}A B x x A B x A B ⊕=∈∉ 且，已知}|{},|{d x c x N b x a x M <<=<<=，其中d c b a 、、、满足a b c d +=+，0ab cd <<，则=⊕N MA. (,)(,)a d b cB.(,][,)c a b dC. (,][,)a c d bD.(,)(,)c a d b9．某学校三个社团的人员分布如下表（每名同学只参加一个社团）学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果合唱社被抽出12人，则a =_______________.11．已知不等式组02,20,20x x y kx y ≤≤⎧⎪+-≥⎨⎪-+≥⎩所表示的平面区域的面积为4，则k 的值为__________. 13．对任意实数b a ,，函数|)|(21),(b a b a b a F --+=，如果函数2()23,f x x x =-++ ()1g x x =+，那么函数()()(),()G x F f x g x =的最大值等于 .18．（本题满分13分） 佛山某学校的场室统一使用“佛山照明”的一种灯管，已知这种灯管使用寿命ξ（单位：月）服从正态分布2(,)N μσ，且使用寿命不少于12个月的概率为0.8，使用寿命不少于24个月的概率为0.2.（1）求这种灯管的平均使用寿命μ；（2）假设一间功能室一次性换上4支这种新灯管，使用12个月时进行一次检查，将已经损坏的灯管换下（中途不更换），求至少两支灯管需要更换的概率.19．（本题满分12分）已知圆221:(4)1C x y -+=，圆222:(2)1C x y +-=，动点P 到圆1C ,2C 上点的距离的最小值相等.（1）求点P 的轨迹方程；（2）点P 的轨迹上是否存在点Q ，使得点Q 到点(22,0)A -的距离减去点Q 到点(22,0)B 的距离的差为4，如果存在求出Q 点坐标，如果不存在说明理由.20．（本题满分14分） 合唱社 粤曲社 书法社 高一45 30 a 高二 15 10 20设a R ∈,函数()ln f x x ax =-.(1) 若2a =，求曲线()y f x =在()1,2P -处的切线方程；(2) 若()f x 无零点,求实数a 的取值范围；(3) 若()f x 有两个相异零点12,x x ,求证: 212x x e ⋅>.21．（本题满分14分）设*N n ∈，圆n C ：222(0)n n x y R R +=>与y 轴正半轴的交点为M ，与曲线y x =的交点为1(,)n N y n，直线MN 与x 轴的交点为(,0)n A a .(1)用n 表示n R 和n a ;(2)求证:12n n a a +>>;(3)设123n n S a a a a =++++ ,111123n T n =++++ ,求证:27352n n S n T -<<.答案 4、A ；6、B ；8、C9．30 11．1 13． 318．（本题满分13分）解：（1）∵2(,)N ξμσ ，(12)0.8P ξ≥=，(24)0.2P ξ≥=，∴(12)0.2P ξ<=，显然(12)(24)P P ξξ<=> ……………3分 由正态分布密度函数的对称性可知，1224182μ+==， 即每支这种灯管的平均使用寿命是18个月； …………………5分（2）每支灯管使用12个月时已经损坏的概率为10.80.2-=， ……………6分假设使用12个月时该功能室需要更换的灯管数量为η支，则(4,0.2)B η ， ………10分故至少两支灯管需要更换的概率1(0)(1)P P P ηη=-=-=0413********.80.80.2625C C =--⨯=（写成≈0.18也可以）. …………………13分19．（本题满分13分）解：（1）设动点P 的坐标为(,)x y ，圆1C 的圆心1C 坐标为(4,0)，圆2C 的圆心2C 坐标为(0,2)， …………………2分因为动点P 到圆1C ,2C 上的点距离最小值相等，所以12||||PC PC =, …………3分 即2222(4)(2)x y x y -+=+-，化简得23y x =-，…………………4分因此点P 的轨迹方程是23y x =-； ……………………5分（2）假设这样的Q 点存在，因为Q 点到(22,0)A -点的距离减去Q 点到(22,0)B 点的距离的差为4，所以Q 点在以(22,0)A -和(22,0)B 为焦点，实轴长为4的双曲线的右支上，即Q 点在曲线221(2)44x y x -=≥上， ……………………9分 又Q 点在直线:23l y x =-上， Q 点的坐标是方程组2223144y x x y =-⎧⎪⎨-=⎪⎩的解，………11分 消元得2312130x x -+=，21243130∆=-⨯⨯<，方程组无解，所以点P 的轨迹上不存在满足条件的点Q . …………………13分20．（本题满分14分）解：方法一在区间()0,+∞上,11()ax f x a x x-'=-=. ………1分 （1）当2a =时，(1)121f '=-=-，则切线方程为(2)(1)y x --=--，即10x y ++= …………3分（2）①若0a <,则()0f x '>,()f x 是区间()0,+∞上的增函数,(1)0f a =->Q ,()(1)0a a a f e a ae a e =-=-<,(1)()0a f f e ∴⋅<,函数()f x 在区间()0,+∞有唯一零点. …………6分②若0a =,()ln f x x =有唯一零点1x =. …………7分③若0a >,令()0f x '=得: 1x a=. 在区间1(0,)a 上, ()0f x '>,函数()f x 是增函数; 在区间1(,)a +∞上, ()0f x '<,函数()f x 是减函数;故在区间()0,+∞上, ()f x 的极大值为11()ln1ln 1f a a a =-=--. 由1()0,f a <即ln 10a --<,解得:1a e>. 故所求实数a 的取值范围是1(,)e +∞. …………9分方法二、函数()f x 无零点⇔方程ln x ax =即ln x a x =在()0,+∞上无实数解 ……4分 令ln ()x g x x =，则21ln ()x g x x -'= 由()0g x '=即21ln 0x x-=得：x e = …………6分 在区间(0,)e 上, ()0g x '>,函数()g x 是增函数;在区间(,)e +∞上, ()0g x '<,函数()g x 是减函数;故在区间()0,+∞上, ()g x 的极大值为1()g e e=. …………7分 注意到(0,1)x ∈时，()(),0g x ∈-∞；1x =时(1)0g =；()1,x ∈+∞时，1()0,g x e⎛⎤∈ ⎥⎝⎦ 故方程ln x a x=在()0,+∞上无实数解⇔1a e >.即所求实数a 的取值范围是1(,)e +∞. …………9分[注:解法二只说明了()g x 的值域是1,e ⎛⎤-∞ ⎥⎝⎦,但并没有证明.] (3) 设120,x x >>12()0,()0,f x f x ==Q 1122ln 0,ln 0x ax x ax ∴-=-= 1212ln ln ()x x a x x ∴+=+,1212ln ln ()x x a x x -=-原不等式21212ln ln 2x x e x x ⋅>⇔+>12()2a x x ⇔+>121212ln ln 2x x x x x x -⇔>-+1122122()ln x x x x x x -⇔>+ 令12x t x =,则1t >,于是1122122()2(1)ln ln 1x x x t t x x x t -->⇔>++. ……12分 设函数2(1)()ln 1t g t t t -=-+(1)t >, 求导得: 22214(1)()0(1)(1)t g t t t t t -'=-=>++ 故函数()g t 是()1,+∞上的增函数, ()(1)0g t g ∴>= 即不等式2(1)ln 1t t t ->+成立,故所证不等式212x x e ⋅>成立. ………………14分 21．（本题满分14分）解： (1)由点N 在曲线y x =上可得11(,)N n n, ……………………1分 又点在圆n C 上，则2221111(),n n n n R R n n n n ++=+==, ……………………2分 从而直线MN 的方程为1n nx y a R +=, ……………………4分 由点11(,)N n n 在直线MN 上得: 111n nna n R +=⋅,将1n n R n +=代入 化简得: 1111n a n n=+++. ……………………6分 (2) 1111,11n n +>+> ,*11,112n n N a n n∴∀∈=+++> ……………7分又111111,1111n n n n +>++>+++ , 11111111111n n a a n n n n +∴=+++>+++=++ ……………………9分 (3)先证:当01x ≤≤时,1(21)112x x x +-≤+≤+. 事实上, 不等式1(21)112x x x +-≤+≤+ 22[1(21)]1(1)2x x x ⇔+-≤+≤+ 22212(21)(21)114x x x x x ⇔+-+-≤+≤++ 222(223)(21)04x x x ⇔-+-≤≤ 后一个不等式显然成立,而前一个不等式2001x x x ⇔-≤⇔≤≤. 故当01x ≤≤时, 不等式1(21)112x x x +-≤+≤+成立. 1111(21)112n n n∴+-≤+<+, ……………………11分 1113221122n a n n n n∴+⋅≤=+++<+(等号仅在n =1时成立) 求和得: 32222n n n n T S n T +⋅≤<+⋅ 273252n n S n T -∴<≤< ……………………14分。

2012年佛山市普通高中高三教学质量检测（一）文科综合能力测试2012.1本试卷共 10页，满分300分．考试时间150分钟．注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号填写在答题卡上．用2B铅笔将答题卡试卷类型（A）填涂在答题卡上，并在答题卡右上角的“试室号”和“座位号”栏填写试室号、座位号，将相应的试室号、座位号信息点涂黑．2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案答在试题卷上无效．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答卷上各题目指定区域内相应位置上，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁．考试结束后，将答卷和答题卡一并交回．第一部分选择题（共 140分）一、本大题共35小题，每小题4分，共140分。

在每小题列出的四个选项中，只有一项是符合题目要求的。

1．下列四图(图1)中能够正确表示地理事物和现象之间关系的是A．① B ．② C．③D．④图12.我国现行流通人民币20元的背面图案（图2）取景于广西桂林，该景观图2图2A.天然植被为落叶阔叶林B.受流水化学和物理作用C.山体的基岩是岩浆岩D.山体连绵，是褶皱山3．读某区域流域图(图3)，可能导致该区域海岸线变迁的人类活动是A.发展海水养殖业B.河流中上游修建水库C.大量开采地下水D.营造沿海防护林4.由表中信息直接可以反映出甲省比乙省A ．城市化水平更高B ．机械增长率更高C ．人口合理容量更大D ．老龄化问题更突出 5.2011年夏季，乙省某城市多次出现严重内涝现象。

它的形成与下列人类活动无关．．的是 A.城市人工绿地面积增多，使地下水位上升 B.城市空气中尘埃多，增加暴雨形成机率 C.城市“热岛效应”，使大气对流运动增强 D.城市建设使地面硬化，地表水下渗能力弱6．我国房价上涨引起社会关注，图4中影响保障性住房布局的主导因素是A ．交通条件和环境因素B ．配套设施和土地价格C ．土地价格和交通条件D ．土地利用效益和地租支付能力图4图32012年高三质量检测（一）文科综合试题 第3页 共14页泰国兰花生产条件优越，2011年1月，泰国农业部推出2011—2016泰国兰花发展 战略计划。

2012届高三年级第二次月考数学试题（文科）（考试范围：集合与简易逻辑、不等式（含绝对值不等式）、函数、导数、三角函数及解三角形、数列、平面向量、立体几何、直线和圆）本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷l 至2页，第Ⅱ卷3至5页，共150分。

考试时间120分钟。

注意事项： 1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和座位号填写在答题卡上。

2．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

参考公式：球的表面积、体积公式24S πR =，343V πR =，其中R 为球的半径．第Ⅰ卷 （选择题60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求． 1．已知集合}21|{},|{<<=<=x x B a x x A 且R =B C A R ,则实数a 的取值范围是（ ） A ．1≤aB ．1<aC ．2≥aD ．2>a2．若直线210ax y ++=与直线20x y +-=互相垂直，那么a 的值等于（ ）A ．1B ．13-C ．23- D ．2-3．设平面向量(1,2),(1,)a b m ==-，若//a b ，则实数m 的值为（ ）A ．1-B ．2-C ．1D ．24．下列四个几何体中，每个几何体的三视图中有且仅有两个视图相同的是（ ）A ．①②B ．①③C ．③④D ．②④5．已知x ，y 满足条件5003x y x y x -+≥⎧⎪≥⎨⎪≤⎩，+，，则z=13y x -+的最大值 （ ）A ．3B ．76 C ．13D ．-236．现有四个函数：①x x y sin ⋅= ②x x y cos ⋅= ③x x y cos ⋅= ④x x y 2⋅=的图象（部分）如下，则按照从左到右图像对应的函数序号安排正确的一组是 （ ） A ．①④③② B ．④①②③ C ．①④②③． D ．③④②①7．已知f （x ）=(3)4,1log ,1a x a x x x a--≥⎧⎨⎩ 是（-∞，+∞）上的增函数，那么a 的取值范围是（ ）A ．（1，+∞）B ．（-∞,3）C ．（ 35,3） D ．（1,3）8．已知三条不重合的直线m 、n 、l 与两个不重合的平面α、β，有下列命题：[ ] ①若m ∥n ，n ⊂α，则m ∥α；②若l ⊥α，m ⊥β且l ∥m ，则α∥β；③若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β；④若α⊥β，α∩β＝m ，n ⊂β，n ⊥m ，则n ⊥α．其中正确的命题个数是 （ ） A ．1 B ．2 C ．3 D ．49．三棱锥P-ABC 的三条侧棱PA 、PB 、PC 两两互相垂直，且长度分别为3、4、5，则三棱锥P-ABC 外接球的表面积是 （ ）A． B． C ．50πD ．200π10．若点P在曲线上移动，经过点P 的切线的倾斜角为，x则角的取值范围是（ ）A ．B ．C ．D ．11．一束光线从点(1,1)A -出发，经x 轴反射到圆22:(2)(3)1C x y -+-=上的最短路径是（ ）A ．4B ．5C ．1D ．12．不等式2313x x a a +--≤-对任意实数x 恒成立，则实数a 的取值范围为（ ）A ．(,1][4,)-∞-+∞B ．(,2][5,)-∞-+∞C ．[1,2]D ．(,1][2,)-∞+∞第Ⅱ卷（非选择题90分）二、填空题：本大题共4个小题，每小题5分，共20分．13．已知数列1-,1a ,2a ,4-成等差数列,1-,1b ,2b ,3b ,4-成等比数列，则212b a a -的值为14．若圆2221:240C x y mx m +-+-=与圆2222:24480C x y x my m ++-+-=相离，则m 的取值范围是 ．15．在四边形ABCD 中，AB =DC =（1，1），11B A B C B A B C B D+=，则四边形ABCD 的面积是16．下面四个命题：①函数sin ||y x =的最小正周期为π；②在△ABC 中，若0>⋅，则△ABC 一定是钝角三角形； ③函数2log (2)(01)a y x a a =+->≠且的图象必经过点（3，2）；④cos sin y x x =-的图象向左平移4π个单位，所得图象关于y 轴对称； ⑤若命题“2,0x R x x a ∃∈++<”是假命题，则实数a 的取值范围为1[,)4+∞；其中所有正确命题的序号是 。

2012学年度第一学期高三年级期末质量检测文科数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。

考试时间120分钟。

注意事项：1、答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、班级和考号填写在答题卷上。

2、必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内相应位置上；如需改动，划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

参考公式：锥体的体积公式：13V Sh =（其中S 是锥体的底面积，h 是锥体的高） 第Ⅰ卷 选择题（共50分）一、选择题（本大题共10小题，每小题5分，满分50分）1．已知集合{1,2},{,},aA B a b ==若1{}2AB =,则A B 为（ ）A ．1{,1,}2bB ．1{1,}2-C ．1{1,}2D ．1{1,,1}2-2．已知复数z 的实部为1-，虚部为2，则5iz=（ ）A ．2i -B ．2i +C ．2i --D ．2i -+3．已知1sin 3α=，则cos(2)πα+的值为（ ）A ．79B ．79-C ．29D ．23-4．已知{}n a 是等差数列，6720a a +=，7828a a +=，则该数列前13项和13S =（ ） A ．156 B ．132C ．110D ．1005．下列命题中的假命题是（ ）A ．3,0x R x ∃∈< B ．“0>a ”是“0a >”C ．,20xx R ∀∈> D ．“x<2”是“|x|<2”的充分不必要条件 6．如图，函数()y f x =的图象是折线段ABC （包括端点）， 其中A B C ，，的坐标分别为（0，4），（2，0），（6，4）， 则((0))f f = （ ） A ．0 B ．2 C ．4 D ．6DCBANMA BCDB1C1 7．如图是一正方体被过棱的中点M、N和顶点A、D、1C截去两个角后所得的几何体，则该几何体的主视图（或称正视图）为（）8．已知m是两个正数8,2的等比中项，则圆锥曲线122=+myx的离心率为（）A．23或25B．23C．5D．23或59．在右程序框图中，当n∈N*（n>1）时，函数()nf x表示函数1n-f x()的导函数.若输入函数1sin cos=+()f x x x，则输出的函数()nf x可化为（）A+xπ)4B．-xπ)4C-xπ)4D．+xπ)410．定义平面向量之间的一种运算“”如下：对任意的(,)a m n=，(,)b p q=，令a b mq np=-，下面说法错误的是（）A．若a与b共线，则0a b =B．a b b a=C．对任意的Rλ∈，有()()a b a bλλ=D．2222()()||||a b a b a b+∙=第Ⅱ卷非选择题（共100分）二、填空题：本大题共５小题，考生作答４小题，每小题5分，满分20分。

广东省佛山市2012届高三4月教学质量检测（二） 文科数学 一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、复数z满足，则z＝ 2、集合，定义集合 已知，则的子集为 3、设函数若f（x）为奇函数，则g（－4）的值是A、－2B、－C、－D、2 4、已知非零向量的（ ） A．B．C．D．是两个不重合的平面，下列命题中正确的是（ ） 6、若，则m＋3n的最小值等于（　） 7.随机抽取某花场甲，乙两种计划在植树节期间移种的树苗各10株，测量它们的高度（单位：cm）,获得高度数据的茎叶图如图，则下列关于甲、乙两种各10株树苗高度的结论正确的是（ ）A.甲种树苗高度的方差较大B.甲种树苗高度的平均值较大C.甲种树苗高度的中位数较大D.甲种树苗高度在175以上的株数较多 8、设等差数列{}的前n项和是，且，那么下列不等式中不成立的是 二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分。

（二）选做题（14、15题,考生只能从中选做一题,两题全答的,只计前一题的得分） 14.(坐标系与参数方程选做题)在极坐标系中,射线与曲线:的异于极点的交点为,与曲线:的异于极点的交点为,则________. 15.(几何证明选做题)如图,已知圆中两条弦与相交于点,是 延长线上一点,且,,若 与圆相切,则线段的长为 ． 三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤。

16.空气质量指数PM2.5(单位：μg/m3)表示每立方米空气中可入肺颗粒物的含量，这个值越高，解代表空气污染越严重： PM2.5日均浓度0~3535~7575~115115~150150~250>250空气质量级别一级二级三级四级五级六级空气质量类别优良轻度污染中度污染重度污染严重污染某市2012年3月8日—4月7日(30天)对空气质量指数PM2.5进行检测，获得数据后整理得到如下条形图： (1)估计该城市一个月内空气质量类别为良的概率； (2)从空气质量级别为三级和四级的数据中任取2个，求至少有一天空气质量类别为中度污染的概率。

2012届高三年级第二次月考数学试卷（文科）命题人：黄友泰一、选择题（10×5=50分）1、已知复数221iz z i==-，则 A ．2iB ．－2iC ．2－2iD ．2＋2i2、已知(1,sin ),(3sin ,1),//cos2a b a b θθθ===且，则A ．－13B ．23-C ．23D ．133、设Sn 是等差数列｛a n ｝的前n 项和，且552833()aS a a a =+，则的值为（ ）A ．512B ．56C ．53D ．524、偶函数()log ||(01)(,0)a f x x b a a =->≠-∞且，在上单调递增，则(1)(2f a f b ++与的大小关系是（ ） A ．(1)(2)f a f b +≥+ B ．(1)(2)f a f b +<+ C ．(1)(2)f a f b +≤+D ．(1)(2)f a f b +>+5、已知两不共线向量(cos ,sin ),(cos ,sin )a b ααββ==，则下列说法不正确的是（ ）A ．()()a b a b +⊥-B ．a b与的夹角等于αβ-C ．||||>2a b a b ++-D ．a b a b +与在方向上的投影相等6、已知函数74sin(2)([0,])66y x x ππ=+∈的图象与直线y=m 有三个交点的横坐标分别为123123123,,(),2x x x x x x x x x <<++那么的值是（ ）A ．34πB ．43π C ．53π D ．32π 7、已知22:,20,:,210,p x R mx q x R x mx p q ∃∈+≤∀∈-+>∨若为假命题，则实数m 的取值范围是（ ）A ．[1,)+∞B ．(,1]-∞-C ．(,2]-∞-D ．[1,1]-8、设｛a n ｝是任意等比数列，它的前n 项和、前2n 项和与前3n 项和分别为X 、Y 、Z ，则下列等式中恒成立的是（ ）A ．X ＋Z ＝2YB ．Y(Y －X)＝Z(Z －X)C ．Y 2＝XZD ．Y(Y －X)＝X(Z －X)9、函数()f x 的定义域为R ，(1)2f -=，对任意,()2x R f x '∈> ，则()24f x x >+的解集为（ ）A ．（-1，1）B ．（-1，+∞）C ．（-∞，-1）D ．（-∞，+∞）10、已知函数2()1,()43,()()x f x e g x x x f a g b =-=-+-=若有，则b 的取值范围为（ ）A．[2 B．(2C ．[1，3]D ．（1，3）二、填空题（5×5=25分）11、若2{|{|1}=A x y B y y x A B ====+⋂，则 。

2012年佛山市普通高中高三教学质量检测（二）数学试题（文科）参考答案和评分标准一、选择题：本大题共10小题，每小题5分，满分50分．11．e12．(1,)-+∞13．114．15三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤．16．（本题满分12分）解析：（1）由条形统计图可知，空气质量类别为良的天数为16天，-------------------------1分所以此次监测结果中空气质量类别为良的概率为1683015=．-------------------------4分（2）样本中空气质量级别为三级的有4天，设其编号为1234,,,a a a a；样本中空气质量级别为四级的有2天，设其编号为12,b b．-------------------------6分则基本事件有：12(,)a a，13(,)a a，14(,)a a，11(,)a b，12(,)a b；23(,)a a，24(,)a a，21(,)a b，22(,)a b；34(,)a a，31(,)a b，32(,)a b；41(,)a b，42(,)a b；12(,)b b．共15个．（注：基本事件可以用树状图或列表等均正确）-------------------------9分其中至少有1天空气质量类别为中度污染的情况为：11(,)a b，12(,)a b，21(,)a b，22(,)a b，31(,)a b，32(,)a b，41(,)a b，42(,)a b，12(,)b b．共9个．所以至少有1天空气质量类别为中度污染的概率为93155=．-------------------------12分17．（本题满分12分）解析：（1）在Rt ABD∆中，DB，6ABDπ∠=，∴1AD=，3DABπ∠=，-------------------------3分又∵1DF=，∴ADF∆为等边三角形，故3ADFπ∠=，-------------------------5分2∴6πα=． -------------------------6分解法二、在BDF ∆中，sinsin 66DF DB ππα=⎛⎫+ ⎪⎝⎭，-------------------------2分即sin 62πα⎛⎫+=⎪⎝⎭， -------------------------3分 注意到03πα<<，所以63ππα+=，即6πα=. -------------------------6分坐标法可相应给分.（2）∵//AD BC ，AD DB ⊥，∴DB BC ⊥，则0AD DB ⋅=，0DB BE ⋅=， -------------------------8分∵AE AD DB BE =++， -------------------------10分 ∴22()3AE DB AD DB BE DB AD DB DB BE DB DB ⋅=++⋅=⋅++⋅==． -------------------12分 18．（本题满分14分）解析：（1）∵四边形ABCD 中，AB AD ⊥，//BC AD ， ∴四边形ABCD 为直角梯形， ∴11()(24)2622ABCD S BC AD AB =+⨯=⨯+⨯=，-------------------2分 又PA ⊥底面ABCD ，∴四棱锥P ABCD -的高为PA ， ∴1162433P ABCD ABCD V S PA -=⋅=⨯⨯=．-------------------4分 （注：只要结果对，就给满分）（2）∵PA ⊥底面ABCD ，CD ⊂平面ABCD ，∴PA CD ⊥， -------------------------6分 又∵直角梯形ABCD 中，AC ==CD =∴222AC CD AD +=，即AC CD ⊥， -------------------------8分又PA AC A =，∴CD ⊥平面PAC ； -------------------------9分文科试题参考答案 第 3 页 共 7 页（3）不存在．-------------------------10分 下面用反证法说明：假设存在点M （异于点C ）使得//BM 平面PAD ． 在四边形ABCD 中，//BC AD ， ∵AD Ì平面PAD ，BC ⊄平面PAD ， ∴//BC 平面PAD ，∵BM ⊂平面PBC ，BC ⊂平面PBC ，BC BM B =，∴平面//PBC 平面PAD而平面PBC 与平面PAD 相交，矛盾． -------------------------14分 （注1：有反证法思想的给1分； 注2：证明面面平行不严密扣1分）19．（本题满分14分） 解析：（1）由题意知，当10x =时， 28u =， ∴22158528(10)48k =--+，解得2k =，-------------------------3分 ∴年销售利润221585(6)(6)[2()]48y x u x x =-⋅=-⋅--+，-------------------------5分 (6,)x ∈+∞．-------------------------6分（2）由（1）知，221585(6)[2()]48y x x =-⋅--+ 2(6)(22118)x x x =-⋅-++，∴222118(6)(421)y x x x x '=-+++--+ -------------------------8分26(1118)6(2)(9)x x x x =--+=---，(6,)x ∈+∞ 令0y '=得，12x =（舍去）或29x =， -------------------------10分 当(6,9)x ∈时，0y '<；当(9,)x ∈+∞时，0y '>； -------------------------12分 因此，9x =是利润函数的极大值点，也是最大值点．故max 135y =万元．-------------------------13分 所以当售价为9元时，最大年利润为135万元． -------------------------14分20．（本题满分14分）解析：（1）解法1：由题意得222231341a b a b ⎧-=⎪⎪⎨⎪+=⎪⎩，-------------------------1分4解得24a =，-------------------------2分； 21b =．-------------------------3分所以椭圆的方程为2214x y +=． -------------------------4分 解法2：椭圆的两个焦点为1(F，2F ，由椭圆的定义可得12712||||422a HF HF =+==+=，（1分） ∴2a =，22221b =-=，（正确解出一个给1分）所以椭圆的方程为2214x y +=． -------------------------4分（2）解法1：由（1）知1(0,1)A ，2(0,1)A -，设00(,)P x y ，-------------------------5分直线1PA 的方程为0011y y x x --=，令0y =，得001N x x y -=-；-------------------------7分 直线2PA 的方程为0011y y x x ++=，令0y =，得001N xx y =+；-------------------------9分 设圆G 的圆心为00001((),)211x x h y y -+-， -------------------------10分则22222000000000011[()]()2111411x x x xx r h h y y y y y =--+=+++-++-，-------------------------11分22200001()411xx OG h y y =-++-，22222220000000011()()411411x x x x OT OG r h h y y y y =-=-+-+-+-+-2021x y =-， -----12分 而220014x y +=，即22004(1)x y =-，-----13分 所以220204(1)4(1)y OT y -==-，所以||2OT =．即线段OT 的长为定值2． -------------------------14分 解法2：由（1）知1(0,1)A ，2(0,1)A -，设00(,)P x y ，------------------------5分文科试题参考答案 第 5 页 共 7 页直线1PA 的方程为0011y y x x --=，令0y =，得001N x x y -=-；-------------------------7分直线2PA 的方程为0011y y x x ++=，令0y =，得001N xx y =+；-------------------------9分则20002000||||||||111x x x OM ON y y y -⋅=⋅=-+-，而220014x y +=，即22004(1)x y =-，∴||||4OM ON ⋅=；取线段MN 的中点Q ，连接,,GQ GM GO ．||r GM =，2222222()()OT OG GM OQ QG MQ QG =-=+-+22(||)(||||)OQ MQ OQ MQ OQ MQ =-=+-||||4OM ON =⋅=∴||2OT =．即线段OT 的长为定值2． -------------------------14分 （注：可不用证明切割线定理） 解法3：过点P 作PR x ⊥轴于点R ．设00(,)P x y ，则12||||1OA OA ==，0||||OR x =，0||||RP y =，------------------------5分 由2PRM A OM ∆∆得2||||||||PR RM A O OM =，即00||||||1||y x OM OM -=，则00||||||1x OM y =+； -------8分 由1PRNAON ∆∆得1||||||||PR RN AO On =，即00||||||1||y ON x ON -=，则00||||1||x ON y =-； ---------11分而220014x y +=，即22004(1)x y =-，-------------------------12分 ∴20002000||||||||4||11||1x x x OM ON y y y ⋅=⋅==+--．-----------13因直线OT 与圆G 相切，且OMN 是圆G 的一条割线，所以2||||4OT OM ON =⋅=，所以||2OT =．即线段OT 的长为定值2． -------------------------14分621．（本题满分14分）解析：（1）设点(,)P x y ，则221x y -=，∴n PA =分==-------------------------2分 ∵y ∈R ，∴当2n a y =时，n PA 取最小值n d，且n d =-------① ------------------3分又1n n a -，∴1n n a +=，1n n d +=，将1n n d +=1n +=-------------------------4分 两边平方得：2212n n a a +-=，又00a =，212a =，-------------------------5分 故数列{}2n a 是首项212a =公差为2的等差数列，∴22n a n =．∵10n n a ->，∴n a = -------------------------6分（2）由点到直线距离公式得n t =，-------------------------7分∴n t ==，=<0+>，∴n t =-------------------------9分 ∴1211()112123n t tt n n+++=+++++-+，-------------------------10分<=-------------------------12分∴112+<L ，故111(212+<L，-------------------------13分∴121122nt t t+++=+<L．-------------------------14分文科试题参考答案第7 页共7 页。