生产规划问题及LINGO求解

例：某工厂生产Ⅰ、Ⅱ两种产品，需要用到A ，B ，C 三种设备，已知有关数据见下表。

企业的经营目标不仅仅是利润，还需要考虑多个方面：（1） 力求使利润不低于1500元；（2） 考虑到市场需求，Ⅰ、Ⅱ两种产品的产量比应尽量保持1：2；（3） 设备A 为贵重设备，严格禁止超时使用；（4） 设备C 可以适当加班，但要控制；设备B 即要求充分利用，又尽可能不加班。

在重要性上，设备C 是设备B 的3倍。

ⅠⅡ设备的生产能力/hA （h/件） 2 2 12B （h/件） 4 0 16C （h/件） 0 5 15 利润 元/件200300解：此题中只有设备A 是刚性约束，其余都是柔性约束。

首先，最重要的指标是企业的利润，将它的优先级列为第一级；其次是Ⅰ、Ⅱ两种产品的产量保持1：2的比例，列为第二级；再次，设备B 、C 的工作时间要有所控制，列为第三级。

在第三级中，设备B 的重要性是设备C 的3倍，因此它们的权重不一样，设备B 的系数是设备C 的3倍。

该计划问题可用数学模型表示为： 目标函数min)33()(433322211++-+--+++++=d d d p d d p d p z满足约束条件 2122x x + 12≤15003002001121=-+++-d d x x022221=-+-+-d d x x 14x 1633=-++-d d155442=-++-d d x3,2,1,0,,,21=≥+-i d d x x i i LINGO 程序为：求第一级目标。

LINGO 程序如下： model: sets:variable/1..2/:x;S_Con_Num/1..4/:g,dplus,dminus; S_con(S_Con_Num,Variable):c; endsets data:g=1500 0 16 15; c=200 300 2 -1 4 0 0 5; enddata min=dminus(1); 2*x(1)+2*x(2)<12;@for(S_Con_Num(i):@sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i)); end求得dminus(1)=0，即目标函数的最优值为0，第一级偏差为0。

一、Lingo 能做什么——Lingo 的简单模型1、简单线性规划求解（目标函数）2134maxx x z += s.t.（约束条件）⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x（决策变量） x 1,x 2手工计算的方法注：Lingo 中“<”代表“<=”，“>”代表“>=”，Lingo 中默认的变量都是大于等于0的，不用显式给出。

求解结果：z=26，x1=2，x2=62、整数规划求解219040Max x x z += ⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x xLingo 程序求解3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x12344、非线性规划求解||4||3||2||min 4321x x x x z +−−=s.t. ⎪⎪⎩⎪⎪⎨⎧−=+−−=−+−=+−−2132130432143214321x x x x x x x x x x x x12345、背包问题一个旅行者的背包最多只能装 6kg 物品，现有4 件物品的重量和价值分别为 2 kg ，3 kg ，3 kg ，4 kg ；1 元，1.2元，0.9元，1.1元。

问应怎样携带那些物品使得携带物品的价值最大?建模：记j x 为旅行者携带第j 件物品的件数, 取值只能为 0 或 1。

求目标函数43211.19.02.1x x x x f +++=在约束条件643324321≤+++x x x x 下的最大值.用Lingo 软件求解0-1规划计算结果6、指派问题有四个工人，要指派他们分别完成4项工作，每人做各项工作所消耗的时间如下表： 问指派哪个人去完成哪项工作，可使总的消耗时间为最小？ 设：第i 个工人做第j 项工作用时ij t ，标志变量ij f 定义如下：变量名 取值⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==×4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作（1） 集合定义部分（从“SETS ：”到“ENDSET ”）：定义集合及其属性，语句“work/A,B,C,D/”其结果正是定义了4个集合元素，没有定义变量名。

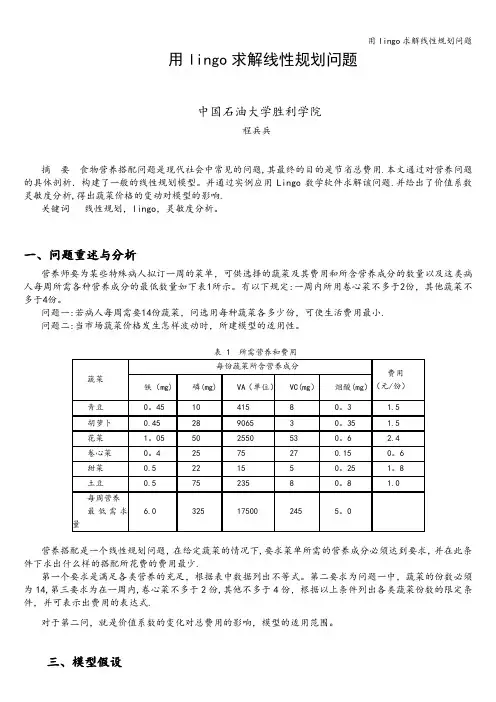
用lingo求解线性规划问题中国石油大学胜利学院程兵兵摘要食物营养搭配问题是现代社会中常见的问题,其最终的目的是节省总费用.本文通过对营养问题的具体剖析．构建了一般的线性规划模型。

并通过实例应用Lingo数学软件求解该问题.并给出了价值系数灵敏度分析,得出蔬菜价格的变动对模型的影响.关键词线性规划，lingo，灵敏度分析。

一、问题重述与分析营养师要为某些特殊病人拟订一周的菜单，可供选择的蔬菜及其费用和所含营养成分的数量以及这类病人每周所需各种营养成分的最低数量如下表1所示。

有以下规定:一周内所用卷心菜不多于2份，其他蔬菜不多于4份。

问题一:若病人每周需要14份蔬菜，问选用每种蔬菜各多少份，可使生活费用最小.问题二:当市场蔬菜价格发生怎样波动时，所建模型的适用性。

表 1 所需营养和费用营养搭配是一个线性规划问题，在给定蔬菜的情况下,要求菜单所需的营养成分必须达到要求，并在此条件下求出什么样的搭配所花费的费用最少.第一个要求是满足各类营养的充足，根据表中数据列出不等式。

第二要求为问题一中，蔬菜的份数必须为14,第三要求为在一周内,卷心菜不多于2份,其他不多于4份，根据以上条件列出各类蔬菜份数的限定条件，并可表示出费用的表达式.对于第二问，就是价值系数的变化对总费用的影响，模型的适用范围。

三、模型假设第一,假设各蔬菜营养成分保持稳定，满足题干要求。

第二,假设各蔬菜价格在一定时间内保持相对稳定。

第三，假设各类蔬菜供应全部到位，满足所需要求量. 第四,假设所求出最优解时不要求一定为整数。

四、符号约定（1)Z 代表目标函数,此题即为费用。

(2）i c 为价值系数，此题即为每份蔬菜的价格。

下标i 代表蔬菜的种类。

(3）i x 为决策变量，表示各种蔬菜的数量。

(4）i b 为最低限定条件,表示蔬菜最低营养需要。

五、模型建立根据以上各种假设和符号约定，建立模型如下。

所求的值就是min,也就是最优化结果.s 。

汽车公司的生产计划与决策摘要当今社会发展迅速，社会的需求也在增加，特别是代步的轿车的需求更是供不应求。

针对问题一：为计算每一种车型的生产成本和预计销售利润，建立成本函数：0i j k C c e d w =+++ 和预计销售利润函数：().*R P C Q =-，根据函数，利用Matlab 程序将算出结果。

针对问题二：首先针对如何计算最大利润的问题建立模型一：最大预计销售利润模型181max R=i i i x r =∑，利用lingo 软件求解出结果为只生产NH16和HA16两种车型；然后运用winQSB 的LP ILP -对模型一进行检验，得出结果为只生产NA18和NH16两种车型，为了计算出题中车型在哪一生产线生产接着建立模型二：0-1规划模型，以求得每条生产线具体生产哪种车型，最后为了计算出该问题的多种最优解我们再次运用Lingo 进行编程计算出生产了NA18、NH16和HA16三种车型并计算出了三种车型分别在哪一生产线上生产。

针对问题三：首先根据dynasearch 算法，建立模型三：最优解模型，得出最优解为只生产HA20；然后为计算出生产HA20具体的量，根据Lingo 中的01-整数规划思想，建立模型四：最优解模型，得出生产HA20300辆且最大利润为930万元。

针对问题四：首先根据销售量的概率分布，利用matlab 编程计算出每种车型预期需求的期望，建立模型五：最大期望获利模型，然后利用Lingo 软件算出最优解为只生产HA20型号车且最大利润为905.2万元。

由于概率是一个预测值，通过matlab 随机产生概率值进行运算得出：最优解在18EH 的销售量小等于293时最优解发生改变，因此此生产方案不具有稳定性。

针对问题五：运用与问题四相同的方法计算得出生产16NH 和16HA 两种车型，同样由于概率是一个预测值，通过matlab 随机产生概率进行运算得出最优解和最优值的大小相同，因此此生产方案具有稳定性。

附1：用LINGO求解线性规划的例子一奶制品加工厂用牛奶生产A1、A2附1:用LINGO求解线性规划的例子一奶制品加工厂用牛奶生产A、A两种奶制品，1桶牛奶可以在设备甲上用12小时加工成3公斤A，121或者在设备乙上用8小时加工成4公斤A。

根据市场需求，生产的A、A能全部售出，且每公斤A获利212124元，每公斤A获利16元。

现在加工厂每天能得到50桶牛奶的供应，每天正式工人总的劳动时间为4802 小时，并且设备甲每天至多能加工100公斤A，设备乙的加工能力没有限制。

试为该厂制定一个生产计划，1使每天获利最大，并进一步讨论以下3个附加问题:1)若用35元可以购买到1桶牛奶，应否作这项投资,若投资，每天最多购买多少桶牛奶,2)若可以聘用临时工人以增加劳动时间，付给临时工人的工资最多是每小时几元,3)由于市场需求变化，每公斤A的获利增加到30元，应否改变生产计划, 1数学模型:设每天用x桶牛奶生产A1 ，用x桶牛奶生产A2 12目标函数:设每天获利为z元。

x桶牛奶可生产3x公斤A1，获利24*3x，x桶牛奶可生产4*x公11122斤A2，获利16*4x，故z=72x+64x212约束条件:原料供应:生产A、A的原料(牛奶)总量不超过每天的供应50桶，即 12x+x?50 12劳动时间:生产A、A的总加工时间不超过每天正式工人总的劳动时间480小时，即 1212x+8x?480 12设备能力:A的产量不得超过设备甲每天的加工能力100小时，即 13x?100 1非负约束:x、x均不能为负值，即x?0，x?0 2121综上所述可得max z=72x+64x 12s.t.x+x?50 1212x+8x?480 123x?100 1x?0，x?0 21显然，目标函数和约束条件都是线性的，这是一个线性规划(LP)，求出的最优解将给出使净利润最大的生产计划，要讨论的问题需要考虑参数的变化对最优解和影响，一般称为敏感性(或灵敏度)分析。

附1：用LINGO求解线性规划的例子一奶制品加工厂用牛奶生产A1、A2附1:用LINGO求解线性规划的例子一奶制品加工厂用牛奶生产A、A两种奶制品，1桶牛奶可以在设备甲上用12小时加工成3公斤A，121或者在设备乙上用8小时加工成4公斤A。

根据市场需求，生产的A、A能全部售出，且每公斤A获利212124元，每公斤A获利16元。

现在加工厂每天能得到50桶牛奶的供应，每天正式工人总的劳动时间为4802 小时，并且设备甲每天至多能加工100公斤A，设备乙的加工能力没有限制。

试为该厂制定一个生产计划，1使每天获利最大，并进一步讨论以下3个附加问题:1)若用35元可以购买到1桶牛奶，应否作这项投资,若投资，每天最多购买多少桶牛奶,2)若可以聘用临时工人以增加劳动时间，付给临时工人的工资最多是每小时几元,3)由于市场需求变化，每公斤A的获利增加到30元，应否改变生产计划, 1数学模型:设每天用x桶牛奶生产A1 ，用x桶牛奶生产A2 12目标函数:设每天获利为z元。

x桶牛奶可生产3x公斤A1，获利24*3x，x桶牛奶可生产4*x公11122斤A2，获利16*4x，故z=72x+64x212约束条件:原料供应:生产A、A的原料(牛奶)总量不超过每天的供应50桶，即 12x+x?50 12劳动时间:生产A、A的总加工时间不超过每天正式工人总的劳动时间480小时，即 1212x+8x?480 12设备能力:A的产量不得超过设备甲每天的加工能力100小时，即 13x?100 1非负约束:x、x均不能为负值，即x?0，x?0 2121综上所述可得max z=72x+64x 12s.t.x+x?50 1212x+8x?480 123x?100 1x?0，x?0 21显然，目标函数和约束条件都是线性的，这是一个线性规划(LP)，求出的最优解将给出使净利润最大的生产计划，要讨论的问题需要考虑参数的变化对最优解和影响，一般称为敏感性(或灵敏度)分析。

LINGO是一个用于求解线性规划问题的优化软件。

以下是一个简单的LINGO例题：
问题描述：
某公司生产A、B两种产品，生产A产品需要10个单位劳动力和2个单位资本，生产B产品需要15个单位劳动力和3个单位资本。

该公司拥有劳动力200个单位和资本150个单位。

A产品的售价为20元，B产品的售价为30元。

目标：最大化总收入。

约束条件：
1.劳动力不超过200个单位。

2.资本不超过150个单位。

3.A产品的产量为整数。

4.B产品的产量为整数。

使用LINGO求解该问题，可以建立以下模型：
目标函数：最大化总收入
@max=20x+30y; // 总收入等于A产品售价乘以A产品产量加上B产品售价乘以B产品产量
约束条件：
@bin(x); // A产品产量为整数
@bin(y); // B产品产量为整数
10x+15y<=200; // 劳动力不超过200个单位
2x+3y<=150; // 资本不超过150个单位
x>=0; // A产品产量非负
y>=0; // B产品产量非负
在LINGO中输入以上模型，即可求解该问题。

基础题：1．目标规划问题最近，某节能灯具厂接到了订购16000套A 型和B 型节能灯具的订货合同，合同中没有对这两种灯具的各自数量做要求，但合同要求工厂在一周内完成生产任务并交货。

根据该厂的生产能力，一周内可以利用的生产时间为20000min ，可利用的包装时间为36000min 。

生产完成和包装一套A 型节能灯具各需要2min ；生产完成和包装完成一套B 型节能灯具各需要1min 和3min 。

每套A 型节能灯成本为7元，销售价为15元，即利润为8元；每套B 型节能灯成本为14元，销售价为20元，即利润为6元。

厂长首先要求必须按合同完成订货任务，并且即不要有足量，也不要有超量。

其次要求满意销售额达到或者尽量接近275000元。

最后要求在生产总时间和包装总时间上可以有所增加，但过量尽量地小。

同时注意到增加生产时间要比包装时间困难得多。

试为该节能灯具厂制定生产计划。

解：将题中数据列表如下：根据问题的实际情况，首先分析确定问题的目标级优先级。

第一优先级目标：恰好完成生产和包装完成节能灯具16000套，赋予优先因子p1；第二优先级目标：完成或者尽量接近销售额为275000元，赋予优先因子p2； 第三优先级目标：生产和包装时间的增加量尽量地小，赋予优先因子p3； 然后建立相应的目标约束。

在此，假设决策变量12,x x 分别表示A 型，B 型节能灯具的数量。

（1） 关于生产数量的目标约束。

用1d -和1d +分别表示未达到和超额完成订货指标16000套的偏差量，因此目标约束为1111211min ,..16000z d d s t x x d d -+-+=+++-=要求恰好达到目标值，即正、负偏差变量都要尽可能地小（2） 关于销售额的目标约束。

用2d -和2d +分别表示未达到和超额完成满意销售指标275000元的偏差值。

因此目标约束为221222min ,..1520-275000.z d s t x x d d --+=++=要求超过目标值，即超过量不限，但必须是负偏差变量要尽可能地小，(另外：d +要求不超过目标值，即允许达不到目标值，就是正偏差变量要尽可能地小) （3） 关于生产和包装时间的目标约束。

实验用LINDO或LINGO求解线性规划问题实验目的1.对于给定的实际应用问题，正确的建立线性规划问题数学模型，并用LINDO或LINGO 求解；2.掌握灵敏度分析以及资源的影子价格的相关分析方法.问题1某工厂在计划期内要安排生产A、B两种产品，已知生产单位产品所需设备台时及对甲、乙两种原材料的消耗，有关数据如表1.1.问：应如何安排生产计划，使工厂获利最大？.LINDO输入语句：max 2x1+3x2stx1+2x2<=84x1<=164x2<=12end在LINGO的MODEL窗口内输入如下模型：model:max=2*x1+3*x2;x1+2*x2<=8;4*x1<=16;4*x2<=12;end选菜单Lingo|Solve(或按Ctrl+S),或用鼠标点击“求解”按纽，如果模型有语法错误，则弹出一个标题为“LINGO Error Message”(错误信息)的窗口，指出在哪一行有怎样的错误，每一种错误都有一个编号（具体含义可查阅相关文献或LINGO的Help）.改正错误以后再求解，如果语法通过，LINGO用内部所带的求解程序求出模型的解，然后弹出一个标题为“LINGO Solver Status”（求解状态）的窗口，其内容为变量个数、约束条件个数、优化状态、耗费内存、所花时间等信息，点击Close关闭窗口，屏幕上出现标题为“Solution Report”（解的报告）的信息窗口，显示优化计算（线性规划中换基迭代）的步数、优化后的目标函数值、列出各变量的计算结果.求解结果：Global optimal solution found at iteration: 5 Objective value: 14.00000Variable Value Reduced Cost X1 4.000000 0.000000 X2 2.000000 0.000000 Row Slack or Surplus Dual Price 1 14.00000 1.000000 2 0.000000 1.500000 3 0.000000 0.1250000 4 4.000000 0.000000该报告说明：运行5步找到全局最优解，目标函数值为14，变量值分别为124,2==x x .“Reduced Cost ”的含义是需缩减成本系数或需增加利润系数（最优解中取值非零的决策变量的Reduced Cost 值等于零）.“Row ”是输入模型中的行号，目标函数是第一行；“Slack or Surplus ”的意思是松弛或剩余，即约束条件左边与右边的差值，对于“≤”的不等式，右边减左边的差值为Slack （松弛），对于“≥”的不等式，左边减的右边差值为Surplus （剩余），当约束条件两边相等时，松弛或剩余的值等于零.“Dual Price ”的意思是对偶价格（或称为影子价格），上述报告中Row2的松弛值为0，表明生产甲产品4单位、乙产品2单位，所需设备8台时已经饱和，对偶价格1.5的含义是：如果设备增加1台时，能使目标函数值增加1.5.报告中Row4的松弛值为4，表明生产甲产品4单位、乙产品2单位，所需原材料乙8公斤还剩余4公斤，因此增加原材料乙不会使目标函数值增加，所以对偶价格为0.对于目标函数系数和约束条件右端常数项的灵敏度分析，可以通过LINGO 软件求解的灵敏度分析给出.如果要看灵敏度分析结果，必须激活灵敏度计算功能才会在求解时给出灵敏度分析结果，默认情况下这项功能是关闭的.想要激活它，必须运行LINGO|Options …命令，选择Gengral Solver ，在Dual Computation 列表框中，选择Prices and Ranges 选项并确定. 法一：打开command window ，输入range ；法二：LINGO ——options ——General Solver ——DualComputations ——Prices&Ranges ， 运行一遍，然后关掉，然后lingo-----range问题2 某公司饲养实验用的动物以供出售，已知这些动物的生长对饲料中3种营养成分（蛋白质、矿物质和维生素）特别敏感，每个动物每周至少需要蛋白质60g ，矿物质3g ，维生素8mg ，该公司能买到5种不同的饲料，每种饲料1kg 所含各种营养成分和成本如表1.2所示，如果每个小动物每周食用饲料不超过52kg ，求既能满足动物生长需要，又使总成本最低的饲料配方.问题3 设有四个化肥厂供应四个地区的农用化肥，假定等量的化肥在这些地区使用效果相同.已知各化肥厂年产量（单位：吨）、各地区年需要量以及从各化肥厂到各地区单位化肥的运价如表3.2.1所示（表中运价中“—”表示不适合）.试决定总的运费最节省的化肥调运方案.表3.2.1 化肥供应的平衡表与运价表问题4 某公司计划在东、西、南、北四个市区建立销售门市部，拟议中有10个位置(1,2,,10)j A j =可供选择，考虑到各地区居民的消费水平及居民居住密集度，在东区由123,,A A A 三个点至多选择两个；在西区由45,A A 两个点中至少选一个；在南区由67,A A 两个点中至少选一个；在北区由8910,,A A A 三个点中至少选两个.j A 各点的设备投资及每年可获利润情况见表3.2.2所示 (单位：万元).但投资总额不能超过72万元，问应选择哪几个销售点，可使年利润为最大?建立整数规划问题的数学模型，并用LINGO 求解.表3.2.2 四个市区的10个位置设备投资及每年利润表问题5 求解整数线性规划问题 12121212max 2535..436,0,379z x x x x s t x x x x =≤≤≥++⎧⎪+⎨⎪⎩全部为整数 思考题1.（1988年美国大学生数学建模竞赛试题）有七种规格的包装箱要装到两辆铁路平板车上去.包装箱的宽和高是一样的，但厚度（t,以厘米计）及重量（w ，以公斤计）是不同的.表3.2.4给出了每种包装箱的厚度、重量以及数量.每辆平板车有10.2米长的地方可用来装包装箱（像面包片那样），载重为40吨.由于当地货运的限制，对567,,C C C 类的包装箱的总数有一个特别的限制：这类箱子在两辆平板车上所占的总空间（厚度）不能超过302.7厘米.试把包装箱（见表3.2.4）装到平板车上去使得浪费的空间最小.。