2020热点重点难点专题透析数学文科 题型1
- 格式:pptx
- 大小:1.55 MB
- 文档页数:45

重难点04 解析几何【命题趋势】解析几何一直是高考数学中的计算量代名词,在高考中所占的比例一直是2+1+1模式.即两道选择,一道填空,一道解答题.高考中选择部分,一道圆锥曲线相关的简单概念以及简单性质,另外一道是圆锥曲线的性质会与直线、圆等结合考查一道综合题目,一般难度诶中等.填空题目也是综合题目,难度中等.大题部分一般是以椭圆抛物线性质为主,加之直线与圆的相关性子相结合,常见题型为定值、定点、对应变量的取值范围问题、面积问题等.双曲线一般不出现在解答题中,一般出现在小题中.即复习解答题时也应是以椭圆、抛物线为主.本专题主要通过对高考中解析几何的知识点的统计,整理了高考中常见的解析几何的题型进行详细的分析与总结,通过本专题的学习,能够掌握高考中解析几何出题的脉略,从而能够对于高考中这一重难点有一个比较详细的认知,对于解析几何的题目的做法能够有一定的理解与应用.【满分技巧】定值问题:采用逆推方法,先计算出结果.即一般会求直线过定点,或者是其他曲线过定点.对于此类题目一般采用特殊点求出两组直线,或者是曲线然后求出两组直线或者是曲线的交点即是所要求的的定点.算出结果以后,再去写出一般情况下的步骤.定值问题:一般也是采用利用结果写过程的形式.先求结果一般会也是采用满足条件的特殊点进行带入求值(最好是原点或是(1,0)此类的点).所得答案即是要求的定值.然后再利用答案,写出一般情况下的过程即可.注:过程中比较复杂的解答过程可以不求,因为已经知道答案,直接往答案上凑即可.关于取值范围问题:一般也是采用利用结果写过程的形式.对于答案的求解,一般利用边界点进行求解,答案即是在边界点范围内.知道答案以后再写出一般情况下的步骤比较好写.一般情况下的步骤对于复杂的计算可以不算.【考查题型】选择,填空,解答题【限时检测】(建议用时:45分钟)一、单选题1.(2020·四川高三期末(文))已知双曲线()222210,0x y a b a b-=>>,点(4,1)在双曲线上,则该双曲线的方程为A .2214x y -= B .221205x y -= C .221123y x -= D .2218x y -= 2.(2019·天津南开中学高考模拟(文))过抛物线24y x =焦点F 的直线与双曲线221(0)y x m m -=>的一条渐近线平行,并交抛物线于,A B 两点,若|||AF BF >且||3AF =,则m 的值为( )A .8B .CD .43.(2020·宁夏高三月考(文))已知直线(2)(0)y k x k =+>与抛物线2:8C y x =相交于A 、B 两点,F 为C 的焦点,若2FA FB =,则k=( )A .13B .3C .23D .34.(2019·山东高考模拟(文))已知抛物线2:4C y x =的焦点F 和准线l ,过点F 的直线交l 于点A ,与抛物线的一个交点为B ,且3FA FB =-u u u v u u u v ,则||AB =( )A .23B .43C .323D .1635 (2019·天津实验中学高考模拟(文))(10)设O 为坐标原点,1F ,2F 是双曲线2222x y 1a b -=(a >0,b >0)的焦点,若在双曲线上存在点P ,满足∠1F P 2F =60°,,则该双曲线的渐近线方程为( )A .BC .=0D ±y=0二、填空题 6.(2020·福建省龙岩第一中学高三期中(文))过双曲线22221(0,0)x y a b a b-=>>的右焦点且垂直于x 轴的直线与双曲线交于,A B 两点,D 为虚轴的一个端点,且ABD ∆为钝角三角形,则此双曲线离心率的取值范围为__________.7.(2019·辽宁高三开学考试(文))已知双曲线C :22221(0,0)x y a b a b-=>>,过双曲线C 的右焦点F 作C 的渐近线的垂线,垂足为M ,延长FM 与y 轴交于点P ,且4FM PM =,则双曲线C 的离心率为__________.三、解答题8.(2020·广东高三期末(文))已知动圆C 过定点()F 1,0,且与定直线x 1=-相切. (1)求动圆圆心C 的轨迹E 的方程;(2)过点()M 2,0-的任一条直线l 与轨迹E 交于不同的两点P,Q ,试探究在x 轴上是否存在定点N (异于点M ),使得QNM PNM π∠∠+=?若存在,求点N 的坐标;若不存在,说明理由.9.(2019·四川高考模拟(文))抛物线C :()220x py p =>的焦点为F ,抛物线过点(),1P p . (∠)求抛物线C 的标准方程与其准线l 的方程;(∠)过F 点作直线与抛物线C 交于A ,B 两点,过A ,B 分别作抛物线的切线,证明两条切线的交点在抛物线C 的准线l 上.10.(2019·广东高考模拟(文))过点()2,0M 的直线l 与抛物线()2:20C y px p =>交于A ,B 两点,O 为坐标原点,OA OB ⊥.(1)求p 的值;(2)若l 与坐标轴不平行,且A 关于x 轴的对称点为D ,求证:直线BD 恒过定点.11.(2020·四川高三期末(文))已知椭圆22122:1(0)x y C a b a b+=>>的左、右焦点分别为1F 、2F ,椭圆的离心率为12,过椭圆1C 的左焦点1F ,且斜率为1的直线l ,与以右焦点2F 2C 相切.(1)求椭圆1C 的标准方程;(2)线段MN 是椭圆1C 过右焦点2F 的弦,且22MF F N λ=u u u u r u u u u r ,求1MF N ∆的面积的最大值以及取最大值时实数λ的值.12.(2019·贵州高考模拟(文))已知椭圆C :22221(0)x y a b a b+=>>的右焦点为F ,上顶点为M ,直线FM 的斜率为FM . (1)求椭圆C 的标准方程;(2)若不经过点F 的直线l :(0,0)y kx m k m =+与椭圆C 交于,A B 两点,且与圆221x y +=相切.试探究ABF ∆的周长是否为定值,若是,求出定值;若不是,请说明理由.13.(2019·河南高考模拟(文))已知O 为坐标原点,过点()1,0M 的直线l 与抛物线C :22(0)y px p =>交于A ,B 两点,且3OA OB u u u r u u u r ⋅=-. (1)求抛物线C 的方程;(2)过点M 作直线'l l ⊥交抛物线C 于P ,Q 两点,记OAB ∆,OPQ ∆的面积分别为1S ,2S ,证明:221211S S +为定值.以下内容为“高中数学该怎么有效学习?”首先要做到以下两点:1、先把教材上的知识点、理论看明白。

冲刺高考文科数学必看题型归纳2020冲刺高考文科数学必看题型归纳一高考文科数学必考题型:三角函数/数列一般全国卷第17题会考三角函数或数列题。
数列是最简单的题目,或许你觉得它难,但它能放在第一道大题的位置,就说明你不应该丢分。
数列题可以多总结一些类型题,分析归类,找到其中规律,题做多了,自然就有思路了。
高考文科数学必考题型:概率一般全国卷第18题会考概率题。
概率题相对比较简单,也是必须得分的题,这道题主要频数分布表、频率分布直方图、回归方程的求法、概率计算、相关系数的计算等等。
主要还是对作图和识图能力考查比较多。
高考文科数学必考题型:立体几何一般全国卷第19题会考立体几何题。
例题几何也不难,但大家一定要敢于尝试,敢于动笔写,不要说没有做题思路就放弃这道题。
只要你按照常规的方法做就可以,然后一步步分析下去,边分析边写步骤,结果自然就出来了。
如果没思路可以尝试2种以上的方法做。
高考文科数学必考题型:解析几何一般全国卷第20题会考解析几何题。
解析几何也不是难题,只要大家平时努力,这些题目都算是相对简单的。
所以大家不要有畏难情绪,认为这是最后2道大题就觉得有多难,其实如果你认认真真去做了,这道题还是有希望做对的。
退一步来说,即便是真的不会了,那也可以得一些步骤分,前一两问还是没问题的。
高考文科数学必考题型:函数一般全国卷第21题会考函数题。
高考对三角函数知识主要考查三角函数及解三角形两部分知识。
主要知识点有三角函数概念。
恒等变形、同角关系等。
三角函数还可以和向量知识结合在一起考,也可以和正弦定理、余弦定理结合起来一起考查。
高考文科数学必考题型:圆/坐标系与参数方程/不等式一般全国卷第22至24题会考圆/坐标系与参数方程/不等式三道选做题。
参数方程是大家选做最多的一道题,参数方程主要考查轨迹方程计算方法、三角换元求最值、极坐标方程和直角坐标方程转化等,这道题相对容易做。
冲刺高考文科数学必看题型归纳二一、三角函数或数列数列是高中数学的重要内容,又是学习高等数学的基础。

高三文科数学2020重要知识点归纳已经进入高二上学期的同学们,在我们顺利度过高中的适应期,积极参与学校社团活动,逐步形成了自我学习模式,初步拟定人生规划后,要将自我的精力集中到学习上,应将自己的学业做到一个高度的时候了。
接下来是小编为大家整理的高三文科数学2020重要知识点归纳,希望大家喜欢!高三文科数学2020重要知识点归纳一第一:高考数学中有函数、数列、三角函数、平面向量、不等式、立体几何等九大章节。
主要是考函数和导数,这是我们整个高中阶段里最核心的板块,在这个板块里,重点考察两个方面:第一个函数的性质,包括函数的单调性、奇偶性;第二是函数的解答题,重点考察的是二次函数和高次函数,分函数和它的一些分布问题,但是这个分布重点还包含两个分析就是二次方程的分布的问题,这是第一个板块。
第二:平面向量和三角函数。
重点考察三个方面:一个是划减与求值,第一,重点掌握公式,重点掌握五组基本公式。
第二,是三角函数的图像和性质,这里重点掌握正弦函数和余弦函数的性质,第三,正弦定理和余弦定理来解三角形。
难度比较小。
第三:数列。
数列这个板块,重点考两个方面:一个通项;一个是求和。
第四:空间向量和立体几何。
在里面重点考察两个方面:一个是证明;一个是计算。
第五:概率和统计。
这一板块主要是属于数学应用问题的范畴,当然应该掌握下面几个方面,第一……等可能的概率,第二………事件,第三是独立事件,还有独立重复事件发生的概率。
第六:解析几何。
这是我们比较头疼的问题,是整个试卷里难度比较大,计算量的题,当然这一类题,我总结下面五类常考的题型,包括第一类所讲的直线和曲线的位置关系,这是考试最多的内容。
考生应该掌握它的通法,第二类我们所讲的动点问题,第三类是弦长问题,第四类是对称问题,这也是2008年高考已经考过的一点,第五类重点问题,这类题时往往觉得有思路,但是没有答案,当然这里我相等的是,这道题尽管计算量很大,但是造成计算量大的原因,往往有这个原因,我们所选方法不是很恰当,因此,在这一章里我们要掌握比较好的算法,来提高我们做题的准确度,这是我们所讲的第六大板块。

2020年高考数学文科考点解读和命题热点突破专题01 集合与常用逻辑用语【考向解读】集合与常用逻辑用语在高考中是以选择题或填空题的形式进行考查的,属于容易题.但命题真假的判断,这一点综合性较强,联系到更多的知识点,属于中挡题.预测2020年高考会以集合的运算和充要条件作为考查的重点.【命题热点突破一】集合的关系及运算集合是高考每年必考内容,题型基本都是选择题、填空题,题目难度大多数为最低档,有时候在填空题中以创新题型出现,难度稍高.在复习中,本部分应该重点掌握集合的表示、集合的性质、集合的运算及集合关系在常用逻辑用语、函数、不等式、三角函数、解析几何等方面的应用.同时注意研究有关集合的创新问题,研究问题的切入点及集合知识在相关问题中所起的作用.1.集合的运算性质及重要结论(1)A ∪A =A ,A ∪∅=A ,A ∪B =B ∪A .(2)A ∩A =A ,A ∩∅=∅,A ∩B =B ∩A .(3)A ∩(∁U A )=∅,A ∪(∁U A )=U .(4)A ∩B =A ⇔A ⊆B ,A ∪B =A ⇔B ⊆A .2.集合运算中的常用方法(1)若已知的集合是不等式的解集,用数轴求解;(2)若已知的集合是点集,用数形结合法求解;(3)若已知的集合是抽象集合,用Venn 图求解.例1、设集合{}{}|(2)(3)0,|0S x x x T x x =--≥=> ,则S T =I ( )(A) [2,3] (B)(-∞ ,2]U [3,+∞) (C) [3,+∞) (D)(0,2]U [3,+∞)【答案】D【解析】由(2)(3)0x x --≥解得3x ≥或2x ≤,所以{|23}S x x x =≤≥或,所以{|023}S T x x x =<≤≥I 或,故选D .【变式探究】(1)已知集合A ={x |x 2-4x +3<0},B ={x |2<x <4},则A ∩B 等于( )A .(1,3)B .(1,4)C .(2,3)D .(2,4)【答案】C(2)设U 为全集,A ,B 是集合,则“存在集合C 使得A ⊆C ,B ⊆∁U C ”是“A ∩B =∅”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】C【命题热点突破二】四种命题与充要条件逻辑用语是高考常考内容,充分、必要条件是重点考查内容,题型基本都是选择题、填空题,题目难度以低、中档为主.在复习中,本部分应该重点掌握四种命题的真假判断、否命题与命题的否定的区别、含有量词的命题的否定的求法、充分必要条件的判定与应用.这些知识被考查的概率都较高,特别是充分、必要条件几乎每年都有考查.1.四种命题中原命题与逆否命题同真同假,逆命题与否命题同真同假.2.若p ⇒q ,则p 是q 的充分条件,q 是p 的必要条件;若p ⇔q ,则p ,q 互为充要条件.例2、设{a n }是首项为正数的等比数列,公比为q ,则“q <0”是“对任意的正整数n ,a 2n −1+a 2n <0”的( )(A )充要条件 (B )充分而不必要条件(C )必要而不充分条件 (D )既不充分也不必要条件【答案】C【解析】由题意得,22212(1)21210()0(1)0(,1)n n n n n a a a q q q q q ----+<⇔+<⇔+<⇔∈-∞-,故是必要不充分条件,故选C.【变式探究】(1)设α,β是两个不同的平面,m 是直线且m ⊂α.则“m ∥β”是“α∥β”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】 B(2)给出下列命题:①若A ,B ,C ,D 是不共线的四点,则AB →=DC →是四边形ABCD 为平行四边形的充要条件;②a =b 的充要条件是|a |=|b |且a ∥b ;③在△ABC 中,sin A >sin B 的充要条件为A >B ;④在△ABC 中,设命题p :△ABC 是等边三角形,命题q :a ∶b ∶c =sin B ∶sin C ∶sin A ,那么命题p 是命题q 的充分不必要条件.其中正确的命题为________.(把你认为正确的命题序号都填上)【答案】①③【命题热点突破三】 逻辑联结词、量词1.命题p ∨q ,只要p ,q 有一真,即为真;命题p ∧q ,只有p ,q 均为真,才为真;綈p 和p 为真假对立的命题.2.命题p ∨q 的否定是(綈p )∧(綈q );命题p ∧q 的否定是(綈p )∨(綈q ).3.“∀x ∈M ,p (x )”的否定为“∃x 0∈M ,綈p (x 0)”;“∃x 0∈M ,p (x 0)”的否定为“∀x ∈M ,綈p (x )”. 例3、命题“*x n ∀∈∃∈,R N ,使得2n x >”的否定形式是( )A .*x n ∀∈∃∈,R N ,使得2n x <B .*x n ∀∈∀∈,R N ,使得2n x <C .*x n ∃∈∃∈,R N ,使得2n x <D .*x n ∃∈∀∈,R N ,使得2n x <【答案】D【解析】∀的否定是∃,∃的否定是∀,2n x ≥的否定是2n x <.故选D .【变式探究】(1)已知m ,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )A .若α,β垂直于同一平面,则α与β平行B .若m ,n 平行于同一平面,则m 与n 平行C .若α,β不平行,则在α内不存在与β平行的直线D .若m ,n 不平行,则m 与n 不可能垂直于同一平面(2)已知命题p :若x >y ,则-x <-y ;命题q :若x >y ,则x 2>y 2.在命题①p ∧q ;②p ∨q ;③p ∧(綈q );④(綈p )∨q 中,真命题是( )A .①③B .①④C .②③D .②④【答案】(1)D (2)C【高考题型解读】1.设集合{}2430A x x x =-+< ,{}230x x ->,则A B =I ( )(A )33,2⎛⎫-- ⎪⎝⎭ (B )33,2⎛⎫- ⎪⎝⎭ (C )31,2⎛⎫ ⎪⎝⎭(D )3,32⎛⎫ ⎪⎝⎭【答案】D 【解析】因为23{|430}={|13},={|},2A x x x x xB x x =+<<<>-所以33={|13}{|}={|3},22A B x x x x x x <<><<I I 故选D. 2.设集合{}{}|(2)(3)0,|0S x x x T x x =--≥=> ,则S T =I ( )(A) [2,3] (B)(-∞ ,2]U [3,+∞) (C) [3,+ ∞) (D)(0,2]U [3,+∞)【答案】D【解析】由(2)(3)0x x --≥解得3x ≥或2x ≤,所以{|23}S x x x =≤≥或,所以{|023}S T x x x =<≤≥I 或,故选D .3.设集合{|22}A x x =-≤≤,Z 为整数集,则A I Z 中元素的个数是( )(A )3 (B )4 (C )5 (D )6【答案】C【解析】由题意,{2,1,0,1,2}A Z =--I ,故其中的元素个数为5,选C.4.设集合2{|2,},{|10},x A y y x B x x ==∈=-<R 则A B U =( )(A )(1,1)-(B )(0,1) (C )(1,)-+∞ (D )(0,)+∞ 【答案】C【解析】}0|{>=y y A ,}11|{<<-=x x B ,则A B =∞U (-1,+),选C. 5.已知集合{1,}A =2,3,{|(1)(2)0,}B x x x x =+-<∈Z ,则A B =U ( )(A ){1} (B ){12}, (C ){0123},,, (D ){10123}-,,,, 【答案】C6.已知集合{|||2}A x x =<,{1,0,1,2,3}B =-,则A B =I ( )A.{0,1}B.{0,1,2}C.{1,0,1}-D.{1,0,1,2}-【答案】C【解析】由}22|{<<-=x x A ,得}1,0,1{-=B A I ,故选C.7.已知集合{}{}213,4,P x x Q x x =∈≤≤=∈≥R R 则()P Q ⋃=R ð( )A .[2,3]B .( -2,3 ]C .[1,2)D .(,2][1,)-∞-⋃+∞【答案】B8. 命题“*x n ∀∈∃∈,R N ,使得2n x >”的否定形式是( )A .*x n ∀∈∃∈,R N ,使得2n x <B .*x n ∀∈∀∈,R N ,使得2n x <C .*x n ∃∈∃∈,R N ,使得2n x <D .*x n ∃∈∀∈,R N ,使得2n x <【答案】D【解析】∀的否定是∃,∃的否定是∀,2n x ≥的否定是2n x <.故选D .9.已知直线a ,b 分别在两个不同的平面α,β内.则“直线a 和直线b 相交”是“平面α和平面β相交”的( )(A )充分不必要条件(B )必要不充分条件 (C )充要条件(D )既不充分也不必要条件 【答案】A【解析】直线a 与直线b 相交,则,αβ一定相交,若,αβ相交,则a,b 可能相交,也可能平行,故选A.10.设{a n }是首项为正数的等比数列,公比为q ,则“q <0”是“对任意的正整数n ,a 2n −1+a 2n <0”的( )(A )充要条件 (B )充分而不必要条件(C )必要而不充分条件 (D )既不充分也不必要条件【答案】C11.已知集合{1,2,3,4},{|32},A B y y x x A ===-∈,则A B I =( )(A ){1}(B ){4} (C ){1,3} (D ){1,4}【答案】D【解析】{1,4,7,10},A B {1,4}.B ==I 选D.12.已知集合{1,2,3,6},{|23},A B x x =-=-<<则=A B I ________▲________.【答案】{}1,2-【解析】{1,2,3,6}{|23}{1,2}A B x x =--<<=-I I13.设R a ∈,则“1>a ”是“12>a ”的( )(A )充分非必要条件 (B )必要非充分条件(C )充要条件 (D )既非充分也非必要条件【答案】A【解析】2211,111a a a a a >⇒>>⇒><-或,所以是充分非必要条件,选A.14.设集合2{|2,},{|10},x A y y x B x x ==∈=-<R 则A B U = (A )(1,1)- (B )(0,1) (C )(1,)-+∞ (D )(0,)+∞【答案】C15.已知全集U ={1,2,3,4,5,6,7,8},集合A ={2,3,5,6},集合B ={1,3,4,6,7},则集合A ∩(∁U B )等于( )A .{2,5}B .{3,6}C .{2,5,6}D .{2,3,5,6,8}【答案】 A【解析】 由题意知,∁U B ={2,5,8},则A ∩(∁U B )={2,5},选A.16.“x <0”是“ln(x +1)<0”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】 B【解析】 ∵ln(x +1)<0,∴0<x +1<1,∴-1<x <0.∵x <0是-1<x <0的必要不充分条件,故选B.17.设集合M ={x |x 2=x },N ={x |lg x ≤0},则M ∪N 等于( )A .[0,1]B .(0,1]C .[0,1)D .(-∞,1]【答案】 A【解析】 由题意得M ={0,1},N =(0,1],故M ∪N =[0,1],故选A.18.设集合A={x||x-1|<2},B={y|y=2x,x∈[0,2]},则A∩B等于()A.[0,2] B.(1,3)C.[1,3) D.(1,4)【答案】 C【解析】由|x-1|<2,解得-1<x<3,由y=2x,x∈[0,2],解得1≤y≤4,∴A∩B=(-1,3)∩[1,4]=[1,3).19.已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A B ={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A B中元素的个数为()A.77B.49C.45D.30【答案】 C20.已知集合P={x|x2-2x≥0},Q={x|1<x≤2},则(∁R P)∩Q等于()A.[0,1) B.(0,2]C.(1,2) D.[1,2]【答案】 C【解析】∵P={x|x≥2或x≤0},∁R P={x|0<x<2},∴(∁R P)∩Q={x|1<x<2},故选C.21.设a1,a2,…,a n∈R,n≥3.若p:a1,a2,…,a n成等比数列;q:(a21+a22+…+a2n-1)·(a22+a23+…+a2n)=(a1a2+a2a3+…+a n-1a n)2,则()A.p是q的必要条件,但不是q的充分条件B.p是q的充分条件,但不是q的必要条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件【答案】 B【解析】若p成立,设a1,a2,…,a n的公比为q,则(a21+a22+…+a2n-1)(a22+a23+…+a2n)=a21(1+q2+…+q2n-4)·a22(1+q2+…+q2n-4)=a21a22(1+q2+…+q2n-4)2,(a1a2+a2a3+…+a n-1a n)2=(a1a2)2(1+q2+…+q2n-4)2,故q成立,故p是q的充分条件.取a1=a2=…=a n=0,则q成立,而p不成立,故p不是q的必要条件,故选B.22.设命题p:∃n∈N,n2>2n,则綈p为()A.∀n∈N,n2>2n B.∃n∈N,n2≤2nC.∀n∈N,n2≤2n D.∃n∈N,n2=2n【答案】 C【解析】 将命题p 的量词“∃”改为“∀”,“n 2>2n ”改为“n 2≤2n ”.23函数f (x )在x =x 0处导数存在.若p :f ′(x 0)=0;q :x =x 0是f (x )的极值点,则( )A .p 是q 是充分必要条件B .p 是q 的充分条件,但不是q 的必要条件C .p 是q 的必要条件,但不是q 的充分条件D .p 既不是q 的充分条件,也不是q 的必要条件【答案】 C24.原命题为“若a n +a n +12<a n ,n ∈N *,则{a n }为递减数列”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )A .真,真,真B .假,假,真C .真,真,假D .假,假,假【答案】 A【解析】 a n +a n +12<a n ⇔a n +1<a n ⇔{a n }为递减数列. 原命题与其逆命题都是真命题,所以其否命题和逆否命题也都是真命题,故选A.25.若m ∈R, 命题“若m >0,则方程x 2+x -m =0有实根”的逆否命题是( )A .若方程x 2+x -m =0有实根,则m >0B .若方程x 2+x -m =0有实根,则m ≤0C .若方程x 2+x -m =0没有实根,则m >0D .若方程x 2+x -m =0没有实根,则m ≤0【答案】 D。

2020年普通高等学校招生全国统一考试(新课标卷I)文科数学试题解析一、选择题,本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x|x2-3x-4≤0},B={-4,1,3,5},且A∩B=( )A.{-4,1} B.{1,5} C.{3,5} D.{1,3}解析:A={x|-1≤x≤4},∴A∩B={1,3},故选D2.若z=1+2i+i3,则|z|=( )A.0 B.1 C2D.2解析:z=1+i,∴|z2 C3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.514B.512C.514D.512解析:设四棱锥的高为h,底面边长为2a,侧面三角形的高为m,依题h2=am,且h2+a2=m2,联立消去h得m2-am -a2=0,152 hm±∴=,舍去负号,故选C. 4.设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )A.15B.25C.12D.45解析:任取三点有:O-A-B,C,D,O-B-C,D,O-C-D,A-B-C,D,A-C-D,B-C-D,共有10种。
其中3点共线的有2种,故选A.5.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:°C)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(x i. y i)(i=1,2,···,20)得到散点图:由此散点图,在10°C 至40°C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是( )A .y=a+bxB .y=a+bx 2C .y=a+be xD .y=a+b ln x解析:根据散点图可排除A .B .C .故选D.6.已知圆x 2+y 2-6x =0,过点(1,2)的直线被该圆所截得的弦的长度的最小值为( ) A .1 B .2 C .3D .4解析:依题圆心为C (3,0),半径r =3,过点A (1,2)的最短弦是垂直AC 的弦. 又AC 2,由勾股关系可得最短弦长=2,故选B. 7.设函数f (x )=cos(ωx +6π)在[-π,π]的图像大致如下图, 则f (x )的最小正周期为( ) A .109πB .76π C .43π D .32π 解析:依图49π-是(-π,0)的一个零点。

重难点01 数列【高考考试趋势】高考中考查数列难度不大,知识点考查比较简单,也是高考中务必拿分题目,对于大部分人来说,数列这一知识点是不容失分的.本重点专题是通过对高考中常见高考题型对应知识点的研究而总结出来的一些题目,通过本专题的学习补充巩固,让你对高考中数列题目更加熟练,做高考数列题目更加得心应手.【高考常见题型分类总结】通项公式的求法q pa a n n +=1-的形式,主要是利用)()(1-m a p m a n n +=+的形式进行转化对于 11-++=n n p pa a n ,主要采用m p a p a n n n n =1-1--的形式进行转化运算 对于11n-n n-n a =pa -a a 一般采用转化成=p a -a n-n 111的形式进行转化运算. 对于求和问题 裂项求和形如)12)(1-2(1+=n n a n 的形式一般采用裂项)121-1-21(21+=n n a n 的形式,注意前面的21此系数,是由系数只差确定与1212+n n-. 错位相减求和问题,本专题题目中有出现.分组求和问题,分为两种,一种是绝对值分组求和问题,另外一种是两种不同数列的分组求和问题.【常见题型限时检测】(建议用时:35分钟)一、单选题1.(2019·全国高考模拟(文))在等差数列{}n a 中,157913100a a a a a ++++=,6212a a -=,则1a =( )A .1B .2C .3D .42.(2019·广东佛山实验中学高三月考(理))已知{}n a 是公差为1的等差数列,n S 为{}n a的前n 项和,若844S S =,则4a =( )A .52B .3C .72D .43.(2019·河南高三月考(文))设{}n a 是首项为1a ,公差为-1的等差数列,n S 为其前n 项和,若124,,S S S 成等比数列,则1a =( )A .2B .-2C .12D .12- 4.(2018·河南高考模拟(文))已知{}n a 为等差数列,135105a a a ++=,24699a a a ++=,以n S 表示{}n a 的前n 项和,则使得n S 达到最大值的n 是( )A .21B .20C .19D .185.(2019·湖南高考模拟(文))等差数列{}n a 中,12019a =,2019201516a a =-,则数列{}n a 的前n 项和n S 取得最大值时n 的值为( )A .504B .505C .506D .507二、填空题6.(2019·广东高考模拟(文))设数列{}n a 的前n 项和为n S ,且满足11222n n a a a n -++⋯+=,则5S =____.7.(2017·安徽淮北一中高考模拟(文))若数列{}n a 满足111n nd a a +-=(*n N ∈,d 为常数),则称数列{}n a 为“调和数列”,已知正项数列1{}nb 为“调和数列”,且12990b b b +++=L ,则46b b 的最大值是__________.8.(2019·广东高考模拟(文))已知数列{}n a 满足()*12(1)2(1)1(1)3n n n n n a a n n N +⎡⎤⎡⎤--++-=+-⨯∈⎣⎦⎣⎦,则251a a -=____.三、解答题9.(2019·山东高考模拟(文))已知数列{}n a 的前n 项和为n S ,且满足2n n S a n =-.(1)求证{}1n a +为等比数列;(2)求数列{}n S 的前n 项和n T .10.(2019·甘肃高三月考(文))已知公差不为0的等差数列{}n a 的首项12,a =且1241,1,1a a a +++成等比数列.(1)求数列{}n a 的通项公式;(2)设*11,,n n n n b n S a a +=∈N 是数列{}n b 的前n 项和,求使319n S <成立的最大的正整数n .11.(2019·四川高考模拟(文))已知等差数列{}n a 的公差大于0,且47a =,2a ,612a a -,14a 分别是等比数列{}n b 的前三项.()1求数列{}n a 的通项公式;()2记数列{}n b 的前n 项和n S ,若39n S >,求n 的取值范围.12.(2019·四川双流中学高考模拟(文))设数列{}n a 的前n 项之和为13322n n S +=-,数 列{}n b 满足2132113(21)log n n n b n a -+=+-. (1)求数列{}n a 的通项公式;(2)求数列{}n b 前n 项之和n T .13.(2019·辽宁高考模拟(文))已知数列{}n a 的前n 项和为n S ,且1,n a ,n S 成等差数列.(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足12n n n a b na =+,求数列{}n b 的前n 项和n T .14.(2019·安徽合肥一中高考模拟(文))设等比数列{}n a 满足132420,10a a a a +=+=.(1)令123n n T a a a a =L ,求n T 的最大值;(2)令2log n n b a =,求数列{}n n a b 的前 n 项和n S .15.(2019·江西临川一中高考模拟(文))已知数列{}n a 中,1a m =,且()*1321,n n n n a a n b a n n N +=+-=+∈.(1)判断数列{}n b 是否为等比数列,并说明理由; (2)当2m =时,求数列{}(1)nn a -的前2020项和2020S .以下内容为“高中数学该怎么有效学习?”首先要做到以下两点:1、先把教材上的知识点、理论看明白。

2020 高考数学知识难点复习梳理失败是什么?没有什么,只是更走近成功一步;成功是什么?就是走过了所有通向失败的路,只剩下一条路,那就是成功的路。
接下来是小编为大家整理的2020 高考数学知识难点复习,希望大家喜欢!第一、基本公式用错等差数列的首项为a1、公差为 d,则其通项公式an=a1+(n-1)d,前 n 项和公式 Sn=na1+n(n-1)d/2= (a1+an)d/2 ;等比数列的首项为 a1、公比为 q,则其通项公式 an=a1pn-1,当公比 q≠1时,前 n 项和公式 Sn=a1(1-pn)/(1-q)= (a1-anq)/(1-q),当公比 q=1 时,前 n 项和公式 Sn=na1。
在数列的基础题中,等差、等比数列公式是解题的根本,一旦用错了公式,解题也失去了方向。
第二、an,Sn 关系不清致误在数列题中,数列的通项 an 与其前 n 项和Sn 之间存在着关系。
这个关系对任意数列都是成立的,但要注意的是关系式分段。
在 n=1 和 n≥2 时,关系式具有完全不同的表现形式,这也是考生答题过程中经常出错的点,在使用关系式时,要牢牢记住其“分段”的特点。
当题目中给出了数列{an}的an 与Sn 之间的关系时,这两者之间可以进行相互转换,知道了an 的具体表达式,就可以通过数列求和的方法求出Sn;知道了 Sn,也可以求出an。
在答题时,一定要体会这种转换的相互性。
第三、等差、等比数列性质理解错误等差数列的前 n 项和在公差不为 0 时是关于n 的常数项为 0 的二次函数。
一般来说,有结论“若数列{an}的前 N 项和 Sn=an2+bn+c(a,b,c∈R),则数列{an}为等差数列的充要条件是 c=0”;在等差数列中,Sm,S2m-Sm,S3m-S2m(m∈N_是等差数列。
解答此类题时,要求考生全面考虑问题,考虑各种可能性,认为正确的就给予证明,不正确就举出反例驳斥。
等比数列中,公比等于-1 是特殊情况,在解决相关题型问题时值得注意。

【2018年高考考纲解读】 高考对本内容的考查主要有:(1)数列的概念是A 级要求,了解数列、数列的项、通项公式、前n 项和等概念,一般不会单独考查; (2)等差数列、等比数列是两种重要且特殊的数列,要求都是C 级,熟练掌握等差数列、等比数列的概念、通项公式、前n 项求和公式、性质等知识,理解其推导过程,并且能够灵活应用. (4)通过适当的代数变形后,转化为等差数列或等比数列的问题. (5)求数列的通项公式及其前n 项和的基本的几种方法. (6)数列与函数、不等式的综合问题.试题类型可能是填空题,以考查单一性知识为主,同时在解答题中经常与不等式综合考查,构成压轴题. 【重点、难点剖析】1.等差、等比数列的通项公式等差数列{a n }的通项公式为a n =a 1+(n -1)d =a m +(n -m )d ;等比数列{a n }的通项公式为a n =a 1q n -1=a m qn -m.2.等差、等比数列的前n 项和 (1)等差数列的前n 项和为S n =n a 1+a n 2=na 1+n n -2d .特别地,当d ≠0时,S n 是关于n 的二次函数,且常数项为0,即可设S n =an 2+bn (a ,b 为常数). (2)等比数列的前n 项和S n =⎩⎪⎨⎪⎧na 1,q =1,a 1-q n 1-q=a 1-a n q1-q ,q ≠1,特别地,若q ≠1,设a =a 11-q ,则S n =a -aq n.3.等差数列、等比数列常用性质(1)若序号m +n =p +q ,在等差数列中,则有a m +a n =a p +a q ;特别的,若序号m +n =2p ,则a m +a n =2a p ;在等比数列中,则有a m ·a n =a p ·a q ;特别的,若序号m +n =2p ,则a m ·a n =a 2p ;(2)在等差数列{a n }中,S k ,S 2k -S k ,S 3k -S 2k ,…成等差数列,其公差为kd ;其中S n 为前n 项的和,且S n ≠0(n ∈N *);在等比数列{a n }中,当q ≠-1或k 不为偶数时S k ,S 2k -S k ,S 3k -S 2k ,…成等比数列,其中S n 为前n 项的和(n∈N*).4.数列求和的方法归纳(1)转化法:将数列的项进行分组重组,使之转化为n个等差数列或等比数列,然后应用公式求和;(2)错位相减法:适用于{a n·b n}的前n项和,其中{a n}是等差数列,{b n}是等比数列;(3)裂项法:求{a n}的前n项和时,若能将a n拆分为a n=b n-b n+1,则a1+a2+…+a n=b1-b n+1;(4)倒序相加法:一个数列倒过来与原数列相加时,若有公因式可提,并且剩余的项的和容易求出,那么这样的数列求和可采用此法.其主要用于求组合数列的和.这里易忽视因式为零的情况;(5)试值猜想法:通过对S1,S2,S3,…的计算进行归纳分析,寻求规律,猜想出S n,然后用数学归纳法给出证明.易错点:对于S n不加证明;(6)并项求和法:先将某些项放在一起先求和,然后再求S n.例如对于数列{a n}:a1=1,a2=3,a3=2,a n+2=a n+1-a n,可证其满足a n+6=a n,在求和时,依次6项求和,再求S n.5.数列的应用题(1)应用问题一般文字叙述较长,反映的事物背景陌生,知识涉及面广,因此要解好应用题,首先应当提高阅读理解能力,将普通语言转化为数学语言或数学符号,实际问题转化为数学问题,然后再用数学运算、数学推理予以解决.(2)数列应用题一般是等比、等差数列问题,其中,等比数列涉及的范围比较广,如经济上涉及利润、成本、效益的增减,解决该类题的关键是建立一个数列模型{a n},利用该数列的通项公式、递推公式或前n项和公式.【题型示例】题型1、等差、等比数列中基本量的计算【例1】(2017·高考全国卷Ⅰ)记S n为等差数列{a n}的前n项和.若a4+a5=24,S6=48,则{a n}的公差为( ) A.1 B.2C.4 D.8(a 4+a 5)-(a 4+a 3)=8, ∴d =4,故选C.【2017江苏,9】等比数列{}n a 的各项均为实数,其前n 项的和为n S ,已知3676344S S ==,,则8a = ▲ .【答案】32【解析】当1q =时,显然不符合题意;当1q ≠时,3161(1)714(1)6314a q q a q q ⎧-=⎪-⎪⎨-⎪=⎪-⎩,解得1142a q ⎧=⎪⎨⎪=⎩,则7812324a =⨯=. 【变式探究】【2016年高考北京文数】已知{}n a 错误!未找到引用源。
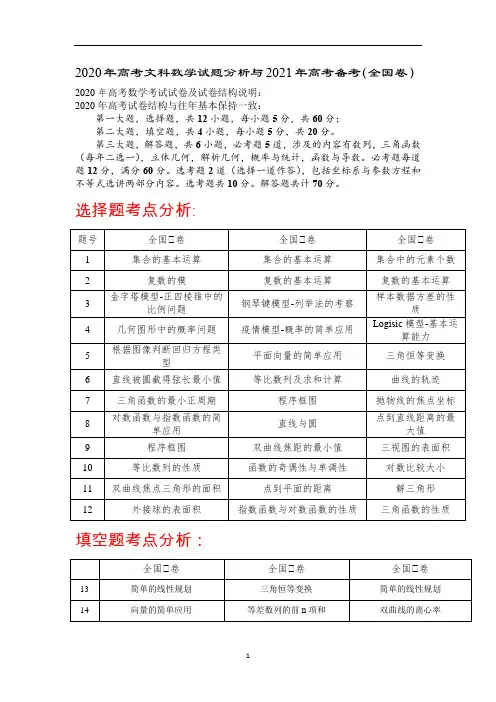
2020年高考文科数学试题分析与2021年高考备考(全国卷)2020年高考数学考试试卷及试卷结构说明:2020年高考试卷结构与往年基本保持一致:第一大题,选择题,共12小题,每小题5分,共60分;第二大题,填空题,共4小题,每小题5分,共20分。
第三大题,解答题,共6小题,必考题5道,涉及的内容有数列,三角函数(每年二选一),立体几何,解析几何,概率与统计,函数与导数。
必考题每道题12分,满分60分。
选考题2道(选择一道作答),包括坐标系与参数方程和不等式选讲两部分内容。
选考题共10分。
解答题共计70分。
选择题考点分析:填空题考点分析:选择填空题主干知识比重分析:解答题考点分析:试卷整体主干知识比重分析:试卷分析:选择题:①在全国卷三套高考试题中,1-4题,均出现了创新题型,如全国Ⅰ卷的胡夫金字塔,全国Ⅱ卷的钢琴键的大小和弦,全国Ⅲ卷考察的Logisic模型均体现了高考的创新性,题目虽然新颖,但是细分析后一切又变得清晰,剥离了材料背景,剩下的就是数学计算,题目考察学生对于数学知识的掌握程度和理解程度,除创新题目以外,其他题型的考察较为常规,考生一般都能够顺利解答。
②选择题的其他题目都较为常规,考察的内容涉及数列,三角函数,统计概率,立体几何,函数与导数等主干知识点,总体而言,选择题重在考察大家的基础知识与基本能力,难度不是很大。
这也告诉我们高考不出偏题,怪题。
平时训练的时候,要筑牢基础,夯实能力,不要一味去钻研偏题,难题和怪题。
填空题:①填空题部分13-15题难度较小,大多数同学们都能够顺利完成,第16题的难度稍大,综合性较强,同学们需要充分挖掘题目中的隐含条件,综合解决。
总体而言,填空题考察的仍然是同学们的基础知识,只要认真,细心,一定能够取得一个不错的分数。
②数学考试填空题在作答时一定要清晰,书写清晰,不能模棱两可,而且在做填空题时要注意答题的位置,不能够答错位置。
解答题:①综合来看,今年的六道解答题总体来看计算量都比较大,所以对于考生来说,耐心计算就成了能否取得高分的关键,解答题在理解题目上设置了一定的难度,同学们需要花一定的时间去分析题意,但是今年的大多数题目较为常规,与2019年高考相比而言,难度有所下降,考生们作答起来比去年可能要轻松许多。

高考文科数学知识点归纳高考文科数学必考考点有哪些呢?那么,下面是小编为大家整理的关于高考文科数学知识点归纳,希望对您有所帮助。
欢迎大家阅读参考学习!2020高考文科数学知识点第一,函数与导数主要考查集合运算、函数的有关概念定义域、值域、解析式、函数的极限、连续、导数。
第二,平面向量与三角函数、三角变换及其应用这一部分是高考的重点但不是难点,主要出一些基础题或中档题。
第三,数列及其应用这部分是高考的重点而且是难点,主要出一些综合题。
第四,不等式主要考查不等式的求解和证明,而且很少单独考查,主要是在解答题中比较大小。
是高考的重点和难点。
第五,概率和统计这部分和我们的生活联系比较大,属应用题。
第六,空间位置关系的定性与定量分析主要是证明平行或垂直,求角和距离。
主要考察对定理的熟悉程度、运用程度。
第七,解析几何高考的难点,运算量大,一般含参数。
2020高考文科数学知识点:文科数学高频必考考点第一部分:选择与填空1.集合的基本运算(含新定集合中的运算,强调集合中元素的互异性);2.常用逻辑用语(充要条件,全称量词与存在量词的判定);3.函数的概念与性质(奇偶性、对称性、单调性、周期性、值域最大值最小值);4.幂、指、对函数式运算及图像和性质5.函数的零点、函数与方程的迁移变化(通常用反客为主法及数形结合思想);6.空间体的三视图及其还原图的表面积和体积;7.空间中点、线、面之间的位置关系、空间角的计算、球与多面体外接或内切相关问题;8.直线的斜率、倾斜角的确定;直线与圆的位置关系,点线距离公式的应用;9.算法初步(认知框图及其功能,根据所给信息,几何数列相关知识处理问题);10.古典概型,几何概型理科:排列与组合、二项式定理、正态分布、统计案例、回归直线方程、独立性检验;文科:总体估计、茎叶图、频率分布直方图;11.三角恒等变形(切化弦、升降幂、辅助角公式);三角求值、三角函数图像与性质;12.向量数量积、坐标运算、向量的几何意义的应用;13.正余弦定理应用及解三角形;14.等差、等比数列的性质应用、能应用简单的地推公式求其通项、求项数、求和;15.线性规划的应用;会求目标函数;16.圆锥曲线的性质应用(特别是会求离心率);17.导数的几何意义及运算、定积分简单求法18.复数的概念、四则运算及几何意义;19.抽象函数的识别与应用;第二部分:解答题第17题:向量与三角交汇问题,解三角形,正余弦定理的实际应用;第18题:(文)概率与统计(概率与统计相结合型)(理)离散型随机变量的概率分布列及其数字特征;第19题:立体几何①证线面平行垂直;面与面平行垂直②求空间中角(理科特别是二面角的求法)③求距离(理科:动态性)空间体体积;第20题:解析几何(注重思维能力与技巧,减少计算量)①求曲线轨迹方程(用定义或待定系数法)②直线与圆锥曲线的关系(灵活运用点差法和弦长公式)③求定点、定值、最值,求参数取值的问题;第21题:函数与导数的综合应用这是一道典型应用知识网络的交汇点设计的试题,是考查考生解题能力和文科数学素质为目标的压轴题。

⾼考2020⽂科数学知识难点整理 知识掌握的巅峰,应该在⼀轮复习之后,也就是在你把所有知识重新捡起来之后。
这样看来,应对⾼⼆这⼀变化的较优选择,是在⾼⼆还在学习新知识时,有意识地把⾼⼀内容从头捡起,⾃⼰规划进度,提前复习。
接下来是⼩编为⼤家整理的⾼考2020⽂科数学知识难点整理,希望⼤家喜欢! ⾼考2020⽂科数学知识难点整理⼀ 1.不等式证明的依据 (2)不等式的性质(略) (3)重要不等式:①|a|≥0;a2≥0;(a-b)2≥0(a、b∈R) ②a2+b2≥2ab(a、b∈R,当且仅当a=b时取“=”号) 2.不等式的证明⽅法 (1)⽐较法:要证明a>b(a0(a-b<0),这种证明不等式的⽅法叫做⽐较法. ⽤⽐较法证明不等式的步骤是:作差——变形——判断符号. (2)综合法:从已知条件出发,依据不等式的性质和已证明过的不等式,推导出所要证明的不等式成⽴,这种证明不等式的⽅法叫做综合法. (3)分析法:从欲证的不等式出发,逐步分析使这不等式成⽴的充分条件,直到所需条件已判断为正确时,从⽽断定原不等式成⽴,这种证明不等式的⽅法叫做分析法. 证明不等式除以上三种基本⽅法外,还有反证法、数学归纳法等. ⾼考2020⽂科数学知识难点整理⼆ 导数是微积分中的重要基础概念。
当函数y=f(x)的⾃变量x在⼀点x0上产⽣⼀个增量Δx时,函数输出值的增量Δy与⾃变量增量Δx的⽐值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
导数是函数的局部性质。
⼀个函数在某⼀点的导数描述了这个函数在这⼀点附近的变化率。
如果函数的⾃变量和取值都是实数的话,函数在某⼀点的导数就是该函数所代表的曲线在这⼀点上的切线斜率。
导数的本质是通过极限的概念对函数进⾏局部的线性逼近。
例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数,⼀个函数也不⼀定在所有的点上都有导数。
2020年高考全国卷三文科数学试题分析解析解读考查关键能力,注重数学应用2020年高考数学试题继续坚持素养导向、能力为重的命题原则,试题重视数学本质、突出理性思维、批判质疑、勇于探究的科学素养,形成了“考查关键能力,注重数学应用”的命题特点。
同时,试题紧密实际生活,特别突出了当下科学抗疫的实际背景,让学生体会和思考生活中数学的存在、作用与魅力,激发学生的思考热情和科学精神。
试卷命题兼具了基础性、综合性、应用性和创新性,难度合理、区分度强,很好起到了的对学生检验和选拔的作用。
考查内容全面,突出主干知识集合、复数、函数、数列、三角函数、线性规划、平面向量、二项式定理、立体几何、圆锥曲线等内容都得到了考查。
除此之外,试卷还强调对主干内容的重点考查,如圆锥曲线和立体几何版块,都直接考查了2道选择题和1道解答题,分值达到了22分;而函数作为高中数学的主线,包含导数部分直接考查了4道选择填空题以及1道解答题,总计分值达到了32分。
总而言之,今年全国三卷文科数学试题知识点覆盖全面,在强调通性通法的同时,还坚持能力立意,难度设计科学合理,很好把握了稳定和创新,对高中数学的教与学起到了很好的积极作用。
发挥学科特色,“战疫”科学入题用数学模型揭示病毒传播规律,全国Ⅲ卷文、理科第4题以新冠肺炎疫情传播的动态研究为背景,选择适合学生知识水平的Logistic模型作为试题命制的基础,考查学生对指数函数基本知识的理解和掌握,以及使用数学模型解决实际问题的能力。
对信息整理能力的考查第18题以当前社会关心的空气质量状况和在公园进行体育锻炼为背景,给出了某市100天中每天的空气质量等级和当天到某公园锻炼的人次的数据表,重点考查学生对概率统计基本思想、基本统计模型的理解和运用。
题不算难,但估计学生做得不理想,因为很多题目可能基本上不在大家平时练习的套路上例如22题的参数方程,参数t二次,不常见,不在套路上。
但只要能理解参数方程的本质,做出来非常轻松。
高考数学考纲解读与热点难点突破导数的热点问题 教案【2020年高考考纲解读】利用导数探求函数的极值、最值是函数的基本问题,高考中常与函数零点、方程根及不等式相结合,难度较大.【题型示例】题型一、利用导数证明不等式用导数证明不等式是导数的应用之一,可以间接考查用导数判定函数的单调性或求函数的最值,以及构造函数解题的能力.例1、(2018·全国Ⅰ)已知函数f(x)=aex -ln x -1.(1)设x =2是f(x)的极值点,求a ,并求f(x)的单调区间; (2)证明:当a ≥1e时,f(x)≥0.(1)解 f(x)的定义域为(0,+∞),f ′(x)=aex -1x .由题设知,f ′(2)=0,所以a =12e2. 从而f(x)=12e2ex -ln x -1,f ′(x)=12e2ex -1x .当0<x<2时,f ′(x)<0;当x>2时,f ′(x)>0.所以f(x)的单调递增区间为(2,+∞),单调递减区间为(0,2). (2)证明 当a ≥1e 时,f(x)≥exe-ln x -1.设g(x)=ex e -ln x -1(x ∈(0,+∞)),则g ′(x)=ex e -1x.当0<x<1时,g ′(x)<0;当x>1时,g ′(x)>0. 所以x =1是g(x)的最小值点. 故当x>0时,g(x)≥g(1)=0. 因此,当a ≥1e时,f(x)≥0.【方法技巧】用导数证明不等式的方法(1)利用单调性:若f(x)在[a ,b]上是增函数,则①∀x ∈[a ,b],则f(a)≤f(x)≤f(b);②对∀x1,x2∈[a ,b],且x1<x2,则f(x1)<f(x2).对于减函数有类似结论.(2)利用最值:若f(x)在某个范围D 内有最大值M(或最小值m),则对∀x ∈D ,有f(x)≤M(或f(x)≥m).(3)证明f(x)<g(x),可构造函数F(x)=f(x)-g(x),证明F(x)<0. 【变式探究】(2018·全国Ⅲ)已知函数f(x)=ax2+x -1ex .(1)求曲线y =f(x)在点(0,-1)处的切线方程; (2)证明:当a ≥1时,f(x)+e ≥0.题型二利用导数讨论方程根的个数方程的根、函数的零点、函数图象与x轴的交点的横坐标是三个等价的概念,解决这类问题可以通过函数的单调性、极值与最值,画出函数图象的走势,通过数形结合思想直观求解.例2、(2018·天津)设函数f(x)=(x-t1)·(x-t2)(x-t3),其中t1,t2,t3∈R,且t1,t2,t3是公差为d的等差数列.(1)若t2=0,d=1,求曲线y=f(x)在点(0,f(0))处的切线方程;(2)若d=3,求f(x)的极值;(3)若曲线y=f(x)与直线y=-(x-t2)-63有三个互异的公共点,求d的取值范围.解(1)由已知,可得f(x)=x(x-1)(x+1)=x3-x,故f′(x)=3x2-1.因此f(0)=0,f′(0)=-1.又因为曲线y=f(x)在点(0,f(0))处的切线方程为y-f(0)=f′(0)(x-0),故所求切线方程为x+y=0.(2)由已知可得f(x)=(x-t2+3)(x-t2)(x-t2-3)=(x-t2)3-9(x-t2)=x3-3t2x2+(3t22-9)x-t32+9t2.故f′(x)=3x2-6t2x+3t22-9.令f′(x)=0,解得x=t2-3或x=t2+ 3.当x变化时,f′(x),f(x)的变化情况如下表:所以函数f(x)的极大值为f(t2-3)=(-3)3-9×(-3)=63,函数f(x)的极小值为f(t2+3)=(3)3-9×3=-63.(3)曲线y =f(x)与直线y =-(x -t2)-63有三个互异的公共点等价于关于x 的方程(x -t2+d)(x -t2)·(x -t2-d)+(x -t2)+63=0有三个互异的实数解.令u =x -t2,可得u3+(1-d2)u +63=0.设函数g(x)=x3+(1-d2)x +63,则曲线y =f(x)与直线y =-(x -t2)-63有三个互异的公共点等价于函数y =g(x)有三个零点.g ′(x)=3x2+(1-d2).当d2≤1时,g ′(x)≥0,这时g(x)在R 上单调递增,不合题意. 当d2>1时,令g ′(x)=0,解得x 1=-d2-13,x2=d2-13. 可得g(x)在(-∞,x1)上单调递增,在[x1,x2]上单调递减,在(x2,+∞)上单调递增. 所以g(x)的极大值为 g(x1)=g ⎝⎛⎭⎪⎪⎫-d2-13=23d2-1329+63>0.g(x)的极小值为 g(x2)=g ⎝⎛⎭⎪⎪⎫d2-13=-23d2-1329+6 3.若g(x2)≥0,则由g(x)的单调性可知函数y=g(x)至多有两个零点,不合题意.若g(x2)<0,即(d2-1)32>27,也就是|d|>10,此时|d|>x2,g(|d|)=|d|+63>0,且-2|d|<x1,g(-2|d|)=-6|d|3-2|d|+63<-6210+63<0,从而由g(x)的单调性,可知函数y =g(x)在区间(-2|d|,x1),(x1,x2),(x2,|d|)内各有一个零点,符合题意.所以d的取值范围是(-∞,-10)∪(10,+∞).【感悟提升】(1)函数y=f(x)-k的零点问题,可转化为函数y=f(x)和直线y=k的交点问题.(2)研究函数y=f(x)的值域,不仅要看最值,而且要观察随x值的变化y值的变化趋势.【变式探究】设函数f(x)=(x-1)ex-k2x2.(1)当k<1时,求函数f(x)的单调区间;(2)当k≤0时,讨论函数f(x)的零点个数.(2)f(0)=-1,①当k<0时,f(1)=-k2>0,又f(x)在[0,+∞)上单调递增,所以函数f(x)在[0,+∞)上只有一个零点. 在区间(-∞,0)中,因为f(x)=(x -1)ex -k2x2>x -1-k2x2,取x =2k-1∈(-∞,0),于是f ⎝ ⎛⎭⎪⎪⎫2k -1>⎝ ⎛⎭⎪⎪⎫2k -1-1-k 2⎝ ⎛⎭⎪⎪⎫2k -12=-k2>0,又f(x)在(-∞,0)上单调递减, 故f(x)在(-∞,0)上也只有一个零点,所以函数f(x)在定义域(-∞,+∞)上有两个零点;②当k =0时,f(x)=(x -1)ex 在单调递增区间[0,+∞)内,只有f(1)=0. 而在区间(-∞,0)内,f(x)<0, 即f(x)在此区间内无零点.所以函数f(x)在定义域(-∞,+∞)上只有唯一的零点.综上所述,当k<0时,函数f(x)有两个零点,当k =0时,f(x)只有一个零点. 题型三 利用导数解决生活中的优化问题生活中的实际问题受某些主要变量的制约,解决生活中的优化问题就是把制约问题的主要变量找出来,建立目标问题即关于这个变量的函数,然后通过研究这个函数的性质,从而找到变量在什么情况下可以达到目标最优.例3、罗源滨海新城建一座桥,两端的桥墩已建好,这两墩相距m 米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x 米的相邻两墩之间的桥面工程费用为(2+x)x 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y 万元.(1)试写出y 关于x 的函数关系式;(2)当m =96米时,需新建多少个桥墩才能使余下工程的费用y 最小? 解 (1)设需新建n 个桥墩, 则(n +1)x =m ,即n =mx -1.所以y =f(x)=32n +(n +1)(2+x)x=32⎝ ⎛⎭⎪⎪⎫m x -1+m x (2+x)x=m ⎝⎛⎭⎪⎪⎫32x+x +2m -32(0<x<m). (2)当m =96时,f(x)=96⎝⎛⎭⎪⎪⎫32x+x +160, 则f ′(x)=96⎝ ⎛⎭⎪⎪⎫12x -32x2=48x2(32x -64). 令f ′(x)=0,得32x =64,所以x =16.当0<x<16时,f ′(x)<0,f(x)在区间(0,16)内为减函数; 当16<x<96时,f ′(x)>0,f(x)在区间(16,96)内为增函数, 所以f (x)在x =16处取得最小值,此时n =9616-1=5.答 需新建5个桥墩才能使余下工程的费用y 最小. 【感悟提升】利用导数解决生活中的优化问题的一般步骤(1)建模:分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系式y =f(x).(2)求导:求函数的导数f ′(x),解方程f ′(x)=0.(3)求最值:比较函数在区间端点和使f ′(x)=0的点的函数值的大小,最大(小)者为最大(小)值.(4)作答:回归实际问题作答.【变式探究】图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,其中四边形ABCD 是矩形,弧CmD 是半圆,凹槽的横截面的周长为4.若凹槽的强度T 等于横截面的面积S 与边AB 的乘积,设AB =2x ,BC =y.(1)写出y 关于x 的函数表达式,并指出x 的取值范围; (2)求当x 取何值时,凹槽的强度最大. 解 (1)易知半圆CmD 的半径为x , 故半圆CmD 的弧长为πx. 所以4=2x +2y +πx , 得y =42x 2.依题意知0<x<y ,得0<x<44+π. 所以y =42x 2⎝ ⎛⎭⎪⎪⎫0<x<44+π. (2)依题意,得T =AB ·S =2x ⎝ ⎛⎭⎪⎪⎫2xy -12πx2=8x2-(4+3π)x3.令T ′=16x -3(4+3π)x2=0,得x =0或x =169π+12.因为0<169π+12<4π+4,所以当0<x<169π+12时,T ′>0,T 为关于x 的增函数;当169π+12<x<44+π时,T ′<0,T 为关于x 的减函数,所以当x =169π+12时凹槽的强度最大.专题练习1.在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为v(米/单位时间),每单位时间的用氧量为⎝ ⎛⎭⎪⎪⎫v 103+1(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为v2(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为y(升).(1)求y 关于v 的函数关系式;(2)若c ≤v ≤15(c>0),求当下潜速度v 取什么值时,总用氧量最少.(2)y ′=6v50-240v2=3(v3-2 000)25v2,令y ′=0,得v =1032,当0<v<1032时,y ′<0,函数单调递减,当v>1032时,y ′>0,函数单调递增, ∴当0<c<1032时,函数在(c,1032)上单调递减,在(1032,15)上单调递增, ∴当v =1032时总用氧量最少,当c ≥1032时,y 在[c,15]上单调递增,∴当v =c 时总用氧量最少.综上,若0<c<1032,则当v =1032时总用氧量最少;若c ≥1032,则当v =c 时总用氧量最少.2.已知函数f(x)=x +a x .(1)判断函数f(x)的单调性;(2)设函数g(x)=ln x +1,证明:当 x ∈(0,+∞)且a>0时,f(x)>g(x).(1)解 因为f ′(x)=1-a x2=x2-a x2()x ≠0,①若a ≤0,则f ′(x)>0在定义域内恒成立,∴f(x)在(-∞,0),(0,+∞)上单调递增;②若a>0,则由f ′(x)>0,解得x<-a 或x>a ,由f ′(x)<0,解得-a<x<a ()x ≠0,∴函数f(x)在⎝⎛⎭⎫-∞,-a ,⎝⎛⎭⎫a ,+∞上单调递增,在⎝⎛⎭⎫-a ,0,⎝⎛⎭⎫0,a 上单调递减.(2)证明 令h(x)=f(x)-g(x)=x +ax -ln x -1(x>0),h ′(x)=1-a x2-1x =x2-x -ax2(x>0),设p(x)=x2-x -a ,则由a>0知,方程p(x)=0的判别式Δ=1+4a>0,设p(x)=0的正根为x0,∴x20-x0-a =0,∵p(1)=1-1-a =-a<0,∴x0>1,又p(0)=-a<0,∴h(x)在(0,x0)上为减函数,在(x0,+∞)上为增函数,h(x)min=h(x0)=x0+ax0-ln x0-1=x0+x20-x0x0-ln x0-1=2x0-ln x0-2,令F(x)=2x-ln x-2()x>1,F′(x)=2-1x=2x-1x>0恒成立,∴F(x)在(1,+∞)上为增函数,又∵F(1)=2-0-2=0,∴F(x)>0,即h(x)min>0,∴当x∈(0,+∞)且a>0时,f(x)>g(x).3.已知函数f(x)=ln x,g(x)=x+m(m∈R).(1)若f(x)≤g(x)恒成立,求实数m的取值范围;(2)已知x1,x2是函数F(x)=f(x)-g(x)的两个零点,且x1<x2,求证:x1x2<1.(1)解令F(x)=f(x)-g(x)=ln x-x-m(x>0),则F′(x)=1x-1=1-xx(x>0),当x>1时,F′(x)<0,当0<x<1时,F′(x)>0,所以F(x)在(1,+∞)上单调递减,在(0,1)上单调递增,F(x)在x=1处取得最大值-1-m,若f(x)≤g(x)恒成立,则-1-m≤0,即m≥-1.(2)证明由(1)可知,若函数F(x)=f(x)-g(x)有两个零点,则m<-1,0<x1<1<x2,要证x1x2<1,只需证x2<1x1,由于F(x)在(1,+∞)上单调递减,从而只需证F(x2)>F ⎝ ⎛⎭⎪⎪⎫1x1,由F(x1)=F(x2)=0,m =ln x1-x1,即证ln 1x1-1x1-m =ln 1x1-1x1+x1-ln x1<0,令h(x)=-1x +x -2ln x(0<x<1),则h ′(x)=1x2+1-2x =x2-2x +1x2>0,故h(x)在(0,1)上单调递增,h(x)<h(1)=0,所以x1x2<1.4.已知f(x)=(ax -1)ex +x2.(1)当a =1时,讨论函数f(x)的零点个数,并说明理由;(2)若x =0是f(x)的极值点,证明f(x)≥ln(ax -1)+x2+x +1.(1)解 当a =1时,f(x)=(x -1)ex +x2,f ′(x)=x ()ex +2,由f ′(x)>0得x>0,由f ′(x)<0得x<0,∴f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,又∵f(-2)=4-3e2>0,f(0)=-1<0,f(1)=1>0,∴f(x)有两个零点.(2)证明 ∵f ′(x)=ex ()ax -1+a +2x ,∵x =0是f(x)的极值点,∴f ′(0)=a -1=0,∴a =1,∴f(x)=(x -1)ex +x2,故要证(x -1)ex ≥ln(x -1)+x +1,令x -1=t ,t>0,即证tet +1≥ln t +t +2(t>0),设h(x)=ex ·ex -ln x -x -2(x>0),即证h(x)≥0(x>0),h ′(x)=e ·ex(x +1)-1x -1=e(x +1)⎝ ⎛⎭⎪⎪⎫ex -1ex (x>0),令u(x)=ex -1ex (x>0),u ′(x)=ex +1ex2>0,∴u(x)在(0,+∞)上单调递增,又u(1)=e -1e >0,u ()e -2=2e e --e<0,故u(x)=0有唯一的根x0∈(0,1),0e x =1ex0,当0<x<x0时,u(x)<0,h ′(x)<0,当x>x0时,u(x)>0,h ′(x)>0,∴h(x)≥h(x0)=ex0·0e x -ln x0-x0-2=ex0·1ex0+ln 01e x +-x0-2=1+x0+1-x0-2=0.综上得证.5.已知函数f(x)=1-x ax +ln x(其中a>0,e ≈2.7).(1)当a =1时,求函数f(x)在(1,f(1))点处的切线方程;(2)若函数f(x)在区间[2,+∞)上为增函数,求实数a 的取值范围;(3)求证:对于任意大于1的正整数n ,都有ln n>12+13+…+1n .(1)解 ∵f(x)=1-x x +ln x ,∴f ′(x)=x -1x2(x>0),∴f ′(1)=0,∵f(1)=0,∴f(x)在点(1,f(1))处的切线方程为y =0.(3)证明 当a =1时,f(x)=1-x x +ln x ,f ′(x)=x -1x2,当x>1时,f ′(x)>0,f(x)在(1,+∞)上是增函数.则当x>1时,f(x)>f(1)=0,当n>1时,令x =nn -1>1,∴f(x)=1-n n -1nn -1+ln n n -1=-1n +ln nn -1>0, ∴ln n n -1>1n ,ln 21>12,ln 32>13,…,ln n n -1>1n, ∴ln 21+ln 32+…+ln nn -1>12+13+ (1), 即ln ⎝ ⎛⎭⎪⎪⎫21×32×...×n n -1>12+13+...+1n , ∴ln n>12+13+ (1), 即对于任意大于1的正整数n ,都有ln n>12+13+ (1). 6.已知函数f(x)=ex +2ln x ,g(x)=x2+ax +b(a ,b ∈R).(1)若对任意的x ∈(0,+∞),不等式f(x)>x2+m +2ln x 恒成立,求实数m 的取值范围;(2)若对任意的实数a ,函数F(x)=f(x)-g(x)+x2-2ln x 在(0,+∞)上总有零点,求实数b 的取值范围.解 (1)对任意的x ∈(0,+∞),不等式f(x)>x2+m +2ln x 恒成立可转化为不等式m<ex -x2在(0,+∞)上恒成立.令m(x)=ex -x2,x ∈[0,+∞),则m ′(x)=ex -2x ,令n(x)=m ′(x)=ex -2x ,则n ′(x)=ex -2,故当x ∈(0,ln 2)时,n ′(x)<0,n(x)单调递减;当x ∈(ln 2,+∞)时,n ′(x)>0,n(x)单调递增.从而当x ∈[0,+∞)时,n(x)≥n(ln 2)=2-2ln 2>0,即m ′(x)>0,所以m(x)在[0,+∞)上单调递增,m(x)的最小值是m(0)=1,所以m ≤1,即m 的取值范围为(-∞,1].(2)函数F(x)=f(x)-g(x)+x2-2ln x 在(0,+∞)上总有零点,即F(x)=ex -ax -b 在(0,+∞)上总有零点.若a<0,则F(x)=ex -ax -b 在(0,+∞)上单调递增,故F(x)在(0,+∞)上总有零点的必要条件是F(0)<0,即b>1.以下证明:当b>1时,F(x)=ex -ax -b 在(0,+∞)上总有零点.①若a<0,由于F(0)=1-b<0,F ⎝ ⎛⎭⎪⎪⎫-b a =e ba --a ⎝ ⎛⎭⎪⎪⎫-b a -b =e ba->0,且F(x)在(0,+∞)上连续,故F(x)在⎝ ⎛⎭⎪⎪⎫0,-b a 上必有零点;②若a ≥0,F(0)=1-b<0,由(1)知ex>x2+1>x2在x ∈(0,+∞)时恒成立,取x0=a +b>0,则F(x0)=F(a +b)=ea +b -a(a +b)-b>(a +b)2-a2-ab -b =ab +b(b -1)>0,由于F(0)=1-b<0,F(a +b)>0,故F(x)在(0,a +b)上必有零点.综上,实数b 的取值范围是(1,+∞).7.已知x =1为函数f(x)=(x2-ax)ln x +x 的一个极值点.(1)求实数a 的值,并讨论函数f(x)的单调性;(2)若方程f(x)=mx2+2x 有且只有一个实数根,求实数m 的值.解 (1)函数f(x)的定义域为(0,+∞).f ′(x)=(x2-ax)×1x +(2x -a)ln x +1=x +(2x -a)ln x -(a -1).因为x =1为函数f(x)的一个极值点,所以f ′(1)=1+(2-a)ln 1-(a -1)=2-a =0,解得a =2.故f(x)=(x2-2x)ln x +x ,f ′(x)=x +(2x -2)ln x -1=(x -1)(1+2ln x).令f ′(x)=0,解得x1=1,x2=12e -=ee .当x ∈⎝ ⎛⎭⎪⎪⎫0,e e 时,f ′(x)>0,函数f(x)单调递增;当x ∈⎝ ⎛⎭⎪⎪⎫e e ,1时,f ′(x)<0,函数f(x)单调递减;当x ∈(1,+∞)时,f ′(x)>0,函数f(x)单调递增.(2)方程f(x)=mx2+2x ,即(x2-2x)ln x +x =mx2+2x ,整理得(x2-2x )ln x -x =mx2.因为x>0,所以m =(x2-2x )ln x -x x2=(x -2)ln x -1x .令g(x)=(x -2)ln x -1x =⎝ ⎛⎭⎪⎪⎫1-2x ln x -1x ,则g ′(x)=2x2ln x +⎝ ⎛⎭⎪⎪⎫1-2x ×1x +1x2=2ln x +x -1x2.令h(x)=2ln x +x -1,则h ′(x)=2x+1>0恒成立, 所以函数h(x)在(0,+∞)上单调递增.又h(1)=0,所以当x =(0,1)时,h(x)<0,即g ′(x)<0,g(x)单调递减;当∈(1,+∞)时,h(x)>0,即g ′(x)>0,g(x)单调递增.所以g(x)的最小值为g(1)=-1<0,当x →0或x →+∞时,g(x)→+∞,所以当f(x)=mx2+2x 有且只有一个实数根时,m =-1.8.已知f(x)=asin x ,g(x)=ln x ,其中a ∈R ,y =g -1(x)是y =g(x)的反函数.(1)若0<a ≤1,证明:函数G(x)=f(1-x)+g(x)在区间(0,1)上是增函数;(2)证明:∑k =1nsin 1(1+k )2<ln 2;(3)设F(x)=g -1(x)-mx2-2(x +1)+b ,若对任意的x>0,m<0有F(x)>0恒成立,求满足条件的最小整数b 的值.(1)证明 由题意知G(x)=asin(1-x)+ln x ,G ′(x)=1x-acos(1-x)(x>0), 当x ∈(0,1),0<a ≤1时,1x >1,0<cos(1-x)<1, ∴acos(1-x)<1,∴G ′(x)>0,故函数G(x)在区间(0,1)上是增函数.(2)证明 由(1)知,当a =1时,G(x)=sin(1-x)+ln x 在(0,1)上单调递增. ∴sin(1-x)+ln x<G(1)=0,sin(1-x)<ln 1x (0<x<1).令1-x =1(1+k )2,所以x =k2+2k(1+k )2.∵sin 1(1+k )2=sin ⎣⎢⎢⎡⎦⎥⎥⎤1-k2+2k (1+k )2<ln (1+k )2k2+2k =ln k +1k -ln k +2k +1,∴∑k =1nsin 1(1+k )2<⎝ ⎛⎭⎪⎪⎫ln 2-ln 32+⎝ ⎛⎭⎪⎪⎫ln 32-ln43+…+⎝ ⎛⎭⎪⎪⎫lnn +1n -ln n +2n +1,=ln 2-ln n +2n +1<ln 2.∴m =0e x -22x0,∵b>-0e x +0e x -22x0·x20+2x0+221 =⎝ ⎛⎭⎪⎪⎫x02-10ex+x0+2,又m<0,则x0∈(0,ln 2),∵b>⎝ ⎛⎭⎪⎪⎫x02-10e x +x0+2,x0∈(0,ln 2)恒成立,令m(x)=⎝ ⎛⎭⎪⎪⎫x 2-1ex +x +2,x ∈(0,ln 2), 则m ′(x)=12(x -1)ex +1,令n(x)=12(x -1)ex +1,则n ′(x)=12xex>0,∴m ′(x)在(0,ln 2)上单调递增, ∴m ′(x)>m ′(0)=12>0,∴m(x)在(0,ln 2)上单调递增, ∴m(x)<m(ln 2)=2ln 2, ∴b ≥2ln 2,又b 为整数, ∴最小整数b 的值为2.。
热点01多选题与多空题(新高考)【变化情况】☆题型(顺序)新高考的选择题由原“12个单选题”变为“8个单选题和4个多选题”;填空题由原“4个单空题”变为“3个单空题和1个多空题”;解答题由原“5个必考题和2个选考题”变为“6个必考题,无选考题”.☆题量(小题量)新高考的选择题总题量不变,共12个;填空题总题量不变,共4个;解答题原来是必考题5个,选考题二选一,现在是必考题6个,无选考题,故总题量不变,但试卷上呈现的解答题的数量减少一个.☆分值新高考的选择题和填空题总分值无变化,解答题分值有变化,解答题分值有变化,解答题第一题10分,其余5道大题每题12分.☆考查知识点的分布(各模块的知识占比、是否为常规意义的高频等)新高考的选择题的多选题的难度增加,重视统计、圆锥曲线、立体几何的部分以及函数专题,但也要注意三角、向量等其他知识的多选题,对其要求的学科思想与学科核心素养要求较高.填空题,增加一道多空题(有一个空变成了两个空),难度加大,但所占的分值比重与全国卷的相当.解答题,原来的全国卷,17题的位置是解三角的问题及数列的问题二选其一,且考查形式较新颖,新高考对数列及解三角形的模块地位一样考查.注意不分文理之后,文科生增加了立体几何空间向量的部分,19题的第二问正是很好的体现.选考题第22,23题不再考查,故不等式的选讲及极坐标与参数方程不作考试要求.其余专题部分基本保持不变.【满分技巧】☆掌握规则多项选择题由1个题干和4个备选项组成,备选项中至少有2个正确选项,所选正确答案将是2个、3个或4个.因此,在做多项选择题时应该注意,如果应考者所选答案中有错误选项,该题得零分;如果全部选对得5分,如果所选答案中没有错误选项,但是正确选项未全部选出,则得3分.多空题只是填空题有原来的一个空改成了两个空,原来一道题一个空5分,现在这道题的两个空一个2分一个3分.实际上得分的几率更高,一般前一个空较简单,如果太难的试题,至少能拿到2分.☆常规方法通用做多项选择题同样可以用直接选择法、排除法、比较法等常用的选择题做题方法,而且,有时可以综合使用多种方法来完成一个题目.做多空题也同样用平时求解一般填空题的方法即可.☆注意内容互相对立的选项在多项选择题中,如果存在一对内容互相对立的选项,而其他三项不存在内容对立的情况,那么在此对立两项中至少有一个正确项;若存在两对内容互相对立的选项,则应该从两对对立项中分别选择一个选项作为正确选项.例如,ABCD四个待选项中,AB互相对立,CD互相对立,则两个正确选项往往需从AB组以及CD组中分别择一产生.当然,该规则也存在例外情况.☆注意互近选项或类似选项在多项选择题中,如果存在两对内容互近选项或类似选项,而这两对选项内容对立,则其中一对互近或类似选项应该为正确选项.例如,ABCD四个待选项中,AB两项内容相近、类似,CD两项内容相近、类似,而AB组与CD组内容对立.如果判断A项正确,那么AB组都正确;如果判断C项正确,那么CD组都正确.☆注意有承接关系或递进关系的选项在多项选择题中,如果两个或两个以上的选项之间存在承接关系或递进关系,即数个选项能同时成立,则往往这几个选项应一起被选择.例如在ABCD四个待选项中,ABC三个选项间存在承接、递进关系,能同时成立,若A正确,则ABC都应该为正确选项.☆坚持宁缺勿滥做多项选择题时,谨慎选择的意识要更加明确.一般首先选出最有把握的2个选项,同时,在有足够把握确定还有其他正确答案时才继续选择,否则不选,以免选出错误选项.这样,才能保证该题目得分.因此,要坚持宁缺勿滥,这一点与单项选择题不同.☆重点保证多项选择题有一定难度,考试成绩的高低往往取决于多项选择题的得分.所以应考者应抓紧时间,保证在考试时间内把所有的多项选择题题目都做完.无论是单选还是多选,都要注意看清楚题目要求是选择正确选项还是选择错误选项.一般规范的考试应该是要求选择正确选项,但是,有时也因为某个知识点的特殊性,不便要求选择正确选项,只能要求选择错误选项,因此,也要谨慎.【常考知识】此类考题常与函数、向量、三角函数、概率、统计、圆锥曲线、立体几何等.【限时检测】(建议用时:30分钟)1.已知向量(1,2)=-a ,||4||=b a ,a b ∥,则b 可能是A .(4,8)B .(4,8)-C .(4,8)--D .(4,8)-【答案】BD【解析】设(),x y =b,依题意有20y x =+=⎪⎩48x y =⎧⎨=-⎩或48x y =-⎧⎨=⎩.故选BD.【名师点睛】本小题主要考查平面向量模的坐标运算,考查两个向量平行的坐标表示,属于基础题.求解时,设出b 的坐标,根据已知条件列方程组,解方程组求得b 的可能取值.2.设a ,b ,c 都是正数,且469a b c ==,那么A .2ab bc ac +=B .ab bc ac +=C .221c a b =+D .121c b a=-【答案】AD【解析】由于a ,b ,c 都是正数,故可设469a b c M ===,∴4log a M =,6log b M =,9log c M =,则1log 4M a =,1log 6M b =,1log 9M c=. log 4log 92log 6M M M +=,∴112a c b +=,即121c b a =-,去分母整理得,2ab bc ac +=.故选AD.【名师点睛】本题考查对数的定义及运算性质,属于基础题.求解时,利用与对数定义求出a ,b ,c ,再根据对数的运算性质可得log 4log 92log 6M M M +=,然后进行化简变形即可得到.3.已知函数()π2sin 23()1f x x =-+,则下列说法中正确的是A .函数()f x 的图象关于点π(,0)3对称B .函数()f x 图象的一条对称轴是π12x =-C .若ππ,32x ⎡⎤∈⎢⎥⎣⎦,则函数()fx 1+D .若120πx x <<<,则()()12f x f x <【答案】BC【解析】A.令π2π()3x k k -=∈Z ,知函数()f x 关于点ππ(,1)()62k k +∈Z 对称,所以A 不成立;B.令ππ2π()32x k k -=+∈Z ,知函数()f x 关于轴5ππ()122k x k =+∈Z 对称,所以B 成立;C.若ππ,32x ⎡⎤∈⎢⎥⎣⎦,ππ2π2,,333x ⎡⎤-∈⎢⎥⎣⎦则函数()f x 1+,C 成立;D.由于当120πx x <<<时,()f x 不单调,所以不成立.故答案选择BC.【名师点睛】研究三角函数性质,我们只需牢记sin ;cos ;tan y x y x y x ===的图象及性质,其他都可以通过整体思想进行类比完成.求解时,()π2sin 23(1f x x =-+的性质的研究,我们更多去考虑()(si )n f x A x B ωϕ=-+的性质,利用整体思想能解决本题.4.下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:空调类冰箱类小家电类其它类营业收入占比90.10% 4.98% 3.82% 1.10%净利润占比95.80%﹣0.48%3.82%0.86%则下列判断中正确的是A .该公司2018年度冰箱类电器销售亏损B .该公司2018年度小家电类电器营业收入和净利润相同C .该公司2018年度净利润主要由空调类电器销售提供D .剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低【答案】ACD【解析】根据表中数据知,该公司2018年度冰箱类电器销售净利润所占比为﹣0.48%,是亏损的,所以A 正确;小家电类电器营业收入所占比和净利润所占比是相同的,但收入与净利润不一定相同,所以B 错误;该公司2018年度净利润空调类电器销售所占比为95.80%,是主要利润来源,所以C 正确;剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低,所以D 正确.故选ACD .【名师点睛】本题考查了数据分析与统计知识的应用问题,考查了读表与分析能力,是基础题.求解时,根据题意,分析表中数据,即可得出正确的选项.5.已知三个数1,,9a 成等比数列,则圆锥曲线2212x y a +=的离心率为AB.3C .102D【答案】BC【解析】由三个数1,,9a 成等比数列,得29a =,即3a =±.当3a =时,圆锥曲线为22132x y +=,曲线为椭圆,则e ==当3a =-时,曲线为22123y x -=,曲线为双曲线,e ==则离心率为:3或2.故选BC.【名师点睛】本题考查等比数列的性质,离心率的求解,易错点为漏解a 的取值,属于中档题.求解时,由等比数列的性质求出a ,再判断曲线类型,进而求出离心率.6.在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且()()()::9:10:11a b a c b c +++=,则下列结论正确的是A .sin :sin :sin 4:5:6ABC =B .ABC △是钝角三角形C .ABC △的最大内角是最小内角的2倍D .若6c =,则ABC △外接圆半径为7【答案】ACD【解析】因为()()()::9:10:11a b a c b c +++=,所以可设:91011a b x a c x b c x +=⎧⎪+=⎨⎪+=⎩(其中0x >),解得:4,5,6a x b x c x ===,所以sin :sin :sin ::4:5:6A B C a b c ==,所以A 正确;由上可知:c 边最大,所以三角形中C 角最大,又()()()2222224561cos 022458x x x a b c C ab x x +-+-===>⨯⨯,所以C 角为锐角,所以B 错误;由上可知:a 边最小,所以三角形中A 角最小,又()()()2222226543cos 22654x x x c b a A cb x x +-+-===⨯⨯,所以21cos22cos 18A A =-=,所以cos2cos A C =,由三角形中C 角最大且C 角为锐角可得:()20,πA ∈,π0,2C ⎛⎫∈ ⎪⎝⎭,所以2A C =,所以C 正确;由正弦定理得:2sin c R C =,又sin 8C ==,所以2R =,解得:7R =,所以D 正确.故选ACD.【名师点睛】本题主要考查了正弦定理及余弦定理的应用,还考查了二倍角的余弦公式及计算能力,考查方程思想及转化能力,属于中档题.求解时,由已知可设91011a b x a c x b c x +=⎧⎪+=⎨⎪+=⎩,求得4,5,6a x b x c x ===,利用正弦定理可得A 正确;利用余弦定理可得cos 0C >,三角形中的最大C 角为锐角,可得B 错误;利用余弦定理可得3cos 4A =,利用二倍角的余弦公式可得:cos2cos A C =,即可判断C 正确;利用正弦定理即可判断D 正确,问题得解.7.关于x 的方程2||0ax x a -+=有四个不同的实数解,则实数a 的值可能是A .12B .13C .14D .16【答案】BCD【解析】方程20ax x a -+=中,0a =时,只有一个解0x =,因此方程20ax x a -+=有四个不同的解,则0a ≠,0x ≠,因此方程可变为211x a x+=1x x =+.作出函数1y x x =+的图象和直线1y a=,如图,函数1y x x =+的最小值为2,因此当12a>时,直线1y a =与函数1y x x =+的图象有四个不同的交点,即原方程有四个解,满足12a>的有BCD .故选BCD .【名师点睛】本题考查函数的零点与方程根的关系,在解决方程解的个数问题时常常采用分离参数法,把问题转化为直线与函数的图象的交点问题.求解时,分离参数,把方程变为211x a x+=1x x =+.利用勾形函数的性质求解.8.若函数()f x 具有下列性质:①定义域为(1,1)-;②对于任意的,(1,1)x y ∈-,都有()()f x f y +=1x y f xy ⎛⎫+ ⎪+⎝⎭;③当10x -<<时,()0f x >,则称函数()f x 为δ的函数.若函数()f x 为δ的函数,则以下结论正确的是A .()f x 为奇函数B .()f x 为偶函数C .()f x 为单调递减函数D .()f x 为单调递增函数【答案】AC【解析】()f x 定义域关于原点对称,令y x =-则有:()()(0)f x f x f +-=,令0x y ==,则有(0)0f =,所以()()f x f x -=-,故()f x 是奇函数,A 正确,B 错误;令1x x =,2y x =-,且12x x <,所以121212()()()1x x f x f x f x x -+-=-,又120x x -<且111x -<<,211x -<<,则122112(1)()(1)(1)0x x x x x x ---=+->,即1212101x x x x --<<-,所以12())0(f x f x ->,所以()f x 是单调减函数,C 正确,D 错误.故选AC.【名师点睛】判断抽象函数的单调性和奇偶性,一般采用令值的方法解决问题.令值的时候注意构造出()f x 与()f x -之间的关系以及12()()f x f x -与0的大小.求解时,分析奇偶性:通过令值找到()f x 与()f x -之间的关系;分析单调性:通过令值找到12()()f x f x -与0的大小关系.9.如图1,点E 为正方形ABCD 边BC 上异于点,B C 的动点,将ABE ∆沿AE 翻折,得到如图2所示的四棱锥B AECD -,且平面BAE ⊥平面AECD ,点F 为线段BD 上异于点,B D 的动点,则在四棱锥B AECD -中,下列说法正确的有A .直线BE 与直线CF 必不在同一平面上B .存在点E 使得直线BE ⊥平面DCEC .存在点F 使得直线CF 与平面BAE 平行D .存在点E 使得直线BE 与直线CD 垂直【答案】AC【解析】A.假设直线BE 与直线CF 在同一平面上,所以E 在平面BCF 上,又E 在线段BC 上,BC I 平面BCF =C ,所以E 与C 重合,与E 异于C 矛盾,所以直线BE 与直线CF 必不在同一平面上,A 正确;B.若存在点E 使得直线BE ⊥平面DCE ,AE ⊂平面AECD ,所以BE AE ⊥,又AB BE ⊥,所以△ABE 中有两个直角,与三角形内角和为180 矛盾,所以不存在点E 使得直线BE ⊥平面DCE ,B 不正确;C.取F 为BD 的中点,12EC AD =,再取AB 的中点G ,则EC FG 且EC =FG ,四边形ECFQ 为平行四边形,所以FC EG ,则直线CF 与平面BAE 平行,C 正确;D.过B 作BO ⊥AE 于O ,因为平面BAE ⊥平面AECD ,平面BAE 平面AECD =AE ,所以BO ⊥平面AECD .过D 作DH ⊥AE 于H ,因为平面BAE ⊥平面AECD ,平面BAE 平面AECD =AE ,所以DH ⊥平面BAE ,所以DH BE ⊥.若存在点E 使得直线BE 与直线CD 垂直,DH ⊂平面AECD ,DC ⊂平面AECD ,DH DC D = ,所以AE ⊥平面AECD ,所以E 与O 重合,与三角形ABE 是以B 为直角的三角形矛盾,所以不存在点E 使得直线BE 与直线CD 垂直,D 不正确.故选AC.【名师点睛】本题考查空间想象能力,逻辑推理能力,空间直线、平面之间的位置关系,反证法的运用,属于难题.求解时,分别判断各个选项是否正确,对于A ,证明两直线异面考虑用反证法;对于B ,C ,D 只要能找到某个位置成立,则命题正确,否则利用反证法进行证明.10.已知12F F 、分别是双曲线()222210,0x y a b a b-=>>的左、右焦点,过点2F 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点P ,若点P 在以线段12F F 为直径的圆外,则双曲线离心率的取值可能为A .2B .3C .4D .5【答案】BCD【解析】不妨设过点2(,0)F c 与双曲线的一条渐近线平行的直线为()by x c a=-,与双曲线另一条渐近线b y x a =-交点为(,)22c bcP a-,因为点P 在以线段12F F 为直径的圆外,所以120PF PF ⋅>uuu r uuu r ,即22222233(,)(,)0,0,30,222244c bc c bc c b c a b a a a-⋅>-+>-+>222230,4a c a e -+->>,2e ∴>,故选BCD.【名师点睛】解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于,,a b c 的方程或不等式,再根据,,a b c 的关系消掉b 得到,a c 的关系式,而建立关于,,a b c 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.求解时,先求点P 坐标,再根据向量数量积列不等式,化简得到关于离心率e 的不等式,解得离心率取值范围.11.设函数()3,2,x x af x x x a ⎧≤=⎨->⎩.①若0a =,则()f x 的最大值为______;②若()f x 无最大值,则实数a 的取值范围是______.【答案】0(,0)-∞【解析】①若0a =,则()3,02,0x x f x x x ⎧≤=⎨->⎩,当0x ≤时,3()f x x =,此时函数为增函数,当0x >时,()2f x x =-,此时函数为减函数,故当0x =时,()f x 的最大值为()00f =;②当0a >时,()3,2,x x af x x x a⎧≤=⎨->⎩图象如图所示:由图可知存在最大值;当0a <时,()3,2,x x af x x x a ⎧≤=⎨->⎩图象如图所示:由图可知此时不存在最大值;由(1)知当0a =时,函数()f x 有最大值,综上所述,若()f x 无最大值,则0a <.故答案为:0;(,0)-∞.【名师点睛】本题考查的知识点是分段函数的应用,函数的最值,难度中档.求解时,①当0a =时,研究其单调性,根据单调性求出最大值;②若()f x 无最大值,则302a a a <⎧⎨->⎩,解不等式组即可得答案.12.已知数列{}n a 的前n 项和公式为2n S n =,若2n a n b =,则n a =________;数列{}n b 的前n 项和n T =__________.【答案】21n -()2413n -【解析】当111,1n a S ===2,n ≥121n n n a S S n -=-=-,满足11a =,故n a =21n -,若2n a n b =,则212n n b -=,故数列{}n b 的前n 项和()()214241143n n n T -==--.故答案为:21n -;()2413n -.【名师点睛】本题考查利用前n 项和求通项公式,考查等比数列求和,是基础题.求解时,由2,n ≥1n n n a S S -=-得数列{}n a 的通项,利用等比数列求和得数列{}n b 的前n 项和.热点02集合与常用逻辑用语【命题趋势】1.在新一轮课改中集合仍然作为一个必考内容出现,集合之间的混合运算以及集合信息的迁移一直高考的一个热点,主要还是放在选择题前两题为主,此部分内容较为简单,常与函数、方程、不等式结合起来考查.2.常见的逻辑用语部分对于数学来说是一种工具类的知识点,很容易与各个知识点相结合起来进行考查.立体几何,数列,三角函数,解析几何等.但是近几年全国卷出现的频率较少.但随着新课标的进行,综合一些趋势方向,相信常用逻辑用语也会逐渐加入高考行列.【考查题型】选择题【满分技巧】给定集合是不等式的解集的用数轴.给定集合是点集的用数形结合去求.给定集合是抽象几何的用Venn 图去求.对于常见的逻辑词来说,重难点是要分清楚命题的否定与否命题之间的区别于联系.原命题与你否命题等价,剩下两个等价.亦可以采用逆向思维去求.对于充分必要条件问题,最好的理解方法亦是转化成集合与子集的观点去探究.充分亦是子集.充要亦是集合相等.主要是观察两个集合哪一个范围更大一些.范围小的就是范围大的的充分,亦是范围大的是范围小的的必要即可.【常考知识】集合常与不等式,基本函数结合,常见逻辑用语常与立体几何,三角函数,数列,线性规划等结合.【限时检测】(建议用时:30分钟)1.(2019全国Ⅰ文2)已知集合{}{}{}1,2,3,4,5,6,72,3,4,52,3,6,7UA B ===,,,则U B A = ðA .{}1,6B .{}1,7C .{}6,7D .{}1,6,7【答案】C【解析】因为{}1234567234{}}23{567U A B ===,,,,,,,,,,,,,,,所以C 17{}6U A =,,,则{67 }U B A =I ,ð.故选C .2.(2019全国Ⅱ文1)已知集合={|1}A x x >-,{|2}B x x =<,则A ∩B =A .(–1,+∞)B .(–∞,2)C .(–1,2)D .∅【答案】A【解析】(1,)A =-+∞,(,2)B =-∞,(1,2)A B =- .故选C.【名师点睛】对于有关不等式的集合之间的运算画数轴是最简便,不容易出错的3.(2019天津文1)设集合{}1,1,2,3,5A =-,{}2,3,4B =,{|13}C x R x =∈< ,则()A C B = (A ){2}(B ){2,3}(C ){-1,2,3}(D ){1,2,3,4}【答案】D【解析】设集合{}1,1,2,3,5A =-,{}13C x x =∈<R ,则{}1,2A C = .又{}2,3,4B =,所以{}{}{}{}1,22,3,41,2,3,4A C B == .故选D.4.已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=,则集合A B 中的元素个数为A .5B .4C .3D .2【答案】D【解析】集合{|32,}A x x n n N ==+∈,当0n =时,322n +=,当1n =时,325n +=,当2n =时,328n +=,当3n =时,3211n +=,当4n =时,3214n +=,∵{6,8,10,12,14}B =,∴A B 中元素的个数为2,选D .【名师点睛】集合运算中,应当特别注意集合中的取值范围5.已知集合22{(,)|1,,}A x y x y x y Z =+∈≤,{(,)|||2,B x y x =≤||2,,}y x y Z ∈≤,定义集合12121122{(,)|(,),(,)}A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为A .77B .49C .45D .30【答案】C 【解析】由题意知,22{(,)1,,}{(1,0),(1,0),(0,1),(0,1)}A x y x y x y =+≤∈=--Z ,{(,)||2,||2,,}B x y x y x y =≤≤∈Z ,所以由新定义集合A B ⊕可知,111,0x y =±=或110,1x y ==±.当111,0x y =±=时,123,2,1,0,1,2,3x x +=---,122,1,0,1,2y y +=--,所以此时A B ⊕中元素的个数有:7535⨯=个;当110,1x y ==±时,122,1,0,1,2x x +=--,123,2,1,0,1,2,3y y +=---,这种情形下和第一种情况下除12y y +的值取3-或3外均相同,即此时有5210⨯=,由分类计数原理知,A B ⊕中元素的个数为351045+=个,故应选C .【名师点睛】本题主要考查学生的运算能力以及细心程度,属于新定义问题.通过理解新定义计算法则,此题容易遗漏某些点.6.设整数4n ≥,集合{}1,2,3,,X n = ,令集合{(,,)|,,S x y z x y z X =∈,且三条件,,x y z y z x z x y <<<<<<恰有一个成立},若(),,x y z 和(),,z w x 都在S 中,则下列选项正确的是A .(),,y z w S ∈,(),,x y w S∉B .(),,y z w S ∈,(),,x y w S ∈C .(),,y z w S ∉,(),,x y w S∈D .(),,y z w S ∉,(),,x y w S∉【答案】B【解析】特殊值法,不妨令2,3,4x y z ===,1w =,则()(),,3,4,1y z w S =∈,()(),,2,3,1x y w S =∈,故选B .如果利用直接法:因为(),,x y z S ∈,(),,z w x S ∈,所以x y z <<…①,y z x <<…②,z x y <<…③三个式子中恰有一个成立;z w x <<…④,w x z <<…⑤,x z w <<…⑥三个式子中恰有一个成立.配对后只有四种情况:第一种:①⑤成立,此时w x y z <<<,于是(),,y z w S ∈,(),,x y w S ∈;第二种:①⑥成立,此时x y z w <<<,于是(),,y z w S ∈,(),,x y w S ∈;第三种:②④成立,此时y z w x <<<,于是(),,y z w S ∈,(),,x y w S ∈;第四种:③④成立,此时z w x y <<<,于是(),,y z w S ∈,(),,x y w S ∈.综合上述四种情况,可得(),,y z w S ∈,(),,x y w S ∈.7.已知全集为R ,集合112x A x ⎧⎫⎪⎪⎛⎫=≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,{}2|680B x x x =-+≤,则R A C B =A .{}|0x x ≤B .{}|24x x ≤≤C .{|024}x x x ≤<>或D .{|024}x x x ≤≤≥或【答案】C 【解析】[)0,A =+∞,[]2,4B =,∴[0,2)(4,)R A B =+∞ ð【名师点睛】考查指数函数有关性质,注意指数函数底数为0到1的数,是单调递减函数另外集合属于一元二次不等式的解法.8.已知,A B 均为集合U ={1,3,5,7,9}的子集,且{3}A B = ,{9}U B A = ð,则A =A .{1,3}B .{3,7,9}C .{3,5,9}D .{3,9}【答案】D【解析】因为{3}A B = ,所以3∈A ,又因为{9}U B A = ð,所以9∈A ,所以选D .本题也可以用Venn 图的方法帮助理解.9.(2019北京文6)设函数f (x )=cos x +b sin x (b 为常数),则“b =0”是“f (x )为偶函数”的(A )充分而不必要条件(B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件【答案】C.【解析】若0b =,则()cos f x x =是偶函数;反之,若()f x 为偶函数,则()()f x f x -=,即()()cos sin cos sin cos sin x b x x b x x b x -+-=-=+,即sin 0b x =对x ∀成立,可得0b =,故“0b =”是“()f x 为偶函数”的充分必要条件.故选C.10.(2019浙江5)若a >0,b >0,则“a +b ≤4”是“ab ≤4”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【解析】因为a >0,b >0,若a +b ≤4,则4a b + ,则4ab ,即44a b ab +⇒ .反之,若4ab ,取1a =,4b =,则44ab = ,但5a b +=,即4ab 推不出a +b ≤4,所以a +b ≤4是4ab 的充分不必要条件.故选A .11.(2019全国Ⅲ文11)记不等式组6,20x y x y +⎧⎨-≥⎩表示的平面区域为D .命题:(,),29p x y D x y ∃∈+ ;命题:(,),212q x y D x y ∀∈+ .下面给出了四个命题①p q ∨②p q ⌝∨③p q ∧⌝④p q⌝∧⌝这四个命题中,所有真命题的编号是A .①③B .①②C .②③D .③④【答案】A 【解析】作出不等式组620x y x y +⎧⎨-⎩的平面区域如图阴影部分所示.由图可知,命题():,,29p x y D x y ∃∈+ ;是真命题,则p ⌝假命题;命题():,,212q x y D x y ∀∈+ 是假命题,则真命题;所以:由或且非逻辑连词连接的命题判断真假有:p q ∨真; p q ⌝∨假;●p q ∧⌝真;❍p q ⌝∧⌝假;故答案●正确.故选A.【名师点睛】线性规划与逻辑词相结合是比较新颖的题型,需要对线性规划一个充分的理解,需要对图像有一个比较清晰的认识理解.从图形中去挖掘信息.另此题比较简单的方法在所在的区域找特殊点进行验证.12.(2018浙江)已知平面α,直线m ,n 满足m α⊄,n α⊂,则“m ∥n ”是“m ∥α”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【解析】若m α⊄,n α⊂,m ∥n ,由线面平行的判定定理知m ∥α.若m ∥α,m α⊄,n α⊂,不一定推出m ∥n ,直线m 与n 可能异面,故“m ∥n ”是“m ∥α”的充分不必要条件.故选A .13.(2018北京)设a ,b ,c ,d 是非零实数,则“ad bc =”是“a ,b ,c ,d 成等比数列”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】a ,b ,c ,d 是非零实数,若ad bc =,则b d a c=,此时a ,b ,c ,d 不一定成等比数列;反之,若a ,b ,c ,d 成等比数列,则a c b d =,所以ad bc =,所以“ad bc =”是“a ,b ,c ,d 成等比数列”的必要而不充分条件.故选B .14.(2017山东)已知命题p :,x ∃∈R 210x x -+≥;命题q :若22a b <,则a b <.下列命题为真命题的是A .p q∧B .p q ⌝∧C .p q ⌝∧D .p q⌝⌝∧【答案】B【解析】取0x =,知1p 成立;若22a b <,得||||a b =,q 为假,所以p q ⌝∧为真.选B .15.(2017浙江)已知等差数列{}n a 的公差为d ,前n 项和为n S ,则“0d >”是“465+2S S S >”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】.C【解析】∵655465()()S S S S a a d ---=-=,当0d >,可得465+2S S S >;当465+2S S S >,可得0d >.所以“0d >”是“465+2S S S >”充分必要条件,选C .16.已知直线,a b 分别在两个不同的平面α,b 内,则“直线a 和直线b 相交”是“平面α和平面β相交”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】根据已知,如果直线,a b 相交,则平面,αβ一定存在公共点,故其一定相交;反之,如果平面,αβ相交,分别位于这两个平面内的直线不一定相交,故为充分不必要条件,选A .17.“sin cos αα=”是“cos 20α=”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【解析】∵22cos 2cos sin ααα=-,当sin cos αα=时,cos 20α=,充分性成立;当cos 20α=时,即22cos sin 0αα-=,∴cos sin αα=或cos sin αα=-,必要性不成立.18.函数()f x 在0=x x 处导数存在,若()00p f x '=:,0:q x x =是()f x 的极值点,则A .p 是q 的充分必要条件B .p 是q 的充分条件,但不是q 的必要条件C .p 是q 的必要条件,但不是q 的充分条件D .p 既不是q 的充分条件,也不是q 的必要条件【答案】C【解析】设3()f x x =,(0)0f '=,但是()f x 是单调增函数,在0x =处不存在极值,故若p 则q 是一个假命题,由极值的定义可得若q 则p 是一个真命题,故选C .【名师点睛】充分必要条件的选择与应用通过集合的观点去认识理解,对于这种题目迎刃而解.主要看的是谁的范围更小谁的范围更大.热点03函数及其性质【命题趋势】在新一轮高考改革中,函数仍旧是高中数学中的以后重难点.高中数学的学习当中,函数贯穿于整个数学内容,是学生最头疼的内容,也会高考当中最能拉开分值的考点,占有的分数比重比较高.内容量比较大,近年文科数学中,函数奇偶性,零点问题,恒成立问题,周期性问题以及单调性问题是高考函数中的核心.容易把具体函数与相应的性质相结合.通过列举了高考数学高频率考点,组合成了本专题,通过本函数及性质的专题的学习,让你对高中数学函数及其性质部分有充分的的理解,在以后遇到高考中的高频题型能够快速找到最佳解法.【考查题型】选择题,填空题【满分技巧】图像题是高考数学中函数及其性质高考必考题型,第一种解法三步走,第一步奇偶性判定,第二步单调性的判定,第三步特殊值的带入.第二种解法:也是三步走,第一步奇偶性判定,第二步特殊值带入.第三步特殊值带入.零点问题是近几年高考常考题目,此类题目务必采用数形结合.将复杂函数分割化,从而求出对应函数的交点问题.对于恒成立问题一般采用函数单调性的方法去做.M x f ≥)(恒成立则M 小于等于函数最小值,M x f ≤)(恒成立,则M 大于等于函数最大值,对于存在使的M x f ≤)(成立,则M 大于函数最小值.对于选择题则可以采用特殊值代入法.恒成立问题另外注意问题是双变量问题,双变量问题一般是指的是两个未知数相互不影响,即若)()(21x ≥g x f 恒成立,只要满足)(x f 定义域范围内最小值大于)(x g 最大值即可.分段函数单调性问题是简单题目也是最容易出错的问题,一般容易遗漏边界点.采用特殊值代入法时应采用多次带入方不会出错.函数及其性质一般会放在选择题的最后四题左右,相对来说比较难,在常规方法的同时应注意特殊点代入,抽象函数具体化.【常考知识】基本函数图像变换,奇偶性应用,周期性应用,单调性,不等式问题.【限时检测】(建议用时:60分钟)1(2018·全国高考真题(文))设函数()2010x x f x x -⎧≤=⎨>⎩,,,则满足()()12f x f x +<的x 取值范围是()A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,【答案】D 【解析】分析:首先根据题中所给的函数解析式,将函数图像画出来,从图中可以发现若有()()12f x f x +<成立,一定会有2021x x x <⎧⎨<+⎩,从而求得结果.详解:将函数()f x 的图像画出来,观察图像可知会有2021x x x <⎧⎨<+⎩,解得0x <,所以满足()()12f x f x +<的x 的取值范围是()0-∞,,故选D.点睛:该题考查的是有关通过函数值的大小来推断自变量的大小关系,从而求得相关的参数的值的问题,在求解的过程中,需要利用函数解析式画出函数图像,从而得到要出现函数值的大小,绝对不是常函数,从而确定出自变量的所处的位置,结合函数值的大小,确定出自变量的大小,从而得到其等价的不等式组,从而求得结果.2.(2019·全国高考真题(文))设()f x 是定义域为R 的偶函数,且在()0,∞+单调递减,则()A .233231log 224f f f --⎛⎫⎛⎫⎛⎫>> ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭B .233231log 224f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭。
2020高考全国二卷文科数学试题分析解析解读2020年高考数学试题继续坚持素养导向、能力立意的命题原则,试题重视数学本质、突出理性思维,考查数学素养,,注重数学应用价值。
多道试题源自真实的生活情境,让学生体会和思考生活中数学的存在、作用与魅力,激发学生的思考热情和科学精神。
试卷命题兼具了基础性、综合性、应用性和创新性,难度合理、区分度强,很好的体现了高考题的选拔功能。
2020年文科数学的高考题相对于2019年的真题,稳重有变,文理数学相同的题的数量由19年的9道题到今年的11道题,文理差异略有减小。
趋向新高考改革的思路。
下面来谈谈,2020年文科数学高考题的特征。
基础题比例合理,注重主干知识的考查试卷中有14道基础题,这些题学生比较容易找到解题思路,题型相对稳定,与平时训练的题相似度较高。
有助于考生在考场上稳定情绪,增强信心。
综合性与应用性的问题及解答题顺序与难度的调整综合性较强的题如11.12.16都是文理相同的题,如试卷的第11题对球的问题进行考查,核心是球小圆半径的计算,学生需要读懂题,画明白图,并且精准计算。
第12题函数题,则要求学生从中分离变量,再进一步提炼出函数:进行分析,这体现了函数思想的综合应用。
我校学生在模考中见过与第11题 12题相似度在90%的题。
第16题立体几何题,则综合了平面的基本性质(这个是容易被学生忽略的知识点)、空间中的平行、垂直关系和逻辑进行考查,同时要求学生写出"所有真命题的序号" ,这种考法也衔接了新高考中的"不定项选择题”,是一个综合性强、难度合理、区分度大的题目,作为选填的最后一题非常合适。
应用性较强的题,就是我们平时所说的情景题,第3题以音乐乐理中的原位大三和弦、原位小三和弦为背景进行考察,体现了数学与音乐之间的联系,渗透了数学之美无处不在。
同时,对于没有学过乐理的考生,只要能读懂题干信息中数学语言,肯动手列举,就能发现规则背后的本质。
2020年普通高等学校招生全国统一考试高三文科数学压轴(一)试题1.已知集合{}M x y x ==和{}2N y y x ==,则下列结论正确的是( )A .M N =B .M N ⋂=∅C .M N R =UD .MN2.复数()221i z i +=-在复平面内对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限3.中央电视台每天晚上的“焦点访谈”是时事、政治性较强的一个节目,其播出时间是在晚上看电视节目人数最多的“黄金时间”,即晚上7点与8点之间的一个时刻开始播出,这一时刻是时针与分针重合的时刻,以高度显示“聚焦”之意,比喻时事、政治的“焦点”,则这个时刻大约是( ) A .7点36分B .7点38分C .7点39分D .7点40分4.以椭圆22194y x +=的长轴端点作为短轴端点,且过点()4,1-的椭圆的焦距是( ) A .16B .12C .8D .65.2019年北京世园会的吉祥物“小萌芽、小萌花”,是一对代表着生命与希望、勤劳与美好、活泼可爱的园艺小兄妹,造型创意来自东方文化中百子图的“吉祥娃娃”,通过头饰、道具、服装创意的巧妙组合,被赋予了普及园艺知识、传播绿色理念的特殊使命.现将三张分别印有“小萌芽”、“小萌花”、“牡丹花”这三个图案的卡片(卡片的形状和大小相同,质地也相同)放入盒子中.若从盒子中依次有放回的取出两张卡片,则一张为小萌芽,一张为小萌花的概率是( ) A .23B .13C .29D .196.古代人家修建大门时,贴近门墙放置两个石墩.石墩其实算是门墩,又称门枕石,在最初的时候起支撑固定院门的作用,为的是让门栓基础稳固,防止大门前后晃动.不过后来不断演变,一是起到装饰作用,二是寓意“方方圆圆”.如图所示,画出的是某门墩的三视图,则该门墩从上到下分别是( )A .半圆柱和四棱台B .球的14和四棱台 C .半圆柱和四棱柱D .球的14和四棱柱7.已知等比数列{}n a 的前n 项和为n S ,若公比为12q =-,6214S =,则数列{}n a 的前n 项之积n T 的最大值为( ) A .16B .32C .64D .1288.若函数()ln f x x =与()21263g x x x k =+-的图象只有一个公共点,且在这个公共点处的切线相同,则实数k =( ) A .13B .23C .16D .569.为了计算333333333333333S =++++,设计了如图所示的程序,则判断框内应填入( )A .3?i >B .4?i >C .5?i >D .6?i >10.某纺织企业通过电脑设计各种美丽的布料图案,设计者考虑用一条长度为a 的线段EF ,其端点E 、F 在边长为3的正方形ABCD 的四条边上滑动,如图所示,当EF 绕着正方形的四边滑动一周时,以A 为原点,AB 、AD 所在直线分别为x 轴、y 轴,探究EF 的中点M 所形成的轨迹.其中2a =时,点M 的轨迹是( )A .B .C .D .11.已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ,过点2F 作一条直线与C 的右支交于A 、B 两点,且190F AB ∠=︒,若1F AB V 的内切圆直径等于实轴的长,则C 的离心率为( )A B C D 12.若定义在R 上的偶函数()f x 满足()()2f x f x +=,且在区间[]1,2上是减函数,()11f =,()01f =-现有下列结论,其中正确的是:( )①()f x 的图象关于直线1x =对称;②()f x 的图象关于点3,02⎛⎫⎪⎝⎭对称;③()f x 在区间[]3,4上是减函数;④()f x 在区间()4,4-内有8个零点. A .①③B .②④C .①③④D .②③④13.已知(),1a k =r ,()2,4b =-r ,()4,3c =-r ,若()c a b R λλ=+∈r r r ,则a r 与b r的夹角为______.14.已知n S 为等差数列{}n a 的前n 项和,公差0d ≠,且1224S =,1a ,7a ,5a 成等比数列,则1a =__________.15.已知函数()()()sin 0,02f x x ωϕωϕπ=+><<满足:①()f x 的图象关于点,012π⎛⎫- ⎪⎝⎭对称;②()f x 的图象关于直线6x π=对称.则满足①和②的ω,ϕ的一组值分别是______.16.在圆锥SO 中,A 、B 、M 是底面圆周上的点,且OA OB ⊥,N 是线段OA 上的一点,且//MN OB ,2SO OA ==,则三棱锥S MON -体积V 的最大值是______;当V 取得最大值时,SM 与OB 所成角的大小为______.17.某市数学教研室对全市2018级15000名的高中生的学业水平考试的数学成绩进行调研,随机选取了200名高中生的学业水平考试的数学成绩作为样本进行分析,将结果列成频率分布表如下:根据学业水平考试的数学成绩将成绩分为“优秀”、“合格”、“不合格”三个等级,其中成绩大于或等于80分的为“优秀”,成绩小于60分的为“不合格”,其余的成绩为“合格”.(1)根据频率分布表中的数据,估计全市学业水平考试的数学成绩的众数、中位数(精确到0.1);(2)市数学教研员从样本中又随机选取了()*n n N∈名高中生的学业水平考试的数学成绩,如果这n 名高中生的学业水平考试的数学成绩的等级情况恰好与按照三个等级分层抽样所得的结果相同,求n 的最小值;(3)估计全市2018级高中生学业水平考试“不合格”的人数.18.在ABC V 中,120BAC ∠=︒,sin 7ABC ∠=,D 是CA 延长线上一点,且24AD AC ==.(1)求sin ACB ∠的值; (2)求BD 的长.19.在三棱柱111ABC A B C -中,侧面11ACC A ⊥底面ABC ,11AA BC ==,12A B AC ==,AB =E 为AB 的中点.(1)求证:1//BC 平面1A CE ; (2)求1A C 的长.20.在平面直角坐标系xOy 中,已知1F 、2F 分别为椭圆22143x y +=的左、右焦点,直线1l 过点1F 且垂直于椭圆的长轴,动直线2l 垂直于直线1l 于点P ,线段2PF 的中垂线交2l 于点Q .记点Q 的轨迹为曲线E .(1)求曲线E 的方程,并说明E 是什么曲线;(2)若直线:l y x k =+与曲线E 交于两点A 、B ,则在圆()22:22C x y -+=上是否存在两点M 、N ,使得MA MB =,NA NB =?若存在,请求出k 的取值范围;若不存在,请说明理由.21.已知函数()()2ln af x ax x a R x=--∈. (1)讨论函数()f x 的极值;(2)设01a <<,若曲线()y f x =在两个不同的点()(),M m f m ,()(),N n f n 处的切线互相平行,求证:()()0f m f n +>.22.在平面直角坐标系xOy 中,圆C的参数方程为,x a y αα⎧=+⎪⎨=⎪⎩(α为参数),直线l的参数方程为,,x y ⎧=⎪⎨=⎪⎩(t 为参数),设原点O 在圆C 的内部,直线l 与圆C 交于M 、N 两点;以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求直线l 和圆C 的极坐标方程,并求a 的取值范围; (2)求证:22OMON +为定值.23.(1)已知0x >,0y >,0z >,证明:222111y z x x y z x y z++≥++; (2)已知1a >,1b >,1c >,且8abc =,若222log log log log log log b c a a a b b c c k ⋅+⋅+⋅≥恒成立,求实数k 的最大值.参考答案1.A 【解析】 【分析】利用函数的定义域可知0x ≥求出集合M ,根据二次函数值域的求法求出N ,再利用集合之间的基本关系即可求解. 【详解】[)0,M =+∞,[)0,N =+∞,所以M N =,故选:A. 【点睛】本题主要考查了集合的基本运算,同时考查了函数的定义域、值域的求法,属于基础题. 2.C 【解析】 【分析】利用复数的乘、除运算可得13z i =--,再利用导数的几何意义即可求解. 【详解】()()()()()2222113111i i i z i i i i ++--===------,对应点的坐标为()1,3--, 故选:C. 【点睛】本题考查了导数的几何意义以及导数的四则运算,属于基础题. 3.B 【解析】 【分析】设7点t 分()060t <<时针OA 与分针OB 重合,在7点时,时针、分针所成的夹角为210︒,根据时针每分钟转0.5︒,分针每分钟转6︒,可得60.5210t t ︒=︒+︒,解方程即可. 【详解】设7点t 分()060t <<时针OA 与分针OB 重合.在7点时,时针OC 与分针OD 所夹的角为210︒, 时针每分钟转0.5︒,分针每分钟转6︒,则分针从OD 到达OB 需旋转6t ︒,时针从OC 到达OA 需旋转0.5t ︒, 于是60.5210t t ︒=︒+︒,解得2383811t =≈(分),故选:B. 【点睛】本题考查了任意角的表示以及终边相同角的表示,考查了基本运算能力,属于基础题. 4.D 【解析】 【分析】设所求椭圆的方程为22219x y a +=,将点()4,1-代入,求出a ,由222c a b =-即可求解.【详解】设所求椭圆的方程为2221,(3)9x y a a +=>,将点()4,1-代入,解得218a =,则2221899c a b =-=-=,即3c =,26c =, 故选:D. 【点睛】本题考查了待定系数法求椭圆的标准方程,椭圆的简单几何性质,属于基础题. 5.C 【解析】 【分析】将卡片分别为A 、B 、C ,根据抽取方法列出基本事件个数,然后再利用古典概型的概率计算公式即可求解. 【详解】记印有“小萌芽”、“小萌花”、“牡丹花”图案的卡片分别为A 、B 、C , 则基本事件分别为(),A B ,(),A C ,(),B C ,(),A A ,(),B B ,(),C C ,(),B A ,(),C A ,(),C B ,共9种情况.其中一张为小萌芽,一张为小萌花是(),A B ,(),B A 共2种情况, 所以所求的概率为29P =, 故选:C. 【点睛】本题主要考查了古典概型的概率计算公式,解题的关键是列出基本事件个数,属于基础题. 6.D 【解析】 【分析】根据几何体的三视图直观想象出几何体的直观图,从而可得几何体的结构特征. 【详解】由几何体的三视图可知: 该几何体上面是球的14,下面是放倒的四棱柱. 故选:D 【点睛】本题考查了几何体的三视图还原直观图,考查了空间想象能力,属于基础题. 7.C 【解析】 【分析】利用等比数列的前n 项和公式求出18a =,从而可求出前n 项之积n T 的最大值. 【详解】由12q =-,6214S =,得61112211412a ⎡⎤⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦=⎛⎫-- ⎪⎝⎭,解得18a =, 所以数列{}n a 为8,4-,2,1-,12,14-,……,前4项乘积最大为64.故选:C. 【点睛】本题主要考查了等比数列的前n 项和公式基本量的运算,需熟记公式,属于基础题. 8.D 【解析】 【分析】设公共点为()00,P x y ,根据导数的几何意义可得()()()()0000f x g x f x g x ''⎧=⎪⎨=⎪⎩,根据函数表达式以及导函数解方程组即可. 【详解】设两个函数图象的公共点为()00,P x y ,根据题意,得()()()()0000,,f x g x f x g x ''⎧=⎪⎨=⎪⎩即()()20000012ln ,163112,233x x x k x x ⎧=+-⎪⎪⎨⎪=+⎪⎩,解()2式得01x =或03x =-(舍去),代入第()1式,解得56k =. 故选:D. 【点睛】本题考查了导数的几何意义以及基本初等函数的导数公式,熟记导数公式、运算法则是解题的关键,属于基础题. 9.C 【解析】 【分析】根据流程图,写出每次循环运行的结果即可得出结果. 【详解】13a =,13S =,2i =;233a =,2333S =+,3i =;3333a =,3333333S =++,4i =;43333a =,43333333333S =+++,5i =;533333a =,5333333333333333S =++++,6i =,此时满足5i >,则输出5333333333333333S =++++.故选:C.【点睛】本题考查了程序框图,考查了基本的运算能力,属于基础题.10.B【解析】【分析】 根据题意可得12AM EF =,设()0,E m ,(),0F n ,(),M x y ,利用两点间的距离公式直接列方程即可求解.【详解】 由题意,得12AM EF =, 设()0,E m ,(),0F n ,(),M x y ,1212==⨯=,解得)01y x =<≤,将函数)01y x =<≤的图象(记为1C )关于直线32x =对称,可得函数)23y x =<≤的图象(记为2C ); 将1C 和2C 的图象分别关于直线32y =对称, 可分别得到以正方形ABCD 的顶点D 、C 为圆心、1为半径的14圆弧. 故选:B.【点睛】本题考查了圆的轨迹方程,解题的关键是列出方程,属于基础题.11.C【解析】【分析】 设1AF m =,()2AF n m n =>,根据双曲线的定义可得2m n a -=,结合2224m n c +=,解得224mn b =,在1Rt F AB V 中,内切圆直径1212r m AB F B m n F B F B =+-=++-,再根据22a a =即可求解.【详解】 设1AF m =,()2AF n m n =>,由题意,得2224m n c +=,2m n a -=,解得224mn b =,则()22222244m n m n mn c b +=++=+,即m n +=;1Rt F AB V 的内切圆直径12122r m AB F B m n F B F B a =+-=++-=,根据题意,得22a a =,解得e , 故选:C.【点睛】本题考查了双曲线的简单几何性质、双曲线的定义以及焦点三角形,属于中档题.12.C【解析】【分析】根据题意可得()()2f x f x -=-,再由函数为偶函数可得()()2f x f x -=,从而可判断①;无法推出()()3f x f x -=-,可判断②;利用周期为2可判断③;利用对称性可判断④.【详解】由()()2f x f x +=,得()()2f x f x -=-,结合()f x 为偶函数,得()()2f x f x -=,则曲线()y f x =关于直线1x =对称,则①正确;无法推出()()3f x f x -=-,则②不一定正确;由曲线()()12y f x x =≤≤可得曲线()()01y f x x =≤≤,即得曲线()()02y f x x =≤≤,恰好是在一个周期内的图象;再根据()f x 是以2为周期的函数,得到曲线()()24y f x x =≤≤,因为在()y f x =在[]1,2上是减函数,()y f x =在[]3,4上是减函数,则③正确; 因为()y f x =在[]1,2上是减函数,()110f =>,()210f =-<,所以()y f x =在[]1,2上有唯一的一个零点,根据对称性,()f x 在区间()4,4-内有8个零点.故选:C.【点睛】本题考查了函数的奇偶性、周期性、单调性的应用,考查了函数性质的应用,属于基础题. 13.90°【解析】【分析】利用向量线性运算的坐标表示求出1λ=,2k =,从而可得()2,1a =r ,再利用向量数量积的坐标表示即可求解.【详解】由已知,得()()()4,3,12,4k λ-=+-,即()()4,32,14k λλ-=+-,解得1λ=,2k =,则()2,1a =r ,所以0a b ⋅=r r ,从而a r 与b r 的夹角为90°.故答案为:90°【点睛】本题考查了向量线性运算的坐标表示、向量数量积的坐标表示,根据向量的数量积求向量的夹角,属于基础题.14.-9【解析】【分析】由1224S =,利用等差数列的前n 项和公式,求得12114a d +=,又由1a ,7a ,5a 成等比数列,利用等差数列的通项公式,求得1290a d +=,联立方程组,即可求解.【详解】由题意知1224S =,则1121112242a d ⨯+=,即12114a d +=, 又由1a ,7a ,5a 成等比数列,则2715a a a =,所以()()211164a d a a d +=+,即1290a d +=,联立方程组,解得19a =-.【点睛】本题主要考查了等差数列的通项公式,以及前n 项和公式的应用,其中解答中熟记等差数列的通项和前n 项和公式,准确计算是解答的关键,着重考查了运算与求解能力,属于基础题.15.2;6π 【解析】【分析】 根据题意可得4612T πππ⎡⎤⎛⎫=-= ⎪⎢⎥⎝⎭⎣⎦,再由2T πω=求出2ω=,将点,012π⎛⎫- ⎪⎝⎭代入表达式求出6π=ϕ即可. 【详解】 可将,012π⎛⎫- ⎪⎝⎭和6x π=视为()f x 在一个周期内的相邻的对称中心与对称轴, 则4612T πππ⎡⎤⎛⎫=-= ⎪⎢⎥⎝⎭⎣⎦,于是2ω=; 将,012π⎛⎫- ⎪⎝⎭代入()sin 2y x ϕ=+,得sin 2012πϕ⎡⎤⎛⎫⨯-+= ⎪⎢⎥⎝⎭⎣⎦,结合02ϕπ<<,可取6π=ϕ. 故答案为:2;6π 【点睛】 本题考查了利用三角函数的性质求解析式,需熟记三角函数的对称轴以及对称中心与函数周期的关系,属于基础题.16.2360° 【解析】【分析】由题意设()02ON x x =<<,可得MN =11232V =⨯⨯⨯60SMN ∠=︒,由//MN OB 即可求解.【详解】由//MN OB 及OA OB ⊥,得OA MN ⊥;设()02ON x x =<<,则MN =所以三棱锥S MON -体积为:()2241111112232323323x x V SO ON MN +-=⋅⋅=⨯⨯⨯=⨯=(当且仅当x =时取等号),即max 23V =. 由SO ⊥平面AOB ,得SO MN ⊥, 结合OA MN ⊥,得MN ⊥平面SOA ,从而MN SN ⊥.由ON =2OM =,得MN =SM =60SMN ∠=︒;由//MN OB ,得SM 与OB 所成角为60SMN ∠=︒. 故答案为:23;60° 【点睛】本题考查了三棱锥的体积公式、异面直线所成的角,同时考查了线面垂直的判定定理,属于基础题.17.(1)众数、中位数分别为75,74.3;(2)n 的最小值为10;(3)1500.【解析】【分析】(1)由频率分布表中的数据,众数为70802+,设中位数为70x +,根据各组频率可得0.0250.0750.250.0350.5x +++=,解方程即可.(2)首先求出“优秀”、“合格”、“不合格”的人数,再根据分层抽样法可得()*6310N n k k k k k =++=∈即可.(3)根据“不合格”的人数所占的比例即可估计出总体.【详解】解:(1)此样本的众数为7080752+=; 设中位数为70x +,则0.0250.0750.250.0350.5x +++=,解得 4.3x ≈,所以中位数约为74.3.运用此样本的数字特征,可以估计总体的数字特征,所以全市学业水平考试的数学成绩的众数、中位数分别为75,74.3.(2)“优秀”、“合格”、“不合格”的人数分别为60,120,20,则“优秀”、“合格”、“不合格”的比例为3:6:1,所以按照分层抽样法,选取的人数为()*6310N n k k k k k =++=∈,故n 的最小值为10.(3)全市2018级高中生学业水平考试“不合格”的人数为115000150010⨯=. 【点睛】本题考查了样本的数字特征、分层抽样的特征、根据样本数字特征估计总体,考查了考生的数据分析、处理能力,属于基础题.18.(1)14(2【解析】【分析】(1)首先利用同角三角函数的基本关系求出cos ABC ∠=,根据三角形的内角和性质可得()sin sin 180120ACB ABC ∠=︒-︒-∠,利用诱导公式以及两角差的正弦公式即可求解.(2)在ABC V 中,利用正弦定理求出AB ,在ABD △中,利用余弦定理即可求解.【详解】解:(1)由sin 7ABC ∠=,得cos ABC ∠==, 所以()sin sin 180120ACB ABC ∠=︒-︒-∠()sin 60ABC =︒-∠sin60cos cos60sin ABC ABC =︒∠-︒∠1272714=-⨯=. (2)由正弦定理,得sin sin AB AC ACB ABC=∠∠,即2sin 1sin 7AC ACB AB ABC∠===∠. 由余弦定理,得BD==【点睛】本题考查了正弦定理、余弦定理解三角形、同角三角函数的基本关系、两角差的正弦公式,需熟记公式,属于基础题.19.(1)证明见解析;(2【解析】【分析】(1)连接1AC ,设11A C AC F ⋂=,可得1//EF BC ,再利用线面平行的判定定理即可证出. (2)由题意可得AC BC ⊥,结合面面垂直的性质定理可证出BC ⊥平面11ACC A ,从而可得1BC A A ⊥,根据线面垂直的判定定理可得1A A ⊥平面1A BC ,即可证出11⊥A A AC ,在1Rt AAC V 中,利用勾股定理即可求解 【详解】解:(1)连接1AC ,设11A C AC F ⋂=,则F 为1AC 的中点,因为E 为AB 的中点,所以1//EF BC .又1BC ⊄平面1A CE ,EF ⊂平面1A CE ,所以1//BC 平面1A CE .(2)在ABC V 中,由1BC =,2AC =,AB =得90ACB ∠=︒,即AC BC ⊥;在1A AB V 中,同理可得11A A A B ⊥.因为侧面11ACC A ⊥底面ABC ,侧面11ACC A I 底面ABC AC =,所以BC ⊥平面11ACC A ,又1A A ⊂平面11ACC A ,所以1BC A A ⊥,又1A B BC B =I ,所以1A A ⊥平面1A BC .因为1A A ⊥平面1A BC ,1AC ⊂平面1A BC , 所以11⊥A A AC . 在1Rt AAC V 中,由11AA =及2AC =,得1AC ===【点睛】本题考查了线面平行的判定定理、线面垂直的判定定理、线面垂直的性质定理,面面垂直的性质定理,考查了学生的逻辑推理能力,属于基础题.20.(1)24y x =;E 是以()21,0F 为焦点,1 : =-1l x 为准线的抛物线(2)存在;01k << 【解析】【分析】(1)根据题意可得2QP QF =,再根据抛物线的定义即可求出曲线E 的方程.(2)将直线:l y x k =+与曲线E :24y x =联立,由直线l 与曲线E 交于点()11,A x y ,()22,B x y ,>0∆,利用韦达定理可得1242x x k +=-,从而求出AB 的中垂线方程,由MA MB =,NA NB =,可得AB 的中垂线与圆C 交于两点M 、N ,利用点到直线的距离公式使圆心到直线的距离小于半径即可求解.【详解】(1)由题意,得2QP QF =,则动点Q 的轨迹是以()21,0F 为焦点,1 : =-1l x 为准线的抛物线,所以点Q 的轨迹E 的方程为24y x =.(2)由2,4,y x k y x =+⎧⎨=⎩得()22240x k x k +-+=. 由直线l 与曲线E 交于点()11,A x y ,()22,B x y ,得()222440k k =-->△,解得1k <.由韦达定理,得1242x x k +=-.设AB 的中点为()00,G x y , 则12022x x x k +==-,0022y x k k k =+=-+=, 即()2,2G k -,所以AB 的中垂线方程为()22y x k -=--+,即40x y k ++-=, 由MA MB =,NA NB =,得AB 的中垂线与圆C 交于两点M 、N ,<04k <<.由①和②,得01k <<.综上,当01k <<时,圆C 上存在两点M 、N ,使得MA MB =,NA NB =.【点睛】本题考查了抛物线的定义、直线与抛物线的位置关系,考查了考生的运算求解能力,属于难题.21.(1)答案不唯一,具体见解析(2)证明见解析;【解析】【分析】(1)求出()222ax x a f x x-+'=,分类讨论0a ≤或0a >,判断()f x '的正负即可求解. (2)根据题意可得()()f m f n ''=,代入导函数整理可得()()()222a m n m n m n m n mn-+-=,利用基本不等式证出2mn a >,从而()()22ln 2f m f n mn mn +=--,令mn t =,不妨设()()222ln 2g t t t t a=-->,利用导数判断()g t 的单调性,求出最小值即可证出.【详解】 解:(1)()22222a ax x a f x a x x x-+'=-+=,()0,x ∈+∞.(i )当0a ≤时,()0f x '<,则()f x 在()0,∞+上是减函数,此时()f x 无极值.(ii )当0a >时,考虑二次函数()22h x ax x a =-+,则()()()241411a a a =-=--+△. 当1a ≥时,0∆≤,则()0h x ≥,即对任意的()0,x ∈+∞恒成立,所以在()0,∞+上是增函数,此时()f x 无极值.当01a <<时,>0∆,则()0h x =的两根为1x =2x =当10x x <<时,()0f x '>;当12x x x <<时,()0f x '<;当2x x >时,()0f x '>,所以()f x 在()10,x 上是增函数,在()12,x x 上是减函数,在()2,x +∞上是增函数,所以()f x 在1x x =处有极大值,在2x x =处有极小值.(2)由题意,得()()f m f n ''=,0m >,0n >,m n ≠, 且2222a a a a m m n n-+=-+. 移项整理,得()()()222a m n m n m n m n mn -+-=. 因为0m >,0n >,m n ≠,所以()2mn a m n a =+>⋅,即2mn a >.()()2ln 2ln a a f m f n am m an n m n+=--+-- ()()()2ln 22ln 2a m n a m n mn mn mn mn+=+--=--. 令mn t =,则2t a >. 设()()222ln 2g t t t t a =-->,则()()2122t g t t t-'=-=. 当21a t <<时,()0g x '<;当1t >时,()0g t '>,所以()g t 在()2,1a 上是减函数,在()1,+∞上是增函数, 所以1t =是()g t 的极小值点,也是()g t 的最小值点,即()()10g t g >=,故()()0f m f n +>成立.【点睛】本题考查了利用导数研究函数的单调性、利用导数证明不等式,考查了分类讨论的思想,属于难题.22.(1)()4R πθρ=∈;()222cos 50a a ρθ-+-=;a 的取值范围是((2)证明见解析;【解析】【分析】(1)消参可得直线l 的直角坐标方程,利用直角坐标与极坐标的互化可得直线l 和圆C 的极坐标方程,根据原点在圆的内部可得()22005a -+<,解不等式即可.(2)将直线的极坐标方程代入圆的极坐标方程可得2250a ρρ+-=,由222212OM ON ρρ+=+,利用韦达定理即可求解. 【详解】解(1)将直线l 的参数方程化为直角坐标方程,得y x =,所以直线l 的极坐标方程为()4R πθρ=∈;将圆C 的参数方程化为直角坐标方程,得()225x a y -+=,所以圆C 的极坐标方程为()222cos 50a a ρθρ-+-=.由原点O 在圆C 的内部,得()22005a -+<,解得a <<故a的取值范围是(.(2)将4πθ=代入()222cos 50a a ρθρ-+-=,得2250a ρρ-+-=.则12ρρ+=,2125a ρρ=-, 所以()222221212122OM ON ρρρρρρ+=+=+-)()222510a =--=, 故22OM ON +为定值.【点睛】本题考查了直线的参数方程与普通方程的互化、普通方程与极坐标方程的互化、极坐标方程的应用,属于基础题.23.(1)证明见解析;(2)实数k 的最大值为3【解析】【分析】(1)利用基本不等式可得212y x y x+≥=,再根据不等式的性质:同向相加即可求解. (2)利用换底公式可得原式222222222222log 2log 2log 2log log log log log log log 2log 2log 2b c a a b c a b c b c a =++=++,结合(1)即可证出.【详解】(1)证明:由0x >,0y >,得212y x y x+≥=,即212y x y x +≥, 同理212z y z y +≥,212x z x z+≥,以上三式相加,得222111222y z x x y z x y z x y z+++++≥++ (当且仅当x y z ==时取等号), 故222111y z x x y z x y z++≥++成立. (2)解:222log log log log log log b c a a a b b c c ⋅+⋅+⋅222222222log log log log log log a b c b c a=++ 222log 2log 2log 2log 2log 2log 2b c a a b c =++, 根据(1),得222log 2log 2log 2111log 2log 2log 2log 2log 2log 2b c a a b c a b c ++≥++ ()2222log log log log a b c abc =++=2log 83==,所以,3k ≤,故实数k 的最大值为3.【点睛】本题考查了基本不等式证明不等式、不等式的性质、换底公式,属于基础题.。
2020年高考数学考点题型全归纳(文)微信公众号:数学研讨2019年6月29日第一章 集合与常用逻辑用语第一节 集 合一、基础知识1.集合的有关概念(1)集合元素的三个特性:确定性、无序性、互异性.元素互异性,即集合中不能出现相同的元素,此性质常用于求解含参数的集合问题中. (2)集合的三种表示方法:列举法、描述法、图示法. (3)元素与集合的两种关系:属于,记为∈;不属于,记为∉. (4)五个特定的集合及其关系图:N *或N +表示正整数集,N 表示自然数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.2.集合间的基本关系(1)子集:一般地,对于两个集合A ,B ,如果集合A 中任意一个元素都是集合B 中的元素,则称A 是B 的子集,记作A ⊆B (或B ⊇A ).(2)真子集:如果集合A 是集合B 的子集,但集合B 中至少有一个元素不属于A ,则称A 是B 的真子集,记作AB 或B A .AB ⇔⎩⎪⎨⎪⎧A ⊆B ,A ≠B .既要说明A 中任何一个元素都属于B ,也要说明B 中存在一个元素不属于A .(3)集合相等:如果A ⊆B ,并且B ⊆A ,则A =B .两集合相等:A =B ⇔⎩⎪⎨⎪⎧A ⊆B ,A ⊇B .A 中任意一个元素都符合B 中元素的特性,B 中任意一个元素也符合A 中元素的特性.(4)空集:不含任何元素的集合.空集是任何集合A的子集,是任何非空集合B的真子集.记作∅.∅∈{∅},∅⊆{∅},0∉∅,0∉{∅},0∈{0},∅⊆{0}.3.集合间的基本运算(1)交集:一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集,记作A∩B,即A∩B={x|x∈A,且x∈B}.(2)并集:一般地,由所有属于集合A或属于集合B的元素组成的集合,称为A与B的并集,记作A∪B,即A∪B={x|x∈A,或x∈B}.(3)补集:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作∁U A,即∁U A={x|x∈U,且x∉A}.求集合A的补集的前提是“A是全集U的子集”,集合A其实是给定的条件.从全集U中取出集合A 的全部元素,剩下的元素构成的集合即为∁U A.二、常用结论(1)子集的性质:A⊆A,∅⊆A,A∩B⊆A,A∩B⊆B.(2)交集的性质:A∩A=A,A∩∅=∅,A∩B=B∩A.(3)并集的性质:A∪B=B∪A,A∪B⊇A,A∪B⊇B,A∪A=A,A∪∅=∅∪A=A.(4)补集的性质:A∪∁U A=U,A∩∁U A=∅,∁U(∁U A)=A,∁A A=∅,∁A∅=A.(5)含有n个元素的集合共有2n个子集,其中有2n-1个真子集,2n-1个非空子集.(6)等价关系:A∩B=A⇔A⊆B;A∪B=A⇔A⊇B.考点一集合的基本概念[典例] (1)(2017·全国卷Ⅲ)已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为( )A.3 B.2C.1 D.0(2)已知a ,b ∈R ,若⎩⎨⎧⎭⎬⎫a ,b a,1={a 2,a +b,0},则a 2 019+b 2 019的值为( )A .1B .0C .-1D .±1[解析] (1)因为A 表示圆x 2+y 2=1上的点的集合,B 表示直线y =x 上的点的集合,直线y =x 与圆x 2+y 2=1有两个交点,所以A ∩B 中元素的个数为2.(2)由已知得a ≠0,则b a=0,所以b =0,于是a 2=1,即a =1或a =-1.又根据集合中元素的互异性可知a =1应舍去,因此a =-1,故a2 019+b2 019=(-1)2 019+02 019=-1.[答案] (1)B (2)C[提醒] 集合中元素的互异性常常容易忽略,求解问题时要特别注意. [题组训练]1.设集合A ={0,1,2,3},B ={x |-x ∈A,1-x ∉A },则集合B 中元素的个数为( ) A .1 B .2 C .3D .4解析:选A 若x ∈B ,则-x ∈A ,故x 只可能是0,-1,-2,-3,当0∈B 时,1-0=1∈A ;当-1∈B 时,1-(-1)=2∈A ;当-2∈B 时,1-(-2)=3∈A ;当-3∈B 时,1-(-3)=4∉A ,所以B ={-3},故集合B 中元素的个数为1.2.若集合A ={x ∈R|ax 2-3x +2=0}中只有一个元素,则a 等于( ) A.92 B.98C .0D .0或98解析:选D 若集合A 中只有一个元素,则方程ax 2-3x +2=0只有一个实根或有两个相等实根. 当a =0时,x =23,符合题意.当a ≠0时,由Δ=(-3)2-8a =0,得a =98,所以a 的值为0或98.3.(2018·厦门模拟)已知P ={x |2<x <k ,x ∈N},若集合P 中恰有3个元素,则k 的取值范围为 .解析:因为P 中恰有3个元素,所以P ={3,4,5},故k 的取值范围为5<k ≤6. 答案:(5,6]考点二 集合间的基本关系[典例] (1)已知集合A ={x |x 2-3x +2=0,x ∈R},B ={x |0<x <5,x ∈N},则( ) A .B ⊆A B .A =B C .AB D .BA(2)(2019·湖北八校联考)已知集合A ={x ∈N *|x 2-3x <0},则满足条件B ⊆A 的集合B 的个数为( )A .2B .3C .4D .8(3)已知集合A ={x |-1<x <3},B ={x |-m <x <m },若B ⊆A ,则m 的取值范围为________. [解析] (1)由x 2-3x +2=0得x =1或x =2,∴A ={1,2}.由题意知B ={1,2,3,4},比较A ,B 中的元素可知AB ,故选C.(2)∵A ={x ∈N *|x 2-3x <0}={x ∈N *|0<x <3}={1,2},又B ⊆A ,∴满足条件B ⊆A 的集合B 的个数为22=4,故选C.(3)当m ≤0时,B =∅,显然B ⊆A . 当m >0时,因为A ={x |-1<x <3}. 若B ⊆A ,在数轴上标出两集合,如图,所以⎩⎪⎨⎪⎧-m ≥-1,m ≤3,-m <m .所以0<m ≤1.综上所述,m 的取值范围为(-∞,1]. [答案] (1)C (2)C (3)(-∞,1] [变透练清]1.(变条件)若本例(2)中A 不变,C ={x |0<x <5,x ∈N},则满足条件A ⊆B ⊆C 的集合B 的个数为( ) A .1 B .2 C .3D .4解析:选D 因为A ={1,2},由题意知C ={1,2,3,4},所以满足条件的B 可为{1,2},{1,2,3},{1,2,4},{1,2,3,4}.2.(变条件)若本例(3)中,把条件“B ⊆A ”变为“A ⊆B ”,其他条件不变,则m 的取值范围为________.解析:若A ⊆B ,由⎩⎪⎨⎪⎧-m ≤-1,m ≥3得m ≥3,∴m 的取值范围为[3,+∞). 答案:[3,+∞)3.已知集合A ={1,2},B ={x |x 2+mx +1=0,x ∈R},若B ⊆A ,则实数m 的取值范围为________. 解析:①若B =∅,则Δ=m 2-4<0,解得-2<m <2; ②若1∈B ,则12+m +1=0,解得m =-2,此时B ={1},符合题意; ③若2∈B ,则22+2m +1=0,解得m =-52,此时B =⎩⎨⎧⎭⎬⎫2,12,不合题意.综上所述,实数m 的取值范围为[-2,2). 答案:[-2,2)考点三 集合的基本运算考法(一) 集合的运算[典例] (1)(2018·天津高考)设集合A ={1,2,3,4},B ={-1,0,2,3},C ={x ∈R|-1≤x <2},则(A ∪B )∩C =( )A.{-1,1} B.{0,1}C.{-1,0,1} D.{2,3,4}(2)已知全集U=R,集合A={x|x2-3x-4>0},B={x|-2≤x≤2},则如图所示阴影部分所表示的集合为( )A.{x|-2≤x<4}B.{x|x≤2或x≥4}C.{x|-2≤x≤-1}D.{x|-1≤x≤2}[解析] (1)∵A={1,2,3,4},B={-1,0,2,3},∴A∪B={-1,0,1,2,3,4}.又C={x∈R|-1≤x<2},∴(A∪B)∩C={-1,0,1}.(2)依题意得A={x|x<-1或x>4},因此∁R A={x|-1≤x≤4},题中的阴影部分所表示的集合为(∁R A)∩B={x|-1≤x≤2}.[答案] (1)C (2)D考法(二) 根据集合运算结果求参数[典例] (1)已知集合A={x|x2-x-12>0},B={x|x≥m}.若A∩B={x|x>4},则实数m的取值范围是( )A.(-4,3) B.[-3,4]C.(-3,4) D.(-∞,4](2)(2019·河南名校联盟联考)已知A={1,2,3,4},B={a+1,2a},若A∩B={4},则a=( )A.3 B.2C.2或3 D.3或1[解析] (1)集合A={x|x<-3或x>4},∵A∩B={x|x>4},∴-3≤m≤4,故选B.(2)∵A ∩B ={4},∴a +1=4或2a =4.若a +1=4,则a =3,此时B ={4,6},符合题意;若2a =4,则a =2,此时B ={3,4},不符合题意.综上,a =3,故选A.[答案] (1)B (2)A[题组训练]1.已知集合A ={1,2,3},B ={x |(x +1)(x -2)<0,x ∈Z},则A ∪B =( ) A .{1} B .{1,2} C .{0,1,2,3}D .{-1,0,1,2,3}解析:选C 因为集合B ={x |-1<x <2,x ∈Z}={0,1},而A ={1,2,3},所以A ∪B ={0,1,2,3}. 2.(2019·重庆六校联考)已知集合A ={x |2x 2+x -1≤0},B ={x |lg x <2},则(∁R A )∩B =( )A.⎝ ⎛⎭⎪⎫12,100B.⎝ ⎛⎭⎪⎫12,2C.⎣⎢⎡⎭⎪⎫12,100 D .∅解析:选 A 由题意得A =⎣⎢⎡⎦⎥⎤-1,12,B =(0,100),则∁R A =(-∞,-1)∪⎝ ⎛⎭⎪⎫12,+∞,所以(∁R A )∩B =⎝ ⎛⎭⎪⎫12,100.3.(2019·合肥质量检测)已知集合A =[1,+∞),B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R ⎪⎪⎪12a ≤x ≤2a -1,若A ∩B ≠∅,则实数a 的取值范围是( )A .[1,+∞)B.⎣⎢⎡⎦⎥⎤12,1C.⎣⎢⎡⎭⎪⎫23,+∞ D .(1,+∞)解析:选A 因为A ∩B ≠∅, 所以⎩⎨⎧2a -1≥12a -1≥12a ,解得a ≥1.[课时跟踪检测]1.(2019·福州质量检测)已知集合A={x|x=2k+1,k∈Z},B={x|-1<x≤4},则集合A∩B中元素的个数为( )A.1 B.2C.3 D.4解析:选B 依题意,集合A是由所有的奇数组成的集合,故A∩B={1,3},所以集合A∩B中元素的个数为2.2.设集合U={1,2,3,4,5,6},A={1,3,5},B={3,4,5},则∁U(A∪B)=( )A.{2,6} B.{3,6}C.{1,3,4,5} D.{1,2,4,6}解析:选A 因为A={1,3,5},B={3,4,5},所以A∪B={1,3,4,5}.又U={1,2,3,4,5,6},所以∁U(A∪B)={2,6}.3.(2018·天津高考)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=( ) A.{x|0<x≤1} B.{x|0<x<1}C.{x|1≤x<2} D.{x|0<x<2}解析:选B ∵全集为R,B={x|x≥1},∴∁R B={x|x<1}.∵集合A={x|0<x<2},∴A∩(∁R B)={x|0<x<1}.4.(2018·南宁毕业班摸底)设集合M={x|x<4},集合N={x|x2-2x<0},则下列关系中正确的是( )A.M∩N=M B.M∪(∁R N)=MC.N∪(∁R M)=R D.M∪N=M解析:选D 由题意可得,N=(0,2),M=(-∞,4),所以M∪N=M.5.设集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12≤2x<2,B ={x |ln x ≤0},则A ∩B 为( ) A.⎝ ⎛⎭⎪⎫0,12B .[-1,0)C.⎣⎢⎡⎭⎪⎫12,1 D .[-1,1]解析:选 A ∵12≤2x <2,即2-1≤2x <212,∴-1≤x <12,∴A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-1≤x <12.∵ln x ≤0,即ln x ≤ln 1,∴0<x ≤1,∴B ={x |0<x ≤1},∴A ∩B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪0<x <12. 6.(2019·郑州质量测试)设集合A ={x |1<x <2},B ={x |x <a },若A ∩B =A ,则a 的取值范围是( ) A .(-∞,2] B .(-∞,1] C .[1,+∞)D .[2,+∞)解析:选D 由A ∩B =A ,可得A ⊆B ,又因为A ={x |1<x <2},B ={x |x <a },所以a ≥2.7.已知全集U =A ∪B 中有m 个元素,()∁U A ∪()∁U B 中有n 个元素.若A ∩B 非空,则A ∩B 的元素个数为( )A .mnB .m +nC .n -mD .m -n解析:选D 因为()∁U A ∪()∁U B 中有n 个元素,如图中阴影部分所示,又U =A∪B 中有m 个元素,故A ∩B 中有m -n 个元素.8.定义集合的商集运算为A B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =m n ,m ∈A ,n ∈B,已知集合A ={2,4,6},B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k 2-1,k ∈A,则集合BA ∪B 中的元素个数为( )A .6B .7C .8D .9解析:选B 由题意知,B ={0,1,2},B A =⎩⎨⎧⎭⎬⎫0,12,14,16,1,13,则BA ∪B =⎩⎨⎧⎭⎬⎫0,12,14,16,1,13,2,共有7个元素.9.设集合A ={x |x 2-x -2≤0},B ={x |x <1,且x ∈Z},则A ∩B =________.解析:依题意得A ={x |(x +1)(x -2)≤0}={x |-1≤x ≤2},因此A ∩B ={x |-1≤x <1,x ∈Z}={-1,0}.答案:{-1,0}10.已知集合U =R ,集合A =[-5,2],B =(1,4),则下图中阴影部分所表示的集合为 ________.解析:∵A =[-5,2],B =(1,4),∴∁U B ={x |x ≤1或x ≥4},则题图中阴影部分所表示的集合为(∁UB )∩A ={x |-5≤x ≤1}.答案:{x |-5≤x ≤1}11.若集合A ={(x ,y )|y =3x 2-3x +1},B ={(x ,y )|y =x },则集合A ∩B 中的元素个数为________. 解析:法一:由集合的意义可知,A ∩B 表示曲线y =3x 2-3x +1与直线y =x 的交点构成的集合.联立得方程组⎩⎪⎨⎪⎧y =3x 2-3x +1,y =x ,解得⎩⎪⎨⎪⎧x =13,y =13或⎩⎪⎨⎪⎧x =1,y =1,故A ∩B =⎩⎨⎧⎭⎬⎫⎝ ⎛⎭⎪⎫13,13,1,1,所以A ∩B 中含有2个元素. 法二:由集合的意义可知,A ∩B 表示曲线y =3x 2-3x +1与直线y =x 的交点构成的集合.因为3x2-3x +1=x 即3x 2-4x +1=0的判别式Δ>0,所以该方程有两个不相等的实根,所以A ∩B 中含有2个元素.答案:212.已知集合A ={x |log 2x ≤2},B ={x |x <a },若A ⊆B ,则实数a 的取值范围是__________. 解析:由log 2x ≤2,得0<x ≤4, 即A ={x |0<x ≤4},而B ={x |x <a },由于A⊆B,在数轴上标出集合A,B,如图所示,则a>4.答案:(4,+∞)13.设全集U=R,A={x|1≤x≤3},B={x|2<x<4},C={x|a≤x≤a+1}.(1)分别求A∩B,A∪(∁U B);(2)若B∪C=B,求实数a的取值范围.解:(1)由题意知,A∩B={x|1≤x≤3}∩{x|2<x<4}={x|2<x≤3}.易知∁U B={x|x≤2或x≥4},所以A∪(∁U B)={x|1≤x≤3}∪{x|x≤2或x≥4}={x|x≤3或x≥4}.(2)由B∪C=B,可知C⊆B,画出数轴(图略),易知2<a<a+1<4,解得2<a<3.故实数a的取值范围是(2,3).第二节命题及其关系、充分条件与必要条件一、基础知识1.命题的概念用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.一个命题要么是真命题,要么是假命题,不能模棱两可.2.四种命题及其相互关系3.充分条件、必要条件与充要条件(1)如果p⇒q,则p是q的充分条件;①A是B的充分不必要条件是指:A⇒B且B A;②A的充分不必要条件是B是指:B⇒A且A B,在解题中要弄清它们的区别,以免出现错误.(2)如果q⇒p,则p是q的必要条件;(3)如果既有p⇒q,又有q⇒p,记作p⇔q,则p是q的充要条件.充要关系与集合的子集之间的关系设A={x|p(x)},B={x|q(x)},①若A⊆B,则p是q的充分条件,q是p的必要条件.②若A B,则p是q的充分不必要条件,q是p的必要不充分条件.③若A=B,则p是q的充要条件.二、常用结论1.四种命题中的等价关系原命题等价于逆否命题,否命题等价于逆命题,所以在命题不易证明时,往往找等价命题进行证明.2.等价转化法判断充分条件、必要条件p是q的充分不必要条件,等价于非q是非p的充分不必要条件.其他情况以此类推.考点一四种命题及其真假判断[典例] (2019·菏泽模拟)有以下命题:①“若xy=1,则x,y互为倒数”的逆命题;②“面积相等的两个三角形全等”的否命题;③“若m≤1,则x2-2x+m=0有实数解”的逆否命题;④“若A∩B=B,则A⊆B”的逆否命题.其中真命题是( )A.①②B.②③C.④ D.①②③[解析] ①原命题的逆命题为“若x,y互为倒数,则xy=1”,是真命题;②原命题的否命题为“面积不相等的两个三角形不全等”,是真命题;③若m≤1,Δ=4-4m≥0,所以原命题是真命题,故其逆否命题也是真命题;④由A∩B=B,得B⊆A,所以原命题是假命题,故其逆否命题也是假命题,故①②③正确.[答案] D[题组训练]1.(2019·长春质监)命题“若x2<1,则-1<x<1”的逆否命题是( )A.若x2≥1,则x≥1或x≤-1B.若-1<x<1,则x2<1C.若x>1或x<-1,则x2>1D.若x≥1或x≤-1,则x2≥1解析:选D 命题的形式是“若p,则q”,由逆否命题的知识,可知其逆否命题是“若非q,则非p ”的形式,所以“若x 2<1,则-1<x <1”的逆否命题是“若x ≥1或x ≤-1,则x 2≥1”.2.已知集合P =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k +12,k ∈Z,Q =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k2,k ∈Z,记原命题:“x ∈P ,则x ∈Q ”,那么,在原命题及其逆命题、否命题、逆否命题中,真命题的个数为( )A .0B .1C .2D .4解析:选C 因为P =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k +12,k ∈Z=⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =2k +12,k ∈Z,Q =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k2,k ∈Z, 所以P Q ,所以原命题“x ∈P ,则x ∈Q ”为真命题,则原命题的逆否命题为真命题.原命题的逆命题“x ∈Q ,则x ∈P ”为假命题, 则原命题的否命题为假命题,所以真命题的个数为2.考点二 充分、必要条件的判断[典例] (1)(2019·湖北八校联考)若a ,b ,c ,d ∈R ,则“a +d =b +c ”是“a ,b ,c ,d 依次成等差数列”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件(2)(2018·天津高考)设x ∈R ,则“⎪⎪⎪⎪⎪⎪x -12<12”是“x 3<1”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件(3)已知p :x +y ≠-2,q :x ,y 不都是-1,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件[解析] (1)定义法当a =-1,b =0,c =3,d =4时,a +d =b +c ,但此时a ,b ,c ,d 不成等差数列;而当a ,b ,c ,d 依次成等差数列时,由等差数列的性质知a +d =b +c .所以“a +d =b +c ”是“a ,b ,c ,d 依次成等差数列”的必要不充分条件,故选B.(2)集合法由⎪⎪⎪⎪⎪⎪x -12<12,得0<x <1,则0<x 3<1,即“⎪⎪⎪⎪⎪⎪x -12<12”⇒“x 3<1”; 由x 3<1,得x <1,当x ≤0时,⎪⎪⎪⎪⎪⎪x -12≥12,即“x 3<1”“⎪⎪⎪⎪⎪⎪x -12<12”. 所以“⎪⎪⎪⎪⎪⎪x -12<12”是“x 3<1”的充分而不必要条件.(3)等价转化法因为p :x +y ≠-2,q :x ≠-1或y ≠-1, 所以非p :x +y =-2,非q :x =-1且y =-1,因为非q ⇒非p 但非p非q ,所以非q 是非p 的充分不必要条件,即p 是q 的充分不必要条件.[答案] (1)B (2)A (3)A[提醒] 判断条件之间的关系要注意条件之间关系的方向,要注意“A 是B 的充分不必要条件”与“A 的充分不必要条件是B ”的区别,要正确理解“p 的一个充分不必要条件是q ”的含义.[题组训练]1.[集合法]已知x ∈R ,则“x <1”是“x 2<1”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件解析:选B 若x 2<1,则-1<x <1,∵(-∞,1)⊇(-1,1),∴“x <1”是“x 2<1”的必要不充分条件.2.[定义法](2018·南昌调研)已知m ,n 为两个非零向量,则“m ·n <0”是“m 与n 的夹角为钝角”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选B 设m ,n 的夹角为θ,若m ,n 的夹角为钝角,则π2<θ<π,则cos θ<0,则m ·n <0成立;当θ=π时,m ·n =-|m |·|n |<0成立,但m ,n 的夹角不为钝角.故“m ·n <0”是“m 与n 的夹角为钝角”的必要不充分条件.3.[等价转化法]“xy ≠1”是“x ≠1或y ≠1”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件解析:选A 设p :xy ≠1,q :x ≠1或y ≠1, 则非p :xy =1,非q :x =1且y =1. 可知非q ⇒非p ,非p非q ,即非q 是非p 的充分不必要条件.故p 是q 的充分不必要条件,即“xy ≠1”是“x ≠1或y ≠1”的充分不必要条件.考点三 根据充分、必要条件求参数的范围[典例] 已知P ={x |x 2-8x -20≤0},非空集合S ={x |1-m ≤x ≤1+m }.若x ∈P 是x ∈S 的必要条件,则m 的取值范围是________.[解析] 由x 2-8x -20≤0,得-2≤x ≤10, 所以P ={x |-2≤x ≤10},由x ∈P 是x ∈S 的必要条件,知S ⊆P . 则⎩⎪⎨⎪⎧1-m ≤1+m ,1-m ≥-2,1+m ≤10,所以0≤m ≤3.所以当0≤m ≤3时,x ∈P 是x ∈S 的必要条件,即所求m 的取值范围是[0,3]. [答案] [0,3][变透练清]1.[变结论]若本例条件不变,问是否存在实数m ,使x ∈P 是x ∈S 的充要条件. 解:若x ∈P 是x ∈S 的充要条件,则P =S , 所以{ 1-m =-21+m =10,解得{ m =3m =9,即不存在实数m ,使x ∈P 是x ∈S 的充要条件.2.(变条件)若本例将条件“若x ∈P 是x ∈S 的必要条件”变为“若非P 是非S 的必要不充分条件”,其他条件不变,求实数m 的取值范围.解:由例题知P ={x |-2≤x ≤10}, ∵非P 是非S 的必要不充分条件, ∴S 是P 的必要不充分条件,∴P ⇒S 且S P .∴[-2,10][1-m,1+m ].∴⎩⎪⎨⎪⎧1-m ≤-2,1+m >10或⎩⎪⎨⎪⎧1-m <-2,1+m ≥10.∴m ≥9,即m 的取值范围是[9,+∞).[课时跟踪检测]1.已知命题p :“正数a 的平方不等于0”,命题q :“若a 不是正数,则它的平方等于0”,则q 是p 的( )A .逆命题B .否命题C .逆否命题D .否定解析:选B 命题p :“正数a 的平方不等于0”可写成“若a 是正数,则它的平方不等于0”,从而q 是p 的否命题.2.命题“若x2+3x-4=0,则x=4”的逆否命题及其真假性为( )A.“若x=4,则x2+3x-4=0”为真命题B.“若x≠4,则x2+3x-4≠0”为真命题C.“若x≠4,则x2+3x-4≠0”为假命题D.“若x=4,则x2+3x-4=0”为假命题解析:选C 根据逆否命题的定义可以排除A、D,因为x2+3x-4=0,所以x=-4或1,故原命题为假命题,即逆否命题为假命题.3.原命题为“若z1,z2互为共轭复数,则|z1|=|z2|”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )A.真,假,真B.假,假,真C.真,真,假 D.假,假,假解析:选B 当z1,z2互为共轭复数时,设z1=a+b i(a,b∈R),则z2=a-b i,则|z1|=|z2|=a2+b2,所以原命题为真,故其逆否命题为真.取z1=1,z2=i,满足|z1|=|z2|,但是z1,z2不互为共轭复数,所以其逆命题为假,故其否命题也为假.4.(2018·北京高考)设a,b,c,d是非零实数,则“ad=bc”是“a,b,c,d成等比数列”的( ) A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件解析:选B a,b,c,d是非零实数,若a<0,d<0,b>0,c>0,且ad=bc,则a,b,c,d不成等比数列(可以假设a=-2,d=-3,b=2,c=3).若a,b,c,d成等比数列,则由等比数列的性质可知ad=bc.所以“ad=bc”是“a,b,c,d成等比数列”的必要而不充分条件.5.已知命题α:如果x<3,那么x<5;命题β:如果x≥3,那么x≥5;命题γ:如果x≥5,那么x≥3.关于这三个命题之间的关系中,下列说法正确的是( )①命题α是命题β的否命题,且命题γ是命题β的逆命题;②命题α是命题β的逆命题,且命题γ是命题β的否命题;③命题β是命题α的否命题,且命题γ是命题α的逆否命题.A.①③ B.②C .②③D .①②③解析:选A 本题考查命题的四种形式,逆命题是把原命题中的条件和结论互换,否命题是把原命题的条件和结论都加以否定,逆否命题是把原命题中的条件与结论先都否定然后互换所得,故①正确,②错误,③正确.6.(2018·北京高考)设a ,b 均为单位向量,则“|a -3b |=|3a +b |”是“a ⊥b ”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件解析:选C 由|a -3b |=|3a +b |,得(a -3b )2=(3a +b )2, 即a 2+9b 2-6a ·b =9a 2+b 2+6a ·b . 因为a ,b 均为单位向量,所以a 2=b 2=1, 所以a ·b =0,能推出a ⊥b .由a ⊥b 得|a -3b |=10,|3a +b |=10, 能推出|a -3b |=|3a +b |,所以“|a -3b |=|3a +b |”是“a ⊥b ”的充分必要条件. 7.如果x ,y 是实数,那么“x ≠y ”是“cos x ≠cos y ”的( ) A .充要条件 B .充分不必要条件 C .必要不充分条件D .既不充分也不必要条件解析:选C 设集合A ={(x ,y )|x ≠y },B ={(x ,y )|cos x ≠cos y },则A 的补集C ={(x ,y )|x =y },B 的补集D ={(x ,y )|cos x =cos y },显然C D ,所以B A .于是“x ≠y ”是“cos x ≠cos y ”的必要不充分条件.8.(2019·湘东五校联考)“不等式x 2-x +m >0在R 上恒成立”的一个必要不充分条件是( ) A .m >14B .0<m <1C .m >0D .m >1解析:选C 若不等式x 2-x +m >0在R 上恒成立,则Δ=(-1)2-4m <0,解得m >14,因此当不等式x 2-x +m >0在R 上恒成立时,必有m >0,但当m >0时,不一定推出不等式在R 上恒成立,故所求的必要不充分条件可以是m >0.9.在△ABC 中,“A =B ”是“tan A =tan B ”的________条件.解析:由A =B ,得tan A =tan B ,反之,若tan A =tan B ,则A =B +k π,k ∈Z.∵0<A <π,0<B <π,∴A =B ,故“A =B ”是“tan A =tan B ”的充要条件.答案:充要10.在命题“若m >-n ,则m 2>n 2”的逆命题、否命题、逆否命题中,假命题的个数是________. 解析:若m =2,n =3,则2>-3,但22<32,所以原命题为假命题,则逆否命题也为假命题,若m =-3,n =-2,则(-3)2>(-2)2,但-3<2,所以逆命题是假命题,则否命题也是假命题.故假命题的个数为3.答案:311.已知p (x ):x 2+2x -m >0,若p (1)是假命题,p (2)是真命题,则实数m 的取值范围为________. 解析:因为p (1)是假命题,所以1+2-m ≤0,解得m ≥3. 又p (2)是真命题,所以4+4-m >0,解得m <8. 故实数m 的取值范围为[3,8). 答案:[3,8)12.(2019·齐鲁名校调研)给出下列说法:①“若x +y =π2,则sin x =cos y ”的逆命题是假命题;②“在△ABC 中,sin B >sin C 是B >C 的充要条件”是真命题;③“a =1”是“直线x -ay =0与直线x +ay =0互相垂直”的充要条件;④命题“若x <-1,则x 2-2x -3>0”的否命题为“若x ≥-1,则x 2-2x -3≤0”. 以上说法正确的是________(填序号). 解析:对于①,“若x +y =π2,则sin x =cos y ”的逆命题是“若sin x =cos y ,则x +y =π2”,当x =0,y =3π2时,有sin x =cos y 成立,但x +y =3π2,故逆命题为假命题,①正确;对于②,在△ABC 中,由正弦定理得sin B >sin C ⇔b >c ⇔B >C ,②正确;对于③,“a =±1”是“直线x -ay =0与直线x +ay =0互相垂直”的充要条件,故③错误;对于④,根据否命题的定义知④正确.答案:①②④13.写出命题“已知a,b∈R,若关于x的不等式x2+ax+b≤0有非空解集,则a2≥4b”的逆命题、否命题、逆否命题,并判断它们的真假.解:(1)逆命题:已知a,b∈R,若a2≥4b,则关于x的不等式x2+ax+b≤0有非空解集,为真命题.(2)否命题:已知a,b∈R,若关于x的不等式x2+ax+b≤0没有非空解集,则a2<4b,为真命题.(3)逆否命题:已知a,b∈R,若a2<4b,则关于x的不等式x2+ax+b≤0没有非空解集,为真命题.第三节简单的逻辑联结词、全称量词与存在量词一、基础知识1.简单的逻辑联结词(1)命题中的“且”“或”“非”❶叫做逻辑联结词.①用联结词“且”把命题p和命题q联结起来,得到复合命题“p且q”,记作p∧q;②用联结词“或”把命题p和命题q联结起来,得到复合命题“p或q”,记作p∨q;③对命题p的结论进行否定,得到复合命题“非p”,记作非p.❷❶“且”的数学含义是几个条件同时满足,“且”在集合中的解释为“交集”;“或”的数学含义是至少满足一个条件,“或”在集合中的解释为“并集”;“非”的含义是否定,“非p”只否定p的结论,“非”在集合中的解释为“补集”.❷“命题的否定”与“否命题”的区别(1)命题的否定只是否定命题的结论,而否命题既否定其条件,也否定其结论.(2)命题的否定与原命题的真假总是相对立的,即一真一假,而否命题与原命题的真假无必然联系.(2)命题真值表:命题真假的判断口诀p∨q→见真即真,p∧q→见假即假,p与非p→真假相反.2.全称量词与存在量词3.4.全称命题与特称命题的否定二、常用结论含逻辑联结词命题真假的等价关系(1)p∨q真⇔p,q至少一个真⇔(非p)∧(非q)假.(2)p∨q假⇔p,q均假⇔(非p)∧(非q)真.(3)p∧q真⇔p,q均真⇔(非p)∨(非q)假.(4)p∧q假⇔p,q至少一个假⇔(非p)∨(非q)真.考点一判断含有逻辑联结词命题的真假[典例] (1)(2017·山东高考)已知命题p:∀x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是( )A.p∧q B.p∧非qC.非p∧q D.非p∧非q(2)(2019·安徽安庆模拟)设命题p:∃x0∈(0,+∞),x0+1x0>3;命题q:∀x∈(2,+∞),x2>2x,则下列命题为真的是( )A.p∧(非q) B.(非p)∧qC.p∧q D.(非p)∨q[解析] (1)当x>0时,x+1>1,因此ln(x+1)>0,即p为真命题;取a=1,b=-2,这时满足a>b,显然a2>b2不成立,因此q为假命题.由复合命题的真假性,知B为真命题.(2)对于命题p,当x0=4时,x0+1x0=174>3,故命题p为真命题;对于命题q,当x=4时,24=42=16,即∃x0∈(2,+∞),使得2x0=x20成立,故命题q为假命题,所以p∧ (非q)为真命题,故选A.[答案] (1)B (2)A[题组训练]1.(2019·惠州调研)已知命题p,q,则“非p为假命题”是“p∧q是真命题”的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件解析:选B 充分性:若非p为假命题,则p为真命题,由于不知道q的真假性,所以推不出p∧q是真命题.必要性:p∧q是真命题,则p,q均为真命题,则非p为假命题.所以“非p为假命题”是“p∧q是真命题”的必要不充分条件.2.已知命题p:“若x2-x>0,则x>1”;命题q:“若x,y∈R,x2+y2=0,则xy=0”.下列命题是真命题的是( )A.p∨(非q) B.p∨qC.p∧q D.(非p)∧(非q)解析:选B 若x2-x>0,则x>1或x<0,故p是假命题;若x,y∈R,x2+y2=0,则x=0,y=0,xy=0,故q是真命题.则p∨q是真命题.考点二全称命题与特称命题[典例] (1)命题∀x∈R,e x-x-1≥0的否定是( )A.∀x∈R,e x-x-1≤0B.∀x∈R,e x-x-1≥0C.∃x0∈R,e x0-x0-1≤0D.∃x0∈R,e x0-x0-1<0(2)对命题∃x0>0,x20>2x0,下列说法正确的是( )A.真命题,其否定是∃x0≤0,x20≤2x0B.假命题,其否定是∀x>0,x2≤2xC.真命题,其否定是∀x>0,x2≤2xD.真命题,其否定是∀x≤0,x2≤2x[解析] (1)改全称量词为存在量词,把不等式中的大于或等于改为小于.故选D.(2)已知命题是真命题,如32=9>8=23,其否定是∀x>0,x2≤2x.故选C.[答案] (1)D (2)C[题组训练]1.命题“∀x∈R,∃n∈N*,使得n≤x2”的否定形式是( )A.∀x∈R,∃n∈N*,使得n>x2B.∀x∈R,∀n∈N*,使得n>x2C.∃x0∈R,∃n∈N*,使得n>x20D.∃x0∈R,∀n∈N*,使得n>x20解析:选D ∀改写为∃,∃改写为∀,n≤x2的否定是n>x2,则该命题的否定形式为“∃x0∈R,∀n∈N*,使得n>x20”.2.已知命题p:∃n∈R,使得f(x)=nxn2+2n是幂函数,且在(0,+∞)上单调递增;命题q:“∃x0∈R,x20+2>3x0”的否定是“∀x∈R,x2+2<3x”.则下列命题为真命题的是( ) A.p∧q B.(非p)∧qC.p∧(非q) D.(非p)∧(非q)解析:选C 当n=1时,f(x)=x3为幂函数,且在(0,+∞)上单调递增,故p是真命题,则非p 是假命题;“∃x0∈R,x20+2>3x0”的否定是“∀x∈R,x2+2≤3x”,故q是假命题,非q是真命题.所以p∧q,(非p)∧q,(非p)∧(非q)均为假命题,p∧(非q)为真命题,选C.考点三根据命题的真假求参数的取值范围[典例] 已知p:存在x0∈R,mx20+1≤0,q:任意x∈R,x2+mx+1>0.若p或q为假命题,求实数m的取值范围.[解] 依题意知p,q均为假命题,当p是假命题时,则mx2+1>0恒成立,则有m≥0;当q是真命题时,则Δ=m2-4<0,-2<m<2.因此由p,q均为假命题得{m≥0m≤-2或m≥2,即m≥2.所以实数m 的取值范围为[2,+∞).[变透练清]1.(变条件)若本例将条件“p 或q 为假命题”变为“p 且q 为真命题”,其他条件不变,则实数m 的取值范围为________.解析:依题意,当p 是真命题时,有m <0; 当q 是真命题时,有-2<m <2,由⎩⎪⎨⎪⎧m <0,-2<m <2,可得-2<m <0.所以m 的取值范围为(-2,0). 答案:(-2,0)2.(变条件)若本例将条件“p 或q 为假命题”变为“p 且q 为假,p 或q 为真”,其他条件不变,则实数m 的取值范围为________.解析:若p 且q 为假,p 或q 为真,则p ,q 一真一假.当p 真q 假时⎩⎪⎨⎪⎧m <0,m ≥2或m ≤-2,所以m ≤-2;当p 假q 真时⎩⎪⎨⎪⎧m ≥0,-2<m <2,所以0≤m <2.所以m 的取值范围为(-∞,-2]∪[0,2). 答案:(-∞,-2]∪[0,2)3.(变条件)若本例将条件q 变为:存在x 0∈R ,x 20+mx 0+1<0,其他条件不变,则实数m 的取值范围为________.解析:依题意,当q 是真命题时,Δ=m 2-4>0,所以m >2或m <-2.由⎩⎪⎨⎪⎧m ≥0,-2≤m ≤2,得0≤m ≤2,所以m 的取值范围为[0,2]. 答案:[0,2][课时跟踪检测]1.(2019·西安摸底)命题“∀x >0,xx -1>0”的否定是( )A .∃x 0≥0,x 0x 0-1≤0 B .∃x 0>0,0≤x 0≤1C .∀x >0,xx -1≤0 D .∀x <0,0≤x ≤1解析:选B ∵x x -1>0,∴x <0或x >1,∴xx -1>0的否定是0≤x ≤1, ∴命题的否定是“∃x 0>0,0≤x 0≤1”. 2.下列命题中,假命题的是( ) A .∀x ∈R,21-x>0B .∃a 0∈R ,y =xa 0的图象关于y 轴对称C .函数y =x a的图象经过第四象限 D .直线x +y +1=0与圆x 2+y 2=12相切解析:选C 对于A ,由指数函数的性质可知为真命题;对于B ,当a =2时,其图象关于y 轴对称;对于C ,当x >0时,y >0恒成立,从而图象不过第四象限,故为假命题;对于D ,因为圆心(0,0)到直线x +y +1=0的距离等于12,等于圆的半径,命题成立.3.(2019·陕西质检)已知命题p :对任意的x ∈R ,总有2x>0;q :“x >1”是“x >2”的充分不必要条件,则下列命题为真命题的是( )A .p ∧qB .(非p )∧(非q)C .(非p )∧qD .p ∧(非q)解析:选D 由指数函数的性质知命题p 为真命题.易知x >1是x >2的必要不充分条件,所以命题q 为假命题.由复合命题真值表可知p ∧(非q)为真命题.4.(2018·湘东五校联考)下列说法中正确的是( )A .“a >1,b >1”是“ab >1”成立的充分条件B .命题p :∀x ∈R,2x>0,则非p :∃x 0∈R,2x0<0 C .命题“若a >b >0,则1a <1b”的逆命题是真命题D .“a >b ”是“a 2>b 2”成立的充分不必要条件解析:选A 对于选项A ,由a >1,b >1,易得ab >1,故A 正确.对于选项B ,全称命题的否定是特称命题,所以命题p :∀x ∈R,2x>0的否定是非p :∃x 0∈R,2x0≤0,故B 错误.对于选项C ,其逆命题:若1a <1b,则a >b >0,可举反例,如a =-1,b =1,显然是假命题,故C 错误.对于选项D ,由“a >b ”并不能推出“a 2>b 2”,如a =1,b =-1,故D 错误.故选A.5.(2019·唐山五校联考)已知命题p :“a >b ”是“2a>2b”的充要条件;命题q :∃x 0∈R ,|x 0+1|≤x 0,则( )A .(非p )∨q 为真命题B .p ∧(非q)为假命题C .p ∧q 为真命题D .p ∨q 为真命题解析:选D 由题意可知命题p 为真命题.因为|x +1|≤x 的解集为空集,所以命题q 为假命题,所以p ∨q 为真命题.6.下列说法错误的是( )A .命题“若x 2-5x +6=0,则x =2”的逆否命题是“若x ≠2,则x 2-5x +6≠0” B .若命题p :存在x 0∈R ,x 20+x 0+1<0,则非p :对任意x ∈R ,x 2+x +1≥0 C .若x ,y ∈R ,则“x =y ”是“xy ≥⎝⎛⎭⎪⎫x +y 22”的充要条件D .已知命题p 和q ,若“p 或q ”为假命题,则命题p 与q 中必一真一假解析:选D 由原命题与逆否命题的关系,知A 正确;由特称命题的否定知B 正确;由xy ≥⎝⎛⎭⎪⎫x +y 22⇔4xy ≥(x +y )2⇔4xy ≥x 2+y 2+2xy ⇔(x -y )2≤0⇔x =y ,知C 正确;对于D ,命题“p 或q ”为假命题,则命题p 与q 均为假命题,所以D 不正确.7.(2019·长沙模拟)已知命题“∀x ∈R ,ax 2+4x +1>0”是假命题,则实数a 的取值范围是( )A .(4,+∞)B .(0,4]C .(-∞,4]D .[0,4)解析:选C 当原命题为真命题时,a >0且Δ<0,所以a >4,故当原命题为假命题时,a ≤4. 8.下列命题为假命题的是( ) A .存在x >y >0,使得ln x +ln y <0B .“φ=π2”是“函数y =sin(2x +φ)为偶函数”的充分不必要条件C .∃x 0∈(-∞,0),使3x 0<4x 0成立D .已知两个平面α,β,若两条异面直线m ,n 满足m ⊂α,n ⊂β且m ∥β,n ∥α,则α∥β 解析:选C 对于A 选项,令x =1,y =1e ,则ln x +ln y =-1<0成立,故排除A.对于B 选项,“φ=π2”是“函数y =sin(2x +φ)为偶函数”的充分不必要条件,正确,故排除B.对于C 选项,根据幂函数y =x α,当α<0时,函数单调递减,故不存在x 0∈(-∞,0),使3x 0<4x 0成立,故C 错误.对于D 选项,已知两个平面α,β,若两条异面直线m ,n 满足m ⊂α,n ⊂β且m ∥β,n ∥α,可过n 作一个平面与平面α相交于直线n ′.由线面平行的性质定理可得n ′∥n ,再由线面平行的判定定理可得n ′∥β,接下来由面面平行的判定定理可得α∥β,故排除D ,选C.9.若命题p 的否定是“∀x ∈(0,+∞),x >x +1”,则命题p 可写为________________________. 解析:因为p 是非p 的否定,所以只需将全称量词变为特称量词,再对结论否定即可. 答案:∃x 0∈(0,+∞),x 0≤x 0+110.已知命题p :x 2+4x +3≥0,q :x ∈Z ,且“p ∧q ”与“非q ”同时为假命题,则 x =________. 解析:若p 为真,则x ≥-1或x ≤-3, 因为“非q ”为假,则q 为真,即x ∈Z ,又因为“p ∧q ”为假,所以p 为假,故-3<x <-1, 由题意,得x =-2. 答案:-211.已知p :a <0,q :a 2>a ,则非p 是非q 的________条件(填:充分不必要、必要不充分、充要、。