下载文档原格式
第四章基础知识归纳知识点1线段、射线、直线1.下面是四个图形，以及对每个图形的描述：○1线段AB与射线CD不相交：○2点C在线段AB上：③直线a与直线b不相交：○4射线OB会通过点A.其中正确的个数是（）.A.1个 B 2个 C.3个 D.4个2.如图，点A.B.C是直线l上的三个点，图中共有线段（）.A.1条B.2条C.3条D.4条3.下列说法正确的是（）.A.两点之间的所有连线中，直线最短B.若P是线段AB的中点，则AP=BPC.若AP=BP，则P是线段AB的中点D.两点之间的线段叫作这两点之间的距离4.如图，C是AB的中点，D是BC的中点，下列等式不正确的是（）.A.CD=AC-DB в.CD=AD-BCC.CD=12AB-BD D.CD=13AB5.如图，A，B，C，D为直线1上的四个点，图中共有条线段，以点C为端点的射线有条，它们是。
6.已知点O在直线AB上，且线段OA的长度为4cm，线段OB的长度为6cm，E，F分别为线段OA，OB的中点，则线段EF的长度为cm.7.如图，C为线段AD上一点，点B为CD的中点，且AD=8cm，BD=2 cm（1）求AC的长；（2）若点E在直线AD上，且EA=3cm，求BE的长.8.已知点A，B如图所示，请你按照下列要求画图（延长线都画成虚线）：（1）过点A，B画直线AB，并在直线AB上方任取两点C，D；（2）画射线AC，线段CD；（3）延长线段CD，与直线AB相交于点M；（4）画线段DB，反向延长线段DB，与射线AC相交于点N.9.（1）已知点C在线段AB上，AC=8厘米，BC-6厘米，点M，N分别是AC，BC的中点，求线段MN的长.（2）根据（1）的计算过程和结果，设AC+BCa，其他条件不变，你能猜测出MN的长度吗？你发现了其中的规律了吗？知识点2角的度量10.如图所示，下列表示角的方法错误的是（）A.∠1与∠AOB表示同一个角B.∠β表示的是∠BOCC.图中共有三角：∠AOB，∠AOC，∠BOCD.∠AOC也可用∠O来表示11.下列说法中，正确的是（）.A.平角是一条直线B.直角就是900C.大于直角的角叫做钝角D.两个锐角的和不一定是钝角12.如图所示，下列说法错误的是（）.A.OA的方向是北偏东50°B.OB的方向是南偏东40°C的方向是西偏南30°D.OD的方向是西北方向13.把15024'36"化成以度表示的角等于14.如图，过直线AB上一点O作射线OC，∠BOC=29o 18'，则∠AOC的度数为15.小斌在暑假参加了书法班和音乐班，第一天时，它的地图被墨染了，已经看不清音乐班的位置，但他知道音乐班是在书法班的南偏东60 o方向，在家的北偏东30 o方向，图中已经画出他家和书法班的位置，你能帮他确定音乐班的位置吗？知识点3角的比较16.若OC是∠AOB内部的一条射线，则下列式子中，不能表示“OC是∠AOB的平分线”的是（）∠АОВA.∠AOC=∠BOC В.∠AOC=12C.AOB=2∠BOCD.∠AOC+ ∠BOC=∠AOB17.在∠AOB的内部任取一点C，作射线0C，则一定有（）.A. ∠AOB>∠AOCB.∠AOC >∠BOCC. ∠BOC>∠AOCD.∠AOC= ∠BOC18.如果∠1-∠2=∠3，且∠4+∠2=∠1，那么∠3和∠4之间的关系是（）.A. ∠3>∠4B.∠3=∠4C.不能确定D. ∠3<∠419.已知∠AOB=3∠BOC，若∠BOC=30o，则∠AOC=（）А.120° B.120°或60 °С.30° D.30°或90°20.如图，直线AB，CD相交于点O，EO⊥AB于点O，∠EOD=50°，则∠BOC的度数为21.如图，∠AOB=90°，OE是∠AOB的平分线，OD是∠BOC平分线，若∠EOD=60°，则∠BOC的度数是∠EOC，∠22.如图，OE为∠AOD的平线，∠COD=14COD=15°.求：（1）∠EOC的度数；（2）∠AOD的度数.23.如图，∠AOB=90°，OM平分∠BOC，ON平分∠ACC，求∠MON 的度数.知识点4多边形和圆的初步认识24.一个多边形从一个顶点最多能引出2019条对角线，这个多边形的边数是（）.А.2 019 B.2 020 C.2021 D.2 022 25.如图，A，B，C.D四个扇形中最大与最小圆心角的差是o26.从n边形一个顶点出发，可以将n边形分为个三角形.27.一个半径是3cm的圆中，有一个圆心角是90的扇形，它的面积是cm.28.一个圆被分为1：5两部分，则较小的弧所对的圆心角是29.如图，正方形ABCD的内部有若干个点，利用这些点以及正方形ABCD的顶点A，B，C，D把原正方形分割成一些小三角形（互相不重叠）：（1）填写下表：（2）原正方形能否被分割成2020个小三角形？若能，求此时正方形ABCD的内部有多少个点·若不能，请说明理由.。
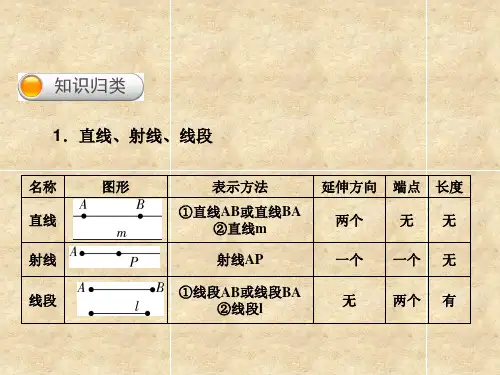
第四章：基本平面图形知识梳理一、线段、射线、直线1、线段、射线、直线的定义（1）线段：线段可以近似地看成是一条有两个端点的崩直了的线。
线段可以量出长度。
（2）射线：将线段向一个方向无限延伸就形成了射线，射线有一个端点。
射线无法量出长度。
（3）直线：将线段向两个方向无限延伸就形成了直线，直线没有端点。
直线无法量出长度。
： 联系：射线是直线的一部分。
线段是射线的一部分，也是直线的一部分。
2、点和直线的位置关系有两种：①点在直线上，或者说直线经过这个点。
②点在直线外，或者说直线不经过这个点。
3、直线的性质（1）直线公理：经过两个点有且只有一条直线。
简称两点确定一条直线。
（2）过一点的直线有无数条。
（3）直线是是向两方面无限延伸的，无端点，不可度量，不能比较大小。
（4）直线上有无穷多个点。
（5）两条不同的直线至多有一个公共点。
4、线段的比较（1）叠合比较法（用圆规截取线段）；（2）度量比较法（用刻度尺度量）。
5、线段的性质（1）线段公理：两点之间的所有连线中，线段最短。
（2）两点之间的距离：两点之间线段的长度，叫做这两点之间的距离。
（3）线段的中点到两端点的距离相等。
（4）线段的大小关系和它们的长度的大小关系是一致的。
6、线段的中点：如果线段上有一点，把线段分成相等的两条线段，这个点叫这条线段的中点。
若C 是线段AB 的中点，则：AC=BC=21AB 或AB=2AC=2BC 。
二、角1、角的概念：（1）角可以看成是由两条有共同端点的射线组成的图形。
两条射线叫角的边，共同的端点叫角的顶点。
（2）角还可以看成是一条射线绕着它的端点旋转所成的图形。
2、角的表示方法：角用“∠”符号表示，角的表示方法有以下四种： ①用数字表示单独的角，如∠1，∠2，∠3等。
②用小写的希腊字母表示单独的一个角，如∠α，∠β，∠γ，∠θ等。
③用一个大写英文字母表示一个独立（在一个顶点处只有一个角）的角，如∠B ，∠C 等。
