北京市北京市西城区2016年中考数学二模试卷
- 格式:pdf
- 大小:432.57 KB
- 文档页数:14
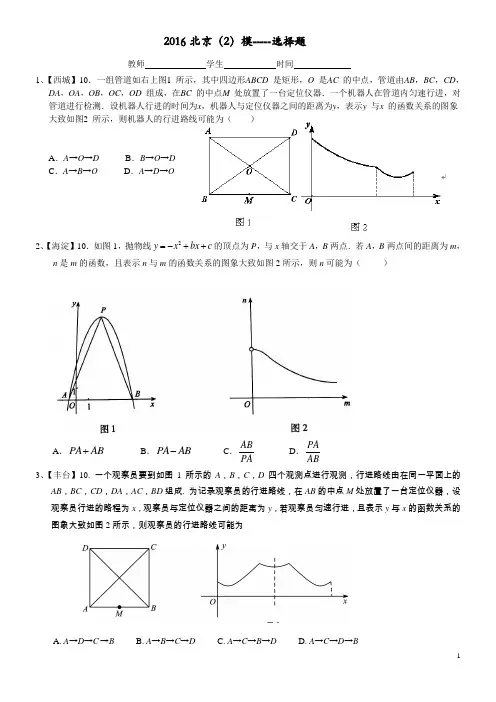
2016北京(2)模-----选择题教师 学生 时间1、【西城】10.一组管道如右上图1 所示,其中四边形ABCD 是矩形,O 是AC 的中点,管道由AB ,BC ,CD ,DA ,OA ,OB ,OC ,OD 组成,在BC 的中点M 处放置了一台定位仪器.一个机器人在管道内匀速行进,对管道进行检测.设机器人行进的时间为x ,机器人与定位仪器之间的距离为y ,表示y 与x 的函数关系的图象大致如图2 所示,则机器人的行进路线可能为( )A .A →O →DB .B →O →DC .A →B →OD .A →D →O2、【海淀】10.如图1,抛物线2y x bx c =-++的顶点为P ,与x 轴交于A ,B 两点.若A ,B 两点间的距离为m , n 是m 的函数,且表示n 与m 的函数关系的图象大致如图2所示,则n 可能为( )A .PA AB +B .PA AB -C .AB PA D .PAAB3、【丰台】10. 一个观察员要到如图1所示的A ,B ,C ,D 四个观测点进行观测,行进路线由在同一平面上的AB ,BC ,CD ,DA ,AC ,BD 组成. 为记录观察员的行进路线,在AB 的中点M 处放置了一台定位仪器,设观察员行进的路程为x ,观察员与定位仪器之间的距离为y ,若观察员匀速行进,且表示y 与x 的函数关系的图象大致如图2所示,则观察员的行进路线可能为A. A →D →C →BB. A →B →C →DC. A →C →B →DD. A →C →D →B图1图24、【石景山】 10.如图1,在等边△ABC 中,点D 是BC 边的中点,点P 为AB 边上的一个动点,设AP =x ,图1中线段DP 的长为y ,若表示y 与x 的函数关系的图象如图2所示,则等边△ABC 的面积为( )A .4 B . C.12 D .5、【朝阳】10.如图,ABC ∆为等边三角形,点O 在过点A 且平行于BC 的直线上运动,以ABC ∆的高为半 径的⊙O 分别交线段AB 、AC 于点E 、F ,则所对的圆周角的度数( )A .从︒0到︒30变化B .从︒30到︒60变化C .总等于︒30D .总等于︒606、【东城】10. 某班有20位同学参加乒乓球、羽毛球比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5人.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( ) A.若甲对,则乙对 B.若乙对,则甲对 C.若乙错,则甲错 D.若甲错,则乙对7、【房山】10.如图,正方形的顶点(0,)2A ,(2B ,顶点C 、D 位于第一象限,直线:(0l x t t =≤ 将正方形ABCD 分成两部分,记位于直线l 左侧阴影部分的面积为S ,当t 由小变大时S关于t 的函数图象大致是( )8、【顺义】10.已知点M 为某封闭图形边界上一定点,动点P 从点M 出发,沿其边界 逆时针运动一周,设点P 走过的路程为x ,线段MP 的长为y ,表示y 与x 的函数关系的图象大致如图所示,则该封闭图形可能是MABCDCB 第10题图PCBA图1 图29、【通州】10. 如图,在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG ,动点P 从点A 出发,沿A→D→E→F→G→B 的路线绕多边形的边匀速运动到点B 时停止(不含点A 和点B ),那么ΔABP 的面积S 随着时间t 变化的函数图象大致为( )t10、【怀柔】10.如右图,点M 从等边三角形的顶点A 出发,沿直线匀速运动到点B, 再沿直线匀速运动到点C,在整个过程中,设M 与A 的距离为y ,点M 的运动时 间为x ,那么y 与x 的图象大致为( )A B C D11、【昌平】10. 如图1,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,AB =2厘米,∠BAD =60°. P ,Q 两点同时从点O 出发,以1厘米/秒的速度在菱形的对角线及边上运动. 设运动的时间为x 秒,P ,Q 间的距离为y 厘米,y 与x 的函数关系的图象大致如图2所示,则P ,Q 的运动路线可能为( )图1图2DO CB AA. 点P : O —A —D —C ,点Q : O —C —D —OB. 点P : O —A —D —O ,点Q : O —C —B —OC. 点P : O —A —B —C ,点Q : O —C —D —OD. 点P : O —A —D —O ,点Q : O — C —D — 12、【燕山】.13、【门头沟】 14、【平谷】 15、【大兴】 16、【延庆】1.(14朝阳一模)8.C;2.(14东城一模)8.B;3.(14西城一模)8.C;5.(14海淀一模)8.C;5.(14昌平一模)8.B;6.(14房山一模)8.C;7.(14石景山一模)8.D;8.(14顺义一模)D.;9.(14通州一模)8.B;10.(14丰台一模)8. D;11.(14怀柔一模)8.A;。

北京市西城区2016年初三二模试卷数 学2016.6一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的。
1.调查显示,2016年“两会”期间,通过手机等移动端设备对“两会”相关话题的浏览量高达115 000 000次.将115 000 000用科学记数法表示应为 A.91.1510⨯B.11.510⨯7C.81.1510⨯D.81.152.“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为A B C D 3.下列各式中计算正确的是 A.246x x x ⋅=B.()2121mnm n -+=-+ C.551023x x x +=D.()3322a a =4.有一个可以自由转动且质地均匀的转盘,被分成6个大小相同的扇形.在转盘的适当地方涂上灰色,未涂色部分为白色.为了使转动的转盘停止时,指针指向灰色的概率为23,则下列各图中涂色方案正确的是A B C D5.利用复印机的缩放功能,将原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,则放大前后的两个三角形的面积比为A.1:2B.1:4C.1:8D.1:166.如图,AB是⊙O的一条弦,直径CD AB⊥于点E.若24,5,AB OE==则⊙O的半径为A.15B.13C.12D.107.如图,在一次定向越野活动中,“超越”小组准备从目前所在的A处前往相距2km的B处,则相对于A处来说,B处的位置是A.南偏西50 ,2kmB.南偏东50 ,2kmC.北偏西40 ,2kmD.北偏东40 ,2km8.教材中“整式的加减”一章的知识结构如图所示,则A和B分别代表的是A.分式,因式分解B.二次根式,合并同类项C.多项式,因式分解D.多项式,合并同类项9.某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过..200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过..200元的部分可以享受的优惠是A.打八折B.打七折C.打六折D.打五折10.一级管道如图1所示,其中四边形ABCD是矩形,O是AC是中点,管道由AB BC CD DA OA OB OC OD组成,在BC的中点M处放置了一台定位仪器.,,,,,,,一个机器人在管道内匀速行进,对管道进行检测.设机器人行进的时间为x,机人与定位仪器之间的距离为y,表示y与x的函数关系的图象大致如图2所示,则机器人的行进路线可能为图1 图2A.A O D →→B.B O D →→C.A B O -→→D.A D O →→二、填空题(本题共18分,每小题3分)11.若20x +=,则xy 的值为.12.一个扇形的半径长为5,且圆心角为72 ,则此扇形的弧长为.13.有一张直角三角形纸片,记作△ABC ,其 中90B ∠= .按如图方式剪去它的一个角(虚线部 分),在剩下的四边形ADEC 中,若1165∠= , 则2∠的度数为°.14.某班级进行了一次诗歌朗诵比赛,甲、乙两组学生的成绩如下表所示(满分10分):你认为哪一组的成绩更好一些?并说明理由. 答:组(填“甲”或“乙”),理由是.15.有一列有序数对:()()()()1,2,4,5,9,10,16,17,......,按此规律,第5对有序数对为;若在平面直角坐标系xOy 中,以这些有序数对为坐标的点都在同一条直线上,则这条直线的表达式为.16.在平面直角坐标系xOy 中,点A 的坐标为()1,0,P 是第一象限内任意一点,连接,PO PA .若,POA m PAO n ∠=∠= ,则我们把(),m n 叫做点P 的“双角坐标”.例如,点()1,1的“双角坐标”为()45,90 .(1)点12⎛ ⎝⎭的“双角坐标”为;(2)若点P 到x 轴的距离为12,则m n +的最小值为. 三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)解答应写出文字说明,演算步骤或证明过程.17.计算:()()39222sin 30--+-+ .18.如图,在△ABC 中,D 是AB 边上一 点,且DC DB =.点E 在CD 的延长线 上,且EBC ACB ∠=∠. 求证:AC EB =.19.先化简,再求值:x x 2-1¸x +22x -2-1x -1æèçöø÷,其中1x =.20.如图,在中,对角线,AC BD 相交于点O , 5,6,8AB AC BD ===.(1)求证:四边形ABCD 是菱形;(2)过点A 作AH BC ⊥于点H ,求AH 的长.21.已知关于x 的方程224490x mx m -+-=.(1)求证:此方程有两个不相等的实数根;(2)设此方程的两个根分别为12,x x ,其中12x x <.若1221x x =+,求m 的值.22.列方程或方程组解应用题:为祝贺北京成功获得2022年冬奥会主办权,某工艺品厂准备生产纪念北京申办冬奥会成功的“纪念章”和“冬奥印”.生产一枚“纪念章”需要用甲种原料4盒,乙种原料3盒;生产一枚“冬奥印”需要用甲种原料5盒,乙种原料10盒.该厂购进甲、乙两种原料分别为20000盒和30000盒,如果将所购进原料正好全部都用完,那么能生产“纪念章”和“冬奥印”各多少枚?23.在平面直角坐标系xOy 中,反比例函数1ky x=的图象与一次函数2y ax b =+的图象交于点()1,3A 和()3,B m -. (1)求反比例函数1ky x=和一次函数2y ax b =+的表达式; (2)点C 是坐标平面内一点,//BC x 轴,AD BC ⊥交直线BC 于点D ,连接AC .若AC =,求点C 的坐标.24.如图,四边形ABCD 内接于⊙O ,点E 在CB 的 延长线上,连接,,45AC AE ACB BAE ∠=∠= . (1)求证:AE 是⊙O 的切线;(2)若,3AB AD AC ADC ==∠=,求CD 的长.25.阅读下列材料:根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化.从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果.所谓“老年人口抚养比”是指某范围人口中,老年人口数(65岁及以上人口数)与劳动年龄人口数(15-64岁人口数)之比,通常用百分比表示,用以表明每100名劳动年龄人口要负担多少名老年人. 以下是根据我国近几年的人口相关数据制作的统计图和统计表.2011-2014年全国人口年龄分布图2011-2014年全国人口年龄分布表*以上图表中数据均为年末的数据.根据以上材料解答下列问题:(1)2011年末,我国总人口约为亿,全国人口年龄分布表中m的值为;(2)若按目前我国的人口自然增长率推测,到2027年末我国约有14.60亿人.假设0-14岁人口占总人口的百分比一直稳定在16.5%,15-64岁人口一直稳定在10亿,那么2027年末我国0-14岁人口约为亿,“老年人口抚养比”约为;(精确到1%)(3)2016年1月1日起我国开始施行“全面二孩”政策,一对夫妻可生育两个孩子.在未来..,假设出生率显著提高,这(填“会”或“不..10..年内会”)对我国的“老年人口抚养比”产生影响.26.【探究函数9y x x =+的图象与性质】 (1)函数9y x x=+的自变量x 的取值范围是;(2)下列四个函数图象中,函数9y x x=+的图象大致是;(3)对于函数9y x x=+,求当0x >时,y 的取值范围. 请将下面求解此问题的过程补充完整: 解:∵x >09y x x∴=+ 22=+2=+.()23xx -≥0,y ∴.【拓展运用】(4)若函数259x x y x -+=,则y 的取值范围是.27.在平面直角坐标系xOy 中,抛物线211:44C y ax ax =--的顶点在x 轴上,直线2:5l y x =-+与x 轴交于点A .(1)求抛物线211:44C y ax ax =--的表达式及其顶点坐标;(2)点B 是线段OA 上的一个动点,且点B 的坐标为(),0t .过点B 作直线BD x ⊥轴交直线l 于点D ,交抛物线223:44C y ax ax t =--+于点E .设点D 的纵坐标为m ,点E 的纵坐标为n ,求证:m n ≥;(3)在(2)的条件下,若抛物线223:44C y ax ax t =--+与线段BD 有公共点,结合函数的图象,求t 的取值范围.28.在等腰直角三角形ABC 中,,90AB AC BAC =∠= .点P 为直线AB 上一个动点(点P 不与点,A B 重合),连接PC ,点D 在直线BC 上,且PD PC =.过点P 作PE PC ⊥,点,D E 在直线AC 的同侧,且PE PC =,连接BE . (1)情况一:当点P 在线段AB 上时,图形如图1所示;情况二:如图2,当点P 在BA 的延长线上,且AP AB <时,请依题意补....全图..2.; (2)请从问题(1)的两种情况中,任选一种情况......,完成下列问题: ①求证:ACP DPB ∠=∠;②用等式表示线段,,BC BP BE 之间的数量关系,并证明.图1 图229.在平面直角坐标系xOy 中,对于点(),P x y ,以及两个无公共点的图形1W 和2W ,若在图形1W 和2W 上分别存在点()11,M x y 和()22,N x y ,使得P 是线段MN 的中点,则称点M 和N 被点P “关联”,并称点P 为图形1W 和2W 的一个“中位点”,此时,,P M N 三个点的坐标满足1212,22x x y y x y ++==.(1)已知点()()()()0,1,4,1,3,1,3,2A B C D --,连接,AB CD .①对于线段AB 和线段CD ,若点A 和C 被点P “关联”,则点P 的坐标为;②线段AB 和线段CD 的一个“中位点”是12,2Q ⎛⎫- ⎪⎝⎭,求这两条线段上被点Q “关联”的两个点的坐标;(2)如图1,已知点()2,0R -和抛物线21:2W y x x =-,对于抛物线1W 上的每一个点M ,在抛物线2W 上都存在点N ,使得点N 和M 被点R “关联”,请在图1中画出符合条件的抛物线2W ;(3)正方形EFGH 的顶点分别是()()()()4,1,4,1,2,1,2,1E F G H ------,⊙T 的圆心为()3,0T ,半径为1.请在图2中画出由正方形EFGH 和⊙T 的所有“中位点”组成的图形(若涉及平面中某个区域时可以用阴影表示),并直接写出该图形的面积.图1 图2北京市西城区2016年初三二模数学试卷参考答案2016.6 一、选择题(每小题3分,共30分)二、填空题(每小题3分,共18分)11. -612. 2π13. 105°14. 理由包含表格所给信息,如:乙,乙组的平均成绩较高,方差较小,成绩相对稳定15. (25, 26),y=x+116. (60°,60°),90°三、解答题(第17~26题,每小题5分,第27题7分,第28题7分,第29题8分)17.原式=9+−8+5−2+2×12=9−8+5−2+1=518. 证明:∵DC=DB,∴∠DCB=∠DBC, ∵∠ACB=∠EBC∴∠ACD=∠EBD又∴∠CDA=∠BDE,CD=BD∴∆ACD≅∆EBD∴AC=EB19. 原式=x(x−1)(x+1)÷x+22x−1−22x−1=x(x−1)(x+1)÷x2(x−1)=x(x−1)(x+1)×2(x−1)x =2x+1=2−1+1=220. (1)证明:∵四边形ABCD为平行四边形,∴AO=CO=12AC=3,BO=DO=12BD=4,又∵AB=5∴AB2=AO2+BO2,∴BO⊥AO,又∵AO=CO ∴BA=BC,∴四边形ABCD是菱形.(2)∵BO⊥AO∴S∆ABC=12AC∙BO=12×6×4=12,又AH⊥BC,∴S∆ABC=12AH∙BC,∴12AH×5=12∴AH=24521. (1)证明:∵∇=(−4m)2−44m2−9=36>0∴此方程有两个不相等的实数根。

北京市西城区2016年初三二模试卷语文 2016.5一、基础·运用(共23分)1.阅读下面的文字,完成第(1)-(3)题(共6分)丝绸是中国古老文明的象征。
几千年前,当丝绸乘.坐在骆驼的脊背之上,一路辗转向欧洲进发的时候,它就已经成为了东方技术与文明的传播者。
在距今五六千年前的新石器时代中期,中国便开始养蚕、取丝、织绸了,其复杂工艺曾被中国长期(lǒng)断。
西周及春秋战国时期,丝绸的品种丰富起来,主要分为绢、绮、锦三大类,其中锦的出现是中国丝绸史上一个重要的里程碑。
锦把蚕丝的优秀性能和美术结合,使丝绸不再只是高贵的衣料,而成为了可以进行创作的艺术品,大大提高了丝绸产品的文化内涵和历史价值,影响很是深远,我们可以从丝绸店常用的对联‚,经纶山海大文章‛中,看出业内对它的推崇。
秦汉时期,丝织业得到了大发展,丝绸贸易也达到了空前的繁荣。
在丝绸贸易的推动下,中国和东西邻邦的经济文化交流也得到了进一步的发展,从而形成了著名的‚丝绸之路‛。
这条路从古长安出发,经甘肃、新疆一直向西,经过中亚、西亚,最终抵达欧洲,沿途聚(lǒng)了诸多的城市群及经济圈。
(1)对文中加点字的注音和对画线字笔顺的判断,全都正确的一项是(2分)A.乘.坐(chéng)“里”字的第五笔是“一”B.乘.坐(chéng)“里”字的第五笔是“丨”C.乘.坐(chèng)“里”字的第五笔是“一”D.乘.坐(chèng)“里”字的第五笔是“丨”(2)理解文意,依据文中括号里的注音填写汉字,全都正确的一项是(2分)A.拢拢B.拢垄C. 垄拢D.垄垄(3)结合文意,为文中丝绸店的对联选择上联,最恰当的一项是(2分)A.驼铃古道丝绸路B.银针绣出彩鸾飞C.罗绮丛中花样新D.锦绣乾坤真事业2.阅读下列文字,完成第(1)-(3)题(共5分)‚武‛,甲骨文由‚戈‛(表兵器)和‚止‛(脚趾,表示行进)组成,表示持戈而行。

2016年各区二模《统计与概率》选择、填空题汇总1(西城4).有一个可以自由转动且质地均匀的转盘,被分成6个大小相同的扇形.在转盘的适当地方涂上灰色,未涂色部分为白色.为了使转动的转盘停止时,指针指向灰色的概率为23,则下列各图中涂色方案正确的是A B C D2(西城14).某班级进行了一次诗歌朗诵比赛,甲、乙两组学生的成绩如下表所示(满分10分):你认为哪一组的成绩更好一些?并说明理由. 答: 组(填“甲”或“乙”),理由是 .3(昌平4). 在一个不透明的袋子里装有3个白球和m 个黄球,这些球除颜色外其余都相同.若从这个袋子里任意摸出1个球,该球是黄球的概率为14,则m 等于A .1B . 2C . 3D . 44(昌平7).在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示: 这些运动员跳高成绩的中位数和众数分别是A .1.65,1.70B .1.70,1.70C .1.70,1.65D .3,4 5(昌平15).市运会举行射击比赛,射击队从甲、乙、丙、丁四人中选拔一人参赛. 在选拔赛中,每人射击10次,计算他们10次成绩(单位:环)的平均数及方差如下表. 根据表中提供的信息,你认为最合适的人选是,理由是.圆矩形平行四边形直角三角形6(顺义5).在下列调查中,适宜采用全面调查的是A. 了解七(1)班学生校服的尺码情况B.了解我市中学生视力情况C.检测一批电灯泡的使用寿命D.调查顺义电视台《师说》栏目的收视率7(顺义7).四张质地、大小相同的卡片上,分别画上如下图所示的四个图形,在看不到图形的情况下从中任意抽出一张卡片,则抽出的卡片上的图形是轴对称图形的概率为A .12B . 14C . 34D .1 8(顺义12). 甲、乙两地某月上旬的日平均气温如图所示,则甲、乙两地这10天日平均气温方差大小关系为S 甲2 S 乙2(填>或<).9这10名学生所得分数的平均数是A .86B .88C .90D .9210(海淀15).在某次试验数据整理过程中,某个事件发生的频率情况如下表所示.估计这个事件发生的概率是_________________(精确到0.01),试举出一个随机事件的例子,使它发生的概率与上述事件发生的概率大致相同:___________________________________________________________________________________.11(东城3).一个不透明的盒子中装有6个除颜色外完全相同的乒乓球,其中4个是黄球,2个是白球.从该盒子中任意摸出一个球,摸到黄球的概率是A.13B.25C.12D.2312(东城7).某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是13(东城10).某班有20位同学参加乒乓球、羽毛球比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5人.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是A.若甲对,则乙对B.若乙对,则甲对C.若乙错,则甲错D.若甲错,则乙对14(东城14). 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是.15(朝阳4).一个袋子中只装有黑、白两种颜色的球,这些球的形状、质地等完全相同,其中白色球有2个,黑色球有n个.在看不到球的条件下,随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀.同学们进行了大量重复试验,发现摸出白球的频率稳定在0.4附近,则n的值为A.2 B.3 C.4 D.516(朝阳6).某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是A.16,15 B.15,15.5C.15,17 D.15,1617(丰台3). 一枚质地均匀的正方体骰子,六个面上分别刻有1、2、3、4、5、6六个数字,投掷这个骰子一次,则向上一面的数字大于4的概率是A.21 B.31 C.32 D.61 18(丰台7). 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.6环,方差分别是2甲S =0.96,2乙S =1.12,2丙S =0.56,2丁S =1.58.在本次射击测试中,成绩最稳定的是 A. 甲B. 乙C. 丙D. 丁19(丰台15). 北京市2010-2015年机动车保有量统计如图所示.根据统计图中提供的信息,预估2016年北京市 机动车的保有量约________万辆, 你的预估理由是______________.20(房山4).小明掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,那么向上一面的点数大于4的概率为A .23 B .12 C .13 D .1621(房山7).国家气象局监测2015年某日24小时PM2.5的值,其中6个时刻的数值如下则这组数据的中位数和平均数分别是A. 331;332.5B. 329;332.5C.331;332D.333;33222(石景山5).从长度分别是2,3,4的三条线段中随机抽出一条,与长为1,3的两条线段首尾顺次相接,能构成三角形的概率是 A .1B .32 C .31D .0 23根据表中的信息,估计掷一枚这样的瓶盖,落地后盖面朝上的概率为.(精确到0.01) 24(石景山14).甲、乙两名队员在5次射击测试中,成绩如下表所示:若需要你根据两名队员的5次成绩,选择一名队员参加比赛,你会选择队员,选择的理由是.25(怀柔3).从0,π,31,22这四个数中随机取出一个数,取出的数是无理数的概率是 A. 41 B. 43 C.31 D.2126(怀柔7).甲、乙、丙、丁四人参加训练,近期10次百米测试平均成绩都是13.2秒,方差如表:则这四人中近期百米测试发挥最稳定的是( )A .甲B .乙C .丙D .丁 27(怀柔13).我市某一周的日最高气温统计如下表:则这组数据的中位数是,众数是.28(通州5).本学期的四次数学单元练习中,甲、乙两位同学的平均成绩一样,方差分别为1.0,0.6,由此可知A. 甲比乙的成绩稳定B. 甲乙两人的成绩一样稳定C. 乙比甲的成绩稳定D. 无法确定谁的成绩更稳定29(通州7).一个盒子中装有四张完全相同的卡片,分别写着2cm ,3cm ,4cm 和5cm ,盒子外有两张卡片,分别写着3cm 和5cm ,现随机从盒中取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是 A.41 B. 31 C 21D. 43成绩/环 五次射击测试成绩30(通州14).如图是根据某班50名同学一周的体育锻练情况绘制的条形统计图,那么这个班50名同学一周参加体育锻炼时间的众数是(小时),中位数是(小时)。


代数综合1、(16朝阳二模)27.在平面直角坐标系xOy 中,抛物线22(9)6y x m x =-++-的对称轴是2x =.(1)求抛物线表达式和顶点坐标;(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A ,求点A 的坐标;(3)抛物线22(9)6y x m x =-++-与y 轴交于点C ,点A 关于平移后抛物线的对称轴的对称点为点B ,两条抛物线在点A 、C 和点A 、B 之间的部分(包含点A 、B 、C )记为图象M .将直线22y x =-向下平移b (b>0)个单位,在平移过程中直线与图象M 始终有两个公共点,请你写出b 的取值范围_________.2、(16东城二模)27.二次函数21:C y x bx c =++的图象过点A (-1,2),B (4,7). (1)求二次函数1C 的解析式;(2)若二次函数2C 与1C 的图象关于x 轴对称,试判断二次函数2C 的顶点是否在直线AB 上;(3)若将1C 的图象位于A ,B 两点间的部分(含A ,B 两点)记为G ,则当二次函数221y x x m =-+++与G 有且只有一个交点时,直接写出m 满足的条件.3、(16 西城二模)27.在平面直角坐标系xOy 中,抛物线C1 : y 1 = ax 2 - 4ax - 4的顶点在x 轴上, 直线l : y 2 = -x + 5与x 轴交于点A.(1)求抛物线C 1 : y 1 = ax 2 - 4ax - 4的表达式及其顶点坐标;(2)点B 是线段OA 上的一个动点,且点B 的坐标为(t,0).过点B 作直线BD ⊥x 轴交直线l 于点D , 交抛物线C 2 : y 3 = ax 2 - 4ax - 4 + t 于点E.设点D 的纵坐标为m ,点E.设点E 的纵坐标为n , 求证:m ≥n(3)在(2)的条件下,若抛物线C 2 : y 3 = ax 2 - 4ax - 4 + t 与线段BD 有公共点,结合函数的图象,求t 的取值范围.4、(16海淀二模)27.已知:点(,)P m n 为抛物线24y ax ax b =-+(0a ≠)上一动点.(1) 1P (1,1n ),2P (3,2n )为P 点运动所经过的两个位置,判断1n ,2n 的大小,并说明理由; (2) 当14m ≤≤时,n 的取值范围是14n ≤≤,求抛物线的解析式.5、(16昌平二模)27. 在平面直角坐标系xOy 中,直线y=kx+b 的图象经过(1,0),(-2,3)两点,且与y 轴交于点A.(1)求直线y=kx+b 的表达式;(2)将直线y=kx+b 绕点A 沿逆时针方向旋转45º后与抛物线21:1(0)G y ax a =->交于B ,C 两点. 若BC ≥4,求a 的取值范围;(3)设直线y=kx+b 与抛物线22:1G y x m =-+交于D ,E 写出m 的取值范围.6、(16房山二模)27.如图,在平面直角坐标系xoy 中,已知点P (-1,0),C ()11-2,,D (0,-3),A ,B 在x 轴上,且P 为AB 中点,1=∆CAP S .(1)求经过A 、D 、B 三点的抛物线的表达式.(2)把抛物线在x 轴下方的部分沿x 轴向上翻折,得到一个新的图象G ,点Q 在此新图象G 上,且APC APQ S S ∆∆=,求点Q 坐标. (3)若一个动点M 自点N (0,-1)出发,先到达x 轴上某点(设为点E ),再到达抛物线的对称轴上某点(设为点F ),最后运动到点D ,求使点M 运动的总路程最短的点E 、点F 的坐标.7、(16石景山二模)27.已知关于x 的方程()021222=-+-+m m x m x . (1)求证:无论m 取何值时,方程总有两个不相等的实数根;(2)抛物线()m m x m x y 21222-+-+=与x 轴交于()0,1x A ,()0,2x B 两点,且210x x <<,抛物线的顶点为C ,求△ABC 的面积;(3)在(2)的条件下,若m 是整数,记抛物线在点B ,C 之间的部分为图象G (包含B ,C 两点),点D 是图 象G 上的一个动点,点P 是直线b x y +=2上的一个动点,若线段DP 的最小值是55,请直接写出b 的值.8、(16顺义二模)27.已知关于x 的一元二次方程2(21)20x m x m -++=. (1)求证:不论m 为任何实数时,该方程总有两个实数根;(2)若抛物线2(21)2y x m x m =-++与x 轴交于A 、B 两点(点A 与点B 在y 轴异侧),且4AB =,求此抛物线的表达式;(3)在(2)的条件下,若抛物线2(21)2y x m x m =-++向上平移b 个单位长度后,所得到的图象与直线y x =没有交点,请直接写出b 的取值范围.9、(通州二模)27. 已知:二次函数c bx -x y ++=2的图象过点A (-1,0)和C (0,2). (1)求二次函数的表达式及对称轴;(2)将二次函数c bx -x y ++=2的图象在直线y=1上方的部分沿直线y=1翻折,图象其余的部分保持不变,得到的新函数图象记为G ,点M (m ,1y )在图象G 上,且0y 1≥,求m 的取值范围。
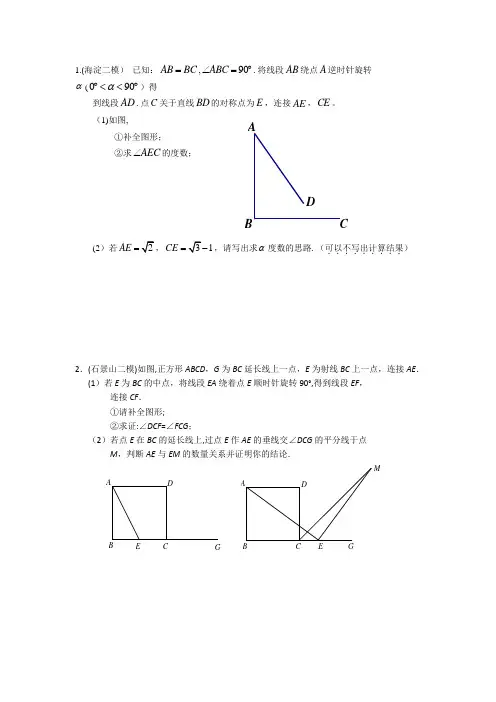
1.(海淀二模) 已知:AB BC =,90ABC ∠=︒.将线段AB 绕点A 逆时针旋转α(090α︒<<︒)得到线段AD .点C 关于直线BD 的对称点为E ,连接AE ,CE 。
(1)如图, ①补全图形;②求AEC ∠的度数;(2)若AE =1CE =,请写出求α度数的思路.(可以不写出计算结果.........)2.(石景山二模)如图,正方形ABCD ,G 为BC 延长线上一点,E 为射线BC 上一点,连接AE . (1)若E 为BC 的中点,将线段EA 绕着点E 顺时针旋转90°,得到线段EF ,连接CF . ①请补全图形; ②求证:∠DCF =∠FCG ;(2)若点E 在BC 的延长线上,过点E 作AE 的垂线交∠DCG 的平分线于点M ,判断AE 与EM 的数量关系并证明你的结论.EGD CBAMABCDGE3.(顺义二模)已知:如图,90ACD ∠=︒,MN 是过点A 的直线,AC DC =,DB MN ⊥于点B .图2图3图1ABCDNMABCDNMNMABCD(1)在图1中,过点C 作CE CB ⊥,与直线MN 于点E ,①依题意补全图形;②求证:BCE ∆是等腰直角三角形;③图1中,线段BD 、AB 、CB 满足的数量关系是 ; (2)当MN 绕A 旋转到如图(2)和图(3)两个位置时,其它条件不变. 在图2中,线段BD 、AB 、CB 满足的数量关系是 ; 在图3中,线段BD 、AB 、CB 满足的数量关系是 ; (3)MN 在绕点A 旋转过程中,当30BCD ∠=︒,BD =则CB = .4.(通州二模) 已知,在菱形ABCD 中,∠ADC=60°,点F 为CD 上任意一点(不与C 、D 重合),过点F 作CD 的垂线,交BD 于点E ,连接AE 。
(1)①依愿意补全图1;②线段EF 、CF 、AE 之间的等量关系是 . (2)在图1中将ΔDEF 绕点D 逆时针旋转,当点F 、E 、C 在一条直线上(如图2). 线段EF 、CE 、AE 之间的等量关系是 。

北京市西城区2016年初三一模试卷数学试卷参考答案及评分标准 2016.4一、选择题(本题共30分,每小题3分)三、解答题(本题共72分,第17﹣26题,每小题5分,第27题7分,第28题7分,第29题8分) 17.解:原式=2319++ ……………………………………………………4分 =11. …………………………………………………………………………5分18.解:原式=222232()a a b a b ---- ……………………………………………………2分 =222a a -. ……………………………………………………………………3分 ∵230a a --=,∴23a a -=. ………………………………………………………………………4分 ∴原式=22()a a -=6. ……………………………………………………………5分 19.证明:∵AB=AC ,AD 是BC 边上的中线, ∴BD=21BC , ………………………………1分 AD ⊥BC . …………………………………2分 ∵BE=21BC , ∴BD =BE . …………………………………3分 ∵AE ⊥BE 于点E ,∴点B 在∠EAD 的平分线上.∴AB 平分∠EAD . ………………………………………………………………5分20.解:原不等式组为2(12)4,35 1.2x x x x +-≥-⎧⎪⎨+>-⎪⎩ 解不等式①,得2x ≤. ……………………………………………………………2分①②解不等式②,得53x >-. …………………………………………………………4分 ∴原不等式组的解集为523x -<≤. ……………………………………………5分21.(1)证明:如图1.∵四边形ABCD 是平行四边形, ∴AB ∥DC ,即AF ∥ED . ∵DF ∥EA ,∴四边形AEDF∵AE ⊥DE , ∴∠E=90°.∴四边形AEDF 是矩形. …………………………………………………2分(2)解:如图2.∵四边形AEDF 是矩形,∴FD =AE =2, ……………………3分 ∠F =90°. ∵在Rt △AFD 中,tan ∠F AD =FD AF =25,∴AF =5. ∵AB =2,∴BF =AB +AF =7.∴在Rt △BFD 中,BD ……………………………5分22.解:(1)∵对于直线314y x =+,令0y =,则43x =-,∴点A 的坐标为(43-,0). ………………………………………………1分∵点B (83,m )在直线314y x =+上,∴38143m ⨯+=,解得3m =.∵点B (83,3)在双曲线k y x =上,∴8k =.∴双曲线的表达式为8y x=. ………………………………………………2分 (2)当点C 在直线AB 的上方时,过点C 作E ,如图1. ∵BC ∥y 轴, ∴CE ⊥x 轴.∴∠BEA =90°,OE∴AE = AO + OE =4.∵在Rt △ABE 中,BE =3,∴AB5=.∴sin ∠45. ∵CD ⊥AB 于点D ,点C 到直线AB 的距离为2, ∴∠CDB =90°,CD =2. ∵∠CBD =∠ABE ,∴在Rt △CDB 中,sin ∠45. ∴ ……………………………………………………………………3分 ∴CE =CB .∴点C 的纵坐标为11. ……………4分∴点C 的纵坐标为12.……………5分综上所述,点C 的纵坐标为112或12.23.解:设如果小芳家选择住在乐园内,预计在迪士尼乐园内游玩x 天.………………1分根据题意,得981098101.51x x =⨯+.……………………………………………2分 解得 2x =. ……………………………………………………………………3分 经检验,2x =是原方程的解,且符合题意. ……………………………………4分 24.(1)证明:连接BD,如图1.∵AB 是⊙O 的直径,∴∠ADB=90°. ∴∠DAB +∠1=90°.∵∠1=∠2, …………………………1分 ∠2=∠3, ∴∠1=∠3.∴∠DAB +∠3=90°. ∴∠CF A=180°-(∠DAB +∠3)=90°. ∴CF ⊥AB . (2)解:连接OE ,如图2.∵∠ADB =90°,∴∠CDB =180°-∠ADB =90°.∵在Rt △CDB 中,CD =4,CB =∴8BD . …………………3分∵∠1=∠3, ∴cos ∠1=cos ∠3=45. ∵在Rt △ABD 中,cos ∠1=DB AB=∴AB =10. ∴OA =OE =5,6AD .∵CD =4,∴AC =AD +CD =10.∴在Rt △ACF 中,CF =AC ·cos ∠3=8.∴6AF =. …………………………………………………4分 ∴OF =AF -OA =1.∴在Rt △OEF中,EF = ……………………………5分25.解:(1)172,35; ………………………………………………………………………2分(2)统计表如下:3分 (3)不同意. ………………………………………………………………………4分因为通过计算2015年重污染天数约为42天,而2014年重污染天数为45天,所以2015年全年的PM2.5重污染天数比2014年少. ……………………5分26.解:(1)已知:如图,筝形ABCD 中,AB =AD ,CB =CD . 求证: ∠B =∠D . ……………………1分 证明:连接AC ,如图1.在△ABC 和△ADC 中, ,,,AB AD CB CD AC AC =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC .∴∠B =∠D .…………………………………………………………2分(2)筝形的其他性质:①筝形的两条对角线互相垂直. ②筝形的一条对角线平分一组对角. ③筝形是轴对称图形.……(写出一条即可) ……………………………3分 (3)不成立.反例如图2所示.………………………4 在平行四边形ABCD 中,AB ≠AD ,对角线AC ,图1BD 相交于点O .由平行四边形性质可知此图形满足∠ABC =∠ADC ,AC 平分BD .但是该四边形不是筝形.(答案不唯一)………………………………5分27.解:(1)∵抛物线1C :2y x bx c =++经过点A (2,3-),且与x 轴的一个交点为B(3,0),∴22223,330.b c b c ⎧++=-⎪⎨++=⎪⎩ …………………………………………………………1分解得 2,3.b c =-⎧⎨=-⎩∴抛物线1C 的表达式为223y x x =--. …………………………………2分 (2)①过A 作AF ⊥x 轴于点F ,如图1.∵223y x x =--2(1)4x =--,∴抛物线1C 的对称轴为直线1x =.∴点D 的坐标为(1-,0).∵点E 的坐标为(m ,0),且m >0, ∴11213224ADE S DE AF DE ∆=⋅=⨯=. ∴DE =72.∴m =OE =DE -OD =52. …………………………………………………4分 ②设抛物线2C 的表达式为2(1)4y x n =--+.情况一:如图2. 当抛物线2C 经过点E (52,0)时, 25(1)402n --+=,解得74n =; 当抛物线2C 经过原点O 时,2(1)40n --+=,解得3n =; ……………5∵当502x ≤≤时,抛物线2C 与x ∴结合图象可知,当734n ≤<时,符合题意.……………………………6分 情况二:如图2.当4n =时,抛物线2C 的表达式为2(1)y x =-,它与x 轴只有一个公共点(1,0),符合题意. …………………………………………………………7分综上所述,n 的取值范围是734n ≤<或4n =. 28.解:(1)等腰直角三角形; (2)①补全图形,如图1所示; ②△QPM 证明:延长BC 至E ,使CE =如图2.∵PB = CE ,∴PB +BC = CE +BC ∵四边形ABCD ∴AB = DC ,∠ABC =∠DCB =90°. 在△DCP 和△ABE ,,,D C A B D C P A BE C P B E =⎧⎪∠=∠⎨⎪=⎩∴△DCP ≌△ABE . ………………………………………………4分 ∴∠1=∠E .∵M 为BC 的中点, ∴MB =MC .∴MB +BP = MC +CE ,即MP =ME . ∴M 为PE 的中点. ∵N 为AP 的中点, ∴NM ∥AE . ∴∠2=∠E . ∴∠1=∠2. ∴QP =QM .∴△QPM 是等腰三角形. …………………………………………5分 (3)求解思路如下:a .由题意画出图形,并延长BC 至E ,使CE =BP 连接AE ,如图3.b .由(2)可得QM ∥AE ,可证''P Q P MQA ME=; c .由P P'∥AD ,可证△P'PQ ∽△ADQ ,从而''P Q P PQA AD =; d .可得''P M P PME AD=; e .由点P'与点P 关于直线AB 对称,得到BP'=BP =CE ,设BP'=BP =CE =x ,由AD =BC =2,可分别表示P'M ,ME ,P'P ,可求BP 的长. ………7分29.解:(1)①1P ,4P ;……………………………………………………………………2分图2②(2,6);……………………………………………………………………3分(2)情况一:如图1,当⊙E与y轴相切时,设切点为F,连接EF.∵⊙E与y轴相切于点F,∴EF⊥y轴.∵⊙E的半径为32,∴EF=32.∴此时点E的横坐标为32. (4)情况二:如图2,设直线l分别与x轴,y轴交于点G,H,连接CD,CO,过点O作⊙C的另一条切线OI,切点为I,直线OI与直线l交于点J.当⊙E与直线OI相切时,过点E作EK⊥y∵⊙C与y轴相切于点D,∴CD⊥y轴.∵点C的坐标为(1,∴tan COD∠=CDOD=.∴∠COD=30°.∵⊙C与OI相切于点I,∴∠COI=∠COD=30°.∴∠HOJ=∠COI +∠COD=60°.∵直线l:y=+分别与x轴,y∴点G(4,0),H(0,.∴tan OHG∠=OGOH=.∴∠OHG=30°.∴∠OJH=180°-∠HOJ-∠OHJ=90°.∴HG⊥OJ.∵⊙E与直线OJ相切,∴切点为点J.∴EJ=32.∵在Rt△OHJ中,HJ=OH·cos∠OHJ =6,∴HE=HJ-EJ=92.∴KE=12HE=94.∴此时点E的横坐标为94.………………………………………………5分可知,点E在直线l上,从情况一中的位置运动到情况二中的位置时,都满足题意,所以点E的横坐标的取值范围是3924Ex≤≤.………………6分(3)9625.……………………………………………………………………………8分。

2016年各区二模几何综合题汇编1.(顺义)28.已知:如图,90ACD ∠=︒,MN 是过点A 的直线,AC DC =,DB MN ⊥于点B .图2图3图1ABCDNMABCDNMNMABCD(1)在图1中,过点C 作CE CB ⊥,与直线MN 于点E ,①依题意补全图形;②求证:BCE ∆是等腰直角三角形;③图1中,线段BD 、AB 、CB 满足的数量关系是 ; (2)当MN 绕A 旋转到如图(2)和图(3)两个位置时,其它条件不变. 在图2中,线段BD 、AB 、CB 满足的数量关系是 ; 在图3中,线段BD 、AB 、CB 满足的数量关系是 ; (3)MN 在绕点A 旋转过程中,当30BCD ∠=︒,BD =则CB = .2.(昌平)28. 在等边△ABC 中,AB =2,点E 是BC 边上一点,∠DEF =60°,且∠DEF 的两边分别与△ABC 的边AB ,AC 交于点P ,Q (点P 不与点A ,B 重合).(1)若点E 为BC 中点.①当点Q 与点A 重合,请在图1中补全图形;②在图2中,将∠DEF 绕着点E 旋转,设BP 的长为x ,CQ 的长为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围;(2)如图3,当点P 为AB 的中点时,点M ,N 分别为BC ,AC 的中点,在EF 上截取EP '=EP ,连接NP '. 请你判断线段NP '与ME 的数量关系,并说明理由.图3图1A BE C图2DPQF3.(东城)28.【问题】在△ABC 中,AC =BC ,∠ACB =90°,点E 在直线BC 上(B ,C 除外),分别经过点E 和点B 做AE 和AB 的垂线,两条垂线交于点F ,研究AE 和EF 的数量关系.【探究发现】某数学兴趣小组在探究AE ,EF 的关系时,运用“从特殊到一般”的数学思想,他们发现当点E 是BC 的中点时,只需要取AC 边的中点G (如图1),通过推理证明就可以得到AE 和EF 的数量关系,请你按照这种思路直接写出AE 和EF 的数量关系;图1【数学思考】那么当点E 是直线BC 上(B ,C 除外)(其它条件不变),上面得到的结论是否仍然成立呢?请你从“点E 在线段BC 上”;“点E 在线段BC 的延长线”;“点E 在线段BC 的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论;图2【拓展应用】当点E 在线段CB 的延长线上时,若BE =nBC (01n <<),请直接写出ABC S △:AEFS △的值.4.(海淀)28. 已知:AB BC =,90ABC ∠=︒.将线段AB 绕点A 逆时针旋转α(090α︒<<︒)得到线段AD .点C 关于直线BD 的对称点为E ,连接AE ,CE . (1)如图, ①补全图形; ②求AEC ∠的度数;(2)若AE1CE =,请写出求α度数的思路.(可.以不写出计算结果........) 5.(西城)28.在等腰直角三角形ABC 中,AB =AC ,∠BAC =90°.点P为直线AB 上一个动点(点P 不与点A ,B 重合),连接PC ,点D 在直线BC 上,且PD =PC .过点P 作EP ⊥PC 于点P ,点D ,E 在直线AC 的同侧,且PE =PC ,连接BE .(1)情况一:当点P 在线段AB 上时,图形如图1所示;情况二:如图2,当点P 在BA 的延长线上,且AP <AB 时,请依题意补全图......2.; (2)请从问题(1)的两种情况中,任选..一种情况....,完成下列问题: ①求证:∠ACP =∠DPB ;②用等式表示线段BC ,BP ,BE 之间的数量关系,并证明.图1 图26.(朝阳)28.在ABC ∆中,点D 、E 分别在AB 、AC 上,BE 、CD 相交于点O ,且A EBC DCB ∠=∠=∠21.(1)如图1,若AB =AC ,则BD 与CE 的数量关系是______________;(2)如图2,若AC AB ≠,请你补全图2,思考BD 与CE 是否仍然具有(1)中的数量关系,并说明理由;(3)如图3,︒=∠105BDC ,BD =3,且BE 平分∠ABC ,请写出求BE 长的思路.(不用写出计算结果)7.(房山)28.在△ABC中,BD平分∠ABC(∠ABC<60°)(1)如图28-1,当点D在AC边上时,若∠ABC=42°,∠ACB=32°,请直接写出AB,DC和BC之间的数量关系.(2)如图28-2,当点D在△ABC内部,且∠ACD=30°时,①若∠BDC=150°,直接写出AB,AD和BC之间的数量关系,并写出结论成立的思路.②若∠ABC=2α,∠ACB=60°-α,请直接写出∠ADB的度数(用含α的式子表示).8.(丰台) 28.在△ABC中,AC=BC,∠ACB=90°. 点D为AC的中点.将线段DE绕点D逆时针旋转90°得到线段DF,连接EF,CF.过点F作FH FC,交直线AB于点H.(1)若点E在线段DC上,如图1,①依题意补全图1;②判断FH与FC的数量关系并加以证明.(2)若E为线段DC的延长线上一点,如图2,且CE=的面积请求出∠FCHCFEΔ,15=,20∠CFE=12°,请写出求△FCH的面积的思路.(可以不写....出计算...结果..)EDADAABAB9.(石景山)28.如图,正方形ABCD ,G 为BC 延长线上一点,E 为射线BC 上一点,连接AE .(1)若E 为BC 的中点,将线段EA 绕着点E 顺时针旋转90°,得到线段EF ,连接CF .①请补全图形; ②求证:∠DCF =∠FCG ;(2)若点E 在BC 的延长线上,过点E 作AE 的垂线交∠DCG 的平分线于点M ,判断AE 与EM 的数量关系并证明你的结论.10.(怀柔)28.在△ABC 中,∠ABC=90°,D 为△ABC 内一动点,BD=a,CD=b(其中a ,b 为常数,且a<b).将△CDB 沿CB 翻折,得到△CEB. 连接AE. (1)请在图1中补全图形;(2)若∠ACB=α,AE ⊥CE ,则∠AEB=;(3)在(2)的条件下,用含a,b,α的式子表示AE 的长.图1 备用图11.(通州)28. 已知,在菱形ABCD 中,∠ADC=60°,点F 为CD 上任意一点(不与C 、D 重合),过点F 作CD 的垂线,交BD 于点E ,连接AE.(1)①依愿意补全图1; ②线段EF 、CF 、AE 之间的等量关系是。

北京市西城区2017年初三统一测试数学试卷2017.4考生须知1.本试卷共8页,共三道大题,29道小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上认真填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,请将本试卷、答题卡一并交回。
一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.据报道,到2020年北京地铁规划线网将由19条线路组成,总长度达到561 500米.将561 500用科学记数法表示为 (A) .05615×106 (B) 5.615×105 (C) 56.15×104 (D) 5 61.5×1032.下列运算正确的是(A) 3362a a a += (B) 532a a a -= (C) 2242a a a = (D) 5210()a a = 3. 不等式 x -1 >0的解集在数轴上表示正确的是(A) (B) (C) (D)4.在一个不透明的袋子里装有5个完全相同的乒乓球,把它们标号分别记为1,2,3,4,5,从中随机摸出一个小球,标号为奇数的概率为 (A)15 (B) 25 (C) 35 (D) 4555大小在下列哪两个实数之间(A) 0与1 (B) 1与2 (C) 2与3 (D) 3与4 6.右图是由射线AB , BC , CD , DE , EA 组成的平面图形,若∠1+∠2+∠3+∠4=225°,ED ∥AB ,则∠1的度数为(A)55° (B)45° (C)35° (D)25°7.已知反比例函数6y x=,当1<x <2时,y 的取值范围是 (A) 1<y <3 (B) 2<y <3 (C) 1<y <6 (D) 3<y <68.如图,以点O 为圆心,AB 为直径的半圆经过点C ,若C 为弧AB 的中点,若AB =2,则图中阴影部分的面积是( ) (A)2π (B) 122π+ (C)4π (D) 124π+9. 如图,点A 在观测点的北偏东方向30 °,且与观测点的距离为8千米,将点A 的位置记作A (8,30°),用同样的方法将点B ,点C 的位置分别记作B (8,60°),C (4,60°),则观测点的位置应在(A) O 1 (B)O 2 (C) O 3 (D) O 410.某大型文体活动需要招募一批学生作为志愿者参与服务.已知报名的男生有420人,女生有400人,他们身高在155≤x <175,随机抽取该校男生、女生进行抽样调查.已知该校共有女生400人,男生420人,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:根据统计图表提供的信息,下列说法中① 估计报名者中男生的身高的众数在D 组;② 估计报名者中女生的身高的中位数在B 组; ③ 抽取的样本中,抽取女生的样本容量是38;④ 估计报名者中身高在160≤x <170之间的学生约有400人 其中合理的是 (A)①② (B) ) ①④ (C)②④(D) ③④二、填空题(本题共18分,每小题3分) 11. 如图, 在长方体中,所有与棱AB 平行的棱是 .12.关于x 的方程240x x k -+=有两个相等的实数根,则k 的值为 .13.如图,正方形ABCD ,AC 为对角线,点E 在AC 上,且AE =AB ,则∠BED 的度数为 °.14. 在平面直角坐标系xOy 中,⊙O 半径是5,点A 为⊙O 上一点, AB ⊥x 轴于点B ,AC ⊥y 轴于点C ,若四边形ABOC 面积为12, 写出一个符合条件的点A 坐标 .15. 右图是由三个直角三角形组成的梯形,根据图形,写出一个正确的等式 .16.《数书九章》中的秦九韶算法是我国南宋时期的数学家秦九韶提出的一种多项式简化算法.在现代,利用计算机解决多项式的求值问题时,秦九韶算法依然是最优的算法.例如在计算“当8=x 时,多项式8354323+--x x x 的值”,按照秦九昭算法,可先将多项式8354323+--x x x 一步地进行改写:()8354383543223+--=+--x x x x x x ()[]83543+--=x x x按改写后的方式计算,它一共做了3次乘法,3次加法,与直接计算相比节省了乘法次数,使计算量减少. 计算当8x =时,多项式的值为1008.请参考上述方法,将多项式3221x x x ++-改写为: ,当8x =时,多项式的值为 .ACEMH FDB三、解答题(本题共72分,第17~26题,每小题5分,第27题7分,第28题7分,第29题8分)解答应写出文字说明,演算步骤或证明过程.171012()4sin 453π----o .18.方程组为 1328y x x y =-⎧⎨+=⎩19.已知2340x x --=,求代数式22(1)(1)(3)2x x x x +--++的值.20.列方程(组)解应用题某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,但每件进价比第一批的每件进价少了10元,且进货量是第一批进货量的一半,求第一批购进这种衬衫每件进价是多少元.21.如图, 在Rt △ABC 中,∠ABC =90 °错误!未指定书签。

2016北京市各区初三数学二模 双曲线与直线综合问题归纳整理(西城2016二模) 23.在平面直角坐标系xOy 中,反比例函数xky =1的图象与一次函数2y ax b =+的图象交于点A (1,3)和(3)B m -,. (1)求反比例函数xky =1和一次函数2y ax b =+的表达式; (2)点C 是坐标平面内一点,BC ∥x 轴,AD ⊥BC 交直线BC 于点D ,连接AC .若AC ,求点C 的坐标. 23.解:(1)∵反比例函数xky =1的图象与一次函数2y ax b =+的图象交于点A (1,3)和(3)B m -,.∴点A (1,3)在反比例函数xky =1的图象上, ∴3k =.∴反比例函数的表达式为13y x=.…………………………………………1分 ∵点(3)B m -,在反比例函数13y x=的图象上, ∴1m =-.……………………………………………………………………2分 ∵点A (1,3)和点(31)B --,在一次函数2y ax b =+的图象上,∴3,3 1.a b a b +=⎧⎨-+=-⎩解得1,2.a b =⎧⎨=⎩∴一次函数的表达式为22y x =+.…………………………………………3分(2)如图.∵BC ∥x 轴,∴点C 的纵坐标为1-.∵AD ⊥BC 于点D , ∴∠ADC =90°,点D 的坐标为(1,1-). ∴AD =4. ∵在Rt △ACD 中,222AC AD CD =+,且AC ,∴222)4CD =+. 解得2CD =.∴点C 1的坐标为(3,1-),点C 2的坐标为(1-,1-).……………5分 综上可得,点C 的坐标为(3,1-)或(1-,1-).评述:考点:考查双曲线以及直线的解析式,利用两点间的距离关系,逆向求点C 的坐标 方法:勾股定理,注意分类讨论思想. 问题:没有分类讨论.这类题目的考查比前几年难度加大,条件不直接,需要自己画图,是一道区分度较大的题目.(2016海淀二模)23.在平面直角坐标系xOy 中,直线1l :12y x b =+与双曲线6y x =的一个交点为(,1)A m .(1)求m 和b 的值;(2)过(1,3)B 的直线交1l 于点D ,交y 轴于点E .若2BD BE =,求点D 的坐标. 23.解:(1)∵点)1,(m A 在双曲线xy 6=上, ∴6=m .………………………1分 ∵点)1,6(A 在直线b x y +=21上, ∴2-=b .………………………2分 (2)当点B 在线段DE 上时,如图1,过点D 作DP ⊥y 轴于P ,过点B 作BQ ⊥y 轴于Q .可得EQB △∽EPD △. ∵BE BD 2=, ∴13BQ BE DP DE ==. ∵1BQ =, ∴3DP =. ∵点D 在直线1l 上,∴)213(-,的坐标为点D .………………4分 当点B 在线段DE 的延长线上时,如图2, 同理,由BE BD 2=,可得点D 的坐标为图15(1)2--,.综上所述,点D 的坐标为)213(-,或5(1)2--,.…………… 5分(2016朝阳二模)23.如图,在平面直角坐标系xOy 中,反比例函数4y x=的图象 与正比例函数y =kx 的图象的一个交点为M (1,b ). (1)求正比例函数y =kx 的表达式;(2)若点N 在直线OM 上,且满足MN=2OM , 直接写出点N 的坐标. 23.解:(1)∵双曲线4y x=过点M (1,b ), ∴4b =.……………………………………………………………………1分 ∵正比例函数y kx =的图象过点M (1,4),∴4k =.……………………………………………………………………2分 ∴正比例函数的表达式为4y x =.………………………………………3分 (2)(-1,-4),(3,12).…………………………………………………5分 (2016顺义二模)23.在平面直角坐标系xOy 中,一次函数y x k =-+的图象与反比例函数4y x=-的图象交于点A (-4,n )和点B .(1)求k 的值和点B 的坐标;(2)若P 是x 轴上一点,且=AP AB ,直接写出点P 的坐标.23. 解:(1)把A (-4,n )代入4y x=-中,得1n =, …………………....….1分把A (-4,1)代入y x k =-+中,得3k =- ……………….….…….2分解方程组3,4.y x y x =--⎧⎪⎨=-⎪⎩得4,1.x y =-⎧⎨=⎩ , 1,4.x y =⎧⎨=-⎩∴点B 的坐标是(1,4)- ……………………………………….…...…3分 (2)点P 的是坐标(3,0)或(11,0)- ……………………………….…...…5分(2016丰台二模)23. 已知反比例函数y =xk(k ≠0)的图象经过点A (-1,6). (1)求k 的值;(2)过点A 作直线AC 与函数y =xk的图象交于点B ,与x 轴交于点C , 且AB =2BC ,求点B 的坐标.(2016通州二模)22. 如图。
北京市2016年各区中考二模汇编四边形一、四边形与三角形1. 【2016年西城二模,第10题】一级管道如图1所示,其中四边形是矩形,是是中点,管道由组成,在的中点处放置了一台定位仪器.一个机器人在管道内匀速行进,对管道进行检测.设机器人行进的时间为,机人与定位仪器之间的距离为,表示与的函数关系的图象大致如图2所示,则机器人的行进路线可能为图1 图2A. B. C. D.2. 【2016年房山二模,第14题】如图,在正方形网格中,每个小正方形的边长均为1,△ABC 的三个顶点均在格点上,则△A BC 的面积为 .3. 【2016年昌平二模,第10题】如图1,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,AB =2厘米,∠BAD =60°.P ,Q 两点同时从点O 出发,以1厘米/秒的速度在菱形的对角线及边上运动. 设运动的时间为x 秒,P ,Q 间的距离为y 厘米,y 与x 的函数关系的图象大致如图2所示,则P ,Q 的运动路线可能为ABCD O AC ,,,,,,,AB BC CD DA OA OB OC OD BC M x y yx A O D →→B O D →→A B O -→→A D O →→ABCA. 点P : O —A —D —C ,点Q : O —C —D —OB. 点P : O —A —D —O ,点Q : O —C —B —OC. 点P : O —A —B —C ,点Q : O —C —D —OD. 点P : O —A —D —O ,点Q : O — C —D —O4. 【2016年通州二模,第23题】如图,四边形ABCD 中,∠A=∠ABC=90°,AD=1,BC=3,E 是边CD 的中点,连接BE 并延长与AD 的延长线相较于点F.连接CF. (1)求证:四边形BDFC 是平行四边形; (2)已知CB=CD ,求四边形BDFC 的面积。
5. 【2016年通州二模,第28题】已知,在菱形ABCD 中,∠ADC=60°,点F 为CD 上任意一点(不与C 、D 重合),过点F 作CD 的垂线,交BD 于点E ,连接AE. (1)①依愿意补全图1;②线段EF 、CF 、AE 之间的等量关系是 。
2016年北京市西城区高三二模数学文试卷第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合{|10}A x x =->,集合3{|}B x x =≤,则A B =I ( ) (A )(1,3)-(B )(1,3](C )[1,3)(D )[1,3]-3. 设命题p :函数1()ex f x -=在R 上为增函数;命题q :函数()cos 2f x x =为奇函数. 则下列命题中真命题是( )(A )p q ∧ (B )()p q ⌝∨ (C )()()p q ⌝∧⌝ (D )()p q ∧⌝4.执行如图所示的程序框图,若输入的{1,2,3}n ∈, 则输出的s 属于( ) (A ){1,2} (B ){1,3} (C ){2,3}(D ){1,3,9}2.已知平面向量,,a b c 满足(1,1)=-a ,(2,3)=b ,(2,)k =-c ,若()//+a b c ,则实数k =( ) (A )4 (B )4- (C )8 (D )8-5. 一个几何体的三视图中,正(主)视图和侧(左)视图如图所示,则俯视图可以为()(A)(B)(C)(D)6. 某生产厂商更新设备,已知在未来x年内,此设备所花费的各种费用总和y(万元)与x满足函数关系2464y x=+,若欲使此设备的年平均花费最低,则此设备的使用年限x 为()(A)3(B)4(C)5(D)67. “3m>”是“曲线22(2)1mx m y--=为双曲线”的()(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件8. 在长方体1111ABCD A B C D-中,11AB BC AA===,点P为对角线1AC上的动点,点Q为底面ABCD上的动点(点P,Q可以重合),则1B P PQ+的最小值为()(A(B(C)32(D)2第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数10i3i=+____. 10. 抛物线24C y x =:的准线l 的方程是____;以C 的焦点为圆心,且与直线l 相切的圆的 方程是____.11.设函数,11,1()2,.x x f x xx -⎧>⎪=⎨⎪-⎩≤ 则[(2)]f f =____;函数()f x 的值域是____. 12.在ABC ∆中, 角A ,B ,C 所对的边分别为,,a b c ,若a =,3b =,2c =, 则A =____;ABC ∆的面积为____.13. 若,x y 满足,2,1,y x y x x y +⎧⎪⎨⎪⎩≥≤≤若z x my =+的最大值为53,则实数m =____. 14. 如图,正方形ABCD 的边长为2,O 为AD 的中点,射线OP 从OA 出发,绕着点O 顺时针方向旋转至OD ,在旋转的过程中,记AOP ∠为([0,π])x x ∈,OP 所经过的在正方形ABCD 内的区域(阴影部分)的面积()S f x =,那么对于函数()f x 有以下三个结论: ○1π()3f =○2 函数()f x 在区间π(,π)2上为减函数;○3 任意π[0,]2x ∈,都有()(π)4f x f x +-=.其中所有正确结论的序号是____.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分) 已知函数cos 2(sin cos )()cos sin x x x f x x x+=-.(Ⅰ)求函数()f x 的定义域; (Ⅱ)求函数()f x 的单调增区间. 16.(本小题满分13分)设数列{}n a 的前n 项和为n S ,且11a =,*11()n n a S n +=+∈N . (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 为等差数列,且11b a =,公差为21a a . 当3n ≥时,比较1nb +与121n b b b ++++L 的大小.17.(本小题满分14分)如图,在四棱锥E ABCD -中,AE DE ⊥,CD ⊥平面ADE , AB ⊥平面ADE ,6CD DA ==,2AB =,3DE =.(Ⅰ)求棱锥C ADE -的体积; (Ⅱ)求证:平面ACE ⊥平面CDE ;(Ⅲ)在线段DE 上是否存在一点F ,使//AF 平面BCE ?若存在,求出EF ED的值;若不存在,说明理由.18.(本小题满分13分)某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.(Ⅰ)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;(Ⅱ)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求a >b 的概率; (Ⅲ)若a =1,记乙型号电视机销售量的方差为s 2,根据茎叶图推断b 为何值时,s 2达到最小值.(只需写出结论) (注:方差2222121[()()()]n s x x x x x x n=-+-++-L ,其中x 为1x ,2x ,…,n x 的平均数)19.(本小题满分14分)设1F ,2F 分别为椭圆2222 + 1(0)x y E a b a b=>>:的左、右焦点,点A 为椭圆E 的左顶点,点B 为椭圆E 的上顶点,且||2AB =.(Ⅰ)若椭圆E E 的方程;(Ⅱ)设P 为椭圆E 上一点,且在第一象限内,直线2F P 与y 轴相交于点Q . 若以PQ 为直径的圆经过点1F ,证明:点P 在直线20x y +-=上.20.(本小题满分13分)已知函数21()1x f x ax -=+,其中a ∈R .(Ⅰ)当14a =-时,求函数()f x 的图象在点(1,(1))f 处的切线方程;(Ⅱ)当0a >时,证明:存在实数0m >,使得对任意的x ,都有()m f x m -≤≤成立; (Ⅲ)当2a =时,是否存在实数k ,使得关于x 的方程()()f x k x a =-仅有负实数解?当12a =-时的情形又如何?(只需写出结论)北京市西城区2015年高三二模试卷参考答案及评分标准高三数学(文科) 2015.5一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.D 3.D 4.A 5.C 6.B 7.A 8.C 二、填空题:本大题共6小题,每小题5分,共30分.9.13i + 10.1x =- 22(1)4x y -+=11.52- [3,)-+∞ 12.π313.2 14.○1 ○3 注:第10,11题第一问2分,第二问3分. 第14题多选、漏选或错选均不得分. 三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:由题意,得cos sin 0x x -≠, ……………… 1分即 tan 1x ≠, ……………… 2分 解得 ππ4x k ≠+, ……………… 4分 所以函数()f x 的定义域为π{|π,}4x x k k ≠+∈Z . ……………… 5分 (Ⅱ)解:cos 2(sin cos )()cos sin x x x f x x x+=-22(cos sin )(sin cos )cos sin x x x x x x-+=-……………… 7分(cos sin )(sin cos )x x x x =++sin 21x =+, ……………… 9分 由 ππ2π22π22k x k -++≤≤, 得 ππππ44k x k -++≤≤, ……………… 11分 又因为 ππ4x k ≠+,所以函数()f x 的单增区间是ππ(π,π)44k k -++,k ∈Z . (或写成ππ[π,π)44k k -++) ……………… 13分16.(本小题满分13分)(Ⅰ)证明:因为11n n a S +=+, ○1 所以当2n ≥时,11n n a S -=+, ○2由 ○1○2两式相减,得1n n n a a a +-=,即12n n a a +=(2)n ≥, ………………3分 因为当1n =时,2112a a =+=,所以212a a =, ………………4分 所以 *12()n nan a +=∈N . ………………5分所以数列{}n a 是首项为1,公比为2的等比数列,所以 12n n a -=. ………………7分 (Ⅱ)解:因为1(1)221n b n n =+-⨯=-, ………………9分所以121n b n +=+,212(121)1112n n n b b b n +-++++=+=+L , ………………11分 因为2(1)(21)(2)n n n n +-+=-, ………………12分 由3n ≥,得(2)0n n ->,所以当3n ≥时,1121n n b b b b +<++++L . ………………13分17.(本小题满分14分) (Ⅰ)解:在Rt ΔADE中,AE ==. ………………1分因为CD ⊥平面ADE ,所以棱锥C ADE -的体积为Δ11332C ADE ADE AE DEV S CD CD -⋅==⋅⋅=⋅. ………………4分(Ⅱ)证明:因为 CD ⊥平面ADE ,AE ⊂平面ADE ,所以CD AE ⊥. ………………5分 又因为AE DE ⊥,CD DE D =I ,所以AE ⊥平面CDE . ………………7分 又因为AE ⊂平面ACE ,所以平面ACE ⊥平面CDE . …………………8分 (Ⅲ)结论:在线段DE 上存在一点F ,且13EFED =,使//AF 平面BCE .…………………9分解:设F 为线段DE 上一点, 且13EF ED =, ………………10分过点F 作//FM CD 交CE 于M ,则1=3FM CD .因为CD ⊥平面ADE ,AB ⊥平面ADE , 所以//CD AB . 又因为3CD AB =所以MF AB =,//FM AB ,所以四边形ABMF 是平行四边形,则//AF BM . ………………12分 又因为AF ⊄平面BCE ,BM ⊂平面BCE ,所以//AF 平面BCE . ………………14分18.(本小题满分13分) (Ⅰ)解:根据茎叶图, 得甲组数据的平均数为101014182225273041432410+++++++++=, ………2分由茎叶图,知甲型号电视机的“星级卖场”的个数为5. ………………4分 (Ⅱ)解:记事件A 为“a >b ”, ………………5分因为乙组数据的平均数为26.7, 所以10182022233132(30)(30)4326.710a b +++++++++++=,解得 8a b +=. ………………7分 所以 a 和b 取值共有9种情况,它们是:(0,8),(1,7),(2,6),(3,5),(4,4),(5,3),ABCE DF M(6,2),(7,1),(8,0), ………………8分其中a >b 有4种情况,它们是:(5,3),(6,2),(7,1),(8,0), ………………9分 所以a >b 的概率4()9P A =. ………………10分 (Ⅲ)解:当b =0时,2s 达到最小值. ………………13分19.(本小题满分14分)(Ⅰ)解:设c =,由题意,得224a b +=,且c a =………………2分解得a =1b =,c =. ………………4分所以椭圆E 的方程为2213x y +=. ………………5分 (Ⅱ)解:由题意,得224a b +=,所以椭圆E 的方程为222214x y a a +=-, 则1(,0)F c -,2(,0)F c,c ==. 设00(,)P x y ,由题意,知0x c ≠,则直线1F P 的斜率10F P y k x c=+, ………………6分 直线2F P 的斜率200F P y k x c=-, 所以直线2F P 的方程为00()y y x c x c=--, 当0x =时,00y cy x c -=-,即点00(0,)Q y c x c--, 所以直线1F Q 的斜率为1F Q y k c x =-, ………………8分 因为以PQ 为直径的圆经过点1F , 所以11PF F Q ⊥.所以1100001F P F Q y y k k x c c x ⨯=⨯=-+-, ………………10分 化简,得22200(24)y x a =--, ○1 又因为P 为椭圆E 上一点,且在第一象限内,所以22002214x y a a +=-,00x >,00y >, ○2 由○1○2,解得202a x =,20122y a =-, ………………12分 所以002x y +=,即点P 在直线20x y +-=上. ………………14分20.(本小题满分13分)(Ⅰ)解:当14a =-时,函数21()114x f x x -=-, 求导,得22222224(1)3()114(1)4(1)44x x x f x x x -+----'==--, ………………2分 因为(1)0f =,(1)43f '=-, ………………3分 所以函数()f x 的图象在点(1,(1))f 处的切线方程为4340x y +-=.………………4分 (Ⅱ)证明:当0a >时,21()1x f x ax -=+的定义域为R . 求导,得22221()(1)ax ax f x ax --'=+, ………………5分 令()0f x '=,解得110x =-<,211x =+>, ………………6分当x 变化时,()f x '与()f x 的变化情况如下表:………………8分 所以函数()f x 在1(,)x -∞,2(,)x +∞上单调递增,在12(,)x x 上单调递减.又因为(1)0f =,当1x <时,21()01xf x ax -=>+;当1x >时,21()01xf x ax -=<+,所以当1x ≤时,10()()f x f x ≤≤;当1x >时,2()()0f x f x <≤.记12max{()|,()|}||M f x f x =,其中12max{()|,()|}||f x f x 为两数1()||f x , 2()||f x 中最大的数,综上,当0a >时,存在实数[,)m M ∈+∞,使得对任意的实数x ,不等式()m f x m -≤≤ 恒成立. ………………10分(Ⅲ)解:当12a =-与2a =时,不存在实数k ,使得关于实数x 的方程()()f x k x a =-仅 有负实数解.。
北京市西城区2016年高三二模试卷数 学(理科)第Ⅰ卷(选择题 共40分)一、 选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 设全集U =R ,集合2{|0}A x x =<<,{|1}B x x =<,则集合()UA B =( )(A )(,0)-∞ (B )(,0]-∞ (C )(2,)+∞(D )[2,)+∞2. 若复数z 满足+i 23i z z ⋅=+,则在复平面内z 对应的点位于( ) (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限3. 在∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若1sin()3A B +=,3a =,4c =,则sin A =( ) (A )23(B )14(C )34(D )164. 某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ) (A )2 (B )5 (C )3 (D )225. “,,,a b c d 成等差数列”是“ad b c ”的( )正(主)视图侧(左)视图俯视图 11(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件6. 某市家庭煤气的使用量x (m 3)和煤气费()f x (元) 满足关系, 0<,()(), .C x A f x CB x A xA ≤ 已知某家庭今年前三个月的煤气费如下表:月份 用气量 煤气费 一月份 4 m34 元 二月份 25 m 314元 三月份35 m319 元若四月份该家庭使用了20 m 3的煤气,则其煤气费为( ) (A )11.5元 (B )11元 (C )10.5元 (D )10元7. 如图,点A ,B 在函数2log 2yx 的图象上,点C 在函数2log y x 的图象上,若ABC 为等边三角形,且直线//BC y 轴,设点A 的坐标为(,)m n ,则m ( ) (A ) 2 (B ) 3 (C )2 (D )38. 设直线l :340xy a,圆22 (2)2C x y :,若在圆C 上存在两点,P Q ,在直线l 上存在一点M ,使得90PMQ ,则a 的取值范围是( )(A )[18,6] (B )[652,652] (C )[16,4](D )[652,652]第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.yO xB ACE AFDCB9. 在62()x x+的展开式中,常数项等于____.10. 设x ,y 满足约束条件2,1,10,y x x y y ++⎧⎪⎨⎪⎩≤≤≥ 则3z x y =+的最大值是____.11. 执行如图所示的程序框图,输出的S 值为______.12.设双曲线C 的焦点在x 轴上,渐近线方程为22y x =±,则其离心率为____;若点(4,2)在C 上,则双曲线C 的方程为____.13. 如图, △ABC 为圆内接三角形,BD 为圆的弦,且//BD AC . 过点A 做圆的切线与DB 的延长线交于点E ,AD 与BC 交于点F . 若4AB AC ==,5BD =,则AFFD=_____; AE =_____.14. 在某中学的“校园微电影节”活动中,学校将从微电影的“点播量”和“专家评分”两个角度来进行评优. 若A 电影的“点播量”和“专家评分”中至少有一项高于B 电影,则称A 电影不亚于B 电影. 已知共有10部微电影参展,如果某部电影不亚于其他9部,就称此部电影为优秀影片. 那么在这10部微电影中,最多可能有____部优秀影片.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数2()(13tan )cos f x x x =+.输出S 否 是2,1i S ==开始11i S S i -=⨯+1i i =+ 21i i =-10i <结束(Ⅱ)求函数()f x 的定义域和值域.16.(本小题满分13分)某中学有初中学生1800人,高中学生1200人. 为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],并分别加以统计,得到如图所示的频率分布直方图.(Ⅰ)写出a 的值;(Ⅱ)试估计该校所有学生中,阅读时间不小于30个小时的学生人数;(Ⅲ)从阅读时间不足10个小时的样本学生中随机抽取3人,并用X 表示其中初中生的人数,求X 的分布列和数学期望.17.(本小题满分14分)如图,正方形ABCD 的边长为4,,E F 分别为,BC DA 的中点. 将正方形ABCD 沿着线段EF 折起,使得60DFA ∠=. 设G 为AF 的中点.(Ⅰ)求证:DG EF ⊥;) 高中生组初中生组(Ⅱ)求直线GA 与平面BCF 所成角的正弦值;(Ⅲ)设,P Q 分别为线段,DG CF 上一点,且//PQ 平面ABEF ,求线段PQ 长度的最小值.18.(本小题满分13分)设a ∈R ,函数2()()x af x x a -=+.(Ⅰ)若函数()f x 在(0,(0))f 处的切线与直线32y x =-平行,求a 的值; (Ⅱ)若对于定义域内的任意1x ,总存在2x 使得21()()f x f x <,求a 的取值范围.19.(本小题满分14分)已知椭圆C :)0(12222>>=+b a by a x 的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为24.(Ⅰ)求椭圆C 的方程;(Ⅱ)设过点)0)(,0(>m m B 的直线l 与椭圆C 相交于,E F 两点,点B 关于原点的对称点为D ,若点D 总在以线段EF 为直径的圆内,求m 的取值范围.20.(本小题满分13分)已知任意的正整数n 都可唯一表示为1100112222k k k k n a a a a --=⋅+⋅++⋅+⋅,其中01a =,12,,,{0,1}k a a a ∈,k ∈N .对于n *∈N ,数列{}n b 满足:当01,,,k a a a 中有偶数个1时,0n b =;否则1n b =.如数5可以ECF E GA BD C ⇒唯一表示为2105120212=⨯+⨯+⨯,则50b =.(Ⅰ)写出数列{}n b 的前8项;(Ⅱ)求证:数列{}n b 中连续为1的项不超过2项;(Ⅲ)记数列{}n b 的前n 项和为n S ,求满足1026n S =的所有n 的值.(结论不要求证明)北京市西城区2016年高三二模试卷参考答案及评分标准 高三数学(理科) 2016.5一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.A 3.B 4.C 5.A 6.A 7.D 8.C 二、填空题:本大题共6小题,每小题5分,共30分.9.160 10.7311.527 12.62 22184x y -=13.456 14.10 注:第12,13题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:因为 α是第二象限角,且6sin α=, 所以23cos 1sin αα=--………………2分 所以sin tan 2cos ααα==- ………………4分 所以2316()(132)()f α-=. ………………6分 (Ⅱ)解:函数()f x 的定义域为{|x x ∈R ,且ππ,}2x k k ≠+∈Z . ………………8分化简,得2()(13)cos f x x x = 2sin (13cos xx x= 2cos 3sin cos x x x =1cos 2322x x +=………………10分 π1sin(2)62x =++, ………………12分 因为x ∈R ,且ππ2x k ≠+,k ∈Z , 所以π7π22π66x k +≠+,所以1π1sin(2)6x -+≤≤.所以函数()f x 的值域为13[,]22-. ………………13分(注:或许有人会认为“因为ππ2x k ≠+,所以()0f x ≠”,其实不然,因为π()06f -=.)16.(本小题满分13分)(Ⅰ)解:0.03a =. ………………3分 (Ⅱ)解:由分层抽样,知抽取的初中生有60名,高中生有40名. ………………4分 因为初中生中,阅读时间不小于30个小时的学生频率为(0.020.005)100.25+⨯=, 所以所有的初中生中,阅读时间不小于30个小时的学生约有0.251800450⨯=人, ………………6分 同理,高中生中,阅读时间不小于30个小时的学生频率为(0.030.005)100.35+⨯=,学生人数约有0.351200420⨯=人.所以该校所有学生中,阅读时间不小于30个小时的学生人数约有450420870+=人. ………………8分 (Ⅲ)解:初中生中,阅读时间不足10个小时的学生频率为0.005100.05⨯=,样本人数为0.05603⨯=人.同理,高中生中,阅读时间不足10个小时的学生样本人数为(0.00510)402⨯⨯=人. 故X 的可能取值为1,2,3. ………………9分则 123235C C 3(1)C 10P X ⋅===, 213235C C 3(2)C 5P X ⋅===, 3335C 1(3)C 10P X ===. 所以X 的分布列为:……………… 12分 所以3319()123105105E X =⨯+⨯+⨯=. ………………13分17.(本小题满分14分)(Ⅰ)证明:因为正方形ABCD 中,,E F 分别为,BC DA 的中点, 所以EF FD ⊥,EF FA ⊥,又因为FD FA F =,所以EF ⊥平面DFA . ………………2分 又因为DG ⊂平面DFA ,所以DG EF ⊥. ………………4分 (Ⅱ)解:因为60DFA ∠=,DF FA =,AG GF =, 所以DFA ∆为等边三角形,且DG FA ⊥. 又因为DG EF ⊥,EFFA F =,所以DG ⊥平面ABEF . ………………5分 设BE 的中点为H ,连接GH ,则,,GA GH GD 两两垂直,故以,,GA GH GD 分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系,则(0,0,0)G ,(1,0,0)A ,(1,4,0)B ,(0,)3C ,(1,0,0)F -,所以(1,0,0)GA =,(13)BC =-,(2,4,0)BF =--. ………………6分 设平面BCF 的一个法向量为(,,)x y z =m ,由0BC ⋅=m ,0BF ⋅=m ,得30,240,x z x y ⎧-=⎪⎨--=⎪⎩令2z =,得(2,3,2)3=-m . ………………7分设直线GA 与平面BCF 所成角为α, 则||257sin |cos ,|19||||GA GA GA α⋅=<>==m m m .即直线GA 与平面BCF 所成角的正弦值为25719. ………………9分(Ⅲ)由题意,可设(0,0,)(03)P k k ≤≤,(01)FQ FC λλ=≤≤, 由(1,3)FC =,得(,43)FQ λλλ=,所以(1,43)Q λλλ-,(1,43)PQ k λλλ--=. ………………10分 由(Ⅱ),得3)GD =为平面ABEF 的法向量. 因为//PQ 平面ABEF ,所以0GD PQ ⋅=30k λ-=. ………………11分 所以222||(1)(4)(3)PQ k λλλ=-++-222(1)(4)1721λλλλ-+=-+=,HyF EA BD C xzG………………12分 又因为221172117()171716λλλ-+=-+,所以当117λ=时,min 417||17PQ =.所以当117λ=,3k =PQ 长度有最小值41717. ………………14分18.(本小题满分13分)(Ⅰ)证明:函数()y f x =的定义域{|}D x x x a =∈≠-R 且, ………………1分由题意,(0)f '有意义,所以0a ≠.求导,得244()()2()()(3)()()()x a x a x a x a x a f x x a x a +--⋅++⋅-'==-++. ………………3分由题意,得243(0)3a f a'==,解得1a =±.验证知1a =±符合题意. ………………5分 (Ⅱ)解:“对于定义域内的任意1x ,总存在2x 使得21()()f x f x <”等价于“()f x 不存在最小值”. ………………6分① 当0a =时, 由1()f x x=,得()f x 无最小值,符合题意. ………………7分 ② 当0a >时, 令4()(3)()0()x a x a f x x a +⋅-'=-=+,得x a =- 或 3x a =. ………………8分随着x 的变化时,()f x '与()f x 的变化情况如下:x (,)a -∞- a -(,3)a a -3a(3,)a +∞()f x '-不存在 +0 -()f x↘不存在↗极大↘所以函数()f x 的单调递减区间为(,)a -∞-,(3,)a +∞,单调递增区间为(,3)a a -.………………9分因为当x a >时,2()0()x af x x a -=>+,当x a <时,()0f x <,所以只要考虑1(,)x a ∈-∞,且1x a ≠-即可. 当1(,)x a ∈-∞-时,由()f x 在(,)a -∞-上单调递减,且1111||2x x x a a <++<-, 得1111()(||)2f x f x x a >++, 所以存在2111||2x x x a =++,使得21()()f x f x <,符合题意; 同理,当1(,)x a a ∈-时,令2111||2x x x a =-+, 得21()()f x f x <,也符合题意;故当0a >时,对于定义域内的任意1x ,总存在2x 使得21()()f x f x <成立.………11分 ③ 当0a <时,随着x 的变化时,()f x '与()f x 的变化情况如下表:x (,3)a -∞ 3a(3,)a a - a - (,)a -+∞()f x '-0 +不存在 -()f x↘极小↗不存在↘所以函数()f x 的单调递减区间为(,3)a -∞,(,)a -+∞,单调递增区间为(3,)a a -.因为当x a >时,2()0()x af x x a -=>+,当x a <时,()0f x <,所以min ()(3)f x f a =.所以当13x a =时,不存在2x 使得21()()f x f x <.综上所述,a 的取值范围为[0,)a ∈+∞. ………………13分19.(本小题满分14分)(Ⅰ)解:由题意,得:,442,a b c ⎧⎪⎨⎪⎩== ………………2分 又因为222c b a +=解得2a =1b =,1c =, ………………4分 所以椭圆C 的方程为1222=+y x . ………………5分(Ⅱ)解:(方法一)当直线l 的斜率不存在时,由题意知l 的方程为0=x , 此时E ,F 为椭圆的上下顶点,且2=EF ,因为点(0,)D m -总在以线段EF 为直径的圆内,且0m >, 所以10<<m .故点B 在椭圆内. ………………6分 当直线l 的斜率存在时,设l 的方程为m kx y +=.由方程组22,1,2y kx m x y =+⎧⎪⎨+=⎪⎩ 得222(21)4220k x kmx m +++-=, ………………8分 因为点B 在椭圆内,所以直线l 与椭圆C 有两个公共点,即0)22)(12(4)4(222>-+-=∆m k km . 设),(),,(2211y x F y x E ,则122421km x x k -+=+,21222221m x x k -=+. ………………9分设EF 的中点),(00y x G , 则12222210+-=+=k kmx x x ,12200+=+=k m m kx y ,所以)12,122(22++-k mk km G . ………………10分 所以2222)12()122(m k m k km DG ++++-=124124224+++=k k k m , 2122124)(1x x x x k EF -++=12121222222+-++=k m k k . ………………11分因为点D 总在以线段EF 为直径的圆内, 所以2EF DG <对于k ∈R 恒成立.所以 1212121241242222224+-++<+++k m k kk k k m . 化简,得1323722422242++<++k k m k m k m ,整理,得31222++<k k m , ………………13分而2221221()113333k g k k k +==--=++≥(当且仅当0=k 时等号成立).所以312<m ,由0>m ,得330<<m .综上,m 的取值范围是330<<m . ………………14分(方法二) … …则122421km x x k -+=+,21222221m x x k -=+. …………………9分因为点D 总在以线段EF 为直径的圆内,所以0DE DF ⋅<. ………………11分 因为11(,)DE x y m =+,22(,)DF x y m =+, 所以2121212()DE DF x x y y m y y m ⋅=++++2121212()()()x x kx m kx m m kx m kx m m =++++++++ 221212(1)2()4k x x km x x m =++++22222224(1)2402121m kmk km m k k --=+++<++,整理,得31222++<k k m . ………………13分(以下与方法一相同,略)20.(本小题满分13分)(Ⅰ)解:1,1,0,1,0,0,1,1. ………………3分 (Ⅱ)证明:设数列{}n b 中某段连续为1的项从m b 开始,则1m b =.由题意,令1100112222k k k k m a a a a --=⋅+⋅++⋅+⋅,则01,,,k a a a 中有奇数个1.(1)当01,,,k a a a 中无0时,因为1102222k k m -=++++,所以111011202020202k kk m +-+=⨯+⨯+⨯++⨯+⨯,111021202020212k k k m +-+=⨯+⨯+⨯++⨯+⨯.所以1m b =,11m b +=,20m b +=,此时连续2项为1. ………………5分(2)当01,,,k a a a 中有0时,① 若0k a =,即11001122202k k k m a a a --=⋅+⋅++⋅+⨯,则110011122212k k k m a a a --+=⋅+⋅++⋅+⨯,因为01,,,k a a a 中有奇数个1,所以10m b +=,此时连续1项为1. ………………7分 ② 若1k a =,即111001 122202121212ik k s s s m a a --=⋅+⋅++⨯+⨯++⨯+⨯连续个乘以,则111001 0212212020202ik k s s s m a a --+=⋅+⋅++⨯+⨯++⨯+⨯连续个乘以,111001(1)0222212020212ik k s s s m a a ---+=⋅+⋅++⨯+⨯++⨯+⨯连续个乘以,(其中i ∈N ) 如果s 为奇数,那么11m b +=,20m b +=,此时连续2项为1. 如果s 为偶数,那么10m b +=,此时仅有1项1m b =.综上所述,连续为1的项不超过2项. ………………10分 (Ⅲ)解:2051n =或2052n =. ………………13分。