浙江省衢州二中2019-2020学年第二学期高三第一 次模拟考试数学试卷
- 格式:pdf
- 大小:737.76 KB
- 文档页数:4

2019届浙江省衢州二中高三下学期第一次模拟考试数学试题一、单选题1.集合{}25,M y N y x x Z =∈=-+∈的真子集个数是( ) A .5B .6C .7D .82.设i 是虚数单位,则复数53i i-=( ) A .4i -B .2i -C .2iD .4i3.已知直线m ,n 和平面α,m α⊂,则“n α⊄”是“n 与m 异面” ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.在梯形ABCD 中,//AD BC ,2224BC AB AD DC ====,AC 与BD 相交于O ,过点A 作AE BD ⊥于E ,则AE AC ⋅=u u u r u u u r( ) ABC .3D.5.若实数x ,y ,对任意实数m ,满足()()222122211x y m x y m x y m ⎧-≤-⎪⎪+≥+⎨⎪-+-≤⎪⎩,则由不等式组确定的可行域的面积是( ) A .14π B .12πC .πD .32π 6.已知定义在R 上的函数()||32x m f x -+=+m 为实数)为偶函数,记()0.2log 3a f =,()5log b f e =,()c f m π=+,则( )A .c b a <<B .c a b <<C .a c b <<D .a b c <<7.等比数列{}n a 中,11a =,128a =,函数()()()1212()f x x x a x a x a =--⋅⋅-…,则(0)f '=( ). A .122B .152C .182D .2128.已知双曲线22221x y a b-=(0a >,0b >)的左,右顶点是A ,B ,P 为双曲线右支上一点,()0BA BP AP +⋅=u u u r u u u r u u u r 且285ABP S a =△,则双曲线的离心率为( )A 15B 15C 15D 15 9.已知函数()222,2log 1,2x x x f x x x ⎧-+≤=⎨->⎩,设12116n x x x ≤<<<≤L ,若()()()()()()12231n n f x f x f x f x f x f x M --+-++-≤L ,则M 的最小值为( ) A .3B .4C .5D .610.设*N n ∈,n a 为()()41nnx x +-+的展开式的各项系数之和,7c t =-,R t ∈,1222555n n n na a a b ⎡⎤⎡⎤⎡⎤=+++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦L ([]x 表示不超过实数x 的最大整数).则()()22n n t b c -++的最小值为( )A .12B .22C .22D .32二、双空题11.已知()3sin cos f x x x ωω=-(0>ω)的最小正周期为2,则ω=________,函数()f x 在11,62⎡⎤-⎢⎥⎣⎦上的值域是________.12.直线20(R)mx y m +-=∈与圆22:210C x y y +--=相交于A ,B 两点,弦长||AB 的最小值为________,若ABC ∆的面积为32,则m 的值为_________.13.袋子中装有若干个均匀的红球和白球,从中摸出一个红球的概率是13,现从袋子中有放回地摸球,每次摸出一个,有2次摸到红球即停止,则恰好摸4次停止的概率p =________;若记4次之内(含4次)摸到红球的次数为ξ,则随机变量ξ的数学期望E ξ=________.14.如图,在ABC V 中,2AB BC ==,150ABC ∠=︒,若平面ABC 外的点P 和线段AC 上的点D ,线段BC 上的点Q ,满足PD DA =,PB BA =,则四面体P BCD -的体积的最大值是________;当P BCD -体积取最大值时,min PQ =________. 三、填空题15.已知平面向量1e u r ,2e u u r ,c r 满足12121e e e e ==-=u r u u r u r u u r ,2123(2)02c e e c -+⋅+=u r u u r r r ,则对任意的R t ∈,1c te -的最小值记为M ,则M 的最大值为________. 16.在数列{}n a 及{}n b中,11111,1n n n n n n a a b b a b a b ++=++=+==.设112n n n n c a b ⎛⎫=+ ⎪⎝⎭,则数列{}n c 的前n 项和为_____________.17.已知函数64,2()25,02x x f x xx x ⎧+-≥⎪=⎨⎪-+⎩<<,若方程()f x a =恰有两个实数解12,x x ()12x x <,且126x x ⋅>,则实数a 的取值范围是__________.四、解答题18.在ABC V 中,()sin 1A B -=,1sin 3C =. (1)求cos B 的值;(2)若AB =ABC V 的面积.19.数列{}n a 中,11a =,12nn n a a +⋅=(*N n ∈).(1)求数列{}n a 的通项公式;(2)设数列{}n b 的前n 项和为n S ,且()()1,2121251,2n n n k n n b n ka ⎧=-⎪++⎪=⎨⎪-=⎪⎩(*N k ∈),求使2n S 取最小值时n 的值.20.如图,已知矩形BCDE 所在平面与ABE △所在平面互相垂直,AB AE ⊥,AB AE >.(1)若M 为AC 中点,N 为BE 中点,证明://MN 平面ADE ; (2)若2BE =,1DE =,且DE 与平面DAC 所成角的正弦5,求ABE ∠的大小.21.已知抛物线L :22y px =(0p >)的焦点为F ,过点()5,0M 的动直线l 与抛物线L 交于A ,B 两点,直线AF 交抛物线L 于另一点C ,直线AC 的最小值为4.(1)求椭圆C 的方程;(2)若过点A 作y 轴的垂线m ,则x 轴上是否存在一点()0,0P x ,使得直线PB 与直线m 的交点恒在一条定直线上?若存在,求该点的坐标及该定直线的方程;若不存在,请说明理由.22.已知函数()()21233ln 2f x ax b a x x =+-++,其中0a >,b R ∈. (1)当3b =-时,求函数()f x 的单调区间; (2)当3a =且0b <时.①若()f x 有两个极值点1x ,2x (12x x <),求证:()192f x <-; ②若对任意的[]1,x t ∈,都有()213922e f x -≤≤-成立,求正实数t 的最大值.。

2020年浙江省衢州二中高考数学一模试卷一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(4分)设{1U =-,0,1,2},集合2{|1A x x =<,}x U ∈,则(U A =ð ) A .{0,1,2}B .{1-,1,2}C .{1-,0,2}D .{1-,0,1}2.(4分)本场考试需要2小时,在这场考试中钟表的时针转过的弧度数为( ) A .3πB .3π-C .23π D .23π-3.(4分)已知复数z 满足202020191z i i =+g (其中i 为虚数单位),则复数z 的虚部是( ) A .1-B .1C .i -D .i4.(4分)已知直线1:240l ax y ++=,2:(1)20l x a y +-+=,则“1a =-”是“12//l l ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.(4分)某几何体的三视图如图所示,则该几何体的体积为( )A .83B .3C .113D .46.(4分)函数()f x 的图象如图所示,则它的解析式可能是( )A .()2(||1)xf x x =- B .21()2x x f x -=C .()||||f x ln x = D .()1x f x xe =-7.(4分)已知数列{}n a 的前n 项和为n S ,11a =,22a =,且*112(1)(1,)n n n S S S n n N +-+=+>∈.则( ) A .47a =B .16240S =C .1019a =D .20381S =8.(4分)已知1F ,2F 是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,若点2F 关于双曲线渐近线的对称点A 满足11(F AO AOF O ∠=∠为坐标原点),则双曲线的渐近线方程为( ) A .2y x =±B .3y x =±C .2y x =±D .y x =±9.(4分)已知平面向量,,a b c r r r,满足||2,||1,b a b c a b λμ=+==+r r r r r r 且21λμ+=,若对每一个确定的向量a r ,记||c r 的最小值为m ,则当a r变化时,m 的最大值为( )A .14B .13C .12D .110.(4分)已知函数2()1|21|()f x ax x ax a R =+++-∈的最小值为0,则(a = ) A .12B .1-C .1±D .12±二、填空题:本大题共7小题,多空每空格3分,单空每空格4分,共36分. 11.(6分)若2log 3a =,3log 2b =,则a b =g ,lga lgb += .12.(6分)《九章算术》是中国古代的数学名著,其中《方田》一章给出了弧田面积的计算公式.如图所示,弧田是由圆弧¶AB 和其所对弦AB 围成的图形,若弧田的弧¶AB 长为4π,弧所在的圆的半径为6,则弧田的弦AB 长是 ,弧田的面积是 .13.(6分)已知实数x 、y 满足121y y x x y m ⎧⎪-⎨⎪+⎩…„„,且可行域表示的区域为三角形,则实数m 的取值范围为 ,若目标函数z x y =-的最小值为1-,则实数m 等于 .14.(6分)有2名老师和3名同学,将他们随机地排成一行,用ξ表示两名老师之间的学生人数,则1ξ=对应的排法有 种;()E ξ= ;15.(4分)已知函数2,()4,x x m f x x x x m <⎧=⎨+⎩…,且p m ∀<,q m ∃…,使得()()0f p f q +=,则实数m 的取值范围是 .16.(4分)已知实数a ,b ,c 满足22221a b c ++=,则ab c +的最小值是 . 17.(4分)若四棱锥P ABCD -的侧面PAB 内有一动点Q ,已知Q 到底面ABCD 的距离与Q 到点P 的距离之比为正常数k ,且动点Q 的轨迹是抛物线,则当二面角P AB C --平面角的大小为30︒时,k 的值为 .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18.(14分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知3A π=,2223b c abc a +-=. (1)求a 的值;(2)若1b =,求ABC ∆的面积.19.(15分)已知等腰梯形ABCD 中(如图1),4AB =,2BC CD DA ===,F 为线段CD 的中点,E ,M 为线段AB 上的点,1AE EM ==,现将四边形AEFD 沿EF 折起(如图2). (Ⅰ)求证:||AM 平面BCD ;(Ⅱ)在图2中,若6BD =,求直线CD 与平面BCFE 所成角的正弦值.20.(15分)已知数列{}n a 的前n 项和n S 满足:1(1)2n n S a =--.(Ⅰ)求{}n a 的通项公式; (Ⅱ)设11111n n n c a a +=++-,数列{}n c 的前n 项和为n T .求证:123n T n >-. 21.(15分)已知椭圆2222:1(0)x y E a b a b+=>>的离心率为3e =,且短轴的一个端点B 与两焦点A ,C 3(Ⅰ)求椭圆E 的方程;(Ⅱ)若点P 为椭圆E 上的一点,过点P 作椭圆E 的切线交圆222:O x y a +=于不同的两点M ,N (其中M 在N 的右侧),求四边形ACMN 面积的最大值. 22.(15分)已知函数()()f x ax lnx a R =+∈有两个零点1x ,2x . (1)求a 的取值范围;(2)是否存在实数λ,对于符合题意的任意1x ,2x ,当012(1)0x x x λλ=+->时均有0()0f x '<?若存在,求出所有λ的值;若不存在,请说明理由.。


2020年高考模拟高考数学一模试卷一、选择题1.设U={﹣1,0,1,2},集合A={x|x2<1,x∈U},则∁U A=()A.{0,1,2}B.{﹣1,1,2}C.{﹣1,0,2}D.{﹣1,0,1} 2.本场考试需要2小时,在这场考试中钟表的时针转过的弧度数为()A.B.C.D.3.已知复数z满足z•i2020=1+i2019(其中i为虚数单位),则复数z的虚部是()A.﹣1B.1C.﹣i D.i4.已知直线l1:ax+2y+4=0,l2:x+(a﹣1)y+2=0,则“a=﹣1”是“l1∥l2”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.某几何体的三视图如图所示,则该几何体的体积为()A.B.3C.D.46.函数f(x)的图象如图所示,则它的解析式可能是()A.f(x)=2x(|x|﹣1)B.f(x)=C.f(x)=|ln|x||D.f(x)=xe x﹣17.已知数列{a n}的前n项和为S n,a1=1,a2=2,且.则()A.a4=7B.S16=240C.a10=19D.S20=3818.已知F1,F2是双曲线的左、右焦点,若点F2关于双曲线渐近线的对称点A满足∠F1AO=∠AOF1(O为坐标原点),则双曲线的渐近线方程为()A.y=±2x B.C.D.y=±x9.已知平面向量,满足且λ+2μ=1,若对每一个确定的向量,记的最小值为m,则当变化时,m的最大值为()A.B.C.D.110.已知函数f(x)=ax+1+|2x2+ax﹣1|(a∈R)的最小值为0,则a=()A.B.﹣1C.±1D.±二、填空题11.若a=log23,b=log32,则a•b=,lga+lgb=.12.《九章算术》是中国古代的数学名著,其中《方田》一章给出了弧田面积的计算公式.如图所示,弧田是由圆弧和其所对弦AB围成的图形,若弧田的弧长为4π,弧所在的圆的半径为6,则弧田的弦AB长是,弧田的面积是.13.已知实数x、y满足,且可行域表示的区域为三角形,则实数m的取值范围为,若目标函数z=x﹣y的最小值为﹣1,则实数m等于.14.有2名老师和3名同学,将他们随机地排成一行,用ξ表示两名老师之间的学生人数,则ξ=1对应的排法有种;E(ξ)=;15.已知函数f(x)=,且∀p<m,∃q≥m,使得f(p)+f(q)=0,则实数m的取值范围是.16.已知实数a,b,c满足a2+b2+2c2=1,则ab+c的最小值是.17.若四棱锥P﹣ABCD的侧面PAB内有一动点Q,已知Q到底面ABCD的距离与Q到点P的距离之比为正常数k,且动点Q的轨迹是抛物线,则当二面角P﹣AB﹣C平面角的大小为30°时,k的值为.三、解答题18.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知,.(1)求a的值;(2)若b=1,求△ABC的面积.19.已知等腰梯形ABCD中(如图1),AB=4,BC=CD=DA=2,F为线段CD的中点,E,M为线段AB上的点,AE=EM=1,现将四边形AEFD沿EF折起(如图2).(Ⅰ)求证:AM||平面BCD;(Ⅱ)在图2中,若,求直线CD与平面BCFE所成角的正弦值.20.已知数列{a n}的前n项和S n满足:.(Ⅰ)求{a n}的通项公式;(Ⅱ)设,数列{c n}的前n项和为T n.求证:.21.已知椭圆E:+=1(a>b>0)的离心率为e=,且短轴的一个端点B与两焦点A,C组成的三角形面积为.(Ⅰ)求椭圆E的方程;(Ⅱ)若点P为椭圆E上的一点,过点P作椭圆E的切线交圆O:x2+y2=a2于不同的两点M,N(其中M在N的右侧),求四边形ACMN面积的最大值.22.已知函数f(x)=ax+lnx(a∈R)有两个零点x1,x2.(1)求a的取值范围;(2)是否存在实数λ,对于符合题意的任意x1,x2,当x0=λx1+(1﹣λ)x2>0时均有f′(x0)<0?若存在,求出所有λ的值;若不存在,请说明理由.参考答案一、选择题:共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设U={﹣1,0,1,2},集合A={x|x2<1,x∈U},则∁U A=()A.{0,1,2}B.{﹣1,1,2}C.{﹣1,0,2}D.{﹣1,0,1}【分析】化简集合A,求出A的补集即可.解:设U={﹣1,0,1,2},集合A={x|x2<1,x∈U}={0},∴∁U A={﹣1,1,2},故选:B.2.本场考试需要2小时,在这场考试中钟表的时针转过的弧度数为()A.B.C.D.【分析】根据弧度制的定义,即可求解.解:由于时针是顺时针转动,形成的角是负角,又由于时针转动1小时,转动的弧度数为,因此时针转过2小时所形成的弧度数为,故选:B.3.已知复数z满足z•i2020=1+i2019(其中i为虚数单位),则复数z的虚部是()A.﹣1B.1C.﹣i D.i【分析】由虚数单位i的运算性质可得z=1﹣i,则答案可求.解:∵i4=1,∴i2020=i4×505=1,i2019=i4×504+3=﹣i,则z•i2020=1+i2019化为z=1﹣i,∴z的虚部为﹣1.故选:A.4.已知直线l1:ax+2y+4=0,l2:x+(a﹣1)y+2=0,则“a=﹣1”是“l1∥l2”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【分析】由两直线平行的充要条件得:“l1∥l2”的充要条件为:,即:a=﹣1,即“a=﹣1”是“l1∥l2”的充分必要条件,得解.解:已知直线l1:ax+2y+4=0,l2:x+(a﹣1)y+2=0,又“l1∥l2”的充要条件为:,解得:a=﹣1,即“a=﹣1”是“l1∥l2”的充分必要条件,故选:C.5.某几何体的三视图如图所示,则该几何体的体积为()A.B.3C.D.4【分析】首先把三视图转换为几何体,进一步求出几何体的体积.解:根据几何体的三视图转换为几何体为:该几何体为由一个三棱柱体,切去一个三棱锥体,如图所示:故:V==.故选:C.6.函数f(x)的图象如图所示,则它的解析式可能是()A.f(x)=2x(|x|﹣1)B.f(x)=C.f(x)=|ln|x||D.f(x)=xe x﹣1【分析】结合图象,运用排除法得解.解:当x=﹣1时,函数值为0,由此排除D;当x=0时,函数值为﹣1,由此排除C;当x→+∞时,函数值→+∞,由此排除B.故选:A.7.已知数列{a n}的前n项和为S n,a1=1,a2=2,且.则()A.a4=7B.S16=240C.a10=19D.S20=381【分析】首先利用数列的递推关系式的应用求出数列的通项公式,进一步求出数列的项和数列的和.解:数列{a n}的前n项和为S n,a1=1,a2=2,且.当n≥2时,S n+2+S n=2(S n+1+1),当n=2时,解得a3=4,所以a n+2+a n=2a n+1,所以数列{a n}是以2为首项公差d=4﹣2=2的等差数列.所以a n=2+2(n﹣2)=2n﹣2,所以,故=226.a4=2×4﹣2=6.a10=2×10﹣2=18.S20=a1+a2+…+a20=1+=381.故选:D.8.已知F1,F2是双曲线的左、右焦点,若点F2关于双曲线渐近线的对称点A满足∠F1AO=∠AOF1(O为坐标原点),则双曲线的渐近线方程为()A.y=±2x B.C.D.y=±x【分析】设F1(﹣c,0),F2(c,0),渐近线方程为y=x,对称点为A(m,n),运用中点坐标公式和两直线垂直的条件:斜率之积为﹣1,求出对称点A的坐标,A满足∠F1AO=∠AOF1,可得|AF1|=|OF1|=c,由两点的距离公式,可得所求渐近线方程.解:设F1(﹣c,0),F2(c,0),渐近线方程为y=x,F2的对称点为A(m,n),即有=﹣,且•n=•,解得m=,n=,A满足∠F1AO=∠AOF1,可得|AF1|=|OF1|=c,即有(+c)2+=c2,结合c2=a2+b2,化为c=2a,即b=a,可得双曲线的渐近线方程为y=±x.故选:B.9.已知平面向量,满足且λ+2μ=1,若对每一个确定的向量,记的最小值为m,则当变化时,m的最大值为()A.B.C.D.1【分析】先假设,=,从而得到点A的轨迹是圆,再由计算,将其化简为关于λ的二次函数,因此得到的最小值为m 与x的关系,再利用导数求其最大值即可.解:设,=,∵,∴(x+2)2+y2=1即点A的轨迹是以(﹣2,0)为圆心,1为半径的圆,x∈[﹣3,﹣1].∵λ+2μ=1,∴=(λx+1﹣λ,λy),∴+2(x﹣1)λ+1=(﹣6x﹣2)λ2+2(x﹣1)λ+1,∵x∈[﹣3,﹣1],∴﹣6x﹣2>0,则关于λ的二次函数开口向上,当时,取得最小值,即=,令(x∈[﹣3,﹣1]),则,∴函数f(x)在[﹣3,]上单调递增,在(,﹣1]上单调递减,∴,即,∴m的最大值为.故选:B.10.已知函数f(x)=ax+1+|2x2+ax﹣1|(a∈R)的最小值为0,则a=()A.B.﹣1C.±1D.±【分析】设,解得g(x),h(x)的解析式,通过图象的特点,结合f(x)的最小值为0,可得所求值.解:设,所以,则f(x)=g(x)+h(x)+|g(x)﹣h(x)|=,由于g(x)=x(x+a)的图象恒过(0,0),(﹣a,0),h(x)的图象为开口向下,且过(﹣1,0),(1,0)的抛物线,且f(x)的最小值为0,结合图象可得﹣a=1或﹣a=﹣1,即有a=±1.故选:C.二、填空题:共7小题,多空每空格3分,单空每空格4分,共36分.11.若a=log23,b=log32,则a•b=1,lga+lgb=0.【分析】利用对数运算性质即可得出.解:∵a=log23,b=log32,则a•b=•=1,lga+lgb=lgab=lg1=0.故答案为:1,0.12.《九章算术》是中国古代的数学名著,其中《方田》一章给出了弧田面积的计算公式.如图所示,弧田是由圆弧和其所对弦AB围成的图形,若弧田的弧长为4π,弧所在的圆的半径为6,则弧田的弦AB长是6,弧田的面积是12π﹣9.【分析】由已知利用弧长公式可求∠AOB,可得∠AOD=,OA=6,即可求解AB的值,由弧田的面积S=S扇形OAB﹣S△OAB即可计算得解.解:∵如图,弧田的弧长为4π,弧所在的圆的半径为6,∴α=∠AOB==,可得∠AOD=,OA=6,∴AB=2AD=2OA sin=2×=6,∴弧田的面积S=S扇形OAB﹣S△OAB=4π×6﹣=12π﹣9.故答案为:6,12π﹣9.13.已知实数x、y满足,且可行域表示的区域为三角形,则实数m的取值范围为m>2,若目标函数z=x﹣y的最小值为﹣1,则实数m等于5.【分析】作出平面区域,结合线性规划的知识及目标函数的几何意义即可求解.解:作出可行域如图,则要为三角形需满足B(1,1)在直线x+y=m下方,即1+1<m,m>2;目标函数可视为y=x﹣z,则z为斜率为1的直线纵截距的相反数,该直线截距最大在过点A时,此时z min=﹣1,直线PA:y=x+1,与AB:y=2x﹣1的交点为A(2,3),该点也在直线AC:x+y=m 上,故m=2+3=5,故答案为:m>2;5.14.有2名老师和3名同学,将他们随机地排成一行,用ξ表示两名老师之间的学生人数,则ξ=1对应的排法有36种;E(ξ)=1;【分析】ξ的可能取值为0,1,2,3,ξ=1对应的排法有:=36.分别求出P (ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出E(ξ).解:有2名老师和3名同学,将他们随机地排成一行,用ξ表示两名老师之间的学生人数,则ξ的可能取值为0,1,2,3,ξ=1对应的排法有:=36.∴ξ=1对应的排法有36种;P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,∴E(ξ)==1.故答案为:36,1.15.已知函数f(x)=,且∀p<m,∃q≥m,使得f(p)+f(q)=0,则实数m的取值范围是(﹣∞,0].【分析】根据条件转化为函数y=﹣f(x)在(﹣∞,m)上的值域是函数y=f(x)在[m,+∞)上的值域的子集;分别求值域即可得到结论.解:依题意,f(q)=﹣f(p),即函数y=﹣f(x)在(﹣∞,m)上的值域是函数y=f(x)在[m,+∞)上的值域的子集.因为y=f(x)在[m,+∞)上的值域为[﹣4,+∞)(m≤﹣2)或[m2+4m,+∞](m>﹣2),y=﹣f(x)在(﹣∞,m)上的值域为(﹣m,+∞),故或,解得m≤0故答案为:(﹣∞,0].16.已知实数a,b,c满足a2+b2+2c2=1,则ab+c的最小值是﹣.【分析】先分离出a2+b2,应用基本不等式转化为关于c的二次函数,进而求出最小值.解:若ab+c取最小值,则ab异号,c<0,根据题意得:1﹣2c2=a2+b2,又由a2+b2≥2|ab|=﹣2ab,即有1﹣2c2≥﹣2ab,则ab+c≥c2+c﹣=(c+)2﹣,即2ab+c的最小值为﹣,故答案为:﹣.17.若四棱锥P﹣ABCD的侧面PAB内有一动点Q,已知Q到底面ABCD的距离与Q到点P的距离之比为正常数k,且动点Q的轨迹是抛物线,则当二面角P﹣AB﹣C平面角的大小为30°时,k的值为.【分析】二面角P﹣AB﹣C平面角为θ,点Q到底面ABCD的距离为|QH|,点Q到定直线AB得距离为d,则d=.再由点Q到底面ABCD的距离与到点P的距离之比为正常数k,可得|PQ|=,由此可得sinθ=k,则由cosθ=cos30°=可求k值.解:如图,设二面角P﹣AB﹣C平面角为θ,点Q到底面ABCD的距离为|QH|,点Q到定直线AB得距离为d,则|QH|=d sinθ,即d=.∵点Q到底面ABCD的距离与到点P的距离之比为正常数k,∴=k,则|PQ|=,∵动点Q的轨迹是抛物线,∴|PQ|=d,即=.则sinθ=k.∴二面角P﹣AB﹣C的平面角的余弦值为cosθ===cos30°=.解得:k=(k>0).故答案为:.三、解答题:共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知,.(1)求a的值;(2)若b=1,求△ABC的面积.【分析】(1)由题意可得,,结合余弦定理可求(2)由正弦定理可求B,C,代入三角形面积公式可得解:(1)由题意可得,,由余弦定理可得,cos A=即=,∴a=(2)∵a=,b=1,由正弦定理可得,sin B===∵a>b,∴B=,C=π﹣A﹣B=∴S△ABC===19.已知等腰梯形ABCD中(如图1),AB=4,BC=CD=DA=2,F为线段CD的中点,E,M为线段AB上的点,AE=EM=1,现将四边形AEFD沿EF折起(如图2).(Ⅰ)求证:AM||平面BCD;(Ⅱ)在图2中,若,求直线CD与平面BCFE所成角的正弦值.【分析】(Ⅰ)证明四边形ADCM为平行四边形,可得AM∥CD,进而得证;(Ⅱ)建立如图所示的空间直角坐标系,再根据已知条件求得点D的坐标以及平面BCEF 的一个法向量,利用向量公式即可得所求正弦值.解:(Ⅰ)证明:连接CM,由AD平行且等于EF,MC平行且等于EF可知,AD平行且等于MC,∴四边形ADCM为平行四边形,∴AM∥CD,又AM不在平面BCD内,CD在平面BCD内,∴AM||平面BCD;(Ⅱ)建立如图所示的空间直角坐标系,则,设D(x,y,z),由,可得,∴,易知平面BCEF的一个法向量为,设直线CD与平面BCFE所成角为θ,则,即直线CD与平面BCFE所成角的正弦值为.20.已知数列{a n}的前n项和S n满足:.(Ⅰ)求{a n}的通项公式;(Ⅱ)设,数列{c n}的前n项和为T n.求证:.【分析】(Ⅰ)运用数列的递推式和等比数列的定义、通项公式,可得所求;(Ⅱ)运用数列的裂项相消求和和不等式的性质,可得证明.解:(Ⅰ)∵,∴,即,∴,当n≥2时,,得,即{a n}是等比数列;∴.(Ⅱ)证明:==,由得,所以,从而==.即.21.已知椭圆E:+=1(a>b>0)的离心率为e=,且短轴的一个端点B与两焦点A,C组成的三角形面积为.(Ⅰ)求椭圆E的方程;(Ⅱ)若点P为椭圆E上的一点,过点P作椭圆E的切线交圆O:x2+y2=a2于不同的两点M,N(其中M在N的右侧),求四边形ACMN面积的最大值.【分析】(Ⅰ)结合已知可得,bc=求出a,b的值,即可得椭圆方程;(Ⅱ)由题意可知,直线的斜率存在,设出直线方程,联立直线方程与椭圆方程,利用判别式等于0可得m2=4k2+1,联立直线方程与圆的方程,结合根与系数的关系求得S△MCO+S△ANO,利用弦长公式及点到直线的距离公式,求出S△MON,得到S ACMN=S△MON+S+S△ANO,整理后利用基本不等式求最值.△MCO解:(Ⅰ)可得,bc=结合a2=b2+c2,解得a=2,c=,b=1.得椭圆方程;(Ⅱ)易知直线MN的斜率k存在,设MN:y=kx+m,由,得(4k2+1)x2+8kmx+4(m2﹣1)=0,由△=64k2m2﹣16(4k2+1)(m2﹣1)=0,得m2=4k2+1,∵S ACMN=S△MON+S△MCO+S△ANO,设点O到直线MN:kx﹣y+m=0的距离为d,d=,|MN=2=2.S△MON+==d=,由,得(k2+1)x2+2kmx+m2﹣4=0,,,∴y1+y2=kx1+m+kx2+m=k(x1+x2)+2m=k(﹣+2m=.∴S△MCO+S△NAO=×(|y1|+|y2|)=(|y1+y2|=,∴S ACMN=S△MON+(S△NAO+S△MCO)=+而m2=4k2+1,k2=,易知k2≥0,∴m2≥1,则|m|≥1,四边形ACMN的面积S==当且仅当=|m|,即m=时取“=”.∴四边形ACMN面积的最大值为4.22.已知函数f(x)=ax+lnx(a∈R)有两个零点x1,x2.(1)求a的取值范围;(2)是否存在实数λ,对于符合题意的任意x1,x2,当x0=λx1+(1﹣λ)x2>0时均有f′(x0)<0?若存在,求出所有λ的值;若不存在,请说明理由.【分析】(1)f′(x)=a+(x>0),求导讨论a以确定导数的正负,从而确定函数的单调区间,求得f(﹣)>0,求得a的取值范围;(2)由于(1)可知:f′(x0)<0,f′(x1)•f′(x2)<0可知λ≠0,且λ≠1,x1,x2是f(x)=0的两个根,求得a的表达式,λ+(1﹣λ)>,t=,构造辅助函数g(t)=lnt﹣(t>0),求导化简整理,令μ=,利用μ的取值范围,即可判断g(t)的单调性,即可求得λ的值.解:(1)f′(x)=a+(x>0),当a≥0时,f′(x)>0对x>0恒成立,与题意不符,当a<0,f′(x)=a+=,∴0<x<﹣时,f′(x)>0;x>﹣时f′(x)<0,即函数f(x)在(0,﹣)单调递增,在(﹣,+∞)单调递减,∵x→0和x→+∞时均有f(x)→﹣∞,∴f(﹣)=﹣1+ln(﹣)>0,解得:﹣<a<0,综上可知:a的取值范围(﹣,0);(2)由(1)可知f′(x0)<0⇔x0>﹣(﹣<a<0),由x1,x2的任意性及f′(x1)•f′(x2)<0知,λ≠0,且λ≠1,∴a=﹣,故x0=λx1+(1﹣λ)x2>,又∵λ+(1﹣λ)>,令t=,则t>0,t≠1,且λ+(1﹣λ)t>>0恒成立,令g(t)=lnt﹣(t>0),而g(﹣1)=0,∴t>1时,g(t)>0,0<t<1时,g(t)<0.(*)∴g′(t)=﹣=,令μ=,若μ<1,则μ<t<1时,g′(t)<0,即函数在(μ,1)单调递减,∴g(t)>g(1)=0,与(*)不符;若μ>1,则1<t<μ时,g′(t)<0,即函数g(t)在(1,μ)单调递减,∴g(t)<g(1)=0,与(*)式不符;若μ=1,解得λ=,此时g′(t)≥0恒成立,(g′(t)=0⇔t=1),即函数g(t)在(0,+∞)单调递增,又g(1)=0,∴t>1时,g(t)>0;0<t<1时,g(t)<0符合(•)式,综上,存在唯一实数λ=符合题意.。


高考模拟数学试卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合}{}{22,4A x x B x x x =≤=<,则RA B =( )A .(],0-∞B .(),0-∞C .[]1,1-D .()0,2 2.已知(),0,a b ∈+∞,则“2ab >”是“22log log 0a b +>”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.如图,这是计算111124620+++⋅⋅⋅+的一个程序框图,其中判断框内应填入的条件是( ) A .19?i >B .20?i >C .20?i <D .21?i <4.下列函数中既有奇函数,又在区间[]1,1-上单调递增的是( ) A .()sin 2f x x = B .()tan f x x x =+ C .()3f x x x =-D .()22x x f x -=+5.甲、乙、丙、丁、戊共5人站成一排,其中甲、乙两人中间恰有1人的站法种数是( ) A .18B .24C .36D .486.设1F 、2F 分别为双曲线22221(0)x y a b a b -=>>的左、右焦点,若双曲线上存在点P ,使得122130,120PF F PF F ∠=∠=,则双曲线的离心率为( )A .2B .3C .31+D .31+ 7.已知函数()23,11,0121,0x x f x x x x x ->⎧⎪=+≤≤⎨⎪+<⎩,若数列{}n a 的前n 项和为Sn ,且()111,3n n a a f a +==,则2014S =( )A .895B .896C .897D .8988.函数()f x 的图像如图,则()f x 的解析式可能是 ( ) A .()cos 2f x x =B .()sin 4f x x π⎛⎫=-+ ⎪⎝⎭C .()3cos 28f x x π⎛⎫=- ⎪⎝⎭D .()5sin 34f x x π⎛⎫=- ⎪⎝⎭9.如图,梯形ABCD 中,AD//BC ,∠ABC=90,AD :BC :AB=234,E 、F 分别是AB 、CD 的中点,将四边形ADFE 沿直线EF 进行翻折.给出四个结论:①DF ⊥BC ;②BD ⊥FC ;③平面DBF ⊥平面BFC ;④平面DCF ⊥平面BFC .在翻折过程中,可能成立的结论是( )A .①③B .②③C .②④D .③④10.若直线1ax by +=与不等式组1210210y x y x y ≤⎧⎪--≤⎨⎪++≥⎩表示的平面区域无公共点,则23a b +的取值范围是( )A .()7,1--B .()3,5-C .()7,3-D .R二、 填空题:本大题共7小题,每小题4分,共28分.11.已知复数z 满足()21z i i -=+(i 是虚数单位),则z =__________. 12.等比数列{}n a 前n 项的乘积为n T ,且2342a a =,则9T =__________.13.若()()8880182121x x a a x a x ++-=++⋅⋅⋅+,则02468a a a a a ++++=__________.14.已知某几何体的三视图如图,则该几何体的体积是_________.15.如图在等腰直角三角形ABC 中,AB=AC=2,D 、E 是线段BC 上的两点,且13DE BC =,则AD AE ⋅的取值范围是___________.16.焦点为F 的抛物线24y x =上有三点A 、B 、C 满足:①△ABC 的重心是F ;②|FA|、|FB|、|FC|成等差数列.则直线AC 的方程是________________________. 17.已知集合()()()()}222,0,,1,2,32a A f x y f x y x a y a a ⎧⎪===-+--=±±±⎨⎪⎩,()(){},0,,1,2,3A g x y g x y x y b b ===+-=±±±,则A 中方程的曲线与B 中方程的曲线的交点个数是_________.三. 解答题 本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18. (本题满分14分)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且sin 2sin b Ca A=(Ⅰ)若512C π=,求角B 的大小; (Ⅱ)若2,32b C ππ=≤<,求△ABC 面积的最小值.19. (本题满分14分)如图,四棱锥P —ABCD 中,PA ⊥平面ABCD ,AD//BC ,PA=AB=AD=2BC=2,∠BAD=θ,E 是棱PD 的中点.(Ⅰ)若60θ=,求证:AE ⊥平面PCD ;(Ⅱ)求θ的值,使二面角P —CD —A 的平面角最小.20. (本题满分14分)有A 、B 、C 三个盒子,每个盒子中放有红、黄、蓝颜色的球各一个,所有的球仅有颜色上的区别. (Ⅰ)从每个盒子中任意取出一个球,记事件S 为“取得红色的三个球”,事件T 为“取得颜色互不相同的三个球”,求P (S )和P (T );(Ⅱ)先从A 盒中任取一球放入B 盒,再从B 盒中任取一球放入C 盒,最后从C 盒中任取一球放入A 盒,设此时A 盒中红球的个数为ξ,求ξ的分布列与数学期望E ξ.21. (本题满分15分)如图,设椭圆22221(0)x y a b a b+=>>长轴的右端点为A ,短轴端点分别为B 、C ,另有抛物线2y x b =+.(Ⅰ)若抛物线上存在点D ,使四边形ABCD 为菱形,求椭圆的方程;(Ⅱ)若2a =,过点B 作抛物线的切线,切点为P ,直线PB 与椭圆相交于另一点Q,求PQ QB的取值范围.•BACEPD(第19题)21. (本题满分15分)已知a R ∈,函数()()()2,ln 2m x x n x a x ==+. (Ⅰ)令()()(),0,0m x x f x n x x ⎧≤⎪=⎨>⎪⎩,若函数()f x 的图像上存在两点A、B满足OA ⊥OB (O 为坐标原点),且线段AB 的中点在y 轴上,求a 的取值范围;(Ⅱ)若函数()()()g x m x n x =+存在两个极值点1x 、2x ,求()()12g x g x +的取值范围.理科数学 参考答案一、选择题(本大题共10小题,每题5分,共50分)1.A ; 2.A ; 3.D ; 4.B ; 5.C ; 6.D ;7.A ;8.D ;9.B ;10.C .第9题提示:考虑①:因为AD BC //,AD 与DF 相交不垂直,所以BC 与DF 不垂直,则①不成立;考虑②:设点D 的在平面BCF 上的射 影为点P ,当CF BP ⊥时就有FC BD ⊥,而4:3:2::=AB BC AD 可使条件满足,所以②正确;考虑③:当点P 落在BF 上时,⊂DP 平面BDF ,从而平面⊥BDF 平面BCF ,所以③正确.考虑④:因为点D 的射影不可能在FC 上,所以④不成立.第10题提示:不等式组⎪⎩⎪⎨⎧≥++≤--≤0120121y x y x y 表示的平面区域是由)1,0(),1,1(),1,1(--C B A 围成的三角形区域(包含边界).因为直线1=+by ax 与⎪⎩⎪⎨⎧≥++≤--≤0120121y x y x y 表示的平面区域无公共点, 所以b a ,满足:⎪⎩⎪⎨⎧>-->-+->-+010101b b a b a 或⎪⎩⎪⎨⎧<--<-+-<-+010101b b a b a . ),(b a 在如图所示的三角形区域(除边界且除原点).所以b a 32+的取值范围是)3,7(-. BAC DEFP二、填空题(本大题共7小题,每题4分,共28分) 11.10; 12.512;13.138+(或6562); 14.38; 15.]38,916[; 16.012=-±y x ; 17.14. 第17题提示:集合A 中的方程表示圆心在直线x y =上的六个圆, 由对称性只需考虑第一象限. 记3,2,1=a 对应的圆分别为⊙1C , ⊙2C ,⊙3C ,易知⊙1C 与⊙3C 外切, ⊙2C 与⊙1C , ⊙3C 相交,且经过⊙1C 的圆心.3,2,1=b 对应的三条直线321,,l l l ,1l 与⊙1C 外切,2l 与⊙2C 外切且与⊙1C 相交,3l 与⊙1C 与⊙3C 的外公切线且与⊙2C 相交,由图知在第一象限共有7个交点,故共有14个交点.三、解答题(本大题共5小题,共72分) 18.(本题满分14分)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且ACa b sin 2sin =. (Ⅰ)若π125=C ,求角B 的大小; (Ⅱ)若2=b ,23ππ<≤C ,求△ABC 面积的最小值.18.(Ⅰ)(本小题7分)由正弦定理,得ACA B a b sin 2sin sin sin ==. ∴ 2165sin 2sin sin ===πC B .∴ 6π=B (65π=B 舍).(Ⅱ)(本小题7分)由(Ⅰ)中C B 2sin sin =可得C B 2=或π=+C B 2. 又 C B 2=时,23ππ<≤C ,π32≥B ,即π≥+C B ,矛盾. 所以π=+C B 2,ππ=+--C C A 2,即C A =. 所以3tan 21≥==∆C hb S ABC , 即当3π=C 时,ABC S ∆的最小值是3.19.(本题满分15分)如图,四棱锥ABCD P -中,⊥PA 平面ABCD ,BC AD //,22====BC AD AB PA ,θ=∠BAD ,E 是棱PD 的中点.(Ⅰ)若︒=60θ,求证:⊥AE 平面PCD ;(Ⅱ)求θ的值,使二面角A CD P --的平面角最小. 19.(Ⅰ)(本小题7分) 当︒=60θ时,∵BC AD //,22===BC AD AB . ∴AD CD ⊥.又⊥PA 平面ABCD ,∴CD PA ⊥. ∴⊥CD 平面PAD . 又⊂AE 平面PAD , ∴AE CD ⊥.又AD PA =,E 是棱PD 的中点, ∴AE PD ⊥. ∴⊥AE 平面PCD .(Ⅱ)(本小题8分)如图,建立空间直角坐标系xyz A -,则)2,0,0(P ,)0,cos 2,sin 2(θθB , )0,1cos 2,sin 2(+θθC ,)0,2,0(D .∴)2,2,0(-=DP 、)0,1cos 2,sin 2(-=θθDC . 设平面PCD 的法向量为),,(z y x n =, 则⎩⎨⎧=-+=+-⎪⎩⎪⎨⎧⇒⊥⊥0)1cos 2()sin 2(022y x z y DC n DP n θθ 取1=y ,得)1,1,sin 21cos 2(θθ-=n .又易知平面ABCD 的法向量为)1,0,0(=m . 设二面角A CD P --的平面角为α, 则2)sin 21cos 2(1||||cos 2+-=⋅=θθαn m要使α最小,则αcos 最大,即0sin 21cos 2=-θθ,∴ 21cos =θ,得3πθ= 20.(本题满分14分)有A 、B 、C 三个盒子,每个盒子中放有红、黄、蓝颜色的球各一个,所有的球仅有颜色上的区别. (Ⅰ)从每个盒子中任意取出一个球,记事件S 为“取得红色的三个球”,事件T 为“取得颜色互不相同的三个球”,求)(S P 和)(T P ;(Ⅱ)先从A 盒中任取一球放入B 盒,再从B 盒中任取一球放入C 盒,最后从C 盒中任取一球放入A 盒,设此时A 盒中红球的个数为ξ,求ξ的分布列与数学期望ξE .(第19题)20.(Ⅰ)(本小题6分)271313131)(=⨯⨯=S P ,92)(131313111213==C C C C C C T P . (Ⅱ)(本小题8分)ξ的可能值为2,1,0.①考虑0=ξ的情形,首先A 盒中必须取一个红球放入B 盒,相应概率为31,此时B 盒中有2红2非红;若从B 盒中取一红球放入C 盒,相应概率为21,则C 盒中有2红2非红,从C 盒中只能取一个非红球放入A 盒,相应概率为21;若从B 盒中取一非红球放入C 盒,相应概率为21,则C 盒中有1红3非红,从C 盒中只能取一个非红球放入A 盒,相应概率为43.故2454321212131)0(=⎥⎦⎤⎢⎣⎡⨯+⨯⨯==ξP .②考虑2=ξ的情形,首先A 盒中必须取一个非红球放入B 盒,相应概率为32,此时B 盒中有1红3非红;若从B 盒中取一红球放入C 盒,相应概率为41,则C 盒中有2红2非红,从C 盒中只能取一个红球放入A 盒,相应概率为21;若从B 盒中取一非红球放入C 盒,相应概率为43,则C 盒中有1红3非红,从C 盒中只能取一个红球放入A 盒,相应概率为41.故2454143214132)2(=⎥⎦⎤⎢⎣⎡⨯+⨯⨯==ξP .③1272452451)1(=--==ξP . 所以ξ的分布列为ξ0 1 2 P245127 245 ξ的数学期望1245212712450=⨯+⨯+⨯=ξE . 21.(本题满分15分)如图,设椭圆)0(12222>>=+b a by a x 长轴的右端点为A ,短轴端点分别为B 、C ,另有抛物线b x y +=2.(Ⅰ)若抛物线上存在点D ,使四边形ABCD 为菱形,求椭圆的方程;(Ⅱ)若2=a ,过点B 作抛物线的切线,切点为P ,直线PB 与椭圆相交于另一点Q ,求||||QB PQ 的取值范围.21.(Ⅰ)(本小题6分) 由四边形ABCD 是菱形, 得),(2b a a D +,且⎩⎨⎧=+=+b b a b b a 22222,解得33=a ,31=b , 所以椭圆方程为19322=+yx .(Ⅱ)(本小题9分) 不妨设),(2b t t P +(0≠t ), 因为t x y t x t x 2|2|'====,所以PQ 的方程为b t t x t y ++-=2)(2,即b t tx y +-=22. 又因为直线PQ 过点B ,所以b b t -=+-2,即22t b =.所以PQ 的方程为222ttx y -=.联立方程组⎪⎪⎩⎪⎪⎨⎧=+-=144224222t y x t tx y ,消去y ,得032)64(22=-+tx x t . 所以点Q 的横坐标为64322+=t tx Q , 所以132||||22+=--=t x x x x QB PQ B Q Q P .又)4,0(22∈=b t ,所以||||QB PQ 的取值范围为)89,1(. 22.(本题满分14分)已知R ∈a ,函数2)(x x m =,)2ln()(+=x a x n .(Ⅰ)令⎩⎨⎧>≤=0,)(0,)()(x x n x x m x f ,若函数)(x f 的图象上存在两点A 、B 满足OB OA ⊥(O 为坐标原点),且线段AB 的中点在y 轴上,求a 的取值集合;(Ⅱ)若函数)()()(x n x m x g +=存在两个极值点1x 、2x ,求)()(21x g x g +的取值范围. 22.(Ⅰ)(本小题6分)由题意,不妨设))2ln(,(+t a t A ,),(2t t B -,且0>t , ∴0=⋅OB OA ,即0)2ln(22=++-t at t ,∴)2ln(1+=t a .∵),2(ln )2ln(+∞∈+t , ∴a 的取值集合是}2ln 10|{<<x x . (Ⅱ)(本小题8分))2ln()(2++=x a x x g ,242)('2+++=x ax x x g . 要使)(x g 存在两个极值点,则0)('=x g 即0422=++a x x 在),2(+∞-上存在两不等的实根.令a x x x p ++=42)(2,∵)(x p 的图象的对称轴为1-,∴0816>-=∆a 且0)2(>-p . ∴20<<a .由上知⎪⎩⎪⎨⎧=⋅-=+222121a x x x x . ∴)2ln()2ln()()(22212121+++++=+x a x x a x x g x g]4)(2ln[2)(212121221++++-+=x x x x a x x x x ]4)2(22ln[22)2(2+-⋅++⋅--=aa a 42ln+-=a aa . 令42ln )(+-=x xx x q ,)2,0(∈x , ∴02ln )('<=xx q ,)(x q 在)2,0(上单调递减, ∴ 442ln2<+-<a aa . 故)()(21x g x g +的取值范围是)4,2(.高考模拟数学试卷第Ⅰ卷(共60分)一.选择题本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合}0|{≥=x x A ,且B B A = ,则集合B 可能是 A.}2,1{B.}1|{≤x xC.}1,0,1{-D.R2.下列函数中,最小正周期为π,且图象关于直线3π=x 对称的是A.)62sin(π+=x y B.)32sin(π+=x yC.)32sin(π-=x yD.)62sin(π-=x y3.已知110a b<<,则下列结论错误的是 A.22b a < B.2b aa b+> C.2b ab > D.2lg lg a ab <4.规定2,a b ab a b a b R +⊗=++∈ 、,若14k ⊗=,则函数()f x k x =⊗的值域A.(2,)+∞ B .),1(+∞ C .7[,)8+∞ D .7[,)4+∞ 5.设命题:p 函数xy 1=在定义域上为减函数;命题:q ,(0,)a b ∃∈+∞,当1a b +=时,113a b +=,以下说法正确的是A.p ∨q 为真B.p ∧q 为真C.p 真q 假D.p ,q 均假6.若向量a 、b 满足)1,2(-=+b a ,)2,1(=a,则向量a 与b 的夹角等于A.︒45 B .︒60 C .︒120 D .︒135 7.某流程图如图所示,现输入如下四个函数,则可以输出的 函数是 A .()x f x x=B .()()2ln1f x x x =+-C .()x x x xe ef x e e --+=- D .|4||3|1)(2x x x x f -++-= 8.已知锐角α且α5的终边上有一点)130cos ),50(sin(0-P ,则α的值为 A .08 B .044 C .026 D .040 9.下列命题正确的个数是①“在三角形ABC 中,若sin sin A B >,则A B >”的否命题是真命题; ②命题:2p x ≠或3y ≠,命题:5q x y +≠则p 是q 的必要不充分条件;③“32,10x R x x ∀∈-+≤”的否定是“01,23>+-∈∃x x R x ”. A.0 B.1 C.2 D.3 10.已知锐角B A ,满足)tan(tan 2B A A +=,则B tan 的最大值为A . 22B .2 C .22 D .42 11.已知函数()2014sin (01)(),log 1x x f x x x π⎧≤≤⎪=⎨>⎪⎩若c b a 、、互不相等,且)()()(c f b f a f ==,则c b a ++的取值范围是A .(1,2014)B .(1,2015)C .(2,2015)D .[2,2015] 12.下列四个图中,函数10ln 11x y x +=+的图象可能是二、填空题:本大题共4小题,每小题5分,共20分13. 已知2||=a,3||=b,b a,的夹角为60,则=-|2|b a___________.14.设420cos =a ,函数,0,()log ,0,x a a x f x x x ⎧<=⎨≥⎩,则211()(log )46f f +的值等于 .15. 在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知6π=C ,1=a ,3=b ,则=B ____________.16.实数y x ,满足⎪⎩⎪⎨⎧≤->≤≥,0),1(,1y x a a y x 若目标函数y x z +=的最大值为4,则实数a 的值为.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)已知α为锐角,且tan()24πα+=.(Ⅰ)求tan α的值; (Ⅱ)求sin 2cos sin cos 2αααα-的值.18.(本小题满分12分)已知幂函数2242()(1)m m f x m x -+=-在(0,)+∞上单调递增,函数()2x g x k =-.(Ⅰ)求m 的值;(Ⅱ)当[1,2]x ∈时,记()f x ,()g x 的值域分别为集合,A B ,若A B A ⋃=,求实数k 的取值范围.20.(本小题满分12分)已知函数]1)1()1lg[()(22+++-=x a x a x f ,设命题p :“()f x 的定义域为R ”; 命题q “()f x 的值域为R ” .(Ⅰ)分别求命题p 、q 为真时实数a 的取值范围; (Ⅱ)p ⌝是q 的什么条件?请说明理由.21.(本小题满分12分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,且55sin ,43==A C π. (Ⅰ)求B sin 的值;(Ⅱ)若105-=-a c ,求ABC ∆的面积.22.(本小题满分12分)已知函数()()()22211xf x ax a x a a e ⎡⎤=+-+--⎣⎦(其中R a ∈).(Ⅰ)若0x =为()f x 的极值点,求a 的值; (Ⅱ)在(Ⅰ)的条件下,解不等式()()21112f x x x x ⎛⎫>-++ ⎪⎝⎭.因为1tan 3α=,所以cos 3sin αα=,又22sin cos 1αα+=, 所以21sin 10α=,…………………9分 又α为锐角,所以10sin α=所以sin 2cos sin 10cos 2αααα-=.…………………10分 18.解:(Ⅰ)依题意得:2(1)1,0m m -=⇒=或2m =当2m =时,2()f x x -=在(0,)+∞上单调递减,与题设矛盾,舍去∴0m =. ……………5分(Ⅱ)当[1,2]x ∈时,()f x ,()g x 单调递增,∴[1,4],[2,4]A B k k ==--,A B A ⋃=,∴B A ⊆,∴210144k k k -≥⎧⇒≤≤⎨-≤⎩. ……………12分 19. (Ⅰ) ()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x . ……………4分当226222πππππ+≤-≤-k x k 时,解得36ππππ+≤≤-k x k ,)62sin()(π-=∴x x f 的单调递增区间为)](3,6[Z k k k ∈+-ππππ. ……………8分(Ⅱ)上的图像知,在,由标准函数时,当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈. ]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f .所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为21,1-. ……………12分20.解(Ⅰ)命题p 为真,即)(x f 的定义域是R ,等价于01)1()1(22>+++-x a x a 恒成立,等价于1-=a 或⎩⎨⎧<--+=>-.0)1(4)1(Δ,01222a a a 解得1-≤a 或35>a .∴实数a 的取值范围为-∞(,35(]1 -,)∞+ ……………4分命题q 为真,即)(x f 的值域是R , 等价于1)1()1(22+++-=x a x a u 的值域),0(∞+⊇,等价于1=a 或⎩⎨⎧≥--+=>-.0)1(4)1(Δ,01222a a a 解得351≤≤a .∴实数a 的取值范围为1[,]35……………8分 (Ⅱ)由(Ⅰ)(Ⅱ)知,p ⌝]35,1(-∈a ;q ]35,1[∈a .而]35,1[]35,1(≠⊃-,∴p ⌝是q 的必要而不充分的条件 ……………12分 21. 解:(1)因为55sin ,43==A C π 所以552sin 1cos 2=-=A A 由已知得A B -=4π.所以A A A B sin 4coscos 4sin)4sin(sin πππ-=-=1010552225222=⋅-⋅=……………………………………………………6分 (2)由(1)知43π=C 所以22sin =C 且1010sin =B .由正弦定理得510sin sin ==C A c a .又因为105-=-a c ,所以10,5==a c .所以25101051021sin 21=⋅⋅==∆B ac S ABC ………………………………12分 22. (Ⅰ)因为()()()22211x f x ax a x a a e ⎡⎤=+-+--⎣⎦()()()()()22222221111x x x f x ax a e ax a x a a e ax a x a e ⎡⎤⎡⎤⎡⎤'∴=+-++-+--=+++⎣⎦⎣⎦⎣⎦因为0x =为()f x 的极值点,所以由()000f ae '==,解得0a =检验,当0a =时,()xf x xe '=,当0x <时,()0f x '<,当0x >时,()0f x '>.所以0x =为()f x 的极值点,故0a =. ……………4分 (Ⅱ) 当0a =时,不等式()()21112f x x x x ⎛⎫>-++ ⎪⎝⎭()()211112x x e x x x ⎛⎫⇔-⋅>-++ ⎪⎝⎭, 整理得()211102x x e x x ⎡⎤⎛⎫--++>⎪⎢⎥⎝⎭⎣⎦, 即2101102x x e x x ->⎧⎪⎨⎛⎫-++> ⎪⎪⎝⎭⎩或2101102x x e x x -<⎧⎪⎨⎛⎫-++< ⎪⎪⎝⎭⎩令()2112x g x e x x ⎛⎫=-++⎪⎝⎭,()()()1x h x g x e x '==-+,()1x h x e '=-, 当0x >时,()10xh x e '=->;当0x <时,()10xh x e '=-<,所以()h x 在(),0-∞单调递减,在(0,)+∞单调递增,所以()()00h x h >=,即()0g x '>, 所以()g x 在R 上单调递增,而()00g =; 故211002x e x x x ⎛⎫-++>⇔>⎪⎝⎭;211002x e x x x ⎛⎫-++<⇔< ⎪⎝⎭, 所以原不等式的解集为{}01x x x <>或. ……………12分高考模拟数学试卷理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟. 注意事项:1.答卷前,考生务必将自已的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人的准考证号、姓名是否一致.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答题无效.3.考试结束后,监考员将答题卡收回. 参考公式:圆锥侧面积公式:S rl π=,其中r 为底面圆的半径,l 为母线长.第Ⅰ卷(选择题部分,共60分)一.选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知2(1)z m mi =-+在复平面内对应的点在第二象限,则实数m 的取值范围是( ) A . (1,1)- B .(1,0)- C .(,1)-∞ D . (0,1) 2.已知集合{|05}A x R x =∈<≤,2{|log 2}B x R x =∈<,则()A CB Z =( )A .{4}B .{5}C .[45],D .{45},3.我国古代数学名著《九章算术》有“米谷粒分”题:发仓募粮,所募粒中秕不百三则收之(不超过3%),现抽样取米一把,取得235粒米中夹秕n 粒,若这批米合格,则n 不超过( ) A .6粒 B .7粒 C .8粒 D .9粒 4.已知332333233332612201+2=()1+2+3=()1+2+3+4=()222,,,,若333331+2+3+4++=3025n ,则n =( )A .8B . 9C .10D .11 5.221a b +=是sin cos 1a b θθ+≤恒成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 6.函数sin ()2xxf x e=的图象的大致形状是( )4226sin360°否结束输出ns ≥3.102nn=6开始7.已知直线:=-l y kx k 与抛物线C :24=y x 及其准线分别交于,M N 两点,F 为抛物线的焦点,若2FM MN =,则实数k等于( )A .B .1±C .D .2±8.已知12,F F 是椭圆和双曲线的公共焦点,P 是它们的一个公共点,且124F PF π∠=,则椭圆和双曲线的离心率乘积的最小值为( ) A .12B .2C .1D9.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n 的值为()A .12B .24C .36D .48 10.已知函数'()f x 是函数()f x 的导函数,1(1)f e=,对任意实数都有()()0f x f x '->,则不等式2()x f x e-<的解集为( )A. (,)e -∞ B .(1,)+∞ C. (1,)e D .(,)e +∞11.一个几何体的三视图如图所示,则该几何体的体积等于( ) A .72 B .48 C .24 D .16 12.函数2231119()cos(2)4cos 2([,])331212f x x x x x ππππ=-+--∈--所有零点之和为( ) A .3π2 B .43π C . π2 D . 83π第Ⅱ卷(非选择题部分,共90分)本卷包括必考题和选考题两个部分. 第13题~第21题为必考题,每个考生都必须作答. 第22题~第23题为选考题,考生根据要求作答.二.填空题:本大题共4小题,每小题5分,共20分.13.已知6(1)(1)x ax -+展开式中含2x 项的系数为0,则正实数a = .14.已知向量(,),(1,2)a m n b ==-,若||25,(0)a a b λλ==<,则m n -= .15.对任意[1,5]k ∈,直线:1l y kx k =--都与平面区域620x a x y x y ≥⎧⎪+≤⎨⎪-≤⎩有公共点,则实数a 的最大值是 .16.定义域为R 的函数()f x 满足(+3)=2()f x f x ,当[1,2)x ∈-时,2|1|,[1,0)()=1(),[0,2)2x x x x f x x -⎧+∈-⎪⎨-∈⎪⎩ .若存在[4,1)x ∈--,使得不等式234()t t f x -≥成立,则实数t 的取值范围是 . 三.解答题:本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分) 已知数列{}n a 满足2312232222nn a a a a n n ++++=+ (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若(1)2n nn a b -=,求数列{}n b 的前n 项和n S .18.(本小题满分12分) 为备战2018年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得3分,负者得0分,在每一场比赛中,甲胜乙的概率为35,丙胜甲的概率为34,乙胜丙的概率为p ,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为110. (Ⅰ)求p 的值;(Ⅱ)设在该次对抗比赛中,丙得分为X ,求X 的分布列和数学期望.19.(本小题满分12分) 如图,四棱锥ABCD P -的底面ABCD 为平行四边形,平面⊥PAB 平面ABCD ,PC PB =,︒=∠45ABC ,点E 是线段PA 上靠近点A (Ⅰ)求证AB PC ⊥;(Ⅱ)若PAB ∆是边长为2的等边三角形, 求直线DE 与平面PBC 所成角的正弦值.20.(本小题满分12分) 如图,已知直线:1(0)l y kx k =+>关于直线1y x =+对称的直线为1l ,直线1,l l 与椭圆22:14x E y +=分别交于点A 、M 和A 、N ,记直线1l (Ⅰ)求1k k ⋅的值;(Ⅱ)当k 变化时,试问直线MN 是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.21.(本小题满分12分)已知函数()axf x ebx =+(0)a <在点(0,(0))f 处的切线方程为51y x =+,且(1)(1)12f f '+=.(Ⅰ)求函数()y f x =的极值;(Ⅱ)若2()3f x x >+在[1,]x m ∈上恒成立,求正整数m 的最大值.请考生在第(22)、(23)两题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B 铅笔在答题卡上把所选题目的题号涂黑,把答案填在答题卡上. 22.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,以原点O 为极点,x 轴的非负半轴为极轴,建立极坐标系,曲线C 的参数方程为1cos sin x y θθ=+⎧⎨=⎩ (θ为参数).(Ⅰ)求曲线C 的极坐标方程;(Ⅱ)若曲线C 向左平移一个单位,再经过伸缩变换2xxy y'=⎧⎨'=⎩得到曲线C ',设(,)M x y 为曲线C '上任一点,求224x y --的最小值,并求相应点M 的直角坐标.23.(本小题满分10分)选修4-5:不等式选讲设函数()|23||1|.f x x x =++- (Ⅰ)解不等式()4f x >; (Ⅱ)若存在3[,1]2x ∈-使不等式1()a f x +>成立,求实数a 的取值范围.理科数学 参考答案及评分标准一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.二、填空题本大题共4小题,每小题5分,满分20分. 13.25; 14. 6-; 15. 2; 16. (,1][2,)-∞+∞ 三、解答题:本大题共6小题,共70分. 解答应写出文字说明.证明过程或演算步骤. 17.【解析】(Ⅰ)2312232222nn a a a a n n ++++=+……①, ∴当2n ≥时,23112231(1)12222n n a a a a n n --++++=-+-② ①②得2(2)2nn a n n =≥,∴12(2)n n a n n +=⋅≥. …………5分 又∵当1n =时,1112a =+, ∴14a =,∴12n n a n +=⋅. …………6分 (Ⅱ)(1)(2)2n n nn a b n -==-,1231(2)2(2)3(2)(2)n n S n =⨯-+⨯-+⨯-++⨯-……③2341(2)1(2)2(2)3(2)(1)(2)+(2)n n n S n n +-=⨯-+⨯-+⨯-++-⨯--……④∴234112[1(2)]3(2)+(2)(2)(2)(2)(2)(2)3n nn n n S n n ++---=--+-+-++---=--∴1(31)(2)29n n n S ++-+=-. …………12分18.【解析】(Ⅰ)由已知,甲获第一名且乙获第三名的概率为110. 即甲胜乙、甲胜丙且丙胜乙概率为110, …………2分 ∴311(1)5410p ⨯⨯-=, ∴13p =. …………6分 (Ⅱ)依题意丙得分X 可以为0,3,6,丙胜甲的概率为34,丙胜乙的概率为23…………7分 111(0)4312P X ==⨯=,31125(3)434312P X ==⨯+⨯=,326(6)4312P X ==⨯= …………10分∴ 1()0361212124E X =⨯+⨯+⨯=. (12)分 19.【解析】(Ⅰ)作PO AB ⊥于O ……①,连接OC , ∵平面⊥PAB 平面ABCD ,且PABABCD AB =面面 ,∴PO ⊥面ABCD . ………2分∵PC PB =,∴POB POC ∆≅∆,∴OB OC =, 又∵︒=∠45ABC ,∴OC AB ⊥……② 又POCO O =,由①②,得AB ⊥面POC,又PC ⊂面POC ,∴AB PC ⊥. ………6分(Ⅱ)∵PAB ∆是边长为2的等边三角形,∴1PO OA OB OC ====如图建立空间坐标系,(1,0,0)P - 设面PBC 的法向量为(,,)n x y z =,(1,0,3),(1,1,0)PB BC=-=-0n PB x n BC x y ⎧⋅=-=⎪⎨⋅=-+=⎪⎩,令x =(3,3,1)n = 11(1,0,3),(,0,33AP AE AP ===,(1,1,0)CB DA ==- 4(,1,33DE DA AE =+=-,设DE 与面PBC 所成角为θsin |cos ,|||||16n DE n DE n DE θ-⋅====∴直线DE 与平面PBC 所成角的正弦值7. …………12分 20.【解析】(Ⅰ)设直线l 上任意一点(,)P x y 关于直线1y x =+对称点为000(,)P x y 直线l 与直线1l 的交点为(0,1),∴11:1,:1l y kx l y k x =+=+01011,y y k k x x --==,由00122y y x x ++=+ 得002y y x x +=++……..① 由1y y x x -=--得00y y x x -=-…….②, 由①②得 0011y x y x =+⎧⎨=+⎩0000100()1(1)(1)(2)11yy y y x x x x kk xx xx -++++-+++===. …………6分(Ⅱ)设点1122(,),(,)M x y N x y ,由12211114y kx x y =+⎧⎪⎨+=⎪⎩得2211(41)80k x kx ++=, ∴2841M kx k -=+,∴221441M k y k -=+. 同理:122188414N k k x k k --==++,221221144414N k k y k k--==++ …………8分 224222222144881414888(33)3414M N MNM N k k y y k k k k k k k x x k k k k k-----+++====------++ …………9分 :()M MN M MN y y k x x -=-,∴22221418()41341k k ky x k k k -+--=--++即:22222218(1)141533(41)4133k k k k y x x k k k k ++-+=--+=--++ …………11分 ∴当k 变化时,直线MN 过定点5(0,)3-. …………12分21.【解析】(Ⅰ)()ax f x e bx =+,那么'()axf x ae b =+由'(0)5(1)'(1)12f f f =⎧⎨+=⎩,得512a aa b ae b b e +=⎧⎨+++=⎩,化简得(2)(1)0a e a -+= 由0a <得1,6a b =-=,∴()6xf x e x -=+ …………3分即'()60xf x e-=-+=,得ln6x =-,∴()f x 在(,ln 6)-∞-单调递减,在(ln 6,)-+∞单调递增,∴ln6()(ln6)6ln666ln6f x f e =-=-=-极小值,无极大值. …………5分(Ⅱ)2()3f x x >+在[]1,x m ∈上恒成立,等价于2630x e x x --+->在[]1,x m ∈上恒成立.设2()63xg x ex x -=-+-,则'()26x g x e x -=--+设()'()26xh x g x e x -==--+,则'()2x h x e -=-, …………6分∵1x m ≤≤,有'()0h x <, ∴()h x 在区间[]1,m 上是减函数, 又∵123(1)40,(2)20,(3)0h eh e h e ---=->=->=-<,∴存在0(2,3)x ∈,使得00()'()0h x g x ==,当01x x ≤<时,有'()0g x >,当0x x >时,有'()0g x <.∴()y g x =在区间[]01,x 上递增,在区间0(,)x m 上递减, 又∵123(1)20,(2)5>0,(3)6>0,g e g eg e ---=+>=+=+456(4)5>0,(5)20,(6)30.g e g e g e ---=+=+>=-<∴当15x ≤≤时,恒有()0g x >;当6x ≥时,恒有()0g x <;∴使命题成立的正整数m 的最大值为5. …………12分 22.【解析】(I )由 1cos sin x y θθ=+⎧⎨=⎩(θ为参数)得曲线C 的普通方程为22(1)1x y -+=得曲线C 的极坐标方程为2cos ρθ=. …………4分(Ⅱ)22(1)1x y -+=,向左平移一个单位再经过伸缩变换2x xy y'=⎧⎨'=⎩得到曲线C '的直角坐标方程为2214x y +=,设(2cos ,sin )M αα,则2222cos cos sin 4x y a a αα-=--cos222cos(2)3a παα==+ …………7分当3k παπ=+时,224x y -的最小值为2-,此时点M的坐标为(1,2或(1,2--. …………10分 23.【解析】(Ⅰ)()|23||1|.f x x x =++-33223()412321x x f x x x x x ⎧--<-⎪⎪⎪∴=+-≤≤⎨⎪+>⎪⎪⎩,∴3311()42232432444x x x f x x x x ⎧⎧><--≤≤⎧⎪⎪>⇔⎨⎨⎨+>⎩⎪⎪-->+>⎩⎩或或211x x x ⇔<-<≤>或0或. 综上,不等式()4f x >的解集为(,2)(0,)-∞-+∞. …………5分(Ⅱ)存在3[,1]2x ∈-使不等式1()a f x +>成立min 1(())a f x ⇔+> 由(Ⅰ)得,3[,1]2x ∈-时,()4f x x =+,()4f x x =+时,min 5(())2f x = ∴512a +>, ∴32a >,∴实数a 的取值范围为3+2∞(,). …………10分高考模拟数学试卷本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第(22)- (23)题为选考题,其他题为必考题。


浙江衢州二中高三数学模拟卷(理)高三数学(理)一、选择题(每小题5分,共50分)1.已知集合A={1,2,3},B={2,4,6},C={|,,}x x a b a A b B =⋅∈∈,则集合C 的元素之和为(A )84 (B )50 (C )38 (D )18 2.0a =是复数(,)a bi a b R +∈为纯虚数的( )条件(A )充分 (B )必要 (C )充要 (D )既非充分又非必要3.正三棱锥V-ABC 的底面边长为2,那么侧棱VC 在平面V AB 上的射影长(A )0 (B )1 (C (D )234.已知二次函数2()2(0)f x ax x a =->对任意[0,1],|()|1x f x ∈≤恒成立,则a 的取值范畴(A )0a <≤ (B )1a <≤(C )1a << (D )1a ≤≤ 5.已知数列11{},1,(2)2n n n a a a S n ==≥,则S 8= ( )(S n 为数列的前n 项和) (A )127 (B )128 (C )256 (D )2576.已知,l P αα⊂∉,过点P 引与直线l 成60°角的直线交平面α于Q ,则Q 点的轨迹是(A )两个点 (B )抛物线 (C )椭圆 (D )双曲线 7.O 为∆ABC 内一点,且3OA OC OB O ++=,则:AOB AOC S S ∆∆=(A )1:2 (B )1:3 (C )2:1 (D )3:18.已知双曲线22221x y a b-=,F 为右焦点,右准线与一条渐近线的交点P ,且|OP|、|PF|、|OF|成等差数列,则双曲线的离心率(A (B (C )53 (D )549.矩形的边长为2和5,通过它的短边上的点作直线,使得所截得的直角三角形的周长为8,则矩形留下部分面积的最小值(A)6+ (B)38 (C )223(D)48- 10.已知函数1()ln2f x x x =++有以下命题: ①方程()0f x =只有一个实根②(2,1]--上为减函数,[1,)-+∞上为增函数 ③有极小值1- ④21lim0()x f x →-= 其中正确的命题是(A )①③④ (B )②③④ (C )②③ (D )①②④二、填空题(每小题4分,共16分)11.一个平均的四面体,一个面上标0,两个面上标1,一个面上标2,连续抛掷两次,则面向下的数之和的数学期望________________12.已知实数,x y 满足220240330x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩,则|1|z x y =+-取值范畴______________13.过抛物线214y x =的焦点F 作弦|AB|,若||2||FA FB =,则|AB|=_________ 14.已知函数()y f x =的反函数11(),(1)fx f x --+若的反函数(1)f x +,且(1)2,(2007)f f ==则_____________高三数学(理)模拟考试答题卷二、填空题(每题4分,共12分)11 12 13 14 三、解答题(每题14分,共84分) 15.已知向量2(sin,1),(2,sin )2xm n x ==. (1)当0x π≤≤时,求m n ⋅的取值范畴.(2)定义函数()|1|f x m n =⋅-,求函数的递增区间.16.正三角形ABC 的中心为O ,D 、E 、F 分别为各边的中点,三角形ABC 的面积为4.(1)以上述七个点为顶点的三角形全体记为集合M ,那么集合M 中共有几个元素?其中面积为1的三角形有几个?(2)从集合M 中,任取两个元素,面积均为1的概率是多少?(3)从M 中有放回地取三角形,若取出面积为1时停止,求恰好取3次后停止摸取的概率.班级________________ 姓名_______________ 准考证号___________________………………………………………………密………………………………封………………………………线………………………………………………17.已知M 68(,)55-关于直线2y x =的对称点N 在椭圆22221(0)x y a b a b +=>>上,离心率2e =. (1)求椭圆方程.(2)过N 点引两条互相垂直的直线交椭圆于A 、B 两点,求证直线AB 恒过定点,并求出定点坐标.18.如图,三棱锥P-ABC 中,ABC ∆为正三角形,D 为AC 的中点,E 为PD的中点,,36PB PBD BE PB AC =∠==⊥. (1)求证:平面PAC PBD ⊥平面. (2)求三棱锥P-ABC 的体积.AC19.已知函数()lg(1)f x x =+,当点M (,)x y 在()y f x =的图象上运动时. (1)求对应点1(,2)()2x a N y a R -+∈确定的函数关系()y g x =. (2)若[0,1]x ∈时,()(2)g x f x ->恒成立,求参数a 的取值范畴.20.数列11{},(1),n n n n a a S n+=-是数列的前n 项和,S n 具有以下性质: 11=11122-=111112323-+=+11111123434-+-=+111111112345345-+-+=++11111111123456456-+-+-=++(1)依照以上规律,写出n=9与n=10时,S n 满足的等式; (2)依照以上规律,归纳出S n 满足的等式关系,并加以证明..高三理科模拟考试参考答案一、BBADB DBCCC 二、2 []0,4922004- 三、15. (1)2sin()4mn x π⋅=-1⎡⎤∈⎣⎦ (2)3,,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦16. (1)27629C -=,面积为1的三角形的个数有10个;(2) 21022945406C C = (3)23191036102924389⨯= 17. (1)2222(2,0),,4,1,124x N e a b y -===+= (2)设AN (2)y k x =+ BN 1(2)y x k=-+, 由22(2)440y k x x y =+⎧⎨+-=⎩得222284(,)4141k k A k k -++,因此222284(,)44k kB k k --++ 因此254(1)ABkk k -=-,AB 的方程为22224528()414(1)41k k k y x k k k --=--+-+ 令0y =,可得2224665(41)5k x k --==-+,即过定点(6,05-)18. (2)由题意2BD BP BE +=,两边平方得28280,0,233x x x x +-=>=13PBDV AC S =⋅⋅=19. (1)用代入法得()2lg(2)g x x a =+(2)由(),(2)g x f x -的定义域得122ax -<<,它包含[]0,1,因此2a >, ()(2)g x f x >得22211024a a x x +--+>,令22211()24a a h x x x +-=-+其对称轴为2114a x +=>(2a >),2min 41()(1)04a a h x h -+==>,2a >+20.(1) 11111111119,12348956789n =-+-+-+=++++ 1111111111110,12348910678910n =-+-+-+-=++++(2)n 为偶数时1111111112234112n n n n n-+-++-=++++--n 为奇数时1111111111234112n n n n n-+-++-=++++--用数学归纳法证,当1,2n =时由已知等式成立 假设n=2k 时等式成立,即1111111112342121212k k k k k-+-++-=+++-+-, 当n=2k+2时,111111112342122122111111212212211111()22211221111222122k k k k k k k k k k k k k k k k k k -+-++-+-=-+-++++-+--+=++++-+--+=+++++-+等式也成立因此,当n 为偶数时,1111111111234112n n nn n-+-++-=++++-- 成立。

2020年浙江省衢州二中高考数学模拟试卷(6月份)一、选择题(本大题共10小题,共30.0分)1.已知集合A={x|0<x<5},B={x|x2−2x−3>0},则A∩∁R B()A. (0,3)B. (3,5)C. (−1,0)D. (0,3]2.双曲线2x2−y2=8的实轴长是()A. 4√2B. 4C. 2√2D. 23.若实数x,y满足约束条件{x−3y+4≥03x−y−4≤0x+y≥0,则z=3x−2y的最大值是()A. 2B. 1C. 5D. 74.设a,b是实数,则“a>b>1”是“a+1a >b+1b”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件5.将函数f(x)=2sin xcos x的图象向右平移φ(φ>0)个单位长度,若所得的图象过点(π3,12),则φ的最小值为()A. π6B. π4C. π3D. 2π36.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A. 28B. 30C. 36D. 427.已知某8个数的期望为5,方差为3,现又加入一个新数据5,此时这9个数的期望记为E(X),方差记为D(X),则().A. E(X)=5,D(X)>3B. E(X)=5,D(X)<3C. E(X)<5,D(X)>3D. E(X)<5,D(X)<38.2019年成都世界警察与消防员运动会期间,需安排甲、乙、丙、丁四名志愿者去A、B、C三个场馆参与服务工作,要求每个场馆至少一人,则甲乙被安排到同一个场馆的概率为()A. 112B. 18C. 16D. 149.在长方体ABCD−A1B1C1D1中,AB=BC=1,AA1=√3,则异面直线AD1与DB1所成角的余弦值为()A. 15B. √56C. √22D. √5510.函数f(x)=x2+x−ln x的零点的个数是()A. 0B. 1C. 2D. 3二、填空题(本大题共7小题,共21.0分)11.洛书,古称龟书,是阴阳五行术数之源.在古代传说中有神龟出于洛水,其甲壳上心有此图像,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五.方.白.圈.皆.阳.数.,.四.隅.黑.点.为.阴.数.,其各行各列及对角线点数之和皆为15.如图,若从五.个.阳.数.中.随机抽取三个数,则能使这三个数之和等于15的概率是.12.已知i为虚数单位,复数z=3+i2−i,则z−等于______.13.若(1−2x)2016=a0+a1x+a2x2+⋯+a2016x2016(x∈R),则a12+a222+a323+⋯+a201622016=______.14.设F1,F2是椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点,过F2的直线l与C交于A,B两点.若AB⊥AF1,且|AB|:|AF1|=4:3,则椭圆的离心率为______.15.若函数f(x)=√x2+ax+1的值域为,则实数a取值范围是_________ .16.已知a∈R,函数f(x)=|x+4x−a|+a在区间[1,4]上的最大值是5,则a的取值范围是______ .17.已知平面向量a⃗、 b⃗ 满足|2a⃗+3b⃗ |=1,则a⃗⋅b⃗ 的最大值为______ .三、解答题(本大题共5小题,共63.0分)18.在△ABC中,角A,B,C的对边分别为a,b,c,且满足(sinC−sinA)a=(sinC−sinB)(c+b),△ABC的外接圆的半径为2√3,3(1)求角B的大小;(2)若a+c=4,求△ABC的面积.19.在三棱锥A−BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边,且AD=√3,BD=CD=1,另一个侧面ABC是等边三角形.(1)求证:AD⊥BC.(2)在线段AC上是否存在一点E,使直线ED与平面BCD的夹角为30°?若存在,确定点E的位置;若不存在,请说明理由.20. 已知等差数列{a n }的前n 项和为S n ,且a 2=3,S 5=20.(1)求数列{a n }的通项公式;(2)设数列{b n }的前n 项和为T n ,且b n =(12)a n ,求证:14≤T n <12.21. 已知椭圆E :x 2a 2+y 2b 2=1(a >b >0)的一焦点F 在抛物线y 2=4x 的准线上,且点M(1,−√22)在椭圆上.(Ⅰ)求椭圆E 的方程;(Ⅱ)过直线x =−2上一点P 作椭圆E 的切线,切点为Q ,证明:PF ⊥QF .22. 已知函数f(x)=e x−1−x ,求f(x)的最小值.-------- 答案与解析 --------1.答案:D解析:解:由B中不等式变形得:(x−3)(x+1)>0,解得:x>3或x<−1,即B=(−∞,−1)∪(3,+∞),∵全集为R,A=(0,5),∴∁R B=[−1,3],则A∩(∁R B)=(0,3],故选:D.求出B中不等式的解集确定出B,根据全集R求出B的补集,找出A与B补集的交集即可.此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.2.答案:B解析:解:双曲线2x2−y2=8,可化为x24−y28=1∴a=2,∴双曲线2x2−y2=8的实轴长是4故选B.双曲线方程化为标准方程,即可确定实轴长.本题考查双曲线的几何性质,考查学生的计算能力,属于基础题.3.答案:C解析:本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.解:由实数x,y满足约束条件{x−3y+4⩾03x−y−4⩽0x+y⩾0作出可行域如图,联立{x +y =03x −y −4=0,解得C(1,−1),化目标函数z =3x −2y 为y =32x −12z ,由图可知,当直线y =32x −12z 过C(1,−1)时,直线在y 轴上的截距最大, 即z 有最大值5. 故选:C .4.答案:A解析:设f(a)=a +1a ,f(b)=b +1b ,由于f(x)=x +1x 图象如下图.∴根据函数的单调性可判断:若“a >b >1”则“a +1a >b +1b ”成立,反之若“a +1a >b +1b ”则“a >b >1”不一定成立.根据充分必要条件的定义可判断:“a >b >1”是“a +1a >b +1b ”的充分不必要条件.5.答案:B解析:本题考查了函数y=Asin(ωx+φ)的图象与性质的应用问题,属于基础题.根据正弦函数的图象平移法则及图象性质即可求出答案.解:由f(x)=sin2x的图象平移后所得的函数表达式为g(x)=sin(2x−2φ),由题意,知sin(2π3−2φ)=12,所以2π3−2φ=π6+2kπ(k∈Z)或2π3−2φ=5π6+2k′π(k′∈Z),所以φ=π4−kπ(k∈Z),或φ=−π12−k′π(k′∈Z).又φ>0,所以φ的最小值为π4.故选B.6.答案:D解析:解:由题意可知几何体的直观图如图:是3个长方体的组合体:几何体的表面积为:2×(1+3+1+3)+2×(1×3)+2×(1+1+1+1)+2×(1+2+1+2)=42.故选:D.画出几何体的直观图,利用三视图的数据求解几何体的表面积即可.本题考查三视图求解几何体的表面积,画出直观图是解题的关键.7.答案:B解析:本题考查随机娈量期望和方差的运算,可利用平均数、方差的定义直接求解.解:某8个数据的平均数为5,方差为3,现又加入一个新数据5,此时这9个数的平均数为x¯,方差为s2,x=8×5+59=5,S2=8×3+(5−5)29=83<3,所以B选项是正确的.故选B.8.答案:C解析:本题主要考查了排列、组合的综合应用,考查了学生的分析与计算能力,属基础题. 根据排列组合知识得出甲乙被安排到同一个场馆的概率.解:由题意可知安排方法有C 42A 33=36种,甲乙被安排到同一个场馆方法有A 33=6种, ∴甲乙被安排到同一个场馆的概率为636=16. 故选C .9.答案:D解析:以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,利用向量法能求出异面直线AD 1与DB 1所成角的余弦值. 【详解】以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,∵在长方体ABCD −A 1B 1C 1D 1中,AB =BC =1,AA 1=√3,,∴A(1,0,0),D 1(0,0,√3),D(0,0,0),B 1(1,1,√3),AD 1⃗⃗⃗⃗⃗⃗⃗ =(−1,0,√3),DB 1⃗⃗⃗⃗⃗⃗⃗⃗ =(1,1,√3),设异面直线AD 1与DB 1所成角为θ,则cosθ=|AD 1⋅DB 1⃗⃗⃗⃗⃗⃗⃗⃗||AD 1||DB 1|=2√5=√55.,∴异面直线AD 1与DB 1所成角的余弦值为√55.故选:D .本题考查异面直线所成角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.。
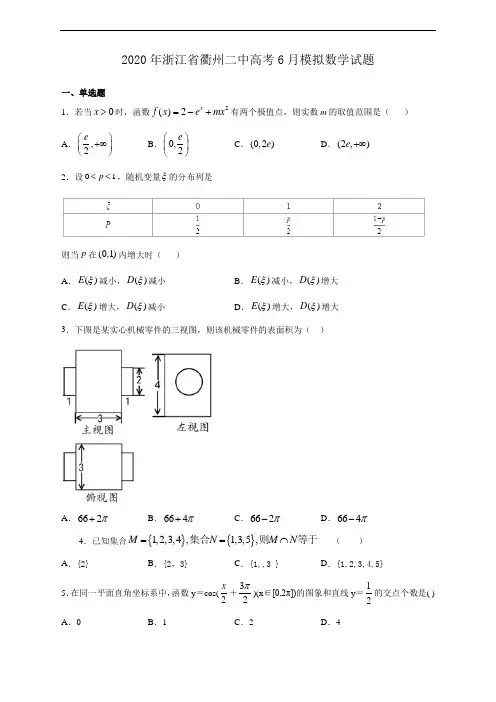
2020年浙江省衢州二中高考6月模拟数学试题一、单选题1.若当0x >时,函数2()2x f x e mx =-+有两个极值点,则实数m 的取值范围是( )A .,2e ⎛⎫+∞⎪⎝⎭B .0,2e ⎛⎫ ⎪⎝⎭C .(0,2)eD .(2,)e +∞2.设01p <<,随机变量ξ的分布列是则当p 在(0,1)内增大时( ) A .()E ξ减小,()D ξ减小 B .()E ξ减小,()D ξ增大 C .()E ξ增大,()D ξ减小D .()E ξ增大,()D ξ增大3.下图是某实心机械零件的三视图,则该机械零件的表面积为( )A .662π+B .664π+C .662π-D .664π-4.已知集合{}{}1,2,3,4,1,3,5,M N M N ==⋂集合则等于 ( ) A .{2}B .{2,3}C .{1,,3 }D .{1,2,3,4,5}5.在同一平面直角坐标系中,函数y =cos(2x +32π)(x ∈[0,2π])的图象和直线y =12的交点个数是( ) A .0B .1C .2D .46.设变量x ,y 满足约束条件250{200x y x y x +-≤--≤≥则目标函数z =2x +3y 的最大值是( )A .8B .9C .10D .117.2013年第12届全国运动会举行期间,某校4名大学生申请当A ,B ,C 三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务A 比赛项目,则不同的安排方案共有( ) A .20种B .24种C .30种D .36种8.已知条件1:p k =,条件:q 直线1y kx =+与圆2212x y +=相切,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件9.直三棱柱111ABC A B C -底面是等腰直角三角形,AB AC ⊥,1BC BB =,则直线1AB 与1BC 所成角的余弦值为( ) AB .23CD .1210.双曲线221x my -=的实轴长是虚轴长的14,则实数m = A .116B .14C .4D .16二、填空题11.函数222231x x y x x ++=+-的值域为________. 12.已知O 是椭圆E 的对称中心,1F ,2F 是E 的焦点,以O 为圆心,1OF 为半径的圆与E 的一个交点为A .若1AF 与2AF 的长度之比为2:1,则E 的离心率等于______.13.在平面直角坐标系中,已知向量(2,1)a =,O 是坐标原点,M 是曲线||2||2x y +=上的动点,则a OM --→⋅的取值范围为__________. 14.函数arcsin tan()4y x x π=+的值域是________三、解答题15.已知ABC ∆的内角,,A B C 的对边分别为,,a b c ,若21cos cos cos c a B b A C=+,4c =.(Ⅰ)求C ;(Ⅱ)当ABC ∆的面积取最大值时,求b 的值. 16.已知212ln ()xf x x+=. (1)求()f x 的最大值;(2)存在()12,1,x x ∈+∞且12x x ≠,使1212()()ln ln f x f x k x x -≥-成立,求k 的取值范围. 17.已知抛物线()2:20C y px p =>上两点()11,A x y 、()()2212,B x y x x ≠,焦点F 满足10AF BF +=,线段AB 的垂直平分线过()6,0Q .(1)求抛物线C 的方程;(2)过点F 作直线l ,使得抛物线C 上恰有三个点到直线l 的距离都为2,求直线l 的方程. 18.如图,四棱锥P ABCD -中,PD ⊥平面ABCD ,底面ABCD 是正方形,2PD AB ==,E 为PC 上一点,当F 为DC 的中点时,EF 平行于平面P AD .(Ⅰ)求证:DE ⊥平面PCB ; (Ⅱ)求二面角E BD P --的余弦值.19.首项为O 的无穷数列{}n a 同时满足下面两个条件: ①1n n a a n +-=;②12n n a -≤(1)请直接写出4a 的所有可能值;(2)记2n n b a =,若1n n b b +<对任意*n N ∈成立,求{}n b 的通项公式; (3)对于给定的正整数k ,求12...k a a a +++的最大值. 四、双空题20.袋中有2个红球,2个白球,2个黑球共6个球,现有一个游戏:从袋中任取3个球,恰好三种颜色各取到1个则获奖,否则不获奖.则获奖的概率是______,有3个人参与这个游戏,则恰好有1人获奖的概率是______.21.已知()()()()2*012111nn n x a a x a x a x n N =++++++∈…+对任意x ∈R 恒成立,则0a=__________;若450a a +=,则n =_________________.22.已知复数z :满足1)3i z i +=+((i 为虚数单位),则复数z 的实部为①________,z =②________.【答案与解析】1.A求出()'f x ,使()0f x '=在()0,x ∈+∞上有两个根,然后利用参变分离思想处理.因为函数2()2x f x e mx =-+,则()2xf x e mx '=-+, 若当0x >时,函数2()2xf x e mx =-+有两个极值点,则()20xf x e mx '=-+=在()0,x ∈+∞上有两根,即2xe m x=在()0,x ∈+∞上有两解,令()2=x e g x x ,则()()22122xx x x exe e g x x x--'==, 当1x >时,()0g x '>,则()g x 在()1,x ∈+∞上递增, 当01x <<时,()0g x '<,则()g x 在()0,1x ∈上递减,所以函数()2=xe g x x在1x =处取得最小值,即()12e g =,故2e m >.故选:A.本题考查利用函数的极值点个数求参数的取值范围问题,难度一般,解答时注意灵活转化,注意参变分离思想的运用. 2.A根据随机变量的期望,方差公式计算出()E ξ,()D ξ后根据函数的单调性可得. 由题意得11()01212222p p pE ξ-=⨯+⨯+⨯=-,所以当p 在(0,1)内增大时,()E ξ减少; 221()[0(1)][1(1)]2222p p p D ξ=--⨯+--⨯22132[2(1)]222p p p p --++--⨯=231()242p --=, 所以当p 在(0,1)内增大时,()D ξ减少. 故选A .本题考查了离散型随机变量的期望与方差的计算问题,也考查了运算求解能力,属中档题. 3.B由三视图可知该机械零件是一个长方体中间穿一个圆柱,结合题中所给的数据求解组合体的表面积即可.由三视图可知该机械零件是一个长方体中间穿一个圆柱,其中长方体的长宽高分别为为3,3,4,圆柱的底面半径为1r =,圆柱的高为5, 据此可得,组合体的表面积2(333434)212664S ππ=⨯⨯+⨯+⨯+⨯⨯=+. 本题选择A 选项.(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和. 4.C因为{}13M N ⋂=, ,所以选C. 5.C试题分析:因为y =cos(2x +32π)(x ∈[0,2π]),即sin 2xy =(x ∈[0,2π])的图像是半个周期的图像,所以它与直线y =12的交点有两个. 考点:三角函数的诱导公式及正弦函数的图像. 点评:本小题关键是利用诱导公式3cos()sin 2παα+=把y =cos(2x +32π)(x ∈[0,2π])转化为sin 2xy =(x ∈[0,2π])然后画出它的图像从图像上观察它与直线y =12的交点个数.6.B试题分析:约束条件对应的可行域为直线250,20,0x y x y x +-=--==围成的三角形及其内部;三顶点为()()50,,0,2,3,12⎛⎫- ⎪⎝⎭,当23z x y =+过点()3,1时取得最大值9考点:线性规划问题 7.B分两种情况,①其中有一个人与甲在同一个项目,有11232212C C A =种情况,②没有人与甲在同一个项目,则有12C C 32•A 22=12种情况;则若甲要求不去A 项目,则不同的分配方案有12+12=24种; 故选B .考点:本题主要考查排列、组合的应用,计数原理.点评:易错题,注意题意中“每个比赛项目至少分配一人”这一条件,再分配甲之后,需要对其余的三人分情况讨论. 8.A先求出直线1y kx =+与圆2212x y +=相切时k 的值,再由充分必要条件的定义判定,即可得出结论.设圆心(0,0)O 到直线1y kx =+距离为d , 由直线1y kx =+与圆2212x y +=相切,则2d ==,解得1k =±, ∴p 成立则q 成立,q 成立p 不一定成立,所以p 是q 的充分不必要条件. 故选:A .本题考查充分不必要条件的判定以及直线与圆的位置关系,属于基础题. 9.A建立空间直角坐标系,用空间向量法求异面直线所成的角. 因为直三棱柱111ABC A B C -底面是等腰直角三角形,AB AC ⊥, 故以AB 为x 轴,AC 为y 轴,1AA 为z 轴建立空间直角坐标系,如图, 设1AB =,则1BB =(1,0,0)B ,(0,1,0)C,1(1B,1(0,1C ,1(1AB =,1(1,1BC =-,111111cos ,63AB BC ABBC AB BC ⋅<>===. ∴直线1AB 与1BC . 故选:A .本题考查求异面直线所成的角,解题方法是建立空间直角坐标系,用空间向量法求解. 10.A本题可以先将双曲线转化为标准式方程,得出实轴长与虚轴长,最后根据题意解得结果.双曲线方程可化为2211y x m-=,则实轴长为2,虚轴长为由题意可得124=⨯116m =.故选A . 本题考查双曲线方程,双曲线的标准方程为22221x y a b -=或22221y x b a-=.11.(,2](2,)-∞-⋃+∞首先分离常数,再求出21x x +-的范围,得出211x x +-的范围,即可逐步求出函数的值域.2222235211x x y x x x x ++==++-+-, 因为221551244x x x ⎛⎫+-=+-- ⎪⎝⎭,所以21415x x ≤-+-或2101x x >+-, 则25221x x +≤-+-或25221x x +>+-,即(,2](2,)y ∈-∞-⋃+∞. 故答案为:(,2](2,)-∞-⋃+∞本题考查具体函数的值域问题,属于中档题. 12.1e =因为2 AOF 为正三角形,故可根据椭圆的定义可得,a c 的关系,从而得到离心率.我们也可以根据已知条件得到12A c ⎛⎫ ⎪ ⎪⎝⎭,把A 代入椭圆整理,得42840e e -+=,由此能够求出椭圆的离心率.解法1:如图,设122F F c =,1OF c =,因为1AF 与2AF 的长度之比为2:1,故1120AOF ∠=,260AOF ∠=, 所以2AOF △为正三角形,故2AF c =.在等腰1AOF △中,求得1AF =.根据椭圆的定义,可得)1221a AF AF c =+=,故椭圆的离心率212c c e a a ====. 解法2:如图,设椭圆的方程为22221(0)x y a b a b+=>>,122F F c =.由题意,易知1120AOF ∠=,260AOF ∠=,所以2AOF △为正三角形,故12A c ⎛⎫⎪ ⎪⎝⎭,因为点A 在椭圆上,所以22223144c c a b+=,即()222223144c c a a c +=-,即()22231441e e e +=-, 整理,得()22221344e eee -+=-,即42840e e -+=,解得24e =+24e =-,所以1e =.本题考查椭圆的本题考查了椭圆的定义,性质和应用,解题时要认真审题,注意公式的灵活运用. 13.[]4,4-先作出曲线||2||2x y +=对应的图像,再结合简单的线性规划问题,观察图像即可得解. 解:曲线||2||2x y +=对应的图像为如图所示的菱形ABCD ,设00()M x y ,则()00,OM x y =,因为M 是曲线||2||2x y +=上的动点, 则00||2||2x y +=,又向量(2,1)a =,则002z a OM x y --→=⋅+=,由图可知:目标函数2z x y =+过点(2,0)A -时,函数取最小值2(2)104⨯-+⨯=-, 过点(2,0)C 时,函数取最大值22104⨯+⨯=, 即a OM --→⋅的取值范围为[]4,4-,故答案为:[]4,4-.本题考查了简单的线性规划问题,重点考查了数形结合的数学思想方法,属中档题. 14.[1,1]22ππ--+利用函数的单调性,结合函数的定义域求解即可. 因为函数arcsin tan()4y x x π=+的定义域是[1-,1],函数是增函数,所以函数的最小值为:12π--,最大值为:12π+.所以函数的值域为:[12π--,1]2π+.故答案为[12π--,1]2π+.本题考查函数的单调性以及函数的值域的求法,考查计算能力. 15.(1)3C π=;(2)4b =.分析:(Ⅰ)由正弦定理统一角,可求得cosC .(Ⅱ)由角C 的面积公式与角C 的余弦定理和均值不等式,求得了面积的最大值,同时均值不等式等号成立条件可求得b 边.详解:(Ⅰ)因为()cos cos 2cos a B b A c C +=, 由正弦定理可得()sin cos sin cos 2sin cos A B B A C C +=, 即()sin 2sin cos A B C C +=,sin 2sin cos C C C = 又sin 0C ≠,即可得1cos 2C =,故3C π= (Ⅱ)依题意,ABC ∆的面积1sin 24S ab C ab ==,故只需ab 最大即可; 由余弦定理2222cos c a b ab C =+-,即2216a b ab =+-, 结合基本不等式可得16ab ≤,当且仅当4a b ==时取等号, 所以当ABC ∆的面积取最大值时,4b =.点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向. 第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化 第三步:求结果,判定是否符合条件,或有多解情况. 16.(1)1;(2)2,e ⎛⎫-∞ ⎪⎝⎭. (1)对函数求导,求函数的单调性,利用单调性即可求得最大值.(2)不妨设121x x >>,由(1)知当x ∈(1,+∞)时,y =f (x )单调递减,由题意可得2121()ln ()ln f x k x f x k x +≥+成立,构造函数()()ln h x f x k x =+,得h (x )在(1,+∞)上存在减区间,则()234ln kx xh x x -'=<0有解,即k <24ln x x 有解,则k <2max4ln x x ⎛⎫ ⎪⎝⎭,令t (x )=24ln x x ,求出y =t (x )的最大值即可. (1)()34ln x f x x '=-,令()34ln 0x f x x'=-=,得x =1, 当x ∈(0,1)时,()0f x '>,函数单调递增; 当x ∈(1,+∞)时,()0f x '<,函数单调递减, 所以当x =1时函数取到最大值为f (1)=1.(2)不妨设121x x >>,由(1)知当x ∈(1,+∞)时,y =f (x )单调递减.1212()()ln ln f x f x k x x -≥-即()1122()()ln ln f x f x k x x -≥-,即2121()ln ()ln f x k x f x k x +≥+,存在()12,1,x x ∈+∞且12x x ≠,使2121()ln ()ln f x k x f x k x +≥+成立.令()()ln h x f x k x =+,h (x )在(1,+∞)上存在减区间,则()234ln kx xh x x -'=<0有解, 即k <24ln x x 有解,则k <2max 4ln x x ⎛⎫ ⎪⎝⎭,令t (x )=24ln x x ,t ′(x )=()3412ln x x-. 当x ∈(0时,()0t x '>,y =t (x )单调递增; 当x ∈,+∞)时,()0t x '<,y =t (x )单调递减.所以当x =2e=. 所以k 的取值范围是2,e ⎛⎫-∞ ⎪⎝⎭. 本题考查利用导数研究函数的最值,考查构造函数的思想,利用导数研究函数的单调性,考查分析能力和计算能力,属于中档题.17.(1)24y x =;(2)1x =+.(1)由10AF BF +=,结合抛物线的定义得出1210x x p ++=,再由中垂线的性质得出QA QB =,利用两点间的距离公式得出12122x x p +=-,可求出实数p 的值,由此可得出抛物线C 的方程;(2)设直线l 的方程为1x my =+,将直线l 平移且使得平移后的直线与直线l 之间的距离等于2,可得出直线1:1l x my =++,2:1l x my =+-,可知直线1l 或2l 与抛物线C 相切,并与抛物线C 的方程联立,利用0∆=求出实数m 的值,即可得出直线l 的方程. (1)由抛物线的定义可得1210AF BF x x p +=++=,① 由于线段AB 的垂直平分线过()6,0Q ,则QA QB =,=221112221236212362x x px x x px -++=-++,()()()1212121220x x x x p x x ∴+--+-=,()()12121220x x x x p -+-+=,12x x ≠,12122x x p ∴+=-,②由①②得2p =,因此,抛物线C 的方程为24y x =;(2)设直线l 的方程为1x my =+,将直线l 平移且使得平移后的直线与直线l 之间的距离等于2,设平移后的直线方程为x my t =+2=,得1t =±,得直线1:1l x my =++,2:1l x my =+-, 可知直线1l 或2l 与抛物线C 相切,若直线1l 与抛物线C相切,则214x my y x⎧⎪=++⎨=⎪⎩2440y my ---=,2116160m ∆=++=,此方程无解;若直线2l 与抛物线C相切,则214x my y x⎧⎪=+-⎨=⎪⎩,得2440y my --+=,2216160m ∆=+-=,得23m =,解得m =因此,直线l的方程为10x -=或10x +-=.本题考查抛物线方程的求解,以及抛物线上的点到直线的距离问题,可以利用平移直线法转化为直线与抛物线相切,考查化归与转化思想,属于中等题. 18.(Ⅰ)证明见解析;(Ⅰ)PD ⊥平面ABCD 可得PD BC ⊥,从而证出BC ⊥平面PCD ,则BC DE ⊥, 从而可证出DE ⊥平面PCB ;(Ⅱ)以点D 为坐标原点,分别以直线DA ,DC ,DP 为x 轴,y 轴,z 轴,建立空间直角坐标系,求得各点的坐标,求出平面BDE 和平面PDB 的的一个法向量,再根据法向量求出二面角. (Ⅰ)证:PD ⊥平面ABCD ,PD BC ∴⊥,又∴正方形ABCD 中,CD BC ⊥,PD CD D ⋂=,BC ∴⊥平面PCD , 又DE ⊂平面PCD ,BC DE ∴⊥,PD CD =,当F 为DC 的中点时,EF 平行平面PAD ,所以E 是PC 的中点, DE PC ⊥,PC BC C ⋂=,DE ∴⊥平面PCB ;(Ⅱ)解:以点D 为坐标原点,分别以直线DA ,DC ,DP 为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则(0,0,0)D ,(0,0,2)P ,(2,2,0)B ,(0,1,1)E ,(2,2,0)DB =,(0,1,1)DE =, 设平面BDE 的法向量为(,,)n x y z =,则0n DB ⋅=,0n DE ⋅=,2200x y y z +=⎧∴⎨+=⎩,令1z =,得到1y =-,1x =,(1,1,1)n ∴=-;又(0,2,0)C ,(2,0,0)A ,(2,2,0)=-AC ,且AC ⊥平面PDB ,∴平面PDB 的一个法向量为(1,1,0)m =-;设二面角E BD P --的平面角为α,由图可知角α为锐角,则1cos |cos ,|m n α+=<>==,∴二面角E BD P --. 本题主要考查线面垂直的判定和性质,考查二面角的求法,属于中档题.19.(1)2,0,6--;(2)2n b n =-;(3)当k 为奇数时,k S 的最大值为0; 当k 为偶数时,k S 的最大值为2k-. (1)由递推关系得到4a 的所有可能值;(2)由题意可知数列{}n a 的偶数项2462,,,...,...n a a a a 是单调递增数列,先证明数列{}n a 中相邻两项不可能同时为非负数,即可得到结果;(3) 由(2)的证明知,1,n n a a +不能都为非负数,分类讨论即可得到结果.(1)4a 的值可以取2,0,6-- .(2)因为2n n b a =,因为1n n b b +<对任意*n N ∈成立,所以{}n b 为单调递增数列, 即数列{}n a 的偶数项2462,,,...,...n a a a a 是单调递增数列, 根据条件21a =-,40a =, 所以当20n a ≥对2n ≥成立 ,下面我们证明“数列{}n a 中相邻两项不可能同时为非负数”, 假设数列{}n a 中存在1,i i a a +同时为非负数, 因为1||i i a a i +-=,若1,i i a a i +-= 则有()i 1112i i a a i i ++-=+≥>,与条件矛盾,若i 1,i a a i +-=-则有112i i i a a i i +-=+≥>, 与条件矛盾 , 所以假设错误,即数列{}n a 中相邻两项不可能同时为非负数, 此时20n a ≥对2n ≥成立,所以当2n ≥时,21210,0n n a a -+≤≤,即212212,n n n n a a a a -+<<, 所以 22121n n a a n --=-,()212222n n a a n ---=--,所以()()22121221n n n n a a a a ----+-=, 即2221n n a a --=,其中2n ≥ , 即11n n b b --=,其中2n ≥, 又121b a ==-,240b a ==,所以{}n b 是以11b =-,公差为1的等差数列, 所以()112n b n n =-+-=- . (3) 记1231k k k S a a a a a -=+++++,由(2)的证明知,1,n n a a +不能都为非负数, 当0n a ≥,则1a 0n +<,根据1||n n a a n +-=,得到1n n a a n +=-,所以112212n n n n a a a n n +-+=-≤-≤-, 当10n a +≥,则a 0n <,根据1||n n a a n +-=,得到+1n n a a n =-,所以11112202n n n n a a a n n +++-+=-≤-≤, 所以,总有10n n a a ++≤成立 ,当n 为奇数时,1||n n a a n +-=,故1,n n a a -的奇偶性不同,则1n n a a ++ 1≤-, 当n 为偶数时,10n n a a ++≤ , 当k 为奇数时,()()12310k k k S a a a a a -=+++++≤,考虑数列:01,1,2,2,--,, 12k --,12k -⋯, 可以验证,所给的数列满足条件,且0k S =, 所以k S 的最大值为0,当k 为偶数时,()()1212k k k k S a a a a -=++++≤-,考虑数列:01,1,2,2--,,,-22k -,22k -,2k- ,可以验证,所给的数列满足条件,且2k kS =-,所以k S 的最大值为2k-.本题考查数列的性质和应用,解题时要注意归纳总结能力的培养,考查了转化能力和运算能力,属于难题. 20.25 54125根据计数原理,所有的取球方法共有36C 种,而三种球各有一个共包含()312C 个,故获奖的概率可求.有3个人参与这个游戏,设中奖人数为X ,则2~3,5X B ⎛⎫ ⎪⎝⎭,故恰好有1人获奖的概率可求.设中奖为事件A ,则事件A 包含的基本事件个数为()3128C =,所有的基本事件共有3620C =个,所以中奖概率为82()205P A ==;有3个人参与这个游戏,设中奖人数为X ,则2~3,5X B ⎛⎫ ⎪⎝⎭,2132254(1)155125P X C ⎛⎫==⨯⨯-=⎪⎝⎭; 故答案为:254;5125. 本题主要考查古典概率和二项分布,明确题目的求解模型是解题关键,侧重考查数学建模的核心素养.21.()1n- 9利用1t x =+将问题转化为二项式的问题,然后利用二项式的通项分别表示出即可求解.令1t x =+,则()20121nn n t a a t a t a t -=+++…+,则()01na =-,()4441n n n a C --=-,()5551n n n a C --=-,∵450a a +=,故45n n n n C C --=,即45n n C C =,解得9n =.本题考查二项式定理,二项展开式的项和系数的关系是易错点.22.2根据复数z 满足1)3i z i +=+(,利用复数的乘除化简为2z i =-,再利用复数的概念和模的公式求解.因为复数z 满足1)3i z i +=+(, 所以()()31)32111)i i i z i i i i +-+===-++-((,所以()()31)3111)i i i z i i i +-+====++-((故答案为:①2本题主要考查复数的运算和复数的概念,还考查了运算求解的能力,属于基础题.。

2020届浙江省衢州二中高三下学期第一次模拟考试数学试题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、单选题1.设{1,0,1,2}U =-,集合2{|1,}A x x x U =<∈,则U C A =( ) A .{0,1,2}B .{1,1,2}-C .{1,0,2}-D .{1,0,1}-2.一场考试需要2小时,在这场考试中钟表的时针转过的弧度数为( ) A .3π B .3π-C .23π D .23π-3.已知复数z 满足202020191z i i ⋅=+(其中i 为虚数单位),则复数z 的虚部是( ) A .1-B .1C .i -D .i4.已知直线1:240l ax y ++=,2:(1)20l x a y +-+=,则“1a =-”是“12l l ”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.某几何体的三视图如图所示,则该几何体的体积为( )A .83B .3C .113D .46.函数()f x 的图象如图所示,则它的解析式可能是( )A .()212xx f x -= B .()()21xf x x =-C .()ln f x x =D .()1xf x xe =-7.已知数列{}n a 的前n 项和为n S ,11a =,22a =且对于任意1n >,*n N ∈满足()1121n n n S S S +-+=+,则( )A .47a =B .16240S =C .1019a =D .20381S =8.已知12,F F 是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,若点2F 关于双曲线渐近线的对称点A 满足11F AO AOF ∠=∠(O 为坐标原点),则双曲线的渐近线方程为( )A .2y x =±B .y =C .y =D .y x =±9.已知平面向量,,a b c ,满足||2,||1,b a b c a b λμ=+==+且21λμ+=,若对每一个确定的向量a ,记||c 的最小值为m ,则当a 变化时,m 的最大值为( ) A .14B .13C .12D .110.已知函数()2121f x ax x ax =+++-(a R ∈)的最小值为0,则a =( ) A .12B .1-C .±1D .12±第II 卷(非选择题)请点击修改第II 卷的文字说明二、双空题11.若23log 3,log 2a b ==,则ab =______,lg lg a b +=______.12.《九章算术》是中国古代的数学名著,其中《方田》一章给出了弧田面积的计算公式.如图所示,弧田是由圆弧AB 和其所对弦AB 围成的图形,若弧田的弧AB 长为4π,弧所在的圆的半径为6,则弧田的弦AB 长是__________,弧田的面积是__________.13.已知实数x 、y 满足121y y x x y m ≥⎧⎪≤-⎨⎪+≤⎩,且可行域表示的区域为三角形,则实数m 的取值范围为______,若目标函数z x y =-的最小值为-1,则实数m 等于______. 14.有2名老师和3名同学,将他们随机地排成一行,用ξ表示两名老师之间的学生人数,则1ξ=对应的排法有______种;()E ξ= ______;三、填空题15.已知函数()2,4,x x mf x x x x m<⎧=⎨+≥⎩,且p m ∀<,q m ∃>,使得()()0f p f q +=,则实数m 的取值范围是______.16.已知实数a ,b ,c 满足22221a b c ++=,则ab c +的最小值是______.17.若四棱锥P ABCD -的侧面PAB 内有一动点Q ,已知Q 到底面ABCD 的距离与Q 到点P 的距离之比为正常数k ,且动点Q 的轨迹是抛物线,则当二面角P AB C 平面角的大小为30时,k 的值为______.四、解答题18.在ABC ∆中,内角,,A B C 的对边分别是,,a b c ,已知222,3A b c a π=+=.(1)求a 的值;(2)若1b =,求ABC ∆的面积.19.已知等腰梯形ABCD 中(如图1),4AB =,2BC CD DA ===,F 为线段CD 的中点,E 、M 为线段AB 上的点,1AE EM ==,现将四边形AEFD 沿EF 折起(如图2)(1)求证://AM 平面BCD ;(2)在图2中,若BD =,求直线CD 与平面BCFE 所成角的正弦值. 20.已知数列{}n a 的前n 项和为n S ,()*21n n S a n N +=∈.(1)求数列{}n a 的通项公式; (2)若11111n n n c a a +=++-,n T 为数列{}n c 的前n 项和.求证:123n T n >-. 21.已知椭圆E :22221x y a b +=(0a b >>)的离心率为2e =,且短轴的一个端点B与两焦点A ,C(Ⅰ)求椭圆E 的方程;(Ⅱ)若点P 为椭圆E 上的一点,过点P 作椭圆E 的切线交圆O :222x y a +=于不同的两点M ,N (其中M 在N 的右侧),求四边形ACMN 面积的最大值. 22.已知函数()ln ()f x ax x a R =+∈有两个零点12,x x . (1)求a 的取值范围;(2)是否存在实数λ, 对于符合题意的任意12,x x ,当012(1)0x x x λλ=+-> 时均有()'0f x <?若存在,求出所有λ的值;若不存在,请说明理由.参考答案1.B 【解析】 【分析】先化简集合A,再求U C A . 【详解】由21x < 得: 11x -<< ,所以{}0A = ,因此{}1,1,2UA =- ,故答案为B【点睛】本题主要考查集合的化简和运算,意在考查学生对这些知识的掌握水平和计算推理能力. 2.B 【解析】 【分析】因为时针经过2小时相当于转了一圈的16,且按顺时针转所形成的角为负角,综合以上即可得到本题答案. 【详解】因为时针旋转一周为12小时,转过的角度为2π,按顺时针转所形成的角为负角,所以经过2小时,时针所转过的弧度数为11263ππ-⨯=-. 故选:B 【点睛】本题主要考查正负角的定义以及弧度制,属于基础题. 3.A 【解析】 【分析】由虚数单位i 的运算性质可得1z i =-,则答案可求. 【详解】 解:∵41i =,∴202045051i i ⨯==,201945043i i i ⨯+==-, 则202020191z i i ⋅=+化为1z i =-,∴z 的虚部为1-. 故选:A. 【点睛】本题考查了虚数单位i 的运算性质、复数的概念,属于基础题. 4.C 【解析】 【分析】先得出两直线平行的充要条件,根据小范围可推导出大范围,可得到答案. 【详解】直线1:240l ax y ++=,()2:120l x a y +-+=,12l l 的充要条件是()1221a a a a -=⇒==-或,当a=2时,化简后发现两直线是重合的,故舍去,最终a=-1.因此得到“1a =-”是“12l l ”的充分必要条件. 故答案为C. 【点睛】判断充要条件的方法是:①若p ⇒q 为真命题且q ⇒p 为假命题,则命题p 是命题q 的充分不必要条件;②若p ⇒q 为假命题且q ⇒p 为真命题,则命题p 是命题q 的必要不充分条件;③若p ⇒q 为真命题且q ⇒p 为真命题,则命题p 是命题q 的充要条件;④若p ⇒q 为假命题且q ⇒p 为假命题,则命题p 是命题q 的即不充分也不必要条件.⑤判断命题p 与命题q 所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p 与命题q 的关系. 5.C 【解析】 【分析】首先把三视图转换为几何体,该几何体为由一个三棱柱体,切去一个三棱锥体,由柱体、椎体的体积公式进一步求出几何体的体积. 【详解】解:根据几何体的三视图转换为几何体为: 该几何体为由一个三棱柱体,切去一个三棱锥体, 如图所示:故:111112*********V =⨯⨯⨯-⨯⨯⨯⨯=. 故选:C. 【点睛】本题考查了由三视图求几何体的体积、需熟记柱体、椎体的体积公式,考查了空间想象能力,属于基础题. 6.B 【解析】 【分析】根据定义域排除C ,求出()1f 的值,可以排除D ,考虑()100f -排除A . 【详解】根据函数图象得定义域为R ,所以C 不合题意;D 选项,计算()11f e =-,不符合函数图象;对于A 选项, ()10010099992f -=⨯与函数图象不一致;B 选项符合函数图象特征.故选:B 【点睛】此题考查根据函数图象选择合适的解析式,主要利用函数性质分析,常见方法为排除法. 7.D 【解析】 【分析】利用数列的递推关系式判断求解数列的通项公式,然后求解数列的和,判断选项的正误即可. 【详解】当2n 时,111112(1)22n n n n n n n n n S S S S S S S a a +-+-++=+⇒-=-+⇒=+. 所以数列{}n a 从第2项起为等差数列,1,122,2n n a n n =⎧=⎨-⎩,所以,46a =,1018a =. 21()(1)(1)12n n a a n S a n n +-=+=-+,1616151241S =⨯+=,2020191381S =⨯+=.故选:D . 【点睛】本题考查数列的递推关系式的应用、数列求和以及数列的通项公式的求法,考查转化思想以及计算能力,是中档题. 8.B 【解析】 【分析】先利用对称得2AF OM ⊥,根据11F AO AOF ∠=∠可得1AF c =,由几何性质可得160AFO ∠=,即260MOF ∠=,从而解得渐近线方程. 【详解】 如图所示:由对称性可得:M 为2AF 的中点,且2AF OM ⊥, 所以12F A AF ⊥,因为11F AO AOF ∠=∠,所以11AF F O c ==,故而由几何性质可得160AFO ∠=,即260MOF ∠=,故渐近线方程为y =, 故选B. 【点睛】本题考查了点关于直线对称点的知识,考查了双曲线渐近线方程,由题意得出260MOF ∠=是解题的关键,属于中档题. 9.B 【解析】 【分析】根据题意,建立平面直角坐标系.令,OP a OB b ==OC c =.E 为OB 中点.由1a b +=即可求得P 点的轨迹方程.将c a b λμ=+变形,结合21λμ+=及平面向量基本定理可知,,P C E 三点共线.由圆切线的性质可知||c 的最小值m 即为O 到直线PE 的距离最小值,且当PE 与圆M 相切时,m 有最大值.利用圆的切线性质及点到直线距离公式即可求得直线方程,进而求得原点到直线的距离,即为m 的最大值. 【详解】根据题意,||2,b =设()(),,2,0OP a x y OB b ====,(),1,0OC c E =则2bOE =由1a b +=1=即P 点的轨迹方程为2221x y又因为c a b λμ=+,变形可得22b c a λμ⎛⎫=+ ⎪⎝⎭,即2OC OP OE λμ=+,且21λμ+=所以由平面向量基本定理可知,,P C E 三点共线,如下图所示:所以||c 的最小值m 即为O 到直线PE 的距离最小值 根据圆的切线性质可知,当PE 与圆M 相切时,m 有最大值 设切线PE 的方程为()1y k x =-,化简可得kx y k 0--=由切线性质及点M1=,化简可得281k =即4k =±所以切线方程为044x y --=或044x y +-= 所以当a 变化时, O 到直线PE 的最大值为13m ==即m 的最大值为13故选:B 【点睛】本题考查了平面向量的坐标应用,平面向量基本定理的应用, 圆的轨迹方程问题,圆的切线性质及点到直线距离公式的应用,综合性强,属于难题.10.C 【解析】 【分析】设()()()()2121g x h x ax g x h x x ax ⎧+=+⎪⎨-=+-⎪⎩,计算可得()()()()()()()2,2,g x g x h x f x h x g x h x ⎧≥⎪=⎨<⎪⎩,再结合图像即可求出答案. 【详解】设()()()()2121g x h x ax g x h x x ax ⎧+=+⎪⎨-=+-⎪⎩,则()()221g x x axh x x ⎧=+⎪⎨=-⎪⎩, 则()()()()()()()()()()()2,2,g x g x h x f x g x h x g x h x h x g x h x ⎧≥⎪=++-=⎨<⎪⎩,由于函数()f x 的最小值为0,作出函数()(),g x h x 的大致图像,结合图像,210x -=,得1x =±, 所以1a =±. 故选:C 【点睛】本题主要考查了分段函数的图像与性质,考查转化思想,考查数形结合思想,属于中档题. 11.1 0 【解析】 【分析】①根据换底公式计算即可得解;②根据同底对数加法法则,结合①的结果即可求解. 【详解】①由题:23log 3,log 2a b ==,则22322log 2log 3log 2log 31log 3ab =⋅=⋅=;②由①可得:lg lg lg lg10a b ab +===. 故答案为:①1,②0 【点睛】此题考查对数的基本运算,涉及换底公式和同底对数加法运算,属于基础题目. 12.12π﹣【解析】 【分析】过O 作OC AB ⊥,交AB 于D ,先求得圆心角AOB ∠的弧度数,然后解解三角形求得AB 的长.利用扇形面积减去三角形OAB 的面积,求得弧田的面积. 【详解】∵如图,弧田的弧AB 长为4π,弧所在的圆的半径为6,过O 作OC AB ⊥,交AB 于D ,根据圆的几何性质可知,OC 垂直平分AB . ∴α=∠AOB =46π=23π,可得∠AOD =3π,OA =6,∴AB =2AD =2OA sin3π=2×6=∴弧田的面积S =S 扇形OAB ﹣S △OAB =12⨯4π×6﹣132⨯=12π﹣. 故答案为:12π﹣【点睛】本小题主要考查弓形弦长和弓形面积的计算,考查中国古代数学文化,属于中档题. 13.2m > 5m =【解析】 【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,结合目标函数z x y =-的最小值,利用数形结合即可得到结论. 【详解】作出可行域如图,则要为三角形需满足()1,1B 在直线x y m +=下方,即11m +<,2m >; 目标函数可视为y x z =-,则z 为斜率为1的直线纵截距的相反数, 该直线截距最大在过点A 时,此时min 1z =-,直线PA :1y x =+,与AB :21y x =-的交点为()2,3A , 该点也在直线AC :x y m +=上,故235m =+=, 故答案为:2m >;5m =. 【点睛】本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法,属于基础题. 14.36 ;1. 【解析】 【分析】ξ的可能取值为0,1,2,3,1ξ=对应的排法有:123323C A A 36=.分别求出()0P ξ=,()1P ξ=,()2P ξ=,()3P ξ=,由此能求出()E ξ.【详解】解:有2名老师和3名同学,将他们随机地排成一行,用ξ表示两名老师之间的学生人数,则ξ的可能取值为0,1,2,3,1ξ=对应的排法有:123323C A A 36=.∴1ξ=对应的排法有36种;()242455A A 480A 120P ξ===,()12332355C A A 361A 120P ξ===, ()22232255A A A 242A 120P ξ===,()223255A A 123A 120P ξ===, ∴()4836241201231120120120120E ξ=⨯+⨯+⨯+⨯= 故答案为:36;1. 【点睛】本题考查了排列、组合的应用,离散型随机变量的分布列以及数学期望,属于中档题. 15.(],0-∞ 【解析】 【分析】根据条件转化为函数()y f x =-在(),m -∞上的值域是函数()y f x =在[),m +∞上的值域的子集;分别求值域即可得到结论. 【详解】解:依题意,()()f q f p =-,即函数()y f x =-在(),m -∞上的值域是函数()y f x =在[),m +∞上的值域的子集. 因为()y f x =在[),m +∞上的值域为[)4,-+∞(2m ≤-)或24,m m ⎡⎤++∞⎣⎦(2m >-), ()y f x =-在(),m -∞上的值域为(),m -+∞,故24m m ≤-⎧⎨-≥-⎩或224m m m m >-⎧⎨-≥+⎩, 解得0m ≤ 故答案为:(],0-∞. 【点睛】本题考查了分段函数的值域求参数的取值范围,属于中档题. 16.916-【解析】 【分析】先分离出22a b +,应用基本不等式转化为关于c 的二次函数,进而求出最小值. 【详解】解:若ab c +取最小值,则ab 异号,0c <, 根据题意得:22212c a b -=+,又由2222a b ab ab +≥=-,即有2122c ab -≥-,则221192416ab c c c c ⎛⎫+≥+-=+- ⎪⎝⎭,即2ab c +的最小值为916-, 故答案为:916- 【点睛】本题考查了基本不等式以及二次函数配方求最值,属于中档题. 17.12【解析】 【分析】 二面角PAB C 平面角为θ,点Q 到底面ABCD 的距离为QH ,点Q 到定直线AB 得距离为d ,则sin QHd θ=.再由点Q 到底面ABCD 的距离与到点P 的距离之比为正常数k ,可得QH PQ k =,由此可得sin k θ=,则由cos cos30θ=︒=可求k 值. 【详解】解:如图, 设二面角PAB C 平面角为θ,点Q 到底面ABCD 的距离为QH ,点Q 到定直线AB 的距离为d ,则sin QH d θ=,即sin QHd θ=. ∵点Q 到底面ABCD 的距离与到点P 的距离之比为正常数k , ∴QH k PQ=,则QHPQ k=, ∵动点Q 的轨迹是抛物线, ∴PQ d =,即sin QH QHk θ=则sin k θ=.∴二面角PAB C 的平面角的余弦值为cos cos30θ===︒=解得:12k =(0k >).故答案为:12. 【点睛】本题考查了四棱锥的结构特征,由四棱锥的侧面与底面的夹角求参数值,属于中档题.18.(1(2【解析】 【分析】(1)由222b c a +-=,利用余弦定理可得2cos bc A =,结合3A π=可得结果;(2)由正弦定理1sin 2B =,π6B =, 利用三角形内角和定理可得π2C =,由三角形面积公式可得结果. 【详解】(1)由题意,得2223b c a abc +-=. ∵2222cos b c a bc A +-=.∴2cos 3bc A abc =, ∵π3A =,∴a A ==.(2)∵a =由正弦定理sin sin a b A B =,可得1sin 2B =. ∵a>b ,∴π6B =,∴ππ2C A B =--=.∴1sin 22ABC S ab C ∆==. 【点睛】本题主要考查正弦定理、余弦定理及特殊角的三角函数,属于中档题.对余弦定理一定要熟记两种形式:(1)2222cos a b c bc A =+-;(2)222cos 2b c a A bc+-=,同时还要熟练掌握运用两种形式的条件.另外,在解与三角形、三角函数有关的问题时,还需要记住30,45,60o o o 等特殊角的三角函数值,以便在解题中直接应用.19.(1)见解析;(2【解析】【分析】(1)先连接CM ,根据线面平行的判定定理,即可证明结论成立;(2)在图2中,过点D 作DO EF ⊥,垂足为O ,连接OB ,OC ,证明平面BCFE ⊥平面BOD ,得到点D 在底面BCFE 上的投影必落在直线OB 上,记H 为点D 在底面BCFE 上的投影,连接DH ,HC ,得出DCH ∠即是直线CD 与平面BCFE 所成角,再由题中数据求解,即可得出结果. 【详解】(1)连接CM ,因为等腰梯形ABCD 中(如图1),2AM AE EM CD =+==,//AB CD , 所以AM 与CD 平行且相等,即四边形AMCD 为平行四边形;所以//AD CM ; 又F 为线段CD 的中点,E 为AM 中点,易得:四边形AEFD 也为平行四边形,所以//AD EF ;将四边形AEFD 沿EF 折起后,平行关系没有变化,仍有://AD CM ,且AD CM =, 所以翻折后四边形AMCD 也为平行四边形;故//AM CD ; 因为AM ⊄平面BCD ,CD ⊂平面BCD , 所以//AM 平面BCD ;(2)在图2中,过点D 作DO EF ⊥,垂足为O ,连接OB ,OC ,因为2AD =,1AE =,翻折前梯形ABCD 的高为FM DE == 所以60DAE DFE ∠=∠=,则3sin 602DO DF =⋅=,1cos602OF DF =⋅=;所以32OE EF OF =-=; 又3BE EM MB =+=,60FEM DFE ∠=∠=,所以3602BO ==,即222BO OE BE +=,所以BO OE ⊥; 又DO BO O ⋂=,且DO ⊂平面BOD ,BO ⊂平面BOD , 所以EO ⊥平面BOD ;因此,平面BCFE ⊥平面BOD ; 所以点D 在底面BCFE 上的投影必落在直线OB 上; 记H 为点D 在底面BCFE 上的投影,连接DH ,HC , 则DH ⊥平面BCFE ;所以DCH ∠即是直线CD 与平面BCFE 所成角,因为BD =2221cos 23OB OD BD BOD OB OD +-∠==⋅,因此sin DH DO DOB =⋅∠=,1cos 3OH DO DOB =⋅∠=故BH BO OH =-=; 因为120OFC EFC FCB ∠=∠=∠=,所以3601201209030HBC OBC ∠=∠=---=,因此3CH =,故CD ==所以sin DH DCH CD ∠==. 即直线CD 与平面BCFE【点睛】本题主要考查证明线面平行,以及求直线与平面所成的角,熟记线面平行的判定定理,以及线面角的求法即可,属于常考题型.20.(1)13nn a ⎛⎫= ⎪⎝⎭(2)证明见解析 【解析】 【分析】(1)利用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩求得数列{}n a 的通项公式.(2)先将n c 缩小即111233n n n c +⎛⎫>-- ⎪⎝⎭,由此结合裂项求和法、放缩法,证得不等式成立. 【详解】(1)∵()*21n n S a n N+=∈,令1n =,得113a=. 又()11212n n S a n --+=≥,两式相减,得113n n a a -=. ∴13nn a ⎛⎫= ⎪⎝⎭. (2)∵111111133n nn c +=+⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭1113311231313131n n n n n n +++=+=-++-+- 11123131n n +⎛⎫=-- ⎪+-⎝⎭.又∵11313n n <+,1111313n n ++>-,∴111233n n n c +⎛⎫>-- ⎪⎝⎭. ∴22311111112333333n n n T n +⎡⎤⎛⎫⎛⎫⎛⎫>--+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦111122333n n n +=+->-. ∴123n T n >-. 【点睛】本小题主要考查已知n S 求n a ,考查利用放缩法证明不等式,考查化归与转化的数学思想方法,属于中档题.21.(Ⅰ)2214x y +=;(Ⅱ)4. 【解析】 【分析】(Ⅰ)结合已知可得2c a =,bc =a ,b 的值,即可得椭圆方程; (Ⅱ)由题意可知,直线的斜率存在,设出直线方程,联立直线方程与椭圆方程,利用判别式等于0可得2241m k =+,联立直线方程与圆的方程,结合根与系数的关系求得MCO ANO S S ∆∆+,利用弦长公式及点到直线的距离公式,求出MON S ∆,得到ACMN MON MCO ANO S S S S ∆∆∆=++,整理后利用基本不等式求最值.【详解】解:(Ⅰ)可得c a =bc =222a b c =+, 解得2a =,c =,1b =,得椭圆方程2214x y +=; (Ⅱ)易知直线MN 的斜率k 存在,设MN :y kx m =+,由2244y kx m x y =+⎧⎨+=⎩,得()()222418410k x kmx m +++-=, 由()()222264164110k m k m ∆=-+-=,得2241m k =+,∵ACMN MON MCO ANO S S S S ∆∆∆=++,设点O 到直线MN :0kx y m -+=的距离为d ,d =MN ==12MON S ∆=⨯==,由224y kx m x y =+⎧⎨+=⎩,得()2221240k x kmx m +++-=, 12221km x x k -+=+,212241m x x k -⋅=+, ∴()1212122y y kx m kx m k x x m +=+++=++2222211km m k m k k ⎛⎫=-+=⎪++⎝⎭∴)12121|)2MCO NAO S S y y y y ∆∆+=+=+=∴()ACMN MON NAO MCO S S S S ∆∆∆==++而2241m k =+,2214m k -=,易知20k ≥,∴21m ≥,则1m ≥, 四边形ACMN的面积414S m m ===≤=++ 当且仅当3m m=,即m =“=”. ∴四边形ACMN 面积的最大值为4.【点睛】本题考查了由,,a b c 求椭圆的标准方程,直线与椭圆的位置关系,考查了学生的计算能力,综合性比较强,属于难题.22.(1)1(,0)e -;(2)12λ=. 【解析】【分析】(1)对()f x 求导,对参数进行分类讨论,根据函数单调性即可求得. (2)先根据()0'0f x <,得01x a>-,再根据零点解得2121ln ln x x a x x -=--,转化不等式得()2112211ln ln x x x x x x λλ-+->-,令21x t x =,化简得()11ln t t t λλ-+->,因此min 11,()1ln t t t t λ><--- ,max 101,()1ln t t t tλ<---,最后根据导数研究对应函数单调性,确定对应函数最值,即得λ取值集合.【详解】(1)()1'(0)f x a x x=+>,当0a ≥时,()'0f x >对0x >恒成立,与题意不符,当0a <,()1'1ax a x f x x +=+=, ∴10x a<<-时()'0f x >, 即函数()f x 在10,a ⎛⎫-⎪⎝⎭单调递增,在1,a ⎛⎫-+∞ ⎪⎝⎭单调递减, ∵0x →和x →+∞时均有()f x →-∞, ∴111ln 0f a a ⎛⎫⎛⎫-=-+-> ⎪ ⎪⎝⎭⎝⎭,解得:10a e -<<, 综上可知:a 的取值范围1,0e ⎛⎫- ⎪⎝⎭; (2)由(1)可知()00f x '<,则011(0)x a a e>--<<, 由12,x x 的任意性及()()12''0f x f x ⋅<知,0λ≠,且1λ≠,112200ax lnx ax lnx +=⎧⎨+=⎩∴2121ln ln x x a x x -=--, 故()21012211ln ln x x x x x x x λλ-=+->-, 又∵()22121111ln x x x x x x λλ-+->,令21x t x =, 则0,1t t >≠,且()110ln t t t λλ-+->>恒成立, 令()()1ln (0)1t g t t t tλλ-=->+-,而()10g =, ∴1t >时,()0,01g t t ><<时,()()0.*g t <∴()()()()()()2222211111'11t t g t t t t t λλλλλλλ⎡⎤---⎢⎥-⎢⎥⎣⎦=-=⎡⎤⎡⎤+-+-⎣⎦⎣⎦,令()221λμλ=-, 若1μ<,则1t μ<<时,()'0g t <,即函数在(),1μ单调递减,∴()()10g t g >=,与()*不符;若1μ>,则1t μ<<时,()'0g t <,即函数()g t 在()1,μ单调递减,∴()()10g t g <=,与()*式不符;若1μ=,解得12λ=,此时()'0g t ≥恒成立,()()'01g t t =⇔=, 即函数()g t 在()0,∞+单调递增,又()10g =,∴1t >时,()0g t >;01t <<时,()0g t <符合()*式, 综上,存在唯一实数12λ=符合题意. 【点睛】利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造函数,直接把问题转化为函数的最值问题.。
浙江省两校2019-2020学年高三下学期第一次联考数学试题一、单选题(★) 1 . 已知全集,,,则()A.B.C.或D.(★) 2 . 二项式的展开式中的系数为()A.10B.C.80D.(★) 3 . 已知复数满足( 为虚数单位),则()A.B.C.D.5(★) 4 . 已知直线和平面,已知,()A.若,则B.若,则C.若,则D.若,则(★★) 5 . 实数满足,则的最大值为()A.1B.2C.3D.4(★) 6 . 函数的图像可能是()A.B.C.D.(★★★★) 7 . 随机变量的分布列如下:其中是互不相等的正数,则 的取值范围()A .B .C .D .(★★) 8 . 已知三棱锥中,,,平面于,设二面角,,分别为,则()A .B .C .D .不确定(★★★★) 9 . 如图,已知白纸上有一椭圆 ,它焦点为,长轴,短轴, 是椭圆上一点,将白纸沿直线折成角,则下列正确的是()①当 在 (或 )时, 最大. ②当 在(或)时,最小.A .①②B .①C .②D .都不正确(★★★★) 10 . 实数,满足 ,且 ,则对,的最大值为 ,则()A .B .C .D .二、双空题(★) 11 . 杨辉在《详解九章算法》中给出了三角垛垛积公式:(其中为正整数).据此公式,______,______.(★★) 12 . 某几何体的三视图如图所示(单位:),则该几何体的表面积为:_____ ,体积为_____ .(★) 13 . 双曲线的焦点坐标______,渐近线方程_________.(★★) 14 . 已知,曲线向左平移得曲线,则的解析式为_______,的最大值为_______.三、填空题(★★) 15 . 从中任选4个字母排成一排,要求按字母先后顺序排列(即按先后顺序,但大小写可以交换位置,如或都可以),这样的情况有______种.(★★★★) 16 . 已知,函数的最小值为,则的取值范围是:______.(★★★★) 17 . 如图,已知圆半径为2,是圆内一定点,,圆上的两动点满足,存在点使构成矩形,则的取值范围是:________.四、解答题(★★) 18 . 中,角所对边分别为.已知,,.(1)求;(2)求.(★★) 19 . 如图,已知几何体中,是正方形,为中点,平面,,,.(1)求证:平面;(2)求直线与平面所成角.(★★) 20 . 已知是等差数列,公差,是等比数列,且,,. (1)求,的通项公式;(2)求.(★★★★) 21 . 如图已知抛物线,过点作两条直线分别交抛物线于和(其中位于轴上方),直线交于点.(1)求证:点在定直线上;(2)当分别为的中点时,求出直线的方程.(★★★★) 22 . 已知函数有两个极值点.(1)求实数的取值范围;(2)求证:;(3)求证:.。
2019-2020学年浙江省两校高三(下)第一次联考数学试卷一、单选题(本大题共10小题,共40.0分)1. 设全集U =R ,集合A ={x |x >-1},B ={x |x >2},则A ∩∁U B =( )A. {x |-1≤x <2}B. {x |-1<x ≤2}C. {x |x <-1}D. {x |x >2}2. 二项式(x −2y)5的展开式中x 2y 3的系数为( )A. 10B. −10C. 80D. −803. 已知复数z 满足z(2+i)=3−4i(i 为虚数单位),则|z|=( )A. √3B. √5C. 2√3D. 54. 已知直线a ,b 和平面α,β,已知a//α,b ⊥β,( )A. 若a//b ,则α//βB. 若a//b ,则α⊥βC. 若a ⊥b ,则α//βD. 若a ⊥b ,则α⊥β5. 实数x ,y 满足{x −y ≤0x +y −2≥0x −3y +6≥0,则2x −y 的最大值为( )A. 1B. 2C. 3D. 46. 函数y =x ⋅e cosx 的图象可能是( )A.B.C.D.7. 随机变量ξ的分布列如表:ξa b c Pabc其中a ,b ,c 是互不相等的正数,则Eξ的取值范围( )A. (0,13)B. (0,12)C. (12,1)D. (13,1)8. 已知三棱锥P −ABC 中,PA =PB =PC ,∠APB >∠BPC >∠CPA ,PO ⊥平面ABC于O ,设二面角P −AB −O ,P −BC −O ,P −CA −O 分别为α,β,γ,则( )A. α>β>γB. γ>β>αC. β>α>γD. 不确定9. 如图,已知白纸上有一椭圆C ,它焦点为F 1,F 2,长轴A 1A 2,短轴B 1B 2,P 是椭圆上一点,将白纸沿直线B 1B 2折成90°角,则下列正确的是( )①当P 在B 1(或B 2)时,PF 1+PF 2最大. ②当P 在A 1(或A 2)时,PF 1+PF 2最小.A. ①②B. ①C. ②D. 都不正确10. 实数a 1,a 2,…,a 9,满足a 1=a 9,且|a i +a i+2−2a i+1|≤1(i =1,2,…,7),则对1≤i <j ≤9,|a i −a j |的最大值为M ,则( )A. M =7B. M =8C. M =9D. M =10二、单空题(本大题共3小题,共12.0分)11. 从A ,B ,C ,a ,b ,c 中任选4个字母排成一排,要求按字母先后顺序排列(即按A(a),B(b),C(c)先后顺序,但大小写可以交换位置,如AaBc 或aABc 都可以),这样的情况有______种. 12. 已知a ,b ∈R ,函数f(x)=x 2+ax+b+|x 2−ax−b|2的最小值为b 2,则b 的取值范围是______.13. 如图,已知圆O 半径为2,P 是圆内一定点,OP =1,圆O 上的两动点A ,B 满足PA ⊥PB ,存在点C 使PACB 构成矩形,则OC ⃗⃗⃗⃗⃗ ⋅OP ⃗⃗⃗⃗⃗ 的取值范围是______.三、多空题(本大题共4小题,共24.0分)14. 杨辉在《详解九章算法》中给出了三角垛垛积公式:1+3+6+⋯+n(n+1)2=16n(n +1)(n +2)(其中n 为正整数).据此公式,则1+3+6+10+15+21+28= (1) ;12+22+⋯+102= (2) .15.某几何体的三视图如图所示(单位:cm),则该几何体的表面积为:_cm2,体积为__cm3.16.双曲线y23−x24=1的焦点坐标,渐近线方程.17.已知f(x)=sin(2x−π3),曲线f(x)向左平移π6得曲线g(x),则g(x)的解析式为,f(x)+g(x)的最大值为.四、解答题(本大题共5小题,共74.0分)18.△ABC中,角A,B,C所对边分别为a,b,c.已知b=3,a2=c2−2c+9,A−B=π4.(Ⅰ)求cos A;(Ⅱ)求a.19.如图,已知几何体QPABCD中,ABCD是正方形,O为BD中点,PA⊥平面ABCD,PQ//AD,AB=2,PA=PQ=1.(Ⅰ)求证:PO//平面QCD;(Ⅱ)求直线BD与平面QCD所成角.20.已知{a n}是等差数列,公差d=3,{b n}是等比数列,且b a1=2,b2=4,b a2=16.(Ⅰ)求{a n},{b n}的通项公式;(Ⅱ)求a b1+a b2+⋯+a bn.21.如图已知抛物线y2=2x,过点P(1,0)作两条直线分别交抛物线于A,B和C,D(其中A,C位于x轴上方),直线AC,BD交于点Q.(Ⅰ)求证:点Q在定直线上;(Ⅱ)当A,D分别为QC,QB的中点时,求出直线AB,CD的方程.22.已知函数f(x)=e1−x+alnx有两个极值点x1,x2(x1<x2).(Ⅰ)求实数a的取值范围;(Ⅱ)求证:x1+x2>2;(Ⅲ)求证:x1x2<1.答案和解析1.【答案】B【解析】解:由已知全集U=R,B={x|x>2},得到∁U B={x|x≤2},又集合A={x|x>-1},所以A∩∁U B={x|-1<x≤2},故选:B.根据全集为R,由集合B求出B的补集,然后求出A和B补集的交集即可.此题考查了交集和补集的运算,是一道基础题.2.【答案】D【解析】解:二项式(x−2y)5的展开式的通项为T r+1=C5r x5−r(−2y)r=(−2)r C5r x5−r y r,要求展开式中x2y3的系数,∴r=3,∴展开式中x2y3的系数为(−2)3C53=−80.故选:D.利用二项式定理的展开式的通项公式,求解所求项的系数即可.本题考查二项式定理的通项公式的应用,属于基础题.3.【答案】B【解析】解:由z(2+i)=3−4i,得z=3−4i2+i,∴|z|=|3−4i2+i |=|3−4i||2+i|=√32+(−4)2√22+12=√5=√5.故选:B.把已知等式变形求得z,再由商的模等于模的商求解.本题考查复数模的求法,考查数学转化思想方法,是基础题.4.【答案】B【解析】解:由直线a ,b 和平面α,β,a//α,b ⊥β,知: 对于A ,若a//b ,则α与β相交,故A 错误;对于B ,若a//b ,则由面面垂直的判定定理得α⊥β,故B 正确; 对于C ,若a ⊥b ,则α与β相交或平行,故C 错误; 对于D ,若a ⊥b ,则α与β平行或相交,故D 错误. 故选:B .对于A ,α与β相交;对于B ,由面面垂直的判定定理得α⊥β;对于C ,α与β相交或平行;对于D ,α与β平行或相交.本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力,是中档题.5.【答案】C【解析】解:先根据约束条件画出可行域,目标函数z =2x −y ,z 在点A 处,目标函数的截距取得最小值,z 取得最大值,由{x −y =0x −3y +6=0,解得A(3,3)可得z max =2×3−3=3, 故最大值为3, 故选:C .先根据约束条件画出可行域,再利用几何意义求最值,只需求出直线z =x −2y 过y 轴的截距最小,即z 最大值,从而求解.本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.6.【答案】C【解析】解:∵y =f(x)=x ⋅e cosx ,∴f(−x)=−x ⋅e cos(−x)=−x ⋅e cosx =−f(x), 即f(x)=x ⋅e cosx 为奇函数,排除A ,B , 又f(1)=e cos1>0,排除D ,故选:C.先判断函数为奇函数,再根据函数值的特点即可判断.本题考查了函数图象的识别,考查了函数的奇偶性和函数值的特点,属于中档题.7.【答案】D【解析】解:由题意,可知a+b+c=1,根据分布列,可得Eξ=a2+b2+c2,∵a,b,c是互不相等的正数,∴a2+b2>2ab,a2+c2>2ac,b2+c2>2bc,各式相加,整理得a2+b2+c2>ab+ac+bc,∵1=(a+b+c)2=a2+b2+c2+2ab+2ac+2bc<a2+b2+c2+2(a2+b2+ c2)=3(a2+b2+c2),∴a2+b2+c2>13,又∵ab+ac+bc>0,∴a2+b2+c2=1−2(ab+ac+bc)<1,∴13<a2+b2+c2<1,即13<Eξ<1,故选:D.本题先根据随机变量的知识可知a+b+c=1,然后计算出Eξ=a2+b2+c2,再根据基本不等式的性质进行运用,进一步进行不等式的运算即可得到正确选项.本题主要考查概率统计与不等式的综合运用.考查了转化思想,定义法,基本不等式的应用,以及逻辑推理能力和数学运算能力.本题属中档题.8.【答案】A【解析】解:连接OA,OB,OC,则△POA,POB,POC均为直角三角形,∵PA=PB=PC,PO为公共边,∴△POA≌△POB≌△POC ,∴OA =OB =OC ,故O 为△ABC 的外心,设D ,E ,F 分别是AB ,BC ,AC 的中点,则OD ⊥AB ,OE ⊥BC ,OF ⊥AC , 又PA =PB =PC ,∴PD ⊥AB ,PE ⊥BC ,PF ⊥AC , ∴∠PDO =α,∠PEO =β,∠PFO =γ, ∵cos∠APB 2=PD PA ,cos∠BPC 2=PE PB ,cos∠APC 2=PFPC ,且∠APB >∠BPC >∠CPA ,PA =PB =PC , ∴PD <PE <PF ,又sinα=POPD ,sinβ=POPE ,sinγ=POPF , ∴sinα>sinβ>sinγ, ∴α>β>γ. 故选:A .判断O 点位置,根据∠APB >∠BPC >∠CPA 得出P 到底边的距离的大小关系,从而得出三个二面角的平面角的正弦的大小,再得出结论.本题考查了二面角的平面角的作法,棱锥的结构特征,属于中档题.9.【答案】A【解析】解:设翻折前椭圆方程为:y 2a 2+x 2b 2=1,如图所示建立空间直角坐标系,根据对称性,不妨设P(0,bcosθ,asinθ),θ∈[0,π2], F 1(c,0,0),F 2(0,0,c),则PF 1+PF 2=√c 2+b 2cos 2θ+a 2sinθ+√b 2cos 2θ+(asinθ−c)2 =√a 2+c 2sin 2θ+√a 2+c 2sin 2θ−2acsinθ=√a 2+c 2sin 2θ+a −csinθ, 设f(θ)=√a 2+c 2sin 2θ+a −csinθ,则f′(θ)=2√a 2+c 2sin 2θ−ccosθ<√(a c)+sin θ−ccosθ<0,故函数单调递减,故当θ=0,即当P 在B 1(或B 2)时,PF 1+PF 2最大, 故θ=π2时,当P 在A 1(或A 2)时,PF 1+PF 2最小. 故选:A .如图所示建立空间直角坐标系,根据对称性,不妨设P(0,bcosθ,asinθ),θ∈[0,π2],PF 1+PF 2=√a 2+c 2sin 2θ+a −csinθ,求导证明f(θ)=√a 2+c 2sin 2θ+a −csinθ单调递减,得到答案.本题考查了椭圆内线段最值,利用导数求最值,意在考查学生的计算能力和综合应用能力,属于难题.10.【答案】B【解析】解:令b i =a i+1−a i ,则|b i+1−b i |≤1,此时b 1+b 2+⋯…+b 8=0, 由题意可知,必存在k ,使得b k b k+1<0,则|b k −b k+1|≤1,必有min{|b k |,|b k+1|}≤12, 下面所有正数项和记为S ,所有负数项和记为T ,则有S =T , 下面对正数项的项数n 进行讨论, 若存在8个正数项,显然不成立; 若存在7个正数项时,T ≤1; 若存在6个正数项时,T ≤1+2=3; 若存在5个正数项时,T ≤1+2+3=6;若存在4个正数项时,存在|b k |≤12,此时T ≤12+32+52+72=8; 综上所述,对1≤i ≤j ≤9,|a i −a j |的最大值为8. 故选:B .令b i =a i+1−a i ,则|b i+1−b i |≤1,b 1+b 2+⋯…+b 8=0,且必存在k ,使得b k b k+1<0,则|b k −b k+1|≤1,必有min{|b k |,|b k+1|}≤12,再对正数项的项数进行讨论即可得出结论.本题考查数列中最值的求解,考查递推数列的运用,考查逻辑推理能力,属于较难题目.11.【答案】36【解析】解:若选出的4个字母中有1对大小写字母,则不同的排列顺序有C 31C 21C 21A 22=24种,若选出的4个字母中有2对大小写字母,则不同的排列顺序有C 32A 22A 22=12种,24+12=36. 故答案为:36.讨论选出的4个字母中相同字母的对数,根据组合数公式和排列数公式计算.本题考查了排列组合数公式的应用,属于基础题.12.【答案】[0,1]【解析】解:f(x)={x 2,x 2≥ax +bax +b,x 2<ax +b,即f(x)=max{x 2,ax +b}, ①当y =x 2与y =ax +b 没有交点或交点在y 轴同侧时,此时f(x)min =b 2=0,解得b =0;②当y =x 2与y =ax +b 的交点在y 轴异侧时,则b >0,当a ≥0时,最低点交点坐标为(−b,b 2),此时b 2=−ab +b ,b =−a +1≤1,即0<b ≤1;当a <0时,最低点交点坐标为(b,b 2),此时b 2=ab +b ,b =a +1<1,即0<b <1; 综上,实数b 的取值范围为[0,1]. 故答案为:[0,1].分析可知,f(x)=max{x 2,ax +b},然后以y =x 2与y =ax +b 的交点情况讨论函数f(x)的最小值,结合题意,即可求得实数b 的取值范围.本题考查绝对值函数的最值求解,考查分类讨论思想,属于中档题.13.【答案】[−√7,√7]【解析】解:设矩形PACB 对角线交点为M ,则OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ +OP ⃗⃗⃗⃗⃗ =2OM⃗⃗⃗⃗⃗⃗⃗ , ∴OA ⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2+2OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ 2+OP ⃗⃗⃗⃗⃗ 2+2OC ⃗⃗⃗⃗⃗ ⋅OP ⃗⃗⃗⃗⃗ ,① 又|AB⃗⃗⃗⃗⃗ |=|PC ⃗⃗⃗⃗⃗ |,∴|OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ |=|OC ⃗⃗⃗⃗⃗ −OP ⃗⃗⃗⃗⃗ |, ∴OA ⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−2OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ 2+OP ⃗⃗⃗⃗⃗ 2−2OC ⃗⃗⃗⃗⃗ ⋅OP ⃗⃗⃗⃗⃗ ,② ①+②可得:OA ⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2=OC ⃗⃗⃗⃗⃗ 2+OP ⃗⃗⃗⃗⃗ 2, ∴OC ⃗⃗⃗⃗⃗ 2=OA ⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−OP ⃗⃗⃗⃗⃗ 2=7, ∴|OC⃗⃗⃗⃗⃗ |=√7, ∴OC ⃗⃗⃗⃗⃗ ⋅OP ⃗⃗⃗⃗⃗ =√7cos∠POC , 又−1≤cos∠POC ≤1, ∴−√7≤OC ⃗⃗⃗⃗⃗ ⋅OP ⃗⃗⃗⃗⃗ ≤√7.故答案为:[−√7,√7].根据矩形性质得出|OC|=√7,再根据平面向量的数量积定义得出答案.本题考查了平面向量的数量积计算,向量在几何证明中的应用,属于中档题.14.【答案】84385【解析】解:由1+3+6+⋯+n(n+1)2=16n(n+1)(n+2),所以1+3+6+10+15+21+28=16×7×8×9=84,易得12+22+32+⋯+2=16n(n+1)(2n+1),所以12+22+⋯+102=16×10×11×21=385,故答案为:84 385.由归纳推理得:1+3+6+10+15+21+28=16×7×8×9=84,易得12+22+32+⋯+2=16n(n+1)(2n+1),所以12+22+⋯+102=16×10×11×21=385,得解.本题考查了归纳推理,属中档题.15.【答案】7π,83π【解析】解:由已知可得该几何体是一个圆柱和一个半球的组合体,圆柱的底面半径为1,高(母线)为2,球的半径为1.则该几何体的表面积S=2π×1×2+π×12+12×4π×12=7πcm2,体积为V=π×12×2+12×43π×13=8π3cm3,故答案为:7π,83π.由已知可得该几何体是一个圆柱和一个半球的组合体,求出圆柱的底面半径和母线长,代入球、圆柱表面积公式和体积公式,可得答案.本题考查由三视图求几何体的体积和表面积,根据已知的三视图分析出几何体的形状是关键,属于基础题.16.【答案】(0,±√7)y =±√32x【解析】解:双曲线y 23−x 24=1的a =√3,b =2,c =√7,所以双曲线的焦点坐标(0,±√7),渐近线方程:y =±√32x.故答案为:(0,±√7);y =±√32x.直接利用双曲线的标准方程求解焦点坐标以及渐近线方程即可. 本题考查双曲线的简单性质的应用,是基础题.17.【答案】g(x)=sin2x√3【解析】 【分析】本题考查三角函数图象的变换规律,正余弦型三角函数最值的求法.属于基础题. 根据“左加右减”的规律求出g(x),然后将f(x)+g(x)化简成形如Asin(ωx +φ)三角函数的形式,即可求出最值. 【解答】解:由已知得g(x)=sin[2(x +π6)−π3]=sin2x . 故g(x)=sin2x .所以f(x)+g(x)=sin2x +sin(2x −π3)=sin2x +sin2x ⋅cos π3−cos2x ⋅sin π3=32sin2x −√32cos2x =√3(√32sin2x −12cos2x)=√3sin(2x−π6)≤√3.故答案为:g(x)=sin2x;√3.18.【答案】解:(Ⅰ)△ABC中,角A,B,C所对边分别为a,b,c.已知b=3,a2=c2−2c+9,所以cosA=b2+c2−a22bc =c2+9−a22bc=2c2bc=1b=13.(Ⅱ)由(Ⅰ)cosA=13,所以sinA=2√23,由于A−B=π4,所以sin(A−π4)=sinAcosπ4−cosAsinπ4=2√23×√22−13×√22=4−√26,即sinB=4−√26.利用正弦定理:asinA =bsinB,故a=bsinAsinB =24√2+127.【解析】(Ⅰ)直接利用余弦定理的应用求出结果.(Ⅱ)利用三角函数关系式的变换和正弦定理的应用求出结果平.本题考查的知识要点:余弦定理、正弦定理,三角函数关系式的变换,主要考查学生的运算能力和转换能力及思维能力,属于基础题.19.【答案】解:(Ⅰ)证明:取CD中点H,连接QH,OH,O为BD中点,CD中点H,故OH 平行且相等12BC ,PQ 平行且相等12BC ,故PQ 平行且相等OH ,故四边形OHQP 为平行四边形,故PO//QH , PO ⊄平面QCD ,QH ⊂平面QCD , 故PO//平面QCD . (Ⅱ)如图,以AB ,AD ,AP 分别为x ,y ,z 轴建立空间直角坐标系, 则B(2,0,0),D(0,2,0),C(2,2,0),Q(0,1,1), 设平面QCD 的一个法向量为n ⃗ =(x,y,z), 则{n ⃗ ⋅CD ⃗⃗⃗⃗⃗ =0n⃗ ⋅QD ⃗⃗⃗⃗⃗⃗ =0,即 {−2x =0y −z =0,取y =1,则法向量为n ⃗ =(0,1,1),BD ⃗⃗⃗⃗⃗⃗ =(−2,2,0), 设直线BD 与平面QCD 所成角为θ(0≤θ≤π2), 则sinθ=|cos〈n ⃗ ⋅BD⃗⃗⃗⃗⃗⃗ 〉|=|n ⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ ||n ⃗⃗ |⋅|BD⃗⃗⃗⃗⃗⃗ |=√2×2√2=12,故直线BD 与平面QCD 所成角为π6.【解析】(Ⅰ)取CD 中点H ,连接QH ,OH ,O 为BD 中点,通过证明四边形OHQP 为平行四边形,得到PO//QH ,进而证明PO//平面QCD ;(Ⅱ)以AB ,AD ,AP 分别为x ,y ,z 轴建立空间直角坐标系,求出平面QCD 的法向量,设直线BD 与平面QCD 所成角为θ(0≤θ≤π2),再结合sinθ=|cos〈n ⃗ ⋅BD⃗⃗⃗⃗⃗⃗ 〉|即可求出θ.本题考查线面平行的证明,考查空间向量的应用,考查学生的逻辑推理能力和计算能力,属于中档题.20.【答案】解:(Ⅰ)设{b n }是公比为q 的等比数列,由b a 1=2,b 2=4,b a 2=16,可得b 1q a 1−1=2,b 1q =4,b 1q a 2−1=16, 又a 2−a 1=d =3,可得q 3=8,即q =2,b 1=2,a 1=1, 则a n =1+3(n −1)=3n −2,b n =2n ,n ∈N ∗;(Ⅱ)a b 1+a b 2+⋯+a b n =(3×2−2)+(3×4−2)+⋯+(3×2n −2) =3×(2+4+⋯+2n )−2n =3×2(1−2n )1−2−2n =3×2n+1−6−2n .【解析】(Ⅰ)设{b n }是公比为q 的等比数列,运用等差数列和等比数列的通项公式,解方程可得首项和公比,进而得到所求通项公式;(Ⅱ)求得a b n =3×2n −2,再由数列的分组求和,结合等比数列的求和公式,计算可得所求和.本题考查等差数列和等比数列的通项公式和求和公式的运用,考查方程思想和运算能力,属于中档题.21.【答案】解:(Ⅰ)证明:设A(2t 12,2t 1),B(2t 22,2t 2),C(2t 32,2t 3),D(2t 42,2t 4),(t 1,t 3>0,t 2,t 4<0),则k AC =2t 3−2t 12t 32−2t 12=1t1+t 3,∴直线AC 的方程为:y =1t1+t 3x +2t 1t 3t 1+t 3,同理可得直线BD 的方程为:y =1t 2+t 4x +2t 2t 4t2+t 4,∵PA ⃗⃗⃗⃗⃗ //PB ⃗⃗⃗⃗⃗ ,PA ⃗⃗⃗⃗⃗ =(2t 12−1,2t 1),PB ⃗⃗⃗⃗⃗ =(2t 22−1,2t 2),∴2t 1(2t 22−1)=2t 2(2t 12−1),化简可得t 1t 2=−12,同理可得t 3t 4=−12,由{y =1t 1+t 3x +2t 1t3t 1+t 3y =1t 2+t 4x +2t 2t 4t 2+t4,化简整理可得(t 1+t 3−t 2−t 4)x =2(t 1t 2t 3+t 1t 3t 4−t 1t 2t 4−t 2t 3t 4)=−t 3−t 1+t 4+t 2,∴x =−1,即点Q 在直线x =−1上,即得证; (Ⅱ)∵A ,D 分别为QC ,QB 的中点,∴{4t 12=−1+2t 324t 42=−1+2t 22,则{4t 12=−1+2t 3244t 32=−1+24t 12,即2t 34−t 32−1=0, ∴t 32=1或t 32=−12(舍), ∵t 3>0, ∴t 3=1, ∴t 4=−12,∴C(2,2),A(12,1),B(2,−2),D(12,−1),∴直线AB 的方程为2x +y −2=0,直线CD 的方程为2x −y −2=0.【解析】(Ⅰ)设出A ,B ,C ,D 四点坐标,求出直线AC ,BD 的斜率及方程,由PA ⃗⃗⃗⃗⃗ //PB ⃗⃗⃗⃗⃗ ,可得t 1t 2=−12,t 3t 4=−12,再联立直线方程,化简即可得证;(Ⅱ)依题意,{4t 12=−1+2t 324t 42=−1+2t 22,计算可得t 3=1,t 4=−12,进而求得点A ,B ,C ,D 四点坐标,由此得出所求直线方程.本题考查直线与抛物线的位置关系,考查直线方程的求解,对运算能力的要求较高,属于中档题.22.【答案】解:(Ⅰ)f(x)=e 1−x +alnx,f′(x)=−e 1−x +ax =0,依题意,a =xe 1−x 有两个正数解,设g(x)=xe 1−x ,则g′(x)=e 1−x −xe 1−x =(1−x)e 1−x , 函数g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,g(1)=1, 画出函数g(x)图象如下图所示,由图象可知,0<a <1;(Ⅱ)证明:g(x)=xe 1−x =a 的两个根为x 1,x 2(x 1<1<x 2),构造函数F(x)=g(x)−g(2−x),则F′(x)=g′(x)−g′(2−x)=(1−x)e 1−x +(x −1)e x−1=(x −1)(e x−1−1e x−1), 当x ≥1时,F′(x)≥0;当0<x <1时,F′(x)>0, 故函数F(x)单调递增,且F(1)=0,F(x 2)=g(x 2)−g(2−x 2)>F(1)=0,即g(x 2)>g(2−x 2),亦即g(x 1)>g(2−x 2),x 1∈(0,1),2−x 2∈(0,1),当x ∈(0,1)时,函数g(x)单调递增,故x 1>2−x 2, ∴x 1+x 2>2,得证;(Ⅲ)证明:根据题意,a =x 1e 1−x 1,a =x 2e 1−x 2,两式相除得到:1=x2x 1e x 1−x 2,设x2x 1=t >1,故x 2−x 1=lnt ,解得x 2=tlnt t−1,x 1=lnt t−1,故x 1x 2=tlnt t−1⋅lnt t−1=tln 2t (t−1)2,要证x 1x 2<1,即证√tlntt−1<1,即证√tlnt −t +1<0,设K(t)=√tlnt −t +1,则K′(t)=2√t+√t−1=√t2√t, 设M(t)=lnt +2−2√t ,则M′(t)=1t √t <0,且M(1)=0, ∴K′(t)<0恒成立,∴K(t)单调递减,故K (t)<K(1)=0恒成立,即得证.【解析】(Ⅰ)求导化简可得a =xe 1−x 有两个正数解,构造函数g(x)=xe 1−x ,画出函数图象得答案;(Ⅱ)构造函数F(x)=g(x)−g(2−x),证明函数F(x)单调递增,进而F(x 2)>F(1)=0,得证;(Ⅲ)由题意,a =x 1e 1−x 1,a =x 2e 1−x 2,两式相除得到:1=x2x 1e x 1−x2,构造函数K(t)=√tlnt −t +1,证明K(t)<K(1)=0即得证.本题考查了根据极值点求参数,证明不等式,意在考查学生的计算能力和综合应用能力,属于中档题.。
浙江省衢州二中高三数学下学期第一次综合练习试题 文一、选择题(5×10=50分)1.设R 为实数集,i 是虚数单位,复数21i z +=,集合}1,0,1{-=A ,则( )A .A i ∈B .AC i R ∈ C .A z ∈2D .A z ∈42.设D C B A ,,,是平面α内的四个定点,平面α内的点M 满足=+++这样的点M 的个数是( )A .0B .1C .3D .43.已知三角形ABC 的一个内角是0120,三边长构成公差为4的等差数列,则三角形的面积是( )A .310B .315C .320D .3254.设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥≤--≤-+002052x y x y x ,则y x 32+的大值是( )A .10B .9C .8D .7.55.直线l 平面α相交,若直线l 不垂直于平面α,则( )A .l 与α内的任意一条直线不垂直B .α内与l 垂直的直线仅有1条C .α内至少有一条直线与l 平行D .α内存在无数条直线与l 异面6.一个空间几何体的三视图如图所示,则该几何体的表面积为( ) A .48 B .17832+ C .17848+D .807.设R b a ∈,,则“11>>b a 且”的充要条件是( ) A.2>+b aB .12>>+ab b a 且C .012>+-->+b a ab b a 且D .12>>+b b a 且8.已知双曲线12222=-by a x 的两条渐近线均与圆05622=+-+x y x 相切,且双曲线的右焦点与圆05622=+-+x y x 的圆心重合,则双曲线的方程是( )A .14522=-y xB .15422=-y xC .13622=-y xD .16322=-y x 9.设O 是平行四边形ABCD 两对角线的交点,N M Q P ,,,分别是线段OD OC OB OA ,,,的中点,在C M P A ,,,中任取一点记为E ,在D N Q B ,,,中任取一点记为F ,设+=,则点G 落在平行四边形ABCD 外(不含边界)的概率是( )A .21B .85C .43D .8710.设函数x x x f -+=)12sin(4)(,则在下列区间中函数不存在零点的是( )A .]2,4[--B .]0,2[-C .]2,0[D .]4,2[ 二、填空题(4×7=28分)11.某市有大型超市,中型超市400家,小型超市1400家,为了掌握各类超市的营 业情况, 现按分层抽样方法抽取一个容量 为100的样本,应抽取中型超市___ 家.12.若m 是某已知的正整数,某程序框图如右图所示,该程序运行后输出的数是31,则m =___13.正方形ABCD 四顶点D C B A ,,,按逆时针方向排列,已知A 、B 两点的坐标)1,3(),0,0(B A ,则C 点的坐标是___14.平面上有A 、B 两定点,且1||=AB ,C 是平面内的一动点,满足31cos -=∠ACB ,则||BC 的取值范围是___ ___15.点P 是曲线2ln y x x =-上任意一点,则点P 到 直线2y x =-的最小距离为16.已知0≠a ,函数⎪⎩⎪⎨⎧≥--<+=1,21,2)(x a x x a x x f ,若)1()1(a f a f +=-,则实数a 的值是___ 17.已知32,21≤≤≤≤y x ,当y x ,在可取值范围内变化时,不等式222y ax xy +≤恒成立,则实数a 的取值范围是___ ___三、解答题18.(本题满分14分)设R x ∈,向量)sin 2,sin 3(x x a =,)sin 2,cos 2(x x =,函数1)(-⋅=x f .(Ⅰ)在区间),0(π内,求)(x f 的单调递减区间; (Ⅱ)若1)(=θf ,其中20πθ<<,求)3cos(πθ+.19.(本题满分14分)设等比数列}{n a 的首项为a ,公比10≠>q q 且,前n 项和为n S (Ⅰ)当1=a 时,121321+++,S,SS 三数成等差数列,求数列}{n a 的通项公式;(Ⅱ)对任意正整数n ,命题甲:21),1(,+++n n n S S S 三数构成等差数列.命题乙:321),1(,++++n n n S S S 三数构成等差数列.求证:对于同一个正整数n ,命题甲与命题乙不能同时为真命题.本题满分14分)四棱锥ABCD P -的底面ABCD 是直角梯形,AB ∥CD ,90=∠ABC ,222===CD BC AB ,PD PA PD PA ⊥=,,PC PB =(Ⅰ)求证:平面⊥PAD 平面ABCD ;(Ⅱ)求直线PB 与平面PAD 所成角的正切值.21.(本题满分15分)函数ax bx x x f 22131)(23++-=,)('x f 是它的导函数. (Ⅰ)当1=b 时,若)(x f 在区间),32(+∞存在单调递增区间,求a 的取值范围。
2019-2020学年高考数学模拟试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.定义在R 上的函数()f x 满足(4)1f =,()f x '为()f x 的导函数,已知()y f x '=的图象如图所示,若两个正数,a b 满足(2)1f a b +<,11b a ++则的取值范围是( )A .(11,53)B .1(,)(5,)3-∞⋃+∞C .(1,53)D .(,3)-∞2.函数f x x 2()cos(2)3π=+的对称轴不可能为( ) A .65x π=-B .3x π=-C .6x π=D .3x π=3.若点(3,4)P -是角α的终边上一点,则sin 2α=( ) A .2425-B .725-C .1625D .854.已知命题:p 若1a <,则21a <,则下列说法正确的是( ) A .命题p 是真命题 B .命题p 的逆命题是真命题C .命题p 的否命题是“若1a <,则21a ≥”D .命题p 的逆否命题是“若21a ≥,则1a <”5.已知角α的顶点与坐标原点O 重合,始边与x 轴的非负半轴重合,它的终边过点(3,4)P --,则tan 24πα⎛⎫+ ⎪⎝⎭的值为( )A .247-B .1731-C .247D .17316.已知命题P :x R ∀∈,sin 1x ≤,则p ⌝为( ) A .0x R ∃∈,0sin 1x ≥ B .x R ∀∈,sin 1x ≥ C .0x R ∃∈,0sin 1x > D .x R ∀∈,sin 1x >7.函数2()1cos 1xf x x e ⎛⎫=-⎪+⎝⎭图象的大致形状是( )A .B .C .D .8.已知向量a 与a b +的夹角为60︒,1a =,3b =,则a b ⋅=( ) A .3-B .0C .0或32-D .32-9.已知F 为抛物线2:8C y x =的焦点,点()1,A m 在C 上,若直线AF 与C 的另一个交点为B ,则AB =( )A .12B .10C .9D .810.为了进一步提升驾驶人交通安全文明意识,驾考新规要求驾校学员必须到街道路口执勤站岗,协助交警劝导交通.现有甲、乙等5名驾校学员按要求分配到三个不同的路口站岗,每个路口至少一人,且甲、乙在同一路口的分配方案共有( ) A .12种B .24种C .36种D .48种11.已知函数()f x 的定义域为()0,∞+,且()()2224m f m f f n n ⎛⎫⎪⎝⎭⋅=,当01x <<时,()0f x <.若()42f =,则函数()f x 在[]1,16上的最大值为( ) A .4B .6C .3D .812.如图,在ABC ∆中,点M ,N 分别为CA ,CB 的中点,若5AB =,1CB =,且满足223AG MB CA CB ⋅=+,则AG AC ⋅等于( )A .2B 5C .23D .83二、填空题:本题共4小题,每小题5分,共20分。