第一讲 盈亏问题

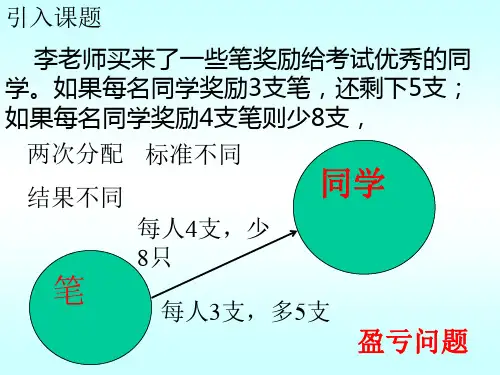
第一讲盈亏问题（一）公式：（盈＋亏）÷两次分配差=份数（大盈－小盈）÷两次分配差=份数（大亏－小亏）÷两次分配差=份数每次分数量×份数＋盈=总数量每次分的数量×份数－亏=总数量例1、学校安排学生宿舍，如果每间4人，就有20人没有床位，如果每间6人，就多出4个空床位，那么有（）间宿舍，有（）个学生。

练习一：1、一个植树小组植树，如果每人植6棵，还剩14棵；如果每人植8棵，就少了4棵，这个小组一共有（）人，共植树（）棵。

2、学生表演团体操，如果每行8人，则多7人；如果每行11人，则少8人。

那么一共有（）行，共有学生（）人。

3、幼儿园小朋友分苹果，如果每人分3个，就多了16个，如果每个小朋友分5个，就差了4个。

问原来有（）个小朋友，有（）个苹果。

4、幼儿园小朋友分饼干，若每人分3块，则余14块；若每人分4块，则还差12块，一共有（）个小朋友，有（）块饼干。

5、同学们植树，如果每人植2棵，则还多了12棵，如果每人植3棵，就少了12棵，问有（）个同学，有（）棵树。

6、少先队员植树，如果每个人植5棵，则还剩13棵；如果每人植7棵，则差21棵。

参加植树的一共有（）人，这批树有（）棵。

例2、学校买来一批小排球，如果每班发9个，就少25个，如果每班发6个，就少7个，那么一共有（）个班，有（）个排球。

练习二：1、学校有一批笔记本奖给三好学生，如果每人发9本，就少12本；如果每人发7本就少了4本，那么三好学生有（）人，有（）本笔记本。

2、一些小朋友分糖块，如果每人分14块就少19块，如果每人分12块，就少11块，一共有（）个小朋友，一共有（）块糖。

3、学校买来一批书奖励三好学生，如果每人奖5本，则差8本，如果每人奖7本，则差30本。

学校有三好学生（）人。

学校买书（）本。

例3、有一批笔记本，如果每人发5本，就多12本；如果每人发8本就多3本，那么有（）本笔记本。

练习三：1、一批书分给小朋友，如果每人分3本，则多了20本；如果每人分5本，则还余8本。

第一讲盈亏问题盈亏问题的特点是问题中每一同类量都要出现两种不同的情况．分配不足时，称之为“亏”，分配有余称之为“盈”；还有些实际问题，是把一定数量的物品平均分给一定数量的人时，如果每人少分，则物品就有余(也就是盈)，如果每人多分，则物品就不足(也就是亏)，凡研究这一类算法的应用题叫做“盈亏问题”．盈亏问题的基本关系式：(盈+亏)÷两次分得之差=人数或单位数(盈-盈)÷两次分得之差=人数或单位数(亏-亏)÷两次分得之差=人数或单位数2、每次分的数量×份数＋盈=总数量每次分的数量×份数－亏=总数量物品数可由其中一种分法和人数求出。

也有的问题两次都有余或两次都不足，不管哪种情况，都是属于按两个数的差求未知数的“盈亏问题”.1、山上有群猴，摘了一篮桃。

1只吃1个，刚好剩1个，1只吃两个，有只没吃着。

你来猜一猜，猴（）只来桃（）个。

※一堆糖果有十几颗，每人分4块多2块，每人分5块少1块，想一想，有（）块糖果，有（）个人。

※一个植树小组植树。

如果每人栽5棵，还剩14棵；如果每人栽7棵，就缺4棵。

这个植树小组（）人，一共有（）棵树。

※幼儿园把一些积木分给小朋友，如果每人分2个，则剩下20个；如果每人分3个，则差40个。

幼儿园有（）个小朋友，一共有（）个积木。

※实验小学学生坐汽车去春游，如果每车坐6人，则多1人；如果每车做8人，则少5人。

问一共有（）辆车，有（）学生。

※某校安排宿舍，如果每间6人，则6人没有床位；如果每间8人，则多出10个床位。

问宿舍有（）间，学生有（）人。

※一袋巧克力，每人分4块，还剩2块，每人分6块，少4块，这袋巧克力有（）块，有（）个人。

2、学校将一批铅笔奖给三好学生。

如果每人奖7支，则缺7支；如果每人奖9支，则缺25支。

三好学生有（）人，铅笔有（）支。

※将月季花插入一些花瓶中，如果每瓶改为插6朵，则缺少1朵；如果每瓶插8朵，则缺少15朵。

一盈一亏类 篮球比赛是根据运动队在规定的比赛时间里得分多少来决定胜负的，因此，篮球比赛的计时计分系统是一种得分类型的系统
李老师买来了一些笔奖励给考试优秀的同 学。如果每名同学奖励3支笔，还剩下5支； 如果每名同学奖励4支笔则少8支，优秀学生 有几人？笔有多少支？
同学
每人4支，少 8只
笔
每人3支，多5支
全班同学去划船，如果减少一条船，每条船正 好坐9个同学；如果增加一条船，每条船正好坐6 个同学。这个班有多少个同学？
练习篮球比赛是根据运动队在规定的比赛时间里得分多少来决定胜负的，因此，篮球比赛的计时计分系统是一种得分类型的系统
一个植树小组植树，如果每人栽5棵，还剩 12棵；如果每人栽7棵，就缺4棵。这个小组 有多少人？一共要栽多少棵树？
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
⑤两盈类
有一个贫困地区遭受雪灾，外地人民献出 爱心，纷纷向灾区捐献大量寒衣。村长分发 寒衣时，每户分给5件，余99件；每户分给7 件，仍然余33件。每户应分多少件可以少余 或不余？
什么叫盈亏问题 篮球比赛是根据运动队在规定的比赛时间里得分多少来决定胜负的，因此，篮球比赛的计时计分系统是一种得分类型的系统 盈：余剩
亏：不足，缺少
把一定数量的物品分配给若干个对象，先 按某一种标准分，结果正好分完，或者多余， 或者不足；再按照另一种标准分，又产生一种 结果（或多，或少，或正好分完）。由此求物 品的数量以及对象的数量，这样的问题叫做盈 亏问题。
松鼠妈妈给小松鼠分松子，如果每只小松鼠 分8个，就差12个；如果每只小松鼠分10个， 就差22个。有多少只小松鼠？

第一讲盈亏问题盈亏问题又叫盈不足问题，是指把一定数量的物品平均分给固定的对象，如果按某种标准分,则分配后会有剩余(盈)；按另一种标准分,分配后又会有不足(亏），求物品的数量和分配对象的数量。

例如：把一代饼干分给小班的小朋友，每人分3块，多12块；如果每人分4块，少8块。

小朋友有多少人?饼干有多少块?这种一盈一亏的情况，就是我们通常说的标准的盈亏问题。

盈亏问题的基本数量关系是：（盈＋亏)÷两次所分之差=人数；还有一些非标准的盈亏问题,它们被分为四类：1.两盈：两次分配都有多余；2。

两不足：两次分配都不够;3。

盈适足:一次分配有余，一次分配够分;4，不足适足:一次分配不够,一次分配正好。

盈亏问题的数量关系是:（1)(盈＋亏)÷两次分配差=份数(大盈－小盈）÷两次分配差=份数（大亏－小亏)÷两次分配差=份数（2）每次分得的数量×份数＋盈=总数量每次分得的数量×份数－亏=总数量例1.一个植树小组,如果每人栽5棵树,还剩14棵,每人栽7棵树,就缺4棵，问一共有几个人?一共有多少棵树?例2、妈妈买来一些桃子分给全家人吃。

如果每人分4个，则多出12个；如果每人分6个，则多出2个.妈妈买来几个桃子？全家共有几人？例3、老师给美术小组的同学分发图画纸.如果每人发5张，则少3张；如果每人发8张,则少48张。

美术小组有几人？练习:1.幼儿园把一些积木分给小朋友，如果每人分2个，则剩下20个；如果每人分3个，则差40个。

幼儿园有多少个小朋友？一共有多少个积木?2。

某校安排宿舍，如果每间6人,则16人没有床位；如果每间8人，则多出10个床位.问宿舍多少间?学生多少人?3.有一个班的同学去划船,他们算了一下，如果增加一条船,正好每条船坐6人；如果减少一条船,正好每条船坐9人.问：这个班共有多少学生？4.将月季花插入一些花瓶中。

如果每瓶插8朵，则缺少15朵；如果每瓶改为插6朵，则缺少1朵。

奥数知识二十八——盈亏问题（1）盈亏问题（1）盈亏问题又叫盈不足问题，是指把固定数量的物品平均分给固定的对象，因为两种不同的分配标准，导致两种不同的分配结果：一种标准分配后有剩余（盈）；另一种标准分配后不够分（亏或不足）。

此类问题，要求通过两种分配结果的比较，求出物品总数量和固定对象的个数。

标准的盈亏问题就是两次分配的结果一盈一亏，所以就叫盈亏问题。

基本的数量关系是：（盈+亏）÷两种分配标准的数量之差＝固定对象数量。

广义的盈亏问题一般还包括以下四种情况：一、两次分配都有余（两盈）；二、两次分配都不够分（两亏）；三、一次有余，一次刚好够分（盈适足）；四、一次分配不够分，一次刚好够分（亏适足）。

解决盈亏问题常用比较的解题策略：通过两次分配盈亏总额与分配数量的比较，先求出固定对象的个数，再求出分配物品的总数量。

此类问题基本数量关系有：①盈适足问题：盈余部分÷两种分配标准的数量之差＝固定对象数量。

②亏适足问题：亏欠部分÷两种分配标准的数量之差＝固定对象数量。

③两盈问题：（盈多－盈少）÷两种分配标准的数量之差＝固定对象数量。

④两亏问题：（亏多－亏少）÷两种分配标准的数量之差＝固定对象数量。

⑤盈亏问题：（盈+亏）÷两种分配标准的数量之差＝固定对象数量。

比较常规的盈亏问题，一般可以直接套用上面的数量关系，解决问题。

较复杂的盈亏问题，一般需要先对题中的条件进行适当的转化，将相关问题先转化成典型的盈亏问题，再求解。

【题目】：“雏鹰小队”的同学们参加植树活动，如果每人栽5棵树，还剩12棵树；如果每人栽7棵，就缺4棵。

问这个小队有多少人？一共要栽多少棵树？【解析】：可以画出线段图帮助理解题意，如下图：观察上图，比较每人栽7棵与每人栽5棵的两种情况，雏鹰小队总人数是不变的。

雏鹰小队栽树总棵数多出：12＋4=16（棵）；而每个人多栽：7－5=2（棵）；所以小队人数为：（12＋4）÷（7－5）=8（人）。

实践练习
练：幼儿园把一些积木分给小朋友，如果每人分2个，则剩
下20个；如果每人分3个，则差40个。幼儿园有多少个小朋
友？一共有多少个积木？
步 骤 盈亏图 2 2 2 33 3
总差
剩下 20 个 缺少 40 个
总差： 20+40＝60（个）小朋友的总人数： 60÷（3-1）＝60（人） . 去相同比不同 一共的积木数量： 60×2+20＝140（. 个）
盈亏问题之能力挑战题
实践练习
同学们早餐吃面包，每袋面包10片，开始来了10个同学，老师 给每个人发了同样多片之后，发现还剩下两包，后来又来了5个 同学，老师也给每个发了与之前同样多片之后，发现还剩下5片， 请问：老师开始准备了几片面包？
步骤
总差
剩下 2 包 剩下 5 片
谢 谢！
实践练习
小高准备了一些棒棒糖发给班里的同学，开始发给3个同学，还剩 下20根。后来又来了4名同学，如发给他们同样多的棒棒糖后，还 缺少20根。请问：小高开始一共准备了多少根棒棒糖？
思路解析
剩下 20 颗
两次分得差 盈+亏、盈+盈
缺少 20 颗
总差： 20+20＝40（根）每个同学分到的糖果： 40÷4＝10（根） . 去相同比不同 老师买了的糖果： 3×10+20＝50（.根）
3.前后二次分配的人数
。
4.前后二次分配的物品
。
盈亏问题之人数不同
例：老师给5个同学一样多的糖，还剩下17颗糖，这时又来
了2个同学，老师也给了他们同样多的糖，还剩下11块糖，
你知道每个同学分到多少颗糖吗？老师一共买多少颗糖？
步 骤 盈亏图
总
剩下 17 颗 差

盈亏问题（一）数学钥匙：盈亏问题是指把一定数量的物品平均分给固定的对象，如果按某种标准分，则分配后有剩余（盈）；按另一种标准分，分配后又有不足（亏），求物品的数量和人数。

盈亏问题有五种基本类型：1、一盈一亏：分配对象的个数=（盈+亏）÷两次分配的数量差2、一盈一尽：分配对象的个数= 盈÷两次分配的数量差3、一亏一尽：分配对象的个数= 亏÷两次分配的数量差4、两盈：分配对象的个数=（大盈－小盈）÷两次分配的数量差5、两亏：分配对象的个数=（大亏－小亏）÷两次分配的数量差例题剖析：例1：幼儿园某班小朋友分水果糖，如果每人分4颗，则剩下20颗；如果每人分5颗，则差5颗。

求小朋友的人数和水果糖的颗数。

练习：1、方阿姨给幼儿园小朋友分苹果，如果每人分3个多16个；如果每人分5个，那么就差4个苹果，问有多少个小朋友？多少个苹果？2、小玲带了一些钱去买苹果，如果买3千克，则多出2元；如果买6千克，则少了4元，苹果每千克多少元？小玲带了多少钱？例2：刘阿姨给小朋友分苹果，如果每人分3个苹果，则多16个苹果；如果每人分5个苹果，则正好分完，那么刘阿姨买了多少个苹果，分给几个小朋友？例3：学校买来一些故事书，每班发16本，正好分完；每班发18本，少40本，则买故事书多少本？分给几个班？练习：1、学校安排学生住校，每个房间住3人；则多出40人；每个房间住5人，恰好能安排完。

问房间和学生各有多少人？2、有一堆梨分给一些小朋友，如果每人分10个，还少20个；如果每人分8个，正好分完，问有几个小朋友，有多少个梨？例4：有一些少先队员到山上去种一批树。

如果每人种16棵，还有24棵没种；如果每人种19棵，还有6棵没有种。

问有多少名少先队员？有多少棵树？例5：将月季花插入一些花瓶中。

如果每瓶插8朵，则缺少15朵；如果每瓶改为插6朵，则缺少1朵。

求花瓶的只数和月季花的朵数。

练习：1、学校将一批铅笔奖给三好学生。

课前预热
现在有一筐苹果平均分给一群小朋友.按如下的方法分： 请判断那种分法是盈，哪种分法是亏。
①如果每人分4个苹果，就剩余39个苹果（ ）； ②如果每人分8个苹果，就还差9个苹（ ）；
③如果每人分6个苹果，就剩余15个苹果（ ④如果每人分10个苹果，就还差33个苹（
）； ）；
知识加油站
• 盈亏问题又叫盈不足问题，是指把一定数 量的物品平均分给固定的对象，如果按某 种标准分，则分配后会有剩余（盈）；按 另一种标准分，分配后又会有不足（亏）， 求物品的数量和分配对象的数量。
盈亏问题的分类
• 它们可以分为五类： （1）一盈一亏：一次分配有余，一次分配不
足 （2）两盈：两次分配都有剩余. （3）两亏：两次分配都不够. （4）盈适足：一次分配有余，一次分配正好 （5）亏适足：一次分配不够，一次分配正好.
例1：幼儿园老师给小朋友分苹果，如果每人 分4个，则多9个；如果每人分5个，则少6个. 问有多少个小朋友？有多少个苹果？
• （大亏－小亏）÷两次分配数量的差=分配 对象
如果在题中直接出现了盈亏，大盈小盈， 大亏小亏。则我们可以直接套用基本公式来 计算。如果题中没有这些量，则我们可以利 用题中的已知信息将盈亏，大盈小盈，大亏 小亏挖掘出来，然后利用基本公式来计算。
19
• 两亏 • 解：（17－3）÷（5－3）＝7（人） • 5×7－17＝18（本） • 答：阿乐的同学有7人，她有18本连环画。
练习：
• 六一班第一小队的同学去植树，如果每人 栽8棵则少27棵；如果每人栽6棵则少5棵。 六一班第一小队有多少个同学？他们要栽 多少棵树？
例3：学校分配宿舍，每个房间住3人，则多 出20人；每个房间住5人，恰恰安排好，问房 间和学生各有多少？

推理问题中的条件繁杂交错，解题时必须根据事 情的逻辑关系进行合情推理，仔细分析，寻找突 破口，并且可以借助于图表，步步深入，这样才 能使问题得到较快的解决。
例题1 ： 有8个球编号是（1）——（8）， 其中有6个球一样重，另外两个球都轻1克。 为了找出这两个轻球，用天平称了3次，结 果如下：
第一次：（1）+（2）比（3）+（4）重；
分析：
因为小英获得了语文第一名，所以， 小明获得的第一名只能是英语或数 学，而小明已获得了数学第二名， 不可能再获得数学第一名，因此， 获得英语第一名的一定是小明。
例题4： 小明看一本书，如果看过的 页数每天比前一天增加一倍，7天正好 看完。已知这本书一共96页，他第几 天看到了12页？
分析：
第二次：（5）+（6）比（7）+（8）轻；
第三次：（1）+（3）+（5）与（2）+（4） +（8）一样重。
那么，两个轻球分别是几号？
分析：
从第一次看，（3）、（4）两球中有 一个轻；从第二次看，（5）、（6）两球 中有一个轻；从第三次看，（1）、（3）、 （5）中有一个轻，（2）、（4）、（8） 中也有一个轻。
（1）许兵说：桌凳不是我修的。
（2）李平说：桌凳是张明修的。
（3）刘成说：桌凳是李平修的。
（4）张明说：我没有修过桌凳。
后经了解，四人中只有一个人说的是真话。 请问：桌凳是谁修的？
例题6：虹桥小学举行科技知识竞赛， 同学们对一贯刻苦学习、爱好读书的 四名学生的成绩作了如下估计：
（1）丙得第一，乙得第二。
例题8：六年级有四个班，每个班都有 正、副班长各一人。平时召开年级班 长会议时，各班都只有一人参加。参 加第一次回师的是小马、小张、小刘、 小林；参加第二次会议的是小刘、小 朱、小马、小宋；参加第三次会议的 是小宋、小陈、小马、小张，小徐因 有病，三次都没有参加。你知道他们 哪两个是同班的吗？

投资问题是盈亏问题中较为复杂的一种类型，涉及到资金的投入和回报。在解决这类问题时，需要考虑本金、利 息和收益之间的关系。通过比较投入和回报，可以确定投资是否盈利。
05
练习与巩固
基础练习题
总结词
掌握基本概念
详细描述
提供简单的盈亏问题，让学生理解盈亏问题的基本概念，如“盈利”、“亏损”等，并能够进行简单 的计算。
盈亏问题基本概念
盈与亏的含义
盈
表示盈利、有多余的意思。在盈 亏问题中，盈通常指的是完成任 务后，有多余的人或物。
亏
表示亏损、不足的意思。在盈亏 问题中，亏通常指的是完成任务 后，人或物不足的情况。
盈亏问题的基本公式
公式
盈亏问题可以通过一个简单的公式来 解决：完成任务所需的总人数 = （ 盈 + 亏）÷ （每人完成任务的效率 ）。
解决盈亏问题的重要性
解决盈亏问题可以帮助我们更好地理解公平和公正的概念，并学会如何在现实生活 中应用这些概念。
通过解决盈亏问题，我们可以培养自己的逻辑思维和数学思维能力，提高解决问题 的能力。
在团队合作和组织管理中，解决盈亏问题也是非常重要的，可以帮助团队成员更好 地协作，避免出现不公平的情况。
02
。
举例说明需要选择具有代表性的 问题，并详细解释解题过程和思
路。
通过举例说明，可以帮助学生更 好地掌握解决盈亏问题的方法，
提高解题能力。
04
常见盈亏问题类型
买卖问题
总结词
涉及物品的买入和卖出，需要考虑成本、售价和利润。
详细描述
买卖问题是盈亏问题中最常见的类型，涉及到商品的购买和销售。在解决这类 问题时，需要考虑商品的成本、售价以及利润。通过比较成本和售价，可以确 定是否盈利或亏损。

关系式：人数或单位数=（亏数-亏数）÷两次分配之差
完整版ppt课件
15
1.直接计算型—亏亏问题
例：学校新进了一批书，将它们分给几位老师，如果每人发10本，还差9 本，每人发9本，还差2本，请问有多少老师？多少本书？
【分析】老师的人数是不变的。所以第一次与第二次相比，不够的数减 少了7本，这是由于每个人少发了一本导致的结果。
显然，第二次绕的一圈，实际用掉绳子长为：4+1=5米。 所以，绳子总的长度为49米，绕8圈则剩下：49-8×5=9米
也可以这样计算绕8圈后剩下的绳子：(9-8)×（4+1）+4=9
完整版ppt课件
6
例3、人民路小学三、四、五年级的同学乘汽车去春游，如果每车坐45人， 有10人不能坐车；如果每车多坐5人，又多出一辆车。一共有多少辆 汽车？有多少名同学去春游？
原计划去的人为：22×30+1=661人
完整版ppt课件
9
例6、果树专业队上山植果树，所需栽的苹果树苗是梨树苗的2倍。如果梨 树苗每人栽3棵，还余2棵；苹果树苗每人栽7棵，则少6颗。问：果 树专业队上山植树的有多少人？要栽多少颗苹果树和梨树？
【分析】这个题目需要关注的是苹果树苗与梨树苗不是等值的，而是存在2倍 关系。所以余下的2棵梨树苗应该折算成2×2=4棵苹果树苗。
完整版ppt课件
10
第二讲 提高篇
完整版ppt课件
11
1.直接计算型--盈亏问题
一般情况下，两次分配的结果，一次分配后有多，即“赢”；一次 分配后不足，即“亏”。如基础部分所讲的案例，都是属于这一类。
用下面线段来表示，蓝菊相交点为分配平衡点，蓝线为多余部分， 虚线为不足部分。由于单位内的数量不等，经过单位数的累积，导致蓝 菊线的出现原因。

第一讲：盈亏问题专题分析：在日常生活中有这样的问题，一定数量的物品分给一定数量的人，每人多一些，物品就不够，每人少一些，物品就有余。

盈亏问题就是在已知盈亏的情况下来确定物品总数和参与分配的人数。

解答盈亏问题的关键是弄清盈、亏与两次分得差的关系。

盈亏问题的数量关系式是：1、（盈＋亏）÷两次分配差＝份数2、（大盈－小盈）÷两次分配差＝份数3、（大亏－小亏）÷两次分配差＝份数入门题：1、一个植树小组植树，如果每人栽5棵，还剩14棵；如果每人栽7棵，就缺4棵。

这个植树小组有多少人？2、学校将一批铅笔奖给三好学生。

如果每人奖9支，就缺45支；如果每人奖7支，则缺7支。

三好学生有多少人？铅笔有多少支？3、有一些少先队员到山上种一批树。

如果每人种16棵，还有24棵没种；如果每人种19棵，还有6棵没种。

问有多少名少先队员？有多少棵树？4、学校给一批新入学的学生分配宿舍。

如果每个房间住12人，则34人没有位置；如果每个房间住14人，则空出4个房间。

求学生宿舍有多少间？住宿学生有多少人？5、少先队员去植树。

如果每人挖5个树坑，还有3个树坑每人挖；如果其中2人各挖4个，其余的人各挖6个树坑，就恰好挖完所有树坑。

少先队员一共挖了多少个树坑？练习题：1、某学校安排宿舍。

如果每间住6人，则16人没有床位；如果每间住8人，则多出8个床位。

问宿舍有多少间？学生有多少人？2、王老师给美术兴趣小组的同学分发图画纸。

如果每人发5张，则少32张；如果每人发3张，则少2张。

美术兴趣小组有多少人？一共有多少张图画纸？3、杨老师将一叠练习本分给一组同学。

如果每人分7本，还多7本；如果每人分8本，正好分完。

这一小组有多少人？这叠练习本有多少个？4、育才小学学生乘汽车去春游。

如果每车坐65人，则有15人不能乘车；如果每车多坐5人，恰好多余一辆车。

问有几辆汽车？有多少学生？5、在一次大扫除中，老师分配一些同学擦玻璃。

盈亏问题（第一讲）盈亏问题的特点是问题中每一同类量都要出现两种不同的情况．分配不足时，称之为“亏”，分配有余称之为“盈”；还有些实际问题，是把一定数量的物品平均分给一定数量的人时，如果每人少分，则物品就有余(也就是盈)，如果每人多分，则物品就不足(也就是亏)，凡研究这一类算法的应用题叫做“盈亏问题”。

盈亏问题是一类古老的问题。

它讨论的是：在分配物品时，人数一定，在两种分配方案中，第一种分配有余（盈），第二种分配不足（亏）；或者两种都不足，或者两种都有余。

解答的关键是要求出总差额和两次分配的数量差，然后利用基本公式求出分配者人数，进而求出物品的数量。

盈亏问题的基本关系式：盈亏总额÷两次分配数之差＝份数。

一次有余（盈），一次不够（亏），可用公式：(盈+亏)÷两次每人分配数的差=分的人数或单位数物品数可由其中一种分法和人数求出。

每次分的数量×份数＋盈=总数量每次分的数量×份数－亏=总数量※小朋友分桃子，每人8个多7个，每人10个少9个。

有（）个小朋友，有（）个桃子。

※智康学校三年级精英班的一部分同学分糖果，如果每人分4个就多9个，如果每人分5个则少6个，问：有（）位同学，有（）个糖果。

※一堆糖果有十几颗，每人分4块多2块，每人分5块少1块，想一想，有（）块糖果，有（）个人。

※秋天到了，小白兔收了一些萝卜，它按照计划吃的天数算一下，如果每天吃4个，则多出8个萝卜；如果每天吃6个，则又少8个萝卜，那么小白兔收回有（）个萝卜，计划吃（）天。

※一个植树小组植树。

如果每人栽5棵，还剩14棵；如果每人栽7棵，就缺4棵。

这个植树小组（）人，一共有（）棵树。

※三年级一班少先队员参加学校搬砖劳动，如果每人搬4块，还剩7块；如果每人搬5块，则少2块，参加劳动的少先队员有（）个，要搬的砖共有（）块。

※幼儿园把一些积木分给小朋友，如果每人分2个，则剩下20个；如果每人分3个，则差40个。

小学数学盈亏问题专题讲解，太棒了，家长照着辅导准没错！一、基本题型第一类：一盈一亏例1：阿姨给幼儿园小朋友分饼干.如果每人分3块，则多出16块饼干；如果每人分5块，那么就缺4块饼干.问有多少小朋友，有多少块饼干？分析：依题中条件，我们可知：第一种分法：每人3块，还剩16块第二种分法：每人5块，还少4块我们可以比较看出：由于第二种分法比第一种分法每人多分了2块，所以不仅把那剩下的16块分完，还少4块，总数上，第二次比第一次多16+4=20块。

换句话说：每人多分2块，就得多分20块，我们就可以算出有多少人了，20÷2=10人，那总饼干数就是：10×3+16=46或10×5-4=46第二类：二次都是盈例：阿姨给幼儿园小朋友分饼干.如果每人分3块，则多出16块饼干；如果每人分5块，那么就多4块饼干.问有多少小朋友，有多少块饼干？第二种分法：每人5块，还多4块我们可以比较看出：由于第二种分法比第一种分法每人多分了2块，所以饼干由剩下16块变成只剩下4块，总数上，第二次比第一次多16-4=12块。

换句话说：每人多分2块，就得多分12块，我们就可以算出有多少人了，12÷2=6人，那总饼干数就是：6×3+16=34或6×5+4=34第三类：二次都是亏例：阿姨给幼儿园小朋友分饼干.如果每人分3块，则少4块饼干；如果每人分5块，那么就少16块饼干.问有多少小朋友，有多少块饼干？第一种分法：每人3块，还少4块第二种分法：每人5块，还少16块我们可以比较看出：由于第二种分法比第一种分法每人多分了2块，所以饼干由少4块变成了少16块，总数上，第二次比第一次多16-4=12块。

换句话说：每人多分2块，就得多分12块，我们就可以算出有多少人了，12÷2=6人，那总饼干数就是：6×3-4=14或6×5-16=14二、变化题型语言上的变化例：同学去划船，如果每只船坐4人，则少1只船；如果每只船坐6人，则多出4只船，问同学们共多少人？租了几只船？分析：讲解时，可先让学生练习以下这道题，引导学生在对比两道例题异与同，进行条件转换。

老师给小朋友们分糖果。如果每个小朋友分到7 颗，那么剩下17 颗； 如果每个小朋友分到9 颗，那么剩下1 颗。 （1） 第一种分配方案属于盈亏问题中的_______（填写“盈”或“亏”） ，第二种分配方案属于盈亏问题中的_______（填写“盈”或“亏”）。 （2）两种分配方案的盈数差是_______ 颗。 （3）两种分配方案的分配差是_______ 颗。
盈亏问题初步
一年一度的花果山庆祝大会又 要开始了，齐天大圣孙悟空准 备先把收获的桃子分给第一批 猴子，每人5个余下15个，每 人6个桃子正好分完，问第一 批猴子有多少只？
一年一度的花果山庆祝大会又 要开始了，齐天大圣孙悟空准 备先把收获的桃子分给第一批 猴子，每人5个余下15个，每 人6个桃子正好分完，问第一 批猴子有多少只？
牛刀小试4-2
老师给小朋友们分糖果。如果每个小朋友分到7 颗，那么缺少10 颗； 如果每个小朋友分到5 颗，那么缺少 2 颗。
（1） 第一种分配方案属于盈亏问题中的___亏____（填写“盈”或“亏”） ；第二种分配方案属于盈亏问题中的_亏______（填写“盈”或“亏”）。 （2）两种分配方案的亏数差是__8_____ 颗。 （3）两种分配方案的分配差是__2_____ 颗。
练习1-2
老师给小朋友们分巧克力。如果每个小朋友分到5 块，那么剩下 28块；如果每个小朋友分到9 块，那么刚好分完。有多少个小朋友？ 老师一共有多少块巧克力？
小朋友：28÷（9-5）=7（个） 巧克力：7×9=63（块）
答：有7个小朋友，老师一共有63块巧克力。
牛刀小试2-1
老师给同学们发作业本。每个同学得到同样多的作业本 后，还剩下20 本。后来老师又给新来的2 个同学也发了 同样数量的作业本，这样就只剩下12 本了。每个同学得 到几本作业本？ （1）新来2 个同学对应少剩下_______ 本作业本。 （2）每个同学得到_______ 本作业本。

第一讲：僧多粥少知识精讲：例1：老师给同学们分积分卡,分给5个同学,每人分到的一样多,还剩下22分,后来又来了2个同学,分给他们同样多的积分后,就只剩下6分了,请问:每名同学分到多少分?练习：小高准备了一些棒棒糖发给班里的同学,开始发给7名同学,还剩下14根,后来又来了3名同学,发给他们同样多的棒棒糖后,就只剩下5根了,请问:每名同学分到了多少根棒棒糖?例2：同学们早餐吃面包,开始来了9个同学,老师给每人发了同样多片之后发现,还剩下30片.后来又来了5个同学,老师也给每人发了与之前同样多的面包后,还剩10片,请问:老师开始准备了几片面包？练习：小高准备了一些棒棒糖分给班里的同学,如果开始有3人,给每人发了同样多根棒棒糖,那么最后多20根;后来又来了4人,也给每人发了与之前同样多的棒棒糖后,还多8根,请问:小高一共准备了多少根棒棒糖?知识精讲：一般我们把分配完之后有剩余的情况称作“盈”,不够的情况称作“亏".如果两次分配完之后,东西都有多余,这样的问题我们可以称为“盈盈问题”,解决这类问题的方法就是比较前后两次分配情况的不同。

例3 ：老师给学生分苹果,如果每人分3个苹果,那么就会剩下20个苹果;如果每人分5个苹果,那么就会剩下8个苹果.请问:一共有多少名同学?练习：学校买了一批电灯准备安在教室,如果每间教室安4盏灯,那么就剩50盏灯;如果每间教室安6盏灯,那么就剩10盏灯.学校一共有多少间教室?例4：裁缝要往一些西服上缝扣子,如果每件西服缝3个扣子,还会剩下26个扣子;如果每件缝5个,就只剩下4个扣子了,请问:一共有几件西服?裁缝一共有多少个扣子?练习：小高准备了一些棒棒糖分给班里的同学,如果给每个同学5根棒棒糖,那么最后还能剩27根;如果给每个同学3根棒棒糖,那么最后能剩下79根,请问:小高一共准备了多少根棒棒糖?挑战自我：同学们早餐吃面包,每袋面包有10片,开始来了10个同学,老师给每人发了同样多片之后,发现还剩下两袋面包,后来又来了5个同学,给新来的同学每人发同样多的面包后,发现还剩下5片面包,请问:老师准备了几袋面包?自我巩固：1.绵羊村村长给羊羊们发青草蛋糕,每只羊分得的同样多,还剩下10块青草蛋糕,后来又来了2只小山羊,村长也发给它们同样多的青草蛋糕,这时青草蛋糕恰好全部分完,那么每只羊分得多少块青草蛋糕？2.墨莫买了一些糖,分给4个同学,每人分到的一样多,还剩下24块糖,后来又来了2个同学,分给他们同样多的糖后,就只剩下14块糖了.那么每人分到多少块糖？3.王老师买了5个苹果,还剩10元;后来又买了2个,结果只剩下2元,那么王老师共带了多少元？4.小高买了一些苹果,分给6个同学,每人分到的一样多,还剩下15个苹果,后来又来了3个同学,分给他们同样多的苹果后,就只剩下6个苹果了.那么小高一共买了多少个苹果？5.裁缝要往一些西服上缝扣子,如果每件西服缝4个扣子,还会剩下36个扣子;如果每件缝6个,就只剩下24个扣子,那么裁继要缝制多少件西服？6.学校买了一批电灯准备安在教室,如果每间教室安6盏灯,就剩55盏灯;如果每间教室安8盏灯,就剩15盏灯,那么学校一共有多少间教室？7.小高准备了一些棒棒糖分给班里的同学,如果给每个同学7根棒棒糖,那么最后还能剩28根;如果每个同学分3根棒棒糖,那么最后能剩下80根,那么小高一共准备了多少根棒棒糖？8.老师给学生分苹果,如果每人分2个苹果,就会剩下26个苹果;如果每人分5个苹果,就会剩下14个苹果,那么一共有多少名同学？9.裁键做好了一些西服,现在要往上面缝扣子,如果每件西服缝3个扣子,还会剩下26个扣子;如果每件缝5个,扣子正好用完,裁缝一共有多少个扣子？10.王老师去买包子,开始他买了8个包子,还剩下7元3角;后来又买了3个包子,结果只剩下3元7角了.王老师一共带了多少角？课内培优：小题精写：1.红红在一个长为25米的泳池中游了2个来回游了（）米；2.22×39的积是（）位数，最高位是（）位。

五年级秋季培优第一讲盈亏问题在日常生活中有这样的问题，一定数量的物品分给一定数量的人，每人多一些，物品就不够（称作“亏”）；每人少一些，物品就有余（称作“盈”）。

盈亏问题就是在已知盈亏的情况下确定物品总数和参加分配的人数。

解答盈亏问题的关键是弄清盈、亏与两次分得的差的关系。

基本解题方法有以下几种：一盈一尽类：盈数÷两次分得之差＝份数一亏一尽类：亏数÷两次分得之差＝份数一盈一亏类：（盈＋亏）÷两次分得之差＝份数两次皆盈类：（大盈－小盈）÷两次分得之差＝份数两次皆亏类：（大亏－小亏）÷两次分得之差＝份数每次分的数量×份数＋盈＝总数量每次分的数量×份数－亏＝总数量典例精讲例1 学校将一批铅笔奖给三好学生。

如果每人奖9支，则缺45支；如果每人奖7支，则缺7支。

三好学生有多少人？铅笔有多少支？【思路点拨】分析两种分配方法：每人9支，少45支；每人7支，少7支。

这是两亏的问题。

由题意知：三好学生人数和铅笔支数是不变的。

比较两种分配方案，结果差45－7＝38（支）。

这是因为两种分配方案每人得到的铅笔数相差9－7＝2（支）。

所以，三好学生有38÷2＝19（人），铅笔有9×19－45＝126（支）。

【详细解答】例2 学校为新生分配宿舍。

若每个房间住10人，则多出14人；若每个房间住12人，还多出2人。

宿舍多少间？新生有多少人？【思路点拨】这是一个两次剩余（两盈）的问题，经分析，每间住12人比每间住10人多住12－10＝2（人），一间多住2人，共多住14－2＝12（人），则宿舍间数为12÷2＝6（间）。

宿舍数有了，新生数便可求得。

【详细解答】例3 三（1）班学生去公园划船，如果每条船坐4人，则少一条船；如果每条船坐6人，则多出4条船。

公园里有多少条船？三（1）班有多少个学生？【思路点拨】为了帮助理解，我们可以将题目中的条件进行转化。