东城 学年度第二学期期末教学目标检测

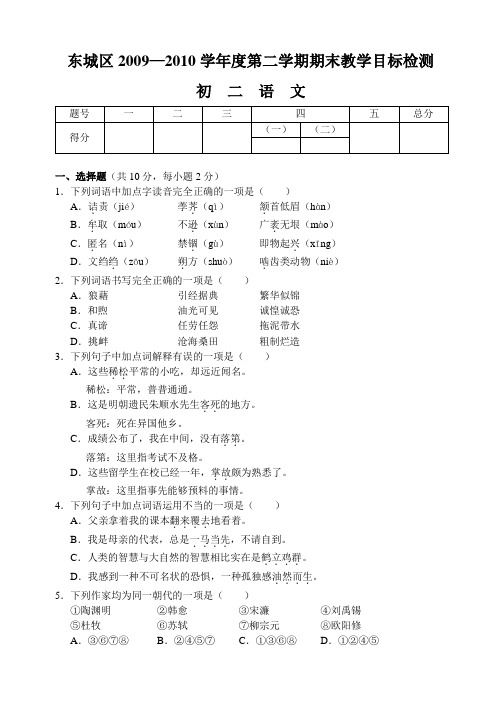
东城区2009—2010学年度第二学期期末教学目标检测初二语文一、选择题（共10分，每小题2分）1．下列词语中加点字读音完全正确的一项是（）A．诘．责（jié）荸荠．（qì）颔．首低眉（hàn）B．牟．取（móu）不逊．（xùn）广袤．无垠（mào）C．匿．名（nì）禁锢．（gù）即物起兴．（xīng）D．文绉绉．（zōu）朔．方（shuò）啮．齿类动物（niè）2．下列词语书写完全正确的一项是（）A．狼藉引经据典繁华似锦B．和煦油光可见诚惶诚恐C．真谛任劳任怨拖泥带水D．挑衅沧海桑田粗制烂造3．下列句子中加点词解释有误的一项是（）A．这些稀松．．平常的小吃，却远近闻名。

稀松：平常，普普通通。

B．这是明朝遗民朱顺水先生客死．．的地方。

客死：死在异国他乡。

C．成绩公布了，我在中间，没有落第．．。

落第：这里指考试不及格。

D．这些留学生在校已经一年，掌故．．颇为熟悉了。

掌故：这里指事先能够预料的事情。

4．下列句子中加点词语运用不当的一项是（）A．父亲拿着我的课本翻来覆去．．．．地看着。

B．我是母亲的代表，总是一马当先．．．．，不请自到。

C．人类的智慧与大自然的智慧相比实在是鹤立鸡群．．．．。

D．我感到一种不可名状的恐惧，一种孤独感油然而生．．．．。

5．下列作家均为同一朝代的一项是（）①陶渊明②韩愈③宋濂④刘禹锡⑤杜牧⑥苏轼⑦柳宗元⑧欧阳修A．③⑥⑦⑧B．②④⑤⑦C．①③⑥⑧D．①②④⑤二、简答题（16分）6．默写（8分）（1）至若春和景明，________，________，一碧万顷。

（范仲淹《岳阳楼记》）（2）作亭者谁？________。

名之者谁？________。

（欧阳修《醉翁亭记》）（3）沉舟侧畔千帆过，________________。

________________，暂凭杯酒长精神。

（刘禹锡《酬乐天扬州初逢席上见赠》）（4）《水调歌头》“此事古难全”中的“此事”是指：___________，___________。

第1页（共7页）东城区2023-2024学年度第二学期期末教学统一检测高二数学参考答案及评分标准2024.7一、选择题（共10小题，每小题4分，共40分）（1）B（2）A （3）D （4）A （5）C （6）B （7）B （8）C （9）A （10）D二、填空题（共5小题，每小题5分，共25分）（11）(1,)+∞（12）2213y x -=（13）540（14）20（15）①③三、解答题（共6小题，共85分）（16）（共13分）解：（Ⅰ）设事件A ：单局比赛中甲4:0领先，则44114()552225P A =⨯⨯⨯=．……………………………………6分所以单局比赛中甲4:0领先的概率是425．（Ⅱ）设事件B ：乙以3:1赢得比赛，则133212()()3327P B C =⨯⨯=．所以乙以3:1赢得比赛的概率为227．……………………………………13分（17）（共13分）解：（Ⅰ）依题意，(0)f a b ==.因为()e 1x f x a '=+，所以(0)1f a '=+.依题意，(0)1f '=-，故11a +=-，得2a =-.所以2a b ==-.……………………………………7分第2页（共7页）(Ⅱ)由(Ⅰ)知，()21x f x e '=-+.令()0f x '=，解得ln 2x =-.令()0f x '>，得ln 2x <-，所以()f x 在区间(,ln 2)-∞-上单调递增；令()0f x '<，得ln 2x >-，所以()f x 在区间(ln 2,)-+∞上单调递减.所以()f x 的单调递增区间为(,ln 2)-∞-；单调递减区间为(ln 2,)-+∞.………………………………………….……13分（18）（共14分）解：（Ⅰ）设事件A ：遥遥在6个新能源汽车品牌中选出2个品牌作比较，品牌1A 被选中，则15261()3C P A C ==．所以遥遥在6个新能源汽车品牌中选出2个品牌作比较，品牌1A 被选中的概率是13．………………………………………….……4分（Ⅱ）12个整点或半点中，“峰时”有6个，“平时”有4个，“谷时”有2个．X 的所有可能取值为36，45，54．2(36)12P X ==，4(45)12P X ==，6(54)12P X ==，所以X 的分布列为X364554P 161312所以111()36455448632E X =⨯+⨯+⨯=（元）.…………………….……9分（Ⅲ）按新车使用8年计算，燃油汽车使用的燃油费为30000831440005⨯⨯=（元），新能源汽车使用电费最多为300008(1.00.8)864005⨯⨯+=（元），因为购买新能源汽车比燃油汽车多花费40000元，第3页（共7页）所以144000400008640017600--=（元）．新能源汽车至少比燃油车总花费少17600元，所以选择新能源汽车总花费更少．…………………….……14分（19）（共15分）解：（Ⅰ）由椭圆2222:1(0)x y E a b a b+=>>过点0（，得b =.因为3AFB π∠=，所以1c =．由于222a b c =+，解得24a =.所以E 的方程为22143x y +=．…………………….……4分（Ⅱ）设直线PQ 的方程为1x my =+．由221,143x my x y =+⎧⎪⎨+=⎪⎩，得22(34)690m y my ++-=,所以222(6)36(34)1441440m m m ∆=++=+>.设1122(,),(,)P x y Q x y ，则122634m y y m +=-+，122934y y m =-+.直线AP 的方程为11(2)2y y x x =++，令4x =，得点M 的纵坐标为11116623M y y y x my ==++.同理可得点N 的纵坐标为2263N y y my =+.()()12121244141339N M N M y y y y y y k k my my =⋅==--++12212123()94y y m y y m y y +++=22222363491893434m m m m m =-+--+++1=-.所以12k k 为定值.…………………….……15分（20）（共15分）解：（Ⅰ）函数()f x 的定义域为(0,)+∞.第4页（共7页）当2a =时，222(1)()2x f x x x x-'=-=.令()0f x '=，解得1x =，或1x =-(舍).当x 变化时，()f x '，()f x 的变化情况如下表所示：x (0,1)1(1,)+∞()f x '-0+()f x 单调递减0单调递增因此，当1x =时，()f x 有极小值，极小值为(1)0f =.（Ⅱ）22()2a x a f x x x x-'=-=.(1)当2a ≤时，因为(1,)x ∈+∞，所以220x a ->.所以()0f x '>.所以()f x 在区间(1,)+∞上单调递增.故()(1)0f x f >=，满足题意.(2)当2a >时，令()0f x '<，得212x <<.所以()f x 在区间22上单调递减.所以2((1)02f f <=,不符合题意.综上可知，(,2]a ∈-∞.…………………….……9分（Ⅲ）当2a ≤时，由（Ⅱ）知，对任意(1,)x ∈+∞，()0f x >恒成立，所以()f x 在区间(1,)+∞没有零点，不符合题意.当2a >时，因为()fx 在区间上单调递减，且(1)0f =，所以()f x 在区间上无零点.因为()f x 在区间(1,)+∞上存在唯一零点0x ，所以022x >.因为当2x >时，()0f x '>，所以函数()f x 在()2+∞上单调递增.要证20e a x -<，只要证20()(e )a f x f -<，即只要证2(e )0a f ->.224(e )e (2)1a a f a a --=---，令20t a =->，只要证2e (2)10t t t -+->.第5页（共7页）令2()e (2)1(0)x g x x x x =-+->，2()2e 22x g x x '=--.令2()2e 22x h x x =--，当0x >时，24e 2)0(x h x -'=>，所以()g x '在区间(0,)+∞上单调递增，则有()(0)0g x g ''>=.所以()g x 在区间(0,)+∞上单调递增，则有()(0)0g x g >=，于是2(e )0a f ->得证.故20e a x -<.…………………….……15分（21）（共15分）解：（Ⅰ）因为数列4:1,2,3,4A ，4():3,1,4,2T A ，所以24():4,3,2,1T A ，34():2,4,1,3T A ，44():1,2,3,4T A ．…………….……4分（Ⅱ）对数列4A 的任意变换T ，①若存在{1,2,3,4}i ∈，有()i i T a a =，则35()i i i T a a a -=≠，则T 不是4A 的3阶逆序变换．②若对{,,,}{1,2,3,4}i j s t =，有()i j T a a =，()j i T a a =，()s t T a a =，()t s T a a =，则32()()()i j i T a T a T a ==，3()()j j T a T a =，3()()s s T a T a =，3()()t t T a T a =．所以34()T A 和4()T A 是相同的数列．若34()T A 是4A 的逆序排列，则4()T A 也是4A 的逆序排列．所以T 不是3阶逆序变换．③若对{,,,}{1,2,3,4}i j s t =，有()i j T a a =，()j s T a a =，()s t T a a =，()t i T a a =，则32()()()i j s t T a T a T a a ===，32()()()t i j s i T a T a T a a a ===≠．所以T 不是4A 的3阶逆序变换．综上所述，对于4项数列4A ，不存在3阶逆序变换．………………….……9分（Ⅲ）由（Ⅱ）知，4项数列4A 不存在3阶逆序变换．第6页（共7页）对于3项数列3123:,,A a a a ，①若11()T a a =，则3113()T a a a =≠，所以变换T 不是3A 的3阶逆序变换．②若12()T a a =，当21()T a a =时有33()T a a =，则3331()T a a a =≠，所以变换T 不是3A 的3阶逆序变换．当23()T a a =时有31()T a a =，则3212313()()()T a T a T a a a ===≠，所以变换T 不是3A 的3阶逆序变换．③若13()T a a =，同②可知，变换T 不是3A 的3阶逆序变换．所以3项数列3A 不存在3阶逆序变换．对于5项数列512345:,,,,A a a a a a ，若存在3阶逆序变换T ，则315()T a a =，324()T a a =，333()T a a =，342()T a a =，351()T a a =．①若33()T a a =，则对于数列41245:,,,A a a a a 和上述的变换T ，有315()T a a =，324()T a a =，342()T a a =，351()T a a =．所以这个4项数列41245:,,,A a a a a 存在3阶逆序变换，与（Ⅱ）结论矛盾．②若33()T a a ≠，因为333()T a a =，则存在,{1,2,4,5}i j ∈，有3()i T a a =，()i j T a a =，3()j T a a =．此时，3235()()()i j i i T a T a T a a a -===≠，与T 是3阶逆序变换矛盾．所以，5项数列5A 不存在3阶逆序变换．第7页（共7页）对于6项数列6123456:,,,,,A a a a a a a ，存在变换T 使得6236145():,,,,,T A a a a a a a ，则26365214():,,,,,T A a a a a a a ，36654321():,,,,,T A a a a a a a ．所以6项数列6A 存在3阶逆序变换．综上，n 的最小值为6．…………………….……15分。

东城区2014—2015学年度第二学期期末教学目标检测高一物理第 I 卷（机读卷 共48分）本题共12小题，在每小题给出的四个选项中，只有一个选项．．．．．．是符合题意的。

（每小题4分，共48分）请将答案填写在下面的表格中。

1．下列各物理量的国际单位中，能量的单位是A ．牛顿B ．焦耳C ．瓦特D ．赫兹 2．下列几种运动中，不属于．．．匀变速运动的是 A ．竖直上抛运动 B ．自由落体运动 C ．平抛运动 D ．匀速圆周运动3．降落伞在下落一定时间后的运动是匀速的。

若在有风的天气，风可以使跳伞员以3m/s 的速度沿水平方向向东运动，且无风时跳伞员竖直匀速下落的速度为4m/s ，有风时跳伞员落地时速度的大小为A ．3m/sB ．4m/sC ．5m/sD ．7m/s 4．如图1所示，在光滑水平面上，质量为m 的小球在绳的拉力作用下做半径为r 的匀速圆周运动，小球运动的角速度为ω，则绳的拉力F 大小为A ．m ωrB ．m ωr 2C ．m ω2r D ．2m r5．火星探测器“凤凰”号曾经在火星上进行科学探究。

在“凤凰”号飞向火星的过程中，距地心的距离为r 时，所受地球的引力为F ，则当“凤凰”号距地心的距离为2r 时，所受地球的引力为 A ．41F B ．31F C ．F D ．3F6．下列所述的实例中（均不计空气阻力），机械能守恒的是A ．小球在竖直平面内做匀速圆周运动的过程B ．电梯在竖直平面内加速向上运动的过程C ．木箱沿粗糙斜面匀速向下滑行的过程D ．铅球被抛出后在空中运动的过程图1图5v7．如图2所示的皮带传动装置，皮带与圆盘O 、O ’之间不打滑．将三个相同的小物块分别放在圆盘O 、O ’边缘的A 、B 两点和圆盘O 上的C 点，三个小物块随圆盘做匀速圆周运动。

A 、B 、C 三物块做圆周运动的半径r A ＝2r B ，r C ＝r B 。

小物块A 、B 运动的线速度之比和小物块B 、C 运动的周期之比分别为A ．1:1；1:2B ．2:1；1:1C ．1:1；2:1D ．2:1；1:28．如图3所示，若从同一炮台的某高度处沿水平方向发射炮弹，忽略空气阻力，则以下说法中正确的是A ．炮弹的质量可以影响炮弹在空中的飞行时间B ．炮弹的质量可以影响炮弹在空中的飞行轨迹C ．炮弹的初始速度可以影响其在空中的飞行时间D ．炮弹的初始速度可以影响其在空中的飞行轨迹9．2004年，中国正式开展月球探测工程，并命名为“嫦娥工程”。

东城区第二学期期末教学统一检测高二数学(理科)本试卷共4页，共100分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共24分）一、选择题 （本大题共8小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．复数12i z =-+，则z 在复平面内对应的点所在象限为A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．直线3,112x y t ⎧=⎪⎪⎨⎪=+⎪⎩（t 为参数）的斜率为 A．3-B．2-C．3 D ．123．在()102x -的展开式中，6x 的系数为A ．41016CB ．41032CC ．6108C -D ．61016C -4．一名老师和四名学生站成一排照相，学生请老师站在正中间，则不同的站法为 A ．4种 B ．12种 C ．24种 D ．120种 5．在极坐标系中，点(2,)3π到直线cos 2ρθ=的距离为A ．12B ．1C ．2D ．3 6．袋子中装有大小完全相同的6个红球和4个黑球，从中任取2个球，则所取出的两个球中恰有1个红球的概率为A ．541 B ．1225C ．158D ．35 7．函数||e cos x y x =-的图象大致为OxyA B C 8．甲、乙两人约好一同去看《变形金刚5》，两人买完了电影票后，偶遇丙也看这场电影，此时还剩9张该场电影的电影票，电影票的座位信息如下表．丙从这9张电影票中挑选了一张，甲、乙询问丙所选的电影票的座位信息，丙只将排数告诉了甲，只将号数告诉了乙．下面是甲、乙关于丙所选电影票的具体座位信息的一段对话：甲对乙说：“我不能确定丙的座位信息，你肯定也不能确定．” 乙对甲说：“本我不能确定，但是现在我能确定了．” 甲对乙说：“哦，那我也能确定了！” 根据上面甲、乙的对话，判断丙选择的电影票是A ．4排8号B ．3排1号C ．1排4号D ．1排5号第二部分（非选择题 共76分）二、填空题（本大题共6小题，每小题4分，共24分．请把答案填在答题卡中相应题中横线上）9．i 是虚数单位，复数13i1i-=- ． 10．定积分11(2sin )x x dx -+⎰的值为 ．11．在高台跳水运动中，某运动员相对于水面的高度h （单位：m ）与起跳后的时间t （单位：s ）存在函数关系2() 4.9 6.510h t t t =-++．则该运动员在0.5t s =时的瞬时速度为v = /m s ．12．若52345012345(21)x a a x a x a x a x a x +=+++++，则012345a a a a a a -+-+-的值为___________．13． 随着中国电子商务的发展和人们对网购的逐渐认识，网购鲜花速递行业迅速兴起．佳佳为祝福母亲的生日，准备在网上定制一束混合花束．客服为佳佳提供了两个系列，如下表：束．请问佳佳可定制的混合花束一共有 种．14．已知平面向量(,)m n =a ，平面向量(,)p q =b ，（其中,,,Z m n p q ∈）．定义：(,)mp nq mq np ⊗=-+a b ．若(1,2)=a ，(2,1)=b ，则⊗a b =_____________； 若(5,0)⊗a b =，且||5<a ，||5<b ，则=a _________，=b __________（写出一组满足此条件的a 和b 即可）．三、解答题（本大题共6个小题，共52分，解答应写出文字说明，证明过程或演算步骤．） 15．（本题满分9分）已知函数32()1f x x x =-+． （I ）求函数()f x 在点(1,(1))f 处的切线方程； （II ）求函数()f x 的极值．16．（本题满分8分）电视连续剧《人民的名义》自3月28日在湖南卫视开播以，引发各方关注，收视率、点击率均占据各大排行榜首位．我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查，共调查了600人，得到结果如下：其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图；表1是不同年龄段的观众选择不同观看方式的人数．求：（I ）假设同一组中的每个数据用该组区间的中点值代替，求非常喜欢《人民的名义》这部电视剧的观众的平均年龄；（II ）根据表1，通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关？附：()()()()d b c a d c b a bc ad n K ++++-=2217．（本题满分8分）已知数列{}n a 的前n 项和为n S ，且满足2n n S a n =-，求数列{}n a 的通项公式．勤于思考的小红设计了下面两种解题思路，请你选择其中一种并将其补充完整．思路1：先设n 的值为1，根据已知条件，计算出1____a =，2____a =，3____a =．猜想：____.n a =观看方式年龄（岁）电视网络[)1545, 150 250 []4565,12080()2k K P ≥0.50 0.40 0.25 0.15 0.10 0.05 0.0250.010 0.005 0.0010k0.4550.7081.3232.0722.7063.8415.0246.6357.87910.828表1年龄6555453525150频率组距0.0400.0100.0150.020图1然后用数学归纳法证明．证明过程如下： ①当1n =时， ，猜想成立②假设n k =（k ∈N *）时，猜想成立，即k a = ． 那么，当1n k =+时，由已知2n n S a n =-，得1k S += ．又2k k S a k =-，两式相减并化简，得1__________k a +=（用含k 的代数式表示）． 所以，当1n k =+时，猜想也成立． 根据①和②，可知猜想对任何k ∈N*都成立．思路2：先设n 的值为1，根据已知条件，计算出1______a =．由已知2n n S a n =-，写出1n S +与1n a +的关系式：1__________n S +=， 两式相减，得1n a +与n a 的递推关系式：1__________n a +=． 整理：11n a ++= ．发现：数列{1}n a +是首项为________，公比为_______的等比数列．得出：数列{1}n a +的通项公式1____n a +=，进而得到n a = ．18．（本题满分9分）为响应市政府“绿色出行”的号召，王老师每个工作日上下班由自驾车改为选择乘坐地铁或骑共享单车这两种方式中的一种出行．根据王老师从3月到5月的出行情况统计可知，王老师每次出行乘坐地铁的概率是0.4，骑共享单车的概率是0.6．乘坐地铁单程所需的费用是3元，骑共享单车单程所需的费用是1元．记王老师在一个工作日内上下班所花费的总交通费用为元，假设王老师上下班选择出行方式是相互独立的． （I ）求的分布列和数学期望()E X ；（II ）已知王老师在6月的所有工作日（按22个工作日计）中共花费交通费用110元，请判断王老师6月份的出行规律是否发生明显变化，并依据以下原则说明理由．原则：设a 表示王老师某月每个工作日出行的平均费用，若|()|a E X -?，则有95％的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化．（注：21()(())ni i i D X x E X p ==-å）19．（本题满分9分）已知函数()ln (1)f x x a x +-=，a R ∈． （I ）求()f x 的单调区间；（II ）若对任意的(0,)x ??，都有()22f x a ≤-，求实数a 的取值范围．20．（本题满分9分）已知随机变量ξ的取值为不大于n 的非负整数值，它的分布列为：其中i p （0,1,2,,i n =L L ）满足：[0,1]i p ∈，且0121n p p p p ++++=L L ．定义由ξ生成的函数2012()nn f x p p x p x p x =++++L L ，令()()g x f x '=．（I ）若由ξ生成的函数23111()424f x x x x =++，求(2)P ξ=的值； （II ）求证：随机变量ξ的数学期望()(1)E g ξ=， ξ的方差2()(1)(1)((1))D g g g ξ'=+-；（2()(())ni i D i E p ξξ==-⋅∑）（Ⅲ）现投掷一枚骰子两次，随机变量ξ表示两次掷出的点数之和，此时由ξ生成的函数记为()h x ，求(2)h 的值．东城区第二学期期末教学统一检测高二数学（理科）答案一、选择题（本大题共8小题，每小题3分，共24分．在每小题给出的四个选项中，选出符合题目要求的一项）二、填空题（本大题共6小题，每小题4分，共24分．请把答案填在答题卡中相应题目的横线上．）三、解答题（本大题共6个小题，共52分，解答应写出文字说明，证明过程或演算步骤．） 15．（本题满分9分）解：（I ）32()1f x x x =-+，2'()32f x x x =-． ………………………………………1分则(1)1,'(1)321f f ==-=． ………………………………………3分则函数()f x 在点(1,(1))f 处的切线方程为11y x -=-，化简得y x =． …………4分 （II ）令2'()320f x x x =-=，解得1220,3x x ==． ………………5分 当x 变化时，'()f x ，()f x 的变化情况如下表：因此，当0x =时，()f x 有极大值，并且极大值为(0)1f =；当23x =时，()f x 有极小值，并且极小值为223()327f =． ……………………9分16．（本题满分8分） 解：（I ）平均年龄为：411506020050400401003015020=⨯+⨯+⨯+⨯+⨯=.....x ． …………4分（II ）根据列联表中的数据，利用公式可得2K 的观测值()272711300200400330270250120801506002.k ≈=⨯⨯⨯⨯-⨯=． …………6分Q 27.27 6.635k ≈≥，∴ 有99%把握认为观看该剧的方式与年龄有关． …………………………………8分17．（本题满分8分） 解：思路1：11a =， ………………………………………………………1分23a =， ………………………………………………………2分 37a =， ………………………………………………………3分 21n n a =-， ………………………………………………………4分11211a =-=，………………………………………………………5分21k k a =-， ………………………………………………………6分112(1)k k S a k ++=-+，………………………………………………7分1121k k a ++=-． …………………………………………8分思路2：11a =， ………………………………………………………1分112(1)n n S a n ++=-+， …………………………………………………2分 121n n a a +=+， ………………………………………………………3分 112(1)n n a a ++=+， …………………………………………………4分2， ………………………………………………………5分 2， ………………………………………………………6分12n n a +=， ………………………………………………………7分21n n a =-． ………………………………………………………8分18．（本题满分9分）解：（I ）依题意，可能的取值是2，4，6，因此的分布列为由此可知，的数学期望为()20.3640.4860.16 3.6E X =⨯+⨯+⨯=． (5)分（II ）判断：有95％的把握认为王老师该月的出行规律与3~5月的出行规律相比有明显变化． ………………………………6分 理由如下：Q 6月共有22个工作日，共花费交通费用110元， ∴平均每天出行的费用110225a =?（元）． .......................................7分 又222()(2 3.6)0.36(4 3.6)0.48(6 3.6)0.16 1.92D X =-?-?-?， (8)分则|()||5 3.6| 1.4a E X -=-=>． ∴有95％的把握认为王老师该月的出行规律与3~5月的出行规律相比有明显变化． ………………………………………9分19．（本题满分9分） 解：（I ）11'()(0)axf x a x x x-=-=>， ………………………………………………1分当0a ≤时，'()0f x >恒成立，则()f x 在(0,)+∞上单调递增； ………………2分 当0a >时，令'()0f x >，则10x a<<． 则()f x 在区间1(0,)a上单调递增，在区间1(,)a+∞上单调递减．……………………4分 （II ）方法1：①当0a ≤时，因为(1)022f a =>-，所以不会有(0,)x "??，()22f x a ≤-． …………………………………………5分 ②当0a >时，由（I ）知，()f x 在(0,)+?上的最大值为111()ln()(1)ln 1f a a a a a a=+-=-+-． ………………………6分所以(0,)x "??，()22f x a ≤-等价于1()ln 122f a a aa=-+-?．即ln 10a a +-?． ………………………………………………7分设()ln 1ln (1)g x x x x x =+-=--，由（I ）知()g x 在(0,)+?上单调递增．又(1)ln1110g =+-=，所以ln 10a a +-?的解为1a ≥． ………………………………8分故(0,)x "??，()22f x a ≤-时，实数a 的取值范围是[1,)+∞． ………………9分方法2：(0,)x "??，()22f x a ≤-等价于ln 21x a x +≥+． ……………………5分令ln 2()1x g x x +=+，则21ln 1'()(1)x x g x x --=+． ………………………………6分 令1()ln 1h x x x =--，则2211(1)'()x h x x x x-+=--=． 因为当(0,)x ??，'()0h x <恒成立，所以()h x 在(0,)+?上单调递减． ………………………………7分 又(1)1ln110h =--=，可得()g x 和'()g x 在(0,)+?上的情况如下：所以()g x 在(0,)+?上的最大值为(1)111g ==+．………………………………8分 因此(0,)x "??，()a g x ≥等价于(1)=1a g ≥．故(0,)x "??，()22f x a ≤-时，实数a 的取值范围是[1,)+∞． …………………9分20．（本题满分9分） 解：（I ） 1(2)2P ξ==． ……………………………………2分（II ）由于012()012n E p p p n p ξ=⋅+⋅+⋅++⋅L L ，112()()2n n g x f x p p x np x -'==+++L L ，所以()g(1)E ξ=． ………………………………………………4分由ξ的方差定义可知2220000220002222222()(())()2()(1)()2()(1)()()2()(1)()()(1)(1)(1)n n n ni i i i i i i i n n n ni i i i i i i i n i i n i i ni i D i E p i p E p E i p i i p i p E p E i p i i p E E E i i p E E i i p g g ξξξξξξξξξξξ============-⋅=⋅+⋅-⋅=-⋅+⋅+⋅-⋅=-⋅++-=-⋅+-=-⋅+-∑∑∑∑∑∑∑∑∑∑.∑由于112g()2n n x p p x np x -=+++L L ，所以有223()232(1)n n g x p p x n n p x -'=+⨯⋅++-⋅L L ，这样232(1)232(1)(1)nn i i g p p n n p i i p ='=+⨯⋅++-=-∑L L ，所以有2()(1)(1)((1))D g g g ξ'=+-． ………………………………………………6分 （III ）方法1．投掷一枚骰子一次，随机变量ξ的生成的函数为：234561()()6f x x x x x x x =+++++． ………………………………7分投掷骰子两次次对应的生成函数为 2345621()[()]6h x x x x x x x =+++++ ． ……… 8分 所以2(2)21441h ==． ………………………………………………9分方法2：ξ的取值为2,3,4,5,6,7,8,9,10,11,12． ……………………………………………7分则ξ的分布列为分则2345678910111212345654321()+3636363636363636363636h x x x x x x x x x x x x =+++++++++． 则4(1412328019232051276810241024)(2)36h ++++++++++= 3969=4419=． ………………………………9分。

北京市东城区2019-2020学年度第二学期期末统一检测北京市东城区2019-2020学年度第二学期期末教学统一检测 高二数学参考答案及评分标准 2020.7一、选择题（共10小题，每小题4分，共40分）（1）A （2）B （3）B （4）D （5）D（6）C （7）C （8）B （9）A （10）C二、填空题（共5小题，每小题4分，共20分）（11）58− （12）①③ （13）12（14）42 （15）1ln 2−+注：（12）题给出的结论中，有多个符合题目要求。

全部选对得4分，不选或错选得0分，其他得2分。

三、解答题（共5小题，共40分）（16）（共8分）解：由题意可知函数()f x 的定义域为(0,)+∞.（Ⅰ）因为21()23ln 2f x x x x =−−， 所以3'()2f x x x=−−， ………1分 '(1)4f =−. ………2分因为3(1)2f =−， ………3分 所以曲线()y f x =在点(1,(1))f 处的切线方程为8250x y +−=.………4分 （Ⅱ） ()f x 的定义域为(0,)+∞. ………5分 因为2323(1)(3)'()2x x x x f x x x x x−−+−=−−==， 由'()0f x =，得11x =−，23x =. ………6分 因为函数()f x 的定义域为(0,)+∞，当x 变化时，'()f x ，()f x 的变化情况如下表： 单调递减单调递增 7分所以，()f x 的单调递增区间为(3,)+∞，()f x 的单调递减区间为(0,3). ………8分（17）（共8分）解：（Ⅰ）共需要填6个空，对2个空 ……1分对4个空 ………2分全对 ………4分（Ⅱ）由题可知，22()=()()()()n ad bc K a b c d a c b d −++++，经过计算， 4.762k ≈，………7分 参照附表，所以在犯错误的概率不超过0.05的前提下，可以认为“爱好冰上运动与性别有关”. ………8分（18）（共8分）解：（Ⅰ）由题意可知，样本中垃圾种类一共200种，辨识度高的垃圾种数是：700.9600.6300.9400.6150+++=⨯⨯⨯⨯.………1分 所求概率为1500.75200=. ………3分 （Ⅱ）X 的可能取值为0,1,2,3. ………4分依题意可知，(3,0.6)X B ~.033(0)(10.6)0.064P X C ===−,123(1)0.6(10.6)0.288P X C ===−,223(2)0.6(10.6)0.432P X C ===−,333(3)0.60.216P X C ===. ………6分所以X 的分布列为………7分()30.6 1.8E X =⨯=. ………………8分（19）（共8分）解：由题意可知函数()f x 的定义域为R .（Ⅰ）因为2()e x f x x =，所以22'()2e e e (2)e (2)x x x x f x x x x x x x =⋅+⋅=⋅+=⋅+⋅. ………1分由'()0f x =，得12x =−，20x =. ………2分当x 变化时，'()f x ，()f x 的变化情况如下表：因此，当2x =−时，()f x 有极大值，并且极大值为24(2)ef −=； 当0x =时，()f x 有极小值，并且极小值为(0)0f =.………4分（全对给1分）（Ⅱ）因为()y f x ax =−，所以2()e e x x ax y x x x a −=−=⋅.所以0x =为一个零点.所以“函数2e x x a y x =−在定义域内有三个零点”可以转化为“方程e x a x =⋅有两个非零实根”. ………5分令()e x h x x =，则'()e e (1)e x x x h x x x =+=+⋅，所以，当1x <−时，'()0h x <，()h x 在(,1)−∞−上单调递减； 当1x >−时，'()0h x >，()h x 在(1,)−+∞上单调递增.当1x =−时，()h x 有最小值1(1)e h −=−. ………6分 若方程e x a x =⋅有两个非零实根，则1(1)e h −=−a <，即1e a >−. 又0a ≥，(,1)x ∈−∞−，e 0x x a ⋅−<恒成立，不存在零点，………7分所以0a <．综上，10ea −<<. 所以当1(,0)e a ∈−时，函数()y f x ax =−在定义域内有三个零点．………8分（20）（共8分）（Ⅰ）解：当3n =时，{3,4,5}n S =.n S 的所有奇子集为{3}{5}{3,4}{4,5}，，，. ………3分（少写或写错扣1分）（Ⅱ）证明：首先证明n S 的奇子集与偶子集个数相等.设奇数n k S ∈，对于n S 的每个奇子集A ，当k A ∈时，取{|B x x A =∈且}x k ≠.当k A ∉时，取{}B A k =，则B 为n S 的偶子集.反之，亦然.所以，n S 的奇子集与偶子集是一一对应的.所以，n S 的奇子集与偶子集个数相等.对于n i S ∀∈，1>i ，含i 的n S 的子集共有12−n 个， …4分其中必有一半是奇子集，一半是偶子集，从而对于每个数i ，在奇子集的和与偶子集的和中，i 所占的个数是一样的.所以n S 的所有奇子集的容量的和与所有偶子集的容量的和相等. …6分（Ⅲ）解：由于每个元素在奇子集中都出现22−n 次，故奇子集的容量和为23(121)2(31)2n n n n n n n −−++++−⨯=−⨯． ………8分。

东城区2022-2023学年度第二学期期末教学统一检测初二数学参考答案及评分标准 2023.7一、选择题(本题共16分，每小题2分) 题号 1 2 3 4 5 6 7 8 答案DCBBADBC二、填空题(本题共16分，每小题2分) 9.1x ≥ 10. 15 11. −1 12.(5，4) 13.3 14. 5 15. 116. ①②③三、解答题(本题共68分，第17题8分，第18-20题，每小题各5分，第21题6分，第22-26题，每小题5分，第27-28题，每小题7分) 解答应写出文字说明、演算步骤或证明过程.17.（1）解：112+232 23+232分23+2= . ----------------------------------------------------------4分(2) ()()2542548÷解：()()2542548÷(22=25422⎡⎤-÷⎢⎥⎣⎦2分 ()201622=-÷42=÷=2---------------------------------------------------------------------------------------------------------4分18. 解：()2125x x --+=22125x x x -+-+ =246x x -+=()222x -+.-----------------------------------------------------------------------------------------------3分将23x =()222x -+, 得()22322+=5.----------------------------------------5分注：若直接代入求值，代入后去掉2个括号正确3分，结果2分.19. 证明：∵BE ⊥AC 于点E ，DF ⊥AC 于点F ，∴∠AEB =∠FCD =90°. ----------------------------------------1分∵四边形ABCD 为平行四边形,∴ AB ∥CD ，AB=CD. ----------------------------------------2分 ∴ ∠BAE =∠DCF . ----------------------------------------3分 ∴ △ABE ≌△CDF （AAS ）. ----------------------------------------4分 ∴ AE =CF . --------------5分20. 解： （1）补全图形如图.—————————————————————————————————2分 （2）四条边相等的四边形是菱形;30; 150-----------------------------5分21.解：（1）将（1，-1），（2，-7）代入y ＝kx ＋b （k ≠0），得127.k b k b +=-⎧⎨+=-⎩，解得65.k b =-⎧⎨=⎩，∴k =6-，b=5. ------------------------2分 （2）由（1）得y ＝6-x ＋5. 当y=10-时，m=2.5；当x=3.5时，n=16-. ------------------------4分 （3）∵k ＝6-＜0，∴y 随着x 的增大而减小.∵当x ＝4时，y ＝-19；当x ＝7时，y ＝-37， ∴-37≤y ≤-19.∴气温y 的变化范围是-37≤y ≤-19. --------------------6分22. 解：（1）画图如下.-------------------------------------------------2分 （2）∵A (-3,0)， ∴OA ＝3. ∵S △OP A ＝6，∴1=62P OA y ⋅⋅. ---------3分 ∴=4P y . ∴=4P y ±.将=4P y 代入2y x =-+，则=2P x -;将=4P y -代入2y x =-+，则=6P x .综上所述，P 1（-2,4）, P 2（6, -4）. -----------------5分22.证明：方法一ODCBAABC DO∵BO 是斜边AC 的中线， ∴AO =CO . ----------2分又∵DO =BO .∴四边形ABCD 是平行四边形. ------------3分 ∵∠ABC =90°， ∴四边形ABCD 是矩形.∴BD =AC . -------------------------4分 ∴BO =12BD =12AC . ------------------5分 方法二∵BO 是斜边AC 的中线， ∴AO =CO .------------------2分 ∴OD 是△ABC 的中位线. ∴OD ∥AB .---------------3分∴∠ODC =∠ABC . ∵∠ABC =90°， ∴∠ODC =90°.∴OD ⊥BC .---------------4分 ∴BO =CO .∴BO =12AC .--------------------5分24. 解：（1）527. ----------------------2分（2）18.----------------------------------------------- 3分（3）①③.----------------------------------------------- 5分 25.解：（1）y 1＝26x ＋15(24- x )＝11 x ＋360；y 2＝25(20- x )＋20(x ＋6)＝- 5x ＋620.----- 3分 （2）由题意可知，0≤x ≤20.由y 1＝y 2，得x 465. 所以(1)中两个函数图象的交点的横坐标为654. 因为y 1随着x 的增大而增大，y 2随着x 的增大而减小， 所以当x 465＞时，y 1＞y 2. 综上，x 的取值范围是＜465x ≤20.-------------------------5分 26.解：（1）∵直线y ＝kx ＋b (k ≠0)由函数y ＝2x 的图象平移得到， ∴k=2.-------------1分∴一次函数的解析式为y ＝2x ＋b .将（-1,3）代入y ＝2x ＋b ，得3＝-2+b , 解得b ＝5.--------2分 ∴一次函数的解析式为y ＝2x ＋5. ----------3分 （2）m ≥7.----------------5分 27.解：（1）补全图形如下,------------------------------------------------------------------------------2分（2）∠AEB= 90°- α，∠AEC= 45°. ---------4分 (3)结论：()=. --------------------5分CE AE2+1.证明：如图，作BF⊥CE于点F.∵点A关于射线BP的对称点为点E,AE .∴AE⊥BP,EG=12∴∠BGE=90°,BE=BA.由（2）知∠AEC =45°，∴∠GHE=45°.∴△EGH是等腰直角三角形.由勾股定理得，2.=EH EG∵四边形ABCD是正方形,∴BA=BC.∴BE=BC.∵BF⊥CE，∴∠BFH=90°,EF=CF.∵∠EHG=∠FHB,EH=BH,∴△EGH≌△BFH（AAS）.∴EG=GH=BF=FH.∴CE=2(EH+FH)=)())EG EG EG AE+==2222121.-------------------------------7分28. 解：（1）①（0，2）；-------------------------1分②∵E（1,-1），F（3,-1），∴点E，点F关于OM的“关联点”点'E(1，3)，点'F（-1，3）. 当点P在线段EF上时，点Q在线段''E F∥EF.E F上，且''因此，如图1，当点P与点E重合时，PQ长取得最小值4；如图2，当点P与点F重合时，PQ长取得最大值42；综上所述，PQ长的取值范围是：4≤PQ≤42-----5分（3）32m2≤≤.------7分--m≤≤或3。

2023-2024学年广东省东莞市东城街道五年级数学第二学期期末监测模拟试题一、认真填一填。

(每小题2分，共20分）1．一件衣服原价80元，打8折出售是（__________）元．一件衣服打8折出售是80元，原价是（__________）元．2．在下面括号里填上适当的分数。

40分＝（____）时1500毫升＝（____）立方分米3．0.25表示有（）个1100，也就是( )100，化成最简分数是（）。

4．的分子加上9，要使分数的大小不变，分母应加上_____．5．如果A是B的3倍（AB均不为0），那么A，B的最大公因数是_____，最小公倍数是_____．6．下图长方体盒子里一个小立方体的棱长为1分米，那么这个长方体盒子的容积是（__________）立方分米．7．已知A＝5B（A、B为非0的自然数），则A与B的最小公倍数是（________），最大公因数是（________）。

8．(?)20＝1．5÷( )=2．15＝( )％＝180×( )9．把三个棱长为3cm的正方体拼成一个长方体，那么棱长总和减少（________）cm，表面积减少了（________）cm2。

10．把3米长的绳子平均分成5段，每段长（）米，每段占3米的．二、是非辨一辨。

(每小题2分，共12分）11．一瓶油重千克，吃了，还剩4千克．（____）12．比1大的自然数的倒数一定是真分数。

（______）13．两个质数相乘的积还是质数．（_______）14．把一个正方体橡皮泥捏成一个长方体后，虽然它的形状变了，但是它所占空间的大小不变．（______）15．一堆煤的14与这堆煤的13，合起来是28吨，这堆煤有48吨。

（__________）16．分母越大，分数单位越小。

（____）三、细心选一选。

请把正确答案的序号填在括号里。

(每小题2分，共10分）17．一根绳子长20米，用去15米，还剩（）。

A．45B．45米C．995米D．16米18．棱长为6分米的正方体，表面积和体积相比，( )．A．相等B．体积大C．表面积大D．无法比较19．一条裤子原价是100元，商店按原价的出售，便宜了( )元． A ．80 B ．20 C ．5 D ．1020．周长相等的正方形、长方形和圆形，（ ）的面积最大。

高二数学第1页（共8页）东城区2023-2024学年度第二学期期末教学统一检测高二数学2024.7本试卷共6页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共10小题，每小题4分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合2{0,,}M a a =，{2,1,0,1,2}N =--，若1M ∈，则M N =（A ）{0,1}（B ）{1,0,1}-（C ）{0,1,2}（D ）{2,1,0,1,2}--（2）某校学生科研兴趣小组为了解1~12岁儿童的体质健康情况，随机调查了20名儿童的相关数据，分别制作了肺活量、视力、肢体柔韧度、BMI 指数和身高之间的散点图，则与身高之间具有正相关关系的是（A ）肺活量（B ）视力（C ）肢体柔韧度（D ）BMI 指数（3）已知,x y ∈R ，且x y >，则下列不等式中一定成立的是（A ）22x y >（B ）11x y>（C ）ln ln >x y（D ）22x y>（4）袋中有10个大小相同的小球，其中7个黄球，3个红球.每次从袋子中随机摸出一个球，摸出的球不再放回.则在第一次摸到黄球的前提下，第二次又摸到黄球的概率为（A ）23（B ）12（C ）13（D ）310高二数学第2页（共8页）（5）已知23a =，4log 5b =，则22-a b 的值为（A ）15（B ）53（C ）35（D ）2-（6）A ，B ，C 三所大学发布了面向高二学生的夏令营招生计划，每位学生只能报一所大学.某中学现有四位学生报名.若每所大学都有该中学的学生报名，则不同的报名方法共有（A ）30种（B ）36种（C ）72种（D ）81种（7）2024年3月20号，我国成功发射鹊桥二号中继卫星，其通过一个大型可展开的星载天线，实现了月球背面与地球之间的信号传输.星载天线展开后形成一把直径（口经）为4.2m 的“金色大伞”，它的曲面与轴截面的交线为抛物线，在轴截面内的卫星波束呈近似平行状态射入接收天线，经反射聚集到焦点F 处.若“金色大伞”的深度为0.49m ，则“金色大伞”的边缘A 点到焦点F 的距离为（A ）2.25m （B ）2.74m （C ）4.5m（D ）4.99m（8）已知直线l ：250--+=mx y m 被圆22(3)(4)4x y -+-=截得的弦长为整数，则满足条件的直线l 共有（A ）1条（B ）2条（C ）3条（D ）4条（9）已知函数2()()()()f x a x a x b a,b =--∈R ，则“0b a >>”是“b 为()f x的极小值点”的A高二数学第3页（共8页）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件（10）《孙子算经》是中国南北朝时期重要的数学著作,书中的“中国剩余定理”对同余除法进行了深入的研究．现给出一个同余问题：如果a 和b 被m 除得的余数相同，那么称a和b 对模m 同余，记为()mod a b m ≡．若0120242024C C 3a =⨯+222024202420242024C 3C 3+⨯+⨯+ ，()mod5a b ≡，则b 的值可以是（A ）2023（B ）2024（C ）2025（D ）2026第二部分（非选择题共110分）高二数学第4页（共8页）二、填空题共5小题，每小题5分，共25分。

东城区2022-2023学年度第二学期期末教学统一检测初二数学2023.7一、选择题(本题共16分，每小题2分)第1-8题均有四个选项，符合题意的选项只有．．一个.1.在下列四个式子中，最简二次根式为A．()22− B．12 C．34D．72.在平行四边形ABCD中，∠A∶∠B∶∠C∶∠D可以是A．1∶2∶3∶4 B．1∶2∶2∶1C．1∶2∶1∶2 D．1∶1∶2∶23. 下列各式中，计算结果正确的是A．()211−=− B．233= C．42=± D. (222−=−4.奥运会的跳水项目是优美的水上运动，中国跳水队被称为“梦之队”.在一次女子单人10米台跳水比赛中，甲、乙两名选手五轮得分的折线统计图如图所示. 设甲、乙的平均分依次为x甲，x乙，方差依次为2s甲，2s乙，在以下四个推断中，正确的是A. 22x x s s甲乙甲乙＞，＞ B. 22x x s s甲乙甲乙＞，＜C. 22x x s s甲乙甲乙＜，＞ D. 22x x s s甲乙甲乙＜，＜5. 如图，矩形ABCD 的两条对角线相交于点O .若∠ACB =30°,AB =2，则边AD 的长为A ．23B ．2C 3D ．16. 在平面直角坐标系xOy 中，点P （1x ，1y ），Q (2x ,2y )都在函数y＝-2x +3的图象上.若12x x ＜＜0,则下列四个推断中错误．．的是 A ．点P 在第二象限 B. 坐标原点不在此函数图象上C ．12y ＞yD ． 2y ＜37. 在平面直角坐标系xOy 中，已知点A (-2,1),B （1,1）.若直线y =mx 与线段AB 有交点，则m 的值不可能是 A. 1 B. 12 C. -12D. -18. 画一个四边形，使得该四边形的面积等于已知图形面积的一半.（1）如图1，已知等腰△ABC ，D ,E 是AB ,AC 的中点，画四边形DBCE ;(2) 如图2，已知四边形ABCD ,AC ⊥BD .四边的中点分别为E ,F ,G ,H ,画四边形EFGH ;(3)如图3，已知平行四边形ABCD , 点E ,G 分别在AD ,BC 上，且EG ∥AB .点F ,H 分别在AB ,CD 上，画四边形EFGH .在以上三种画法中，所有正确画法的序号是A. (1) (3)B. (2)C. (2) (3)D.(1) (2) (3)二、填空题(本题共16分，每小题2分)9.若二次根式1x−x的取值范围是．10. 北京某月连续10天的最低气温（单位：℃）分别是：13 14 1515 15 16 16 18 19 21 . 这组数据的众数是. 11. 若最简二次根式42m−与6是同类二次根式，则m的值是．12.如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的（2，0），点D在y轴上，则点C的坐标是_______．坐标分别为（-3，0），13.如图，在平行四边形ABCD中，AC⊥BC，对角线AC，BD交于点O,点E为边AB的中点若AB=10，AC=8，则OE的长为.14.如图，将矩形纸片ABCD沿AE折叠，顶点B落在CD边上点F处.若AB ＝3，BC＝2，则DF＝ .15. 如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E，F分别在BC，CD上，则△EFC的面积为．16.已知A，B两地相距240 km.甲、乙两辆货车分别从A，B两地同时出发，匀速相向而行.图1表示甲、乙两辆货车距A地的距离s（单位：km）与行驶时间t（单位：h）的数量关系；图2表示甲、乙两辆货车间的距离d（单位：km）与行驶时间t（单位：h）的数量关系.根据以上信息得到以下四个推断：①甲货车从A地到B地耗时6小时，即a＝6；②出发后2.4小时甲、乙两货车相遇，即b＝2.4；③乙货车的速度是60 km/h；④点P的坐标是（4,180）.所有正确推断的序号是 .三、解答题(本题共68分，第17题8分，第18-20题，每小题各5分，第21题6分，第22-26题，每小题5分，第27-28题，每小题7分) 解答应写出文字说明、演算步骤或证明过程.17. 计算：;（1）112+232(2)()()(÷254254818. 已知23x =+求代数式()2125x x −−+的值.19.如图，在平行四边形ABCD 中，AC 是对角线，BE ⊥AC 于点E ，DF ⊥AC 于点F .求证：AE =CF ．20. 如图，△ABC 为等边三角形.求作：菱形ABFE ,使得∠BAE =150°.作法：如图，① 作∠BAC 的平分线AD ，交BC 于点D ；② 以点A 为圆心，AB 长为半径画弧交DA 的延长线于点E ；③ 分别以点B ，E 为圆心，AB 长为半径画弧，两弧交于点F ；（不是点A ）⑤连接BF ,EF .则四边形ABFE 为所求作的菱形.（1）使用直尺和圆规，依作法补全尺规作图（保留作图痕迹）；（2）完成下面的证明.证明：∵AB=AE=BF=EF ,∴四边形ABFE 为菱形（ ）（填推理依据）.∵△ABC为等边三角形，∴∠BAC=60°.∵AD平分∠BAC，∴∠BAD =1∠BAC= °.2∵∠BAE=180°-∠BAD,∴∠BAE= °.21.某数学兴趣小组研究某地区气温与海拔的关系.下表记录的是气温随海拔变化的情况：海拔x/km … 1 1.5 2 m 3.5 …气温y/℃…-1 -4 -7 -10 n…小组研究发现，气温y与海拔x满足一次函数关系：y＝kx＋b（k≠0）.根据小组的研究发现，回答下列问题.（1）求出k，b的值；（2）求表格中m,n的值；（3）当海拔x满足4≤x≤7时，求气温y的变化范围.22.在平面直角坐标系xOy中，点P（x，y）的坐标满足2=−.y x （1）当点P在第一象限时，画出点P组成的图形；（2）已知点A(-3,0),当△OP A的面积为6时，求点P的坐标.23.下面是证明直角三角形的一个性质的两种添加辅助线的方法，选择其中一种，完成证明. 性质：直角三角形斜边上的中线等于斜边的一半.已知：如图，Rt △ABC 中，∠ABC =90°，BO 是斜边AC 的中线.求证：BO =12AC .方法一 证明：如图，延长BO 至点D ，使得OD =OB ，连接AD ，CD .方法二 证明：如图，取BC 中点D ，连接OD .24. 为了解北京市的水资源情况，收集了1978-2020年北京的年降水量（单位：毫米）共43个数据，并对数据进行整理、描述和分析.下面给出了部分信息.注：降水量是指一定时间段内降落在某一点或某一区域的水层深度，通常以毫米表示.a. 43个数据的频数分布直方图如下（数据分成7组：200≤x＜300, 300≤x＜400, 400≤x＜500, 500≤x＜600, 600≤x＜700, 700≤x＜800, 800≤x≤900）:b.43个数据中，在500≤x＜600这一组的是：507 523 527 542 544 547 573 576 579c. 43个数据的平均数、中位数如下：平均数中位数547n根据以上信息，回答下列问题：（1）表中n的值为；（2）1978-2020年北京降水量高于547 毫米的年份共个：（3）若2021年，2022年北京的年降水量分别是698 毫米,493毫米,则下列推断合理的是（填写序号）；①因为698大于n，所以北京2021年降水量比1978-2020年中一半年份的降水量高；②已知1978-2000年北京的降水量的方差为21 249若2021年，2001-2022年北京的年降水量的方差为13 486，由此推断2001-2022年北京的年降水量的波动较大；③1个底面边长为10分米的正方体集水箱2022年共可收集降水约493升.注：1升=1立方分米.25.A,B两地分别有垃圾20吨，30吨,现要把这些垃圾全部运到C，D两个垃圾处理厂,其中24吨运到C厂. 运费标准（单位：元/吨）如下表：始发地目的地C厂D厂A地26 25B地15 20当从A地运送多少吨垃圾到C厂时，从A,B两地到C厂的总运费大于运到D厂的总运费?(1)建立函数模型设从A地运到C厂x吨垃圾.从A,B两地到C厂的总运费为y1元，到D厂的总运费为y2元.求y1，y2关于x的函数关系式；（2）根据函数的图象与性质，解决问题：当y1＞y2时，求x的取值范围.26.在平面直角坐标系xOy中，一次函数y＝kx＋b(k≠0)的图象由函数y＝2x的图象平移得到，且经过点（-1,3）.（1）求一次函数的解析式；（2）当x＞1时，对于x的每一个值，函数y＝mx的值均大于函数y ＝kx＋b（k≠0）的值，直接写出m的取值范围.27.如图，正方形ABCD.过点B作射线BP，交DA的延长线于点P. 点A关于直线BP的对称点为E，连接BE，AE，CE.其中AE，CE分别与射线BP交于点G,H.（1）依题意补全图形;（2）设∠ABP=α，∠AEB=（用含α的式子表示），∠AEC=°；（3）若EH=BH,用等式表示线段AE与CE之间的数量关系，并证明.28. 在平面直角坐标系xOy中，对于线段MN和点P作出如下定义：若点M，N分别是线段PP1，PP2的中点，连接P1P2，我们称线段P1P2的中点Q是点P关于线段MN的“关联点”.（1）已知点M（2,2），点P关于线段OM的“关联点”是点Q.①若点P的坐标是（2,0），则点Q的坐标是；②若点E的坐标是（1,-1），点F的坐标是（3,-1）.点P是线段EF上任意一点，求线段PQ长的取值范围；（2）点A是直线l:y=x+1上的动点.在矩形ABCD中，边AB∥x轴，AB＝3，BC＝2.点P是矩形ABCD边上的动点，点P关于其所在边的对边的“关联点”是点Q.过点A作x轴的垂线，垂足为点G.设点G的坐标是（t，0）.当点A沿着直线l运动到点'A时，点G沿着x 轴运动到点'G（t+m，0），点Q覆盖的区域的面积S满足20≤S≤30，直接写出m的取值范围.。