沪科版数学七年级上册第1课时 等积变形和行程问题
- 格式:doc
- 大小:236.50 KB
- 文档页数:4
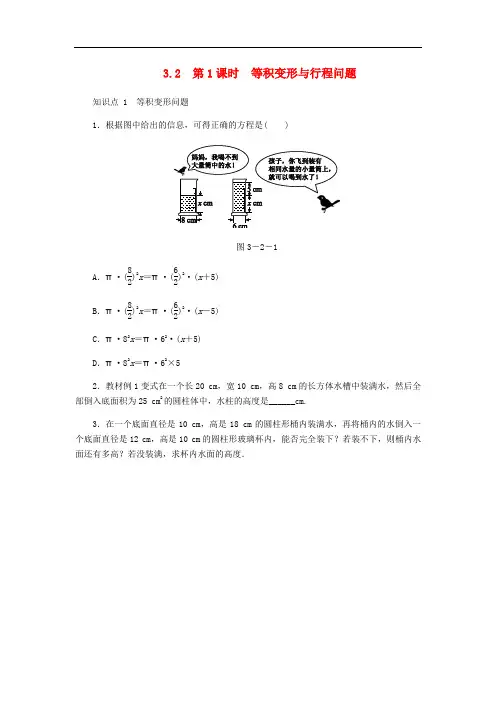
3.2 第1课时 等积变形与行程问题知识点 1 等积变形问题1.根据图中给出的信息,可得正确的方程是( )图3-2-1A .π·(82)2x =π·(62)2·(x +5)B .π·(82)2x =π·(62)2·(x -5)C .π·82x =π·62·(x +5) D .π·82x =π·62×52.教材例1变式在一个长20 cm ,宽10 cm ,高8 cm 的长方体水槽中装满水,然后全部倒入底面积为25 cm 2的圆柱体中,水柱的高度是______cm.3.在一个底面直径是10 cm ,高是18 cm 的圆柱形桶内装满水,再将桶内的水倒入一个底面直径是12 cm ,高是10 cm 的圆柱形玻璃杯内,能否完全装下?若装不下,则桶内水面还有多高?若没装满,求杯内水面的高度.知识点 2 行程问题——相遇4.快车从甲地到乙地要行10小时,慢车从乙地到甲地要行15小时,两车分别从甲、乙两地同时出发,相向而行,________小时后两车相遇.5.甲、乙两车分别从距离360千米的两地同时相向开出,已知甲车的速度是60千米/时,乙车的速度是40千米/时,若甲车先开出1小时,则乙车开出多长时间后两车相遇?知识点 3 行程问题——追及6.甲、乙两人分别从两地同时出发,若相向而行,则6 h相遇;若同向而行,则12 h 甲追上乙.那么甲的速度是乙的速度的( )A.32倍 B.23C.3倍 D.137.已知A,B两地相距48千米,甲骑自行车每小时走18千米,乙步行每小时走6千米,甲、乙两人分别从A,B两地同时出发,同向而行,开始时乙在前,经过多少小时甲追上乙?知识点 4 行程问题——环形跑道8.甲、乙两人在400 m的环形跑道上练习跑步,甲的速度是5 m/s,乙的速度是7 m/s.两人站在同一起点,同时同向出发,那么当乙第一次恰好追上甲时,甲跑了________m.知识点 5 行程问题——顺(逆)风(水)9.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3 h,若静水时船速为26 km/h,水速为2 km/h,则A港和B港相距________km.10.如图3-2-2所示,在水平桌面上有甲、乙两个内部呈圆柱形的容器,容器内部底面积分别为80 cm2,100 cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8 cm,则甲容器的容积为( )图3-2-2A.1280 cm3 B.2560 cm3C.3200 cm3 D.4000 cm311.甲、乙两人从相距140千米的两地同时相向而行,甲骑车的速度为80 km/h,乙骑车的速度为60 km/h,________ h后两人相距70 km.12.家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:(1)他下山时的速度比上山时的速度每小时快1千米;(2)他上山2小时到达的位置,离山顶还有1千米;(3)抄近路下山,下山路程比上山路程近2千米;(4)下山用1个小时.根据上面的信息,他做出如下计划:①在山顶游览1个小时;②中午12:00回到家吃中餐.若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?13.一队学生从学校出发去部队军训,行进速度是5千米/时,走了4.5千米时,一名通信员按原路返回学校报信,然后他随即追赶队伍,通信员的速度是14千米/时,他在距部队6千米处追上队伍,则学校到部队的距离是多少(报信时间忽略不计)?14.如图3-2-3,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A 点逆流航行3小时到达B 点后,又继续顺流航行2小时15分钟到达C 点,总共行驶了198 km ,已知游艇的速度是38 km/h.(1)求水流的速度;(2)由于AC 段在建桥,游艇用同样的速度沿原路返回共需要多少时间?图3-2-33.2 第1课时 等积变形与行程问题1.A . 2.643.解: 水的体积为(102)2π×18=450π(cm 3).圆柱形玻璃杯的容积为(122)2π×10=360π(cm 3).∵450π>360π,即水的体积大于圆柱形玻璃杯的容积,故不能完全装下.设桶内水面还有x cm 高,由题意,得(102)2π×18-(122)2π×10=(102)2πx ,解得x =3.6.故桶内水面还有3.6 cm 高. 4.65.解:设乙车开出x 小时后两车相遇,由题意,得 60(x +1)+40x =360, 解得x =3.答:乙车开出3小时后两车相遇. 6.C .7.解:设经过x 小时甲追上乙. 依题意得18x -6x =48, 解得x =4.答:经过4小时甲追上乙. 8.1000 . 9.504 10.C . 11.0.5或1.512 解: 设上山的速度为v ,下山的速度为(v +1),则2v +1=v +1+2, 解得v =2,即上山速度是2千米/时,则下山的速度是3千米/时,山高为5千米. 则计划上山的时间为5÷2=2.5(时), 计划下山的时间为1小时,则共用时间为2.5+1+1=4.5(时), 12-4.5=7.5, 所以出发时间为7:30.答:孔明同学应该在7:30从家出发.13.解:设通信员从开始返回学校到追上队伍的时间为t 小时,由题意可得14t -4.5=4.5+5t ,解得t =1,所以学校到部队的距离是4.5+5×1+6=15.5(千米).14.解: (1)设水流速度为x km /h ,则游艇的顺流航行速度为(x +38)km /h ,游艇的逆流航行速度为(38-x)km /h .根据题意可得3(38-x)+94(38+x)=198.解得x =2.∴水流的速度为2 km /h .(2)由(1)可知,顺流航行的速度为40 km /h ,逆流航行的速度为36 km /h . ∴AB 段的路程为3×36=108(km ),BC 段的路程为94×40=90(km ).故原路返回时间为9036+10840=2.5+2.7=5.2(h ).答:游艇用同样的速度沿原路返回共需要5小时12分钟.。

3.2一元一次方程的应用第1课时等积变形和行程问题【学习目标】1、理解等积变形前后不变的量,速度、时间、路程三个基本量之间的关系.会列一次方程解行程问题。
2、在解决行程问题的过程中,进一步掌握列一元一次方程解简单应用题的方法和步骤。
等积变形和行程问题:等积变形问题:“等积变形”是以形状改变而体积不变为前提.常用等量关系为:①形状面积变了,周长没变;②原料体积=成品体积.行程问题:(1)行程问题中的三个基本量及其关系:路程=速度×时间.(2)基本类型有①相遇问题;②追及问题;常见的还有:相背而行;行船问题;环形跑道问题.等积变形问题常见几何图形的面积、体积、周长计算公式,依据形虽变,但体积不变.①圆柱体的体积公式V=底面积×高=S·h= r2h②长方体的体积V=长×宽×高=abc行程问题基本量之间的关系路程=速度×时间时间=路程÷速度速度=路程÷时间(1)相遇问题快行距+慢行距=原距(2)追及问题快行距-慢行距=原距(3)航行问题顺水(风)速度=静水(风)速度+水流(风)速度逆水(风)速度=静水(风)速度-水流(风)速度抓住两码头间距离不变,水流速和船速(静不速)不变的特点考虑相等关系.【自主学习】1、还记得小学学过的行程问题中的路程 时间和速度三个量之间关系吗?注意:(1)“同时”、“同地”、“相向”、“同向”关键字的含义。
(2)行程问题一般从时间、路程找等量关系。
(3)注意单位的统一。
2、慢车每小时行驶48千米,x 小时可行驶 千米,快车每小时行驶72千米,如果快车先开5/12小时,那么在慢车开出x 小时后快车行驶 千米。
3、(1) 如图甲、乙两人分别从A 、B 两地同时出发相向而行,相遇时他们走的时间的关系是_________________ ______,走的路程关系是_______ __ __.4、 (2)如果甲从A 、乙从B 同时出发同向而行,甲追乙,在C 点追击,那么他们走的路程关系是_ ____________, 时间关系是______ ___________4、用直径为4厘米的圆钢,铸造三个直径为2厘米,高为16厘米的圆柱形零件,问需要截取多长的圆钢?5、某机器加工厂要锻造一个毛胚,上面是一个直径为20毫米,高为40毫米的圆柱,下面也是一个圆柱,直径为60毫米,高为20毫米,问需要直径为40毫米的圆钢多长?【合作探究】问题1:小明与小兵的家分别在相距20千米的甲、乙两地,星期天小明从家出发骑自行车去小兵家,小明骑车的速度为每小时13千米.两人商定到时候小兵从家里出发骑自行车去接小明,小兵骑车速度是每小时12千米。







3.2一元一次方程的应用第1课时等积变形和行程问题教学目标:1.通过学习列方程解决实际问题,进一步感知数学在生活中的作用;2.通过分析等积变形,追及问题中的数量关系,从而建立方程解决实际问题。
进一步发展分析问题,解决问题的能力;3.在合作与交流中学会肯定自己和倾听他人意见。
教学重点:找出等积变形,追及问题中的条件和要求的结论,并找出等量关系,列出方程,解决实际问题。
教学难点:找等量关系,,设未知数列方程.一、创设情境问题:例1:小明每天早上要在7:50之前赶到距家1000米的学校上学。
小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书。
于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他。
(1)爸爸追上小明用了多长时间?(2)追上小明时,距离学校还有多远?分析:当爸爸追上小明时,两人所行距离相等。
在解决这个问题时要抓住这个等量关系。
(引导学生画出线路图)80x5 80x180x相等关系:爸爸走的路程=小明走5分钟的路程 + 小明走x分钟的路程= 小明走的总路程爸爸所用的时间 = 小明所用总时间– 5分钟例2:圆柱体积公式:长方体体积公式:如图,已知圆柱(2)的体积是圆柱(1)的体积的3倍,求圆柱(1)的高(图中φ40表示直径为40毫米)二.合作探究(一)交流展示1.用直径为4cm的圆钢(截面为圆形的实心长条钢材)铸造3个直径为2cm,高为16cm的圆柱形零件,则需要截取多长的圆钢?2.某工厂锻造直径为60毫米,高20毫米的圆柱形瓶内装水,再将瓶内的水倒入一个底面直径6厘米、高10厘米的圆柱形玻璃杯中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离。
3.甲、乙两人从相距为180千米的A,B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶.已知甲的速度为15千米/时,乙的速度为45千米/时.经过多少时间两人相遇?4.甲、乙两人从A、B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶.出发后经3时两人相遇.已知在相遇时乙比甲多行了90千米,相遇后经1时乙到达A地.问甲、乙行驶的速度分别是多少?变题相遇后经过多少时间甲到达B地?在分析应用题中的数量关系时,常用列表分析法与线段图示法,使题目中的条件和结论变得直观明显,因而容易找到它们之间的相等关系.三、议一议:1.育红学校七年级学生步行到郊外旅行。

3.2一元一次方程的应用第1课时等积变形和行程问题【学习目标】1、理解等积变形前后不变的量,速度、时间、路程三个基本量之间的关系.会列一次方程解行程问题。
2、在解决行程问题的过程中,进一步掌握列一元一次方程解简单应用题的方法和步骤。
等积变形和行程问题:等积变形问题:“等积变形”是以形状改变而体积不变为前提.常用等量关系为:①形状面积变了,周长没变;②原料体积=成品体积.行程问题:(1)行程问题中的三个基本量及其关系:路程=速度×时间.(2)基本类型有①相遇问题;②追及问题;常见的还有:相背而行;行船问题;环形跑道问题.等积变形问题常见几何图形的面积、体积、周长计算公式,依据形虽变,但体积不变.①圆柱体的体积公式V=底面积×高=S·h= r2h②长方体的体积V=长×宽×高=abc行程问题基本量之间的关系路程=速度×时间时间=路程÷速度速度=路程÷时间(1)相遇问题快行距+慢行距=原距(2)追及问题快行距-慢行距=原距(3)航行问题顺水(风)速度=静水(风)速度+水流(风)速度逆水(风)速度=静水(风)速度-水流(风)速度抓住两码头间距离不变,水流速和船速(静不速)不变的特点考虑相等关系.【自主学习】1、还记得小学学过的行程问题中的路程 时间和速度三个量之间关系吗?注意:(1)“同时”、“同地”、“相向”、“同向”关键字的含义。
(2)行程问题一般从时间、路程找等量关系。
(3)注意单位的统一。
2、慢车每小时行驶48千米,x 小时可行驶 千米,快车每小时行驶72千米,如果快车先开5/12小时,那么在慢车开出x 小时后快车行驶 千米。
3、(1) 如图甲、乙两人分别从A 、B 两地同时出发相向而行,相遇时他们走的时间的关系是_________________ ______,走的路程关系是_______ __ __.4、(2)如果甲从A 、乙从B 同时出发同向而行,甲追乙,在C 点追击,那么他们走的路程关系是_ ____________,时间关系是______ ___________相遇乙走的乙甲B A甲走的路程C B 乙甲A4、用直径为4厘米的圆钢,铸造三个直径为2厘米,高为16厘米的圆柱形零件,问需要截取多长的圆钢?5、某机器加工厂要锻造一个毛胚,上面是一个直径为20毫米,高为40毫米的圆柱,下面也是一个圆柱,直径为60毫米,高为20毫米,问需要直径为40毫米的圆钢多长?【合作探究】问题1:小明与小兵的家分别在相距20千米的甲、乙两地,星期天小明从家出发骑自行车去小兵家,小明骑车的速度为每小时13千米.两人商定到时候小兵从家里出发骑自行车去接小明,小兵骑车速度是每小时12千米。

3.2 一元一次方程的应用第1课时等积变形和行程问题1.会用一元一次方程解决等积变形和行程问题;(重点、难点)2.通过对“变化中的不变量”的分析提高分析问题、解决问题的能力.一、情境导入一种牙膏出口处直径为5mm,子昂每次刷牙都挤出1cm长的牙膏,这样一支牙膏可以用36次.该品牌牙膏现推出新包装,只是将出口处直径改为6mm,子昂还是按习惯每次挤出1cm的牙膏,这样,这支牙膏能用多少次呢?二、合作探究探究点一:等积变形问题用直径为90mm的圆钢,铸造一个底面长和宽都是131mm,高度是81mm的长方体钢锭.问需要截取多长的一段圆钢?(结果保留π) 解析:圆钢由圆柱体变为长方体,形状变了,但体积不变.解:设截取圆钢的长度为xmm.根据题意,得π⎝ ⎛⎭⎪⎫9022x =131×131×81, 解方程,得x =686.44π. 答:截取圆钢的长度为686.44πmm. 将一个长、宽、高分别为15cm 、12cm 和8cm 的长方体钢坯锻造成一个底面是边长为12cm 的正方形的长方体钢坯.试问:是锻造前的长方体钢坯的表面积大,还是锻造后的长方体钢坯的表面积大?请你计算比较.解析:由锻造前后两长方体钢坯体积相等,可求出锻造后长方体钢坯的高.再计算锻造前后两长方体钢坯的表面积,最后比较大小即可.解:设锻造后长方体的高为xcm ,依题意,得15×12×8=12×12x.解得x =10.锻造前长方体钢坯的表面积为2×(15×12+15×8+12×8)=2×(180+120+96)=792(cm 2),锻造后长方体钢坯的表面积为2×(12×12+12×10+12×10)=2×(144+120+120)=768(cm 2).因为792>768,所以锻造前的长方体钢坯的表面积较大.方法总结:本题的解题关键是根据等积变形中的等量关系确定变化后长方体的高.探究点二:行程问题【类型一】相遇问题小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?解析:本题等量关系:小明所走的路程+爸爸所走的路程=全部路程,但要注意小明比爸爸多走了5分钟,另外也要注意本题单位的统一.解:设小明爸爸出发x分钟后接到小明,如图所示,由题意,得200x +60(x+5)=2900.解得x=10.答:小明爸爸从家出发10分钟后接到小明.方法总结:找出问题中的等量关系是列方程解应用题的关键,对于行程问题,通常借助“线段图”来分析问题中的数量关系.这样可以比较直观地反映出方程中的等量关系.【类型二】追及问题敌我两军相距25km,敌军以5km/h的速度逃跑,我军同时以8km/h的速度追击,并在相距1km处发生战斗,问战斗是在开始追击后几小时发生的?解析:本题相等关系:我军所走的路程-敌军所走的路程=敌我两军相距的路程.解:设战斗是在开始追击后x小时发生的.根据题意,得8x-5x=25-1.解得x =8.答:战斗是在开始追击后8小时发生的.方法总结:追及问题中的等量关系:追及距离=速度差×追及时间.【类型三】 环形问题甲、乙两人在一条长400米的环形跑道上跑步,甲的速度为360米/分,乙的速度是240米/分.(1)两人同时同地同向跑,问第一次相遇时,两人一共跑了多少圈?(2)两人同时同地反向跑,问几秒后两人第一次相遇?解析:(1)题实质上是追及问题,两人第一次相遇,实际上就是快者比慢者多跑一圈,其等量关系是追上时,甲走的路程-乙走的路程=400米;(2)题实质上是相遇问题,两人第一次相遇就是两人所走的路程之和为环行跑道一圈的长,其等量关系是相遇时,甲走的路程+乙走的路程=400米.解:(1)设x 分钟后两人第一次相遇,由题意,得360x -240x =400.解得x =103. ⎝ ⎛⎭⎪⎫103×360+103×240÷400=5(圈). 答:两人一共走了5圈;(2)设x 分钟后两人第一次相遇,由题意,得360x +240x =400.解得x =23(分钟)=40(秒).答:40秒后两人第一次相遇.方法总结:环形问题中的等量关系:两个人同地背向而行:相遇问题(首次相遇),甲的行程+乙的行程=一圈周长;两个人同地同向而行:追及问题(首次追上),甲的行程-乙的行程=一圈周长.三、板书设计1.等积变形问题2.行程问题(1)相遇问题;(2)追及问题;(3)环形问题.教学过程中,通过对开放性问题的探讨与交流,体验生活中数学的应用与价值,感受数学与人类生活的密切联系,激发学生学习数学的兴趣,培养学生的创新意识、团队精神和克服困难的勇气.。
3.2 一元一次方程的应用
第1课时等积变形和行程问题
【知识与技能】
1.通过一元一次方程解决实际问题,进一步体会方程这一数学模型的重要作用,增强数学的应用意识.
2.掌握一元一次方程解应用题的一般步骤,能根据问题的意义,检验结果的合理性.
【过程与方法】
从学生熟悉的一元一次方程及一元一次方程的解法的基础上,引出利用一元一次方程解决实际问题.通过各种师生活动加深学生对“列一元一次方程解应用题的一般步骤”的理解;让学生在经历知识的获得过程中,体会数学模型思想.过程中还培养了学生的运算能力,提高了教学效率.
【情感态度】
经历将数学问题实际化的过程,感受数学在生活中的应用,进一步体会方程模型的重要性.
【教学重点】
重点是掌握列一元一次方程解决实际问题.
【教学难点】
难点是灵活运用一元一次方程解等积变形和行程问题.
一、情境导入,初步认识
【情境1】实物投影,并呈现问题:如图,用直径为200mm的圆柱体钢,锻造一个长、宽、高分别为300mm,300mm和90mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
【情境2】实物投影,并呈现问题:为了适应经济发展,铁路运输再次提速,如果客车行驶的平均速度增加40km/h,提速后由合肥到北京1 110km的路程只需行驶10h.那么,提
速前,这趟客车平均每小时行驶多少千米?
【教学说明】学生独立思考后,小组讨论,教师注意引导学生正确列出方程,在列方程时,注意等量关系的确定及未知数的设法.在解决问题的过程中,让学生总结列方程解应用题的一般步骤,并能根据问题的意义,检验结果的合理性.情境1中设应截取的圆柱体钢长
为x mm.根据题意,得3.14×
2
200
2
⎛⎫
⎪
⎝⎭
x=300×300×90,解这个方程得x≈258.检验:x≈258
适合方程,且符合题意.答:应截取约258mm长的圆柱体钢.情境2中设提速前客车平均每小时行驶x km,那么提速后客车平均每小时行驶(x+40)km.客车行驶路程1 110km,平均速度是(x+40)km/h,所需时间是10h.根据题意,得:10(x+40)=1 110.解方程,得x=71.检验:x=71适合方程,且符合题意.
答:提速前这趟客车的平均速度是71km/h.
【教学说明】通过现实情景再现,让学生体会到实际生活中的数学问题,并使学生体验数学知识与生活实际的联系.学生通过前面的情景引入,在老师的引导下,通过自己的观察,归纳出结论,进而体验到成功的喜悦,同时,也激发了学生学习的兴趣.
二、思考探究,获取新知
列方程解应用题的方法步骤
问题1列方程解应用题的方法步骤是什么?
问题2寻找等量关系的方法有哪些?
【教学说明】学生通过回顾列方程解应用题的过程,再经过观察、分析、类比后能得出结论.
【归纳结论】列方程解应用题的方法步骤:
(1)审:审题,弄清题意,明确各数量之间的关系;(2)找:找出能够表示应用题全部含义的一个相等关系;(3)设:设未知数,通常题目问什么,就可以设什么为未知数;(4)列:根据这个相等关系列出所需的代数式,从而列出方程;(5)解:解所列出的方程,求出未知数的值;(6)答:检验是否符合题意,答题.列方程解应用题的关键是寻找题目中的等量关系,一般有下列三种方法:①从有关数量比较的关键词语中发现等量关系,如大、小、多、少、倍、分等;②借助基本数量关系,探讨数量之间的等量关系,如路程=平均速度×时间;③注意变化中的不变量,寻找隐含的等量关系,如行程问题中,静水速度不变等.
三、运用新知,深化理解
1.甲、乙两站相距1200千米,一列慢车从甲站开出,每小时行80千米,一列快车从乙站开出,每小时行120千米,两车同时开出,出发后()小时两车相距200千米.
A.5
B.7
C.5或7
D.6
2.一块长、宽、高分别为4cm,3cm,2cm的长方体橡皮泥,要用它来捏一个底面半径为1.5cm的圆柱,圆柱的高是多少?
3.小亮与小莹在运动场上跑步,跑道一圈的长为400米,小亮与小莹的速度分别为5米/秒与4米/秒.
(1)如果二人从跑道上某一位置同时相背起跑,那么经过多少秒二人第一次相遇?
(2)如果二人从跑道上某一位置同时同向起跑,那么经过多少分钟小亮第一次追上小莹?
【教学说明】通过新课的讲解以及学生的练习,充分做到讲练结合,让学生更好巩固新知识.通过本环节的讲解与训练,让学生对一元二次方程有了更加明确的认识,同时也尽量让学生明白知识点不是孤立的,需要前后联系,才能更好地处理问题.
【答案】1.C
2.解:设圆柱的高是x cm,根据题意,得4×3×2=π×1.52x,解得x=32
3π
cm.
答:圆柱的高是32
3π
cm.
5.解:(1)设经过x秒二人第一次相遇.根据题意,得5x+4x=400,解这个方程,得x=400 9
.
所以经过400
9
秒二人第一次相遇.
(2)设经过y秒小亮第一次追上小莹.根据题意,得5y-4y=400,
解这个方程,得y=400. 40020 603
=.
所以经过20
3
分钟小亮第一次追上小莹.
四、师生互动,课堂小结
1.列方程解应用题的一般步骤是什么?
2.如何运用一元一次方程解决等积变形问题和行程问题?
3.通过这节课的学习,你还有哪些疑惑,大家交流.
【教学说明】引导学生自己小结本节课的知识要点及数学方法,从而将本节知识点进行很好的回顾以加深学生的印象,同时使知识系统化.
1.布置作业:从教材第94页“练习”和第97页“习题3.2”中选取.
2.完成同步练习册中本课时的练习.
本节课主要是列方程解决等积变形与行程问题,列方程解应用题的过程实际上就是将问题“数学化”的过程.也就是先将实际问题化为数学问题,即方程,也就是“数学模型”,然
后解这个数学问题,即解方程,再将这个数学问题的解转化为实际问题的解.。