交岔点、三心拱及圆弧拱excel计算程序(完整)

定义所谓“三心拱”，即拱形由三段相内切的圆弧构成。

三段圆弧则有三个圆心，故称三心拱。

编辑本段特性任意三心拱，是指三心拱的拱宽和拱高可以任意指定，但拱形本身必须具备下列特点：1.拱作为受力结构的主要特性，是要将覆在其上的载荷作用所产生的内应力，沿拱上任意点的切线方向传递至拱（或墙脚），而拱上任意点的径向应力（拉或压应力）为0，这在理论上就必须要求拱的三段圆弧上的任意点的切线均应垂直通过该点的圆弧半径，包括大小三段弧相切之切点的切线必须垂直大小圆弧半径的重合点。

不具备这一特性，则不是一个标准的拱形。

一心拱即半圆拱和弧形拱具备这一特性，仅是三心拱的特例。

2.大拱的顶部圆弧之圆心在拱的对称轴线上，而两侧小圆弧之圆心的联线被对称轴线垂直平分。

3.拱之大小圆弧相内切，通过其切点的切线垂直大小圆弧半径之重合线。

编辑本段任意三心拱的作法已知三心拱的净高h和净宽w，作三心拱。

步骤：1.作直线ab=w，作ab的中垂线cf=h；2.分别过c点和a点作cf和ab的垂线，并交于d点，连接ca；3.分别过c点和a点作角dca和角dac的角平分线，并交于e点；4.过e点作ac的垂线，与ab交于o2点，与cf的延长线交于o1点；5.以o1为圆心，co1为半径作弧，过c、e两点；以o2为圆心，eo2为半径作弧，过e、a两点；6.然后将弧aec以cf为对称轴镜像，得到完整的三心拱，如图所示。

o1、o2和o3即为一个大圆和两个小圆的圆心。

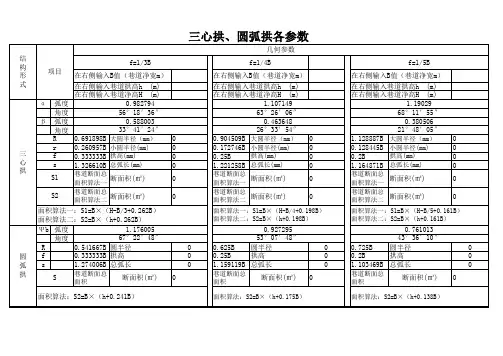
二、三分之一的三心拱的大小圆半径1、大圆半径为R=0.692B（B为巷道宽度）2、小圆半径为r=0.262B（B为巷道宽度）3、大圆圆心角a=67°22′4、小圆圆心角a=56°19′5、1/3三心拱面积为0.264B²三、1/4三心拱1、大圆半径为R=0.904B（B为巷道宽度）2、小圆半径为r=0.173B（B为巷道宽度）3、大圆圆心角a=53°08′4、小圆圆心角a=63°26′5、1/3三心拱面积为0.198B²四、2/5三心拱1、大圆半径为R=0.593B（B为巷道宽度）2、小圆半径为r=0.346B（B为巷道宽度）3、大圆圆心角a=77°19′4、小圆圆心角a=51°21′5、1/3三心拱面积为0.315B²五、1/3圆弧拱1、大圆半径为R=0.542B（B为巷道宽度）2、弧心至拱基线高为r=0.209B（B为巷道宽度）3、大圆圆心角a=134°46′4、面积为0.241B²六、1/4圆弧拱1、大圆半径为R=0.625B（B为巷道宽度）2、弧心至拱基线高为r=0.371B（B为巷道宽度）3、大圆圆心角a=106°16′4、面积为0.175B²七、2/5圆弧拱1、大圆半径为R=0.512B（B为巷道宽度）2、弧心至拱基线高为r=0.110B（B为巷道宽度）3、大圆圆心角a=154°38′4、面积为0.298B²。

三心拱的面积计算公式是什么？如何证明公式？问题补充：对于公式S=B(aB+H)其中：H是表示壁高，还是拱高，亦或者是墙高？已知三心拱的净高h和净宽w，作三心拱。

步骤： 1.作直线ab=w，作ab的中垂线cf=h； 2.分别过c点和a点作cf和ab 的垂线，并交于d点，连接ca； 3.分别过c点和a点作角dca 和角dac的角平分线，并交于e点； 4.过e点作ac的垂线，与ab交于o2点，与cf的延长线交于o1点； 5.以o1为圆心，co1为半径作弧，过c、e两点；以o2为圆心，eo2为半径作弧，过e、a 两点； 6.然后将弧aec以cf为对称轴镜像，得到完整的三心拱，如图所示。

o1、o2和o3即为一个大圆和两个小圆的圆心。

补充回答：心拱断面面积的计算公式三心拱：S＝B（净宽）×（H－B/3+0.263B）B：净宽H：净高S＝B（净宽）×（H－B/4+0.198B）B：净宽H：净高补充回答：巷道面积公式三心拱S=B0(h2+0.262B0)S=B0(h2+0.198B0)S=B0(h2+0.161B0)圆弧拱S=B0(h2+0.241B0)S=B0(h2+0.175B0)S=B0(h2+0.138B0)半园拱S=B0(h2+0.39B0)注：式中h2为墙高Bo为巷道宽度f0为拱高拱形巷道参数表S——为拱弧长f0——拱高B0——巷道宽度α——小圆角度β——大圆角度R——大圆半径r ——小圆半径巷道面积公式三心拱S=B0(h2+0.262B0) S=B0(h2+0.198B0) S=B0(h2+0.161B0) 圆弧拱S=B0(h2+0.241B0) S=B0(h2+0.175B0) S=B0(h2+0.138B0) 半园拱S=B0(h2+0.39B0)注：式中h2为墙高Bo为巷道宽度f0为拱高。

三心拱的面积计算公式是什么？如何证明公式？问题补充：对于公式S=B(aB+H)其中：H是表示壁高，还是拱高，亦或者是墙高？已知三心拱的净高h和净宽w，作三心拱。

步骤： 1.作直线ab=w，作ab的中垂线cf=h； 2.分别过c点和a点作cf和ab 的垂线，并交于d点，连接ca； 3.分别过c点和a点作角dca 和角dac的角平分线，并交于e点； 4.过e点作ac的垂线，与ab交于o2点，与cf的延长线交于o1点； 5.以o1为圆心，co1为半径作弧，过c、e两点；以o2为圆心，eo2为半径作弧，过e、a 两点； 6.然后将弧aec以cf为对称轴镜像，得到完整的三心拱，如图所示。

o1、o2和o3即为一个大圆和两个小圆的圆心。

补充回答：心拱断面面积的计算公式三心拱：S＝B（净宽）×（H－B/3+0.263B）B：净宽H：净高S＝B（净宽）×（H－B/4+0.198B）B：净宽H：净高补充回答：巷道面积公式三心拱S=B0(h2+0.262B0)S=B0(h2+0.198B0)S=B0(h2+0.161B0)圆弧拱S=B0(h2+0.241B0)S=B0(h2+0.175B0)S=B0(h2+0.138B0)半园拱S=B0(h2+0.39B0)注：式中h2为墙高Bo为巷道宽度f0为拱高拱形巷道参数表S——为拱弧长f0——拱高B0——巷道宽度α——小圆角度β——大圆角度R——大圆半径r ——小圆半径巷道面积公式三心拱S=B0(h2+0.262B0) S=B0(h2+0.198B0) S=B0(h2+0.161B0) 圆弧拱S=B0(h2+0.241B0) S=B0(h2+0.175B0) S=B0(h2+0.138B0) 半园拱S=B0(h2+0.39B0)注：式中h2为墙高Bo为巷道宽度f0为拱高。

三心拱的半径计算公式：地下工程的顶面为增加稳定性，常设计为三心拱。

三心拱参数有高跨比（f），但高跨比f 确定以后，三心拱并不能确定。

大弧半径R是弧心角α的函数，对于f=1/3的三心拱，函数式为：R= bcos(α/2)/{6*sin((α/2)+cos(α/2)-1]}+b/3，但是α/2不能大于67°。

所谓“三心拱”，即拱形由三段相内切的圆弧构成。

三段圆弧则有三个圆心，故称三心拱。

2特性任意三心拱，是指三心拱的拱宽和拱高可以任意指定，但拱形本身必须具备下列特点：1.拱作为受力结构的主要特性，是要将覆在其上的载荷作用所产生的内应力，沿拱上任意点的切线方向传递至拱（或墙脚），而拱上任意点的径向应力（拉或压应力）为0，这在理论上就必须要求拱的三段圆弧上的任意点的切线均应垂直通过该点的圆弧半径，包括大小三段弧相切之切点的切线必须垂直大小圆弧半径的重合点。

不具备这一特性，则不是一个标准的拱形。

一心拱即半圆拱和弧形拱具备这一特性，仅是三心拱的特例。

2.大拱的顶部圆弧之圆心在拱的对称轴线上，而两侧小圆弧之圆心的联线被对称轴线垂直平分。

3.拱之大小圆弧相内切，通过其切点的切线垂直大小圆弧半径之重合线。

3任意三心拱的作法已知三心拱的净高h和净宽w，作三心拱。

步骤：1.作直线ab=w，作ab的中垂线cf=h；2.分别过c点和a点作cf和ab的垂线，并交于d点，连接ca；3.分别过c点和a点作角dca和角dac的角平分线，并交于e点；4.过e点作ac的垂线，与ab交于o2点，与cf的延长线交于o1点；5.以o1为圆心，co1为半径作弧，过c、e两点；以o2为圆心，eo2为半径作弧，过e、a两点；6.然后将弧aec以cf为对称轴镜像，得到完整的三心拱，如图所示。

o1、o2和o3即为一个大圆和两个小圆的圆心。

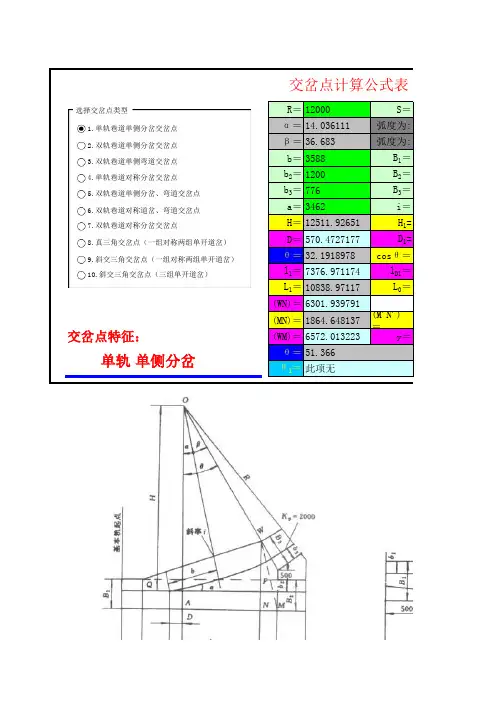
R＝12000S＝1α＝14.036111弧度为:β＝36.683弧度为:b＝3588B 1＝b 2＝1200B 2＝b 3＝776B 3＝a＝3462i＝H＝12511.92651H 1=D＝570.4727177D 1=θ＝32.1918978cos θ＝l 1＝7376.971174l D1＝L 1＝10838.97117L 0＝(WN)＝6301.939791(M N)＝1864.648137(M'N')＝(WM)＝6572.013223y＝θ＝θ1＝此项无单轨单侧分岔交岔点计算公式表交岔点特征：51.366选择交岔点类型1.单轨巷道单侧分岔交岔点2.双轨巷道单侧分岔交岔点3.双轨巷道单侧弯道交岔点4.单轨巷道对称分岔交岔点5.双轨巷道单侧分岔、弯道交岔点6.双轨巷道对称道岔、弯道交岔点7.双轨巷道对称分岔交岔点8.真三角交岔点（一组对称两组单开道岔）9.斜交三角交岔点（一组对称两组单开道岔）10.斜交三角交岔点（三组单开道岔）1.单轨单侧分岔3.双轨单侧弯道5.双轨单侧分岔弯道6.双轨对7.双轨对称分岔9.斜三角（一组对称二组单开）0α1＝142100.244976α1＝14.03611111弧度为:0.2449760.64023914213500α＝2β＝56284010493500β1＝0.3β2＝此项无β1＝此项无β3＝此项无此项无β2＝此项无γ＝此项无0.846269θ1＝此项无cos θ1＝此项无此项无l 2＝此项无P＝此项无9339.799L＝此项无n=此项无m=此项无n 1=此项无m 1=此项无n 2=-365.476m 2=m 3=β3＝γ＝此项无表此项无此项无此项无°°′′″″°′″2.双轨单侧分岔4.单轨对称分岔6.双轨对称道岔8.真三角（一组对称二组单开）10.斜三角（三组单开）。

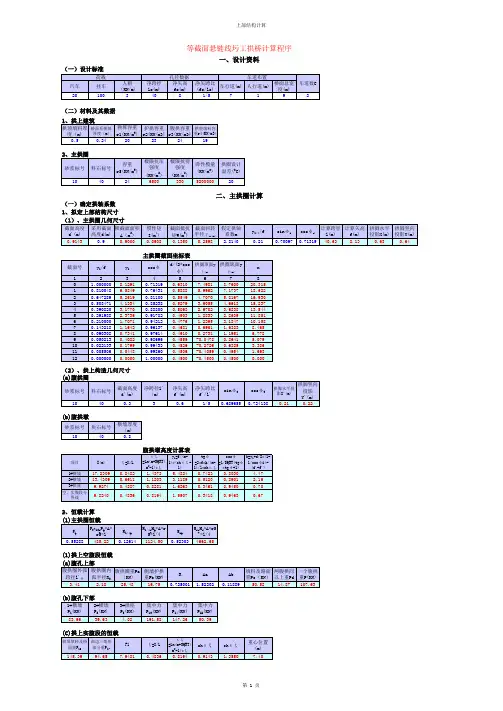
巷道断面、周长计算公式巷道断面三心拱：S=B(0.26B+h2)圆弧拱：S=B(0.24B+h2)半圆拱：S=B (0.39B+h2)梯形断面：S=( B1+B2) / 2 *h巷道周长三心拱：p=2.33B+2 h2圆弧拱：p=2.27B+2 h2半圆拱：p=2.57B+2 h2梯形断面：S=B1+B2 +( 2 h2/sina)以上：B——巷道的净宽度h ——从道渣面起巷道的净高度h2——从道渣面起巷道的墙度B1——巷道的上净宽B2——巷道的下净宽sina——一般取80度17三心拱画法、参数、巷道面积计算公式三心拱的画法：；拱形巷道参数表：；L——拱弧长f——拱高；B——巷道宽度α——小圆角度β——大圆角度R——；巷道断面面积计算公式：三心拱面积公式1：S=B(；S=B(h+0.241B)——f＝B/3S=B(；注：式中B为巷道净宽，h为墙高，f为拱高三心拱面；S＝B×（H－B/3+0.262B）——f＝B/；注：式中B为巷道净宽，H为巷道净高，f为拱高；三心拱的画法：拱形巷道参数表：L——拱弧长 f——拱高1B——巷道宽度α——小圆角度β——大圆角度 R ——大圆半径 r ——小圆半径ψ——圆心角巷道断面面积计算公式：三心拱面积公式1：S=B(h+0.262B) —— f＝B/3 S=B(h+0.198B) —— f＝B/4S=B(h+0.161B) —— f＝B/5 圆弧拱面积公式：S=B(h+0.241B) —— f＝B/3 S=B(h+0.175B) —— f＝B/4 S=B(h+0.138B) —— f＝B/5 半圆拱：S=B(h+0.39B)注：式中B为巷道净宽，h为墙高，f为拱高三心拱面积公式2：S＝B ×（H－B/3+0.262B）—— f＝B/3 S＝B ×（H－B/4+0.198B）—— f＝B/4注：式中B为巷道净宽，H为巷道净高，f为拱高。

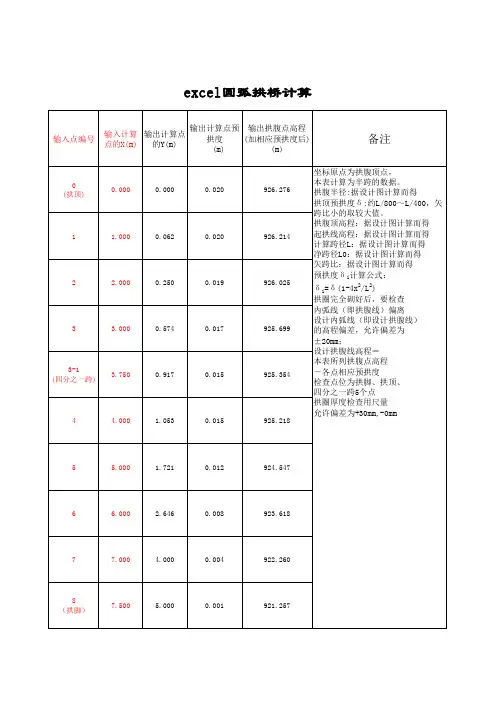
三心拱面积计算公式为了准确计算三心拱的面积，我们需要了解三心拱的定义和结构特点。

三心拱是指由三个通过同一顶点的圆弧构成的拱形结构。

在建筑、桥梁等领域中，三心拱被广泛应用于提供稳定和承重功能。

一、三心拱的定义三心拱是由三个相切于同一顶点的圆弧构成的几何形状。

这三个圆弧的半径分别为r1、r2和r3，顶点处的切线长度为l。

在计算三心拱的面积之前，我们需要先确定这些参数的取值。

二、三心拱的结构特点三心拱具有以下结构特点，这些特点将影响到面积的计算。

1. 顶点切线长度l：顶点切线长度是从顶点处画出的与拱形切线相交的线段长度。

它与半径的取值有关，因为三个圆弧的半径不同，所以l也会有所不同。

2. 上下拱高h：三心拱的上拱和下拱的高度分别为h1和h2。

这两个参数决定了拱形的形状和尺寸，也会影响到拱的面积。

3. 拱脚半径r1、r2和r3：三心拱的圆弧半径将决定拱的大小，它们之间的差异也会对面积的计算产生影响。

三、三心拱的面积计算公式为了准确计算三心拱的面积，我们可以使用以下公式：S = 1/2 * (h1 * r1 + h2 * r2 + l * (r2 - r1))其中，S表示三心拱的面积，h1表示上拱的高度，h2表示下拱的高度，r1表示上拱的半径，r2表示下拱的半径，l表示顶点切线长度。

根据上述公式，我们可以按照以下步骤进行计算：1. 确定三心拱的结构参数，包括h1、h2、r1、r2和l的取值。

2. 将这些参数代入计算公式，进行计算，得到三心拱的面积。

3. 对于复杂的三心拱形状，可以将其分解为多个简单形状的组合，然后分别计算其面积，最后将这些面积求和，得到整个三心拱的面积。

四、三心拱面积计算实例为了更好地理解三心拱面积的计算过程，让我们以一个具体的实例进行说明。

假设上拱高度h1为10米，下拱高度h2为8米，上拱半径r1为5米，下拱半径r2为7米，顶点切线长度l为12米。

首先，代入计算公式：S = 1/2 * (10 * 5 + 8 * 7 + 12 * (7 - 5))经过计算，可以得到三心拱的面积。

三心拱的面积计算公式是什么？如何证明公式?问题补充：对于公式S=B(aB+H)其中：H是表示壁咼，还是拱咼，亦或者是墙咼?已知三心拱的净高h和净宽w，作三心拱。

步骤： 1.作直线ab=w,作ab的中垂线cf=h; 2.分别过c点和a点作cf和ab 的垂线，并交于d点，连接ca; 3•分别过c点和a点作角dca和角dac的角平分线，并交于e点； 4.过e点作ac的垂线，与ab交于o2点，与cf的延长线交于o1点；5•以o1为圆心，col 为半径作弧，过c、e两点；以o2为圆心，eo2为半径作弧，过e、a 两点；6•然后将弧aec以cf为对称轴镜像，得到完整的三心拱，如图所示。

o1、o2和o3即为一个大圆和两个小圆的圆心。

补充回答: 心拱断面面积的计算公式三心拱：S= B (净宽)X( H k B/3+0.263B) B:净宽H:净高S= B (净宽)X( H- B/4+0.198B) B:净宽H:净高补充回答：巷道面积公式三心拱S=B0(h2+0.262B0) S=B0(h2+0.198B0) S=B0(h2+0.161B0) 圆弧拱S=B0(h2+0.241B0) S=B0(h2+0.175B0) S=B0(h2+0.138B0) 半园拱S=B0(h2+0.39B0) 注:式中h2 为墙高Bo为巷道宽度f0为拱高拱形巷道参数表f0 ――拱高B0巷道宽度a 小圆角度(3——大圆角度R――大圆半径r ——小圆半径巷道面积公式三心拱S=B0(h2+0.262B0)S=B0(h2+0.198B0)S=B0(h2+0.161B0) 圆弧拱S=B0(h2+0.241B0)S=B0(h2+0.175B0)S=B0(h2+0.138B0)半园拱S=B0(h2+0.39B0)注：式中h2为墙高Bo为巷道宽度f0为拱高巷道面枳公式.三许Ji ■:禺J 后］爲ABofh^CI 262£g)・37：-h2 >BXh>0 W Bo”% ■护Jo=7^(] S-h(h2f0 】38%卜muS・BMh”Q 39BM a«武中m为堪鬲Bo丸巷遭花度"B为携高・。