北师大版数学高二-选修1-1课时作业 充要条件

[A 组 基础巩固]1．“2a >2b ”是“log 2a >log 2b ”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析：若2a >2b ，则只能得到a >b ，但不能确定a ，b 的正负，当0>a >b 时，log 2a ，log 2b 均无意义，更不能比较其大小；若log 2a >log 2b ，则a >b >0，从而有2a >2b 成立．综上，“2a >2b ”是“log 2a >log 2b ”的必要不充分条件．答案：B2．已知a ，b 都是实数，那么“a 2>b 2”是“a >b ”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析：①当a 2>b 2时，有a 2－b 2>0⇔(a ＋b )(a －b )>0，由此推不出a >b . ②当a >b 时，如若a ＝－2，b ＝－3，有a 2<b 2，故推不出a 2>b 2. 所以“a 2>b 2”是“a >b ”的既不充分也不必要条件． 答案：D3．l 1，l 2表示空间中的两条直线，若p ：l 1，l 2是异面直线，q ：l 1，l 2不相交，则( ) A ．p 是q 的充分条件，但不是q 的必要条件 B ．p 是q 的必要条件，但不是q 的充分条件 C ．p 是q 的充分必要条件D ．p 既不是q 的充分条件，也不是q 的必要条件解析：根据空间两条直线的位置关系和充要条件的定义进行判断．若l 1，l 2异面，则l 1，l 2一定不相交；若l 1，l 2不相交，则l 1，l 2是平行直线或异面直线，故p ⇒q ，q /⇒p ，故p 是q 的充分不必要条件．答案：A4．“x ＝π4”是“函数y ＝sin 2x 取得最大值”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：当x ＝π4时，函数y ＝sin 2x ＝sin π2＝1取得最大值；反过来，当函数y ＝sin 2x 取得最大值时，不能推出x ＝π4，如x ＝5π4时，函数y ＝sin 2x 也可取得最大值．综上所述，“x ＝π4”是“函数y ＝sin 2x 取得最大值”的充分不必要条件，选A.答案：A5．在下列四个结论中，正确的有( ) ①x 2>4是x 3<－8的必要不充分条件；②在△ABC 中，“AB 2＋AC 2＝BC 2”是“△ABC 为直角三角形”的充要条件； ③若a ，b ∈R ，则“a 2＋b 2≠0”是“a ，b 全不为0”的充要条件； ④若a ，b ∈R ，则“a 2＋b 2≠0”是“a ，b 不全为0”的充要条件． A ．①② B ．③④ C ．①④D ．②③解析：对于结论①，由x 3<－8⇒x <－2⇒x 2>4；但是x 2>4⇒x <－2或x >2⇒x 3<－8或x 3>8，不一定有x 3<－8.故x 3<－8⇒x 2>4，但x 2>4⇒/ x 3<－8.所以①正确．根据选择题的特点，对以上的四个结论有选择地进行判断，现已判定①正确，则不必对③进行判定了．因为由①正确可知应淘汰B ，D ，进而只要对A ，C 作进一步的选择，而选A 还是选C ，只需对②或④中的一个作出判定即可，可以从②④中选择容易判定的一个．结论②，“△ABC 为直角三角形”没有明确哪个顶点为直角顶点，因此就不一定有“AB 2＋AC 2＝BC 2”成立．故“AB 2＋AC 2＝BC 2”是“△ABC 为直角三角形”的充分不必要条件．答案：C6．已知p ：x 2＋x －2＞0，q ：x ＞a ，若q 是p 的充分不必要条件，则a 的取值范围可以是________．解析：将p ，q 分别视为集合A ＝{x |x 2＋x －2＞0}＝{x |x ＞1或x ＜－2}，B ＝{x |x ＞a }，已知q 是p 的充分不必要条件，即B A ，在数轴上表示出两个集合(图略)，可知满足题意的a 的取值范围为a ≥1.答案：[1，＋∞)7．设a ，b 为实数，则“0<ab <1”是“a <1b 或b >1a ”的________条件．解析：∵0<ab <1，∴a ，b 同号，且ab <1. ∴当a >0，b >0时，a <1b ；当a <0，b <0时，b >1a .∴“0<ab <1”是“a <1b 或b >1a”的充分条件．而取a ＝－1，b ＝1，显然有a <1b ，但不能推出0<ab <1，∴“0<ab <1”是“a <1b 或b >1a ”的充分不必要条件．答案：充分不必要8．已知p ：x 2－4x －5≤0，q ：|x －3|<a (a >0)．若p 是q 的充分不必要条件，则实数a 的取值范围是__________．解析：设A ＝{x |x 2－4x －5≤0}＝{x |－1≤x ≤5}，B ＝{x ||x －3|<a }＝{x |－a ＋3<x <a ＋3}．因为p 是q 的充分不必要条件，所以A B ，故⎩⎪⎨⎪⎧－a ＋3<－1a ＋3>5，解得a >4，即实数a 的取值范围为(4，＋∞)．答案：(4，＋∞)9．求关于x 的方程ax 2＋2x ＋1＝0的实数根中有且只有一个负实数根的充要条件． 解析：若方程ax 2＋2x ＋1＝0有且仅有一个负实数根，则 a ＝0时，x ＝－12，符合题意．当a ≠0时，方程ax 2＋2x ＋1＝0有实数根，则Δ＝4－4≥0，解得a ≤1， 当a ＝1时，方程有且仅有一个负实数根x ＝－1，当a <1且a ≠0时，若方程有且仅有一个负实数根，则1a<0，即a <0.综上，“方程ax 2＋2x ＋1＝0有且仅有一个负实数根”的充要条件为“a ≤0或a ＝1”． 10．指出下列各组命题中，p 是q 的什么条件，q 是p 的什么条件． (1)已知a 、b 是不等于0的实数，p ：ab >1，q ：a >b ；(2)p ：m <－2，q ：方程x 2－x －m ＝0无实根；(3)已知p ：－2<m <0,0<n <1，q ：关于x 的方程x 2＋mx ＋n ＝0有两个小于1的正根． 解析：(1)由条件“ab >1”可得a －b b >0，若b >0，则a >b ；若b <0，则有a <b ， ∴“ab>1”⇒/ “a >b ”，条件不充分．反过来，a >b ⇔a －b >0，也不能推出a －b b >0⇔ab >1，条件也不必要．∴p 是q 的既不充分也不必要条件，q 也是p 的既不充分也不必要条件． (2)∵m <－2⇒方程x 2－x －m ＝0无实根； 方程x 2－x －m ＝0无实根⇒/ m <－2.∴p 是q 的充分不必要条件，q 是p 的必要不充分条件．(3)若x 2＋mx ＋n ＝0有两根x 1，x 2，则由根与系数的关系，有x 1＋x 2＝－m ，x 1·x 2＝n ， 又0<x 1，x 2<1，∴0<x 1＋x 2<2,0<x 1x 2<1. ∴－2<m <0,0<n <1，∴q ⇒p .当m ＝－1，n ＝12时，方程x 2＋mx ＋n ＝0，即x 2－x ＋12＝0，此方程无实根，故p ⇒/ q .∴p 是q 的必要不充分条件，q 是p 的充分不必要条件．[B 组 能力提升]1．已知定义在R 上的偶函数f (x )满足f (4－x )＝f (x )，且在区间[0,2]上是增函数，那么“f (0)<0”是“函数f (x )在区间[0,6]上有3个零点”的( )A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件解析：依题意，得f (4－x )＝f (x )＝f (－x )，即函数f (x )是以4为周期的函数．因此，当f (0)<0时，不一定能得出函数f (x )在区间[0,6]上有3个零点，如当f (2)<0时，结合该函数的性质及图像，分析可知此时函数f (x )在区间[0,6]上不存在零点；当函数f (x )在区间[0,6]上有3个零点时，结合该函数的性质及图像，分析可知此时f (0)<0.综上，“f (0)<0”是“函数f (x )在区间[0,6]上有3个零点”的必要不充分条件．答案：C2．设0<x <π2，则“x sin 2 x <1”是“x sin x <1”的________条件．解析：因为0<x <π2，所以0<sin x <1.由x ·sin x <1知x sin 2x <sin x <1，因此必要性成立．由x sin 2x <1得x sin x <1sin x ，而1sin x >1，因此充分性不成立．答案：必要不充分 3．给出下列命题：①命题“若b 2－4ac <0，则方程ax 2＋bx ＋c ＝0(a ≠0)无实根”的否命题； ②命题“在△ABC 中，AB ＝BC ＝CA ，那么△ABC 为等边三角形”的逆命题； ③命题“若a >b >0，则3a >3b >0”的逆否命题；④“若m >1，则mx 2－2(m ＋1)x ＋(m －3)>0的解集为R ”的逆命题． 其中真命题的序号为________．解析：①否命题：若b 2－4ac ≥0，则方程ax 2＋bx ＋c ＝0(a ≠0)有实根，真命题；②逆命题：若△ABC 为等边三角形，则AB ＝BC ＝CA ，真命题；③因为命题“若a >b >0，则3a >3b >0”是真命题，故其逆否命题为真；④逆命题：若mx 2－2(m ＋1)x ＋(m －3)>0的解集为R ，则m >1，假命题，因为⎩⎪⎨⎪⎧m >0，[－2(m ＋1)]2－4m (m －3)<0，得m ∈∅. 所以应填①②③. 答案：①②③4．已知条件p ：A ＝{x |x 2－(a ＋1)x ＋a ≤0}，条件q ：B ＝{x |x 2－3x ＋2≤0}，当a 为何值时，(1)p 是q 的充分不必要条件； (2)p 是q 的必要不充分条件； (3)p 是q 的充要条件．解析：由p ：A ＝{x |(x －1)(x －a )≤0}，由q ：B ＝[1,2]． (1)∵p 是q 的充分不必要条件， ∴A ⊆B 且A ≠B ，故A ＝[1，a ]⇒1≤a <2. (2)∵p 是q 的必要不充分条件，∴B ⊆A 且A ≠B ，故A ＝[1，a ]且a >2⇒a >2. (3)∵p 是q 的充要条件，∴A ＝B ⇒a ＝2.5．已知全集U ＝R ，非空集合A ＝⎩⎨⎧⎭⎬⎫x |x －2x －3a －1<0，B ＝⎩⎨⎧⎭⎬⎫x |x －a 2－2x －a <0.记p ：x ∈A ，q ：x ∈B ，若q 是p 的必要条件，求实数a 的取值范围．解析：B ＝{x |a <x <a 2＋2}．①当3a ＋1>2，即a >13时，A ＝{x |2<x <3a ＋1}．∵q 是p 的必要条件，∴A ⊆B ，∴⎩⎪⎨⎪⎧a ≤23a ＋1≤a 2＋2，得13<a ≤3－52. ②当3a ＋1＝2，即a ＝13时，A ＝∅，不符合题意．③当3a ＋1<2，即a <13时，A ＝{x |3a ＋1<x <2}，由A ⊆B ，得⎩⎪⎨⎪⎧a ≤3a ＋1a 2＋2≥2，得－12≤a <13.综上所述，实数a 的取值范围是⎣⎡⎭⎫－12，13∪⎝ ⎛⎦⎥⎤13，3－52.莘莘学子，最重要的就是不要去看远方模糊的，而要做手边清楚的事。

第一章 常用逻辑用语
2．3 充要条件
问题导航 (1)充要条件是如何定义的？ (2)若一个命题及它的逆命题均为真命题，则此命题的条件和 结论等价吗？ (3)若一个命题“若 p，则 q”为真命题，而它的否命题为假命 题，那么 p 是 q 的什么条件？q 是 p 的什么条件？ (4)若一个命题及它的逆命题均为假命题，则此命题的条件是 结论的什么条件？
于 x 的不等式 x2＋mx＋4＞0 的解集为 R，则 p 是 q 成立的( B )
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
解析：(1)因为 0＜a＜b⇒(14)a＞(14)b 成立，反之，由(14)a＞(14)b ⇒a＜b 但推不出 0＜a＜b，故选 A. (2)|x－2|＋|x＋2|≥|x－2－x－2|＝4，由题意可得 p 成立时 m
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
解析：因为 A＝(2，＋∞)，B＝(2，＋∞)∪(－∞，0)，所以
A B，所以“x∈A”是“x∈B”的充分不必要条件．
3．已知 α，β为不重合的两个平面，直线 m α，那么“α⊥β”
是“m⊥β”的( B )
A．充分不必要条件 B．必要不充分条件
[方法归纳] (1)要从 p 推 q，q 推 p 两个方面进行判断； (2)若 p、q 与集合有关时，常利用 p、q 对应集合的基本关系 进行判断．
1．(1)“0＜a＜b”是“(14)a＞(14)b”的( A )
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
(2)已知 p：关于 x 的不等式|x－2|＋|x＋2|＞m 的解集为 R；q：关

§2 充分条件与必要条件课时目标 1.理解充分条件、必要条件、充要条件的意义.2.了解充分而不必要条件，必要而不充分条件，既不充分也不必要条件的含义.3.正确推断充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件.4.通过学习，理解对条件的判定可以归结为推断命题的真假．1．充分条件 “若p ，则q ”形式的命题为真命题是指：由条件p 可以得到结论q .通常记作________，读作“p 推出q ”．此时我们称________________________． 2．必要条件假如“若p ，则q ”形式的命题为真命题，即________，称p 是q 的____________，同时，我们称q 是p 的____________．3．充要条件：由于p ⇒q ，所以p 是q 的充分条件；由于q ⇒p ，所以p 是q 的必要条件，在这种状况下，我们称p 是q 的充分必要条件，简称充要条件． 4．推出与充分条件、必要条件若p ⇒q ，但q ⇒p ，则称p 是q 的________________________； 若p ⇒q ，但q ⇒p ，则称p 是q 的_________________________； 若p ⇒q ，且q ⇒p ，则称p 是q 的________________________．一、选择题1．“A ＝B ”是“sin A ＝sin B ”的( ) A ．充分不必要条件 B ．必要不充分条件C ．既是充分条件，又是必要条件D ．既不充分又不必要条件2．“m <14”是“一元二次方程x 2＋x ＋m ＝0有实数解”的( )A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件3．设0<x <π2，则“x sin 2x <1”是“x sin x <1”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件4．设集合M ＝{x |x >2}，P ＝{x |x <3}，那么“x ∈M ，或x ∈P ”是“x ∈M ∩P ”的( ) A ．必要不充分条件 B ．充分不必要条件 C ．充要条件D ．既不充分也不必要条件5．若f (x )是R 上的减函数，且f (0)＝3，f (3)＝－1，设P ＝{x ||f (x ＋t )－1|<2}，Q ＝{x |f (x )<－1}，若“x ∈P ”是“x ∈Q ”的充分不必要条件，则实数t 的取值范围是( ) A ．{t |t ≤0} B ．{t |t ≥0} C ．{t |t ≥－3} D ．{t |t ≤－3}题 号 1 2 3 4 5 答 案二、填空题6．“lg x >lg y ”是“x >y ”的____________条件．7．p 是q 的充分不必要条件，r 是q 的必要不充分条件，那么p 是r 的____________条件．8．不等式(a ＋x )(1＋x )<0成立的一个充分而不必要条件是－2<x <－1，则a 的取值范围是________．三、解答题9．求证：关于x 的方程x 2＋2ax ＋b ＝0有实数根且两根均小于2的充分但不必要条件是a ≥2且|b |≤4.10.已知p ：实数x 满足x 2－4ax ＋3a 2<0，其中a <0；q ：实数x 满足x 2－x －6≤0或x 2＋2x －8>0，且p 是q 的充分不必要条件，求a 的取值范围．力量提升11．记实数x 1，x 2，…，x n 中的最大数为max{x 1，x 2，…，x n }，最小数为min {}x 1，x 2，…，x n .已知△ABC的三边边长为a ，b ，c (a ≤b ≤c )，定义它的倾斜度为l =max ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ·min ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ，则“l ＝1”是“△ABC 为等边三角形”的( ) A ．必要而不充分条件 B ．充分而不必要条件 C ．充要条件D ．既不充分也不必要条件12．已知数列{a n }的前n 项和为S n ＝(n ＋1)2＋c ，探究{a n }是等差数列的充要条件．。

2.3 充要条件课时目标1．结合实例，理解充要条件的意义.2.会判断(证明)某些命题的条件关系.3.会利用充要条件求一些字母的范围，进一步理解数学概念．1．如果既有p ⇒q ，又有q ⇒p ，就记作__________．这时p 是q 的____________条件，简称________条件，实际上p 与q 互为________条件．如果p ⇒q 且q ⇒p ，则p 是q 的____________________条件．2．我们常用“当且仅当”表达充要条件．命题p 和命题q 互为充要条件，称它们是两个相互等价的命题．一、选择题1．“x >0”是“x ≠0”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件2．设集合M ＝{x |0<x ≤3}，N ＝{x |0<x ≤2}，那么“a ∈M ”是“a ∈N ”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件3．“m <14”是“一元二次方程x 2＋x ＋m ＝0有实数解”的( ) A ．充分非必要条件 B ．充分必要条件C ．必要非充分条件D ．非充分非必要条件4．“k ＝1”是“直线x －y ＋k ＝0与圆x 2＋y 2＝1相交”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件5．设l ，m ，n 均为直线，其中m ，n 在平面α内，“l ⊥α”是“l ⊥m 且l ⊥n ”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．“a <0”是“方程ax 2＋2x ＋1＝0至少有一个负数根”的( )A ．必要不充分条件B ．充分不必要条件C ．充分必要条件二、填空题7．用符号“⇒”或“⇒”填空.(1)a >b ________ac 2>bc 2；(2)a 2c ≠0________c ≠0.8．不等式(a ＋x )(1＋x )<0成立的一个充分而不必要条件是－2<x <－1，则a 的取值范围是________．9．函数y ＝ax 2＋bx ＋c (a >0)在[1，＋∞)上单调递增的充要条件是__________．(填序号)三、解答题10．下列命题中，判断条件p 是条件q 的什么条件：(1)p ：|x |＝|y |，q ：x ＝y .(2)p ：△ABC 是直角三角形，q ：△ABC 是等腰三角形；(3)p ：四边形的对角线互相平分，q ：四边形是矩形．11.设x，y∈R，求证|x＋y|＝|x|＋|y|成立的充要条件是xy≥0.能力提升12．已知P＝{x|a－4<x<a＋4}，Q＝{x|x2－4x＋3<0}，若x∈P是x∈Q的必要条件，求实数a的取值范围．13．记实数x 1，x 2，…，x n 中的最大数为max{x 1，x 2，…，x n }，最小数为min {}x 1，x 2，…，x n .已知△ABC 的三边边长为a ，b ，c (a ≤b ≤c )，定义它的倾斜度为l ＝max ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ·min ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ， 则“l ＝1”是“△ABC 为等边三角形”的( )A ．必要而不充分条件B ．充分而不必要条件C ．充要条件D ．既不充分也不必要条件1．判断条件p 和结论q 之间的关系，可以先尝试确定p 、q 间的推出关系．2．证明充要条件时，既要证明充分性，又要证明必要性，即证明原命题和逆命题都成立，但要分清必要性、充分性是证明怎样的一个式子成立．“A 的充要条件为B ”的命题的证明：A ⇒B 证明了必要性；B ⇒A 证明了充分性．“A 是B 的充要条件”的命题的证明：A ⇒B 证明了充分性；B ⇒A 证明了必要性．2．3 充要条件知识梳理1．p ⇔q 充分必要 充要 充要 既不充分又不必要作业设计1．A [对于“x >0”⇒“x ≠0”，反之不一定成立． 因此“x >0”是“x ≠0”的充分而不必要条件．]2．B [因为N M .所以“a ∈M ”是“a ∈N ”的必要而不充分条件．]3．A [若一元二次方程x 2＋x ＋m ＝0有实数解，则Δ＝1－4m ≥0，因此m ≤14. 故m <14是方程x 2＋x ＋m ＝0有实数解的充分非必要条件．] 4．A [把k ＝1代入x －y ＋k ＝0，推得“直线x －y ＋k ＝0与圆x 2＋y 2＝1相交”；但“直线x －y ＋k ＝0与圆x 2＋y 2＝1相交”不一定推得“k ＝1”．故“k ＝1”是“直线x －y ＋k＝0与圆x 2＋y 2＝1相交”的充分而不必要条件．]5．A [l ⊥α⇒l ⊥m 且l ⊥n ，而m ，n 是平面α内两条直线，并不一定相交，所以l ⊥m 且l ⊥n 不能得到l ⊥α.]6．B [当a <0时，由韦达定理知x 1x 2＝1a<0，故此一元二次方程有一正根和一负根，符合题意；当ax 2＋2x ＋1＝0至少有一个负数根时，a 可以为0，因为当a ＝0时，该方程仅有一根为－12，所以a 不一定小于0.由上述推理可知，“a <0”是“方程ax 2＋2x ＋1＝0至少有一个负数根”的充分不必要条件．]7．(1)⇒ (2)⇒8．(2，＋∞)解析 不等式变形为(x ＋1)(x ＋a )<0，因当－2<x <－1时不等式成立，所以不等式的解为－a <x <－1.由题意有(－2，－1)(－a ，－1)，∴－2>－a ，即a >2. 9．b ≥－2a解析 由二次函数的图象可知当－b 2a≤1，即b ≥－2a 时，函数y ＝ax 2＋bx ＋c 在[1，＋∞)上单调递增．10．解 (1)∵|x |＝|y |⇒x ＝y ，但x ＝y ⇒|x |＝|y |，∴p 是q 的必要条件，但不是充分条件．(2)△ABC 是直角三角形⇒△ABC 是等腰三角形．△ABC 是等腰三角形⇒△ABC 是直角三角形．∴p 既不是q 的充分条件，也不是q 的必要条件．(3)四边形的对角线互相平分⇒四边形是矩形．四边形是矩形⇒四边形的对角线互相平分．∴p 是q 的必要条件，但不是充分条件．11．证明 ①充分性：如果xy ≥0，则有xy ＝0和xy >0两种情况，当xy ＝0时，不妨设x ＝0，则|x ＋y |＝|y |，|x |＋|y |＝|y |，∴等式成立．当xy >0时，即x >0，y >0，或x <0，y <0，又当x >0，y >0时，|x ＋y |＝x ＋y ，|x |＋|y |＝x ＋y ，∴等式成立．当x <0，y <0时，|x ＋y |＝－(x ＋y )，|x |＋|y |＝－x －y ，∴等式成立．总之，当xy ≥0时，|x ＋y |＝|x |＋|y |成立．②必要性：若|x ＋y |＝|x |＋|y |且x ，y ∈R ，则|x ＋y |2＝(|x |＋|y |)2，即x 2＋2xy ＋y 2＝x 2＋y 2＋2|x ||y |，∴|xy |＝xy ，∴xy ≥0.综上可知，xy ≥0是等式|x ＋y |＝|x |＋|y |成立的充要条件．12．解 由题意知，Q ＝{x |1<x <3}，Q ⇒P ，∴⎩⎪⎨⎪⎧ a －4≤1a ＋4≥3，解得－1≤a ≤5.∴实数a 的取值范围是[－1,5]．13．A [当△ABC 是等边三角形时，a ＝b ＝c ，∴l ＝max ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ·min ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ＝1×1＝1. ∴“l ＝1”是“△ABC 为等边三角形”的必要条件．∵a ≤b ≤c ，∴max ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ＝c a.又∵l ＝1，∴min ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ＝a c ， 即a b ＝a c 或b c ＝a c ，得b ＝c 或b ＝a ，可知△ABC 为等腰三角形，而不能推出△ABC 为等边三角形． ∴“l ＝1”不是“△ABC 为等边三角形”的充分条件．]。

C.[1，＋∞)
D.(－∞，－1]
解析 q：x<－1或x>2，由题意知，{x|x≥k} {x|x<－1或x>2}， 则k>2， ∴k的取值范围是(2，＋∞).
3 达标检测
PART THREE
1.“－2<x<1”是“x>1或x<－1”的 A.充分不必要条件 B.必要不充分条件
√C.既不充分又不必要条件
第一章 §2 充分条件与必要条件
2.3 充要条件
学习目标
XUEXIMUBIAO
1.了解充要条件的意义. 2.会判断、证明充要条件. 3.通过学习，弄清对条件的判断应该归结为对命题真假的判断.
内容索引
NEIRONGSUOYIN
自主学习 题型探究 达标检测
1 自主学习
PART ONE
知识点一 充要条件的概念 一般地，如果既有p⇒q，又有q⇒p，就记作 p⇔q .此时，我们说，p是q的_充__分_ 必要条件 ，简称 充要条件 .
题型三 充分条件与必要条件的应用
例4 已知p：3x＋m<0，q：x2－2x－3>0，若p是q的一个充分不必要条件，求
m的取值范围.
解
由 3x＋m<0 得，x<－m3 .∴p：A＝xx <－m3
.
由x2－2x－3>0得，x<－1或x>3. ∴q：B＝{x|x<－1或x>3}. ∵p⇒q 而 q⇏p，∴A 是 B 的真子集，∴－m3 ：x－1＝ x－1； 解 ∵当 x＝1 或 x＝2 时，可得 x－1＝ x－1成立， 反过来，当 x－1＝ x－1时，可以推出 x＝1 或 x＝2， ∴p是q的充要条件. (4)p：sin α>sin β，q：α>β. 解 由sin α>sin β不能推出α>β， 反过来由α>β也不能推出sin α>sin β， ∴p既不是q的充分条件，也不是q的必要条件. 则p是q的既不充分又不必要条件.

1.充要条件的概念 ：
既有p q，又有q p，就 记作 p q.
则 p 是 q 的充分必要条件， 简称充要条件.
2.形如“若p，则q ”的命题中存在以下四种关系 ：
（1）p是q的充分不必要条件 （2）p是q的必要不充分条件 （3）p是q的充要条件 （4）p是q的既不充分又不必要条件
No Image
1.“b＝c＝0”是“二次函数y＝ax2＋bx＋c(a≠0)
经过原点”的( A )
A.充分不必要条件 B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
解析：b＝c＝0⇒y＝ax2，二次函数一定经过原点；
二次函数y＝ax2＋bx＋c经过原点⇒c＝0，b不一
定等于0，故选A.
2.（2012·山东高考）设a＞0且a≠1，则“函数
f(x)=ax在R上是减函数”是“函数g(x)=(2-a)x3在
R上是增函数”的（ A ）
A.充分不必要条件 B.必要不充分条件
C.充分必要条件
D.既不充分又不必要条件
提示：结合函数单调性的定义求解
3.若A是B的必要不充分条件，C是B的充要条件，D 是C的充分不必要条件，那么D是A的_充__分__不__必__要__条__件_. 4.填写“充分不必要，必要不充分，充要，既不充 分又不必要”. （1）sinA>sinB是A>B的_既__不__充__分__又__不__必__要__条件. （2）在Δ ABC中，sinA>sinB是 A>B的_充__要__条件.
由于p q，q p，我们称p是q的充分必要条件, 简称充要条件.
注意：1. p q，q p，通常记作：p q
2.当p是q的充要条件时，q也是p的充要条件. 3.我们常用“当且仅当”来表达充要条件，p是q 的充要条件可以说成：p成立当且仅当q成立.

充要条件同步练习1．在下列括号中填写“充分而不必要条件”“必要而不充分条件”“充要条件”三者中的一种．(1)“a=0”是“ab=0”的( )(2)“|x|＜3”是“|x|＜5”的( )(3)“a3－b3是偶数”是“a－b是偶数”的( )(4)“x＋y=7”是“x2－y2－6x＋8y=7”的( )(5)“x＋y=4”是“2x2－xy－3y2－7x＋13y－4=0”的( )．(1)a＋b＞0________a＞0且b＞0．(2)c2a＞c2b________a＞b．(3)A∪B≠φ________A∩B≠φ．(5)A∩B=φ________A=φ或B=φ．3．用“充分”“必要”填空．(1)“某数能被9整除”是“某数能被3整除”的________条件．(2)“两三角形对应三边相等”是“两三角形对应角相等”的________条件．(4)“(1－|x|)(1＋x)＞0”是“|x|＜1”的________条件．4．用“充分”“必要”填空．(1)“0＜x＜5”是“|x－2|＜3”的________条件．(2)“四边形的对角线相等”是“这个平行四边形为正方形”的________条件．(3)“xy＞0”是|x＋y|=|x|＋|y|”的________条件．(4)“个位数是5的整数”是“这个数能被5整除”的________条件．5．证明：关于x的不等式ax2－ax＋1＞0对于一切实数都成立的必要条件是0＜a＜4．答案:1．(1)充分而不必要条件(2)充分而不必要条件(3)充要条件(4)充分而不必要条件(5)充分而不必要条件3．(1)充分 (2)充分 (3)必要 (4)必要4．(1)充分 (2)必要 (3)充分 (4)充分∴不等式ax2－ax＋1＞0对一切实数都成立的必要条件是0＜a ＜4．。

3 的取值范围是2，2.
判断下列各题中的条件是结论的什么条件． (1)条件 A：ax2＋ax＋1＞0 的解集为 R，结论 B：0＜a＜4； (2)条件 p：A B，结论 q：A∪B＝B.
【错解】 (1)∵Δ＝a2－4a＜0，即 0＜a＜4，
∴当 0＜a＜4 时，ax2＋ax＋1＞0 恒成立，故 B⇒A. 而 ax2＋ax＋1＞0 的解集为 R 时，有 0＜a＜4，故 A⇒B， ∴A 是 B 的充要条件．
此时就有p是q的充分条件，q是p的必要条件．
(2)“p是q的充分条件”中，p是条件，q是结论．“q是p的 必要条件”中，p是结论，q是条件． (3)p 是 q 的充要条件也可以说成： p 成立，当且仅当 q 成 立．如果p、q分别表示两个命题，且它们互为充要条件，我们
通常称命题p和命题q是两个互相等价的命题．
) B．必要而不充分条件 D．既不充分也不必要条件
由a＞b不一定可推出a＞|b|，但由a＞|b|一定可以
推出a＞b.
答案： B
2．设x∈R，则“x＝1”是“x3＝x”的( A．充分而不必要条件
)
B．必要而不充分条件
C．充要条件
解析：
D．既不充分也不必要条件
当 x ＝ 1 时， x3 ＝ x 成立．若 x3 ＝x ， x(x2 － 1) ＝ 0 ，
2
c 负根，所以 Δ＝b －4ac>0，x1x2＝a<0，所以 ac<0 c 充分性：由 ac<0 可推得 Δ＝b －4ac>0 及 x1x2＝a<0
2
所以方程 ax2＋bx＋c＝0 有两个相异实根，且两根异号． 即方程 ax2＋bx＋c＝0 有一正根和一负根．
充分、必要条件的应用

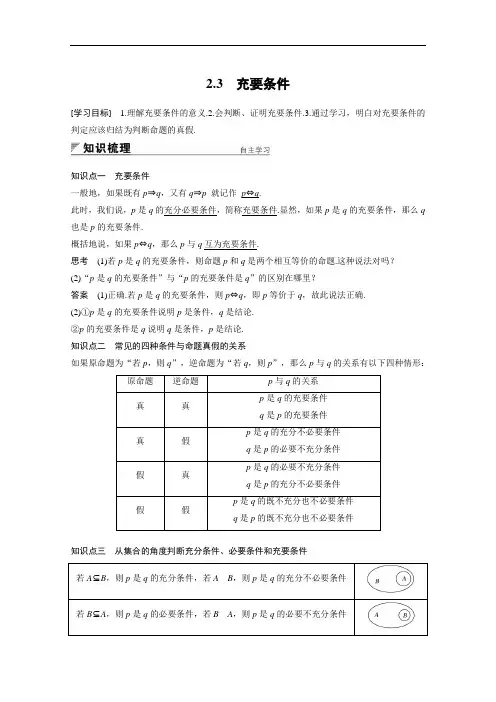
2.3充要条件[学习目标] 1.理解充要条件的意义.2.会判断、证明充要条件.3.通过学习，明白对充要条件的判定应该归结为判断命题的真假.知识点一充要条件一般地，如果既有p⇒q，又有q⇒p就记作_p⇔q.此时，我们说，p是q的充分必要条件，简称充要条件.显然，如果p是q的充要条件，那么q 也是p的充要条件.概括地说，如果p⇔q，那么p与q互为充要条件.思考(1)若p是q的充要条件，则命题p和q是两个相互等价的命题.这种说法对吗？(2)“p是q的充要条件”与“p的充要条件是q”的区别在哪里？答案(1)正确.若p是q的充要条件，则p⇔q，即p等价于q，故此说法正确.(2)①p是q的充要条件说明p是条件，q是结论.②p的充要条件是q说明q是条件，p是结论.知识点二常见的四种条件与命题真假的关系如果原命题为“若p，则q”，逆命题为“若q，则p”，那么p与q的关系有以下四种情形：知识点三从集合的角度判断充分条件、必要条件和充要条件其中p：A＝{x|p(x)成立}，q：B＝{x|q(x)成立}.题型一充要条件的判断例1(1)设x＞0，y∈R，则“x＞y”是“x＞|y|”的()A.充要条件B.充分而不必要条件C.必要而不充分条件D.既不充分也不必要条件答案 C解析分别判断x＞y⇒x＞|y|与x＞|y|⇒x＞y是否成立，从而得到答案.当x＝1，y＝－2时，x＞y，但x＞|y|不成立；若x＞|y|，因为|y|≥y，所以x＞y.所以x＞y是x＞|y|的必要而不充分条件.(2)判断下列各题中，p是否为q的充要条件？①在△ABC中，p：∠A>∠B，q：sin A>sin B；②若a，b∈R，p：a2＋b2＝0，q：a＝b＝0；③p：|x|>3，q：x2>9.解①在△ABC中，显然有∠A>∠B⇔sin A>sin B，所以p是q的充要条件.②若a2＋b2＝0，则a＝b＝0，即p⇒q；若a＝b＝0，则a2＋b2＝0，即q⇒p，故p⇔q，所以p是q的充要条件.③由于p：|x|>3⇔q：x2>9，所以p是q的充要条件.反思与感悟判断p是q的充分必要条件的两种思路(1)命题角度：判断p是q的充分必要条件，主要是判断p⇒q及q⇒p这两个命题是否成立.若p⇒q成立，则p是q的充分条件，同时q是p的必要条件；若q⇒p成立，则p是q的必要条件，同时q是p的充分条件；若二者都成立，则p与q互为充要条件.(2)集合角度：关于充分条件、必要条件、充要条件，当不容易判断p⇒q及q⇒p的真假时，也可以从集合角度去判断，结合集合中“小集合⇒大集合”的关系来理解，这对解决与逻辑有关的问题是大有益处的.跟踪训练1 (1)已知直线a ，b 分别在两个不同的平面α，β内，则“直线a 和直线b 相交”是“平面α和平面β相交”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件答案 A解析 若直线a 和直线b 相交，则平面α和平面β相交；若平面α和平面β相交，那么直线a 和直线b 可能平行或异面或相交，故选A. (2)“函数y ＝x 2－2x －a 没有零点”的充要条件是________. 答案 a <－1解析 函数没有零点，即方程x 2－2x －a ＝0无实根，所以有Δ＝4＋4a <0，解得a <－1.反之，若a <－1，则Δ<0，方程x 2－2x －a ＝0无实根，即函数没有零点. 故“函数y ＝x 2－2x －a 没有零点”的充要条件是a <－1. 题型二 充要条件的证明例2 求证：方程x 2＋(2k －1)x ＋k 2＝0的两个根均大于1的充要条件是k <－2. 证明 ①必要性：若方程x 2＋(2k －1)x ＋k 2＝0有两个大于1的根，不妨设两个根为x 1，x 2，则 ⎩⎪⎨⎪⎧Δ＝(2k －1)2－4k 2≥0，(x 1－1)＋(x 2－1)>0，(x 1－1)(x 2－1)>0，⇒⎩⎪⎨⎪⎧k ≤14，(x 1＋x 2)－2>0，x 1x 2－(x 1＋x 2)＋1>0.即⎩⎪⎨⎪⎧k ≤14，－(2k －1)－2>0，k 2＋(2k －1)＋1>0，解得k <－2.②充分性：当k <－2时，Δ＝(2k －1)2－4k 2＝1－4k >0. 设方程x 2＋(2k －1)x ＋k 2＝0的两个根为x 1，x 2. 则(x 1－1)(x 2－1)＝x 1x 2－(x 1＋x 2)＋1 ＝k 2＋2k －1＋1＝k (k ＋2)>0. 又(x 1－1)＋(x 2－1)＝(x 1＋x 2)－2 ＝－(2k －1)－2＝－2k －1>0， ∴x 1－1>0，x 2－1>0. ∴x 1>1，x 2>1.综上可知，方程x 2＋(2k －1)x ＋k 2＝0有两个大于1的根的充要条件为k <－2.反思与感悟一般地，证明“p成立的充要条件为q”时，在证充分性时应以q为“已知条件”，p是该步中要证明的“结论”，即q⇒p；证明必要性时则是以p为“已知条件”，q为该步中要证明的“结论”，即p⇒q.跟踪训练2求证：一次函数f(x)＝kx＋b(k≠0)是奇函数的充要条件是b＝0.证明①充分性：如果b＝0，那么f(x)＝kx，因为f(－x)＝k(－x)＝－kx，所以f(－x)＝－f(x)，所以f(x)为奇函数.②必要性：因为f(x)＝kx＋b(k≠0)是奇函数，所以f(－x)＝－f(x)对任意x均成立，即k(－x)＋b＝－(kx＋b)，所以b＝0.综上，一次函数f(x)＝kx＋b(k≠0)是奇函数的充要条件是b＝0.充分必要条件的应用例3使得x2＋2x≤0成立的充分不必要条件可以是()A.－1≤x≤1B.－3<x≤0C.－1<x<0D.－1<x<1错解 B错因分析没有分清命题的条件和结论.若p的充分不必要条件是q，应有q⇒p且pD⇒/q.正解 C1.设p：实数x，y满足x>1且y>1，q：实数x，y满足x＋y>2，则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 A解析2.已知集合A＝{1，a}，B＝{1,2,3}，则“a＝3”是“A⊆B”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件 答案 A解析 a ＝3时，A ＝{1,3}，A ⊆B ；当A ⊆B 时，a ＝2或3.3.已知α：“a ＝±2”；β：“直线x －y ＝0与圆x 2＋(y －a )2＝2相切”，则α是β的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D .既不充分也不必要条件 答案 C解析 a ＝±2时，直线x －y ＝0与圆x 2＋(y ±2)2＝2相切；当直线x －y ＝0与圆x 2＋(y －a )2＝2相切时，得|a |2＝2，∴a ＝±2.∴α是β的充要条件. 4.已知直线l 1：x ＋ay ＋6＝0和直线l 2：(a －2)x ＋3y ＋2a ＝0，则l 1∥l 2的充要条件是a ＝________. 答案 －1解析 由1×3－a ×(a －2)＝0得a ＝3或－1， 而a ＝3时，两条直线重合，所以a ＝－1.5.命题p ：x >0，y <0，命题q ：x >y ，1x >1y ，则p 是q 的________条件.答案 充要解析 当x >0，y <0时，x >y 且1x >1y 成立，当x >y 且1x >1y时，得⎩⎪⎨⎪⎧x －y >0，x －yxy <0⇒⎩⎪⎨⎪⎧x >0，y <0. 所以p 是q 的充要条件.1.充要条件的判断有三种方法：定义法、等价命题法、集合法.2.充要条件的证明与探求(1)充要条件的证明分充分性的证明和必要性的证明.在证明时要注意两种叙述方式的区别： ①p 是q 的充要条件，则由p ⇒q 证的是充分性，由q ⇒p 证的是必要性； ②p 的充要条件是q ，则由p ⇒q 证的是必要性，由q ⇒p 证的是充分性.(2)探求充要条件，可先求出必要条件，再证充分性；如果能保证每一步的变形转化过程都可逆，也可以直接求出充要条件.。

1.2.1 充分条件与必要条件一、选择题1．若¬p 是¬q 的必要条件，则q 是p 的( )A ．充分条件B ．必要条件C ．非充分条件D ．非必要条件解析：¬p 是¬q 的必要条件，即¬q ⇒¬p 为真命题，故¬q ⇒¬p 的逆否命题p ⇒q 也为真命题．∴q 是p 的必要条件．答案：B2．对任意实数a ，b ，c ，在下列命题中，真命题是( )A. “ac >bc ”是“a >b ”的必要条件B. “ac ＝bc ”是“a ＝b ”的必要条件C. “ac >bc ”是“a >b ”的充分条件D. “ac ＝bc ”是“a ＝b ”的充分条件解析：当a ＝b 时，ac ＝bc ，而当ac ＝bc 时，若c ＝0，则a 和b 不一定相等． 答案：B3．已知条件p ：y ＝lg(x 2＋2x －3)的定义域，条件q ：5x －6>x 2，则¬p 是¬q 的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件解析：¬p ：x 2＋2x －3≤0，则－3≤x ≤1；¬q ：5x －6≤x 2，即x 2－5x ＋6≥0，∴x ≥3或x ≤2.由小集合⇒大集合，∴¬p ⇒¬q ，但¬q ¬p .故选A.答案：A 4．一次函数y ＝－m n x ＋1n的图像同时经过第一、二、四象限的必要不充分条件是( ) A. m >0，n >0B. mn <0C. m <0，n <0D. mn >0解析：一次函数y ＝－m n x ＋1n 的图像同时经过第一、二、四象限，即⎩⎪⎨⎪⎧ －m n <0，1n >0，得m >0，n >0.由题意可得，m >0，n >0可以推出选项条件，而反之不成立，所以选D.答案：D二、填空题5．用“充分条件”和“必要条件”填空．(1)“xy ＝1”是“lg x ＋lg y ＝0”的__________．(2)“△ABC ≌△A ′B ′C ′”是“△ABC ∽△A ′B ′C ′”的__________．解析：(1)xy ＝1lg x ＋lg y ＝0(如x ＝y ＝－1)，lg x ＋lg y ＝0⇒lg(xy )＝0⇒xy ＝1.(2)△ABC ≌△A ′B ′C ′⇒△ABC ∽△A ′B ′C ′，△ABC ∽△A ′B ′C ′△ABC ≌△A ′B ′C ′.答案：(1)必要条件 (2)充分条件6．已知α、β是不同的两个平面，直线a ⊂α，直线b ⊂β， p ：a 与b 无公共点，q ：α∥β，则p 是q 的________条件．解析：面面平行时定有分别位于两个面内的直线无公共点，但是两个面内的直线无公共点时，这两个面的关系可能是平行的，也可能是相交，故p 是q 的必要不充分条件．答案：必要不充分7．已知p ：x 2＋x －2>0，q ：x >a ，若q 是p 的充分不必要条件，则a 的取值范围是__________．解析：将p ，q 分别视为集合A ＝{x |x 2＋x －2>0}＝{x |x >1或x <－2}，B ＝{x |x >a }，已知q 是p 的充分不必要条件，即B A ，在数轴上表示出两个集合(图略)，可知满足题意的a 的取值范围为a ≥1.答案：a ≥1三、解答题8．下列命题中，判断条件p 是条件q 的什么条件：(1)p ：|x |＝|y |，q ：x ＝y ；(2)p ：△ABC 是直角三角形，q ：△ABC 是等腰三角形；(3)p ：四边形的对角线互相平分，q ：四边形是矩形．解：(1)∵|x |＝|y |x ＝y ，但x ＝y ⇒|x |＝|y |，∴p 是q 的必要条件，但不是充分条件．(2)△ABC 是直角三角形△ABC 是等腰三角形．△ABC 是等腰三角形△ABC 是直角三角形．∴p 既不是q 的充分条件，也不是q 的必要条件．(3)四边形的对角线互相平分四边形是矩形．四边形是矩形⇒四边形的对角线互相平分．∴p 是q 的必要条件，但不是充分条件．9．[2014·河南省郑州一中月考]已知p ：关于x 的不等式3－m 2<x <3＋m 2，q ：x (x －3)<0，若p 是q 的充分不必要条件，求实数m 的取值范围．解：记A ＝{x |3－m 2<x <3＋m2}，B ＝{x |x (x －3)<0}＝{x |0<x <3}，若p 是q 的充分不必要条件，则A B .注意到B ＝{x |0<x <3}≠∅，分两种情况讨论：(1)若A ＝∅，即3－m 2≥3＋m2，求得m ≤0，此时A B ，符合题意；(2)若A ≠∅，即3－m 2<3＋m2，求得m >0，要使A B ，应有⎩⎪⎨⎪⎧ 3－m2>0，3＋m2<3，m >0，解得0<m <3.综上可得，实数m 的取值范围是(－∞，3)．。

2.“条件”和“结论”中均有否定词的充分条件和必要条件的判断方法 对于条件和结论中含有否定词的判断，应从它的等价命题即逆否命题判断.
【变式训练】指出下列各组命题中，p是q的什么条件？ (1)p:x＞1,q:x2＞1. (2)p:△ABC有两个角相等，q:△ABC是正三角形. 【解析】(1)由x＞1⇒x2＞1,∴p⇒q.∵x2＞1, ∴x＞1或x＜-1, ∴q p,∴p是q的充分不必要条件. (2)△ABC有两个角相等，则△ABC是等腰三角形，不一定是正 三角形，所以p q;若△ABC是正三角形，则三个角均相等， 即任意两个角都相等，所以q⇒p,故p是q的必要不充分条件.
显然l1∥l2,
∴aБайду номын сангаас1是l1与l2平行的充分条件.
若l1∥l2，∴
∴a=-2或a=1.
答案：充分不必要
a 2 1, 1 a 1 4
2.(1)(x+1)(x-2)=0,∴x1=-1或x2=2, 由(x+1)(x-2)=0 x+1=0, 由x+1=0⇒(x+1)(x-2)=0. ∴p是q的必要不充分条件.
(2)p:x=y,q:sin x=sin y.
【解题探究】1.充分条件和必要条件是如何定义的？ 2.判断充分条件和必要条件的依据是什么？
探究提示：1.如果“若p,则q”形式的命题为真命题，即p⇒q,称p是q的充分条
件，q是p的必要条件.
2.依据是充分条件和必要条件的定义.
【解析】1.当a=1时，直线l1为x+2y-1=0,直线l2为x+2y+4=0,
1 ＜x＜1 ， 32
【互动探究】改变题2中的集合A如下，p是q的什么条件?
(1)p:A=

1.2.2 充要条件基础过关1.“x ，y 均为奇数”是“x ＋y 为偶数”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[[解析]] 当x ，y 均为奇数时，一定可以得到x ＋y 为偶数；但当x ＋y 为偶数时，不一定必有x ，y 均为奇数，也可能x ，y 均为偶数.[[答案]] A2.设{a n }是等比数列，则“a 1<a 2<a 3”是“数列{a n }是递增数列”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[[解析]] {a n }为等比数列，a n ＝a 1·q n －1，由a 1<a 2<a 3，得a 1<a 1q <a 1q 2，即a 1>0，q >1或a 1<0，0<q <1，则数列{a n }为递增数列.反之也成立.[[答案]] C3.设x ∈R ，则“x ＞12”是“2x 2＋x －1＞0”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[[解析]] 因为{x |2x 2＋x －1＞0}＝⎩⎨⎧⎭⎬⎫x |x ＞12或x ＜－1，所以⎩⎨⎧⎭⎬⎫x |x ＞12{x |2x 2＋x －1＞0}，故选A.[[答案]] A4.函数f (x )＝x 2＋mx ＋1的图象关于直线x ＝1对称的充要条件是________.[[解析]] 当m ＝－2时，f (x )＝x 2－2x ＋1，其图象关于直线x ＝1对称，反之也成立，所以函数f (x )＝x 2＋mx ＋1的图象关于直线x ＝1对称的充要条件是m ＝－2.[[答案]] m ＝－25.下列不等式：①x <1；②0<x <1；③－1<x <0；④－1<x <1.其中，可以为x 2<1的一个充分条件的所有序号为__________.[[解析]] 由于x 2<1即－1<x <1，①显然不能使－1<x <1一定成立，②③④满足题意.[[答案]] ②③④6.试说明0＜m ＜13是方程mx 2－2x ＋3＝0有两个同号且不等实根的什么条件.解 若方程mx 2－2x ＋3＝0有两个同号且不等的实根，则⎩⎪⎨⎪⎧Δ＝4－12m ＞0，m ≠0，3m ＞0，∴0＜m ＜13.反之，若0＜m ＜13，则2m ＞0，3m ＞0，－4＜－12m ＜0，0＜4－12m ＜4，即Δ＞0，且2m ＞0，3m ＞0.因此0＜m ＜13是方程mx 2－2x ＋3＝0有两个同号且不等实根的充要条件.7.求证：一元二次方程ax 2＋bx ＋c ＝0(a ，b ，c 是常数且a ≠0)有一正实根和一负实根的充要条件是ac ＜0.证明 必要性：由于方程ax 2＋bx ＋c ＝0(a ≠0)有一正实根和一负实根，∴Δ＝b 2－4ac ＞0，且x 1x 2＝c a ＜0，∴ac ＜0.充分性：由ac ＜0可推出Δ＝b 2－4ac ＞0及x 1x 2＝c a ＜0，∴方程ax2＋bx＋c＝0(a≠0)有一正一负两实根.因此一元二次方程ax2＋bx＋c＝0(a≠0)有一正实根和一负实根的充要条件是ac ＜0.能力提升8.在△ABC中，“sin(A－B)cos B＋cos(A－B)sin B≥1”是“△ABC是直角三角形”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[[解析]]sin(A－B)cos B＋cos(A－B)sin B＝sin[(A－B)＋B]＝sin A≥1，又因为sin A≤1，所以sin A＝1.又因为0<A<π，所以A＝π2，故△ABC为直角三角形；若△ABC为直角三角形，则A不一定为直角，也可能为锐角，则sin A不一定取到最大值1，即不一定有sin(A－B)cos B＋cos(A－B)sin B＝sin A≥1，故“sin(A－B)cos B＋cos(A－B)sin B≥1”是“△ABC是直角三角形”的充分不必要条件，故选A.[[答案]] A9.若a，b为实数，则“0＜ab＜1”是“a＜1b或b＞1a”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[[解析]]因为0＜ab＜1，所以a，b同号，且ab＜1.当a＞0，b＞0时，显然有a＜1b；当a＜0，b＜0时，显然有b＞1a，故“0＜ab＜1”是“a＜1b 或b＞1a”的充分条件.而当a＜0，b＞0时，显然有a＜1b 且b＞1a，但推不出0＜ab＜1.综上所述，“0＜ab＜1”是“a＜1b 或b＞1a”的充分不必要条件，故选A.[[答案]] A10.圆x2＋y2＝1与直线y＝kx＋2没有公共点的充要条件是________.[[解析]]圆心(0，0)到直线的距离为d＝21＋k2，由题意知d>1，∴21＋k2>1，两边平方得k2<3，∴－3<k< 3.[[答案]]－3<k< 311.已知α，β是不同的两个平面，直线a⊂α，直线b⊂β，p：a与b无公共点，q：α∥β，则p是q的________条件.[[解析]]面面平行时一定有分别位于两个平面内的直线无公共点，但是分别位于两个平面内的直线无公共点时，这两个平面的关系可能是平行，也可能是相交，故p是q的必要不充分条件.[[答案]]必要不充分12.设x，y∈R，求证|x＋y|＝|x|＋|y|成立的充要条件是xy≥0.证明①充分性：如果xy≥0，则有xy＝0和xy>0两种情况，当xy＝0时，不妨设x＝0，得|x＋y|＝|y|，|x|＋|y|＝|y|，∴等式成立.当xy>0，即x>0，y>0或x<0，y<0时.又当x>0，y>0时，|x＋y|＝x＋y，|x|＋|y|＝x＋y，∴等式成立.当x<0，y<0时，|x＋y|＝－(x＋y)，|x|＋|y|＝－x－y＝－(x＋y)，∴等式成立.总之，当xy≥0时，|x＋y|＝|x|＋|y|成立.②必要性：若|x＋y|＝|x|＋|y|且x，y∈R，得|x＋y|2＝(|x|＋|y|)2，即x2＋2xy＋y2＝x2＋y2＋2|x|·|y|，∴|xy|＝xy，∴xy≥0.综上可知，xy≥0是等式|x＋y|＝|x|＋|y|成立的充要条件.13.(选做题)已知函数f(x)＝3－（x＋2）（2－x）的定义域为A，g(x)＝lg[(x－a －1)(2a－x)](a＜1)的定义域为B.(1)求A；(2)记p：x∈A，q：x∈B，若p是q的必要不充分条件，求实数a的取值范围. 解(1)要使f(x)有意义，则3－(x＋2)(2－x)≥0，化简整理得(x＋1)(x－1)≥0，解得x≤－1或x≥1，∴A＝{x|x≤－1或x≥1}.(2)要使g(x)有意义，则(x－a－1)(2a－x)＞0，即(x－a－1)(x－2a)＜0，又∵a＜1，∴a＋1＞2a，∴B＝{x|2a＜x＜a＋1}.∵p 是q 的必要不充分条件， ∴B A ，∴2a ≥1或a ＋1≤－1，解得12≤a ＜1或a ≤－2.∴a 的取值范围为(－∞，－2]∪⎣⎢⎡⎭⎪⎫12，1.。

课时分层作业(二) 充分条件与必要条件(建议用时：60分钟)[基础达标练]一、选择题1．下面四个条件中，使“a >b ”成立的充分条件是( ) A ．a >b ＋1 B ．a >b －1 C ．a 2>b 2D ．a ＋1>bA [“p 的充分条件是q ”即“q 是p 的充分条件”，亦即“q ⇒p ”．因为a >b ＋1⇒a >b ，故选A.]2．函数f (x )＝x 2＋mx ＋1的图像关于直线x ＝1对称的充要条件是( ) A ．m ＝－2 B ．m ＝2 C ．m ＝－1 D ．m ＝1A [由f (x )＝x 2＋mx ＋1＝⎝ ⎛⎭⎪⎫x ＋m 22＋1－m 24，∴f (x )的图像的对称轴为x ＝－m 2，由题意：－m2＝1，∴m ＝－2.]3．已知p ：关于x 的不等式x 2＋2ax －a >0的解集是R ，q ：－1<a <－12，则p 是q 的( )A ．充分条件B ．必要条件C ．既不充分也不必要条件D ．不能确定B [p 所对应的集合为A ＝{a |－1<a <0}，q 所对应的集合为B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪－1<a <－12， ∴B ⊆A ，∴q ⇒p ，∴p 是q 的必要条件．]4．设x ∈R ，则“|x －2|＜1”是“x 2＋x －2>0”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件D ．既不充分也不必要条件A [|x －2|<1⇔1<x <3，x 2＋x －2>0⇔x >1或x <－2. 由于{x |1<x <3}是{x |x >1或x <－2}的真子集，所以“|x －2|<1”是“x 2＋x －2>0”的充分而不必要条件．] 5．有下述说法：①a ＞b ＞0是a 2＞b 2的充要条件；②a ＞b ＞0是1a ＜1b的充要条件；③a ＞b ＞0是a 3＞b 3的充要条件．其中正确的说法有( ) A ．0个 B ．1个 C ．2个D ．3个A [a ＞b ＞0⇒a 2＞b 2，a 2＞b 2⇒|a |＞|b |⇒/a ＞b ＞0，故①错． a ＞b ＞0⇒1a ＜1b ，但1a ＜1b ⇒/a ＞b ＞0，故②错．a ＞b ＞0⇒a 3＞b 3，但a 3＞b 3⇒/a ＞b ＞0，故③错．]二、填空题 6．“cos α＝－32”是“α＝56π”的________条件． [解析] α＝56π时，cos α＝－32，反之不一定成立，故应是必要不充分条件．[答案] 必要不充分7．若“p ：x >a ”是“q ：x >1或x <－3”的充分不必要条件，则a 的取值范围是________． [解析] p 是q 的充分不必要条件，则p ⇒q 且qp .设A ＝{}x |x >a ，B ＝{}x |x >1或x <－3，则A ⊆B ，但B A .如数轴所示，易知a ≥1.[答案] [1，＋∞)8．直线l 1：2x ＋my ＋1＝0与直线l 2：y ＝3x －1垂直的充要条件是________． [解析] l 1⊥l 2，则2×3＋m ×(－1)＝0，即m ＝6. [答案] m ＝6 三、解答题9．已知M ＝{x |(x －a )2<1}，N ＝{x |x 2－5x －24<0}，若N 是M 的必要条件，求a 的取值范围．[解] 由(x －a )2<1，得a －1<x <a ＋1， 由x 2－5x －24<0，得－3<x <8， ∵N 是M 的必要条件， ∴M ⊆N ，∴⎩⎪⎨⎪⎧a －1≥－3，a ＋1≤8，∴－2≤a ≤7.即a 的取值范围是[－2,7]．10．已知p ：ab ≠0，a ＋b ＝1；q ：ab ≠0，a 3＋b 3＋ab －a 2－b 2＝0.求证：p 是q 的充要条件．[证明] ①先证充分性成立． ∵ab ≠0，a ＋b ＝1， ∴b ＝1－a .∴a 3＋b 3＋ab －a 2－b 2＝a 3＋(1－a )3＋a (1－a )－a 2－(1－a )2＝a 3＋1－3a ＋3a 2－a 3＋a －a 2－a 2－1＋2a －a 2＝0. ②再证必要性成立． ∵ab ≠0， ∴a ≠0且b ≠0.∵a 3＋b 3＋ab －a 2－b 2＝0，∴(a ＋b )(a 2－ab ＋b 2)－(a 2－ab ＋b 2)＝0. ∴(a 2－ab ＋b 2)·(a ＋b －1)＝0. ∵a 2－ab ＋b 2≠0， ∴a ＋b ＝1.由①②知，p 是q 的充要条件．[能力提升练]1．设0<x <π2，则“x sin 2x <1”是“x sin x <1”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件B [因为0<x <π2，所以0<sin x <1.由x sin x <1知x sin 2 x <sin x <1，因此必要性成立．由x sin 2x <1得x sin x <1sin x ，而1sin x>1，因此充分性不成立．] 2．若A ：log 2a <1，B ：关于x 的二次方程x 2＋(a ＋1)x ＋a －2＝0的一个根大于零，另一个根小于零，则A 是B 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件A [由log 2a <1，解得0<a <2；而方程x 2＋(a ＋1)x ＋a －2＝0的一个根大于零，另一个根小于零的充要条件是a －2<0，解得a <2.因为命题：“若0<a <2，则a <2”是真命题，而“若a <2，则0<a <2”是假命题，所以“0<a <2”是“a <2”的充分不必要条件，所以A 是B 的充分不必要条件，选A.]3．定义在(－∞，0)∪(0，＋∞)上的奇函数f (x )在(0，＋∞)上为减函数，且f (2)＝0，则“f (x )－f (－x )x<0”是“2x>4”成立的________条件． [解析] ∵f (x )是定义在(－∞，0)∪(0，＋∞)上的奇函数，∴f (x )－f (－x )＝2f (x )，∴f (x )－f (－x )x <0即f (x )x<0，又∵f (x )在(0，＋∞)上为减函数，且f (2)＝0，∴x ∈(2，＋∞)，又∵f (x )是(－∞，0)∪(0，＋∞)上的奇函数，∴x ∈(2，＋∞)∪(－∞，－2)，因为2x>4⇔x >2，所以前者是后者的必要不充分条件．[答案] 必要不充分4．设a 1、b 1、c 1、a 2、b 2、c 2均为非零实数，不等式a 1x 2＋b 1x ＋c 1>0和a 2x 2＋b 2x ＋c 2>0的解集分别为M 和N ，那么“a 1a 2＝b 1b 2＝c 1c 2”是“M ＝N ”的________条件(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)．[解析] 如果a 1a 2＝b 1b 2＝c 1c 2>0，则M ＝N ；如果a 1a 2＝b 1b 2＝c 1c 2<0，则M ≠N ，所以a 1a 2＝b 1b 2＝c 1c 2M＝N .反之，若M ＝N ＝∅，即说明二次不等式的解集为空集、与它们的系数比无任何关系，只要求判别式小于零．因此，M ＝Na 1a 2＝b 1b 2＝c 1c 2. [答案] 既不充分也不必要5．已知条件p ：|x －1|>a 和条件q ：2x 2－3x ＋1>0，求使p 是q 的充分不必要条件的最小正整数a .[解] 依题意得a >0.由条件p ：|x －1|>a ， 得x －1<－a ，或x －1>a ，∴x <1－a ，或x >1＋a . 由条件q ：2x 2－3x ＋1>0，得x <12，或x >1.要使p 是q 的充分不必要条件，即“若p ，则q ”为真命题，逆命题为假命题，应有 ⎩⎪⎨⎪⎧1－a ≤12，1＋a >1，或⎩⎪⎨⎪⎧1－a <12，1＋a ≥1，解得a ≥12.令a ＝1，则p ：x <0，或x >2， 此时必有x <12，或x >1.即p⇒q，反之不成立．∴最小正整数a为1.。

第2课时充分条件与必要条件1.明白得充分条件和必要条件的含义.2.会判定两个条件间的充分必要关系.3.能利用条件间的充分必要关系求参数的取值范围.函数y=x cos x+sin x的图像大致为().图像分析题是高考中比较常见的一种试题,做这种题的要紧思想是排除法,从解析式结合图像咱们很容易找到三个角度来排除,一是利用函数是奇函数能够排除B,二是利用x=π时,y=1,能够排除C,三是利用x=π时,y=-π,能2够排除A,因此答案选D.问题1: 一样地,“假设p,那么q”为真命题,是指由p通过推理能够得出q.这时,咱们就说,由p可推出q,记作, 而且说p是q的充分条件,q是p的必要条件.依照上述情境,结合充分条件、必要条件的概念咱们用充分和必要进行填空:(1)“图像关于原点对称”是“该图像是函数y=x cos x+sin x的图像”的条件;(2)“ y=f(x)的图像是y=x cos x+sin x的图像”是“f(π)>0”的条件;2(3)“ f(π)>0”是“y=f(x)的图像不是y=x cos x+sin x的图像”的条件.问题2:p与q的推出情形和p与q的充分、必要性有何联系?(1)假设,那么p是q的充分没必要要条件;(2)假设,那么p是q的必要不充分条件;(3)假设,那么p是q的充要条件;(4)假设,那么p是q的既不充分也没必要要条件.问题3:如何从集合的角度明白得充分条件、必要条件和充要条件?成立与p、q相应的集合,即p:A={x|p(x)},q:B={x|q(x)}.集合A与B的关系Venn图表示法若A⊆B,则p是q的,若A⫋B,则p是q的若B⊆A,则p是q的,若B⫋A,则p是q的若A⊈B且B⊈A,则p既不是q的,也不是q的若A⊆B且B⊆A,即A=B,则p是q的1.在以下电路图中,表示开关A闭合是灯泡B亮的必要但不充分条件的线路图是().2.在△ABC中,“sin A>√32”是“A>π3”的().A.充分没必要要条件B.必要不充分条件C.充要条件D.既不充分也没必要要条件3.已知q是等比数列{a n}的公比,那么“q<1”是“数列{a n}是递减数列”的条件.4.指出以下各题中,p是q的什么条件?(1)p:∠A=∠B,q:∠A和∠B是对顶角.(2)p:x=1,q:x2=1.充分条件、必要条件、充要条件的判定分析下面的各组命题中p是q的什么条件.(从“充分没必要要条件”“必要不充分条件”“充要条件”“既不充分也没必要要条件”当选一个)(1)在△ABC中,p:∠A=∠B,q:sin A=sin B.(2)非空集合A、B中,p:x∈A∪B,q:x∈B.依照充分条件、必要条件求参数的取值范围已知p:A={x∈R|x2+ax+1≤0},q:B={x∈R|x2-3x+2≤0},假设p是q的充分没必要要条件,求实数a的取值范围.充要条件的探求与证明已知方程x2+(2k-1)x+k2=0,求使方程有两个大于1的根的充要条件.判定以下各题中p是q的什么条件.(1)p:a>b,q:√a>√a.(2)p:a>b,q:2a>2b-1..(3)p:△ABC中,∠A≠60°,q:sin A≠√32已知命题p:1-c<x<1+c(c>0),命题q:x>7或x<-1,而且p是q的既不充分又没必要要条件,那么c的取值范围是.求关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件.1.设集合A,B,那么“A⊆B”是“A∩B=A成立”的().A.充分没必要要条件B.必要不充分条件C.充要条件D.既不充分也没必要要条件2.已知平面α,β,直线m⊂平面α,那么“平面α∥平面β”是“直线m∥平面β”的().A.充分没必要要条件B.充要条件C.必要不充分条件D.既不充分也没必要要条件3.设有如下三个命题:甲: m∩l=A,m,l⊂α,m,l⊄β;乙:直线m,l中至少有一条与平面β相交;丙:平面α与平面β相交.当甲成立时,乙是丙的条件.4.判定以下各题中p是q的什么条件.(1)p:a>0且b>0, q:ab>0.(2)p:aa>1, q:x>y.(2021年·安徽卷)“(2x-1)x=0”是“x=0”的().A.充分没必要要条件B.必要不充分条件C.充分必要条件D.既不充分也没必要要条件考题变式(我来改编):第2课时充分条件与必要条件知识体系梳理问题1:p⇒q (1)必要(2)充分(3)充分问题2:(1)p⇒q,且q⇒/p (2)p⇒/q,且q⇒p (3)p⇒q,且q⇒p (4)p⇒/q,且q⇒/p 问题3:充分条件充分没必要要条件必要条件必要不充分条件充分条件必要条件充要条件基础学习交流开关A闭合,灯泡B不必然亮,灯泡B亮,开关A必然闭合.∵在△ABC中,sin A>√32,那么A∈(π3,2π3),∴“sin A>√32”是“A>π3”的充分条件.∵在△ABC中,取A=5π6,但不能推出sin A>√32,∴“sin A>√32”不是“A>π3”的必要条件.应选A.3.必要不充分由数列{a n}是递减数列可得0<q<1,因此“q<1” 是“数列{a n}是递减数列”的必要不充分条件.4.解:(1)∵p⇒/q且q⇒p,∴p是q的必要不充分条件.(2)∵q :x 2=1⇔x=1或x=-1,∴x=1⇒x 2=1,但x 2=1⇒/ x=1,∴p 是q 的充分没必要要条件.重点难点探讨探讨一:【解析】(1)在△ABC 中,∠A=∠B ⇒sin A=sin B ,反之,假设sin A=sin B ,因为A 与B 不可能互补(因为三角形三个内角和为180°),因此只有A=B.故p 是q 的充要条件.(2)显然x ∈A ∪B 不必然有x ∈B ,但x ∈B 必然有x ∈A ∪B ,因此p 是q 的必要不充分条件.【小结】在判定p 是q 的什么条件时,准确明白得和运用充分条件、必要条件、充要条件的概念是关键,而能综合、灵活地运用已学的知识是难点,故当知识点不能熟练运历时,就容易显现思维受阻的现象.探讨二:【解析】B={x ∈R |x 2-3x+2≤0}={x|1≤x ≤2},∵p 是q 的充分没必要要条件,∴p ⇒q ,即A ⫋B ,可知A=⌀或方程x 2+ax+1=0的两根要在区间[1,2]内,∴Δ=a 2-4<0或{ a ≥0,1≤-a 2≤2,4+2a +1≥0,1+a +1≥0,得-2≤a<2.【小结】p 是q 的充分没必要要条件,利用真子集关系求解.此题易错的地址是解不等式组,请认真体会缘故.探讨三:【解析】(法一)设两根为x 1, x 2,那么有{a 1+a 2>2,a 1·a 2>1,即{-(2a -1)>2,a 2>1,解得k<-1, ∴所求充要条件为k<-1.(法二)由题意,设两根为x 1, x 2,应有{a ≥0,a 1+a 2>2,a 1·a 2>1,即{(2a -1)2-4a 2≥0,-(2a -1)>2,a 2>1,解得k<-1, ∴所求充要条件为k<-1.[问题]使方程有两个大于1的根的充要条件是k<-1吗?[结论]问题的实质是确信所给方程的两根都大于1时k 应知足的充要条件,而上面的解析中所列的不等式组仅是两根x 1、x 2都大于1的必要条件,并非充分,例如,x 1=1,x 2=3,有{a 1+a 2>2,a 1·a 2>1,但没有x 1>1,x 2>1.错误的本质是没有把函数、函数图像和方程三者有机结合起来,从而找出等价关系.于是,正确解答如下:(法一)使两根x 1, x 2都大于1的充要条件为{a ≥0,(a 1-1)+(a 2-1)>0,(a 1-1)(a 2-1)>0,解得k<-2, ∴所求的充要条件为k<-2.(法二)令f (x )=x 2+(2k-1)x+k 2.∵f (x )=0的两根都大于1,∴函数f (x )图像如图,那么x 1,x 2都大于1的充要条件为{ a ≥0,a (1)>0a a 2+2k >0,-2a -12>1,解得k<-2,∴所求的充要条件是k<-2.【小结】(1)解决此类问题一样是把充分条件、必要条件或充要条件转化为集合之间的关系,然后依照集合之间的关系列出关于参数的不等式求解.(2)注意利用转化的方式明白得充分必要条件:假设q是p的充分没必要要(必要不充分、充要)条件,那么p是q的必要不充分(充分没必要要、充要)条件.思维拓展应用应用一:(1)p⇒/q,q⇒p,∴p是q的必要不充分条件.(2)p⇒q,q⇒/p,∴p是q的充分没必要要条件.(3)p⇒/q,q⇒p,∴p是q的必要不充分条件.应用二:c>0命题p对应的集合A={x|1-c<x<1+c,c>0},同理,命题q对应的集合B={x|x>7或x<-1}.因为p是q的既不充分又没必要要条件,因此A∩B=⌀或A不是B的子集且B不是A的子集,因此{1-a≥-1,1+a≤7①或{1+a≥-1,1-a≤7②,解①得c≤2,解②得c≥-2,又c>0,综上所述得c>0.应用三:(1)a=0适合.(2)当a≠0时,显然方程没有零根,假设方程有两异号的实根,那么必需知足{1a<0,a=4-4a>0⇒a<0;假设方程有两个负的实根,那么必需知足{1a>0,-2 a <0,a=4-4a≥0⇒0<a≤1.综上知,假设方程至少有一个负的实根,那么a≤1;反之,假设a≤1,那么方程至少有一个负的实根.因此,关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是a≤1.基础智能检测由A⊆B,得A∩B=A;反过来,由A∩B=A,且(A∩B)⊆B,得A⊆B.因此,“A⊆B”是“A∩B=A成立”的充要条件.因为平面α∥平面β且直线m⊂平面α,因此直线m∥平面β,反之,当直线m∥平面β时,直线m⊂平面α,也可能平面α和平面β相交.3.充要由题意乙⇒丙,丙⇒乙.故当甲成立时,乙是丙的充要条件.4.解:(1)p是q的充分没必要要条件.当a>0且b>0时,ab>0成立;反之,当ab>0时,只要求a、b同号即可.(2)p是q的既不充分也没必要要条件.aa>1在y>0的条件下才有x>y成立.同应当x=2,y=-1时,aa>1不成立.全新视角拓展B由(2x-1)x=0可得x=12或0,因为“x=12或0”是“x=0”的必要不充分条件,故答案选B.思维导图构建充分没必要要必要不充分充要既不充分也没必要要。

第一章 常用逻辑用语第2.1节 充分条件第2.2节 必要条件一、选择题1.“A ∩B=A ”是A=B 的( ).A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件2.下列判断正确的是( ).A.(x+1)(x-2)=0是x=-1的充分条件B.x 2＞4是x 2＞23的必要条件C.｜x+1｜＜1是-2＜x ＜0的充要条件D.(a-2)2+(b+3)2=0是(a-2)(b+3)=0的必要条件3.若条件p ∶｜x+1｜＞2；条件q ∶x 2＜5x-6.则p 是q 的( ).A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.已知A 是B 的必要条件，B 是C 的充分条件，则A 是C 的( )A.充分条件B.必要条件C.充要条件D.无法判断5.“0＜x ＜5”是“｜x-2｜＜3”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件6.“xy ＞0”是“｜x+y ｜=｜x ｜+｜y ｜”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件二、填空题(从“充分而不必要条件”、“必要而不充分条件”、“充要条件”、“既不充分也不必要条件”中选出适当的一种填空)1.复合命题“非p ”为假命题是复合命题“p 或q ”为真命题的 .2.k ＞4,b ＜5是一次函数y=(k-4)x+b-5的图像交y 轴于负半轴，交x 轴于正半轴的 .3.⎩⎨⎧>>+4,4xy y x 是⎩⎨⎧>>2,2y x 的.三、解答题1.分别举出四个例子，说明p 是q 的“充分而不必要条件”、“必要而不充分条件”、“充要条件”、“既不充分也不必要条件”，并说明理由.2.已知全集R ，A=｛x ｜｜x-3｜＞6｝，B=｛x ｜｜x ｜＞a,a ∈N +｝.当a 为何值时.①A是B的充分而不必要条件；②A是B的必要而不充分条件；③A是B的充要条件.3.求关于x的一元二次不等式ax2-ax+1＞0对一切x∈R都成立的充要条件是什么.4.已知p∶x∈Z，y∈Z，m=x2-y2；q∶k∈Z,m=2K+1,或m=4k.求证：p是q的充分条件.参考答案一、1.B 2.C 3.A 4.D 5.A 6.A二、1.充分而不必要条件. 2.充要条件. 3.必要而不充分条件.三、1.略.2.①a=3,2,1.提示：A⊆B，结合数轴观察.②｛a｜a≥9,a∈N+｝.提示：A⊇B.③这样的a不存在.3.0＜a＜4.提示：分a＞0，a＜0两种情况讨论.4.略。

正确运用“条件”的定义解题 典型例题： 例1．在下列各题中，判断A 是B 的什么条件，并说明理由．1． A ：R p p ∈≥,2，B ：方程+++p px x 203=有实根；2． A ：)(,2Z k k ∈=+πβα，B ：)sin(βα+βαsin sin +=；3．A ：132>-x ；B ：061
2>-+x x ；4．A ：圆222r y x =+与直线++by ax 0=c 相切，B ：.
)(2222r b a c += 例2 设集合{}{}2,3M x x N x x =>=<，那么“x M ∈或x N ∈” 是“x M N ∈”的（ ）
A ．充分不必要条件
B ．必要不充分条件
C ．充要条件
D ．既不充分也不必要条件
目标检测： 1：指出下列命题中，p 是q 的什么条件（在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要条件”中选出一种作答）. （1）在△ABC 中，p ：∠A=∠B ，q ：sinA=sinB （2）对于实数x 、y ，p ：x+y ≠8,q:x ≠2或y ≠6; （3）非空集合A 、B 中，p ：x ∈A ∪B ，q ：x ∈B
（4）已知x 、y ∈R ，p ：（x-1）2+（y-2）2=0，q ：（x-1）（y-2）=0. 2. 已知,a b 是实数，则“0a >且0b >”是“0a b +>且0ab >”的 ( )A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件
学后反思：。

§2充分条件与必要条件课后作业提升1若向量a=(x,3)(x∈R),则“x=4”是“|a|=5”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件解析:|a|2=x2+9=25,解方程,得x=±4,故“x=4”是“|a|=5”的充分而不必要条件,选A.答案:A2函数y=x2+bx+c(x∈[0,+∞))是单调函数的充要条件是()A.b≥0B.b≤0C.b>0D.b<0解析:二次函数的单调区间应以对称轴来划分.二次函数y=x2+bx+c的对称轴为x=-,要使函数在[0,+∞)上是单调函数,需使-≤0,即b≥0,反之也成立.答案:A3下面命题中是真命题的是()A.x>2且y>3是x+y>5的充要条件B.A∩B≠⌀是A⫋B的充分条件C.b2-4ac<0是一元二次不等式ax2+bx+c>0的解集为R的充要条件D.一个三角形的三边满足勾股定理的充要条件是此三角形为直角三角形解析:对于选项A,x>2且y>3⇒x+y>5,但x+y>5未必能推出x>2且y>3,如x=0且y=6满足x+y>5,但不满足x>2,故A为假命题.对于选项B,A∩B≠⌀未必能推出A⫋B,如A={1,2},B={2,3},故B为假命题.对于选项C,例如一元二次不等式-2x2+x-1>0的解集为⌀,但满足b2-4ac<0,故C为假命题.答案:D4“a=1”是“函数f(x)=是奇函数”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件解析:若f(x)为奇函数,因为函数f(x)=的定义域为R,所以f(0)=0,即f(0)=-a=0,解得a=±1,所以“a=1”是“函数f(x)=是奇函数”的充分不必要条件,选A.答案:A5设甲是乙的充分不必要条件,乙是丙的充要条件,丁是丙的必要不充分条件,那么甲是丁的条件.答案:充分不必要6指出下列各题中p是q的什么条件:(1)p:直线l的方程为x-y=0,q:直线l平分圆x2+y2=1的周长;(2)p:x>1,q:log2x>1;(3)p:两个三角形相似,q:两个三角形全等;(4)在△ABC中,p:A>B,q:sin A>sin B.解:(1)因为当一条直线平分圆x2+y2=1的周长时,直线过原点即可,所以p⇒q,q p,所以p是q的充分不必要条件.(2)当log 2x>1时,可得x>2.所以p q,q⇒p,所以p是q的必要不充分条件.(3)易知p q,q⇒p,所以p是q的必要不充分条件.(4)在△ABC中,A>B⇔a>b⇔sin A>sin B,所以p是q的充要条件.7求证:关于x的方程x2+mx+1=0有两个负实数根的充要条件是m≥2.证明:(1)充分性:因为m≥2,所以Δ=m2-4≥0.所以x2+mx+1=0有实根.设两根为x1,x2,由根与系数的关系,知x1x2=1>0,所以x1与x2同号.又x1+x2=-m≤-2<0,所以x1,x2同为负实数,即x2+mx+1=0有两个负实数根的充分条件是m≥2.(2)必要性:因为x2+mx+1=0有两个负实数根,设为x1和x2,则x1x2=1,x1+x2=-m,所以m-2=-(x1+x2)-2=--2=-≥0.故m≥2,即x2+mx+1=0有两个负实数根的必要条件是m≥2.综上,m≥2是x2+mx+1=0有两个负实数根的充要条件.8关于x的不等式与x2-3(a+1)x+2(3a+1)≤0的解集依次为A与B,问“A⊆B”是“1≤a≤3或a=-1”的充要条件吗?并说明理由.解:是.理由如下:A={x|2a≤x≤a2+1},B={x|(x-2)[x-(3a+1)]≤0}.①当2≤3a+1,即a≥时,B={x|2≤x≤3a+1}.所以A⊆B⇔⇔1≤a≤3.②当2>3a+1,即a<时,B={x|3a+1≤x≤2}.所以A⊆B⇔⇔a=-1.综上所述:A⊆B⇔a=-1或1≤a≤3.所以“A⊆B”是“1≤a≤3或a=-1”的充要条件.。