计算方法第三章习题

第三章习题答案1.分别用梯形公式、Simpson公式、Cotes公式计算积分1,I=⎰并估计误差。

解：1）用梯形公式有：()()110.51[10.5]10.42678242f f⎛-≈+=+≈⎝⎭⎰()()()333333220.512.6042107.36571012124Tb aE f fηηη-----⎛⎫''=-=--=⨯≤⨯⎪⎝⎭事实上，()()()()()()110.430964410.50.510.4267767210.50.510.00418772Tf x II f fE f f f===-≈+=⎡⎤⎣⎦-∴=-+=⎡⎤⎣⎦⎰⎰2）Simpson公式()110.53111410.43093 642122f f f⎛-⎡⎤⎛⎫⎛⎫≈++=+=⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭⎰[]()()44744211111522 1.1837710180218028Sb a b aE f fηη--⎛⎫--⎪⎛⎫--⎛⎫=-=--≤⨯⎪ ⎪⎪⎝⎭⎝⎭⎪⎝⎭3122()''()48T f fb aE事实上，()()()10.510.50.510.5410.000030462SE f f f f-⎡+⎤⎛⎫=-++=⎪⎢⎥⎝⎭⎣⎦⎰3）由Cotes公式有：()() ()111537270.5321232719084814.9497525.2982210.3923029.9332670.43096180f f f f f-⎡⎤⎛⎫⎛⎫⎛⎫≈++++⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=++++=⎰15732127)18088()6116211294522 2.697410945464C E f η--⎛⎫⨯ ⎪⎛⎫=-⨯-≤⨯ ⎪ ⎪⎝⎭⎪⎝⎭7(6)945*42()()82Cf b aEf事实上，()0.0000003C E f =2．证明Simpson 公式()2.8具有三次代数精度。

计算方法第三章习题答案计算方法第三章习题答案计算方法是一门涵盖了数值计算和计算机编程的学科，它在现代科学和工程中扮演着重要的角色。

第三章是计算方法课程中的重要章节，主要涉及到数值计算中的误差分析和插值方法。

本文将为大家提供第三章习题的详细答案，帮助读者更好地理解和应用这些概念。

1. 误差分析误差分析是计算方法中非常重要的一部分，它帮助我们理解和评估数值计算中的误差来源。

以下是一些常见的误差类型：- 绝对误差：绝对误差是指数值计算结果与真实值之间的差异。

它可以通过计算两者之差来得到。

- 相对误差：相对误差是指绝对误差与真实值之间的比值。

通常以百分比的形式表示。

- 截断误差：截断误差是由于在计算过程中舍入或截断数字而引入的误差。

它通常是由于计算机的有限精度导致的。

- 舍入误差：舍入误差是由于将无限位数的小数截断为有限位数而引入的误差。

它通常是由于计算机的有限精度或计算方法的近似性质导致的。

2. 插值方法插值方法是一种用于通过已知数据点来估计未知数据点的技术。

以下是一些常见的插值方法：- 线性插值：线性插值是一种简单的插值方法，它假设两个已知数据点之间的未知数据点的取值在直线上。

通过已知数据点的斜率和截距，我们可以计算出未知数据点的值。

- 拉格朗日插值：拉格朗日插值是一种使用多项式来逼近已知数据点的方法。

它通过构造一个满足通过已知数据点的多项式来估计未知数据点的值。

- 牛顿插值：牛顿插值是一种使用差商来逼近已知数据点的方法。

它通过构造一个满足通过已知数据点的差商多项式来估计未知数据点的值。

3. 习题答案以下是一些第三章习题的答案，供大家参考：- 习题1：已知函数f(x)在区间[a, b]上连续，且在[a, b]上的导数存在且连续，证明存在一点c∈(a, b)，使得f(b) - f(a) = (b - a)f'(c)。

这是拉格朗日中值定理的一个特例，根据定理的条件，我们可以得到上述结论。

- 习题2：已知函数f(x)在区间[a, b]上连续，且在(a, b)内可导，证明存在一点c∈(a, b)，使得f'(c) = (f(b) - f(a))/(b - a)。

第一章 绪论（12）1、设0>x ，x 的相对误差为δ，求x ln 的误差。

[解]设0*>x 为x 的近似值，则有相对误差为δε=)(*x r ，绝对误差为**)(x x δε=，从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x ， 相对误差为****ln ln )(ln )(ln x x x x rδεε==。

2、设x 的相对误差为2%，求n x 的相对误差。

[解]设*x 为x 的近似值，则有相对误差为%2)(*=x r ε，绝对误差为**%2)(x x =ε，从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε，相对误差为%2)()(ln )(ln ***n x x x nr==εε。

3、下列各数都是经过四舍五入得到的近似数，即误差不超过最后一位的半个单位，试指出它们是几位有效数字：1021.1*1=x ，031.0*2=x ，6.385*3=x ，430.56*4=x ，0.17*5⨯=x 。

[解]1021.1*1=x 有5位有效数字；0031.0*2=x 有2位有效数字；6.385*3=x 有4位有效数字；430.56*4=x 有5位有效数字；0.17*5⨯=x 有2位有效数字。

4、利用公式（3.3）求下列各近似值的误差限，其中*4*3*2*1,,,x x x x 均为第3题所给的数。

（1）*4*2*1x x x ++； [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε；（2）*3*2*1x x x ；[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε；（3）*4*2/x x 。

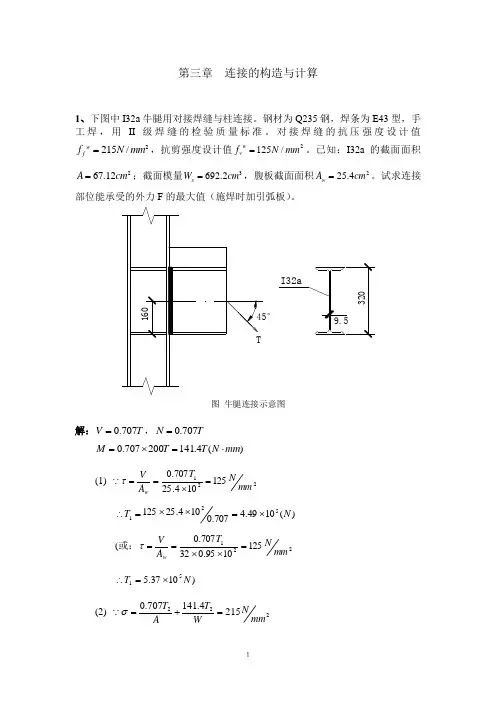
第三章 连接的构造与计算1、下图中I32a 牛腿用对接焊缝与柱连接。

钢材为Q235钢，焊条为E43型，手工焊，用II 级焊缝的检验质量标准。

对接焊缝的抗压强度设计值2215/w f f N mm =，抗剪强度设计值2125/w v f N mm =。

已知：I32a 的截面面积267.12A cm =；截面模量3692.2x W cm =，腹板截面面积225.4w A cm =。

试求连接部位能承受的外力F 的最大值（施焊时加引弧板）。

°图 牛腿连接示意图解：T V 707.0=，T N 707.0=)(4.141200707.0mm N T T M ⋅=⨯=(1) 221125104.25707.0mm N T A V w =⨯==τ )(1049.4707.0104.25125521N T ⨯=⨯⨯=∴(或：2211251095.032707.0mm N T A Vw =⨯⨯==τ )1037.551N T ⨯=∴(2) 2222154.141707.0mm N WT A T =+=σ2232215)102.6924.1411012.67707.0(mm N T =⨯+⨯∴ )(1094.652N T ⨯=∴(3) 折算应力（在顶部中点亦可）()2151.11.1000555.0000278.03000276.03)000233.0104.30707.0( 000278.0104.25707.0000276.01605.26160102.6924.1411012.67707.03322212133213321333231⨯=≤=⨯+=+=⨯==⨯==-⨯⨯+⨯=w f f T T T T T T T T T τσττσ或得：)(1.4263KN T ≤ （KN T f T 3wf 33.484 1.10.000488≤≤或）由T 1、T 2、T 3中取最小值，得T ＝426.1（KN ）m KN M Nmm ⋅=⨯⨯=4104105 N V 5104⨯=f ff f h h W M 6.4283.93331046=⨯==σ22.1=f β， f ff f h h A V 6.14282801045=⨯==τ 2002.1471)6.1428()22.16.428()(2222≤=+=+ff f f f f h h h τβσ mm h f 4.7≥，取mm h f 8=.3、如图所示的牛腿用角焊缝与柱连接。

习 题 一3.已知函数y =4, 6.25,9x x x ===处的函数值，试通过一个二次插值函解：0120124, 6.25,9;2, 2.5,3y x x x y y y =======由题意 （1） 采用Lagrange插值多项式220()()j j j y L x l x y ==≈=∑27020112012010*********()|()()()()()()()()()()()()(7 6.25)(79)(74)(79)(74)(7 6.25)2 2.532.255 2.25 2.75 2.7552.6484848x y L x x x x x x x x x x x x x y y y x x x x x x x x x x x x ==≈------=++------------=⨯+⨯+⨯⨯-⨯⨯= 其误差为(3)25(3)25(3)2[4,9]2()(7)(74)(7 6.25)(79)3!3()83max |()|40.0117281|(7)|(4.5)(0.01172)0.008796f R f x x f x R ξ--=---==<∴<=又则（2）采用Newton插值多项式2()y N x =≈ 根据题意作差商表：224(7)2(74)()(74)(7 6.25) 2.64848489495N =+⨯-+-⨯-⨯-≈4. 设()()0,1,...,k f x x k n ==，试列出()f x 关于互异节点()0,1,...,i x i n =的Lagrange 插值多项式。

注意到：若1n +个节点()0,1,...,i x i n =互异，则对任意次数n ≤的多项式()f x ，它关于节点()0,1,...,i x i n =满足条件(),0,1,...,i i P x y i n ==的插值多项式()P x 就是它本身。

可见，当k n ≤时幂函数()(0,1,...,)kf x x k n ==关于1n +个节点()0,1,...,i x i n =的插值多项式就是它本身，故依Lagrange 公式有()00(),0,1,...,nn n k kk i j j j j j i j ii jx x x l x x x k n x x ===≠-=≡=-∑∑∏特别地，当0k =时，有()0001nn n ij j j i j ii jx x l x x x ===≠-=≡-∑∑∏而当1k =时有()000nnn ij j j j j i j ii jx x x l x x x x x ===≠⎛⎫- ⎪=≡ ⎪- ⎪⎝⎭∑∑∏ 5.依据下列函数表分别建立次数不超过3的Lagrange 插值多项式和Newton 插值多项式，并验证插值多项式的唯一性。

《计算方法》习题答案第一章 数值计算中的误差1．什么是计算方法？（狭义解释）答：计算方法就是将所求的的数学问题简化为一系列的算术运算和逻辑运算，以便在计算机上编程上机，求出问题的数值解，并对算法的收敛性、稳定性和误差进行分析、计算。

2．一个实际问题利用计算机解决所采取的五个步骤是什么？答：一个实际问题当利用计算机来解决时，应采取以下五个步骤： 实际问题→建立数学模型→构造数值算法→编程上机→获得近似结果 4．利用秦九韶算法计算多项式4)(53-+-=x x x x P 在3-=x 处的值，并编程获得解。

解：400)(2345-+⋅+-⋅+=x x x x x x P ，从而 1 0 -1 0 1 -4 -3 -3 9 -24 72 -2191-38-2473-223所以，多项式4)(53-+-=x x x x P 在3-=x 处的值223)3(-=-P 。

5．叙述误差的种类及来源。

答：误差的种类及来源有如下四个方面：（1）模型误差：数学模型是对实际问题进行抽象，忽略一些次要因素简化得到的，它是原始问题的近似，即使数学模型能求出准确解，也与实际问题的真解不同，我们把数学模型与实际问题之间存在的误差称为模型误差。

（2）观测误差：在建模和具体运算过程中所用的一些原始数据往往都是通过观测、实验得来的，由于仪器的精密性，实验手段的局限性，周围环境的变化以及人们的工作态度和能力等因素，而使数据必然带有误差，这种误差称为观测误差。

（3）截断误差：理论上的精确值往往要求用无限次的运算才能得到，而实际运算时只能用有限次运算的结果来近似，这样引起的误差称为截断误差（或方法误差）。

（4）舍入误差：在数值计算过程中还会用到一些无穷小数，而计算机受机器字长的限制，它所能表示的数据只能是一定的有限数位，需要把数据按四舍五入成一定位数的近似的有理数来代替。

这样引起的误差称为舍入误差。

6．掌握绝对误差（限）和相对误差（限）的定义公式。

第3章运算方法和运算部件一、选择题（每题3分）1. 若十进制数据为 137.625，则其二进制数为（）。

A．10001001.11 B．10001001.101 C．10001011.101 D．1011111.101 【答案】B2．如果 [X]补=11110011，则[-X]补是（）。

A．11110011 B．01110011 C．00001100 D．00001101【答案】D3．原码乘法是（）。

A．先取操作数绝对值相乘，符号位单独处理B．用原码表示操作数，然后直接相乘C．被乘数用原码表示，乘数取绝对值，然后相乘D．乘数用原码表示，被乘数取绝对值，然后相乘【答案】A4.定点16位字长的字，采用2的补码形式表示时,一个字所能表示的整数范围是______。

A -215 ~ +（215 -1）B -（215 –1）~ +（215 –1）C -（215 +1）~ +215D -215 ~ +215【答案】A5. （2000）10化成十六进制数是______。

A．（7CD）16 B.（7D0）16 C.（7E0）16 D.（7F0）16【答案】B6. 下列数中最大的数是______。

A．（10011001）2 B.（227）8 C.（98）16 D.（152）10 【答案】A7. ______表示法主要用于表示浮点数中的阶码。

A. 原码B. 补码C. 反码D. 移码【答案】D8.二进制数11001011等于十进制的______。

A.395B.203C.204D.394【答案】B9.设X= —0.1011，则[X]补为______。

A.1.1011B.1.0100C.1.0101D.1.1001【答案】C10. 下列数中最大的数是______。

A.（10010101）2 B.（227）8C.（96）16D.（143）10【答案】B11.设寄存器位数为8位，机器数采用补码形式（含一位符号位）。

对应于十进制数-27，寄存器内容为______。

《必修1 数据与计算》第三章练习题1．单选题（1）随着数据的快速增长，人工处理大量数据的效率与计算机处理相比较正变得（）。

A．更高B．更低C．一样D．无法比较（2）关于用计算机程序解决问题说法中正确的是（）。

A．利用计算机的高速运算能力提高信息处理能力B．提高信息加工的效率C．针对具体问题以专门的程序来实现信息加工的自动化D．以上说法都正确（3）小明编写好解密程序后，调试运行时，程序没有报错且能顺利运行，却不能正确解密，造成这个结果的原因是（）。

A．解密算法逻辑错误B．程序语句语法错误C．程序过期了D．程序设计窗口配置不对（4）算法的重要特征不包括以下哪一项？（）A．有穷性B．确定性C．数据输出D．唯一性（5）执行下面的流程图，最后s=（）。

A．1 B．720 C．120 D．6（6）下列关于算法的叙述，正确的是（）。

A．解决一个问题的算法只有一种B．有穷性是算法的基本特征之一C．可行性不属于算法基本特征D．算法对程序设计没有任何作用2．思考题（1）我们知道求两个数的最大公约数可用辗转相除法，那么怎样求多个数的最大公约数呢，如怎样求四个数的最大公约数？请写出求四个数的最大公约数的算法思想。

（2）不同的程序设计语言，其语句种类、语言格式、语法要求、数据及函数类型等有所不同，我们应该如何选择？3．情境题（1）《一槌定音》是中央电视台财经频道推出的一档大型演播室艺术品投资电视栏目，重点突出大众对艺术品投资的认识和参与，该栏目突破了以往艺术品投资节目以鉴定为主的单一形式，用模拟真实交易的方式，向观众传播艺术品投资的技巧、知识、风险防范，更加凸显财经特色。

节目的最后一个环节是对一个艺术品进行估价，每次估价，主持人均会根据专家的估价对各个嘉宾所报的估价做出“高了”或“低了”的提示。

请问，嘉宾应如何估价才能在有限的次数里更快地估算到？请写出解决这个问题的算法设计思想。

（2）素数问题。

科技节到了，某中学举行了一个科技游园活动，有一个项目是看谁能又快又准地判断一个正整数是否为素数。

第三章练习题及答案五、计算分析题：1、已知:某企业本期有关成本资料如下：单位直接材料成本为10元,单位直接人工成本为5元，单位变动性制造费用为7元，固定性制造费用总额为4000元，单位变动性销售管理费用为4元，固定性销售管理费用为1000元。

期初存货量为零，本期产量为1000件，销量为600件，单位售价为40元.要求：分别按两种成本法的有关公式计算下列指标：（1）单位产品成本（2）期间成本（3）销货成本（4）营业利润.解：1、变动成本法：（1）单位产品成本=10+5+7=22元（2)期间成本=4000+4×600+1000=7400元(3）销货成本=22×600=13200元（4）贡献边际=40×600—（22×600+4×600）=8400元营业利润=8400-（4000+1000)=3400元2、完全成本法：（1）单位产品成本=22+4000/1000=26元(2）期间成本=4×600+1000=3400元(3)销货成本=26×600=15600元（4）营业利润=40×600-15600—3400=5000元2、已知:某厂只生产一种产品，第一、二年的产量分别为30 000件和24 000件，销售量分别为20 000件和30 000件；存货计价采用先进先出法.产品单价为15元/件，单位变动生产成本为5元/件;每年固定性制造费用的发生额为180 000元。

销售及管理费用都是固定性的，每年发生额为25 000元。

要求：分别采用两种成本计算方法确定第一、第二年的营业利润(编制利润表）。

解：贡献式利润表单位:元传统式利润表单位:元3、已知：某厂连续两年的产销量、成本和售价等资料如下表:资料单位：元该厂按变动成本法计算的营业利润第一年为150 000元,第二年为100 000元，存货按先进先出法计价。

要求：用利润差额简算法计算完全成本法的各年营业利润。

第三章 潮流计算习题1. 试写出牛顿-拉夫逊法潮流计算的基本步骤。

（华北电大）2. 牛顿-拉夫逊潮流计算总，极坐标形式的修正方程式可以写成如下形式： ⎥⎦⎤⎢⎣⎡ΔΔ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡ΔΔU U L K N H Q P /δ 说明为什么节点电压相位角的改变主要影响有功潮流，节点电压幅值的改变主要影响无功潮流？并写出PQ 分解法的修正方程式。

（华北电大）3. PQ 分解法潮流计算与牛顿-拉夫逊法潮流计算相比有何优缺点？这两种算法可得相同精度的结果吗？4. 电力系统潮流自然分布与经济分布，各与什么参数有关？5. P-Q 分解法潮流计算的原理和简化条件是什么？写出其修正方程式。

6. 试述电力网络潮流调整和控制的办法。

7. 对于存在R ≥X 的电力网络，是否可以采用P-Q 分解法进行潮流计算？为什么？8. 网络结构如图所示，各支路参数均为电抗标幺值，1-2支路理想变压器的变比是K *=1.1，试写出网络的导纳矩阵。

（数据精确到小数点后两位）（华北电大）9. 系统等值网络如图所示，节点类型：1是PV 节点；2、3、5为PQ 节点；4 是平衡节点。

各元件的标幺参数为电抗：X 12=0.4，X 23=0.5，X 34=0.2，X 24=0.4，X 45=0.2电拿：B 20=0.8，B 40=0.4求：（1）该网络的节点导纳矩阵。

（2）试写出采用直角坐标N-R 法进行潮流计算时的修正方程式结构。

（注：状态变量和运行变量用符号表示，雅可比矩阵中非零元素用“×”表示，零元素用“0” 表示。

）10. 已知两节点系统及标幺值参数如图所示，节点1 是平衡节点，给点电压为1.05pu ，支路阻抗为0.01+j0.03pu,节点2 的负荷为0.5+j0.1pu.求：（1）节点2 的功率方程；（2）牛顿-拉夫逊法直角坐标形式的修正方程式；（3）当给定初值()102=U 时，计算第一次迭代的电压()12U ？11. 5节点电力系统，节点1为PV 节点，节点5为平衡节点，其余为PQ 节点。

第三章总练习题111121221.N ew to n -L eib n iz 1(1).[1,1],.tan (2).tan (0,2)2tan2.,x x xd de d x e e d x d x x d x d x u x xf F F ππ-⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=+⎰⎰为什么用公式于下列积分会得到不正确结果?无界从而不可积在的一些点不可导.证明奇连续函数的原函数为偶函数,而偶连续函数的原函数之一为奇函数.设奇连续函数的原函数为 现在证明是偶证.()().(()())()()()()0,()(),(0)(0)0.()()0.,.()().(()())()()()()0,()().(0)0,(F x f x F x F x F x F x f x f x F x F x C C F F F x F x f F F F x f x F x F x F x F x f x f x F x F x C F C F ''''=--=---=---=--==--=--=''''=-+=--+=--+=--===函数设偶连续函数的原函数为现在证明是奇函数设则3003440010100)(0)0.()()0.sin ,0,3.()()()?0,0., 0,()()()sin co s |1co s .444.sin ().sin ()s b ab b b a aaabF F x F x x x f x f x f x d x a b x x f x d x f x d x f x d x x d x xd xxax b d x t d x d xd d x t d x d xd x--=-+=≥⎧==<>⎨<⎩=+=+=-=+-++=⎰⎰⎰⎰⎰⎰⎰⎰求定积分其中求微商解解()()110001201/2221210221in ()sin (1)sin ().5.lim()(),().1lim()()().6.lim(1).(2)!!(1)co s.(21)!!2x xh x h u xh u xnn nn n n u d u x x f x h t d x f x f x f x h t d u f t d tf x hx d x n x d x td t I n I π+→+→=→∞+++=+-+='+==--===+<⎰⎰⎰⎰⎰⎰⎰试证明其中是实轴上的连续函数求极限证解12210(2)!!(21)!!1,(21)!!(22)!!1100(),lim(1)0.sin co s 7..2sin 3co s sin co s (2sin 3co s )(2sin 3co s )(2sin 3co s )(2co s 3sin )(23)sin (32)co s nn n n n n n n I n x d x x x d x x xx x A x x B x x A x x B x x A B x A B +→∞+=+++<<→→∞-=+-'+=-+-=-++=++-+⎰⎰令解,x23115,,.3211313sin co s 2sin 3co s (2sin 3co s )(2sin 3co s )2sin 3co s ln |2sin 3co s |15ln |2sin 3co s |.1313A B A B A B x xd x x x A x x B x x d xx xA xB x xC x x x C +=⎧=-=⎨-+=⎩+=-'-+-=-=+-+=-+-+⎰⎰222228.:2(1),ln (2),.22222222.(2)(2)222xxu d u x u x u d x uu d u d u x u uu u C C xex x e xd==+=+⎛⎫==- ⎪++⎝⎭⎛⎛=-+=-+ ⎝⎝=-==⎰⎰⎰⎰⎰⎰⎰⎰通过适当的有理化或变量替换求下列积分()24.2).22(3)33.(4)(11ln .2x C x C x CC d x x C ⎛⎫=+⎝=-++==-⨯=-=+-==-+⎰⎰⎰⎰⎰224444224222244sec tan(1)9..sin co s1tan11112111.21111((arctan1)arctansin co sd x xd x u d ux x x uuuu ud xx x+==++++⎛==++⎝⎛⎫⎪⎪=+⎪⎛⎛⎪++-+⎪⎝⎝⎝⎭=+++⎰⎰⎰⎰)1).110.()(,),,()()(),:()()( 3.424)11.()[,],()0.:(,),()0.,()(,),,TxbaCf x Tg x f x f x d xTh x g t d t Tf x a b f x d x a b cf cf x a b ff-+-∞+∞=-===⎰⎰⎰设函数在上连续以为周期令证明函数也以为周期.此即习题第题设函数在区间上连续且证明在内至少存在一点使若不然在没有零点由的连续性和连续函数的中间值定理在证证(,).()0,(,).,,,[,]0.()()()()()0..b c d ba a c da b f x x a b c d a c d b f c dmf x d x f x d x f x d x f x d x m d c>∈<<<>=++≥->⎰⎰⎰⎰不变号不妨设取满足则在取最小值于是矛盾22222212.[,],()0,:()0,[,].[,][,],|()||()|,[,].2|()|()()()0.2.bab ea da b f x d x f x x a bd e a bf cf x x d ef cf x d x f x d x d e=≡∈∈≠⊆>∈≥>->⎰⎰⎰设函数f在区间上连续且证明若不然,存在c[a,b],f(c)0.由f在c的连续性,存在区间矛盾证00222/200013.()(-,),(1),()();sin(2);1co s4sin1(3)(1co s sin()()()()().a aa a aaf xa f x d x f a x d xx xd xxxd xx xf x d x x a t f a t d t f a t d t f a x d xπππ∞+∞=-=+=++=-=--=-=-⎰⎰⎰⎰⎰⎰⎰⎰设在上可积证明对于任意实数有证(1)22220211022222sin ()sin ()sin sin (2),1co s 1co s 1co s 1co s sin co s arctan |.21co s 21co s 14sin sin (/2)(3)co s sin co s(/2)s x x x x x x xI d x d x d x d x I x x xx xd xd x d uI u xxux x I d x x xx ππππππππππππππππ--==-==-++++==-===+++-==+-+⎰⎰⎰⎰⎰⎰⎰/2/20222/2/2/20/2/2/2in (/2)co s co s sin ,2co s sin co s sin co s sin 1|csc(/4)co t(/4)||co s sin 11ln1ln co s s 4d xx x xx d x I d x d xx xx xx xd x d xd x x x x xππππππππππππ==++++===+-++⎡⎤⎛⎫⎢⎥ ⎪=+-⎥ ⎪⎥ ⎪⎢⎥⎝⎭⎣⎦⎰⎰⎰⎰⎰⎰⎰11),in 411).I π⎛⎫⎪-= ⎪ ⎪⎝⎭=232221123222014.()(23)m /s .004m /s,(1);(2)3(1)()23,3,4,34,4,3230.()4.34(4)(1)0, 4.32(5)a t t t x v tx t t x t t C C x t t x t t C tC x t t t x t t t t t s x =-===-''''=-=-+-==--=--+'==--=--=-+===一质点作直线运动,其加速度若时且求质点改变动方向的时刻头5秒钟内质点所走的总路程.解3322543343(4)|(4)|424m.32322t t t t x x t t t t ==⎛⎫⎛⎫-+=-----=⎪⎪⎝⎭⎝⎭000200022002200215.100m ,10.2s,25m ,25m ., 0;(), 10.2., 0;()210.2./2/2253m /s .10010.2a t t t v t a t t t a tt t s t a t t C t t a t a t Ca t a a t C ≤≤⎧=⎨≤≤⎩⎧≤≤⎪=⎨⎪+≤≤⎩⎧=+⎪=≈⎨⎪=+⎩一运动员跑完共用了在跑头时以等加速度进行然后保持等速运动跑完了剩余路程.求跑头时的加速度解16.(1):利用积分的几何意义证明111111ln,1,2,111(2)1ln ,211111ln ,21,.111(3)lim 1ln E u ler 211ln |111ln (1)ln lnn n n n n n n n n nnn n n n nx n n y n n nx y n n n d x d x x n n xn n n n→∞++++<<=+=+++--=++++--⎛⎫++++- ⎪-⎝⎭=<=+++=+-=<⎰⎰令证明序列单调上升而序列单调下降证明极限存在(此极限称为常数).证 (1)1121.1111(2)1ln (1)1ln 22111ln 10((1)).111111ln (1)1ln 21211ln 10((1)).1(3)1ln 20(2)n n n n n n d x n n x x n n n n n n y y n n n n n n n y x x n ++=⎛⎫⎛⎫-=+++-+-+++- ⎪ ⎪-⎝⎭⎝⎭⎛⎫=-+> ⎪⎝⎭⎛⎫⎛⎫-=++++-+-+++- ⎪ ⎪+⎝⎭⎝⎭⎛⎫=-+< ⎪+⎝⎭>>=->>⎰由由n +1n11/22111/1/2222112.,lim .17.:0,11.111111(1/).111/118.()(,),,(2)().2,()0.(2)()n n n xxxxxay y x d t d t ttd t x u d x d t tuutf x x f x f x a f x d x f x f x →∞>=++==⨯=+++-∞+∞-=-≠=-=-⎰⎰⎰⎰⎰⎰单调下降有下界故有极限证明当时设在上连续(书上为可积，欠妥)且对一切实数均有求实数使条件证解(22220221(11)(11))()(2)(),()0.0.19.ln (1)arctan ,0 1.11,[0,1],[0,],1111ln (1)arctan ,0 1.20.(1)x x f x f x f x f x d x f u d u f u d u f x d x a x x x d t d t t x ttttx x x =+-=-+-=-=-==+≤≤≤≤∈≤+++++≤≤≤⎰⎰⎰⎰⎰⎰相当关于为奇函数取即可利用定积分的性质，证明不等式在上积分得设证()()[0,];()()2(2)a f x d x a f x a d x f x f a x =+-⎰在上可积，证明利用(1)中的公式求下列积分的值：22/2222sin ;22sin co s ()()(1)()()()()()()2()()()()()(-)1,.()()()()22a a a a a a a xx d x d xx x x xf x f a u I d x d uf x f a x f u f a u f x f a u I d x d uf x f a x f u f a u f x f a x a d x d x d x a I f x f a x f x f a x xx x π-++-==+-+--=++-+-=+===+-+--⎰⎰⎰⎰⎰⎰⎰⎰⎰证解(2)22222/20222 2.2(2)2sin /2.sin sin (/2)24xd x d x x x xd x x x ππππ==⨯=++-==+-⎰⎰⎰tan 2sin tan tan 22sin sin tan 22222sin tan 32222sin 2()21.()(1).()(1)tan sin ,()sec co s tan sec sin co s sec co s tan sec sin co s 3sec x xx x x xx xxxd f x f x xt d td x d xf x xt d t x x x t d t d f x x x x x x x x x t d td xt x x x x x x x x =+=+=-+=-+-+=-+-+==⎰⎰⎰⎰设求解()()22233222331co s tan sec sin co s tansin 31sec (1tan )co s (1sin )tansin .3x x x x x x x x x x x x x x x x x x -+-+-=+-++-()/22/2/22/220/20/2/2022.co s 3.11co s 3(1co s 6)sin 6|.2412423.|sin co s |.|sin co s ||sin co s ||sin co s ||sin co s ||sin ()2I d I d d I x x d x x x d xx x d x x x d x x x d x t ππππππππππθθππθθθθθπ===+=+==--=-+--++⎰⎰⎰⎰⎰⎰⎰⎰求定积分的值求定积分的值解解I =22=2()()()()/20/2/20/4/2/20/4/4/2/2/40co s()|2|sin co s ||co s sin |(co s sin )(sin co s )(co s sin )2sin co s |(co s sin )|(sin co s )|t d x x x d x t t d xx x d x x x d x t t d xx x x x x x ππππππππππππ⎛⎫-+ ⎪⎝⎭=-++=-+-++=++--+-=⎰⎰⎰⎰⎰⎰221010101010100110()/224.0,.2x x x x x x x x x x x x x x I x I xxx x x x u x --<<====+⎛⎫==- ⎪⎝⎭=⎰⎰⎰⎰⎰设求定积分的值解10()/210222102()2arcsin().28x x a aux x x a u a a x x aππ--==⎡⎤=⎢⎥⎣⎦-==⎰⎰4342(2)16468 4.y x x x y x x x =++-=++-与43323242224342442432164164684,680,6840,680,(2)(4)0,2,4.{(164)(684)][(684)(164)]y x x x x x x x x x x y x x x x x x x x x S x x x x x x d xx x x x x x d x⎧=++-⎪+-=+--+=⎨=++-⎪⎩=-+=--===++--++-+++--++-⎰⎰解222212552233532325.:(1)6827.682768,278150,(3)(5)0.3, 5.(27(68))(815)4415.33y x x y x y x x x x x y x x x x x x x S x x x d x x x d xx x x =-+=-⎧=-+-=-+⎨=-⎩-+=--====---+=-+-⎛⎫=-+-=⎪⎝⎭⎰⎰求下列曲线所围图形的面积与解/2/2/4/45/45/4/2/2(4)sin ,cos /2.(sin -cos )(cos sin )|1;(sin cos )(cos sin )| 1.y x y x x S x x dx x x S x x dx x x πππππππππ=====--==-=--=⎰⎰与解/21102/211226.co s ,1/2,,.,)2arcco s 2arcsin 2(1co s 2).242arcsin arcsin y x y x x V V V x d x y y d y y yd y V x d x V y yd y yd yππσπσππππππππ===⎛⎫=-==⎪⎝⎭=-====⎰⎰⎰⎰⎰⎰设区域由曲线及所围成将绕轴旋转一周得一旋转体试用两种不同的积分表示体积并且求的值. 2解V =(1-c o s 24323222444323202(68)(68)24248.44x x x d x x x x d xx x x x x x =-++-+-⎡⎤⎡⎤=-++-+-=⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰2222212321(3)1 3.(3)1,7100,(2)(5)0,2,5.1,2.[(3)(1)]92.322y x y x x x x x x x x y S y y d x yy y --=-=--=--+=--===-=+-+⎛⎫=-++= ⎪⎝⎭⎰与解4π2π54π112212222arcsin ()1arcsin .22244y y y xyπππππππ=-⨯⎤=-=-=⎥⎦⎰22111/21/2200213397200257025027.:(1)arcsin |.4612(2)(918055801)400.28.()[0,7],()5,()6,() 3.(1)();(2)x xxx d x f x f x d x f x d x f x d x f x d x f πππ-===-=-++====⎰⎰⎰⎰⎰⎰求下列定积分的值设在上可积且一直已知求的值求7552500277557755().(3):(5,7),()0.(1)()()()5611.(2)()()()3118.(3),()0,(5,7),()0,()80,.x d x f x f x d x f x d x f x d x f x d x f x d x f x d x f x x f x d x f x d x <=+=+==-=-=-≥∈≥=-<⎰⎰⎰⎰⎰⎰⎰⎰⎰的值证明在内至少存在一点使若不然但是矛盾解证2/23/21/2/2/2/2/232111, 2,129.()sin ,(),()2, 2.(1)()();(2)()();(3)()().(1)()()sin 0.(2)()()()()()xx f x x h x g x x x f x g x d x g x h x d x f t g t d x f x g x d x xd x g x h x d x g x h x d x g x πππππππππ----≤≤⎧===⎨<≤⎩===+⎰⎰⎰⎰⎰⎰⎰设试求下列定积分的值或表达式:解322323221212/22/2/22()12125.6sin co s ,2(3)()()sin 2sin co s 22co s ,2.xxx h x d x d x d x xxxxtd t x t x f t g t d x td t td t x x πππππ=+=--=⎧=--≤≤⎪=⎨⎪+=-<≤⎩⎰⎰⎰⎰⎰⎰⎰()()30()[,](0),()()()()()().b f b af a f x a b ag y f x f x d x b f b a f a g y d x >=--⎰⎰设函数在区间上连续，严格单调递增是的反函数,利用定积分的几何意义证明下列公式并作图解释这一公式.解11()10031.(1)()[0,),()0,0()()()()()()()(*).00(0),()a B a aa x x x a B a B x d x x d xx x x d x x d x a a B B x x ϕϕϕϕϕϕϕϕϕϕϕϕϕ---+∞→∞→+∞≥≥≤++==>=→∞→+∞⎰⎰⎰⎰⎰设函数在上连续且严格单调递增又设当+时且(0)=0.证明:对于任意实数,下列不等式成立:其中是的反函数.由题时不等式显然成立.设由于+时证30,111101100()11()1()1,0,(),[0,],,0,().,*)()().,()()()()()()()()(())(a B aBa a B a Ba a a B a a a B a a a B x d x x d x a a x d x x d xx d x x d x x d xa a x d xa a a B ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ------'>''>>===+>+=++=++≥+⎰⎰⎰⎰⎰⎰⎰⎰存在在连续根据连续函数的中间值定理存在若则由(得若则1100()()11()11()).,()()()()()()()()(())(()).11(2)(1),0,,11,M in k o w sk i.1aB a a a Ba B pqa a B a a x d x x d xx d x x d x x d xa a x d xa a a a B a B ab p q p qaba b pqp ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ------=<+=+-=-≥--=≥≥+=≤+>⎰⎰⎰⎰⎰⎰若则利用中的不等式,对于任意实数证明下列不等式不妨设证111/(1)1/(1)1/(1)1/0.(),()..1/(1)1/(1)p p pp pp p pqa b ppx x x x abababa b x d x xd x pp pp p pqϕϕ----+-==≤+=+=+=+-+-⎰⎰在中取则(1)232.0,,1,112.xa a y y x a y π>=+===设求的值使由曲线及所围成的区域绕直线旋转所得之旋转体的体积等于b22222202222220002.)2,112,22,2,18,2ln 9,44aa x aa a x x u a d x d x xe d x e d x e d u e a a ππ=====-===⎰⎰⎰⎰⎰20解(y -1) 20033.1sin 21co s 43(1sin 2)(12sin 2).22r S d d ππθθπθθθθ=+-=+=++=⎰⎰作由极坐标方程所确定的函数的图形,并求它所围区域的面积.解。

计算⽅法-刘师少版课后习题答案1.1 设3.14, 3.1415, 3.1416分别作为π的近似值时所具有的有效数字位数解近似值x =3.14＝0.314×101,即m =1，它的绝对误差是－0.001 592 6…，有31105.06592001.0-*?≤=- x x .即n =3，故x =3.14有3位有效数字. x =3.14准确到⼩数点后第2位. ⼜近似值x =3.1416，它的绝对误差是0.0000074…，有 5-1*10?50≤00000740=-.. x x 即m =1,n ＝5，x =3.1416有5位有效数字.⽽近似值x =3.1415，它的绝对误差是0.0000926…，有4-1*10?50≤00009260=-.. x x即m =1,n ＝4，x =3.1415有4位有效数字. 这就是说某数有s 位数，若末位数字是四舍五⼊得到的，那么该数有s 位有效数字1.2 指出下列各数具有⼏位有效数字，及其绝对误差限和相对误差限：2.0004 －0.00200 9000 9000.00解（1）∵ 2.0004＝0.20004×101, m=1绝对误差限：4105.0000049.020004.0-*?≤≤-=-x x xm -n =-4,m =1则n =5,故x =2.0004有5位有效数字1x =2，相对误差限000025.010221102151)1(1=??=??=---n r x ε（2）∵－0.00200= -0.2×10-2, m =-25105.00000049.0)00200.0(-*?≤≤--=-x x xm -n =-5, m =-2则n =3,故x =-0.00200有3位有效数字1x =2，相对误差限3110221-??=r ε=0.0025 (3) ∵ 9000=0.9000×104, m =4，0105.049.09000?<≤-=-*x x xm -n =0, m =4则n =4,故x =9000有4位有效数字4110921-??=r ε＝0.000056 (4) ∵9000.00=0.900000×104, m =4，2105.00049.000.9000-*?<≤-=-x x xm -n =-2, m =4则n =6,故x =9000.00有6位有效数字相对误差限为6110921-??=rε＝0.000 00056 由(3)与(4)可以看到⼩数点之后的0，不是可有可⽆的，它是有实际意义的.1.3 ln2=0.69314718…，精确到310-的近似值是多少？解精确到310-＝0.001，即绝对误差限是ε＝0.0005,故⾄少要保留⼩数点后三位才可以.ln2≈0.693 2.1 ⽤⼆分法求⽅程013=--x x在[1, 2]的近似根，要求误差不超过31021-?⾄少要⼆分多少？解：给定误差限ε＝0.5×10－3，使⽤⼆分法时，误差限为)(211*a b x x k k -≤-+ 只要取k 满⾜ε<-+)(211a b k 即可，亦即 96678.912lg 10lg 35.0lg 12lg lg )lg(=-+-=---≥εa b k只要取n ＝10.2.3 证明⽅程1 -x –sin x ＝0 在区间[0, 1]内有⼀个根，使⽤⼆分法求误差不超过0.5×10-4的根要⼆分多少次？证明令f (x )＝1－x －sin x ，∵ f (0)=1>0，f (1)=－sin1<0∴ f (x )=1－x －sin x =0在[0，1]有根.⼜ f '(x )=-1－c os x<0 (x ∈[0.1]),故f (x ) 在[0，1]单调减少，所以f (x ) 在区间[0，1]内有唯⼀实根.给定误差限ε＝0.5×10－4，使⽤⼆分法时，误差限为)(211*a b x x k k -≤-+ 只要取k 满⾜ε<-+)(211a b k 即可，亦即7287.1312lg 10lg 45.0lg 12lg lg )lg(=-+-=---≥εa b k只要取n ＝14.2.4 ⽅程0123=--x x 在x =1.5附近有根，把⽅程写成四种不同的等价形式，并建⽴相应的迭代公式：（1）211xx +=，迭代公式2111kk x x +=+ （2）231x x +=，迭代公式3211k k x x +=+（3）112-=x x，迭代公式111-=+k k x x （4）13-=x x ，迭代公式131-=+k k x x试分析每种迭代公式的收敛性，并选取⼀种收敛迭代公式求出具有四位有效数字的近似根。

第三章习题3-4 利用标准状态下298K 的熵值数据，计算下列反应在标准压力及298K 条件下的熵变。

（1）)()(21)(212g HCl g Cl g H =+ （2）)(2)(2)(2)(2223l O H g CO g O l COOH CH +=+ 解：（1）)(21)(21)(22H S Cl S HCl S S m m mmr ΘΘΘΘ--=∆111104.10)68.1302107.2232191.186(----⋅⋅=⋅⋅⨯-⨯-=mol K J mol K J （2）)(2),(),(2),(22322O S l COOH CH S g CO S l O H S S m m m m m r ΘΘΘΘΘ--+=∆1111776.2)138.20528.15974.213291.692(----⋅⋅-=⋅⋅⨯--⨯+⨯=mol K J mol K J3-5 试根据标准生成焓m f H ∆（298K ）和标准摩尔熵m S （298K ）的数据，求算下列反应的m r G ∆（298K ）： （1）)()(21)(222l O H g O g H =+（2）)(2)()(2g HCl g Cl g H =+（3）)()(21)(324l OH CH g O g CH =+解：(1)122283.285)(21)()(-ΘΘΘΘ⋅-=∆-∆-∆=∆mol kJ O H H H O H H H m f m f m f mr)(21)()(222O S H S O H S S m mm mr ΘΘΘΘ--=∆111134.163)14.2052168.13091.69(----⋅⋅-=⋅⋅⨯--=mol K J mol K J13]10)34.163(15.29883.295[--ΘΘΘ⋅⨯-⨯--=∆-∆=∆mol kJ S T H G m r m r m r113.237-⋅-=mol kJ(2))()()(222Cl H H H HCl H H m f m f m f m r ΘΘΘΘ∆-∆-∆=∆1)]307.92(2[-⋅-⨯=mol kJ)()()(222Cl S H S HCl S S m m m m r ΘΘΘΘ--=∆111107.20)07.22368.13091.1862(----⋅⋅=⋅⋅--⨯=mol K J mol K J1136.190)1007.2015.298614.184(---ΘΘΘ⋅-=⋅⨯⨯--=∆-∆=∆mol kJ mol kJ S T H G m r m r m r （注：答案31007.2015.298614.184⨯⨯-=∆Θmr G 错误）(3) )(21)()(243O H CH H OH CH H H m f mf mf mr ΘΘΘΘ∆-∆-∆=∆1189.163)]81.74(7.238[--⋅=⋅---=mol kJ mol kJ )(21)()(243O S CH S OH CH S S m m m m r ΘΘΘΘ--=∆1111033.162)138.2052126.1868.126----⋅⋅-=⋅⋅⨯--=mol K J mol K JΘΘΘ∆-∆=∆mr m r m r S T H G 11358.115]10)03.162(15.29889.163[---⋅-=⋅⨯-⨯--=mol kJ mol kJ3-7已知1282.241)15.298,,(-⋅-=∆mol kJ K g O H H m f，R g O H C m V 5.4),(2,=，参加下列反应的气体为理想气体：)()(21)(222g O H g O g H =+该反应系统始态的温度为298.15K ，压力为101.325kPa ，试分别计算在（1）绝热、恒压反应；（2）绝热、恒容反应条件下进行单位反应时，反应系统末态的温度及过程的W 、U r ∆、H r ∆各为若干？解：对绝热恒压反应0==∆p Q H0321=∆+∆+∆=∆H H H H r0)15.298()5.4(02,21=-⨯++∆=+∆+ΘΘ⎰T R R H dT C H m r T T m p mrK K R H T m r 49.558615.298314.85.524182015.2985.52=+⨯=+∆-=Θ由理想气体状态方程：222111V T n V T n =得11249.1215.1985.149.5586V V V =⨯= 11148.11)149.12(21RT n V p pdV U W V V -=-⨯-=-=∆=⎰kJ kJ 7.4215.298314.85.149.11-=⨯⨯⨯-=(2)绝热恒容反应：0==∆V Q U，0=W)15.298()5.4()15.298(2,21-⨯++∆=+∆=∆ΘΘ⎰T R R H dT C K H H m r T T m p m r r1122)(RT n RT n pV U H r r -=∆+∆=∆联合(1)(2)可得Rn RT n R H T m r )5.5(15.2985.52112-+⨯-∆=ΘK K 55.6728314.8)5.51(15.298314.85.115.298314.85.5241820=⨯-⨯⨯+⨯⨯--=1122)(RT n RT n pV U H r r -=∆+∆=∆kJ kJ 2.52)]15.2985.155.67281(314.8[=⨯-⨯⨯=3-8 甲烷与过量50%的空气混合，为使恒压燃烧的最高温度能达到2000℃，则混合气体燃烧前应预热到多少度？计算中N2，O2,H2O （g ）,CH4(g),CO(g)的Cp,m 分别为33.47,33.47，41.84,75.31及54.3911--⋅⋅mol K J。