等分圆周表

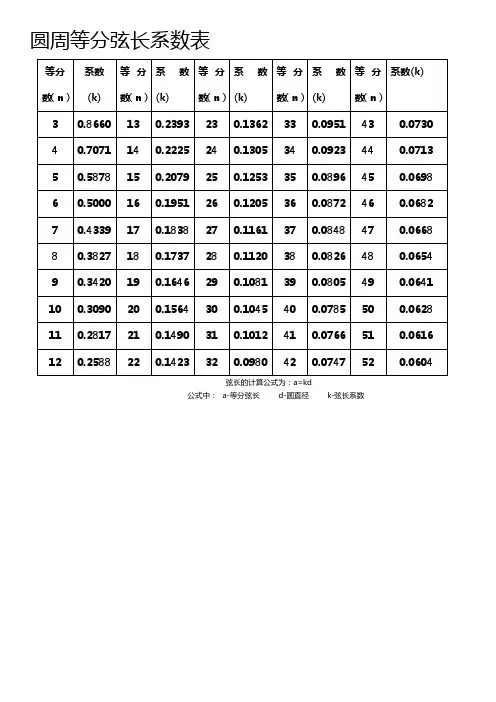
圆周等分弦长系数表弦长的计算公式为：a=kd公式中：a-等分弦长d-圆直径k-弦长系数90度虾米腰弯头放样展开简易计算公式关于虾米腰弯头放样展开的方法，好多网友问到具体的放样展开方便的方法，因为1：1画图展开太麻烦了，也不够精确。

我总结了一下，归纳了下面的计算表格，根据此表格，可以比较方便的展开90度多节（2~19节）弯头。

圆周等分数为16等份只能是90度的虾米腰弯头，请先按照虾米腰节数选出K值，带入到左面表格的公式中，计算出17个点的坐标，然后可在钢板上直接画出第一节展开图或放出样板。

，我举个实际例子比如：5节弯头（取值K=0.1989），直径219，弯曲半径300点1 X=0*219 Y=0.1989*（300-0.5*219）点2 X=0.196*219 Y=0.1989*（300-0.462*219）点3 X=0.393*219 Y=0.1989*（300-0.354*219）点9 X=1.571*219 Y=0.1989*（300+0.5*219多节的弯头叫作“虾米腰”。

手工放样步骤：（以一节为例，其余方法相同）1）先按实际尺寸画出弯头侧面投影。

包括接缝线。

2）按线把每一个封闭线框图形分割成独立的图形。

（可以裁剪，也可以单独再画。

3）取一个图样，（将中心线垂直的设置）画在另一张纸上，沿图样高度画两条上下平行的横线，并与中心线垂直，长度正好是图样直径的圆周长。

（封闭的长方形）4）将图样垂直方向作等分，并作好标记，然后将这些等分线垂直的画到刚才画的展开的长方形内，注意展开图上的点一定要对应投影图样上的点。

5）将图样上斜线沿水平方向作等分。

并平行的拉到展开的图样上，并对应相应的点。

把展开样上得到的交点圆滑连接，就是展开的曲线。

等分作的越密，曲线越准。

6）放出咬口的量，和板厚处理。

弯头下料必须知道弯曲半径，厚度、几节。

图12、画展开图：在端节的一端以aa’为直径画一个半圆弧，将半圆弧六等分（等分的越多就越精确）。

圆等分系数表及计算公式
圆等分系数表是数学中常用的一个工具，用于计算圆的等分问题。

在计算一个圆的等分时，我们通常会遇到需要确定等分点的位置和数量的问题。

而圆等分系数表则提供了一种便捷的方法来解决这些问题。

圆等分系数表由一列数字组成，每个数字代表了圆的等分点的位置。

这些数字的大小和顺序都有特定的规律，可以帮助我们准确地计算出圆的等分点的位置。

具体来说，圆等分系数表可以分为两种类型：一种是等分点的位置系数表，另一种是等分点的数量系数表。

在等分点的位置系数表中，每个数字代表了一个等分点在圆周上的位置。

这些数字通常是小数，可以表达出等分点在圆周上的具体位置。

通过查找圆等分系数表，我们可以找到需要的等分点的位置，并准确地确定它们在圆周上的位置。

而在等分点的数量系数表中，每个数字代表了等分点的数量。

通过查找圆等分系数表，我们可以找到需要的等分点的数量，并根据这个数量来确定等分点的位置。

圆等分系数表的计算公式是一个复杂的数学公式，涉及到圆的几何性质和数学运算。

但在实际应用中，我们并不需要直接使用这个公式来计算，而是通过查找圆等分系数表来获得所需的结果。

圆等分系数表是一个在圆的等分问题中非常实用的工具。

通过使用这个表，我们可以快速准确地确定圆的等分点的位置和数量，从而解决各种与圆的等分相关的问题。

无论是在数学教学中，还是在实际应用中，圆等分系数表都是一个非常有用的工具。

希望这篇文章可以帮助读者更好地理解和应用圆等分系数表。

等分圆周系数表
等分圆周系数表是指在圆周内等分若干份的系数表。

这份系数表可以用于计算圆内接正多边形的面积，以及圆的周长等。

下面是一份等分圆周系数表，其中每一项是一个整数，表示将圆周等分为多少个等份，每个等份的大小为该数字乘以圆的周长。

| 整数 | 等分圆周系数 |
| ----- | -------- |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | 10 |
| 11 | 11 |
| 12 | 12 |
| 13 | 13 |
| 14 | 14 |
| 15 | 15 |
| 16 | 16 |
| 17 | 17 |
| 18 | 18 |
| 19 | 19 |
| 20 | 20 |
这份等分圆周系数表是根据圆的周长和半径计算出的。

当圆的周长为 C，半径为 r 时，圆内接正 n 边形的面积为:
πr^2 × (n-2)!
其中，n 表示正 n 边形的边数，! 表示阶乘运算。

另外，圆的周长为:
C = 2πr
因此，可以通过计算πr^2 和 2πr 之间的系数，来制作等分圆周系数表。

等分圆周系数表还可以用于计算圆的面积、圆周长、正多边形的面积等。

在制作等分圆周系数表时，需要考虑到小数点后的位数，以确保计算结果的准确性。

圆周的等分系数表1. 引言圆周的等分系数表是一种用于计算圆周等分问题的工具。

在几何学中，圆周等分是指将一个圆分成若干个等角的部分。

这个问题在数学和工程领域中有着广泛的应用，例如在建筑设计、航空航天和电子工程等领域。

本文将介绍圆周的等分系数表的定义、用途以及计算方法，并提供一个示例来说明如何使用该表解决实际问题。

2. 定义圆周的等分系数表是一个记录了将一个圆等分成不同数量部分时所需的角度值的表格。

该表格列出了从2份到n份（n为正整数）所需的角度值，并提供了相应的计算方法。

3. 用途圆周的等分系数表可以帮助我们快速计算出将一个圆平均地划分成任意数量部分时每个部分所对应的角度值。

这对于许多需要进行精确角度划分的问题非常有用，比如：•建筑设计：在建筑设计中，经常需要按照一定比例划定室内或室外空间。

通过使用圆周的等分系数表，可以确保每个部分的角度都是均匀的，从而使得设计更加美观和合理。

•航空航天：在航空航天领域中，飞行器的导航和控制往往需要准确的角度划分。

通过使用圆周的等分系数表，可以计算出每个划分区域的角度值，从而帮助飞行器进行准确导航和控制。

•电子工程：在电子工程中，许多设备需要进行精确的角度测量和控制。

圆周的等分系数表可以用于计算出每个部分所对应的角度值，从而帮助实现精确的测量和控制。

4. 计算方法圆周等分系数表中给出了从2份到n份（n为正整数）所需的角度值。

其中，2份时每份对应180°，3份时每份对应120°。

对于其他数量部分时所需的角度值，可以通过以下公式计算：angle = 360 / n其中，angle为每个部分所对应的角度值，n为将圆等分成的部分数量。

5. 示例假设我们需要将一个圆平均地划分成6份，并计算出每个部分所对应的角度值。

根据圆周的等分系数表，我们可以找到6份所对应的角度值为60°。

通过使用计算方法，我们也可以得到相同的结果：angle = 360 / 6= 60°因此，每个部分所对应的角度值为60°。

圆度等分系数表【最新版】目录1.圆度等分系数表的定义与作用2.圆度等分系数表的计算方法3.圆度等分系数表的应用实例4.圆度等分系数表的优缺点分析正文一、圆度等分系数表的定义与作用圆度等分系数表是一种用于衡量圆形物体的圆度精度的工具，其主要作用是将圆周等分，以便于计算圆的各个部分的长度和角度。

在机械制造、仪器仪表、航天航空等领域，圆度等分系数表被广泛应用于检验产品的圆度精度，以确保产品的质量和性能。

二、圆度等分系数表的计算方法圆度等分系数表的计算方法主要包括以下两种：1.直接法：根据圆的直径和圆周长，直接计算出等分点的坐标。

这种方法计算简单，但精度较低，适用于对圆度要求不高的场合。

2.间接法：通过计算圆周上各点的切线长度，从而得出等分点的坐标。

这种方法计算较为复杂，但精度较高，适用于对圆度要求较高的场合。

三、圆度等分系数表的应用实例在实际应用中，圆度等分系数表可以用于以下方面：1.检验产品的圆度精度：通过与标准圆度等分系数表进行对比，可以判断产品的圆度是否达到要求。

2.确定零件的加工工艺：根据零件的圆度要求，可以选用合适的加工工艺，以保证零件的圆度精度。

3.优化生产过程：通过对圆度等分系数表的分析，可以发现生产过程中存在的问题，并采取措施进行改进。

四、圆度等分系数表的优缺点分析圆度等分系数表的优点：1.计算方法成熟，应用广泛；2.可以对圆度进行定量分析，便于判断产品的质量；3.对提高产品质量和生产效率具有重要作用。

圆度等分系数表的缺点：1.计算过程较为繁琐，对计算工具和技能的要求较高；2.受到测量设备和测量方法的限制，计算结果可能存在一定误差。