建筑曲率的计算公式模版
- 格式:pptx
- 大小:291.44 KB
- 文档页数:12





混凝土梁的曲率计算方法一、前言混凝土梁是建筑工程中常见的结构形式,用于承载楼板和其他荷载。
在设计混凝土梁时,需要计算其曲率,以确保其符合建筑要求。
本文将详细介绍混凝土梁的曲率计算方法。
二、混凝土梁的曲率概述混凝土梁的曲率是指梁在受力情况下产生的弯曲变形程度。
曲率是一个重要的参数,影响梁的承载能力和稳定性。
在设计梁时,需要计算其曲率,以保证其能够承受预期的荷载,并满足建筑要求。
三、曲率计算方法1.曲率计算公式混凝土梁的曲率计算可以使用以下公式:κ = M / EI其中,κ是梁的曲率,M是梁上的弯矩,E是混凝土的弹性模量,I是梁的截面惯性矩。
2.弯矩计算方法弯矩是混凝土梁曲率计算的关键参数之一。
以下是计算弯矩的方法:M = Wl^2 / 8其中,M是梁上的弯矩,W是梁的荷载,l是梁的长度。
3.截面惯性矩计算方法截面惯性矩是混凝土梁曲率计算的另一个关键参数。
以下是计算截面惯性矩的方法:I = (bh^3) / 12其中,I是梁的截面惯性矩,b是梁的宽度,h是梁的高度。
4.弹性模量计算方法弹性模量是混凝土梁曲率计算的另一个关键参数。
以下是计算弹性模量的方法:E = 57,000 * sqrt(f_c)其中,E是混凝土的弹性模量,f_c是混凝土的抗压强度。
四、曲率计算实例为了更好地理解混凝土梁曲率计算方法,以下给出一个实例。
假设有一根长度为5m,宽度为0.2m,高度为0.4m的混凝土梁,其承受的荷载为20kN。
试计算该梁的曲率。
首先,计算梁的截面惯性矩:I = (0.2 * 0.4^3) / 12 = 0.0010667 m^4然后,计算混凝土的弹性模量:E = 57,000 * sqrt(20) = 269,258 N/mm^2接着,计算梁上的弯矩:M = 20 * 5^2 / 8 = 62.5 kN*m最后,计算梁的曲率:κ = 62.5 * 10^6 / (0.0010667 * 269,258 * 10^6) = 0.228 /m因此,该梁的曲率为0.228 /m。

曲率公式是什么
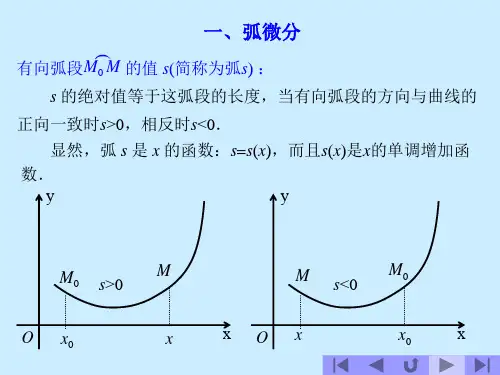
在数学上,曲率是表明曲线在某一点的弯曲程度的数值,曲率的公式可以表示为:K=|dα/ds|。
曲率
曲线的曲率是曲线上一点的切线方向角对弧长的旋转率,由微分定义,表示曲线偏离直线的程度。
数学上表示曲线在某一点的弯曲程度的数值。
曲率越大,曲线的曲率越大。
曲率的倒数就是曲率半径。
曲率的定义
曲率的计算公式
什么是曲率半径
曲率的倒数就是曲率半径,即R=1/K。
平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。
对于曲线,它等于最接近该点处曲线的圆弧的半径。
对于表面,曲率半径是最适合正常截面或其组合的圆的半径。
圆形半径越大,弯曲程度就越小,也就越近似于一条直线。
所以说,曲率半径越大曲率越小,反之亦然。


曲率半径的计算公式是什么?
曲率半径的计算公式是R=1/K。
平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。
对于曲线,它等于最接近该点处曲线的圆弧的半径。
对于表面,曲率半径是最适合正常截面或其组合的圆的半径。
应用:
(1)对于差分几何上的应用,请参阅Cesàro方程。
(2)对于地球的曲率半径(由椭圆椭圆近似),请参见地球的曲率半径。
(3)曲率半径也用于梁的弯曲三部分方程中。
(4)曲率半径(光学)。
(5)半导体结构中的应力。

曲线的参数方程与曲率计算曲线是我们生活中常见的一种形态,它们可以是自然界中的山脉、河流,也可以是人工构建的建筑物、道路等。
曲线的形状和特征对于我们理解和描述事物的运动和变化具有重要意义。
在数学中,我们可以通过参数方程来描述曲线的运动轨迹,而曲率则是衡量曲线弯曲程度的重要指标。
一、曲线的参数方程曲线的参数方程是一种描述曲线运动轨迹的方式。
它由一组参数方程组成,每个参数对应曲线上的一个点。
以二维平面上的曲线为例,我们可以将曲线上的每个点表示为(x, y),其中x和y分别是该点在x轴和y轴上的坐标。
而参数方程则是通过引入一个参数t,将x和y表示为t的函数,即x=f(t),y=g(t)。
通过不同的参数取值,我们可以得到曲线上的不同点。
例如,我们可以通过参数方程x=cos(t),y=sin(t)来描述单位圆的运动轨迹。
当t取0时,对应的点坐标为(1, 0),即单位圆上的起点。
随着t的增大,曲线逐渐绕着原点旋转,最终回到起点。
通过参数方程,我们可以清晰地描述出单位圆的运动轨迹。
二、曲线的曲率计算曲率是衡量曲线弯曲程度的指标。
在曲线上的每一点,曲率可以通过计算曲线在该点处的切线与曲线的弯曲程度来得到。
具体地,我们可以通过曲线的参数方程来计算曲率。
曲线的曲率计算可以分为两步:首先计算曲线的切向量,然后通过切向量来计算曲率。
对于曲线的参数方程x=f(t),y=g(t),我们可以分别求出x和y对t的导数,即dx/dt和dy/dt。
这两个导数分别表示曲线在该点处x和y坐标的变化率,也就是切向量的两个分量。
然后,我们可以通过切向量的两个分量来计算曲线的切向量的模长。
切向量的模长表示曲线在该点处的切线的斜率,也就是曲线的斜率。
最后,通过对切向量的模长求导,我们可以得到曲线的曲率。
曲率的计算公式为k=|dy/dt * d^2x/dt^2 - dx/dt * d^2y/dt^2| / (dx/dt^2 +dy/dt^2)^(3/2),其中d^2x/dt^2和d^2y/dt^2分别表示x和y对t的二阶导数。

参数方程下的曲率公式曲率的定义是物体的曲度,即当物体在特定的参数方程中,其表面自变量的变化程度。
曲率公式是求取曲率的重要工具,它可以帮助我们计算物体表面的曲度,也可以用于曲面的平面展开,以及几何学中的微分几何。
在几何学中,曲率是一个重要的度量,用它可以衡量曲面、曲线在不同空间上的弯曲程度。
它有助于研究曲面、曲线在空间中的特性和轨迹,也可以应用于其他科学研究中。
在参数方程下,可以计算出曲率的一个公式,即曲率公式。
曲率公式可以表示为:κ = R(1 + h^2)^( 3/2)其中,R是曲率半径,h是曲面中自变量的变化率。
曲率公式的求取基础是参数方程,参数方程是由物体表面的参数方程求取的,因此,了解参数方程是非常重要的。
参数方程有三类:抛物面参数方程、凸反平面参数方程和椭圆回形参数方程。
抛物面参数方程可以表示为:X = A + Ucosθ + VsinθY = B + U2sin2θ + V2cos2θZ = C + U2sin2θ + V2cos2θ其中,A,B,C是物体表面的常数参数,U,V是物体表面的自变量,θ是变量θ的参数值。
凸反平面参数方程可以表示为:X = A + Ucosθ + VsinθY = B + U2sin2θ + V2cos2θZ = C + V2cos2θ U2sin2θ它和抛物面参数方程的区别是负号的使用。
椭圆回形参数方程可以表示为:X = A + Ucosθ + VsinθY = B + U2sin2θ + V2cos2θZ = C + U2cos2θ + V2sin2θ它与抛物面参数方程的区别在于自变量的变化率是相反的。
这三类参数方程可以用来求取曲率公式。
我们可以准备三类参数之后,将物体表面的自变量U、V和参数θ代入曲率公式,就可以计算出物体表面的曲率值了。
由于曲率公式可以用来测量物体表面的曲度,因此,在工程中有着广泛的应用。
例如,它可以应用于构件的强度评估,也可以用于测量地形和气象环境的精细变化;它可以用于太阳能电池板的制造,也可以用于油藏的勘察中。
曲率总结曲率是描述曲线或者曲面弯曲程度的一个重要概念,在数学和物理学中都得到广泛应用。
虽然曲率的数学定义可能相对复杂,但是在应用中我们可以通过一些简化的方法来理解和计算曲率。
本文将对曲率的概念、计算方法以及应用领域进行总结。
1. 曲率的概念在数学中,曲率是描述曲线或者曲面弯曲程度的一个量。
对于曲线而言,曲率可以理解为曲线在某一点处的弯曲程度;对于曲面而言,曲率可以理解为曲面在某一点处的弯曲程度。
曲率可以用于描述道路的弯曲程度、几何体的表面形状等。
2. 曲率的计算方法2.1 曲线的曲率计算对于曲线,我们可以通过求导数的方式计算曲线在某一点处的曲率。
具体而言,曲线的曲率可以使用以下公式计算:k = |dθ/ds|其中,k表示曲率,dθ表示弧长元素ds对应的角度变化。
2.2 曲面的曲率计算对于曲面,曲率的计算相对复杂一些。
常用的计算曲率的方法有以下两种:2.2.1 主曲率和法向量法主曲率是曲面上曲率最大和最小的两个方向的曲率。
我们可以通过计算曲面上的法向量和曲面上的两个方向的曲率来求得主曲率。
具体而言,主曲率的计算公式如下:k1 = |H + sqrt(H^2 - K)|k2 = |H - sqrt(H^2 - K)|其中,k1和k2分别表示主曲率,H表示平均曲率,K表示高斯曲率。
2.2.2 曲面的切曲率法曲面的切曲率法是通过计算曲面上某一点处曲线的曲率来求得该点的曲率。
具体而言,曲面的切曲率法计算曲率的公式如下:k = (dN/ds) · B其中,k表示曲率,dN表示曲面上法向量的变化量,ds表示曲线上的弧长元素,B表示曲线的切向量。
3. 曲率的应用领域曲率的概念和计算方法在许多领域中都有广泛的应用。
下面简要介绍几个典型的应用领域:3.1 车辆行驶路径规划曲率可以用于车辆行驶路径规划。
在道路设计中,合理的曲率设计可以提高车辆行驶的安全性和舒适性。
通过计算道路曲线的曲率,可以确定适合车辆行驶的最佳速度和转弯半径等参数。