下载文档原格式
函数单调性，凸性及判定1 单调性判定2凸曲线与凸函数3曲线的渐近线1 函数单调性的判定1212():()().f x x x f x f x <≤单调非减若，则1212():()().f x x x f x f x <<单调增加若，则1212():()().f x x x f x f x <≥单调非增若，则1212():()().f x x x f x f x <>单调减少若，则单调非减单调非增单调增加单调减少命题1I ,f 设在区间处处存在导数1.()0,f x ′≥若()0,f x ′>若().f x 则单调非减().f x 则单调增加证明1.()0,f x ′≥若1212[,],,a b x x x x <则对于中任意满足的两点)()()()(1212x x f x f x f −⋅′=−ξ12(,),x x ξ∈存在使得12()0()().f f x f x ξ′≥≤于是由推出根据拉格朗日定理根据拉格朗日定理，，命题3(),f x 若单调非减或增加()0.f x ′≥则证明证明：：0()()()lim0.x f x x f x f x x+∆→+∆−′=≥∆(),f x 若单调非增或减少()0.f x ′≤则第二个结论可以同样证明第二个结论可以同样证明..只证第一个结论只证第一个结论...)(存在假设x f ′.)()(0x f x x f x ≥∆+>∆时有注意到当所以命题命题444.()0,f x ′≡若()(),f x g x ′′≡若().f x 则恒等于常数.反之亦然()().f x g x c =+则.反之亦然x y tan =π0 ,2x <<求证当时有不等式：.tan 3 3x x x <+例133x x y +=证明;tan x x <首先证明第一个不等式首先证明第一个不等式..()tan f x x x =−令.)2π0(01sec )(2<<>−=′x x x f π()[0,).2f x 于是在单调增加(0)0f =由于，π(0,)()0.2f x >所以在有tan .x x >即xy =3π()tan (0).32x f x x x x =−−≤<令.)2π0(0tan 1sec )(2222<<>−=−−=′x x x x x x f 3tan .3x x x +<再证明π()[0,).2f x 于是在单调增加(0)0f =由于，π(0,)()0.2f x >所以在有21tan .3x x x >+即函数的凸性与曲线的凸性,,,,a b c d 观察同一区间上的四条曲线abcd,,a b 所表示的函数都单调减少,c d 表示的函数都单调增加，;但它们的形态很不相同这给与我们一个提示这给与我们一个提示：：还需要考察函数在区间上的凸性还需要考察函数在区间上的凸性...但它们增加的规律差异很明显仅有单调性不足以精确地反映函数的变化规律仅有单调性不足以精确地反映函数的变化规律..函数下凸严格定义函数下凸严格定义：：.,)(b x a x f y ≤≤=12[,]x x a b ∈如果对于任意两点，，12121()[()()]22x x f f x f x +<+都有.],[)(为下凸函数在则称b a x f a b)(x f y =12()2x x f +121[()()]2f x f x +1x 2x 定理定理11.)(存在导数在区间假设I x f 下凸的充分必要条件是在则I x f )(.)(单调增加在I x f ′证明：只证充分性只证充分性，，略去必要性证明.().f x I ′假设在单调增加)(2121x x x x I <，任取两点在区间)(21210x x x +=))(()()(01101x x f x f x f −′+=ξ根据拉格朗日定理得到20220()()()()f x f x f x x ξ′=+−),(011x x ∈ξ201(,)x x ξ∈))(()()(01101x x f x f x f −′+=ξ20220()()()()f x f x f x x ξ′=+−),(011x x ∈ξ201(,)x x ξ∈12021211()()2()[()()]()2f x f x f x f f x x ξξ′′+=+−⋅−21()()()f x f f ξξ′′′>单调增加推出于是120()()2()f x f x f x +>从而120()()().2f x f x f x +>下凸函数的几何意义下凸函数的图像的特点下凸函数的图像的特点：：ab)(x f y =①弦在上弦在上，，弧在下弧在下..1x 2x 3x ②曲线在上曲线在上，，切线在下这两个结论的证明留给大家研究这两个结论的证明留给大家研究..定理定理22().f x I 假设在区间存在二阶导数()f x I 则在下凸的充分条件是()0.f x ′′>上凸函数定义上凸函数定义：：12121()[()()]22x x f f x f x +>+定理3：()f x 上凸的充要条件：().f x ′单调减少().f x ′若存在定理定理44().f x I 假设在区间存在二阶导数()f x I 则在上凸的充分条件是()0.f x ′′<上凸函数的几何特征上凸函数的几何特征：：2x 1x AB122x x +①弦在下弦在下，，弧在上弧在上..②弧在下弧在下，，切线在上切线在上..1x 2x 3x 4x )1(>=p x y p (1)q y x q =<xy ln =xy e =P >0 下凸下凸；；0<p <1 上凸上凸．．:p x 幂函数(1)x a a >指数函数下凸；(1)x a a >对数函数上凸.xyπ−π；上凸,)π)12(,π2(:sin +=n n x y sin :((21)π,2π),.y x n n =−下凸x yx 拐点的必要条件拐点的必要条件：：，的拐点是曲线假设)())(,(00x f y x f x P =，连续如果)(x f ′′0()0.f x ′′=则必有)2)(1(−−=x x x y )1(6−=′′x y (1)0y ′′=1,6(1)0,x y x ′′<=−<时上凸;1,6(1)0,.x y x ′′>=−>时下凸.)0,1(是拐点P 221e )(x x x f −=例研究单调性和凸性研究单调性和凸性..22112221()e e ()2x x f x x x −−′′=+⋅⋅−2211222()e e x x fx x−−′=−⋅2122e (1)x x −=−2122()[()][e (1)]x f x fx x −′′′′′==−2122e (3)x x x −=−2−4−24xyO221ex x y −=2122()e (1)x f x x −′=−研究单调性研究单调性...0)(:)1,(<′−−∞x f .)(单调减少x f (1,1):()0.f x ′−<().f x 单调增加(1):()0.f x ′+∞<，.)(单调减少x f 研究凸性研究凸性..(,3):()0.f x ′′−∞−<().f x 上凸(30):()0.f x ′′−>，().f x 下凸(0,3):()0.f x ′′<().f x 上凸2122()e(3)x f x x x −′′=−(3):()0.f x ′′+∞>，().f x 下凸拐点拐点：：)3,3(23−−−e A 32(3,3)B e−)0,0(O 2−4−24xyO221ex x y −=自我评估题2302224.limtan xx ex x x−→−+−31−2csc5.lim(cos )xx x →12−016.lim(csc )x x x→+0自我评估题11.,??1y y y x′′′===+sin 2.x y x=3.()ln (0)f x x x x =>?d ?)1(1==′=x y y ??y y ′′′==2)1(sin cos )1(x x x x y +−+=′32)1(sin )12(cos )1(2x xx x x x y +−+++=′′(0)1y ′=2)0(=′′y 研究单调性和凸性研究单调性和凸性．．O12−e xx x x 22ln )ln (−=′。
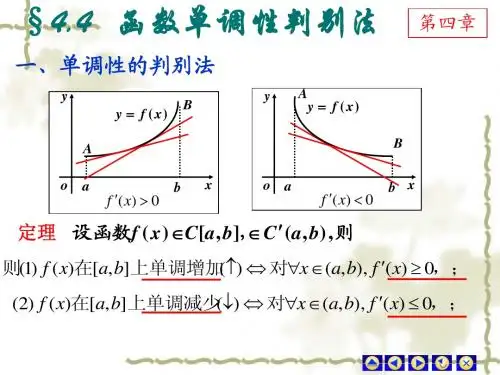
高等数学教学样板教案授课次序09教 学 基 本 指 标教学课题 函数的单调性与凸性的判别方法 课的类型 新知识课 教学方法 讲授教学手段 演示教学重点 掌握函数单调性的判别法、凸性判别方法教学难点利用函数的单调性可以确定某些方程实根的个数和证明不等式教 学 基 本 内 容第九节 函数的单调性与凸性的判别方法一、函数单调性的判别法1、()[,](,),()[,]()()0(0)f x C a b D a b f x a b f x '∈⇒≥≤ 在。
证：不妨设()[,]f x a b 在，00,0()()()lim0,0x x f x x f x f x x x ∆→≥∆>⎧+∆-'=⎨≤∆<∆⎩。
2、函数单调性判别法：设()[,](,)f x C a b D a b ∈ ，那么 ⑴如果(,)x a b ∀∈，有()0f x '>，则()f x 在[,]a b ； ⑵如果(,)x a b ∀∈，有()0f x '<，则()f x 在[,]a b 。
证:),,(,21b a x x ∈∀,21x x <且应用拉氏定理,得)())(()()(211212x x x x f x f x f <<-'=-ξξ,012>-x x ,0)(),(>'x f b a 内，若在,0)(>'ξf 则).()(12x f x f >∴ .],[)(上单调增加在b a x f y =∴,0)(),(<'x f b a 内，若在,0)(<'ξf 则).()(12x f x f <∴.],[)(上单调减少在b a x f y =∴注意：①[,]a b I →，结论仍成立；②,()0(0)x I f x '∈≥≤且只有个别点处()0f x '=，则在I 上()()f x 。
例1、判定sin y x x =-在[0,2]π上的单调性。
备注栏解：在(0,2)π内1cos 0y x '=->，故sin y x x =-在[0,2]π上 。
例2、讨论1x y e x =--的单调性。
解: :(,)D -∞+∞ ，且1x y e '=-。
,)0,(内在-∞,0<'y x y e ∴=-x-1在(,0]-∞ ；,),0(内在+∞,0>'y x y e ∴=-x-1在[0,)+∞ 。
注意:函数的单调性是一个区间上的性质，要用导数在这一区间上的符号来判定，而不能用一点处的导数符号来判别一个区间上的单调性．3、单调区间求法问题；如上例，函数在定义区间上不是单调的，但在各个部分区间上单调。
定义；若函数在其定义域的某个区间内是单调的，则该区间称为函数的单调区间。
关键：导数等于零的点和不可导点，可能是单调区间的分界点.求法：用()0f x '=及()f x '不存在的点来划分()f x 的定义区间，然后判断区间内导数的符号。
例3、32()(25).f x x x =-确定函数的单调区间解:).,(:+∞-∞D 213331010101(),(0)333x f x x x x x--'=-=⋅≠当0x =时，导数不存在；当1x =时，()0f x '=。
用0x =及1x =将(),-∞+∞划分为三部分区间：(,0],[0,1],[1,)-∞+∞。
现将每个部分区间上导数的符号与函数单调性列表如下：x (,0)-∞ 0(0,1)1(1,)+∞()f x ' +不存在-+()f x例4、()cos .f x x x =+判断函数的单调性解:).,(:+∞-∞D ()1sin 0f x x '=-≥，其中等号仅在点2()2x k k Z ππ=+∈处成立，故()f x 在每个区间[2,2(1)]22k k ππππ+++上增加，从而在(,)-∞+∞内增加。
注意：区间内个别点导数为零，不影响区间的单调性。
例5、当0x >时，试证ln(1)x x >+成立。
证；设()ln(1)f x x x =-+，则()1xf x x'=+。
()[0,)(0,)()0,f x C D f x '∈+∞+∞> ，[0,)∴+∞ 在；又(0)0f = ，∴当0x >时，,0)1ln(>+-x x 即ln(1)x x >+。
小结：1、单调性的判别是拉格朗日中值定理的重要应用；2、定理中的区间换成其它有限或无限区间，结论仍然成立；3、应用：利用函数的单调性可以确定某些方程实根的个数和证明不等式。
思考题:若0)0(>'f ，是否能断定)(x f 在原点的充分小的邻域内单调递增？ 练习题1、研究()arctan f x x x =-的单调性。
2、确定2221x x y x -+=-的单调区间。
3、证明下列不等式：若0>x ，则31tan (0)32x x x x π>+<<。
二、函数的凸性及其判别法1、定义：设()()f x C I ∈。
如果对1212,()x x I x x ∀∈≠，对任一(0,1)λ∈，总有1212[(1)](1)()()f x x f x f x λλλλ-+<-+，则称()f x 在I 内是凸的；如果对1212,()x x I x x ∀∈≠，对任一(0,1)λ∈，总有1212[(1)](1)()()f x x f x f x λλλλ-+>-+，则称()f x 在I 内是凹的。
注意：①如果()f x 在I 内是凸（凹）的，则()f x -在I 内是凹（凸）的；②如果()f x 在I 内是凸（凹）的，则()f x 的图形是向下（上）凸的。
2、函数凸性判别法1：设()()f x D I ∈，且导函数()f x '在I 内增加（减少），那么()f x 在I 内是凸（凹）的。
函数凸性判别法2：若x I ∀∈，()0f x ''>，则()f x 在I 内是凸的；若x I ∀∈，()0f x ''<，则()f x 在I 内是凹的。
例1、讨论3y x =的凸性。
解：,32x y =' ,6x y =''当0x <时，0y ''<，3y x ∴=在(,0)-∞内是凹的；当0x >时，,0>''y 3y x ∴=在0,)+∞(内是凸的。
注意：点(0,0)是曲线凹凸的分界点。
3、曲线的拐点及其求法（1）定义：连续曲线()y f x =上凹凸的分界点00(,())x f x 称为曲线的拐点。
注意:①拐点处的切线必在拐点处穿过曲线；②拐点是()f x ''不存在的点或()0f x ''=的点。
（2）拐点的求法：如果)(x f 在),(00δδ+-x x 内存在二阶导数,则点())(,00x f x 是拐点的必要条件是0)(0"=x f 。
例2、32()(25).f x x x =-讨论函数的凸性 解：3101(),(0)3x f x x x-'=⋅≠，从而当0x ≠时，31021();09x f x x x x +''=⋅=当时，导数不存在，二阶导数当然也不存在.当12x =-时，()0f x ''=.于是，0x =与12x =-将函数的定义域11(,),22-∞+∞-∞--∞划分为三个部分区间(],[,0],[0,+).现将每个部分区间上二阶导数的符号与函数的凸性列表表示如下：x 1(,)2-∞- 12-1(,0)2- 0(0,)+∞()f x '' -+不存在 +()f x凹凸凸例3、（1）讨论ln y x =的凸性；（2）,0,01a b λ><<，证明：1(1)a b a b λλλλ-≤-+。
解：（1）211,0y y x x'''==-<，故ln y x =在(0,)+∞是凹的； （2）由ln y x =在(0,)+∞是凹的，故对,0a b ∀>，当a b ≠时，有11ln[(1)](1)ln ln ln ln ln a b a b a b a b λλλλλλλλ---+>-+=+=1(1)a b a b λλλλ--+>当a b =时，“=”成立，故,0,01a b λ><<，1(1)a b a b λλλλ-≤-+。
小结1、函数凹凸性的定义；2、凹凸性的判定；3、曲线改变弯曲方向的点——拐点。
思考题:设)(x f 在),(b a 内二阶可导，且0)(0=''x f ，其中),(0b a x ∈，则,(0x ))(0x f 是否一定为曲线)(x f 的拐点？举例说明。
练习题一、填空题：1、若函数)(x f y =在（b a ,）可导，则曲线)(x f 在(b a ,)内取凹的充要条件是____________.2、曲线上____________的点，称作曲线的拐点.3、曲线)1ln(2x y +=的拐点为__________.4、曲线)1ln(x y +=拐点为_______.二、求函数2sin 4x y x =+的图形的上凸区间与下凸区间。
三、利用函数的凹凸性，证明不等式：22y x yx e e e +>+)(y x ≠。
四、试证明曲线112+-=x x y 有三个拐点位于同一直线上。
五、问a 及b 为何值时，点(1,3)为曲线23bx ax y +=的拐点？。
