当前位置：文档之家 › 人教版初一数学上册第1讲实数及其运算(20210202145128)

人教版初一数学上册第1讲实数及其运算(20210202145128)

  • 格式：docx
  • 大小：157.72 KB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

初一数学(人教版)实数的运算PPT

初一数学(人教版)实数的运算PPT
这四个数中绝对值最大的数对应的点是＿＿＿Q ＿点＿＿＿＿.
M
N
-3
x0
PQ 3y
典型例题
例题 分别写出 6 ，π 3.14 的相反数.
分析：因为根据相反数的意义，
6 6
所以 6 的相反数是 6 .
典型例题
例题 分别写出 6 ，π 3.14 的相反数.
因为 π 3.14 3.14 π
2
先列表再观察求值.
2.5 7 π
2
3
2
0
相反数 2.5 绝对值 2.5
7 7
π 2π
2
3
2
3
2
0 0
反思
复习有理数的 类比 相反数和绝对值
规定实数的相反数和绝对值
通过例题巩固解题方法
加深对实数的认识
再探新知
思考问题 4 ：实数之间可以进行哪些运算？ 在进行实数运算时，有理数的运算法则、运算性质还适用吗？
0.05 6.280.22 1.4
10
所以小重物来回摆动一次所用的时间是 1.4 秒.
用有理数估计无理数大小
解决实际的问题 判断无理数在哪两个 比较实数的大小 相邻整数之间
巩固练习
1. 下列各数中，界于 6 和 7 之间的数是（ B ）.
（A） 25
分析： 25 5.
（B） 43 （C） 58
所以 π3.14 的相反数是 3.14 π .
典型例题 例题 指出 5，1 3 3分别是什么数的相反数.
分析：因为根据相反数的意义，
5 5，
所以 5 是 5 的相反数.
典型例题 例题 指出 5，1 3 3分别是什么数的相反数.
3
3
因为 3 1 1 3

实数完整版课件

实数完整版课件

实数完整版课件一、教学内容1. 实数的定义与分类：有理数和无理数。

2. 实数的性质：实数的加法、减法、乘法、除法运算规则。

3. 实数的运算律：交换律、结合律、分配律。

4. 实数与数的比较：实数的大小比较、实数的绝对值。

二、教学目标1. 让学生掌握实数的定义与分类，理解实数的概念。

2. 让学生掌握实数的性质和运算律，能够熟练进行实数的运算。

3. 培养学生运用实数解决实际问题的能力。

三、教学难点与重点1. 教学难点：实数的分类，特别是无理数的概念。

2. 教学重点：实数的性质，实数的运算律。

四、教具与学具准备1. 教具：黑板、粉笔、多媒体教学设备。

2. 学具：教材、笔记本、文具。

五、教学过程1. 实践情景引入：通过生活实例，如购物时找零钱，引入实数的概念。

2. 知识讲解：讲解实数的定义与分类，重点讲解无理数的概念。

3. 例题讲解：举例子说明实数的性质和运算律的应用。

4. 随堂练习：让学生现场进行实数的运算，巩固所学知识。

5. 板书设计：列出实数的性质和运算律，方便学生记忆。

6. 作业设计：布置有关实数的运算题目，巩固所学知识。

六、作业设计（1）2 + 3 × (4) ÷ 2（2）( 3 )^2 × 3 ÷ ( 6 )（3）√9 √162. 答案：（1）2 + 3 × (4) ÷ 2 = 8（2）( 3 )^2 × 3 ÷ ( 6 ) = 3（3）√9 √16 = 3 4 = 1七、板书设计实数的性质与运算律：性质：1. 加法交换律2. 加法结合律3. 乘法交换律4. 乘法结合律5. 分配律运算律：1. 交换律2. 结合律3. 分配律八、课后反思及拓展延伸本节课通过生活实例引入实数的概念，让学生能够理解实数的重要性。

通过讲解实数的性质和运算律，让学生能够熟练进行实数的运算。

在作业设计中，布置了有关实数的运算题目，让学生能够巩固所学知识。

《讲实数及其运算》课件

《讲实数及其运算》课件

实数与数轴的关系
数轴的定义
数轴是一个直线，它具有正方向、负方向和 原点。每一个实数都可以在数轴上找到一个 与之对应的点。
实数与数轴的关系
实数是数轴上所有点的集合，每一个实数都 可以在数轴上表示出来。反过来，每一个在 数轴上的点也可以表示为一个实数。因此， 实数与数轴之间存在着一一对应的关系。
05
在物理中的应用
测量
热力学
实数在物理中用于表示各种物理量的 测量值，如长度、时间、质量等。物 理量的测量结果通常以实数的形式表 示，并遵循一定的单位制。
在热力学中，温度、压力等物理量可 以用实数表示。通过实数的运算，可 以描述热力学系统的状态变化和热力 学过程。
运动学
在运动学中，物体的位置、速度和加 速度等都是实数。通过实数的运算， 可以描述物体的运动规律，如匀速直 线运动、匀加速运动等。
加法运算
总结词
加法运算的基本性质
详细描述
实数的加法运算满足交换律、结合律和分配律，这些性质有助于简化复杂的加 法运算。
减法运算
总结词
减法运算的特性
详细描述
减法运算可以通过加法转换为加法运算，例如 a - b = a + (-b)。此外，减法运算还有一些重要的特性，如差的 不等式性质和差的商的性质。
实数的表示方法
实数可以用小数、分数、根号等形式表示。小数形式如0.25、1.5等，分数形式 如1/2、3/4等，根号形式如√2、√3等。
实数也可以用数轴上的点来表示。在数轴上，每一个实数都可以找到一个唯一的 点与之对应，反之亦然。这个特性使得实数与数轴上的点形成了一一对应的关系 。
02
实数的运算
实数具有完备性，即实数集在加法、减法、乘法和除法（除 数不为零）下是封闭的，也就是说，任何两个实数的这四种 运算的结果仍为实数。

初中实数ppt课件

初中实数ppt课件
为分数。
实数具有完备性，即实数集在加 法、减法、乘法和除法（除数不
为0）下是封闭的。
实数的分类
有理数
有理数包括整数和分数，其中整 数包括正整数、0和负整数。分数
则可以表示为两个整数的比，如 1/2、2/3等。
无理数
无理数是无法表示为分数的数，常 见的无理数有无限不循环小数，如 π、√2等。
实数的其他分类
实数还可以根据其性质进行分类， 如正数、负数、零、正有理数、负 有理数等。
实数的性质
实数的顺序性
对于任意两个不同的实数a和b，如果 a小于b，那么在它们之间一定存在一 个实数c，使得a小于c且c小于b。
实数的四则运算性质
实数的完备性
实数集在加法、减法、乘法和除法（ 除数不为0）下是封闭的，即任何两 个实数的这四种运算的结果仍然是实 数。
减法运算
总结词
掌握减法运算的基本概念和规则
详细描述
实数的减法可以通过加法来实现，即将减数变为相反数，然后进行加法运算。例如，a - b = a + (-b) 。
乘法运算
总结词
理解乘法运算的基本概念和规则
详细描述
实数的乘法运算需要考虑正负数的特殊情况。例如，正数与正数相乘、负数与负数相乘、正数与负数相乘等。
详细描述
在建筑、工程、机械制造等领域，需要使用实数来表示物体的长度、宽度、高度等参数 。例如，在设计一座桥梁时，需要精确地测量各个部分的长度，并使用实数来表示，以
确保桥梁的安全性和稳定性。
重量测量中的实数应用
总结词
在购买商品时，我们经常需要测量物体 的重量，而实数在重量测量中的应用也 是必不可少的。
值的取值范围。
解决几何问题
在解决与几何图形相关的面积、 体积等问题时，需要比较实数的 大小，以确定相关参数的取值范

人教版初中数学实数第1课时课件(共26张PPT)

人教版初中数学实数第1课时课件(共26张PPT)

2019/2/23
9
教学过程
单击此处编辑母版标题样式 单击此处编辑母版文本样式 第二级 第三级 第四级 第五级
Teaching Process
无理数的诞生
2、探究新知
2019/2/23
10
教学过程
单击此处编辑母版标题样式 单击此处编辑母版文本样式 第二级 第三级 第四级 第五级
Teaching Process
Teaching Process
2、探究新知
2019/2/23
13
教学过程
单击此处编辑母版标题样式
Teaching Process
2、探究新知
有理数
初中阶段对数的认识范围扩充为 单击此处编辑母版文本样式 第二级 新加入 第三级 第四级 第五级
实数
无理数
有理数和无理数统称实数
思考:实数如何分类？
2019/2/23 14
单击此处编辑母版标题样式 单击此处编辑母版文本样式 第二级 第三级 第四级 第五级
单击此处编辑母版标 实 题样式 数（第1课时）
单击此处编辑母版副标题样式
2019/2/23
1
单击此处编辑母版标题样式 单击此处编辑母版文本样式 第二级 第三级 第四级 第五级
2019/2/23
2
教学过程
单击此处编辑母版标题样式 单击此处编辑母版文本样式 第二级 第三级 第四级 第五级
单击此处编辑母版标题样式
Teaching Process
3、运用新知
2单击此处编辑母版文本样式 下列这些数找不到位置，请你帮它找一找
第二级 第三级 第四级 第五级
2019/2/23
有理数集合
无理数集合
17

第1课 实数

第1课 实数

为 整数 ，这种记数法叫做科学记数法.
4.实数的大小比较
（1）利用数轴：
①在数轴上表示两个数的点，右边点表示的数总比左边点表示的数 大 ； ②正数 ＞ 0，负数 ＜ 0；两个负数比较大小，绝对值大的数反而 小 .
（负半轴上距原点越远的数越小）
（2）作差法： 设a、b是任意实数，若a-b>0,则 a＞b ；若a-b=0,则a=b ；若a-b<0,则 a＜b .
（2）相反数：
①代数意义：如果两个数只有 符号 不同，那么我们称其中一 个数是另一个数的相反数.即：实数a的相反数为 -a .
②几何意义：在数轴上，互为相反数的两个数所对应的点 位于 原点 的两旁且到 原点 的距离相等.
（3）绝对值：
实数a的绝对值记作 a
，
a (a≥0 有 | a | Fra bibliotek a(a≤0A
01
例6.（2010山东潍坊）如图，数轴上A、B两点对应的实数分别是1和 3 ,若点 A关于点B的对称点为C点，则点C所对应的实数为（ ）
A. 2 3 1
B.1 3
C. 2 3
D. 2 3 1
拓展提高
1. 将1、2 、3 、6 按右侧方式排列．若规定（m，n）表示第m排从左向右第n个
数，则（5，4）与（15，7）表示的两数之积是
．
1 23 61 2 361 2 3 61 2 3
第1排 第2排 第3排 第4排 第5排
2.如图，A，B，C，D四张卡片上分别写有2，3，5，π 四个实数，从中任取两
7
张卡片．
（1）请列举出所有可能的结果（用字母A，B，C，D表示）；
（2）求取到的两个数都是无理数的概率．
A
B

初中数学精品课件：第一课 实数及其运算

初中数学精品课件：第一课 实数及其运算

A. 51
B. 70 C. 76 D. 81
2.下面每个表格中的四个数都是按相同规律 填写的：
根据此规律确定x的值为
.
3.“梅花朵朵迎春来”，下面四个图形是由小梅花 摆成的一组有规律的图案，按图中规律，第n个 图形中小梅花的个数是 ．
倒数是它本身的数是_-_1__，__1_
平方是它本身的数是_0__，__1 立方是它本身的数是_0__，__1_，_ -1
任何不等于零的数的-p次幂，等于这个数的p 次幂的倒数，即a-p = .(a≠0，p为正整数)
4.实数的运算: 实数的运算顺序是先算 ，再算 ,最
后算 .如果有括号，先算小括号，再算 , 最后算 .
5.实数的大小比较： (1)数轴比较法： (2)差值比较法： (3)作商比较法：
1.在0，2，-3，-1.2中，属于负整数的是( )
平方根是它本身的数是__0___ 立方根是它本身的数是_0_，__1_，-1
算术平方根是它本身的数是_0___，_ 1
把7的平方根和立方根按从小到大的顺序排 列为 ．
②的面积为18 cm2，图③的面积为36 cm2，…，
那么图⑥的面积为 ( )
A．84 cm2
B．90 cm2
C．126 cm2
D．168 cm2
1.如图是由同样大小的棋子按一定的规律组成的， 其中第1个图形有1颗棋子，第2个图形一共有6颗 棋子，第3个图形一共有16颗棋子……则第6个图 形中棋子的个数为 ( )
1.实数的分类 按实数的定义分类：
正整数
整数 零
实数
有理数 无理数
负整数 正分数 分数 负分数 正无理数
负无理数 (1)数轴： 原点，正方向，单位长度
数轴上所有的点与全体实数一一对应

初中数学初一数学上册《实数的运算》教案、教学设计

初中数学初一数学上册《实数的运算》教案、教学设计
1.讲解实数运算的基本概念，如加减乘除，以及实数的优先级和运算顺序。
2.示范实数运算的过程，通过具体的例题，让学生直观地了解实数运算的步骤和技巧。
3.举例讲解实数运算在生活中的应用，使学生认识到实数运算的重要性。
在此过程中，教师注意引导学生积极参与，鼓励他们提出问题，及时解答学生的疑惑，确保学生能够掌握实数运算的基本知识。
初中数学初一数学上册《实数的运算》教案、教学设计
一、教学目标
（一）知识与技能
1.理解实数的概念，掌握实数的分类，包括有理数和无理数，并能准确区分。
2.学会实数的四则运算，包括加减乘除，熟练掌握运算规则，能够正确进行混合运算。
3.能够运用实数运算解决实际问题，提高数学应用能力。
4.理解实数运算的优先级，掌握运算顺序，避免运算错误。
-定期进行小测验，及时了解学生的学习进度和掌握情况，为教学调整提供依据。
-鼓励学生自我评价和同伴评价，培养学生的自我反思能力和批判性思维。
4.教学反馈设想：
-建立良好的师生沟通渠道，及时收集学生的反馈信息，了解他们的学习需求。
-根据学生的反馈调整教学方法和策略，确保教学活动能够满足学生的个性化学习需求。
-注意：此题旨在培养学生的合作能力和团队精神，要求各小组成员积极参与讨论，共同解决问题。
5.反思总结题：要求学生课后对实数运算的学习进行反思总结，撰写学习心得，内容包括学习收获、存在的不足以及改进措施。
-注意：此题旨在帮助学生养成自我反思和总结的好习惯，要求学生认真对待，真实反映自己的学习情况。
教师将根据学生的作业完成情况进行评价和反馈，关注学生的个体差异，鼓励他们在完成作业的过程中积极思考、勇于探索，不断提高实数运算能力。同时，教师要及时发现学生的进步和问题，为下一节课的教学提供参考。

数学人教版七年级上册第一章 数与式(第一节 实数的相关概念)

数学人教版七年级上册第一章 数与式(第一节 实数的相关概念)

第一章数与式第一节实数的相关概念一、教学目标：1．理解实数的有关概念，掌握实数的运算性质，知道实数自身的体系分类；理解数轴、相反数、绝对值等概念，了解数的绝对值的几何意义，掌握科学记数法。

2.强化基本运算，培养数感，形成理性的思维．3.培养计算策略的选择和能力的提高．加强建立数学模型解题的能力．二、教学重难点重点:会求一个数的绝对值、倒数、相反数；注意近似数与有效数字的选取方法以及科学计数法的表示方法。

难点：实数运算性质的掌握与灵活应用三、学情分析掌握实数的运算性质，知道实数自身的体系分类；理解数轴、相反数、绝对值等概念，了解数的绝对值的几何意义，掌握科学记数法。

强化基本运算，培养数感，形成理性的思维。

四、教学手段及运用多媒体课件。

运用多媒体课件让学生更容易观察理解五、教学方法运用复习知识，教师讲解；学生练习。

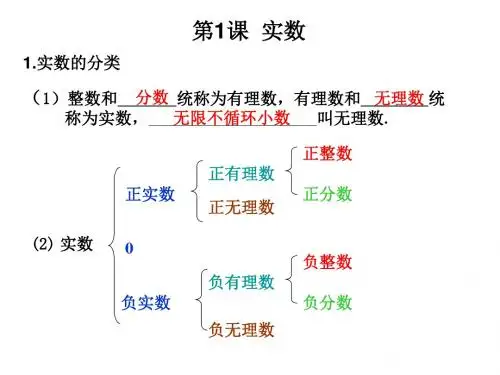
六、教学过程（一）知识复习考点一实数及其分类1. 有理数：①______和②______统称为有理数.2. 无理数：无限③_________小数叫做无理数.失分点1 无理数的判定判定一个数是不是无理数关键在于不同形式表示的数最终结果是不是无限不循环小数.在判定无理数时应注意：（1）用根号表示的数不一定就是无理数，如④_____、⑤______等；（2）用三角函数符号表示的数也不一定就是无理数，如⑥______、⑦______等；（3）最终结果含有π的数是无理数；（4）有规律的无限不循环小数是无理数，如：0.1010010001…（两个1之间依次增加一个0）（2）按正负分类实数可分为正实数，0，负实数.0既不是正数，也不是负数.正负数可用于表示相反意义的量.【归纳总结】“盈”与“亏”，“胜”与“负”，“增加”与“减少”，“收入”与“支出”，“赢”与“输”，“向上”与“向下”等均是具有相反意义的词.考点二数轴、相反数、倒数、绝对值（高频考点）1. 数轴：规定了原点、正方向和单位长度的直线叫做数轴；实数和数轴上的点是一一对应的.2. 相反数（1）只有______不同的两个数叫做互为相反数，即a和-a互为相反数,特别地，0的相反数是0.（2）实数a、b互为相反数a+b＝____.考点三科学记数法（高频考点）1.科学记数法：把一个大于10的数表示成____.的形式（其中1≤a＜10，n是正整数），其中n的值等于原数的整数位数减1.2. 近似数和精确度近似数：对于一个实际数所取的近似值.精确度：近似数与准确数的接近程度，一个近似数四舍五入到哪一位就说这个近似数精确到哪一位.如：3.1是精确到0.1或叫做精确到十分位.（二）‘例题讲解【归纳总结】1. 求一个数的相反数，直接在这个数的前面加上负号，并化简；2. 非零整数a的倒数为，0没有倒数,分数的倒数为；3. 非负数的绝对值是它本身，负数的绝对值是它的相反数.类型二科学记数法例2 （’14白银）节约是一种美德，节约是一种智慧，据不完全统计，全国每年浪费食物总量折合粮食可养活约3亿5千万人.350000000用科学记数法表示为( )A. 3.5×107B. 3.5×108C. 3.5×109D. 3.5×1010【解析】将一个较大数表示成a×10n的形式，其中1≤a＜10，故a＝3.5;n的值等于原数的整数位数减1,因为原数为一个9位数，所以n＝9-1=8，因此350000000=3.5×108.【备考指导】将一个数用科学记数法表示成a×10n的形式时，需要从下面两个方面入手：（1）确定a和n的值：①确定a：a是只有一位整数的数，即1≤a＜10；②确定n：当原数≥10时，n等于原数的整数位数减1，或等于原数变为a时小数点移动的位数；当0＜原数＜1时，n是负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位数的零）或等于原数变为a时小数点移动的位数.（2）对于含有计数单位并需转换单位的科学记数法，可以利用1亿＝1×108，1万＝1×104，1千＝1×103来表示，能提高解题的效率.拓展变式（’14盐城)2014年5月，中俄两国签署了供气购销合同，从2018年起，俄罗斯开始向我国供气最终达到每年380亿立方米，380亿这个数据用科学记数法表示为（）A. 3.8×109B. 3.8×1010C. 3.8×1011D. 3.8×1012（三）、练习p 1-3题（四）、作业：练习本第一页（五）、反思：通过本节学生掌握了实数的运算性质，会求一个数的绝对值、倒数、相反数，掌握科学计数法的表示。

人教版(五四学制)七年级上册数学—1实数课件

人教版(五四学制)七年级上册数学—1实数课件

相关知识： 正方形的面积＝边长之积＝对角线之积的一半
A
D
单位正方形（边长为1的正方形）
B
C
在数轴上找到 2
A
D
B
C
在数轴上作出 5的对应点
2
1 -1 0
1 25 3
一个实数a
-2 -1 0
1A 2
如果将所有的有理数都标到数轴上，那 么数轴将被填满吗？
如果再将所有的无理数都标到数轴上， 那么数轴被填满了吗？
总结：数轴上的任一点必定表示一个实 数；反过来，每一个实数（有理数或无理数） 也都可以用数轴上的一个点来表示。
即：实数与数轴上的点一一对应
让你的思维动起来
想一想：4 是有理数还是无理数？
判断： 带有根号的数一定是无理数（ × ） 无理数一定含有根号（ × ） 无限小数一定是无理数（ × ）
无理数的绝对值一定是无理数 （ √ ）
实数
它们是正确的吗？
1.-4是16的平方根； 2.16的平方根是4与-4； 3.平方根等于本身的数1，0； 4.算术平方根等于本身的数是1； 5.3的算术平方根记作 3 。
视察下图，每个小正方形的边长均是1， 我们可以得到小正方形的面积1， (1)图中阴影正方形的面积是多少？
它的边长是多少？ 2
3
3
；
4绝对值等于 6的数是 6 .
5.一个数的绝对值是π，这个数是 ；
6. 2 3的相反数是 3 2 ;
7. 3.14 3.14 ;
小结
（1）知道实数与数轴上的点一一对应， 能将实数表示在数轴上； （2）相反数、绝对值、数的大小比较法 则同样适用于实数。
随堂练习
比较下列各组里两个数的大小。
49 , 8.131,

第1讲 实数及其运算(可编辑ppt)

第1讲 实数及其运算(可编辑ppt)

变式6-1 若()-(-2)=3,则括号内的数是 ( B ) A.-1 B.1 C.5 D.-5
解析 1-(-2)=3,故选B.
变式6-2 (2)2 .
计算:
1 2
2
-|-
3+2|+(
2 -1.414)0-3tan 30°-
解析
原式=4-(2-
3
)+1-3×
3-2=4-2+
3
3 +1-
3 -2=1.
栏目索引
第1讲 实数及其运算
总纲目录
泰安考情分析 基础知识过关 泰安考点聚焦 随堂巩固练习
总纲目录
栏目索引
泰安考情分析
泰安考情分析 栏目索引
基础知识过关 栏目索引
基础知识过关
知识点一 实数及其分类 知识点二 实数的相关概念及性质 知识点三 实数的大小比较 知识点四 实数的混合运算 知识点五 科学记数法与近似数
借助数轴进行比较;(2)若一组数中含有带根号的无理数,一般可
采用平方法进行比较;(3)若一组数中含有π,一般采用取近似值法
进行比较.
泰安考点聚焦 栏目索引
考点四 科学记数法
中考解题指导 涉及科学记数法的题有两类:一是将一个数用科 学记数法表示;二是将用科学记数法表示的数还原. 例5 (2018泰安)一个铁原子的质量是0.000 000 000 000 000 000 000 000 093 kg,将这个数用科学记数法表示为
9.3×10-26 .
泰安考点聚焦 栏目索引
变式5-1 (2017泰安)“2014年至2016年,中国同‘一带一路’沿 线国家贸易总额超过3万亿美元”.将3万亿用科学记数法表示为
( C) A.3×1014 B.3×1013 C.3×1012 D.3×1011

实数ppt课件人教版

实数ppt课件人教版

实数与复数的关系和转换
实数与复数的关系
实数是特殊的复数，即虚部为0的复数。实 数在复数域中占据了原点附近的区域。
实数与复数的转换
在数学表达上，任何实数都可以视为复数， 只需将其虚部设为0即可。同样地，任何复 数也可以视为实数的扩展，只需将其虚部消 去即可。
THANKS FOR WATCHING
感谢您的观看
绝对值和符号
根据实数的绝对值大小和正负符号，可以将实数分为正数、负数、零和绝对值相 等但符号不同的数等。
03 实数的运算
加法运算
总结词
加法运算的基本性质
详细描述
实数的加法运算满足交换律和结合律，即a+b=b+a和(a+b)+c=a+(b+c)。加法运算还有负数和零的加法性质， 即a+(-a)=0和a+0=a。
过极限来描述。
实数的收敛性和极限理论是数学 分析的基础，它们在解决各种数
学问题中发挥着重要的作用。
实数的其他性质和定理
实数具有完备性，这意味着实数集合 具有一些特殊的性质，使得实数集合 在加法、减法、乘法和除法等运算下 是封闭的。
实数还具有一些其他的性质和定理， 例如实数的有序性、阿基米德性质等 等，这些性质和定理在数学分析和实 数理论中有着广泛的应用。
实数的表示方法
十进制表示法
实数可以用小数或分数形式表示，如 2.5、1/3等。
分数形式表示法
实数可以用分数形式表示，如2/3、 3/4等。
实数的性质和运算，可以确定任意两个实数之间
的大小关系。
实数的四则运算
实数可以进行加、减、乘、除四 则运算，运算规则与有理数相同
实数ppt课件人教版

实数及其运算课件

实数及其运算课件

乘法与除法
总结词
实数之间的乘法和除法运算也是基本的运算，它们同样具有一些共同的性质和法则。
详细描述
实数之间的乘法和除法运算与有理数的运算类似，但也有一些不同。例如，乘法和除法运算的结果不一定是有限 的，还有可能是无穷大或无穷小。此外，实数之间的乘法和除法运算还具有一些特殊的性质，如乘法分配律和乘 法结合律等。
实数的减法运算及应用
总结词
实数的减法运算是加法的逆运算，其实质是 求两个数的差的运算。
详细描述
实数的减法运算可以用以下形式表示：cd=e，其中c和d是任意两个实数，e是它们 的差。减法运算的交换律和结合律与有理数 的减法运算相同。减法运算的结果是一个实 数，它可以表示为数轴上的一点。实数的减 法运算在几何上可以用来表示旋转和平移变 换的合成变换。
应用
开方运算可以用于求解实际问题，例如求解面积、体积等问 题，以及在科学、工程、经济等领域中的各种计算问题。
开方运算的实例及解析
实例1
求81的平方根。
解析
81的平方根是±9，因为9的平 方等于81。
实例2
求256的立方根。
解析
256的立方根是4，因为4的立 方等于256。
THANK YOU
感谢聆听
和平移变换的合成变换的逆变换。
05
实数的幂运算及应用
幂运算的定义及公式
幂运算的定义
幂运算是一种关于幂的数学运算， 幂可以理解为乘方的结果。
幂运算的公式
幂运算的公式包括乘方、开方、 平方等。
幂运算的性质及应用
幂运算的性质
幂运算具有结合律、分配律、交换律 等性质。
幂运算的应用
幂运算在数学、物理、工程等领域都 有广泛的应用。

《初中数学实数》课件

《初中数学实数》课件
总结词
理解实数减法在数学中的重要性和应用，能够运用实数减 法解决实际问题。
详细描述
实数减法在数学中有广泛的应用，如计算差值、速度、加 速度等。通过掌握实数减法的运算法则和性质，可以更好 地解决实际问题。
实数的乘法运算
总结词
理解实数乘法的意义和性质，掌握实数乘法的运算法则 。
详细描述
实数的乘法运算与普通乘法运算类似，但需要考虑正负 数相乘的情况。实数乘法的意义是表示两个数在数轴上 的倍数关系，具有结合律和交换律。
实数的开方运算
04
平方根的定义和性质
平方根的定义
如果一个数的平方等于a，那么这个数就是a的平方根。例如，4的平方根是±2 。
平方根的性质
一个正数的平方根有两个值，一个正数和一个负数；0的平方根是0；负数没有 实数平方根。
立方根的定义和性质
立方根的定义
如果一个数的立方等于a，那么这个 数就是a的立方根。例如，8的立方 根是2。
无限性也是数学和物理学中许 多重要概念的基础，如无穷大 、无穷小等。
实数的运算
03
实数的加法运算
总结词
理解实数加法的意义和性质，掌握实数加法的运算法则 。
详细描述
实数的加法运算与普通加法运算类似，但需要考虑正负 数相加的情况。实数加法的意义是表示两个数在数轴上 的位移，具有结合律和交换律。
总结词
01
02
03
长度测量
实数可以用来表示物体的 长度，例如身高、体重等 。
时间计算
用实数表示时间，例如秒 、分、小时等。
货ห้องสมุดไป่ตู้计算
用实数表示货币，例如元 、角、分等。
实数在数学中的运用
代数运算
实数可以用于代数运算， 例如加、减、乘、除等。

人教版七年级数学课件-实数

人教版七年级数学课件-实数
110, 12.91, 12.96, 0, －52 1.1,
122.5, 182.5,
＋75, 305,
18, －7.5, ＋10.
110 12.91
12.96
0
－52 1. 1
+75
122.5
182.5
305
18
－7.5 +10
2
你沒忘吧?
110, 12.91, 12.96, 0, －52 1.1, 122.5, 182.5, ＋75, 305, 18, －7.5, ＋10.
1.在以上各數中, 是我們以前學過的什麼數?
2.什麼是有理數?他可以分哪幾類?
有理數
整數 分數
正整數
0 負整數 正分數
負分數
正有理數 正整數 有理數 0 正分數
負有理數 負整數 負分數
使用計數器計算,把下列各數寫成小數的形式， 你有什麼發現？
3, 3 , 47 , 9 , 11 , 5 5 8 11 90 9
有理數集合
無理數集合
9
探究實數的分類(一)
由上可知: 1.實數可分為哪兩類數? 2.有理數可分為哪幾類? 3.無理數可分為哪幾類?
正有理數
有理數
實數
無理數
零 負有理數 正無理數 負無理數
實無有數理理數數
正負有有零有理理理數數數
負正無無無理理理數數數
正有理數 零
負有理數 正無理數 負無理數
10
依據實數的分類 （一）示意圖,在右 圖的卡片上填上下 列數的名稱.你發 現實數的分類示意 圖與這棵樹枝幹的 形狀有哪些聯繫嗎?
2
3
—2 — 3
7
你能舉出一些無理數嗎？
例如：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017年中考数学第一轮复习______________ —马寨中心学校九年级数学备课组
第一章教与式
第1节实数及其运算（2）
1・（2014-安徽）（-2）X3的结果是（）
A・—5 B・1 C・—6 D・6
2• （2015•安徽）在一4, 2, -1, 3这四个数中，比一2小的数是（）A • —4 B.2 C.—1 D・ 3
3• （2016-安徽）一2的绝对值是（）
A ・—2 B.2 C・ ±2 D・ 2
赵三年中考）
4.（2016安徽中考）2016年3月份我省农产品实现出口额8362万美元•其中
8362万用科学计数法表示为()
A. 8.362 X107
B. 83.62 X106
C. 0.8362 X IO10
D. 8.362 X108
5. （2015安徽中考）3・移动互联网已经全面进入人们的日常生活.截止
2015年3月，全国4G用户总数达到1・62亿，其中1・62亿用科学记数法表示为（）
B. 1.62X106
C. 1.62X108 D・ 0.162X1()9
A. 1.62X10°
6・（2015安徽中考）一64的立方根是
7 -（2014-安徽）据报载，2014年我国将发展固定宽带接入新用户25000000
户‘其中25000000用科学记数法表示为____ ・
考点»实数的分类
【例1】（2014•合肥模拟）实数71，芥0，T 中，无理数是（）
A ・〃 B.| C・ 0 D・—1
【点评】判断一个数是不是无理数，关键就看它能否写成无限不循环小数，初中常见的无理数共分三种类型：⑴化简后含〃（圆周率）的式子；（2）含根号且开不尽方的数；（3）有规律但不循环的无限小数.掌握常见无理数类型有助于识别无理数.
対应训练即时巩固举一反三
1• (1)下列各数中，3.14159 ，-^8 ，
0.131131113...，-77，迈5, — *无理数的个数有(B )
A • 1个 B. 2个 C. 3个 D. 4个
(2)下列各数中，为负数的是(B)
A • 0 B. -2 C. 1 D#
实数的运算
【例2】（2014蓮庆）计算: 羽+(—考点》
3)2—2014°X I—41+(*)一1
解：原式=2+9—1 X4+6=11—4+6=13
［点评］实数运算要严格按照法则进行，特别是混合运算'注意符号和顺序是非常重要的■
对应训练耶哥元了皋二反三二:
3
2- （2014-东营）计算：（―l）2°】4+（s加30。

）
-】+（芥疋
解：原式=7 +2+7 —3边+3—1 —6—3边
考点少科学记数法与近似值
（1）（2014 •资阳）餐桌边的一蔬一饭，舌尖【例3】
上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心.据统计，中国每年浪费的食物总量折合粮食约500亿千克，这个数据用科学记数法表示为（A ）
A • 5X10】。

千克 B. 50X109千克
C • 5X109千克 D. 0.5X10H千克
⑵下列近似数中精确到千位的是(C )
A - 90200 B. 3.450X102
C • 3.4X104 D. 3.4X102
【点评］(1)科学记数法一般表示的数较大或很
小'所以解题时一定要仔细；(2)科学记数法写岀这个数后可还原成原数进行检验•
对应训练 P卩讦花釦皋二瓦三
3• (1)近似数2.5万精确到千位.
(2)(2014 •内江)一种微粒的半径是0.00004米，这个数据用科学记数法表示为(C )
A • 4X106 B. 4X10—6
C • 4X10T D. 4X105
考点沙与实数相关的概念
【例4】(1)(2014 •河北)—2是2的(B)
A •倒数B.相反数C.绝对值D.平方根
(2)已知\a\ = l，⑹=2，lcl=3，且a>b>c，那么a+b—c—
2或0 .
【点评】⑴互为相反数的两个数和为0 ； (2)正数的
绝对值是它本身'负数的绝对值是它的相反数'0的绝对值是0 ；(3)两个非负数的和为0，则这两个数分别等于0.
对应训练…环時元鹵•皋二瓦三：：
4・（1）（2012-凉山）若x是2的相反数，lyl = 3 ，则x—y的
A • -5 B. 1 C.—1 或5 D
（2）计算:
1 L 1 L 一（-旷亠_；1—孑=
丄
（4）--1；（-計=-2
—■
值是
（D）
.1 或—5
A • a~2.5 C • a+2.5B. 2.5—a D. ~a~2.5
考点身数轴—
【例5】实数a在数轴上的位置如图，则la—2.51 =(B )
--------- 1 ------- 1--------------- 1------------------------ ►
0 a 2.5
［点评］数形结合借助数轴找到数的位置,或由数找到在数轴上的点的位置及其相反数的位置『再根据数轴上右边的数大于左边的数，确定各数的大小或根据大减小为正Z 小减大为负Z以及有理数的加法、乘法法则来确定数的运算后的符号.
对应训练…帝哥元鹵•菇二瓦
三
5.（2014 •呼和浩特）实数a，b，c在数轴上对应的点如下图所示，则下列式子中正确的是（D）
•• ••・
a bo c兀
A • ac>bc B. \a—b\=a~b
C • —a<—b<c D. —a—c>—b—c
考点窃实数的大小比较
【例6] ⑴（2014•绍兴）比较一3，1，—2的大小，下列判断正确的是(A )
A - -3<—2<1 B. -2<-3<1
C • 1<-2<-3 D. 1<-3<-2
(2)(2014•河北)a，b是两个连续整数，若a<V7<b，则a，
b分别是(A)
【点评】实数的大小比较要依据数值特点来灵活运用比较大小的几种方法来进行.
对应训练… P卩時况鹵專二皮三］
6 • (1)(2014•珠海)比较大小：一2 N -3.
(2)比较2.5，-3，"的大小，正确的是(A)
A • -3<2.5<A/7 B. 2.5V—3V曲C • -3<^7<2.5 D.A/7<2.5<-3
丄学法籍导〉
数形结合思想
数形结合思想是指将数（量）与（图）形结合起来进行分直观;形无数，难入微.”数形结合思想可以使问题化难为易、化繁为简•
析、研究、解决问题的一种思想策略•〃数无形，少分类讨论思想
分类讨论思想是“化整为零，各个击破，再积零为整”的数学策略,分类注意按一定的标准进行;分类既不能遗漏'也不能交叉重复•
学出福导~
化归思想
化归也称转化,是指将未知的、陌生的、复杂的问题通过演绎归纳转化为已知的、熟悉的、简单的
问题，从而使问题顺利解决的数学思想，关键是确
定合理、可行的转化目标，掌握基本的方法步骤•
丄学出福导〉
五种大小比较方法实数的大小比较常用以下五种方法：
(1)数轴比较法：将两数表示在数轴上，右边的点表示的数总比左边的点表示的数大•
(2)代数比较法:正数大于零；负数小于零；
正数大于一切负数；两个负数'绝对值大的数
反而小•
学出福导~
⑶差值比较法：设0，b是两个任意实数，则：°> 0 =>a > b } a - b = 0=>a = b；a - b < 0=>a < b・
(4)倒数比较法:若〉*，d>0，b>0，则ovb.
(5)平方比较法:V由a > b > 0可得也 > 边，.•.可以把远与观的大小问题转化成比较Q和b的大小问题.。