2018南航材料力学答案-916

材料力学课后答案第一章材料单向静拉伸载荷下的力学性能一、解释下列名词滞弹性：在外加载荷作用下，应变落后于应力现彖。

静力韧度：材料在静拉仲时单位体积材科从变形到断裂所消耗的功。

弹性极限：试样加载后再卸裁，以不出现残留的永久变形为标准，材料能够完全弹性恢复的最高应力。

比例极限：应力一应变曲线上符合线性关系的最高应力。

包中格效应:指原先经过少量塑性变形，卸载后同向加载，弹性极限（。

P）或屈服强度（。

S）增加；反向加载时弹性极限（。

P）或屈服强度3 s）降低的现象。

解理断裂:沿一定的晶体学平面产生的快速穿晶断裂。

晶体学平面一一解理面，一般是低指数，表面能低的晶面。

解理而:在解理断裂屮具冇低指数，表而能低的品体淫平而。

韧脆转变：材料力学性能从韧性状态转变到脆性状态的现象（冲击吸收功明显下降，断裂机理由微孔聚集型转变微穿晶断裂，断口特征出纤维状转变为结晶状）。

静力韧度：材料在静拉伸时单位体积材料从变形到断裂所消耗的功叫做静力韧度。

是一个强度与塑性的综合指标，是表示静载下材料强度与塑性的最佳配合。

二、金属的弹性模量主要取决于什么？为什么说它是一个对结构不敏感的力学姓能？答案：金屈的弹性模量主要取决于金屈键的本性和原子间的结合力，而材料的成分和组织对它的影响不大，所以说它是一个对组织不皱感的性能指标，这是弹性模量在性能上的主要特点。

改变材料的成分和组织会对材料的强度（如屈服强度、抗拉强度）有显著影响，但对材料的刚度影响不大。

三、什么是包辛格效应，如何解释，它冇什么实际意义？答案：包辛格效应就是指原先经过变形，然后在反向加载时弹性极限或屈服强度降低的现象。

特别是弹性极限在反向加载时几乎下降到零，这说明在反向加载吋犁性变形立即开始了。

包辛格效应可以用位错理论解释。

第一，在原先加载变形时，位错源在滑移而上产生的位错遇到障碍，塞积后便产生了背应力，这背应力反作用于位错源，当背应力（取决于塞积时产生的应力集中）足够大时，可使位错源停止开动。

一、填空题：请将正确答案写在划线内 每空1分，计16分 ⒈ 工程构件正常工作的条件是 ――――――――――――、、――――――――――――、―――――――――――――。

⒉ 工程上将延伸律------- δ的材料称为脆性材料。

⒊ 矩形截面梁横截面上最大剪应力max τ出现在―――――――――――各点，其值=τmax -------------。

4．平面弯曲梁的q 、F s 、M 微分关系的表达式分别为--------------、、-------------、、 ----------------。

5．四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、 ――――――――――――――、―――――――――――――――――――――――――――――――――。

6．用主应力表示的广义虎克定律为 ――――――――――――――――――――― ；――――――――――――――――――――――；－―――――――――――――――――――――――。

二、单项选择题⒈ 没有明显屈服平台的塑性材料，其破坏应力取材料的――――――――――――。

⑴ 比例极限p σ； ⑵ 名义屈服极限2.0σ； ⑶ 强度极限b σ； ⑷ 根据需要确定。

２． 矩形截面的核心形状为----------------------------------------------。

⑴ 矩形； ⑵ 菱形； ⑶ 正方形； ⑷三角形。

3． 杆件的刚度是指――――――――――――――－。

⑴ 杆件的软硬程度； ⑵ 杆件的承载能力； ⑶ 杆件对弯曲变形的抵抗能力； ⑷ 杆件对弹性变形的抵抗能力；4. 图示二向应力单元体，如剪应力改变方向，则―――――――――――――。

⑴ 主应力的大小和主平面的方位都将改变；⑵ 主应力的大小和主平面的方位都不会改变； ⑶ 主应力的大小不变，主平面的方位改变； ⑷ 主应力的大小改变，主平面的方位不变。

由平衡方程，解得：
FBy 5KN; M B 13KN m
微分法画弯矩图
( M B 13KN m; M C M C 3KN m; M D 0)
2.根据强度要求确定 b
max WZ 2 bh 2 3 WZ b 6 3 M
弯矩图
M
（+）
x
3.绘制挠曲轴略图并计算wmax， A , B 令 dw 0 得 x l (0 x l ) 2 dx 所以 wmax w x l
2
挠曲轴略图
w
5ql 4 384 EI
x0
（-）
B
ql 3 24 EI
x
由式（3）知 A
max
M max ymax 176MPa IZ
max
M WZ
K
M max yK 132MPa IZ
3
5-5.图示简支梁，由 NO18 工字钢制成，在集度为q的均匀载荷作用下测得横截 4 面C底边的纵向正应变 =3.0 10 ，试计算梁内的最大弯曲正应力，已知刚的弹 FAy FBy 性模量E=200GPa，a=1m。
M yA Wy 6 M yA M zA 6M zA Wz 2b b 2 b (2b) 2
由 max 解得 b 35.6mm 故
h 2b 71.2mm
14
2.截面为圆形，确定d 由分析图及叠加原理可知： 在1,3区边缘某点分别有最大拉应力，最大压应力 其值均为：
I Z I Z 1 2 I Z 2 1.02 104 m4
2.画弯矩图 由平衡方程得 微分法画弯矩图
FCy 10KN; M C 10KN m

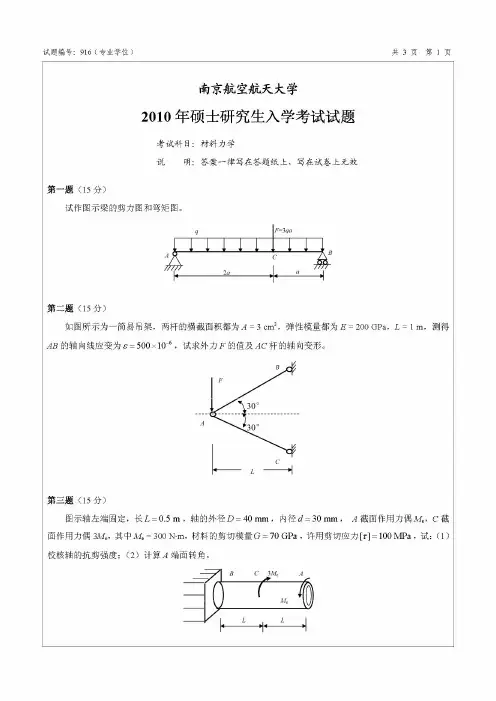
南京航空航天大学2011年硕士研究生入学考试初试试题 A卷 科目代码: 916满分: 150 分科目名称: 材料力学（专业学位）注意: ①认真阅读答题纸上的注意事项；②所有答案必须写在答题纸上，写在本试题纸或草稿纸上均无效；③本试题纸须随答题纸一起装入试题袋中交回！1．承受单向拉伸应力σx的单元体，初始体积为V。

材料的弹性模量为E，泊松系数为ν，求应力引起的体积变化。

（15分）2．一端固支一端自由的受扭圆截面杆，直径为D，杆长为L，材料的弹性模量为E，剪切弹性模量为G，泊松系数为ν，承受未知大小的外力偶矩T作用。

两端面产生了相对扭转角φ。

求（1）杆内最大切应力；（2）杆内最大线应变。

（15分）3．求图示梁的约束反力，作梁的剪力图和弯矩图。

（15分）4 矩形截面梁高h=80mm ，宽b=30mm 。

在梁的B 处联接拉杆BC ，其直径d=20mm ， 梁和杆的许用应力均为［σ］=160MPa ，试求许可载荷q 。

（15分）5. 根据图示点的应力情况，求该点的主应力和最大剪应力。

（15分）6．图示薄壁圆筒的壁厚为δ，平均直径为D ，材料的弹性模量为E ，泊松比为ν，承受内压强p 和轴向拉力F 作用。

试求其外表面周向应变t ε与轴向应变m ε。

（15分）7． 图示重量为P 的物体自由落下冲击于梁上C 点，试求：当梁内最大动应力、静应力之比max st max d /σσ= 4时的h 值。

（15分）C P B 2l /3A EIh l /38． 设有一托架如图所示，在横杆端点D 处受到一力20 kN F =的作用。

已知斜撑杆AB 两端为柱形约束(柱形铰销钉垂直于托架平面)，其截面为环形，外径45 mm D =，内径36 mm d =，材料的弹性模量200 GPa E =，比例极限p 200 MPa σ=。

若杆的稳定安全因数st []2n =，试校核杆AB 的稳定性。

（15分）9． 图示悬臂梁ABC 由AB 段和BC 段在B 处焊接而成，A 端固支，受均布载荷q 作用。

题 2.39 图
第二章 拉伸、压缩与剪切
学号（
） 姓名（mm的两快盖板相联接。各零件材料相同，许用应力均为 [ σ ]=80MPa，[τ ]=60MPa，[ σ bs]=160MPa。若拉杆的厚度t =15mm，拉力P =120kN，试设 计螺栓直径d及拉杆宽度b。
△R R
题 1.12 图
.
第二章 拉伸、压缩与剪切
学号（
） 姓名（
）4
第二章 拉伸、压缩与剪切
一、是非题
2.1 使杆件产生轴向拉压变形的外力必须是一对沿杆件轴线的集中力。
（）
2.2 轴力越大，杆件越容易被拉断，因此轴力的大小可以用来判断杆件的强度。 （ ）
2.3 内力是指物体受力后其内部产生的相互作用力。
（）
2.15 变形与位移关系描述正确的是（ ）
A. 变形是绝对的，位移是相对的
B. 变形是相对的，位移是绝对的
C. 两者都是绝对的
D. 两者都是相对的
2.16 轴向拉压中的平面假设适用于（ ）
A. 整根杆件长度的各处
B. 除杆件两端外的各处
C. 距杆件加力端稍远的各处
2.17 变截面杆如图，设F1、F2、F3分别表示杆件中截面 1-1、2-2、3-3 上的内力，则下
A
B
l
题 1.10 图
第一章 绪论
学号（
） 姓名（
）3
1.11 图示三角形薄板因受外力作用而变形，角点 B 垂直向上的位移为 0.03mm，但 AB 和 BC 仍保持为直线。试求沿 OB 的平均应变，并求 AB，BC 两边在 B 点的角度改变。
B
45º
45º
A
O
C
240
题 1.11 图

北京航空航天大学2017－2018 学年 第二学期期末《 材 料 力 学 A 》考试A 卷班 级______________学 号 _________姓 名______________成 绩 _________2018年06月25 日班号 学号 姓名 成绩《材料力学A 》期末考试试卷一、单项选择题（每题3分，共15分）1．根据圆轴扭转时的平面假设，可以认为圆轴扭转时横截面 A 。

A ．形状尺寸不变，直径线仍为直线；B ．形状尺寸改变，直径线仍为直线；C ．形状尺寸不变，直径线不保持直线；D ．形状尺寸改变，直径线不保持直线。

2．下列四种截面直梁，材料相同，横截面积相等，在xy 面内弯曲（x 轴沿梁轴线），从强度设计考虑，图 D 截面梁能承受的弯矩最大。

（A ） （B ） （C ）题一2图3. 图示低碳钢工字形截面悬臂梁，自由端承受集中力F ， a 点位于腹板与翼缘交界处、b 点为截面形心。

下列说法正确的是 B 。

A. 应采用第一强度理论校核a 点强度；B. 应采用第三或第四强度理论校核a 点强度；C. 应采用第一或第二强度理论校核b 点强度；D. 应采用第二或第三强度理论校核b 点强度。

题一3图F4. 梁的截面为如图放置 T 字形，z 轴通过横截面的形心，弯矩图如图所示，B 截面和C 截面的弯矩大小相等，则有 C 。

A. 最大拉应力和最大压应力位于同一截面B ；B. 最大拉应力位于截面B ，最大压应力位于截面C ；C. 最大拉应力位于截面C ，最大压应力位于截面B ；D. 最大拉应力和最大压应力位于同一截面C 。

题一4图5．如题一5图（1）和（2）所示微体，均处于平面应力状态，设z 是z 轴的方向应变，则 D 。

A ．两微体z 均等于零；B ．两微体z 均小于零；C ．两微体z 均大于零；D ．微体（1）z 小于零，微体（2）z 等于零；E ．微体（1）z 等于零，微体（2）z 小于零。

题一5图x(2)(1)x二、填空题（每空2分，共20分）1．为保证构件正常或安全工作，构件应具备足够的 强度 （即抵抗破坏的能力）、足够的刚度（即抵抗 变形 的能力）、足够的 稳定性 （即保持原有平衡形式的能力）。

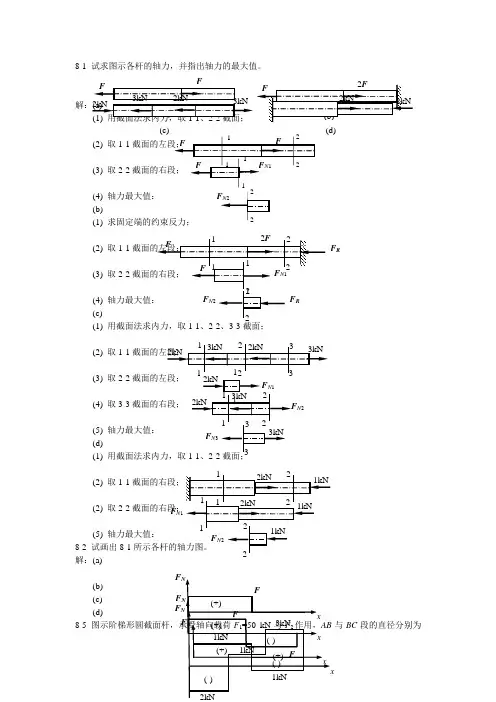
8-1 试求图示各杆的轴力，并指出轴力的最大值。

(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。

解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。

解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。

解：(1) 对节点A(2) 列平衡方程 解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。

解：(1) 对节点A (2) 84 mm 。

8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。

8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形 解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。

由切应力互等定理可知，纵截面上的切应力 τ x 与 τ 2max 一样大。 左、右端面上弯曲正应力构成的轴向合力分别为
Fx1 =
bh Fa 1 σ1max ( ) = 2 2 2h bh Fa 1 Fx 2 = σ 2max ( ) = h 2 2
左、右端面上弯曲切应力构成的竖向合力大小相等，其值为
(也可用左侧题号书签直接查找题目与解)
6-3
图示带传动装置，胶带的横截面为梯形，截面形心至上、下边缘的距离分别为
y1 与 y2，材料的弹性模量为 E。试求胶带内的最大弯曲拉应力与最大弯曲压应力。
题 6-3 图 解：由题图可见，胶带中性层的最小曲率半径为
ρmin = R1
依据
σ=
Ey ρ
可得胶带内的最大弯曲拉应力和最大弯曲压应力分别为
Fy 1 = F y 2 =
1ห้องสมุดไป่ตู้F 6
Fa 2h
顺便指出，纵截面上弯曲切应力构成的轴向合力为
FSx = τ x ( ab) =
3．检查单元体的平衡方程是否满足
∑F ∑F
x
= 0，Fx 2 − Fx1 − FSx = = 0，Fy1 − Fy 2
y
Fa Fa Fa − − =0 h 2 h 2h F F = − =0 6 6
题 6-10 图 解：1.查№18 工字钢的有关数据 工字钢截面大致形状及尺寸符号示如图 6-10。
图 6-10 由附录 F 表 4 查得
h = 180mm，b = 94mm t = 10.7mm，I z = 1660cm 4，Wz = 185cm 3
2．计算顶边 AB 的长度改变量 顶边处有
3
σ max =
计算中用到 h1 = h / 2 − t = 79.3mm。

习题1.3
应用有限元法求解弹性力学问题，包括建立 有限元模型、求解有限元方程等。
习题1.4
应用有限差分法求解弹性力学问题，包括建 立差分模型、求解差分方程等。
思考题解析
思考题1.1
如何理解弹性力学的基本概念？
思考题1.3
如何应用有限元法和有限差分法求解弹性力 学问题？
思考题1.2
如何建立和求解弹性力学的基本方程？
南航材料力学第2讲(第1章-续)
目录
• 材料力学的基本概念 • 材料的力学性质 • 杆件的基本变形 • 应力分析与应变分析 • 材料的失效与强度理论 • 习题与思考题
01 材料力学的基本概念
材料力学的定义
总结词
材料力学是一门研究材料在力作用下 变形、破坏和恢复的学科。
详细描述
材料力学主要关注材料在不同外力作 用下的行为，包括变形、断裂、疲劳 等，以及这些行为对材料性能的影响。
泊松比
描述材料横向变形与纵向变形之比的物理量。
杨氏模量与泊松比的关系
杨氏模量是弹性模量的一种，它描述了材料在单向受力时的弹性性质，而泊松比则描述了材料在横向受 力时的变形性质。
材料的强度和塑性极限
强度极限
材料所能承受的最大应力值，超过这个值材料会发生断裂。
塑性极限
材料在受力过程中所能发生的最大塑性形变量，超过这个值材料的塑性变形会变得不稳定。
应变分析
定义
应变定义为物体形状的改变量与 其原始尺寸的比值，表示物体形 状的相对变化。
分类
应变分为线应变和角应变。线应 变表示长度方向的改变，角应变 表示角度的改变。
应变协调方程
在连续介质中，应变分量之间存 在一定的关系，即应变协调方程， 它确保物体内部各点应变分量的 连续性。

第二章轴向拉(压)变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：（1）求指定截面上的轴力FN =-11FF F N -=+-=-222（2）作轴力图轴力图如图所示。

（b）解：（1）求指定截面上的轴力FN 211=-02222=+-=-F F N （2）作轴力图FF F F N =+-=-2233轴力图如图所示。

（c）解：（1）求指定截面上的轴力FN 211=-FF F N =+-=-222（2）作轴力图FF F F N 32233=+-=-轴力图如图所示。

（d）解：（1）求指定截面上的轴力FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-（2）作轴力图中间段的轴力方程为：x aF F x N ⋅-=)(]0,(a x ∈轴力图如图所示。

[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积2400mm A =，试求各横截面上的应力。

解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力MPa mm N A N 504001020231111-=⨯-==--σMPamm N A N 254001010232222-=⨯-==--σMPa mmN A N 254001010233333=⨯==--σ[习题2-3]试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积21200mm A =，22300mm A =，23400mm A =，并求各横截面上的应力。

解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力MPa mm N A N 10020010202311111-=⨯-==--σMPa mmN A N 3.3330010102322222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-4]图示一混合屋架结构的计算简图。

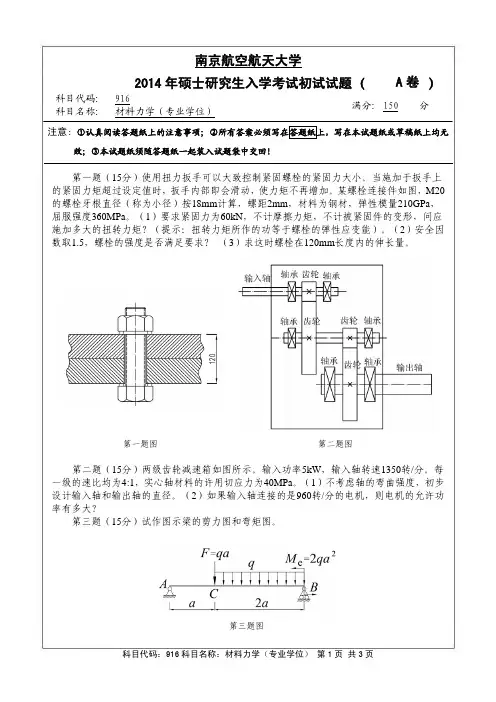
南京航空航天大学2014年硕士研究生入学考试初试试题（A卷）科目代码: 916满分: 150 分科目名称: 材料力学（专业学位）注意: ①认真阅读答题纸上的注意事项；②所有答案必须写在答题纸上，写在本试题纸或草稿纸上均无效；③本试题纸须随答题纸一起装入试题袋中交回！第一题（15分）使用扭力扳手可以大致控制紧固螺栓的紧固力大小。

当施加于扳手上的紧固力矩超过设定值时，扳手内部即会滑动，使力矩不再增加。

某螺栓连接件如图，M20的螺栓牙根直径（称为小径）按18mm计算，螺距2mm，材料为钢材，弹性模量210GPa，屈服强度360MPa。

（1）要求紧固力为60kN，不计摩擦力矩，不计被紧固件的变形，问应施加多大的扭转力矩？（提示：扭转力矩所作的功等于螺栓的弹性应变能）。

（2）安全因数取1.5，螺栓的强度是否满足要求？（3）求这时螺栓在120mm长度内的伸长量。

第一题图第二题图第二题（15分）两级齿轮减速箱如图所示。

输入功率5kW，输入轴转速1350转/分。

每一级的速比均为4:1，实心轴材料的许用切应力为40MPa。

（1）不考虑轴的弯曲强度，初步设计输入轴和输出轴的直径。

（2）如果输入轴连接的是960转/分的电机，则电机的允许功率有多大？第三题（15分）试作图示梁的剪力图和弯矩图。

第三题图第四题（15分）在图示铸铁槽形截面梁上作用均布载荷q ，在A 截面作用集中力偶20.1M ql =，5m l =。

其截面形心位置如图所示，截面对形心轴的惯性矩为84110mm z I =×。

材料的许用拉应力为[]30MPa t σ=，许用压应力[]150MPa c σ=。

试由梁的强度条件确定许可外力q 。

第四题图第五题（15分）某点应力单元体如图所示，100MPa x y xy σστ===，0z σ=。

设材料的弹性模量200GPa E =，泊松比0.3μ=，30α=°。

试计算：（1）该点的3个主应力和最大剪应力。

第九题
2kN/m
B
EI
4m
C EI A 4m
第十题
科目代码：916 科目名称：材料力学(专业学位) 第 3 页 共 3 页
第七题
八、（15 分）图示平面机构 ABCD 由物块 A、光滑滑轮 B 和 C、弹性绳索 ABCD 构成，绳索 D 端连接地 面，物块 A 的重量为120 N ，绳索长度为 0.6 m ，横截面面积为 50 mm2 。已知 E = 200 GPa ，[σ ] = 160 MPa ， 假设物块 A 上移至高度 h = 15 mm 处自由下落，试校核绳索强度。
0.5m 1.5m
AC
B
F 第一题 二、（15 分）图示齿轮传动系统。马达的输入功率 P1 = 30kW，轴 AB 的转速 n1 = 270r/min。B 处齿轮与 C 处齿轮的齿数之比 z1: z2=1:3。实心圆轴 AB 直径 d1=40mm，空心圆轴 CD 外径 D2=50mm，内径 d2=40mm。 两根轴采用相同的材料，其剪切弹性模量 G=100GPa。试求：（1）所有轴中的最大切应力；（2）若将实 心圆轴 AB 的直径减小一半，其他条件不变，则圆轴两端截面的相对扭转角是原来的多少倍？（3）空心 圆轴 CD 的单位长度扭转角。
马达
A
B
C
D
三、（15 分）作梁的剪力图和弯矩图。
第二题
第三题 科目代码：916 科目名称：材料力学(专业学位) 第 1 页 共 3 页
梦想不会辜负每一个努力的人
四、（15 分）箱式变截面梁式起重机（俗称行车）是近年来普遍使用的结构形式（如图）。为简单起见， 梁自重简化为集度 q=1400N/m 的均布载荷，设计起吊载荷为 50kN。梁使用厚度为 10mm 的钢板焊接而 成，中心截面 C 处梁高 H=600mm，两端（A、B 处）梁高 H＝300mm，宽度均为 300mm。设材料为 Q235 钢，σs=230MPa，安全因数取 1.8，试校核结构的强度（注：梁的弯曲正应力强度仅校核中心截面 C 即可， 两端需考虑弯曲切应力强度）。梁的跨度为 l=20m。

第二章轴向拉伸与压缩2- 1 试求图示直杆横截面1- 1、2- 2、3- 3上的轴力，并画出轴力图。

2- 2 图示中部对称开槽直杆，试求横截面1-1 和 2-2上的正应力。

12F.F=14kN..(a)1F1FFFF2F323F N1F N2F N32+F=2kNFF N1= - 2kN1220102044解：1．轴力F N (kN)F1=18kN (b)18kN18kNF N (kN)21 F 2=3kN2F3=25kN12F N1F N33kNF N21815F N2 = 0kNF N3= 2kN3F4=10kN310kN10+F N1= - 18kNF N2= - 15kNF N3= 10kN由截面法可求得，杆各横截面上的轴力为F N F14kN2．应力103F N14175MPa1 1A1 120MPa4F N14 103350 MPa2 2A220MPa210 42- 3 图示桅杆起重机， 起重杆 AB 的横截面是外径为 20 mm 、内径为 18 mm 的圆环， 钢丝绳 BC 的横截面面积为 10 mm 2。

试求起重杆AB 和钢丝绳 BC 横截面上的应力。

yBF N BCB. 45C30o15oxFFN AB. 15F=2kNA.解：1．轴力取节点 B 为研究对象，受力如图所示，F x 0 ： F NBC F NAB cos30 F cos 45F y0 ：F N AB sin 30F sin 45由此解得： FNAB2.83 kN ，FNBC1.04 kN2．应力起重杆横截面上的应力为ABFNAB2.83 103MPa47.4 MPaA AB2 220 184钢丝绳横截面上的应力为BC F N BC1.04 103MPa 104 MPaABC102- 4 图示由铜和钢两种材料组成的等直杆，铜和钢的弹性模量分别为E1100 GPa 和 E2210 GPa 。

若 杆 的 总 伸 长 为l 0.126 mm ，试求载荷 F 和杆横截面上的应力。

练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。

（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（ 是 ） （4）应力是内力分布集度。

（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。

（是 ） （6）若物体产生位移，则必定同时产生变形。

（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。

（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。

（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。

（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。

（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。

（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。

（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。

根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。

（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。

变形。

（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。

（8）根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。

1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。

材料力学课后习题答案6章材料力学课后习题答案6章第六章弯曲应力题号页码 6-3............................................................................. . (1)6-7............................................................................. . (2)6-10............................................................................ (3)6-13............................................................................ (4)6-14............................................................................ (6)6-17............................................................................ (7)6-18............................................................................ (9)6-19............................................................................ .........................................................................10 6-21............................................................................ .........................................................................11 6-23............................................................................ .........................................................................13 6-26............................................................................ .........................................................................15 6-28............................................................................ .........................................................................16 6-31............................................................................ .........................................................................17 6-33............................................................................ .........................................................................18 6-34............................................................................ .........................................................................19 6-36............................................................................ .........................................................................20 6-38............................................................................ .........................................................................22 6-40............................................................................ . (22)(也可用左侧题号书签直接查找题目与解)6-3 图示带传动装置，胶带的横截面为梯形，截面形心至上、下边缘的距离分别为y1与y2，材料的弹性模量为E。

一、填空题：请将正确答案写在划线内 每空1分，计16分⒈ 工程构件正常工作的条件是 ――――――――――――、、――――――――――――、―――――――――――――。

⒉ 工程上将延伸律-------πδ的材料称为脆性材料。

⒊ 矩形截面梁横截面上最大剪应力max τ出现在―――――――――――各点，其值=τmax -------------。

4．平面弯曲梁的q 、F s 、M 微分关系的表达式分别为--------------、、-------------、、----------------。

5．四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、 ――――――――――――――、―――――――――――――――――――――――――――――――――。

6．用主应力表示的广义虎克定律为 ――――――――――――――――――――― ；――――――――――――――――――――――；－―――――――――――――――――――――――。

二、单项选择题⒈ 没有明显屈服平台的塑性材料，其破坏应力取材料的――――――――――――。

⑴ 比例极限p σ； ⑵ 名义屈服极限2.0σ；⑶ 强度极限b σ； ⑷ 根据需要确定。

２． 矩形截面的核心形状为----------------------------------------------。

⑴ 矩形； ⑵ 菱形； ⑶ 正方形； ⑷三角形。

3． 杆件的刚度是指――――――――――――――－。

⑴ 杆件的软硬程度； ⑵ 杆件的承载能力；⑶ 杆件对弯曲变形的抵抗能力；⑷ 杆件对弹性变形的抵抗能力；4. 图示二向应力单元体，如剪应力改变方向，则―――――――――――――。

⑴ 主应力的大小和主平面的方位都将改变；⑵ 主应力的大小和主平面的方位都不会改变；⑶ 主应力的大小不变，主平面的方位改变；⑷ 主应力的大小改变，主平面的方位不变。

练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。

（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（ 是 ） （4）应力是内力分布集度。

（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。

（是 ） （6）若物体产生位移，则必定同时产生变形。

（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。

（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。

（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。

（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。

（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。

（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。

（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。

根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。

（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。

变形。

（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。

（8）根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。

1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。