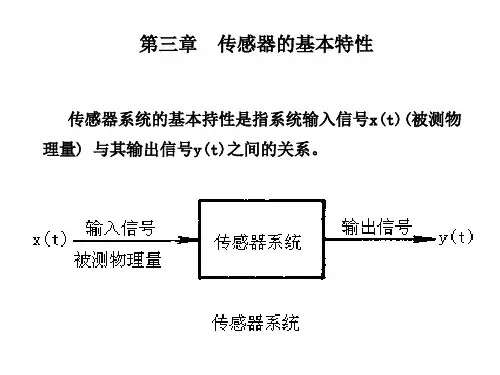
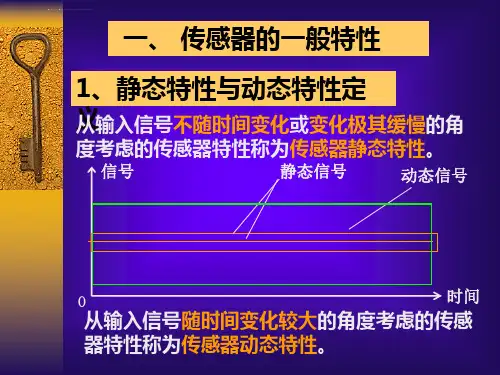
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y2=f2(s1, s2,···, sn) s2=f’2(y1, y2,···, ym)(b)确定函数f1, f2, ···,fn
ym=fm(s1, s2,···, sn) sn=f ’n(y1, y1,···, ym)
传感器系统静态特性建模技术 ——建模方法分类
按是否求取参数分:
1) 参数拟合建模 设定某个模型,以实现对数据拟合,确定该模型的
传感器系统静态特性建模技术(1) ——插值法
从数学上加以概括,可得到样条函数的定义如下:
三次样条函数记作S(x),a x b,满足:
①在每个小区间 [xi , xi1] (i 0,1, , n 1)是三次多项式。 ②在每个内节点 xi (i 1, , n 1) 上具有二次连续导数。
③ S(xi ) yi ,i 0,1, , n
传感器系统静态特性建模技术
——传感器系统模型
(2)多传感器系统 1)多传感器系统结构
Sensor1 y1
s1 s2
Sensor2 y2 ym
计算机或 S 微处理器
检测结果
sn Sensorm
2)建模所要做的工作:
y1=f1(s1, s1,···, sn) s1=f’1(y1, y2,···, ym)(a)获取标定数据;
三角法(线性插值),临近点取值法,多维曲面插值 法。
2)参数拟合建模法 常采用多项式模型,最小二乘法拟合
传感器系统静态特性建模技术(1) ——插值法
(1)线性插值法 T
特点:1)方法简 单,实现容易, 计算量小;2)逼 近精度低。
T(U5) T(U4)
0
U4 Ux U5
U
T
(U x
)
T
(U 4
)
T
(x xn ) (xi xn )
Tn (x)
n
li (x) yi
i0
n
i0
n j0
x xj xi x j
yi
ji
拉格朗日插值法由于存在龙格效应问题,在实践中并
不常用。
传感器系统静态特性建模技术(1)
——插值法 T
被逼近 曲线
T(U5) T(U4)
逼近曲线
误差 曲线
0
U4 Ux U5
U
(U5 ) U5
T (U4 U4
)
•
(U
x
U4
)
传感器系统静态特性建模技术(1)
——插值法
(2)最临近点法 T
把最临近输入
点的输出值作 为该点的输出。 T(U5)
如U于T(xU右是距5)图T离。(U中最x)U近=x,与
T(U4)
特点:1)方法简
单;2)这种方
法不产生新的
0
值,逼近精度
差
U4 Ux U5
U
传感器系统静态特性建模技术(1) ——插值法
(3)多项式插值法
由泰勒级数可知:
f (x) y0 y '0
(x
x0
)
1 2!
y
''0
(x
x0
)2
因此,传感器的逆函数可以用多项式来近似。
已知函数y=f(x)在m个点xi处的函数值及倒数值yi,•••,yj(r1),为求f(x)的近似简单函数φ(x),应当要求φ(x)满足条
传感器系统静态特性建模技术 ——传感器系统模型
(1)单传感器系统 1)单传感器系统结构
s
Sensor
y
计算机或 s 微处理器
检测结果
y=f (s)
s=f (y)
2)建模所要做的工作: (a)制作样本(s(1),y(1)), (s(2),y(2)), ···,(s(N),y(N)); (b)确定函数s=f (y)
传感器系统静态特性建模技术(1)
——插值法
又l0(x0)=1,于是让l0(x)的分母为(x0-x1)(x0-x2) ••• (x0-xn) 即可。依此类推,可得到
li
(x)
(x x0 ) (xi x0 )
(x xi1)(x xi1) (xi xi1)(xi xi1)
于是可以获得拉格朗日插值通式:
x1) T ( x1 x0
x0 T x0
x0 )
( x1
•
)
(
x
x0
)
依此类推可得 Tn(x)=l0(x)y0+ l1(x)y1 +•••+ ln(x)yn
且 l0(x0)=1, l0(x1)=0, l0(x2)=0, •••, l0(xn)=0
明显地:l0(x)含有因式(x- x1)(x- x2) ••• (x- xn)时,可使得 l0(x1)=0, l0(x2)=0, •••, l0(xn)=0。
龙格效应
传感器系统静态特性建模技术(1)
——插值法
2) 三次样条多项式插值法
所谓样条(Spline),本来是指一种绘图工具, 它是一种富有弹性的细长木条,在飞机或轮船 制造过程中,被用于描绘光滑的外形曲线。使 用时,用压铁将其固定在一些给定的节点上, 在其他地方任其自然弯曲,然后依样画下的光 滑曲线,就称为样条曲线。它实际上是由分段 三次曲线拼接而成,在连续点即节点上,不仅 函数自身是连续的,而且它的一阶和二阶导数 也是连续的。
参数的过程。常用方法为最小二乘法(多项式回归)。 (2)无参数拟合建模
只关心由数据得到的平滑曲线/曲面,并不关心拟合 参数,采用方法为插值法(三次样条插值)。
传感器系统静态特性建模技术 ——建模方法
按模型自变量个数(传感器个数)划分可分为:
(1)单输入-输出模型建模 1)无参数拟合建模法: 插值法,临近点取值法 2)参数拟合建模法:选定模型,求参数。 (2)多输入-输出模型建模 1)无参数拟合建模法
传感器系统静态特性建模技术(1)
——插值法
1) 拉格朗日多项式插值法
满足插值条件:Pn(xi)=yi=f(xi),i=0,1,•••,n的n次多项式称 为函数y=f(x)的拉格朗日插值多项式。
线性插值表达式
可改写为:
T (x)
T (x) T (x0
x x0
x1 x1
T
(x0
)
)
T(
x x1
件φ(xi)=yi, φ(xi)=yj, ••• 。这种条件称为插值条件, φ(x)称为插值函数, f(x)称为被插函数,x0,x1,•••,xm称 为插值节点,最小节点与最大节点之间的区间称为
插值区间。
传感器系统静态特性建模技术(1) ——插值法
多项式插值法类别:
拉格朗日插值法; 逐次线性插值法; 牛顿插值法; 样条插值法; Sinc函数插值法。
由三次样条函数中的条件①知,S(x)有个4n待定系数。 由条件②知,S(x)在n-1个内节点上具有二阶连续导数,
即满足条件:
S (xi 0) S (xi 0) S '(xi 0) S '(xi 0) S(xi 0) S "(xi 0)