Minitab做实验设计(田口法)

（完整版）MinitabDOE操作说明（田口法静态范例）Minitab DOE(田口法靜態型)操作說明:製造高爾夫球及設計開發其有效的增加最大飛行距離 ,4個控制因子 , 2水準因子水準1 Core material liquid tungsten2 Core diameter 118 1563 Number of dimples 392 4224 Cover thickness 0.03 0.06交互作用:Core material V.S Core diameter干擾因子: two type of golf clubs(driver and a 5-iron)Step 1:因子數及水準數之決定開啟功能選單Stat > DOE > Taguchi > Create Taguchi Design ?勾選2水準設計及因子數Step 2:實驗次數選定點選Designs按鈕(直交表類型)決定(4因子2水準作8次實驗)Step 3:因子及水準Data輸入點選Factors按鈕依照各因子名稱及水準Data輸入視窗表中Step 4:因子間交互作用選定在Taguchi Design-Factors對話框中 , 點選Interactions按鈕選擇已知交互作用由Available Terms欄位 > Selected Terms欄位Step 5:田口直交表及實驗結果輸入將直交表中C5及C6欄位分別輸入干擾因子Driver及Iron名稱 , 實驗結果Key-in至表中Step 6:實驗結果分析(選項設定)在功能表選擇Stat > DOE > Taguchi > Analyze Taguchi Design 將C5(Driver)及C6(Iron)移至Response data are in欄位中點選Analysis按鈕在選項中勾選Signal to Noise ratios及Means在Analyze Taguchi Design對話框中 , 選擇Options按鈕因此範例為望大特性, 故在Signal to Noise Ratio選項中勾選Larger is better在Analyze Taguchi Design對話框中 , 選擇Analysis Graphs按鈕勾選Four in one設定完成後在Analyze Taguchi Design對話框中 , 按Ok按鈕利用繪圖及視窗分析表作S/N比及最佳組合比較Step 7:實驗結果分析(S/N比及Mean值之視窗分析表及繪圖)在反應表中藉由各因子S/N比之大小來決定因子變異之影響性, 並選擇因子最小變異之水準值降低變異後 , 其他因子將平均值調整至目標設定在ANOVA分析各因子Mean值差異性 , Material、Diameter是顯著的因子1.S/N比以Diameter最大 , 為極顯著因子 , 其水準1又較水準2之效果好2.Thickness與Material/Diameter 有極大關係(成反比)Mean值以Diameter最大 , 為極顯著因子Step 8:結論(最佳組合及圖形解析)此範例因為品質特性設定為望大型(目標為增加高爾夫球最大的飛行距離) , 所以想得到因子水準最高的Mean值 , S/N比最大的因子最佳水準組合在S/N比主效應圖中 , 每個因子水準S/N比較 , 設定最佳組合為在Mean值主效應圖中, 每個因子水準Mean值比較 , 設定最佳組合為綜合以上分析結果得知最佳組合為(代號表示)→→→→A A11B B11C C11D D22Step 9:預測結果目的在於利用Minitab—Predict Taguchi Results指令來預測S/N 比與相對選定因子設定的反應特性在功能表選擇Stat > DOE > Taguchi > Predict Taguchi Results 取消Standard deviation及Natural log of standard deviation 勾選點選Terms按鈕(A,B,C,D)及交互作用(A*B)皆在Selected T erms 欄位中在Predict Taguchi Results對話框中點選Levels按鈕在Method of specifying new factor levels下選擇Select levels from a list , 並將因子最佳水準組合輸入表中選擇的最佳因子組合預測S/N比為53.68及Mean值(球的平均飛行距離)約為276碼 , 接下來 , 以此組合再作一次實驗去驗證與預測結果之正確性。

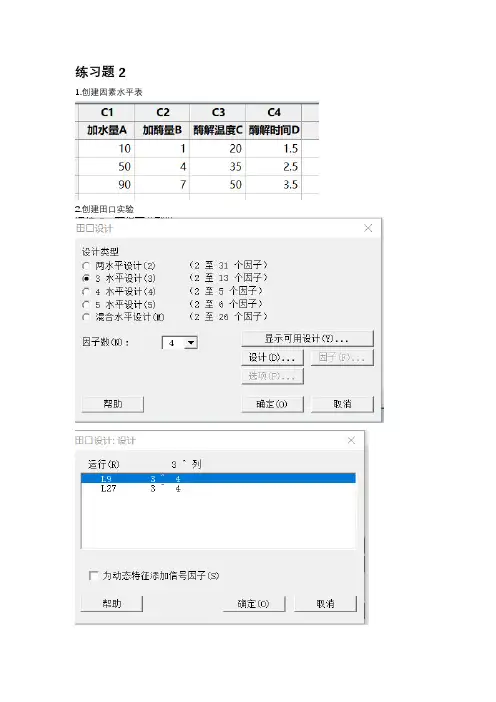
练习题2 1.创建因素水平表2.创建田口实验3.将实验结果添加到田口实验设计表中4.分析田口实验的设置：5.实验结果由上图可知，当加水量为50ml/100g，加酶量为7ml/100g,酶解温度为35℃，酶解时间为3.5h 时，酶法液化工艺能达到最佳效果。

练习题3：1.创建因素水平表2.创建田口实验3.把实验结果输入到生成的正交实验表中4.分析田口实验的设置5.实验结果结果: 工作表2 田口设计田口正交表设计L9(3^3)因子: 3试验次数: 9列 L9(3^4) 阵列1 2 3田口分析:槽宽, 槽深与脉冲能量, 扫描速度, 扫描次数线性模型分析:信噪比与脉冲能量, 扫描速度, 扫描次数信噪比的模型系数估计项系数系数标准误 T P常量 26.5451 0.4169 63.678 0.000脉冲能量 30 -1.8692 0.5895 -3.171 0.087脉冲能量 40 1.1855 0.5895 2.011 0.182扫描速度 20 1.5770 0.5895 2.675 0.116扫描速度 40 -0.3084 0.5895 -0.523 0.653扫描次数 1 -6.6611 0.5895 -11.299 0.008扫描次数 5 1.6008 0.5895 2.715 0.113S = 1.251 R-Sq = 98.7% R-Sq（调整） = 95.0%信噪比的方差分析来源自由度 Seq SS Adj SS Adj MS F P 脉冲能量 2 16.101 16.101 8.050 5.15 0.163 扫描速度 2 12.573 12.573 6.287 4.02 0.199 扫描次数 2 217.618 217.618 108.809 69.57 0.014 残差误差 2 3.128 3.128 1.564合计 8 249.420线性模型分析:均值与脉冲能量, 扫描速度, 扫描次数均值的模型系数估计项系数系数标准误 T P常量 28.6766 0.7242 39.599 0.001脉冲能量 30 -6.0883 1.0241 -5.945 0.027脉冲能量 40 4.0872 1.0241 3.991 0.057扫描速度 20 5.3067 1.0241 5.182 0.035扫描速度 40 -0.8218 1.0241 -0.802 0.507扫描次数 1 -10.0154 1.0241 -9.779 0.010扫描次数 5 -0.4546 1.0241 -0.444 0.701S = 2.173 R-Sq = 99.0% R-Sq（调整） = 96.1%均值的方差分析来源自由度 Seq SS Adj SS Adj MS F P 脉冲能量 2 173.330 173.330 86.665 18.36 0.052 扫描速度 2 146.854 146.854 73.427 15.56 0.060 扫描次数 2 630.414 630.414 315.207 66.78 0.015 残差误差 2 9.440 9.440 4.720合计 8 960.038线性模型分析:标准差与脉冲能量, 扫描速度, 扫描次数标准差的模型系数估计系数标项系数准误 T P常量 8.6890 1.134 7.661 0.017脉冲能量 30 0.2974 1.604 0.185 0.870脉冲能量 40 -1.9812 1.604 -1.235 0.342扫描速度 20 -0.9481 1.604 -0.591 0.614扫描速度 40 0.7025 1.604 0.438 0.704扫描次数 1 7.5172 1.604 4.687 0.043扫描次数 5 -2.6423 1.604 -1.647 0.241S = 3.402 R-Sq = 92.5% R-Sq（调整） = 70.1%标准差的方差分析来源自由度 Seq SS Adj SS Adj MS F P 脉冲能量 2 20.546 20.546 10.273 0.89 0.530 扫描速度 2 4.358 4.358 2.179 0.19 0.842 扫描次数 2 261.762 261.762 130.881 11.31 0.081 残差误差 2 23.154 23.154 11.577合计 8 309.820信噪比响应表望大水平脉冲能量扫描速度扫描次数1 24.68 28.12 19.882 27.73 26.24 28.153 27.23 25.28 31.61Delta 3.05 2.85 11.72排秩 2 3 1均值响应表水平脉冲能量扫描速度扫描次数1 22.59 33.98 18.662 32.76 27.85 28.223 30.68 24.19 39.15Delta 10.18 9.79 20.49排秩 2 3 1标准差响应表水平脉冲能量扫描速度扫描次数1 8.986 7.741 16.2062 6.708 9.392 6.0473 10.373 8.935 3.814Delta 3.665 1.651 12.392排秩 2 3 1均值主效应图标准差主效应图信噪比主效应图信噪比残差图均值残差图标准差残差图由均值-主效应图可知，当脉冲能量为40 j,扫描速度为20mm/s,扫描次数为10次时为切割槽宽和槽深的最佳工艺条件。

过程能力概述一旦过程处于统计控制状态，并且是连续生产，那么你可能想知道这个过程是否有能力满足规范的限制，生产出好的零件（产品），通过比较过程变差的宽度和规范界限的宽度可以确定过程能力。

在评估过程能力之前，过程必须受控。

如果过程不受控，你将得到不正确的过程能力值。

.你能通过画能力柱状图和能力图来评估过程能力。

这些图形能够帮助你评估数据的分布和检验过程是否受控。

你也可以估计包括规范公差与正常过程变差之间比率的能力指数。

能力指数或统计指数都是评估过程能力的一种方法，因为它们都没有单位，所以，可以用能力统计表来比较不同过程的能力。

选择能力命令MINITAB提供了一组不同的能力分析命令，你可以根据数据的性质和分布从中选择命令，你可以对以下情况进行能力分析：——正态或Weibull概率模式（对于测量数据）——不同子组之间可能有很强变差的正态数据——二项式或Poisson概率模式（对于计数数据或属性数据）当进行能力分析时，选择正确的公式是基本要求，例如，MINITAB提供基于正态或Weibull分布模型上的能力分析工具，使用正态概率模型的命令提供了更完全的统计设置，但是，适用的数据必须近似于正态分布.例如，利用正态概率模型，能力分析（正态）可以估计预期零件的缺陷PPM 数。

这些统计分析建立在两个假设的基础上，1、数据来自于一个稳定的过程，2、数据服从近似的正态分布，类似地，能力分析（Weibull）计算零件的缺陷的PPM值利用的是Weibull分布。

在这两个例子中，统计分析正确性依赖于假设分布模型的正确性。

如果数据是歪斜非常严重，那么用正态分布分析将得出与实际的缺陷率相差很大的结果。

在这种情况下，把这个数据转化比正态分布更适当的模型，或为数据选择不同的概率模式.用M INITAB,你可以使用Box-Cox能力转化或Weibull概率模型，非正态数据比较了这两种方法.如果怀疑过程中子组之间有很强的变差来源，可以使用能力分析（组间/组内）或SIXpack能力分析（组间/组内）。

Minitab做实验设计（DOE）（田口法）（3因子3水平）编著：鲁仁山2007.12.271．双击桌面上的Minitab图标。

2．这是打开后的界面。

3.如上所示，将资料输入表中。

4. 数据输入完毕，打开Stat菜单，点选DOE Taguchi Create Taguchi Design…5. 这是弹出的界面。

6.根据水平的数量点选相应的水平设计，根据因子的数量点选相应的数字，然后按下Designs…按钮。

7.在弹出的界面上点选相应的正交方案，本例点选L9，然后按OK确认。

8. 这是弹出的界面，之前的灰色按钮（未激活）的已全部激活，按下Factors按钮。

9. 这是弹出的界面。

10．如图所示，将资料输入弹出的界面，然后按OK确认。

11.按下Options按钮，这是弹出的界面。

12. 如图所示，钩选Store design in worksheet，然后按OK确认。

13.这是弹出的实验设计组合排列表。

14.将根据实验组合进行实验得到的实验数据作为响应填入表中。

15. 打开Stat菜单，点选DOE Taguchi Analyze Taguchi Design…16. 这是弹出的界面。

17.在Response data are in处填入响应所在的栏位号，然后按下Graphs…18. 这是弹出的界面。

19.根据需要，如图所示点选相应的项目，按OK确认，然后按下Analysis。

20. 这是弹出的界面。

21. 根据需要，如图所示点选相应的项目，按OK确认，然后按下Terms。

22. 这是弹出的界面。

23. 如图所示点选相应的项目，按OK确认，然后按下已激活的Analysis Graphs。

24. 这是弹出的界面。

25. 如图所示点选相应的项目，按OK确认，然后按下Options。

26. 如图所示点选相应的项目，按OK确认，然后按下Storage。

27. 这是弹出的界面。

28. 如图所示点选相应的项目，按全部OK确认。

过程能力概述一旦过程处于统计控制状态，并且是连续生产，那么你可能想知道这个过程是否有能力满足规范的限制，生产出好的零件（产品），通过比较过程变差的宽度和规范界限的宽度可以确定过程能力。

在评估过程能力之前，过程必须受控。

如果过程不受控，你将得到不正确的过程能力值。

.你能通过画能力柱状图和能力图来评估过程能力。

这些图形能够帮助你评估数据的分布和检验过程是否受控。

你也可以估计包括规范公差与正常过程变差之间比率的能力指数。

能力指数或统计指数都是评估过程能力的一种方法，因为它们都没有单位，所以，可以用能力统计表来比较不同过程的能力。

选择能力命令MINITAB提供了一组不同的能力分析命令，你可以根据数据的性质和分布从中选择命令，你可以对以下情况进行能力分析：——正态或Weibull概率模式（对于测量数据）——不同子组之间可能有很强变差的正态数据——二项式或Poisson概率模式（对于计数数据或属性数据）当进行能力分析时，选择正确的公式是基本要求，例如，MINITAB提供基于正态或Weibull分布模型上的能力分析工具，使用正态概率模型的命令提供了更完全的统计设置，但是，适用的数据必须近似于正态分布.例如，利用正态概率模型，能力分析（正态）可以估计预期零件的缺陷PPM 数。

这些统计分析建立在两个假设的基础上，1、数据来自于一个稳定的过程，2、数据服从近似的正态分布，类似地，能力分析（Weibull）计算零件的缺陷的PPM 值利用的是Weibull分布。

在这两个例子中，统计分析正确性依赖于假设分布模型的正确性。

如果数据是歪斜非常严重，那么用正态分布分析将得出与实际的缺陷率相差很大的结果。

在这种情况下，把这个数据转化比正态分布更适当的模型，或为数据选择不同的概率模式.用M INITAB,你可以使用Box-Cox能力转化或Weibull概率模型，非正态数据比较了这两种方法.如果怀疑过程中子组之间有很强的变差来源，可以使用能力分析（组间/组内）或SIXpack能力分析（组间/组内）。

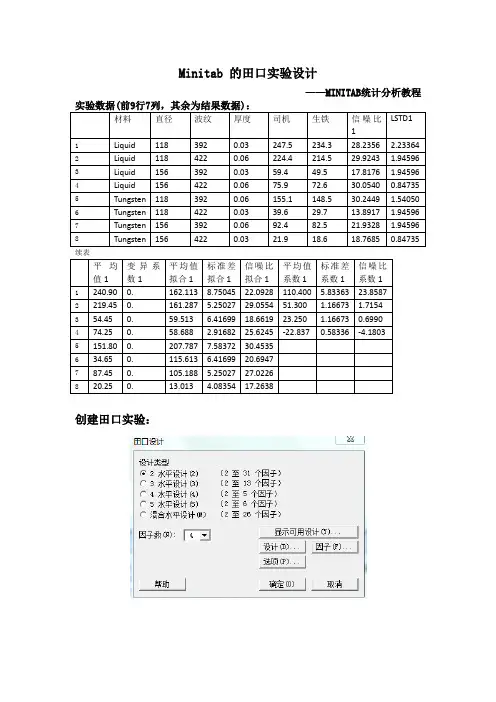
Minitab 的田口实验设计——MINITAB统计分析教程续表创建田口实验：分析田口实验的设置：实验结果：————— :11:22 ————————————————————欢迎使用 Minitab，请按 F1 获得有关帮助。

田口设计田口正交表设计L8(2**4)因子: 4试验次数: 8列 L8(2**7) 阵列1 2 3 4田口分析:司机, 生铁与直径, 波纹, 厚度线性模型分析:信噪比与直径, 波纹, 厚度信噪比的模型系数估计系数标项系数准误 T P常量 23.8587 2.041 11.689 0.000直径 118 1.7154 2.041 0.840 0.448波纹 392 0.6990 2.041 0.342 0.749厚度 0.03 -4.1803 2.041 -2.048 0.110S = 5.773 R-Sq = 55.6% R-Sq（调整） = 22.4%对于信噪比的方差分析来源自由度 Seq SS Adj SS Adj MS F P 直径 1 23.542 23.542 23.542 0.71 0.448 波纹 1 3.909 3.909 3.909 0.12 0.749 厚度 1 139.801 139.801 139.801 4.19 0.110 残差误差 4 133.317 133.317 33.329合计 7 300.569线性模型分析:均值与直径, 波纹, 厚度均值的模型系数估计系数标项系数准误 T P常量 110.40 24.95 4.425 0.011直径 118 51.30 24.95 2.056 0.109波纹 392 23.25 24.95 0.932 0.404厚度 0.03 -22.84 24.95 -0.915 0.412S = 70.56 R-Sq = 59.7% R-Sq（调整） = 29.5%备注：Seq SS： Sum of SquaresAdj MS: Adjusted Mean Square对于均值的方差分析来源自由度 Seq SS Adj SS Adj MS F P 直径 1 21054 21054 21054 4.23 0.109 波纹 1 4324 4324 4324 0.87 0.404 厚度 1 4172 4172 4172 0.84 0.412 残差误差 4 19915 19915 4979合计 7 49465备注：Seq SS： Sum of SquaresAdj MS: Adjusted Mean Square线性模型分析:标准差与直径, 波纹, 厚度标准差的模型系数估计项系数系数标准误 T P常量 5.8336 0.7717 7.559 0.002直径 118 1.1667 0.7717 1.512 0.205波纹 392 1.1667 0.7717 1.512 0.205厚度 0.03 0.5834 0.7717 0.756 0.492S = 2.183 R-Sq = 56.2% R-Sq（调整） = 23.4%对于标准差的方差分析来源自由度 Seq SS Adj SS Adj MS F P 直径 1 10.890 10.890 10.890 2.29 0.205 波纹 1 10.890 10.890 10.890 2.29 0.205 厚度 1 2.722 2.722 2.722 0.57 0.492 残差误差 4 19.058 19.058 4.764合计 7 43.560信噪比响应表望目(10*Log10(Ybar**2/s**2))水平直径波纹厚度1 25.57 24.56 19.682 22.14 23.16 28.04Delta 3.43 1.40 8.36排秩 2 3 1均值响应表水平直径波纹厚度1 161.70 133.65 87.562 59.10 87.15 133.24Delta 102.60 46.50 45.68排秩 1 2 3标准差响应表水平直径波纹厚度1 7.000 7.000 6.4172 4.667 4.667 5.250Delta 2.333 2.333 1.167排秩 1 2 3标准差主效应图信噪比主效应图信噪比残差图标准差残差图。

Minitab 的田口实验设计——MINITAB统计分析教程续表创建田口实验：分析田口实验的设置：实验结果：————— 987351:11:22 ————————————————————欢迎使用 Minitab ，请按 F1 获得有关帮助。

田口设计田口正交表设计L8(2**4)因子: 4试验次数: 8列 L8(2**7) 阵列1 2 3 4田口分析:司机, 生铁与直径, 波纹, 厚度线性模型分析:信噪比与直径, 波纹, 厚度信噪比的模型系数估计系数标项系数准误 T P常量 23.8587 2.041 11.689 0.000直径 118 1.7154 2.041 0.840 0.448波纹 392 0.6990 2.041 0.342 0.749厚度 0.03 -4.1803 2.041 -2.048 0.110S = 5.773 R-Sq = 55.6% R-Sq（调整） = 22.4%对于信噪比的方差分析来源自由度 Seq SS Adj SS Adj MS F P 直径 1 23.542 23.542 23.542 0.71 0.448 波纹 1 3.909 3.909 3.909 0.12 0.749 厚度 1 139.801 139.801 139.801 4.19 0.110 残差误差 4 133.317 133.317 33.329合计 7 300.569线性模型分析:均值与直径, 波纹, 厚度均值的模型系数估计系数标项系数准误 T P常量 110.40 24.95 4.425 0.011直径 118 51.30 24.95 2.056 0.109波纹 392 23.25 24.95 0.932 0.404厚度 0.03 -22.84 24.95 -0.915 0.412S = 70.56 R-Sq = 59.7% R-Sq（调整） = 29.5%备注：Seq SS： Sum of SquaresAdj MS: Adjusted Mean Square对于均值的方差分析来源自由度 Seq SS Adj SS Adj MS F P 直径 1 21054 21054 21054 4.23 0.109 波纹 1 4324 4324 4324 0.87 0.404 厚度 1 4172 4172 4172 0.84 0.412 残差误差 4 19915 19915 4979合计 7 49465备注：Seq SS： Sum of SquaresAdj MS: Adjusted Mean Square线性模型分析:标准差与直径, 波纹, 厚度标准差的模型系数估计项系数系数标准误 T P常量 5.8336 0.7717 7.559 0.002直径 118 1.1667 0.7717 1.512 0.205波纹 392 1.1667 0.7717 1.512 0.205厚度 0.03 0.5834 0.7717 0.756 0.492S = 2.183 R-Sq = 56.2% R-Sq（调整） = 23.4%对于标准差的方差分析来源自由度 Seq SS Adj SS Adj MS F P 直径 1 10.890 10.890 10.890 2.29 0.205 波纹 1 10.890 10.890 10.890 2.29 0.205 厚度 1 2.722 2.722 2.722 0.57 0.492 残差误差 4 19.058 19.058 4.764合计 7 43.560信噪比响应表望目(10*Log10(Ybar**2/s**2))水平直径波纹厚度1 25.57 24.56 19.682 22.14 23.16 28.04Delta 3.43 1.40 8.36排秩 2 3 1均值响应表水平直径波纹厚度1 161.70 133.65 87.562 59.10 87.15 133.24Delta 102.60 46.50 45.68排秩 1 2 3标准差响应表水平直径波纹厚度1 7.000 7.000 6.4172 4.667 4.667 5.250Delta 2.333 2.333 1.167排秩 1 2 3标准差主效应图信噪比主效应图信噪比残差图标准差残差图。

minitab中因子设计与田口设计因子设计和田口设计是统计实验设计中常用的两种方法，它们能够帮助我们有效地确定影响产品质量或过程性能的关键因素，并确定优化的方向。

下面我们将分别介绍这两种设计方法，并说明它们在Minitab软件中的应用。

1.因子设计：因子设计是通过系统地改变关键因素的水平，来研究对应响应变量的影响的一种实验设计方法。

它的主要目的是确定哪些因素对产品质量或过程性能具有显著影响，并确定各个因素的最佳水平。

一般来说，因子设计包括两个主要的步骤：选择因子和水平，以及分析数据。

在Minitab中，我们可以使用因子设计来确定关键因素及其最佳水平。

我们可以通过以下几个步骤来进行因子设计的分析：1.1.数据收集：收集有关因素和响应变量的数据。

通常，这些数据可以通过实际的生产或实验收集。

1.2.设计因子和水平：根据实际情况和经验，选择关键因素和它们的水平。

在Minitab中，我们可以使用"Stat"菜单中的"DOE"子菜单来选择适当的设计。

1.3.运行实验：根据设计的要求，在实验中设置因子的水平，并记录每个试验条件下的响应变量数据。

在Minitab中，我们可以使用"Stat"菜单中的"DOE"子菜单中的"Factorial"设计和"Response"子菜单来运行实验。

1.4.数据分析：使用Minitab中的统计工具来分析收集的数据，以确定因素对响应变量的影响以及各因子的最佳水平。

常用的分析方法包括方差分析（ANOVA）、回归分析等。

因子设计的优点是可以在较少的实验次数中确定关键因素，并且可以比较不同因素对响应变量的影响。

然而，因子设计的主要局限性是不能考虑因素之间的交互作用，可能会忽略一些潜在的复杂因素。

2.田口设计：田口设计是由日本质量管理专家田口玄一所提出的一种实验设计方法，它主要用于优化产品设计和制程控制。

Minitab田口设计学习田口原一博士被认为是稳健性参数设计的最先提出者，该设计是用于产品或过程设计的工程方法，关注的是使变异性和/或对噪声的敏感度最小化。

只要使用得当，田口设计可成为一种高效有力的方法，用于设计能在各种条件下以最优状态一致运行的产品。

田口设计：一种试验设计方法，使用它可以选择在操作环境中执行得更一致的产品或过程。

田口设计认识到，并非所有引起变异的因子都可以真正得到控制。

这些无法控制的因子称为噪声因子。

田口设计尝试确认使噪声因子的效应最小化的可控制因子（控制因子）。

在试验中，对噪声因子进行操作以强制产生变异，然后中找出使过程或产品健壮（即对来自噪声因子的变异有抵抗力）的最优控制因子设置。

田口设计的著名示例来自 20 世纪 50 年代日本的 Ina Tile 公司。

该公司生产了大量在指定尺寸之外的瓦片。

质量小组发现，用于烧制瓷砖的窑中的温度发生了变化，从而导致了瓷砖的尺寸不均匀。

由于建造新窑的成本很高，因此无法消除温度变异。

这样，温度就成了噪声因子。

使用田口设计的试验，小组发现通过增加粘土的石灰含量（一个控制因子），瓷砖对窑内温度变异更具抵抗力（即更健壮），使其可以生产出更均匀的瓷砖。

田口设计使用正交表，后者估计因子对响应均值和变异的效应。

使用正交表可以单独研究每个效应，并可以减少使用部分设计的试验时与试验关联的时间和成本。

在经典设计试验中，主要目标是确认影响均值响应并将其控制在期望水平的因子。

田口设计重点关注减少变异，以及将均值设置为目标。

在稳健性参数设计中，主要目标是在调整（或保持）目标过程的同时，找出使响应变异最小化的因子设置。

确定影响变异的因子之后，可以尝试找出将减小变异、使产品对不可控（噪声）因子的变化不敏感或同时达到这两种效果的可控制因子的设置。

为此目标设计的过程会产生更一致的输出。

以此目标设计的产品可以提供更一致的性能，而无论使用该产品的环境如何。