第9章_决策树算法

决策树算法介绍（DOC）3.1 分类与决策树概述3.1.1 分类与预测分类是⼀种应⽤⾮常⼴泛的数据挖掘技术，应⽤的例⼦也很多。

例如，根据信⽤卡⽀付历史记录，来判断具备哪些特征的⽤户往往具有良好的信⽤；根据某种病症的诊断记录，来分析哪些药物组合可以带来良好的治疗效果。

这些过程的⼀个共同特点是：根据数据的某些属性，来估计⼀个特定属性的值。

例如在信⽤分析案例中，根据⽤户的“年龄”、“性别”、“收⼊⽔平”、“职业”等属性的值，来估计该⽤户“信⽤度”属性的值应该取“好”还是“差”，在这个例⼦中，所研究的属性“信⽤度”是⼀个离散属性，它的取值是⼀个类别值，这种问题在数据挖掘中被称为分类。

还有⼀种问题，例如根据股市交易的历史数据估计下⼀个交易⽇的⼤盘指数，这⾥所研究的属性“⼤盘指数”是⼀个连续属性，它的取值是⼀个实数。

那么这种问题在数据挖掘中被称为预测。

总之，当估计的属性值是离散值时，这就是分类；当估计的属性值是连续值时，这就是预测。

3.1.2 决策树的基本原理1.构建决策树通过⼀个实际的例⼦，来了解⼀些与决策树有关的基本概念。

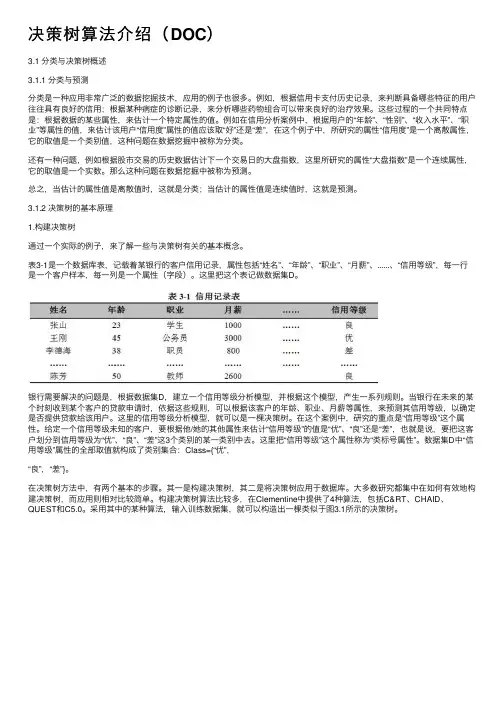
表3-1是⼀个数据库表，记载着某银⾏的客户信⽤记录，属性包括“姓名”、“年龄”、“职业”、“⽉薪”、......、“信⽤等级”，每⼀⾏是⼀个客户样本，每⼀列是⼀个属性（字段）。

这⾥把这个表记做数据集D。

银⾏需要解决的问题是，根据数据集D，建⽴⼀个信⽤等级分析模型，并根据这个模型，产⽣⼀系列规则。

当银⾏在未来的某个时刻收到某个客户的贷款申请时，依据这些规则，可以根据该客户的年龄、职业、⽉薪等属性，来预测其信⽤等级，以确定是否提供贷款给该⽤户。

这⾥的信⽤等级分析模型，就可以是⼀棵决策树。

在这个案例中，研究的重点是“信⽤等级”这个属性。

给定⼀个信⽤等级未知的客户，要根据他/她的其他属性来估计“信⽤等级”的值是“优”、“良”还是“差”，也就是说，要把这客户划分到信⽤等级为“优”、“良”、“差”这3个类别的某⼀类别中去。

机器学习--决策树算法（ID3C4.5）在⽣活中，“树”这⼀模型有很⼴泛的应⽤，事实证明，它在机器学习分类和回归领域也有着深刻⽽⼴泛的影响。

在决策分析中，决策树可以明确直观的展现出决策结果和决策过程。

如名所⽰，它使⽤树状决策模型。

它不仅仅是在数据挖掘中⽤户获取特定⽬标解的策略，同时也被⼴泛的应⽤于机器学习。

如何使⽤树来表⽰算法为此，我们考虑使⽤泰坦尼克号数据集的⽰例，以预测乘客是否会⽣存。

下⾯的模型使⽤数据集中的3个特征/属性/列，即性别，年龄和SIBSP（配偶或⼉童的数量）。

这是⼀棵体现了⼈性光辉的决策树。

树的形状是⼀棵上下颠倒的决策树，叶⼦节点在下，根节点在上。

在图像中，⿊⾊中的粗体⽂本表⽰条件/内部节点，基于树分成分⽀/边缘。

不再分裂的分⽀结束是决策/叶⼦，在这种情况下，乘客是否被死亡或幸存，分别表⽰为红⾊和绿⾊⽂本。

虽然，⼀个真实的数据集将有很多功能，这只是⼀个更⼤的树中的部分分⽀，但你不能忽略这种算法的简单性。

该特征重要性是明确的，可以轻易查看决策关系。

该⽅法更常见于来⾃数据的学习决策树，并且在树上被称为分类树，因为⽬标是将乘客分类为幸存或死亡，上⾯所展⽰的决策树就是分类树。

回归树以相同的⽅式表⽰，例如⽤于预测房⼦价格的连续价值。

通常，决策树算法被称为CART或分类和回归树。

那么，算法⽣成的背后发⽣了什么呢？如何⽣成⼀个决策树取决于选择什么特征和在何种情况下进⾏分裂，以及在什么时候停⽌。

因为⼀棵树通常是随意⽣长的，你需要修剪它，让它看起来漂亮（研究如何⽣成决策树）。

ID3算法ID3算法⽣成决策树ID3算法（Iterative Dichotomiser 3）是决策树⽣成算法的⼀种，基于奥卡姆剃⼑原理(简约原则) 1。

是Ross Quinlan发明的⼀种决策树算法，这个算法的基础就是上⾯提到的奥卡姆剃⼑原理，越是⼩型的决策树越优于⼤的决策树，尽管如此，也不总是⽣成最⼩的树型结构，⽽是⼀个启发式算法。

决策树算法公式
决策树算法公式是机器学习中常用的分类算法，通过构建一个树形结构来实现对数据集的分类。

决策树的主要思路是将数据集分成若干个小部分，每个小部分对应一条分支，直到达到预定的终止条件。

根据数据集的属性特征，决策树算法会选择最优的属性来进行划分，从而得到最优的分类效果。

决策树算法的主要公式包括：
1.信息增益公式：$IG(D, A) = H(D) - H(D|A)$
其中，$H(D)$表示数据集$D$的经验熵，$H(D|A)$表示在属性$A$的条件下，数据集$D$的经验条件熵。

信息增益越大，说明使用属性$A$进行划分能够得到更好的分类效果。

2.基尼系数公式：$Gini(D) =
sum_{k=1}^{|mathcal{Y}|}sum_{k'
eq k}p_kp_{k'} = 1 - sum_{k=1}^{|mathcal{Y}|}p_k^2$ 其中，$|mathcal{Y}|$表示数据集$D$中不同类别的个数，
$p_k$表示数据集$D$中属于第$k$个类别的样本占总样本数的比例。

基尼系数越小，说明使用属性$A$进行划分能够得到更好的分类效果。

通过使用信息增益或基尼系数等公式，决策树算法可以自动选择最优的属性进行划分，从而得到最优的分类效果。

- 1 -。

决策树的算法一、什么是决策树算法？决策树算法是一种基于树形结构的分类和回归方法，其本质是将训练数据集分成若干个小的子集，每个子集对应一个决策树节点。

在决策树的生成过程中，通过选择最优特征对数据进行划分，使得各个子集内部的样本尽可能属于同一类别或者拥有相似的属性。

在预测时，将待分类样本从根节点开始逐层向下遍历，直到到达叶节点并输出该节点所代表的类别。

二、决策树算法的基本流程1. 特征选择特征选择是指从训练数据集中选取一个最优特征用来进行划分。

通常情况下，选择最优特征需要考虑两个因素：信息增益和信息增益比。

2. 决策树生成通过递归地构建决策树来实现对训练数据集的分类。

具体实现方式为：采用信息增益或信息增益比作为特征选择标准，在当前节点上选择一个最优特征进行划分，并将节点分裂成若干个子节点。

然后对每个子节点递归调用上述过程，直到所有子节点都为叶节点为止。

3. 决策树剪枝决策树剪枝是指通过去掉一些无用的分支来降低决策树的复杂度，从而提高分类精度。

具体实现方式为：先在训练集上生成一棵完整的决策树，然后自底向上地对内部节点进行考察，若将该节点所代表的子树替换成一个叶节点能够提高泛化性能，则将该子树替换成一个叶节点。

三、常见的决策树算法1. ID3算法ID3算法是一种基于信息熵的特征选择方法。

其核心思想是在每个节点上选择信息增益最大的特征进行划分。

由于ID3算法偏向于具有较多取值的特征，因此在实际应用中存在一定局限性。

2. C4.5算法C4.5算法是ID3算法的改进版，采用信息增益比作为特征选择标准。

相比于ID3算法，C4.5算法可以处理具有连续属性和缺失值的数据，并且生成的决策树更加简洁。

3. CART算法CART（Classification And Regression Tree）算法既可以用来进行分类，也可以用来进行回归分析。

其核心思想是采用基尼指数作为特征选择标准，在每个节点上选择基尼指数最小的特征进行划分。

决策树计算公式
决策树是一种监督学习算法，用于解决分类问题。

其计算公式如下：
1.特征选择：根据某个特征的信息增益、信息增益比、基尼系数等指标，选择最优的特征进行划分。

2.划分节点：根据选择的最优特征，将数据集划分成多个子集或子节点。

3.递归构建：对每个子节点，重复步骤1和步骤2，直到满足终止条件（例如，节点只含有一类样本，或者达到最大深度等）。

4.终止条件：可以是以下情况之一：
-节点只包含一类样本，无需继续划分；
-达到预设的最大深度；
-无法选择一个特征进行划分。

5.样本分类：根据叶子节点的类别标签进行分类。

需要注意的是，决策树的计算过程是一个递归的过程，通过选择最优特征进行划分，将数据集分成更小的子集，最终得到树形结构的分类模型。

决策树还有其他一些拓展形式，例如随机森林、梯度提升树等。

这些拓展形式在计算公式上可能会有一些差异，但核心的思想和基本的计算过程与原始决策树相似。

决策树算法原理（三种最优属性划分方法）决策树是一种用于分类和回归的机器学习算法，其原理是基于历史数据进行学习，并通过一系列判断条件将数据集划分为不同的类别或者预测目标值。

决策树的主要思想是通过一系列属性值来对数据进行逐层划分，直到达到终止条件为止。

在每一次划分时，决策树需要选择最优的属性来进行划分，以使得划分后的数据纯度最高或者信息增益最大。

三种最优属性划分方法包括信息增益、增益率和基尼指数。

1.信息增益：信息增益是用来衡量划分后数据集纯度提高的程度。

它基于信息论中的熵的概念，计算的是划分前后数据集的信息熵之差。

信息熵可以衡量数据集的不确定性，即数据集中的混乱程度。

在选择划分属性时，我们希望划分后的数据集的不确定性最小，即使得信息增益最大。

2.增益率：增益率是信息增益的一种改进，用于解决信息增益在选择具有较多取值的属性上的偏好问题。

增益率通过考虑属性的分裂信息来衡量属性的纯度提升程度。

分裂信息反映了数据集分裂后的数据集的不确定性。

3.基尼指数：基尼指数是通过测量在给定数据集中随机选择一些样本后，错误分类该样本的概率。

基尼指数可以用于二分类或多分类问题。

在选择划分属性时，我们希望划分后的数据集的基尼指数最小，即使得纯度提高的程度最大。

以上三种最优属性划分方法在决策树学习的过程中都有着重要的应用。

在实际应用中，决策树算法可以通过先验知识或者经验来选择最优属性划分方法。

此外，由于决策树算法在高维数据上容易过拟合的问题，可以通过剪枝等技术来避免过拟合。

决策树算法的优势在于易于理解和解释，但也存在局限性，比如对于处理缺失数据、处理连续数据和处理类别不平衡等问题仍然存在挑战。

基于决策树的算法分析与应用示例在机器学习领域，决策树是一个经典的算法，它可以在面对大量数据时进行快速且可靠的分类或回归。

本文将介绍决策树算法的原理与应用，并通过一个具体的案例来展示其实际应用价值。

一、什么是决策树算法决策树是一种树形结构的分类模型，它的构建过程就像是一次“递归”的决策过程。

假设我们有一组数据，每个数据点都有若干个特征（即不同的属性），我们要根据这些特征来决定其类别（如是/否、高/中/低等）。

而决策树的生成就是一个逐步“分治”的过程，将原始数据分成不同子集，并根据不同特征来分别处理，最终得到一棵带有判定条件的树形结构。

决策树的构建过程可以分为三个步骤：特征选择、决策树生成和决策树剪枝。

其中，特征选择是指从所有特征中选出一个最佳特征来作为当前的分类依据；决策树生成是指利用选定的特征对数据进行划分，生成一棵完整的决策树；决策树剪枝是指对已经生成的决策树进行优化，去除一些不必要的节点和分枝，以避免过拟合等问题。

除了常见的二叉树决策树外，还有多叉树、CART树、C4.5树、ID3树等多种类型的决策树算法。

它们在特征选择、剪枝等方面有所不同，但本质上都是基于“树形结构”来完成分类或回归任务的。

二、决策树算法的应用示例决策树算法有许多实际应用，如金融风险评估、医学诊断、信用卡反欺诈等。

这里我们以一个简单的基于决策树的鸢尾花分类为例来说明决策树的应用过程。

鸢尾花数据集是机器学习中常用的一个数据集，它包含了150条记录，每条记录都有四个特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度。

根据这些特征，我们需要判断鸢尾花属于哪种类型：山鸢尾（Iris-setosa）、变色鸢尾（Iris-versicolor）或维吉尼亚鸢尾（Iris-virginica）。

以下是如何用Python和sklearn库来实现这一任务：```python# 引入相关库和数据集from sklearn.datasets import load_irisfrom sklearn.tree import DecisionTreeClassifierfrom sklearn.model_selection import train_test_splitiris = load_iris()X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=42)# 构建决策树模型并进行训练clf = DecisionTreeClassifier(criterion='entropy', max_depth=10, random_state=42)clf.fit(X_train, y_train)# 预测并评估模型准确率y_pred = clf.predict(X_test)score = clf.score(X_test, y_test)print(score)```上述代码首先引入了相关的Python库和鸢尾花数据集，并将数据集分为训练集和测试集。

决策树算法的原理
决策树算法，也称为决策树学习，是一种常见的机器学习算法。

它根据已有的样本数据，用树形结构（每个非叶节点对应一个属性）来生成一个训练模型用于预测和分类，也就是说，构建一个决策支持系统，为用户做出一系列的决定。

决策树算法的原理是基于贝叶斯决策理论的独特要素，贝叶斯决策理论是以概率模型为基础的，其核心思想是根据给定的训练样本数据集，来学习决策规则，用于进行新样例的分类。

决策树算法的基本流程是：
（1）准备：根据训练数据集，对数据进行预处理，将训练数据集转换成决策树的学习例子；
（2）构建：使用贝叶斯决策理论，一步一步地从根节点开始，根据最大信息增益（或最小错误率）的原则，逐步完善决策树；
（3）剪枝：使用测试集对构建的决策树进行验证，并进行剪枝，从而改善决策树的分类精度；
（4）预测：使用构建好的决策树，对新样例数据进行预测，并将其分类到最终的类别中。

综上，决策树算法就是以贝叶斯决策原则为基础，结合数据集构建、剪枝和预测三个步骤，实现决策模型的一种机器学习算法。

此算法具有易于理解、易于实施，能进行非线性分类，能够用于多分类，但也有其不足之处，例如对训练样本数据集要求较高，相比其他算法效率低等。