九年级数学射影定理
- 格式:pptx
- 大小:603.71 KB
- 文档页数:8

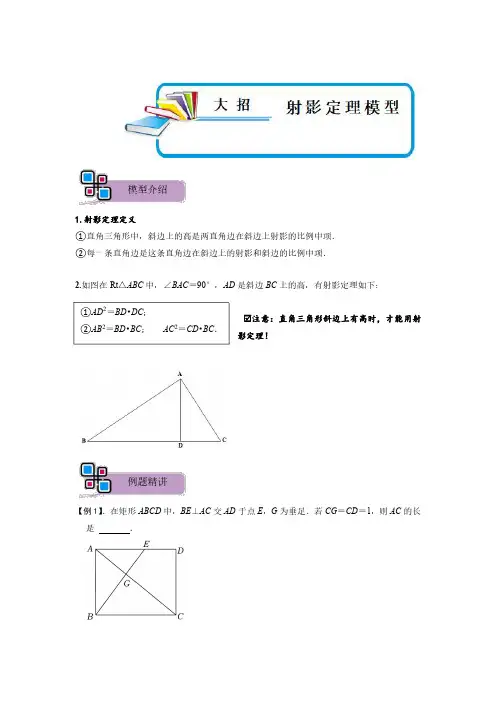
模型介绍1.射影定理定义①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.2.如图在Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高,有射影定理如下: 注意:直角三角形斜边上有高时,才能用射影定理!例题精讲【例1】.在矩形ABCD 中,BE ⊥AC 交AD 于点E ,G 为垂足.若CG =CD =1,则AC 的长是.①AD 2=BD •DC ;②AB 2=BD •BC ;AC 2=CD •BC .解:∵四边形ABCD是矩形,∴AB=CD=1,∠ABC=90°,∵BE⊥AC,∴∠AGB=90°=∠ABC,∵∠BAG=∠CAB,∴△ABG∽△ACB,∴=,∴AG•AC=AB2(射影定理),即(AC﹣1)•AC=12,解得:AC=或AC=(不合题意舍去),即AC的长为,故答案为:.【例2】.如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为()A.﹣B.﹣C.﹣1D.﹣2解:设A(x1,0)(x1<0),B(x2,0)(x2>0),C(0,t),∵二次函数y=ax2+bx+2的图象过点C(0,t),∴t=2;∵AC⊥BC,∴OC2=OA•OB(射影定理),即4=|x1x2|=﹣x1x2,根据韦达定理知x1x2=,∴a=﹣.故选:A.【例3】.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是()A.3B.8C.D.2解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.变式训练【变式1】.如图,在△ABC中,若=AC,BC=2BD=6,DE⊥AC,则AC•EC的值是9.解:如图,∵在△ABC中,若AB=AC,BC=2BD=6,∴AD⊥BC,CD=BD=3.又DE⊥AC,∴∠CED=∠CDA=90°.∵∠C=∠C,∴△CDE∽△CAD.∴=,即AC•EC=CD2=9.(射影定理)故答案是:9.【变式2】.如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC,BD交于O,且BE:ED=1:3,AD=6cm,则AE=cm.解:设BE=x,因为BE:ED=1:3,故ED=3x,根据射影定理,AD2=3x(3x+x),即36=12x2,x2=3;由AE2=BE•ED,AE2=x•3x;即AE2=3x2=3×3=9;AE=3.【变式3】.如图,若抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,若∠OAC=∠OCB.则ac的值为()A.﹣1B.﹣2C.D.解:设A(x1,0),B(x2,0),C(0,c),∵二次函数y=ax2+bx+c的图象过点C(0,c),∴OC=c,∵∠OAC=∠OCB,OC⊥AB,∴△OAC∽△OCB,∴,∴OC2=OA•OB(即射影定理)即|x1•x2|=c2=﹣x1•x2,令ax2+bx+c=0,根据根与系数的关系知x1•x2=,∴,故ac=﹣1,故选:A.【变式4】.如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=____________.解:连接CF、GF,如图:在正方形ABCD中,∠EAD=∠ADC=90°,AF⊥DE,∴△AFD∽△EAD,∴=,又∵DF=5EF=5,∴AD====CD,在Rt△AFD中,AF===,∵∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,∴∠DAF=∠CDF,∵四边形GFCD是⊙O的内接四边形,∴∠FCD+∠DGF=180°,∵∠FGA+∠DGF=180°,∴∠FGA=∠FCD,∴△AFG∽△DFC,∴=,∴=,∴AG=,∴DG=AD﹣AG=﹣【变式5】.如图,在△ABC中,以AC边为直径的⊙O交BC于点D,过点B作BG⊥AC 交⊙O于点E、H,连AD、ED、EC.若BD=8,DC=6,则CE的长为2.解:∵AC为⊙O的直径,∴∠ADC=90°,∵BG⊥AC,∴∠BGC=∠ADC=90°,∵∠BCG=∠ACD,∴△ADC∽△BGC,∴=,∴CG•AC=DC•BC=6×14=84,连接AE,∵AC为⊙O的直径,∴∠AEC=90°,∴∠AEC=∠EGC=90°,∵∠ACE=∠ECG,∴△CEG∽△CAE,∴=,∴CE2=CG•AC=84,∴CE=2.故答案为2.【变式6】.如图,四边形ABCD是平行四边形,过点A作AE⊥BC交BC于点E,点F在实战演练BC 的延长线上,且CF =BE ,连接DF .(1)求证:四边形AEFD 是矩形;(2)连接AC ,若∠ACD =90°,AE =4,CF =2,求EC 和AC的长.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∵CF =BE ∴BE +CE =CF +CE ,即BC =EF ,∴AD =EF ,∵AD ∥EF ,∴四边形AEFD 是平行四边形,∵AE ⊥BC ,∴∠AEF =90°,∴平行四边形AEFD 是矩形;(2)解:如图,∵CF =BE ,CF =2,∴BE =2,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠BAC =∠ACD =90°,∵AE ⊥BC ,∴AE 2=BE •EC (射影定理),∴EC ===8,∴AC ===4.1.如图,在矩形ABCD 中,DE ⊥AC ,垂足为点E .若sin ∠ADE =,AD =4,则AB 的长为()A .1B .2C .3D .4解:∵DE ⊥AC ,∴∠ADE+∠CAD=90°,∵∠ACD+∠CAD=90°,∴∠ACD=∠ADE,∵矩形ABCD的对边AB∥CD,∴∠BAC=∠ACD,∵sin∠ADE=,BC=AD=4,∴=,∴=,∴AC=5,由勾股定理得,AB==3,故选:C.2.如图,在矩形ABCD中,BD=2.对角线AC与BD相交于点O,过点D作AC的垂线,交AC于点E,AE=3CE.则DE2的值为()A.4B.2C.D.4解:∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=2,∵AE=3CE,∴AE=AC=,CE=AC=,∵∠ADC=90°,∴∠DAC+∠ACD=90°,∵DE⊥AC,∴∠AED=∠CED=90°,∴∠ADE+∠DAC=90°,∴∠ADE=∠ACD,∴△ADE∽△DCE,∴=,∴DE2=AE•CE=×=,故选:C.3.如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于()A.B.C.D.解:如图,设点S为BC的中点,连接DP,DS,DS与PC交于点W,作PE⊥BC于点E,PF⊥AB于点F,∴DP=CD=2,PS=CS=1,即DS是PC的中垂线,∴△DCS≌△DPS,∴∠DPS=∠DCB=90°,∴DS===,由三角形的面积公式可得PC=,∵BC为直径,∴∠CPB=90°,∴PB==,∴PE=FB==,∴PF=BE==,∴AF=AB﹣FB=,∴AP==故选:B.4.如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④OA(CP﹣CD)=AP•CD,正确的结论有()个.A.1B.2C.3D.4解:①∵PC与⊙O相切于点C,∴∠PCB=∠A,∠P=∠P,∴△PBC∽△PCA,∴PC2=PA•PB;②∵OC⊥PC,∴PC•OC=OP•CD;③∵CD⊥AB,OC⊥PC,∴OC2=OD•OP,∵OA=OC,∴OA2=OD•OP;④∵AP•CD=OC•CP﹣OA•CD,OA=OC,∴OA(CP﹣CD)=AP•CD,所以正确的有①,②,③,④,共4个.故选:D.5.如图,在Rt△ABC中,∠A=90°,AB=AC=8,点E为AC的中点,点F在底边BC上,且FE⊥BE,则CF长.解:作EH⊥BC于H,如图,∵∠A=90°,AB=AC=8,∴BC=AB=16,∠C=45°,∵点E为AC的中点,∴AE=CE=4,∵△CEH为等腰直角三角形,∴EH=CH==4,∴BH=12在Rt△ABE中,BE==4,在Rt△BEF中,∵EH⊥BF,∴BE2=BH•BF,即BF==,∴CF=BC﹣BF=16﹣=.故答案为.6.如图,在矩形ABCD中,点E在边AD上,把△ABE沿直线BE翻折,得到△GBE,BG 的延长线交CD于点F.F为CD的中点,连结CG,若点E,G,C在同一条直线上,FG=1,则CD的长为2+2,cos∠DEC的值为﹣1.解:∵四边形ABCD是矩形,∴AB=CD,AD∥BC,∠BCD=∠A=∠D=90°,∴∠AEB=∠EBC,∠BCG=∠DEC,由折叠的性质得:BG=BA,∠EGB=∠A=90°,∠GEB=∠AEB,∴CD=BG,∴∠EBC=∠GEB,∴BC=EC,∵点E,G,C在同一条直线上,∴∠CGF=90°,∠CGB=180°﹣∠EGB=90°,∵F为CD的中点,∴CF=DF,设CF=DF=x,则BG=CD=2x,∵∠CFG=∠BFC,∴△CFG∽△BFC,∴=,∴CF2=FG•BF,即x2=1×(1+2x),解得:x=1+或x=1﹣(舍去),∴CD=2x=2+2,∵∠DEC+∠ECD=90°,∠GFC+∠ECD=90°,∴∠DEC=∠GFC,∴cos∠DEC=cos∠GFC===﹣1,故答案为:2+2,﹣1.7.如图,在平面直角坐标系中,直线y=kx+1分别交x轴,y轴于点A,B,过点B作BC ⊥AB交x轴于点C,过点C作CD⊥BC交y轴于点D,过点D作DE⊥CD交x轴于点E,过点E作EF⊥DE交y轴于点F.已知点A恰好是线段EC的中点,那么线段EF的长是.解:因为AB的解析式为y=kx+1,所以B点坐标为(0,1),A点坐标为(﹣,0),由于图象过一、二、三象限,故k>0,又因为BC⊥AB,BO⊥AC,所以在Rt△ABC中,BO2=AO•CO,代入数值为:1=•CO,CO=k,同理,在Rt△BCD中,CO2=BO•DO,代入数值为:k2=1•DO,DO=k2又因为A恰好是线段EC的中点,所以B为FD的中点,OF=1+1+k2,Rt△FED中,根据射影定理,EO2=DO•OF,即(k++)2=k2•(1+k2+1),整理得(k﹣)(k+)(k2+2)(k2+1)=0,解得k=.根据中位线定理,EF=2GB=2DC,DC==,EF=2.8.如图,在菱形ABCD中,过点D作DE⊥CD交对角线AC于点E,连接BE,点P是线段BE上一动点,作P关于直线DE的对称点P',点Q是AC上一动点,连接P'Q,DQ.若AE=14,CE=18,则DQ﹣P'Q的最大值为.解:如图,连接BD交AC于点O,过点D作DK⊥BC于点K,延长DE交AB于点R,连接EP′并延长,延长线交AB于点J,作EJ关于AC的对称线段EJ′,则点P′的对应点P″在线段EJ′上.当点P是定点时,DQ﹣QP′=DQ﹣QP″,当D,P″,Q共线时,QD﹣QP′的值最大,最大值是线段DP″的长,当点P与B重合时,点P″与J′重合,此时DQ﹣QP′的值最大,最大值是线段DJ′的长,也就是线段BJ的长.∵四边形ABCD是菱形,∴AC⊥BD,AO=OC,∵AE=14.EC=18,∴AC=32,AO=OC=16,∴OE=AO﹣AE=16﹣14=2,∵DE⊥CD,∴∠DOE=∠EDC=90°,∵∠DEO=∠DEC,∴△EDO∽△ECD,∴DE2=EO•EC=36,∴DE=EB=EJ=6,∴CD===12,∴OD===4,∴BD=8,=×OC×BD=BC•DK,∵S△DCB∴DK==,∵∠BER=∠DCK,∴sin∠BER=sin∠DCK===,∴RB=BE×=,∵EJ=EB,ER⊥BJ,∴JR=BR=,∴JB=DJ′=,∴DQ﹣P'Q的最大值为.解法二:DQ﹣P'Q=BQ﹣P'Q≤BP',显然P'的轨迹EJ,故最大值为BJ.勾股得CD,OD.△BDJ∽△BAD,BD2=BJ*BA,可得BJ=.故答案为:.9.在矩形ABCD中,点E为射线BC上一动点,连接AE.(1)当点E在BC边上时,将△ABE沿AE翻折,使点B恰好落在对角线BD上点F处,AE交BD于点G.①如图1,若BC=AB,求∠AFD的度数;②如图2,当AB=4,且EF=EC时,求BC的长.(2)在②所得矩形ABCD中,将矩形ABCD沿AE进行翻折,点C的对应点为C',当点E,C',D三点共线时,求BE的长.解:(1)①∵四边形ABCD是矩形,∴AD=BC,∠BAD=90°,∵BC=AB,∴AD=AB,∴tan∠ABD==,∴∠ABD=60°,由折叠的性质得:AF=AB,∴△ABF是等边三角形,∴∠AFB=60°,∴∠AFD=180°﹣∠AFB=120°;②由折叠的性质得:BF⊥AE,EF=EB,∵EF=EC,∴EF=EB=EC,∴BC=2BE,∵四边形ABCD是矩形,∴∠ABC=90°,AD=BC=2BE,AD∥BC,∴△ADG∽△EBG,∴==2,∴AG=2EG,设EG=x,则AG=2x,∴AE=3x,在△ABE中,BG⊥AE,∴AB2=AG•AE(射影定理),即42=2x•3x,解得:x=(负值已舍去),∴AE=3x=2,∴BE===2,∴BC=2BE=4,即BC的长为4;(2)当点E,C',D三点共线时,如图3,由②可知,BC=4,∵四边形ABCD是矩形,∴∠ABC=∠BCD=90°,AD=BC=4,CD=AB=4,AD∥BC,∴∠DCE=90°,∠CED=∠B'DA,由折叠的性质得:AB'=AB=4,∠B'=∠ABC=90°,∴∠DCE=∠B',DC=AB',∴△CDE≌△B'AD(AAS),∴DE=AD=4,∴CE===4,∴BE=BC+CE=4+4.10.如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.(1)求证:PC是⊙O的切线;(2)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合).问GE▪GF是否为定值?如果是,求出该定值;如果不是,请说明理由.解:(1)∵PA=OA=2,AM=OM=1,CM=,又∵∠CMP=∠OMC=90°,∴PC==2,∵OC=2,PO=4,∴PC2+OC2=PO2,∴∠PCO=90°,∴PC与⊙O相切;(2)GE•GF为定值,理由如下:如图2,连接GA、AF、GB,∵点G为弧ADB的中点,∴,∴∠BAG=∠AFG,∵∠AGE=∠FGA,∴△AGE∽△FGA,∴,∴GE•GF=AG2,∵AB为直径,AB=4,∴∠BAG=∠ABG=45°,∴AG=2,∴GE•GF=AG2=8.11.如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.(1)求证:△ABF≌△BCE;(2)如图2,当点E运动到AB中点时,连接DG,求证:DC=DG;(3)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.(1)证明:∵BF⊥CE,∴∠CGB=90°,∴∠GCB+∠CBG=90,∵四边形ABCD是正方形,∴∠CBE=90°=∠A,BC=AB,∴∠FBA+∠CBG=90,∴∠GCB=∠FBA,∴△ABF≌△BCE(ASA);(2)证明:如图2,过点D作DH⊥CE于H,设AB=CD=BC=2a,∵点E是AB的中点,∴EA=EB=AB=a,∴CE=a,在Rt△CEB中,根据面积相等,得BG•CE=CB•EB,∴BG=a,∴CG==a,∵∠DCE+∠BCE=90°,∠CBF+∠BCE=90°,∴∠DCE=∠CBF,∵CD=BC,∠CHD=∠CGB=90°,∴△CHD≌△BGC(AAS),∴CH=BG=a,∴GH=CG﹣CH=a=CH,∵DH=DH,∠CHD=∠GHD=90°,∴△DGH≌△DCH(SAS),∴CD=GD;(3)解:如图3,过点D作DQ⊥CE于Q,S△CDG=•DQ•CG=CH•DG,∴CH==a,在Rt△CQD中,CD=2a,∴DH==a,∵∠MDH+∠HDC=90°,∠HCD+∠HDC=90°,∴∠MDH=∠HCD,∴△CHD∽△DHM,∴=,∴HM=a,在Rt△CHG中,CG=a,CH=a,∴GH==a,∵∠MGH+∠CGH=90°,∠HCG+∠CGH=90°,∴∠CGH=∠CNG,∴△GHN∽△CHG,∴,∴HN==a,∴MN=HM﹣HN=a,∴=12.在平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.(1)求过A,B,C三点的抛物线的解析式;(2)求点D的坐标;(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径;若不存在,请说明理由.解:(1)令二次函数y=ax2+bx+c,则,∴,∴过A,B,C三点的抛物线的解析式为y=﹣x2﹣x+2.(2)以AB为直径的圆的圆心坐标为O′(﹣,0),∴O′C=,OO′=;∵CD为⊙O′切线∴O′C⊥CD,∴∠O′CO+∠OCD=90°,∠CO'O+∠O'CO=90°,∴∠CO'O=∠DCO,∴△O'CO∽△CDO,∴=,即=,∴OD=,∴D坐标为(,0).(3)存在,抛物线对称轴为x=﹣,设满足条件的圆的半径为r,则E的坐标为(﹣+r,|r|)或F(﹣﹣r,|r|),而E点在抛物线y=﹣x2﹣x+2上,∴|r|=﹣(﹣+r)2﹣(﹣+r)+2;∴r1=﹣1+,r2=﹣1﹣(舍去),r3=1+,r4=1﹣(舍去);故以EF为直径的圆,恰好与x轴相切,该圆的半径为或1+.。

射影定理的推导过程射影定理是数学中的一个重要定理,它在几何学和代数学中都有广泛的应用。
下面我将以人类的视角,用自然流畅的语言来描述射影定理的推导过程。
假设我们有一个平面上的点A和一条直线L,我们希望得到点A到直线L的距离。
首先,我们需要找到点A关于直线L的射影点B。
为了找到射影点B,我们可以从点A引一条垂直于直线L的线段,假设这条线段与直线L的交点为B。
现在我们可以看到,点A、B 和直线L形成了一个直角三角形。
根据直角三角形的性质,我们可以利用勾股定理来计算点A到直线L的距离。
假设直线L的方程为ax + by + c = 0,点A的坐标为(x0, y0),则点B的坐标为(x1, y1)。
由于点B是点A关于直线L的射影点,因此直线AB与直线L垂直。
根据直线的斜率性质,我们可以得到直线AB的斜率为-k/a,其中k 是直线L的斜率。
接下来,我们可以利用点斜式来表示直线AB的方程。
假设直线AB 的方程为y = mx + d,其中m是直线AB的斜率,d是直线AB与y 轴的交点。
由于点A在直线AB上,所以点A的坐标(x0, y0)满足直线AB的方程。
将点A的坐标代入直线AB的方程,我们可以得到y0 = m*x0 + d。
将直线AB的方程和直线L的方程联立,我们可以得到一个关于m 和d的方程组。
解出m和d的值后,我们就得到了直线AB的方程。
现在,我们可以计算点A到直线L的距离了。
根据点到直线的距离公式,点A到直线L的距离等于点A到射影点B的距离。
利用两点间距离的公式,我们可以得到点A到射影点B的距离为:distance = sqrt((x0 - x1)^2 + (y0 - y1)^2)至此,我们成功地推导出了射影定理的计算公式。
射影定理的推导过程虽然涉及了一些几何和代数的知识,但通过合理的描述和逻辑推理,我们可以用生动的语言将其阐释清楚。
希望这段文字能够帮助你更好地理解射影定理的推导过程。

射影定理结论射影定理(ProjectiveTheorem)是一种数学定理,它以简洁的方式描述了空间中的点、线和平面的关系。
它揭示了空间中某个点会在线或平面上给出对应的点,也就是说,它提出了射影映射这一结果。
这个定理是著名的法国数学家宗撰写的,他于1822年在他的著作《试论平面曲线理论》中提出了射影定理。
射影定理的结论如下:空间中的任意一点都可以在其他点、线或平面上项给出对应的点,这种对应的点即射影映射(Projection Mapping)。
射影映射有着多种应用。
首先,在从一维空间到二维空间之间的映射过程中,它广泛地用于平面绘图,其中每个像素点都可以进行射影映射。
此外,在从二维空间到三维空间间的映射中,它也可以被用于立体化模型绘制。
在三维空间绘制模型的时候,点和线的对应关系可以很容易地通过射影定理得出。
此外,即使是在从多维空间到多维空间之间的映射过程中,也可以使用射影定理,这种映射也可以应用于复杂的物理过程,例如粒子发射过程。
射影定理的另一个重要优势在于它能够提供一种数学工具,可以用于探究空间中相互关联的点对象,而不需要考虑它们之间的相对位置。
例如,假设有一条直线,它分割开空间中的两个物体,这时,只要通过使用射影定理,就可以轻松地获得物体之间的关联性,而不需要考虑它们的相对位置。
射影定理也能够用来解释很多不同的科学过程,因为它能够提供一种数学方法来分析这些过程中的物理变化。
例如,它可以分析视角变换的物理过程,也能够解释空间中的光的反射和折射过程。
最后,它也可以用于研究立体视觉的结构,这种结构通常是非常复杂的,尤其是在实践活动中。
综上所述,射影定理是一种数学定理,它以简洁的方式描述了空间中的点、线和平面的关系,它提出了平面投影映射这一结果,它能够广泛地用于从一维空间到多维空间之间的映射,能够用于研究物理过程和立体视觉结构。

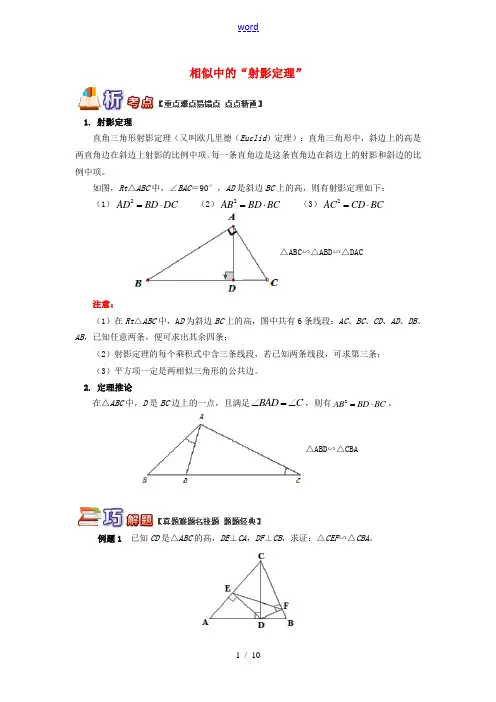
相似中的“射影定理”1. 射影定理直角三角形射影定理(又叫欧几里德(Euclid )定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
如图,Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高,则有射影定理如下: (1)2AD BD DC =⋅ (2)2AB BD BC =⋅ (3)2AC CD BC =⋅△ABC∽△ABD∽△DAC注意:(1)在Rt △ABC 中,A D 为斜边BC 上的高,图中共有6条线段:AC 、BC 、CD 、AD 、DB 、AB ,已知任意两条,便可求出其余四条;(2)射影定理的每个乘积式中含三条线段,若已知两条线段,可求第三条; (3)平方项一定是两相似三角形的公共边。
2. 定理推论在△ABC 中,D 是BC 边上的一点,且满足BAD C ∠=∠,则有2AB BD BC =⋅。
△ABD∽△CBA例题1 已知CD 是△ABC 的高,DE ⊥CA ,DF ⊥CB ,求证:△CEF ∽△CBA 。
解析:根据△CDE ∽△CAD 和△CDB ∽△CFD 得2CD CE CA =和2CD CF CB =⋅利用等量代换和变形,即可证明△CEF ∽△CBA 。
答案:证明:在Rt △ADC 中,由射影定律得,2CD CE CA =⋅, 在Rt △BCD 中,2CD CF CB =⋅ ∴CE CA CF CB ⋅=⋅ ∴CE CFCB CA=∵ECF BCA ∠=∠ ∴△CEF ∽△CBA点拨:本题主要考察了相似三角形的基本模型射影定理的应用。
做题时要善于发现相似,找出等量关系,进行适当的变形。
例题2 已知:如图,AB 为⊙O 的直径,AC 为弦,CD ⊥AB 于D 。
若AE =AC ,BE 交⊙O 于点F ,连接CF 、DE 。
求证:(1)2•AE AD AB = (2)ACF AED ∠=∠解析:(1)根据AE =AC ,可以把结论转化为证明2•AC AD AB =,只需连接BC ,证明△ACD ∽△ABC 即可。

射影定理巧妙记忆
射影定理是在线性代数中非常重要的定理,可以帮助我们理解向量空间中向量之间的关系。
为了帮助大家更好地记忆射影定理,建议采用以下方法:
1. 了解射影定理的数学定义和含义:射影定理指出,一个向量可以被分解为它在一个子空间上的投影和在该子空间的正交补空间上的投影之和。
这个定理可以帮助我们更好地理解线性代数中的向量空间,以及它们之间的关系。
2. 熟记射影定理的公式:射影定理的公式可以写成P = A(A^TA)^(-1)A^T,其中P 表示向量在子空间上的投影,A 表示子空间的基向量或者列向量,A^T 表示A 的转置,而(A^TA)^(-1) 表示A^TA 的逆。
熟记这个公式可以帮助我们更方便地使用射影定理。
3. 利用实际例子加深记忆:结合实际例子可以更加深刻地理解和记忆射影定理。
例如,在三维向量空间中,一个向量可以被分解成在一个平面上的投影和在该平面的法向量上的投影之和,我们可以通过画图或者实际计算,来加深对于射影定理的记忆。
4. 多做练习:多做一些相关的练习和题目可以帮助我们更好地理解和记忆射影定理。
同时也可以加深对于线性代数中其他概念的理解,从而更好地掌握这门学科。
总之,射影定理是线性代数中非常重要的定理,需要我们认真学习和掌握。
通过采用上述方法,可以帮助我们更好地记忆和理解射影定理,从而更加轻松地应对相关考试和课程。


专项32 相似三角形-射影定理综合应用(2种类型) 一、射影定理 直角三角形斜边上的高是它分斜边所得两条线段的比例中项;且每条直角边都是它在斜边上的射影和斜边的比例中项。
如图(1):Rt△ABC中,若CD为高,则有CD2=BD•AD、BC2=BD•AB或AC2=AD•AB。
(证明略)二、变式推广 1.逆用 如图(1):若△ABC中,CD为高,且有DC2=BD•AD或AC2=AD•AB或BC2=BD•AB,则有∠DCB=∠A或∠ACD=∠B,均可等到△ABC为直角三角形。
2.一般化,若△ABC不为直角三角形,当点D满足一定条件时,类似地仍有部分结论成立。
(后文简称:射影定理变式(2)) 如图(2):△ABC中,D为AB上一点,若∠CDB=∠ACB,或∠DCB=∠A,则有△CDB∽△ACB,可得BC2=BD•AB;反之,若△ABC中,D为AB上一点,且有BC2=BD•AB,则有△CDB∽△ACB,可得到∠CDB=∠ACB,或∠DCB=∠A。
【类型1:直角三角形中射影定理】【典例1】(2021秋•南京期末)如图,在Rt△ABC中,∠ACB=90°,点D在AB上,且=.(1)求证△ACD∽△ABC;(2)若AD=3,BD=2,求CD的长.【解答】(1)证明:∵=,∠A=∠A,∴△ACD∽△ABC;(2)解:∵△ACD∽△ABC,∴∠ACD=∠B,∵∠ACB=90°,∴∠A+∠B=90°,∴∠A+∠ACD=90°,∴∠ADC=90°,∴∠ADC=∠BDC,∵∠ACD=∠B,∴△ACD∽△CBD,∴=,∴=,∴CD=.【变式1-1】(2022•义乌市校级开学)如图,在△ABC中,∠ACB=90°,CD⊥AB,若AD=4,BD=8,则CD的长为( )A.4B.4C.4D.【答案】A【解答】解:∵∠ACB=90°,∴∠A+∠B=90°,∵CD⊥AB,∴∠DCB+∠B=90°,∴∠A=∠DCB,∵∠ADC=∠CDB=90°,∴△ADC∽△CDB,∴=,即=,解得:CD=4,故选:A.【变式1-2】(2021秋•漳州期末)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,CD=4,则BD的长为( )A.B.C.D.2【答案】A【解答】解:∵∠BAC=90°,∴∠B+∠C=90°,∵AD⊥BC,∴∠DAC+∠C=90°,∠ADB=∠ADC=90°,∴∠B=∠DAC,∴△BDA∽△ADC,∴=,∵AD=3,CD=4,∴=,解得:BD=,故选:A.【变式1-3】(2020秋•梁平区期末)如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )A.AC2=AD•AB B.CD2=CA•CB C.CD2=AD•DB D.BC2=BD•BA 【答案】B【解答】解:∵∠ACB=90°,CD⊥AB于点D,∴AC2=AD•AB,CD2=DA•DB,BC2=BD•BA.故选:B.【变式1-4】(2015•黄冈中学自主招生)将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )A.3B.8C.D.2【答案】A【解答】解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.【类型2:非直角三角形中射影定理】【典例2】如图,已知∠A=70°,∠APC=65°,AC2=AP•AB,则∠B的度数为( )A.45°B.50°C.55°D.60°【答案】A【解答】解:∵∠A=70°,∠APC=65°,∴∠ACP=180°﹣70°﹣65°=45°.∵AC2=AP•AB,∴=.∵∠B=∠B,∴△BAC∽△CPA.∴∠B=∠ACP=45°.故选:A.【变式2-1】如图,在△ABC中,点D在边AB上,若∠ACD=∠B,AD=3,BD=4,则AC的长为( )A.2B.C.5D.2【答案】B【解答】解:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴,∵AD=3,BD=4,∴AB=AD+BD=3+4=7,∴,∴AC=或﹣(舍去),故选:B.【变式2-2】如图,在△ABC中,点D在AB边上,∠ABC=∠ACD.(1)求证:△ABC∽△ACD;(2)若AD=2,AB=6.求AC的长.【解答】(1)证明:∵∠ABC=∠ACD,∠A=∠A,∴△ABC∽△ACD;(2)解:∵△ABC∽△ACD,∴,∴AC2=2×6=12,∴AC=2.【典例3】如图,在△ABC中,∠A=90°,点D、E分别在AC、BC边上,BD=CD=2DE,且∠C+∠CDE=45°,若AD=6,则BC的长为 .【答案】8【解答】解:∵∠A=90°,∴∠ABD+∠ADB=90°,∵BD=CD,∴∠DBC=∠C,∴∠ADB=∠DBC+∠C=2∠C,∵∠C+∠CDE=45°∴2∠C+∠CDE=90°,∴∠ADB+∠CDE=90°,∴∠BDE=90°,作DF⊥BC于F,如图所示:则BF=CF,△DEF∽△BED∽△BDF,∴===,设EF=x,则DF=2x,BF=CF=4x,∴BC=8x,DE=x,∴CD=BD=2x,AC=6+2x,∵∠DFC=∠A=90°,∠C=∠C,∴△CDF∽△CBA,∴=,即=,解得:x=,∴BC=8;故答案为:8.【变式3】如图,在锐角△ABC中,BD⊥AC于D,DE⊥BC于E,AB=14,AD=4,BE:EC=9:2,则CD= .【答案】2【解答】解:∵BD⊥AC,∴∠ADB=90°,∴BD2=AB2﹣AD2=142﹣42=180,设BE=9x,EC=2x,∵DE⊥BC,∴BD2=BE•BC,即180=9x(9x+2x),解得x2=,∵CD2=CE•CB=2x•11x=22×=40,∴CD=2.1.(2022秋•义乌市月考)如图,小明在A时测得某树的影长为3m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.A.B.C.6D.【答案】B【解答】解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=3m;∵∠E+∠F=90°,∠E+∠ECD=90°,∴∠ECD=∠F,∴△EDC∽△CDF,∴=,即DC2=ED•FD=2×3=6,解得CD=m.故选:B.2.(2012•麻城市校级自主招生)如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2,AC=3,BC=6,则⊙O的半径是( )A.3B.4C.4D.2【答案】D【解答】解:延长EC交圆于点F,连接DF.则根据90°的圆周角所对的弦是直径,得DF是直径.∵DE∥BC,∴△ADE∽△ABC.∴.则DE=4.在直角△ADF中,根据射影定理,得EF==4.根据勾股定理,得DF==4,则圆的半径是2.故选:D.3.(2022春•周村区期末)如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 .【答案】6【解答】解:∵∠BAC=90°,AD⊥BC,∴AD2=CD•BD=36,∴AD=6,故答案为:6.4.(2021春•汉阴县期中)如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC,BD 交于O,且BE:ED=1:3,AD=6cm,则AE= cm.【答案】3【解答】解:设BE=x,因为BE:ED=1:3,故ED=3x,根据射影定理,AD2=3x (3x+x),即36=12x2,x2=3;由AE2=BE•ED,AE2=x•3x;即AE2=3x2=3×3=9;AE=3.5.(2022•武汉模拟)在矩形ABCD中,BE⊥AC交AD于点E,G为垂足.若CG=CD=1,则AC的长是 .【答案】【解答】解:∵四边形ABCD是矩形,∴AB=CD=1,∠ABC=90°,∵BE⊥AC,∴∠AGB=90°=∠ABC,∵∠BAG=∠CAB,∴△ABG∽△ACB,∴=,∴AG•AC=AB2(射影定理),即(AC﹣1)•AC=12,解得:AC=或AC=(不合题意舍去),即AC的长为,故答案为:.6.(2021秋•滦州市期中)已知关于x的方程x2﹣2(a+b)x+c2+2ab=0有两个相等的实数根,其中a、b、c为△ABC的三边长.(1)试判断△ABC的形状,并说明理由;(2)若CD是AB边上的高,AC=2,AD=1,求BD的长.【解答】解:(1)∵两根相等,∴可得:4(a+b)2﹣4(c2+2ab)=0,∴a2+b2=c2,∴△ABC是直角三角形;(2)由(1)可得:AC2=AD×AB,∵AC=2,AD=1,∴AB=4,∴BD=AB﹣AD=3.7.如图,点D在△ABC的边BC上,∠ADC+∠BAC=180°,AB=4,BC=8,求BD的长.【解答】解:∵∠ADC+∠BAC=180°,∠ADC+∠ADB=180°,∴∠ADB=∠BAC,又∵∠B=∠B,∴△BAD∽△BCA,∴=,∴BA2=BD•BC,∵AB=4,BC=8,∴BD=2.即AC⋅CF=CB⋅DF.8.(盐城校级模拟)【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E 在CD上,过点C作CF⊥BE,垂足为F,连接OF,(1)试利用射影定理证明△BOF∽△BED;(2)若DE=2CE,求OF的长.【解答】【问题情境】证明:如图1,∵CD⊥AB,∴∠ADC=90°,而∠CAD=∠BAC,∴Rt△ACD∽Rt△ABC,∴AC:AB=AD:AC,∴AC2=AD•AB;【结论运用】(1)证明:如图2,∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90°,∴BC2=BO•BD,∵CF⊥BE,∴BC2=BF•BE,∴BO•BD=BF•BE,即=,而∠OBF=∠EBD,∴△BOF∽△BED;(2)方法一:∵BC=CD=6,而DE=2CE,∴DE=4,CE=2,在Rt△BCE中,BE==2,在Rt△OBC中,OB=BC=3,∵△BOF∽△BED,∴=,即=,∴OF=.方法二:将△OFC绕O顺时针旋转90度得到△OGB,如图3,由△BOF∽△BED得到∠OFB=45°,∴∠OGB=∠OFC=45°+90°=135°,∵OG=OF,∴△OGF为等腰直角三角形,∴∠OGF=45°,∴G点在BE上,∵BG=CF=,∴GF=,∴OF=GF=.。
证明射影定理射影定理(Projection Theorem)是线性代数中的重要定理,它指出了一组向量之间的线性关系或映射关系。
它指出,如果一组特定的矢量组已经被定义,则任何一个向量可以表示为这组矢量的线性组合;而任何一个向量都可以被投影到这组向量所确定的一维线性空间中。
射影定理可以解释为,如果两个空间上的向量v和w,当w取正则任意值时,都可以用此定理表达v的线性组合:v=w1+w2+w3+ ···根据此定理,用一个向量表示另一个向量,就必须知道两个向量的维数相同,并确定它们在某一维度上的对应,才能采取预先构建的线性表达式。
因此,可以把线性代数的射影定理理解为一种空间向量彼此之间的关系。
由于它在空间上提供了一些线性映射关系,因此我们可以用它来描述和理解向量的组合。
这种关系的重要性体现在它能够以线性表达式形式将一个向量准确地映射到另一个向量,用它来发现和探索现实世界中向量之间的关系,为各种计算机程序提供有用的解决方案以及诸多其他用途。
射影定理具有重要的应用价值,在最优化计算、分类学习和多元时延预测等数学场景中发挥了重要作用。
在材料科学中,射影定理可以用来对液相反应和表面物理力进行分析;在机器学习中,可以用来解决高维数据的压缩和可视化;在信息融合技术中,可以用来加速信号数据的传播;而在数据挖掘,计算机视觉和自然语言处理等领域,则可以利用射影定理进行特征提取和参数优化。
综上所述,射影定理是线性代数中的一种重要定理,它定义了一组向量之间的线性映射关系。
可以说,它具有极高的理论价值和应用价值,可以用来描述、表达、分析和优化线性系统中的向量。
证明射影定理的三个结论证明射影定理的三个结论,这个话题一听就感觉有点学术,但其实说白了,咱们就是想搞清楚一些基本的数学原理。
大家都知道,射影定理在几何学里就像是个老朋友,听起来复杂,其实就藏着许多小秘密。
咱们得先捋清楚,射影定理主要是关于三角形和直线的关系。
想象一下,咱们有一个三角形,里面的每一条边都好像是在讲故事,特别是它们和直线的互动,真是妙趣横生。
好比你走在街上,碰到朋友,顺势就聊起来了。
第一个结论是,任意一点到一条边的距离,其实就是那点投影到边上的垂直距离。
这么说吧,就像你在阳光下站着,影子总是朝着特定的方向伸展,对吧?这就是投影的魅力,谁都能明白,简单又直观。
你只要想象一下,一个小球在地上滚动,它落到地面上时,距离可不就成了一个影子嘛。
让人会心一笑,简单的道理却有着不简单的深意。
第二个结论就更加引人入胜了。
你知道,三角形的重心就在于三个边的中点连成的线,这就像是一群小伙伴围成圈,互相拉扯,保持平衡。
重心的存在就意味着,不论你如何摆动这三角形,它总会回到这个中心点。
真是一个天生的平衡大师。
想想吧,生活中也有很多这样的平衡,比如工作和休闲的时间安排,要学会找个中点,不然就容易翻车。
这个结论让我们明白,数学不仅仅是公式,它还能教我们生活的智慧。
再说说第三个结论,咱们称之为相似三角形的属性。
这部分就像是一场视觉盛宴。
你把一个三角形放大或者缩小,咱们仍然可以看到它的形状依然保持着,这种奇妙的相似关系就像是一对好姐妹,穿着不同的衣服,打扮各异,形态却依旧一脉相承。
举个例子,就像你和你的好朋友一起拍照,虽然身高不同,姿势各异,但你们的笑容却是那么和谐。
这种相似性就让我们的生活充满了乐趣。
数学中的这种美感,有时候就是在这些小细节里展现出来的,令人忍不住想要去探索更深的世界。
综合这三条结论,咱们可以看到射影定理不仅仅是在玩数字游戏,它还蕴藏着许多有趣的生活哲学。
每一个结论都像是打开了一扇窗,窗外的风景各有千秋。