用回归模型预测木材剩余物

货架寿命预测公式(一)货架寿命预测公式1. 货架寿命预测公式的重要性货架寿命预测是对货架寿命进行科学估算的过程，对于企业的库存管理和生产计划具有重要意义。

合理预测货架寿命可以减少库存损失和节省资源，提高资金利用率和客户满意度。

2. 常见的货架寿命预测公式在货架寿命预测中，常见的公式包括：•线性回归模型•指数平滑模型•ARIMA模型•支持向量回归模型线性回归模型线性回归模型是一种常见的预测模型，其公式为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中，Y表示货架寿命，X1、X2、…、Xn表示影响货架寿命的各种因素，β0、β1、β2、…、βn表示线性回归系数，ε表示误差项。

例子：假设我们要预测一个货架的寿命，我们可以考虑以下因素：负载重量、使用时间、环境湿度等。

我们可以收集不同货架的这些数据，并使用线性回归模型拟合，进而预测该货架的寿命。

指数平滑模型指数平滑模型是一种基于历史数据加权平均的预测模型，其公式为：Ft+1 = αYt + (1-α)Ft其中，Ft+1表示第t+1个时期的预测值，Yt表示第t个时期的实际值，Ft表示第t个时期的预测值，α为平滑系数。

例子：假设我们有一系列货架的寿命数据，我们可以使用指数平滑模型预测下一个时间段各货架的寿命情况。

通过调整平滑系数α的大小，可以控制历史数据的权重，进而影响预测结果。

ARIMA模型ARIMA模型是一种常用于时间序列预测的模型，其公式为：Yt = c + ϕ1Yt-1 + ϕ2Yt-2 + ... + ϕpYt-p + εt - θ1εt-1 - θ2εt-2 - ... - θqεt-q其中，Yt表示第t个时期的实际值，c为常数，ϕ1、ϕ2、…、ϕp为自回归系数，εt为误差项，θ1、θ2、…、θq为移动平均系数。

例子：我们收集了某货架每日销售量的时间序列数据，我们可以使用ARIMA模型来预测未来一段时间内货架的寿命。

2000 t0.05 (14) s(2000) = 7.3231 2.15 0.6742
= 5.8736, 8.7726
(2.67)
从而得出预测结果，2000年若采伐木材20万m3，产生木材剩余物的点估 计值是7.3231万m3。平均木材剩余物产出量的置信区间估计是在 [5.8736, 8.7726] 万m3之间。从而为恰当安排2000年木材剩余物的加工生
由图1.1、1.2可以看出国内生产总值与消费的增长都很快。国内生产 总值曲线的波动幅度相比较大。消费曲线的波动幅度相对较小。这与宏 观消费行为具有“惯性”有关。他既不可能随时间突然大幅增加，也不可 能随时间突然大幅减少。
1952-1978
平均增长 年增长率的
率
标准差
GDP 5.76%
0.10
消费 4.79%
案例1：用回归模型预测木材剩余物
（一元线性回归模型（file:b1c3）） 伊春林区位于黑龙江省东北部。全区有森林面积2189732公顷，木 材蓄积量为23246.02万m3。森林覆盖率为62.5%，是我国主要的木材工 业基地之一。1999年伊春林区木材采伐量为532万m3。按此速度44年之 后，1999年的蓄积量将被采伐一空。所以目前亟待调整木材采伐规划与 方式，保护森林生态环境。为缓解森林资源危机，并解决部分职工就业 问题，除了做好木材的深加工外，还要充分利用木材剩余物生产林业产 品，如纸浆、纸袋、纸板等。因此预测林区的年木材剩余物是安排木材 剩余物加工生产的一个关键环节。下面，利用简单线性回归模型预测林 区每年的木材剩余物。显然引起木材剩余物变化的关键因素是年木材采 伐量。 伊春林区16个林业局1999年木材剩余物和年木材采伐量数据见附 表。散点图见图2.14。观测点近似服从线性关系。建立一元线性回归模 型如下：

10.1.3 林分生长和收获预估模型的分类
•
•
•
•
1987年世界林分生长模型和模拟会议上提出林 分生长模型和模拟的定义。 林分生长模型是指一个或一组数学函数，它描 述林木生长与林分状态和立地条件的关系； 模拟是使用生长模型去估计林分在各种特定条 件下的发育过程。 这里明确地指出了林分生长模型不同于大地域 (林区)的模型，如林龄空间模型，收获调整模 型，轮伐预估模型等，也不同于单木级的模型， 例如树干解析生长分析等。
（一）生长和收获模型的分类
(1) Munro(1974)ห้องสมุดไป่ตู้据制作模型的原理把生长模型 分为三类： a)以单木为构成模型的基本单位，立木间的距 离作为已知参数，模拟时按各个立木都由空间 座标确定位置； b)和前一种相同，以单木为构成模型的基本单 位，只是不用立木间的距离作参数，立木的生 长按单木或径阶用数式来记述； c)把林分作为构成模型的基本单位，不需要各 株立木的信息。
相同林分密度时不同立地质量林 分的蓄积生长过程
相同立地质量不同林分密度时林 分的蓄积生长过程
林分生长与收获预估模型
林分生长与收获预估模型就是基于这四个因子采 用生物统计学方法所构造的数学模型。其一般 表达式为：
Y f( A 、 SI 、 SD )
式中：Y——林分每公顷的生长量或收获量， A——林分年龄； SI——地位指数或其它立地质量指标； SD——林分密度指标。
10.1.2 影响林分生长量和收获量的因子
林分生长量和收获量是以一定树种的林分生 长和收获概念为基础，在很大程度上取决于以下 四个因子： 林分的年龄或异龄林的年龄分布； 林分在某一林地上所固有的生产潜力(立地质量)； 林地生产潜力的充分利用程度(林分密度)； 所采取的林分经营措施(如间伐、施肥、竞争植物 的控制等)。

长白山主要树种直径生长的多元回归预测模型：以云杉为例刘洋;亢新刚;郭艳荣;高北延;冯启祥【摘要】A total of 949 trees from 18 clear-cut stands and 78 standard trees of Picea koraiensis in Changbai Mountains were selected to establish a multiple regression prediction model for diameter growth of dominant tree species. In the course of model building, the potential increment of tree diameter was determined to build an equation for diameter growth of open-grown trees. Then three competition indexs were applied to express modified function as a quantitative index to measure mean site quality, stand density, and distances to the nearest neighboring trees in order to correct the potential increment of tree diameter. The data were analyzed with SPSS software. The functions with the highest correlation coefficient and lowest surplus sum of squares were chosen as the realistic diameter growth model. The model could reasonably predict the diameter size of the dominant tree species and diameter structure of the future stand, which has a great significance for mastering the stand dynamics and estimating stand growth condition. In addition, the fitting degree was checked with 432 trees of the analytic trees form 8 clear-cut stands and 23 standard trees of P. Koraiensis which did not participate model building. It is found that the practical application error of the regression model is small, and the model can achieve the better fitting effect and forecast precision.%选取长白山地区18块皆伐标准地的949株云杉解析木和78株云杉标准木,建立长白山主要树种直径生长的多元回归预测模型.在生长模型中,首先确定林木直径的潜在生长量,建立疏开木的直径潜在生长方程,然后用反映立地质量、林分密度、对象木与周围相邻木最近距离3个竞争指数所表示的修正函数对直径潜在生长函数进行修正.采用SPSS软件对参数进行拟合,依据相关系数最大,剩余平方和最小得到直径的实际生长模型.该模型可以合理预测长白山地区主要树种一定时期内未来直径大小和林分的直径结构,这对把握林分动态、预估林分生长状态有极其重要的意义.另外,用未参加建模的8块皆伐标准地的432株云杉解析木和23株云杉标准木,对直径生长的多元回归预测模型的拟合度进行检验,结果显示拟合效果很好.【期刊名称】《东北林业大学学报》【年(卷),期】2012(040)002【总页数】4页(P1-4)【关键词】直径生长;多元回归预测模型;天然异龄林;长白山【作者】刘洋;亢新刚;郭艳荣;高北延;冯启祥【作者单位】省部共建森林培育与保护教育部重点实验室(北京林业大学)北京100083;省部共建森林培育与保护教育部重点实验室(北京林业大学)北京 100083;北京林业大学;吉林省汪清林业局;吉林省汪清林业局【正文语种】中文【中图分类】S758.5林分内各种大小直径的树木的分配状态，直接影响树木的树高、干形、材积、材种及树冠等因子的变化;林木直径可以被快速、方便且准确地测量，同时它是许多森林经营技术及测树制表技术理论的依据［1］。

第10章 林分生长和收获预估模型
内容提要
• 林分生长量和收获量的概念 • 全林分模型 • 径阶分布模型 • 单木生长模型
前言
• 随着森林经营集约程度的不断提高，人们对森林经营 信息的要求也日益增多，这就要求建立不同林分条件 下的林分生长和收获预估模型来提供更为详细而又合 理的有关林分动态信息，从而一方面满足森林经营者 合理经营森林的需要，另一方面又能解释经营者对森 林系统干扰（施肥、间伐、择伐等）所产生效果。
各类模型的优缺点
• 单木生长模型能够提供最多的信息，由此可以 推断林分的径阶分布及林分总收获量。在这3 类模型中，单木生长模型适用性最大。但是， 由于单木生长模型，尤其是与距离有关的模型， 要求输入量多，模拟林木生长时的计算量大， 应用成本高，这使其在实际应用中有较大的限 制。
• 在森林经营实践中，应视其经营技术水平、经 营目的及经营对象的实际状况，选用林分生长 和收获模型。
• 在19世纪80年代中，德国的林学家采用图形的 方法模拟森林的生长量和林分产量。
• 随着数学模型及模拟技术的迅速发展时期，却 始于电子计算机的产生，并可被林学研究者使 用的近代时期。
• 全林分模型可分二类：固定密度的模型和可变 密度的模型，两者的区别在于是否将林分密度 (SD)作为自变量。
10. 2. 1 固定密度的全林分模型
（三）资料的整理
(1) 资料的整理：将各种调查数据建立计算 机数据库，并将所收集的全部标准地数 据,大致按4：1（75%和25%）的比例分 成两组独立样本：建模样本和检验样本， 分别用于构建和检验林分生长和收获模 型。
(2) 资料的分析—取舍：剔除异常点（测错、 计算误差、异常数据） 。
第二节 全林分模型
（2）临时标准地短期观测法（一次测定法） 在规定的建模地域范围内，分别树种设置大量临时标准地。临时标准地分 布于不同t、SD和SI的林分中，实测林分的各调查因子。该法提供资料迅 速、花费较少，但是不能合理地反映林木或林分的生长规律和动态信息。 建模时将取自不同林分相同立地条件的标准地予以归类，修匀后作为该 立地条件下的林分发育过程。这样做的结果是人为地将不相关的林分进 行了组合来反映林分生长过程，只能说明实际林分发育过程的表面现象 （平均结果），而很难从本质上揭示林分生长的内在规律，更甚者会得 到错误的结论。由于我国固定标准地少，以往多采用此方法。容有：1）确定地域和树 种；2）确定标准地的条件、数量；3）确定标准地调 查内容与方法。 （1）标准地设置 • 标准地应分布于不同年龄、不同立地和不同密度，其 数量应在200块以上。 （2）测定项目：1）林分各调查因子：林分年龄（t）、 每木检尺，树高、枝下高、冠幅。建立单木生长模型 还需要通过定株观测，测定每株树木的直径、树高、 冠幅、冠长和树木的相对位置；2）记载标准地的地形、 地势、海拔、植被；3）做土壤剖面进行土壤调查；4） 详细记载林分经营历史，尤其是间伐次数、间伐时间 及间伐强度等。

回归模型的估计方法及在林业中的应用研究的开题报告一、选题背景和意义在林业科学中，建立回归模型是一个重要的研究领域。

回归模型是通过建立某些变量之间的关系，来预测或者解释一个变量的变化。

在林业科学中，回归模型可以用来预测树木的生长情况，森林病理学的研究、森林火灾预测等。

回归模型估计方法是林业研究中的重点之一。

回归模型估计方法包括最小二乘法、广义线性模型、岭回归等。

这些方法用于回归模型的建立和参数估计，是林业研究中不可缺少的一部分。

二、研究目的本研究的目的是探讨回归模型估计方法及其在林业中的应用。

具体目标如下：1. 综述回归模型估计方法的基本原理和主要方法；2. 探究回归模型在林业中的应用领域；3. 运用回归模型分析森林生态系统数据，探讨不同估计方法的优劣；4. 提出可行的林业回归模型估计方法。

三、研究内容本研究的主要内容包括以下几个方面：1. 回归模型估计方法的基本原理和主要方法：综述回归模型和回归分析的基本原理；介绍回归模型估计方法，如最小二乘法、广义线性模型、岭回归等；分析估计方法的优点和局限性。

2. 回归模型在林业中的应用领域：综述回归模型在林业中的应用领域，如树木生长预测、森林火灾预测、生物量估算等。

3. 运用回归模型分析森林生态系统数据：通过收集森林生态系统数据，运用回归模型进行数据分析，探讨不同估计方法的优劣。

4. 提出可行的林业回归模型估计方法：根据数据分析结果和回归模型估计方法的特点，提出可行的林业回归模型估计方法。

四、研究方法和技术路线本研究采用文献综述、案例分析和数理统计方法。

具体流程如下：1. 文献综述：通过检索相关文献，综述回归模型估计方法的基本原理和主要方法，回归模型在林业中的应用领域等。

2. 案例分析：选择森林生态系统数据，运用回归模型分析数据，探讨不同估计方法的优劣。

3. 数理统计方法：运用数理统计方法对回归模型进行参数估计，分析数据，提出可行的林业回归模型估计方法。

五、预期结果和成果本研究的预期结果和成果如下：1. 回归模型估计方法的综述和分析：分析回归模型估计方法的基本原理和主要方法，回归模型在林业中的应用领域，探讨不同估计方法的优劣。

第一节 标准木法
• 标准木 －林分或标准地中，具有平均材积大小的 树木 。 • 标准木法 －采用典型取样的方法，按一定要求选 取标准木，伐倒区分求积，用标准木材积推算林 分蓄积量的方法 。 • 这种方法在没有适用的调查数表或数表不能满足 精度要求的条件下，是一种简便易行的测定林分 蓄积量的方法。 • 标准木法可分为平均标准木法和分级标准木法。
树高曲线模型
序号 1 2 3 4 5 6 7 8 9 10 方程名称 双曲线 柯列尔(Rоляср，1878) Goulding (1986) Schumacher(1939) Wykoff 等人(1982) Ratkowsky （1990） Hossfeld (1822) Bates and Watts (1980) Loetsh 等人 (1973) Curtis (1967) 树高曲线方程
H = 1.3 + ae −be
− cD
H = 1.3 + a (1 − e − cD ) b
H = 1.3 + ae
−be− cD
d
2．由二元材积表导算一元材积表 ．
• 兴安落叶松的树高曲线经验方程为：
D H= 0.6872 + 0.025696 D
• 兴安落叶松二元材积方程为：
V = 0.00005043; bD
V = aD+ bD2
2
V = a + bD + cD
覆赫纳德尔（Hohenadl.W）－克雷恩 （Krenn.K） 伯克霍特（Berkhout）
V = aD b
lg V = a + b lg D + c
D3 V =a 1+ D
1 布里纳克（Brenac） D

t t t t t t t t
t
t
∑ ( x − x )( y − y ) = − x) ∑ (x − x)
t t 2 t
− y)
5.12 案例分析：用回归模型预测木材剩余物 案例分析： 通过这个案例一是掌握怎样利用实际数据建立、分析计量模型并预测 计量模型并预测， 通过这个案例一是掌握怎样利用实际数据建立、分析计量模型并预测， 二是怎样从 怎样从计量经济学专用软件 输出结果中找到这些有关的量。 中找到这些有关的量 二是怎样从计量经济学专用软件 EViews 输出结果中找到这些有关的量。 伊春林区位于黑龙江省东北部。 公顷， 伊春林区位于黑龙江省东北部。全区有森林面积 2 189 732 公顷，木材 蓄积量为 23 246.02 万 m3。 森林覆盖率为 62.5%， ， 是我国主要的木材工业基 地之一。1999 年伊春林区木材采伐量为 532 万 m3。按此速度 44 年之后， 地之一。 年之后， 1999 年的蓄积量将被采伐一空。所以目前亟待调整木材采伐规划与方式， 年的蓄积量将被采伐一空。所以目前亟待调整木材采伐规划与方式， 保护森林生态环境。为缓解森林资源危机 并解决部分职工就业问题， 源危机， 保护森林生态环境。为缓解森林资源危机，并解决部分职工就业问题，除 了做好木材的深加工外，还要充分利用木材剩余物（主要是指伐下的树冠） 了做好木材的深加工外，还要充分利用木材剩余物（主要是指伐下的树冠） 生产林业产品，如纸浆、纸袋、纸板等。 生产林业产品，如纸浆、纸袋、纸板等。因此预测林区的年木材剩余物是 安排木材剩余物加工生产的一个关键环节。下面， 安排木材剩余物加工生产的一个关键环节。下面，利用简单线性回归模型 预测林区每年的木材剩余物。 预测林区每年的木材剩余物。显然引起木材剩余物变化的关键因素是年木 材采伐量。 材采伐量。

第三节 最小二乘估计量的性质三大性质：线性特性、无偏性和最小偏差性 一、 线性特性的含义线性特性是指参数估计值1ˆβ和2ˆβ分别是观测值t Y 或者是扰动项t μ的线性组合，或者叫线性函数，也可以称之为可以用t Y 或者是t μ来表示。

1、2ˆβ的线性特征证明 （1）由2ˆβ的计算公式可得： 222222()ˆt tttt ttttttt tt tt x y x Y x Y xxx xx x x x β--===⎛⎫== ⎪ ⎪⎝⎭∑∑∑∑∑∑∑∑∑∑∑Y Y Y Y需要指出的是，这里用到了因为t x 不全为零，可设2tt tx b x =∑，从而，t b 不全为零，故2ˆt t b β=∑Y 。

这说明2ˆβ是t Y 的线性组合。

（2）因为12t t t Y X ββμ=++，所以有()212122ˆt t t t t t t t t t t tb b X b b X b b βββμββμβμ==++=++=+∑∑∑∑∑∑Y这说明2ˆβ是t μ的线性组合。

需要指出的是，这里用到了220t t t t t x x b x x ===∑∑∑∑∑以及 ()2222222201t t tt t t tt ttttttttx x X x b X X x x x x X x X x x x x x⎛⎫+⎪== ⎪⎝⎭++==+=∑∑∑∑∑∑∑∑∑∑∑∑∑2、1ˆβ的线性特征证明 （1）因为12ˆˆY X ββ=-，所以有 ()121ˆˆ1t t t t tY X Y X b nXb n ββ=-=-⎛⎫=- ⎪⎝⎭∑∑∑Y Y这里，令1a Xb n=-，则有1ˆt a β=∑Y 这说明1ˆβ是t Y 的线性组合。

（2）因为回归模型为12t t t Y X ββμ=++，所以()11212ˆt t t t t t t t t ta a X a a X a βββμββμ==++=++∑∑∑∑∑Y因为111t t t a Xb X b nn⎛⎫=-=-=⎪⎝⎭∑∑∑∑。

林木生长模型及应用林木的生长对于森林资源的可持续利用和气候变化研究具有重要意义。

为了更好地理解和预测林木的生长过程，科学家们发展了各种生长模型。

本文将介绍林木生长模型的种类及其在林业管理和环境保护中的应用。

一、简介林木生长模型是一种数学模型，通过描述和预测林木的生长和发展过程，帮助我们理解林木生态系统的动态变化。

它可以基于林木的生物学特性、环境因素和管护措施等因素来推测林木的生长轨迹和生态系统的发展趋势。

二、林木生长模型的类型1. 统计模型统计模型是基于大量的观测数据和统计分析方法来建立的。

它通过分析林木的生长数据、环境因素和人为干扰等来研究林木的生长规律。

常见的统计模型有线性回归模型、非线性回归模型和广义线性模型等。

2. 生理生态模型生理生态模型是通过考虑林木的生理过程和生态环境的交互作用来建立的。

它基于对林木生理特性、光合作用、养分吸收和水分利用等过程的理解，预测林木的生长和发展。

典型的生理生态模型有森林动态模型、生理因子模型和光合作用模型等。

3. 过程模型过程模型是在理论基础上建立的，通过描述和模拟林木生长的各个过程来实现对整个林木生命周期的模拟。

它包括了从种子萌发到成年树的整个生长过程，并考虑了气候、土壤和种群动力学等因素。

过程模型能够提供详细的生长轨迹和动态变化，为林业管理和生态保护决策提供重要依据。

三、林木生长模型的应用1. 林业管理林木生长模型可以帮助林业管理者制定合理的抚育措施和采伐计划。

通过模拟林木的生长轨迹，可以预测不同管理干扰下林木的生长响应，并优化森林经营和资源利用。

此外，林木生长模型还可用于评估森林经营的效果和预测林木的稳定产量。

2. 气候变化研究气候变化对林木的生长和分布具有显著影响。

林木生长模型能够模拟林木对气候变化的响应，预测不同气候条件下林木的生长变化和物候期的转变。

这对于评估气候变化对生态系统的影响、制定气候适应策略和保护生态系统具有重要意义。

3. 生态环境保护通过模拟林木的生长过程和生态系统的发展，林木生长模型能够评估不同管护措施对生态环境的影响。

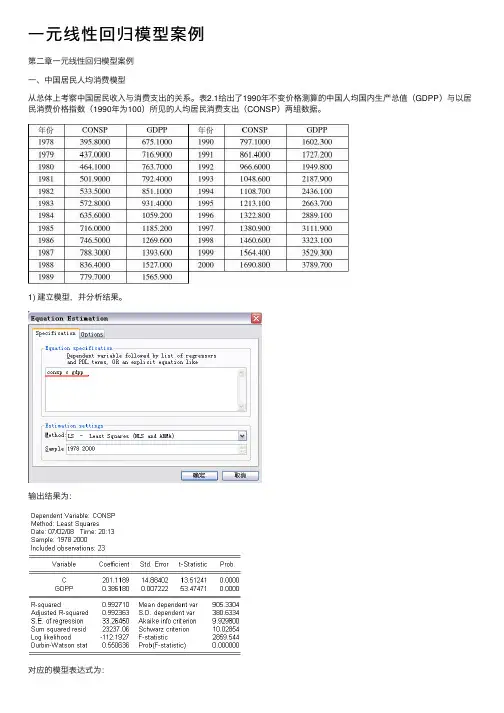
⼀元线性回归模型案例第⼆章⼀元线性回归模型案例⼀、中国居民⼈均消费模型从总体上考察中国居民收⼊与消费⽀出的关系。

表2.1给出了1990年不变价格测算的中国⼈均国内⽣产总值（GDPP）与以居民消费价格指数（1990年为100）所见的⼈均居民消费⽀出（CONSP）两组数据。

1) 建⽴模型，并分析结果。

输出结果为：对应的模型表达式为：201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出，拟合度较好，截距项和斜率项系数均通过了t 检验。

中国⼈均消费增加10000元，GDP 增加3862元。

⼆、线性回归模型估计表2.2给出⿊龙江省伊春林区1999年16个林业局的年⽊材采伐量和相应伐⽊剩余物数据。

利⽤该数据（1）画散点图；（2）进⾏OLS 回归；（3）预测。

表2.2 年剩余物y 和年⽊材采伐量x 数据（1）画散点图先输⼊横轴变量名，再输⼊纵轴变量名得散点图（2）OLS估计弹出⽅程设定对话框得到输出结果如图：由输出结果可以看出，对应的回归表达式为：0.76290.4043t t yx =-+ (-0.625) (12.11)20.9129,146.7166, 1.48R F DW === （3）x=20条件下模型的样本外预测⽅法⾸先修改⼯作⽂件范围将⼯作⽂件范围从1—16改为1—17确定后将⼯作⽂件的范围改为包括17个观测值，然后修改样本范围将样本范围从1—16改为1—17打开x的数据⽂件，利⽤Edit+/-给x的第17个观测值赋值为20将Forecast sample选择区把预测范围从1—17改为17—17，即只预测x=20时的y的值。

由上图可以知道，当x=20时，y的预测值是7.32，yf的分布标准差是2.145。

三、表2.3列出了中国1978—2000年的参政收⼊Y和国内⽣产总值GDP的统计资料。

单木生物量模型构建
单木生物量模型是一种用来估算森林中单棵树木的生物量的模型。

生物量是指树木的质量，包括树木的茎、枝、叶、根和果实等部分。

单木生物量模型可以用来估算森林的生物量总和，从而为森林资源管理、森林碳储存和其他应用提供依据。

构建单木生物量模型的过程如下：
选择样本：选择一定数量的树木作为样本，这些树木的生物量将用来构建模型。

样本的选取应该具有代表性，即能够代表整个森林中不同种类、不同年龄和不同位置的树木。

收集数据：对选定的样本进行测量，收集与生物量相关的数据。

这些数据可能包括树木的高度、胸径、分支结构、叶面积、果实重量等。

建立模型：根据收集的数据，使用统计学方法或机器学习方法建立单木生物量模型。

常见的方法包括线性回归、多项式回归和决策树等。

验证模型：使用已知生物量的树木来验证模型的准确性。

通常使用交叉验证的方法，将样本分成训练集和测试集，用训练集来构建模型，用测试集来验证模型的准确性。

如果模型的预测结果与已知生物量的误差较小，则表明模型较为准确。

应用模型：构建好的单木生物量模型可以用来估算森林中单棵树木的生物量。

可以使用模型对森林中的每棵树木进行预测，并统计出森林的生物量总和。

此外，单木生物
量模型还可以用来研究森林的生物量分布情况，以及影响森林生物量的因素等。

基础理论
基础理论
累积损伤模型是一种用于描述结构损伤演化的模型，它假定结构的损伤是时 间的函数，并随着时间的推移而累积。剩余寿命评估则是预测结构在达到其使用 寿命之前的剩余寿命。这个过程需要对结构进行全面的健康监测和性能评估，以 了解其损伤状况和发展趋势。
分析因素
分析因素
影响古建筑木构件剩余寿命的因素多种多样，主要可分为力学、化学、物理 等方面。
参考内容
古建筑木构件剩余寿命评估：基 于累积损伤模型的方法
引言
引言
古建筑木构件作为历史文化的重要载体，具有极高的艺术、科学和历史价值。 然而，由于自然环境和人为因素的影响，这些木构件常常遭受不同形式的损伤， 影响其结构和功能的稳定性。为了更好地保护和利用这些珍贵的文化遗产，本次 演示基于累积损伤模型，对古建筑木构件的剩余寿命进行评估。
古建筑木构件基于累积损伤的 剩余寿命评估
目录
01 引言
03 剩余寿命评估基础
02
古建筑木构件损伤模 式
04 评估因素分析
05 评估流程
07 参考内容
目录
06 结论与建议
古建筑木构件剩余寿命评估：基 于累积损伤的视角
引言
引言
古建筑木构件作为历史文化遗产的重要组成部分，具有极高的艺术、历史和 经济价值。然而，由于长期遭受环境侵蚀、使用磨损等因素影响，古建筑木构件 的寿命逐渐缩短。为了更好地保护这些珍贵的文化遗产，评估古建筑木构件的剩 余寿命具有重要意义。本次演示将围绕古建筑木构件的损伤模式、剩余寿命评估 基础、评估因素分析及评估流程展开讨论。
结果分析
同时，我们也对模型进行了误差分析和可靠性评估。发现模型的预测结果与 实际情况基本一致，误差在可接受范围内。但是，我们也指出模型存在的局限性， 如数据不足、某些因素未被考虑等，这可能对模型的预测结果产生一定影响。

一种基于随机森林算法的探明储量预测新方法摘要传统的哈伯特模型、翁氏模型等预测方法主要采用一元多项式拟合储量增长趋势，无法解决多变量对储量预测的影响，使得预测结果与客观实际存在较大差距。

文章基于随机森林机器学习模型，建立了一种预测累计探明储量增长趋势的新方法。

该方法通过相关性分析找出影响探明储量增长的可量化指标，从而确定模型训练中的输入属性，以同类盆地油田年度累计探明储量为评价单元，建立随机森林机器学习样本数据集，通过调整决策树个数和单个决策树的最大特征数，对模型进行优化训练，从而建立累计探明储量预测模型，成功解决了多因素叠加下储量非线性增长预测的难题。

该方法在东部断陷盆地油田年度累计探明储量预测中应用成效显著，预测模型拟合的准确率达到88.19%,具有巨大的推广应用价值。

关键词：机器学习；随机森林算法；储量增长趋势；东部断陷盆地；油田年度累计探明储量O引言储量是勘探工作的目标和导向，采用科学的方法预测储量增长趋势和合理确定储量指标对于油公司发展规划编制和勘探工作部署制定具有至关重要的意义。

传统的油气储量增长趋势的预测方法包括基于生命旋回的哈伯特模型、翁氏模型、逻辑斯谛模型、高斯模型等，以及基于概率论与蒙特卡洛统计模拟法的油田规模序列法”51,这些方法在国外广泛应用，国内油公司在学习、引进这些方法的同时，也在实际应用过程中建立了适合本地区储量增长特征的方法，例如对储量发现历史数据进行拟合的“帚状”预测模型以及针对勘探发现中储量“多峰”增长问题建立的多旋回哈伯特模型、多旋回高斯模型等51.现有的方法技术存在的主要问题包括：目前广泛应用的哈伯特模型、翁氏模型等预测的是盆地整个油气勘探生命旋回的资源量、最终探明储量，无法有效解决中短期储量增长预测的问题；现有的预测方法主要研究对象为单一盆地或凹陷，缺少对同种类型盆地的研究；目前的方法主要采用一元多项式拟合储量增长趋势，无法解决多变量对储量预测的影响，使得预测结果与客观实际存在较大差距。

统计学中的回归树模型统计学是一门研究数据收集、分析和解释的学科，而回归树模型是其中一种重要的方法。

回归树模型通过将数据集划分为不同的区域，每个区域内的数据具有相似的特征，从而建立了一棵树状结构。

本文将介绍回归树模型的基本原理、应用场景以及优缺点。

一、回归树模型的基本原理回归树模型的基本原理是通过将自变量空间划分为多个矩形区域，每个区域内的数据具有相似的特征。

在构建回归树时，首先选择一个自变量作为划分变量，并选择一个划分点将数据集分为两部分。

然后，对每个子集重复上述过程，直到满足某个停止准则为止。

最终，每个叶节点都对应一个区域，该区域内的数据通过叶节点上的平均值来预测。

回归树模型的构建过程可以用以下步骤总结：1. 选择一个自变量作为划分变量。

2. 选择一个划分点将数据集分为两部分。

3. 对每个子集重复上述过程，直到满足某个停止准则为止。

4. 每个叶节点对应一个区域，通过叶节点上的平均值来预测。

二、回归树模型的应用场景回归树模型在实际应用中有着广泛的应用场景。

以下是几个常见的应用场景：1. 房价预测：回归树模型可以通过房屋的各种特征（如面积、地理位置等）来预测房价。

通过构建回归树模型，可以将数据集划分为不同的区域，每个区域内的房屋具有相似的特征和价格水平。

2. 股票价格预测：回归树模型可以通过分析股票的历史数据（如交易量、市盈率等）来预测未来的股票价格。

通过构建回归树模型，可以将数据集划分为不同的区域，每个区域内的股票具有相似的特征和价格趋势。

3. 用户行为分析：回归树模型可以通过分析用户的行为数据（如点击量、购买量等）来预测用户的行为。

通过构建回归树模型，可以将数据集划分为不同的区域，每个区域内的用户具有相似的行为特征。

三、回归树模型的优缺点回归树模型作为一种常用的统计学方法，具有以下优点：1. 解释性强：回归树模型可以将数据集划分为不同的区域，每个区域内的数据具有相似的特征，从而更容易理解和解释模型的结果。

3、生物：在生物学领域中，回归树模型可以用于预测生物体的特征和行为。 例如，通过分析基因组数据和环境因素，可以构建回归树模型来预测生物体的表 型特征和行为表现。
4、化学：在化学领域中，回归树模型可以用于预测分子的性质和反应。例 如，通过分析分子的结构和使用量行为。
技术研究
回归树模型是一种基于决策树的预测模型，通过构建一棵树形结构来预测目 标变量的值。回归树模型的优点包括：能够处理各种类型的数据、对数据的预处 理要求较低、易于理解和解释等。然而，回归树模型也存在一些缺点，如容易过 拟合、对噪声数据敏感等。
回归树模型的应用范围非常广泛，可以用于预测连续型的输出变量，如温度、 价格、销售额等。与其他的机器学习模型相比，回归树模型具有较低的复杂度和 易于解释的优点，因此在很多领域都得到了广泛的应用。
未来展望
随着技术的发展和应用的深入，回归树模型的研究和应用也将不断发展和创 新。未来，回归树模型的研究将更加注重以下几个方面：
1、模型的优化：回归树模型的性能和精度还有很大的提升空间。未来将会 有更多的研究致力于优化模型的训练过程和剪枝策略，以减少模型的过拟合和提 高预测精度。
2、多变量预测：目前大多数回归树模型主要处理单变量预测问题。未来， 研究者们将更加注重如何处理多变量预测问题，以实现对更复杂系统的精确预测。
结论
回归树模型作为一种重要的机器学习模型，在各个领域得到了广泛的应用。 本次演示对回归树模型的技术研究、方法与算法、应用场景以及未来发展进行了 深入的探讨。总结来说，回归树模型具有广泛的应用前景和发展空间，值得我们 进一步研究和应用。
感谢观看
在算法方面，常见的回归树模型算法包括：CART（Classification and Regression Trees）、C4.5、ID3等。这些算法的主要区别在于如何选择最优划 分属性，以及如何处理树的剪枝过程。

一元线性回归模型1．一元线性回归模型有一元线性回归模型（统计模型）如下，y t = 0 + 1 x t + u t上式表示变量y t 和x t之间的真实关系。

其中y t 称被解释变量（因变量），x t称解释变量（自变量），u t称随机误差项， 0称常数项， 1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t) = 0 + 1 x t,（2）随机部分，u t。

图2.1 真实的回归直线这种模型可以赋予各种实际意义，收入与支出的关系；如脉搏与血压的关系；商品价格与供给量的关系；文件容量与保存时间的关系；林区木材采伐量与木材剩余物的关系；身高与体重的关系等。

以收入与支出的关系为例。

假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。

但实际上数据来自各个家庭，来自各个不同收入水平，使其他条件不变成为不可能，所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。

随机误差项u t中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。

所以在经济问题上“控制其他因素不变”是不可能的。

回归模型的随机误差项中一般包括如下几项内容，（1）非重要解释变量的省略，（2）人的随机行为，（3）数学模型形式欠妥，（4）归并误差（粮食的归并）（5）测量误差等。

回归模型存在两个特点。

（1）建立在某些假定条件不变前提下抽象出来的回归函数不能百分之百地再现所研究的经济过程。

（2）也正是由于这些假定与抽象，才使我们能够透过复杂的经济现象，深刻认识到该经济过程的本质。

通常线性回归函数E(y t) = 0 + 1 x t是观察不到的，利用样本得到的只是对E(y t) = 0 + 1 x t 的估计，即对 0和 1的估计。

在对回归函数进行估计之前应该对随机误差项u t做出如下假定。

(1) u t 是一个随机变量，u t 的取值服从概率分布。