大学物理波动学公式集复习课程
- 格式:doc
- 大小:111.50 KB
- 文档页数:6


大学物理波动课件引言波动是物理学中的一个重要概念,涉及到的领域广泛,包括声波、电磁波、机械波等。
本文旨在介绍大学物理中波动的基本概念、波动方程、波动特性以及波动在各个领域的应用,以帮助读者更好地理解和掌握波动知识。
一、波动的基本概念1.1波的定义波是一种能量传递的方式,它是由振源产生的振动在介质中传播的过程。
波可以分为两大类:机械波和电磁波。
机械波需要介质来传播,如声波和水波;而电磁波不需要介质,可以在真空中传播,如光波和无线电波。
1.2波的参数波的参数包括波长、波速、频率和振幅。
波长是相邻两个波峰(或波谷)之间的距离,通常用λ表示;波速是波在介质中传播的速度,通常用v表示;频率是单位时间内通过某一点的完整波的个数,通常用f表示;振幅是波的振动幅度,即波的最大偏离度。
二、波动方程2.1机械波方程机械波的波动方程可以表示为:y=Asin(2πft2πx/λ+φ)其中,y表示介质中某一点的位移,A表示振幅,f表示频率,λ表示波长,x表示该点距离振源的距离,φ表示初相位。
2.2电磁波方程电磁波的波动方程可以表示为:E=E0sin(2πft2πx/λ+φ)其中,E表示电场强度,E0表示振幅,其他参数与机械波方程相同。
三、波动特性3.1干涉干涉是指两个或多个波相遇时,它们的振动叠加产生的现象。
当两个波峰相遇时,振动加强;当波峰与波谷相遇时,振动减弱。
干涉现象广泛应用于光学、声学等领域。
3.2衍射衍射是指波传播过程中遇到障碍物或通过狭缝时,波的传播方向发生改变的现象。
衍射现象广泛应用于光学、声学等领域,如光栅、声呐等。
3.3折射折射是指波从一种介质传播到另一种介质时,波的传播方向发生改变的现象。
折射现象广泛应用于光学领域,如透镜、棱镜等。
3.4反射反射是指波遇到界面时,部分能量返回原介质的现象。
反射现象广泛应用于光学、声学等领域,如镜子、回声等。
四、波动应用4.1声学领域波动在声学领域有着广泛的应用,如声音的产生、传播、接收和利用。

大学物理波动光学知识点总结.doc波动光学是物理学中的重要分支,涉及到光的反射、折射、干涉、衍射等现象。
作为大学物理中的一门必修课程,波动光学是大学物理知识体系重要的组成部分。
以下是相关的知识点总结:1. 光的波动性光可以被看作是一种电磁波。
根据电磁波的性质,光具有波动性,即能够表现出干涉、衍射等现象。
光的波长决定了其在物质中能否传播和被发现。
2. 光的反射光在与物体接触时会发生反射。
根据反射定律,发射角等于入射角。
反射给人们带来很多视觉上的感受和体验,如反光镜、镜子等。
当光从一种介质向另一种介质传播时,光的速度和方向都会发生改变,这个现象称为折射。
光在空气、玻璃、水等介质中的折射现象被广泛应用到光学、通信等领域中。
4. 光的干涉当两束光相遇时,它们会相互干涉,产生干涉条纹。
这是因为两束光的干涉条件不同,它们之间产生了相位差,导致干涉现象。
干涉可以分为光程干涉和振幅干涉。
光经过狭缝或小孔时,其波动性会导致光将会分散成多个波阵面。
这种现象称为衍射。
衍射可以改变光的方向和能量分布,被广泛应用于成像和光谱分析等领域。
6. 偏振偏振是光波沿着一个方向振动的现象,产生偏振的方式可以通过折射、反射、散射等途径实现。
光的偏振性质在光学通信、材料研究等领域有着广泛的应用。
总结波动光学是大学物理学知识体系不可或缺的一部分,它涉及到光的波动性、光的反射、折射、干涉、衍射等现象。
对于工程、光学、材料等领域的学生和研究者来说,深入了解波动光学的基本原理和理论,都有助于提高知识和技术水平。


波动光学公式复习波动光学是物理学的一个分支,研究光的传播和相互作用的波动性质。
波动光学的基础是波动理论,利用波动方程和边界条件,可以推导出一系列关于光波的性质,并且与实验结果相符。
在本篇复习中,我将回顾波动光学的一些重要公式。
1.波动方程波动方程是描述波的传播的微分方程。
对于光波,我们可以采用波动方程来描述光的传播行为。
波动方程如下:∇^2ψ-1/c^2∂^2ψ/∂t^2=0其中,∇^2是拉普拉斯算子,ψ是波函数,c是光速。
2.平面波的描述平面波是具有相同频率和波矢的波,具有以下形式的解析表达式:ψ(x,t) = A * e^(i(kx - ωt))其中,A是振幅,k是波矢,x是位置,ω是角频率,t是时间。
平面波描述了波的传播过程,并且可以通过叠加多个平面波得到复杂的波形。
3.折射定律折射定律描述了光线从一个介质射入另一个介质时的偏折现象。
根据斯涅耳定律,入射角i和折射角r满足以下关系:n1 * sin(i) = n2 * sin(r)其中,n1和n2分别是两个介质的折射率。
折射定律告诉我们光线由一种介质传输到另一种介质时的偏折角度,进而影响到光的传播方向。
4.衍射公式衍射是光线通过一个较小孔径或障碍物后产生的弯曲现象。
根据菲涅尔衍射公式,衍射极大值的位置可以由以下方程给出:sin(θ) = nλ/a其中,θ是衍射角,λ是光的波长,a是孔径或障碍物的大小。
衍射公式告诉我们衍射现象的出现与波长、孔径或障碍物的大小有关。
5.直线偏振光直线偏振光是在一个平面上振动的光波,具有以下表达式:ψ(x,t) = A * cos(kx - ωt + φ)其中,A是振幅,k是波矢,x是位置,ω是角频率,t是时间,φ是相位差。
直线偏振光是光学中常见的一种偏振光,其振动方向是固定的。
6.光的干涉干涉是当两束或多束光波相遇时,它们会叠加产生明暗相间的条纹。
根据叠加原理,两束光波的干涉可以通过相干光的波函数叠加得出:ψ(x,t)=ψ1(x,t)+ψ2(x,t)其中,ψ1和ψ2是两束光波的波函数。





⼤学物理波动学公式集复习课程⼤学物理波动学公式集⼤学物理波动学公式集波动学1.定义和概念简谐波⽅程: x 处t 时刻相位振幅ξ=Acos(ωt+φ-2πx/λ) 简谐振动⽅程:ξ=Acos(ωt+φ)=Acos(2πx/λ+φ′)相位Φ——决定振动状态的量振幅A ——振动量最⼤值决定于初态x0=Acos φ初相φ——x=0处t=0时相位(x 0,V 0) V 0= –A ωsin φ频率ν——每秒振动的次数圆频率ω=2πν决定于波源如:弹簧振⼦ω=mk / 周期T ——振动⼀次的时间单摆ω=l g / 波速V ——波的相位传播速度或能量传播速度。
决定于介质如:绳V=µ/T 光速V=C/n空⽓V=ρ/B波的⼲涉:同振动⽅向、同频率、相位差恒定的波的叠加。
光程:L=nx(即光⾛过的⼏何路程与介质的折射率的乘积。
相位突变:波从波疏媒质进⼊波密媒质时有相位π的突变(折合光程为λ/2)。
拍:频率相近的两个振动的合成振动。
驻波:两列完全相同仅⽅向相反的波的合成波。
多普勒效应:因波源与观察者相对运动产⽣的频率改变的现象。
衍射:光偏离直线传播的现象。
⾃然光:⼀般光源发出的光偏振光(亦称线偏振光或称平⾯偏振光):只有⼀个⽅向振动成份的光。
部分偏振光:各振动⽅向概率不等的光。
可看成相互垂直两振幅不同的光的合成。
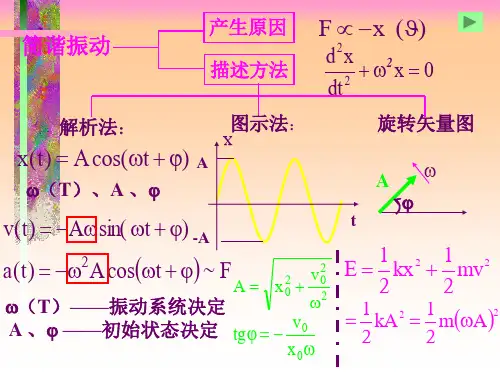
2.⽅法、定律和定理①旋转⽮量法:如图,任意⼀个简谐振动ξ=Acos(ωt+φ)可看成初始⾓位置为φ以ω逆时针旋转的⽮量A 在x⽅向的投影。
相⼲光合成振幅:A=φ?++cos 2212221A A A A其中:Δφ=φ1-φ2–λπ2(r 2–r 1当φ1-φ2=0时,光程差δ=(r 2–r 1②惠更斯原理:波⾯⼦波的包络⾯为新波前。
(⽤来判断波的传播⽅向)③菲涅尔原理:波⾯⼦波相⼲叠加确定其后任⼀点的振动。
④*马吕斯定律:I 2=I 1cos 2θ⑤ *布儒斯特定律:。
大学物理波动学公式
集
大学物理波动学公式集
波动学 1.
定义和概念
简谐波方程: x 处t 时刻相位 振幅
ξ=Acos(ωt+φ-2π
x/λ
) 简谐振动方程:ξ=Acos(ωt+φ)
=Acos(2πx/λ+φ′)
相位Φ——决定振动状态的量
振幅A ——振动量最大值 决定于初态 x0=Acos φ 初相φ——x=0处t=0时相位 (x 0,V 0) V 0= –A ωsin φ 频率ν——每秒振动的次数
圆频率ω=2πν 决定于波源如: 弹簧振子ω=m
k /
周期T ——振动一次的时间 单摆ω=
l
g /
波速V ——波的相位传播速度或能量传播速度。
决定于介质如: 绳V=μ
/T
光速V=C/n
空气V=
ρ
/B
波的干涉:同振动方向、同频率、相位差恒定的波的叠加。
光程:L=nx(即光走过的几何路程与介质的折射率的乘积。
相位突变:波从波疏媒质进入波密媒质时有相位π的突变(折合光程为λ/2)。
拍:频率相近的两个振动的合成振动。
驻波:两列完全相同仅方向相反的波的合成波。
多普勒效应:因波源与观察者相对运动产生的频率改变的现象。
衍射:光偏离直线传播的现象。
自然光:一般光源发出的光
偏振光(亦称线偏振光或称平面偏振光):只有一个方向振动成份的光。
部分偏振光:各振动方向概率不等的光。
可看成相互垂直两振幅不同的光的合成。
2. 方法、定律和定理 ①
旋转矢量法:
如图,任意一个简谐振动ξ=Acos(ωt+φ)可看成初始角位置为φ以ω逆时针旋转的矢
量A
在x方向的投影。
相干光合成振幅: A=φ
∆++cos 2212
22
1A A A A
其中:Δφ=φ1-φ2–λπ2(r 2–r 1当φ1-φ2=0时,光程差δ=(r 2–r 1 ② 惠更斯原理:波面子波的包络面为新波前。
(用来判断波的传播方向) ③
菲涅尔原理:波面子波相干叠加确
定其后任一点的振动。
④ *马吕斯定律:I 2=I 1cos 2θ ⑤
*布儒斯特定律:
当入射光以I p 入射角入射时则反射光为垂直入射面振动的完全偏振光。
I p 称布儒斯特角,其满足: tg i p = n 2/n 1 3.
公式
振动能量:E k =mV 2/2=E k (t) E= E k +E p =kA 2
/2 E p =kx 2/2= (t)
*波动能量:2221A ρωω=
I=V A V 2221
ρωω=∝A 2
*驻波:
波节间距d=λ/2 基波波长λ0=2L 基频:ν0=V/
λ0=V/2L;
谐频:ν=nν0
*多普勒效应: 机械波ν
νs
R
V V V V -+=
'(V R ——观察者速度;V s ——波源速度) 对光波ν
νr
r
V C V C +-=
'
其中V r 指光源与观察者相对速度。
杨氏双缝: dsin θ=kλ(明纹) θ≈sin θ≈y/D 条纹间距Δy=D/λd
单缝衍射(夫琅禾费衍射): asin θ=kλ(暗纹) θ≈sin θ≈y/f
瑞利判据:
θmin =1/R =1.22λ/D (最小分辨角) 光栅:
dsin θ=kλ(明纹即主极大满足条件) tg θ=y/f
d=1/n=L/N (光栅常数) 薄膜干涉:(垂直入射)
δ反=2n2t+δ0
δ0= 0 中 λ/2
极 增反:δ反=(2k+1)λ/2 增透:δ反=k λ
其中:2
211c v -
=
γ因V 总小于C 则γ≥0所以称其为膨胀因子;称β=2
2
1c
v -为收缩因子。
3.狭义相对论的时空观:
①同时的相对性:由Δt=γ(Δt’+v Δx’/c 2),Δt’=0时,一般Δt ≠0。
称x’/c 2为同时性因子。
②运动的长度缩短:Δx=Δx’/γ≤Δx ′ ③运动的钟变慢:Δt=γΔt’≥Δt ′ 4.几个重要的动力学关系: ① 质速关系m=γm 0
② 质能关系E=mc 2 粒子的静止能量为:E 0=m 0c 2 粒子的动能为:E K =mc 2 – m 0c 2= ++=
--
2
402
0212
082)111(
2
2c
V m V
m c m c v 当V<<c 时,E K ≈mV 2/2 *③ 动量与能量关系:E 2–p 2c 2=E 02 *5.速度变换关系:
Σ’系→Σ系: '
1'2x c v x x u v
u u ++= '11'2
2
x c v c v y y u u u +-= '11'2
2
x c v
c v z z u u u +-= Σ系→Σ’系:'
1'2x c v x x u v
u u --= '11'22x c v c v y y u u u --= '11'22
x c v c v z z u u u --=。