静电场中的电偶极子
- 格式:ppt
- 大小:223.50 KB
- 文档页数:2

1、问题的提出近年来,电磁学研究,尤其是电磁学的一些分支前沿学科的研究,例如,电磁散射、计算电磁学、瞬态电磁学等,取得了较大的进展。
随着量子力学的发展和Aharonov-Bohm 效应的发现,人们发现仅采用磁感应强度B 来描述磁场是不够的,它不能解释电子在外磁场中的干涉和散射等现象。
而经典电磁场理论认为运动电荷受到电场力和磁场力的作用,且只有电场强度E 和磁感应强度B 对运动电荷有作用,而不是电磁势A 。
一般认为电磁势A 始终只被看作是数学上的需要而引入的参数。
带电粒子在外磁场中的动力学行为是否会受到矢势A 的直接影响?电磁势A 的影响是否可以独立于磁感应强度B 出现干涉的量子效应?研究人员针对以上问题展开了讨论。
定义电磁势为()A x π=⎰μIdl4r。
式中, r=x-x'为源点到场点的距离,I 为圆环的电流,dl 为线元。
它由磁场的高斯定理推导出,符合式⋅⋅⎰⎰ Adl=Bds。
但此式不唯一,可以加上任意标题函数的梯度。
由于梯度的环路积分恒等于0,可以有无数个电磁势的形式。
这叫做电磁势的规范变换。
而电偶极子是电磁理论与实际生活中经常碰到的一种带电体系,例如,在外电场作用下电介质的原子里正、负电荷即形成电偶极子;无线电天线里电子作周期性运动形成振荡偶极子。
电偶极子是指一对等量异号的点电荷,它们之间的距离l 远小于场点到它们的距离r,其中电偶极矩用p=ql 表示。
在实际生活中,电偶极子的例子经常可以碰到。
匀速直线运动是电偶极子常见的运动形式,因此研究它所产生的电场和磁场具有重要的意义。
例如,天体上的电偶极子所产生的电磁场将对在其附近飞行的宇宙飞船影响甚大。
本文首先利用平面内场强叠加原理和相对论的变换关系,分别计算电偶极子在二维平面内的做沿轴线和沿中垂线匀速运动的电场,然后再由静止电偶极子电磁势出发,计算出电偶极子在惯性系Σ中的电磁势,最后利用(A,φ)和(E,B)关系,即可得出实验室坐标系Σ中匀速运动的电偶极子的电场和磁场在三维空间内的分布。




收稿日期:2003-06-14作者简介:吕宽州(1963-),男,河南扶沟人,郑州经济管理干部学院讲师。
文章编号:1004-3918(2003)05-0512-03电偶极子的场及辐射吕宽州1,姜俊2(1.郑州经济管理干部学院,河南郑州450053;2.河南省科学院,河南郑州450002)摘要:采用了镜像法等方法对电偶极子及其产生的静电场、电磁场及辐射等做了较系统和深入的分析、研究,使分析方便、简化,推出的结论有一定实际指导意义。
关键词:电偶极子;电场;磁场;辐射中图分类号:0442文献标识码:A在很多文献上,缺乏对电偶极子及其产生的静电场、电磁场及辐射等较系统和深入的分析、研究。
本文参考有关文献给出或分析、推出了重要结论,部分内容采用了镜像法,使分析更方便。
!电偶极子及其产生的静电场电偶极子由一对正、负点电荷组成,电量为l ,相距为l ,如图1所示。
其电偶极矩p =l l ,l 的方向由~l 指向+l ,在T 处产生的电场的电势为:#(r )=l 4L e 0T +_l4L e 0T _当T !l 时,#(r )=l l cOs 64L e 0T 2=p ·e r 4L e 0T2(1)电场强度为:E =_"@=e r P cOs 62L e 0T 3+e !P si n 64L e 0T3(2)以上结果表明,电偶极子的电势及电场强度的大小分别与距离的平方、三次方成反比,既存在于近区,且与方位角有关,这些特点都与点电荷的电场显著不同。
图2绘出了电偶极子的电力线与等位面。
图1电偶极子F i g .1E lectric d i p O le图2电偶极子的电力线与等位线F i g .2E lectric p Ow er li ne and e C ui p Otential p laneOf e lectric d i p O le第21卷第5期2003年10月河南科学HENAN SC I ENCEV O l.21N O.50ct .2003!电偶极子产生的电磁场及辐射当P =P 0e -j G t 时,为谐振电偶极子,P 0为常矢,则在近区,即l H T 时,主要地一方面将感应如上所述的静电场,另一方面,相当于I =j G C 、长为l 的电流元还将产生一稳恒磁场,其规律可用毕萨定律描述,且电场与磁场的相位相差为90 ,即电场能量与磁场能量相互转换,而平均波印亭矢量为零,故不产生辐射。
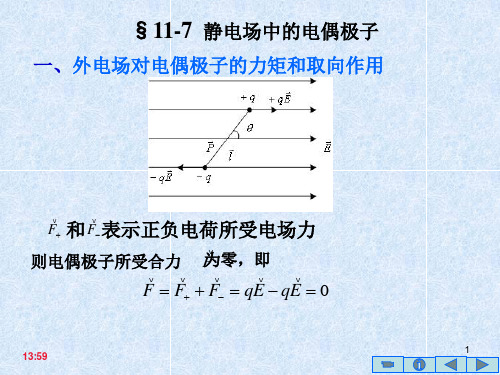
第12讲等势面电势梯度静电场中的电偶极子电场线与等势面的关系♉电场线处处垂直等势面♉电场线指向电势降的方向♉等势面的疏密反映了场的强弱电场强度和电势的关系积分关系式⎰⋅=b a a l Ed ϕ0=b ϕ微分关系式ϕϕ-∇=-=g ra d Ek z j y i x ˆˆˆ∂∂+∂∂+∂∂=∇ϕϕϕϕ电偶极子( )在电场( )中所受的力矩 Ep M ⨯=电偶极子( )在均匀外场( )中的势能 Ep W ⋅-=E p E p 电场中的电偶极子O 图中所示以 O 为心的各球冠面为静电场的等势面,已知ϕ1 < ϕ2 < ϕ3,在图上画出 a 、b 两点的电场强度的方向,并比较它们的大小。
E a E b(填 <、=、>)。
ϕ1 ϕ2 ϕ3 a b = a E b E Q3.12.11.若静电场的某个区域电势等于恒量,则该区域的电场强度分布是 ;若电势随空间坐标作线性变化,则该区域的场强分布是 。
处处为零 不为零的恒量(或均匀分布) Q3.12.2设有两个电偶极矩分别为 和 的电偶极子。
如果它们重叠在一起,此带电系统的电偶极矩为多少? 答:1p 2p Q3.12.3221121l q l q p p p+=+=Q3.12.4电偶极子在均匀电场中总要使自身转向稳定平衡的位置,若此电偶极子处在非均匀电场中,它将怎样运动呢?你能说明吗?答:见视频。
[Q3.12.5] 证明 Q1.3.7 中的电四极子在它的轴线延长线上的电势为式中 Q = 2ql 2 叫做它的电四极矩。
利用梯度验证,所得场强公式与Q1.3.7一致。
)(l r r Q >>= π4130εϕ+q P-2q +q l l r解: 根据电势的叠加原理⎪⎭⎫ ⎝⎛--++=r l r l r q 211π40εϕ+q P-2q +q l l r2π422220)()()()(l r r l r l r r l r r q ---++-=ε)(22202π4l r r l q -=ε当 l << r 时, 30π4r Qεϕ≈r E ∂∂-=ϕ40π43r Q ε=[Q3.12.5]* 电偶极层: 一厚度 l 均匀的曲面薄壳,两面带有符号相反的面电荷 。