【授课】第二章知识点复习

浙教版九年级上册数学第二章本章复习课（解析版）本章复习课_类型之一随机事件1．[2019·长沙]下列说法正确的是(D)A．检测某批次灯泡的使用寿命，适宜用全面调查B．可能性是1%的事件在一次试验中一定不会发生C．数据3，5，4，1，－2的中位数是4D．“367中有2人同月同日出生”为必然事件【解析】A．检测某批次灯泡的使用寿命，调查具有破坏性，应采用抽样调查，此选项错误；B.可能性是1%的事件在一次试验中可能发生，，5，4，1，－2的中位数是3，此选项错误；D.“367中有2人同月同日出生”为必然事件，此选项正确．类型之二概率的意义与计算2．[2019·贺州]从分别标有数－3，－2，－1，0，1，2，3的七张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数的绝对值不小于2的概率是(D)A.17 B.27 C.37 D.473．[2019·杭州]已知一包糖果共有5种颜色(糖果只有颜色差别)，如图2－1是这包糖果颜色分布百分比的统计图，在这包糖果中任意取一粒，则取出糖果的颜色为绿色或棕色的概率是__12__．图2－1【解析】棕色所占的百分比为1－20%－15%－30%－15%＝1－80%＝20%，∴P(绿色或棕色)＝30%＋20%＝50%＝1 2.类型之三用树状图或列表法求概率4．[2019·株洲]三名九年级学生坐在仅有的三个座位上，起身后重新就坐，恰好有两名同学没有坐回原座位的概率为(D)A.19 B.16 C.14 D.12【解析】列表(用A，B，C表示三位同学，用a，b，c表示他们原来的座位)共有6种等可能的结果数，其中恰好有两名同学没有坐回原座位的结果数为3，所以恰好有两名同学没有坐回原座位的概率＝36＝12.5．[2019·泰州]在学校组织的朗诵比赛中，甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛，抽签规则是：在3个相同的标签上分别标注字母A，B，C，各代表1篇文章，一名学生随机抽取一个标签后放回，另一名学生再随机抽取．用画树状图或列表的方法列出所有等可能的结果，并求甲、乙抽中同一篇文章的概率．解：画树状图如答图，第5题答图所有等可能的结果有9种，甲、乙抽中同一篇文章的情况有3种，概率为39＝13.6．[2019·衡阳]有四张背面完全相同的纸牌A，B，C，D，其中正面分别画有四个不同的几何图形(如图2－2)，小华将这四张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸一张．(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A，B，C，D 表示)；(2)求摸出两张纸牌牌面上所画几何图形，既是轴对称图形又是中心对称图形的概率．图2－2解：(1)画树状图如答图，第6题答图则共有16种等可能的结果；(2)∵既是中心对称又是轴对称图形的只有B，C，∴既是轴对称图形又是中心对称图形的有4种情况，∴既是轴对称图形又是中心对称图形的概率为416＝14.类型之四用频率估计概率7．[2019·眉山]一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球．若红球个数是黑球个数的2倍多40个．从袋中任取一个球是白球的概率是1 29.(1)求袋中红球的个数；(2)求从袋中任取一个球是黑球的概率．解：(1)290×129＝10(个)，290－10＝280(个)，(280－40)÷(2＋1)＝80(个)，280－80＝200(个)．故袋中红球的个数是200个；(2)80÷290＝8 29.答：从袋中任取一个球是黑球的概率是8 29.类型之五概率在实际生活中的应用8．[2019·枣庄]为发展学生的核心素养，培养学生的综合能力，某学校计划开设四门选修课：乐器、舞蹈、绘画、书法，学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门)．对调查结果进行整理，绘制成如图2－3的两幅不完整的统计图，请结合图中所给信息解答下列问题：图2－3(1)本次调查的学生共有__50__人，在扇形统计图中，m的值是__30%__；(2)将条形统计图补充完整；(3)在被调查的学生中，选修书法的有2名女同学，其余为男同学，现要从中随机抽取2名同学代表学校参加某社区组织的书法活动，请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率．解：(1)20÷40%＝50(人)，15÷50＝30%；(2)50×20%＝10(人)，50×10%＝5(人)，补全条形统计图如答图；第8题答图(3)∵5－2＝3(名)，∴选修书法的5名同学中，有3名男同学，2名女同学，列表如下：男1男2男3女1女2 男1——男2男1男3男1女1男1女2男1男2男1男2——男3男2女1男2女2男2男3男1男3男2男3——女1男3女2男3女1男1，女1男2女1男3女1——女2女1女2男1女2男2女2男3女2女1女2——所有等可能的情况有20种，其中抽取的2名同学恰好是1名男同学和1名女同学的情况有12种， 则P (一男一女)＝1220＝35. 类型之六 概率与方程(组)、几何、统计等知识的综合运用9．从3，0，－1，－2，－3这5个数中，随机抽取1个数，作为函数y ＝(5－m 2)x 和关于x 的方程(m ＋1)x 2＋mx ＋1＝0中m 的值，恰好使所得函数的图象经过第一、三象限，且方程有实数根的概率为__25__．【解析】 ∵所得函数的图象经过第一、三象限， ∴5－m 2＞0，∴m 2＜5，∴3，0，－1，－2，－3中，3和－3均不符合题意． 将m ＝0代入(m ＋1)x 2＋mx ＋1＝0，得x 2＋1＝0， b 2－4ac ＝－4＜0，无实数根；将m ＝－1代入(m ＋1)x 2＋mx ＋1＝0，得－x ＋1＝0，解得x ＝1，有实数根； 将m ＝－2代入(m ＋1)x 2＋mx ＋1＝0，得x 2＋2x －1＝0，b 2－4ac ＝4＋4＝8＞0，有实数根． ∴所求的概率为25.10．一个不透明的袋子里装有编号分别为1，2，3的球(除编号以外，其余都相同)，其中1号球1个，3号球3个，从中随机摸出1个球是2号球的概率为13.(1)求袋子里2号球的个数；(2)甲、乙两人分别从袋中摸出1个球(不放回)，甲摸出球的编号记为x ，乙摸出球的编号记为y ，用列表法求点A (x ，y )在直线y ＝x 下方的概率． 解：(1)设袋子里2号球的个数为x ， 则x 1＋x ＋3＝13，解得x ＝2，经检验，x ＝2为所列方程的解， ∴袋子里2号球的个数为2； (2)列表：x (x ，y )122333y1(2，1)(2，1)(3，1)(3，1)(3，1) 2(1，2)(2，2)(3，2)(3，2)(3，2) 2(1，2)(2，2)(3，2)(3，2)(3，2) 3(1，3)(2，3)(2，3)(3，3)(3，3) 3(1，3)(2，3)(2，3)(3，3)(3，3) 3(1，3)(2，3)(2，3)(3，3)(3，3)∴共有30种等可能的结果，其中点在直线y＝x下方的有(2，1)，(2，1)，(3，1)，(3，1)，(3，1)，(3，2)，(3，2)，(3，2)，(3，2)，(3，2)，(3，2)，共11种，∴点A(x，y)在直线y＝x下方的概率P＝11 30.。

人教版高中数学必修二第二章知识点汇总第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系2.1.11 平面含义：平面是无限延展的2 平面的画法及表示（1）平面的画法：水平放置的平面通常画成一个平行四边形，锐角画成450，且横边画成邻边的2倍长（如图）（2）平面通常用希腊字母α、β、γ等表示，如平面α、平面β等，也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示，如平面AC 、平面ABCD 等。

3 三个公理：（1）公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内符号表示为A∈LB∈L => L α A∈α B∈αLA· α DCBAα公理1作用：判断直线是否在平面内（2）公理2：过不在一条直线上的三点，有且只有一个平面。

符号表示为：A 、B 、C 三点不共线 => 有且只有一个平面α， 使A∈α、B∈α、C∈α。

公理2作用：确定一个平面的依据。

（3）公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

符号表示为：P∈α∩β =>α∩β=L，且P∈L 公理3作用：判定两个平面是否相交的依据 2.1.2空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系：相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点。

2 公理4：平行于同一条直线的两条直线互相平行。

符号表示为：设a 、b 、c 是三条直线a∥bC·B ·A· α P·αLβ共面直线 =>a ∥cc∥b强调：公理4实质上是说平行具有传递性，在平面、空间这个性质都适用。

公理4作用：判断空间两条直线平行的依据。

3 等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补4 注意点：① a'与b'所成的角的大小只由a 、b 的相互位置来确定，与O 的选择无关，为简便，点O 一般取在两直线中的一条上；② 两条异面直线所成的角∈(0， )；③ 当两条异面直线所成的角是直角时，我们就说这两条异面直线互相垂直，记作a⊥b； ④ 两条直线互相垂直，有共面垂直与异面垂直两种情形；⑤ 计算中，通常把两条异面直线所成的角转化为两条相交直线所成的角。

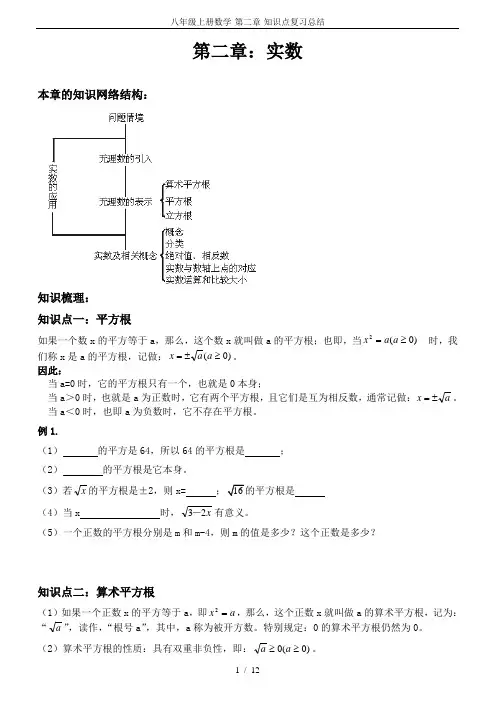
第二章：实数本章的知识网络结构：知识梳理： 知识点一：平方根如果一个数x 的平方等于a ，那么，这个数x 就叫做a 的平方根；也即，当)0(2≥=a a x 时，我们称x 是a 的平方根，记做：)0(≥±=a a x 。

因此：当a=0时，它的平方根只有一个，也就是0本身；当a ＞0时，也就是a 为正数时，它有两个平方根，且它们是互为相反数，通常记做：a x ±=。

当a ＜0时，也即a 为负数时，它不存在平方根。

例1.（1） 的平方是64，所以64的平方根是 ； （2） 的平方根是它本身。

（3）若x 的平方根是±2，则x= ；16的平方根是 （4）当x 时，x 23－有意义。

（5）一个正数的平方根分别是m 和m-4，则m 的值是多少？这个正数是多少？知识点二：算术平方根（1）如果一个正数x 的平方等于a ，即a x =2，那么，这个正数x 就叫做a 的算术平方根，记为：“a ”，读作，“根号a ”，其中，a 称为被开方数。

特别规定：0的算术平方根仍然为0。

（2）算术平方根的性质：具有双重非负性，即：)0(0≥≥a a 。

(3) 算术平方根与平方根的关系：算术平方根是平方根中正的一个值，它与它的相反数共同构成了平方根。

因此，算术平方根只有一个值，并且是非负数，它只表示为：a ；而平方根具有两个互为相反数的值，表示为：a ±。

例2.（1）下列说法正确的是 （ ）A ．1的立方根是1±；B ．24±=； C.81的平方根是3±； D.0没有平方根； （2）下列各式正确的是 （ ）A 、981±=B 、14.314.3-=-ππC 、3927-=-D 、235=- （3）2)3(-的算术平方根是 。

（4）若x x -+有意义，则=+1x ___________。

（5）已知△ABC 的三边分别是,,,c b a 且b a ,满足0)4(32=-+-b a ，求c 的取值范围。

第二章 一元二次方程教学目标1、灵活运用直接开平方法、配方法、公式法、因式分解法解一元二次方程，运用一元二次方程解决简单的实际问题．2、发展学生的独立思考能力和创新精神．3、本节主要是对一元二次方程进行系统复习，巩固所学知识，提升应用能力．重点难点重点：运用知识、技能解决问题；难点：解题分析能力的提高．教学过程一、知识网络图表 一元二次方程解法 直接开平方法 配方法 公式法 因式分解法 判别式 应用 列方程或方程组解应用题二、知识要点归纳（一）一元二次方程1、一元二次方程定义：含有一个未知数，并且未知数的最高次数是2的整式方程叫做一元二次方程。

2、一元二次方程的一般形式： )0(02≠=++a c bx ax 。

它的特征是：等式左边是一个关于未知数x 的二次多项式，等式右边是零； 其中2ax 叫做二次项，a 叫做二次项系数；bx 叫做一次项，b 叫做一次项系数；c 叫做常数项。

二、一元二次方程的解法 ：1、直接开平方法利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。

直接开平方法适用于解形如b a x =+2)(的一元二次方程。

根据平方根的定义可知， a x +是b 的平方根，当0≥b 时，b a x ±=+，b a x ±-=，当b<0时，方程没有实数根。

既：左边是一个完全平方式，右边是一个大于等于0的数例1： 降次—直接开平方法（将被开放式看作一个整体）212:(21)521=55125151,22x x x x x +=+±±-=---==例解：2、配方法配方法是一种重要的数学方法，它不仅在解一元二次方程上有所应用，而且在数学的其他领域也有着广泛的应用。

配方法的理论根据是完全平方公式：222)(2b a b ab a +=+±，把公式中的a 看做未知数x ，并用x 代替，则有222)(2b x b bx x ±=+±。

数学第二章知识点数学第二章知识点在日常过程学习中，是不是听到知识点，就立刻清醒了？知识点也不一定都是文字，数学的知识点除了定义，同样重要的公式也可以理解为知识点。

为了帮助大家掌握重要知识点，下面是店铺帮大家整理的数学第二章知识点，仅供参考，欢迎大家阅读。

数学第二章知识点1数轴的三要素：原点、正方向、单位长度(三者缺一不可)。

任何一个有理数，都可以用数轴上的一个点来表示。

(反过来，不能说数轴上所有的点都表示有理数)如果两个数只有符号不同，那么我们称其中一个数为另一个数的相反数，也称这两个数互为相反数。

(0的相反数是0)在数轴上，表示互为相反数的两个点，位于原点的侧，且到原点的距离相等。

数轴上两点表示的数，右边的总比左边的大。

正数在原点的右边，负数在原点的左边。

绝对值的定义：一个数a的绝对值就是数轴上表示数a的点与原点的距离。

数a的绝对值记作|a|。

正数的绝对值是它本身;负数的绝对值是它的数;0的绝对值是0。

或绝对值的性质：除0外，绝对值为一正数的数有两个，它们互为相反数;互为相反数的两数(除0外)的绝对值相等;任何数的绝对值总是非负数，即|a|0比较两个负数的大小，绝对值大的反而小。

比较两个负数的大小的步骤如下：①先求出两个数负数的绝对值;②比较两个绝对值的大小;③根据两个负数，绝对值大的反而小做出正确的判断。

绝对值的性质：①对任何有理数a，都有|a|0②若|a|=0，则|a|=0，反之亦然③若|a|=b，则a=b④对任何有理数a,都有|a|=|-a|有理数加法法则：①同号两数相加，取相同符号，并把绝对值相加。

②异号两数相加，绝对值相等时和为0;绝对值不等时取绝对值较大的数的符号，并用较大数的绝对值减去较小数的绝对值。

③一个数同0相加，仍得这个数。

加法的交换律、结合律在有理数运算中同样适用。

灵活运用运算律，使用运算简化，通常有下列规律：①互为相反的两个数，可以先相加;②符号相同的数，可以先相加;③分母相同的数，可以先相加;④几个数相加能得到整数，可以先相加。

教资科目二第二章必背知识点一、知识概述《教育的基本规律》①基本定义：教育的基本规律就是教育内部、教育与其他事物之间一些本质性的关系。

比如教育与人的发展规律，就是说教育如何影响人成长、发展的一些内在关系；教育与社会发展规律，则是阐述教育和社会中的政治、经济、文化等方面存在什么样的相互作用关系。

②重要程度：这部分是教资科目二第二章的核心内容，就相当于一栋房子的地基。

如果不掌握教育的基本规律，后面关于教学、德育等内容的理解都会受到影响，因为这些都要遵循这些基本规律。

③前置知识：需要了解一些基本的教育概念，像教育是什么、教育的目的之类的基础知识。

例如，知道教育是有目的地培养人的社会活动，这样有助于理解教育规律中教育与人的关系。

④应用价值：在实际教学过程中，依据教育与社会发展规律，可以知道根据社会的不同需求调整教学内容和方式。

比如现在社会强调创新能力，那教育就应该增加培养创新能力的课程和活动。

根据教育与人的发展规律，教师能根据学生的年龄特点和身心发展阶段进行因材施教。

二、知识体系①知识图谱：教育的基本规律是整个第二章知识体系的基干部分，其他章节像教学、德育等知识都是在遵循这些规律的基础上展开的。

②关联知识：和教育学中的教学原则、德育原则等知识联系紧密。

例如，教学原则中的因材施教原则就是根据教育与人的发展规律制定的，要根据学生的个体差异来教学。

③重难点分析：- 掌握难度：难。

因为这些规律比较抽象，需要深入理解社会、教育、人的复杂关系。

- 关键点：抓住教育与人、教育与社会的相互影响和作用的关键点。

比如教育是如何促进社会文化传承的，又是怎样受社会经济制约的。

④考点分析：- 在考试中的重要性：非常重要。

一般会以选择题、简答题，甚至辨析题的形式考查。

- 考查方式：选择题可能会出一个实例让选择体现了哪种教育规律；简答题就可能直接让阐述教育与社会发展的关系有哪些。

三、详细讲解（以理论概念类为例）①概念辨析：- 教育与人的发展规律：主要谈教育对人的影响以及人的发展规律对教育的要求。