下载文档原格式
数据结构实验报告图的遍历讲解一、引言在数据结构实验中，图的遍历是一个重要的主题。
图是由顶点集合和边集合组成的一种数据结构，常用于描述网络、社交关系等复杂关系。
图的遍历是指按照一定的规则，挨次访问图中的所有顶点，以及与之相关联的边的过程。
本文将详细讲解图的遍历算法及其应用。
二、图的遍历算法1. 深度优先搜索（DFS）深度优先搜索是一种常用的图遍历算法，其基本思想是从一个顶点出发，沿着一条路径向来向下访问，直到无法继续为止，然后回溯到前一个顶点，再选择此外一条路径继续访问。
具体步骤如下：（1）选择一个起始顶点v，将其标记为已访问。
（2）从v出发，选择一个未被访问的邻接顶点w，将w标记为已访问，并将w入栈。
（3）如果不存在未被访问的邻接顶点，则出栈一个顶点，继续访问其它未被访问的邻接顶点。
（4）重复步骤（2）和（3），直到栈为空。
2. 广度优先搜索（BFS）广度优先搜索是另一种常用的图遍历算法，其基本思想是从一个顶点出发，挨次访问其所有邻接顶点，然后再挨次访问邻接顶点的邻接顶点，以此类推，直到访问完所有顶点。
具体步骤如下：（1）选择一个起始顶点v，将其标记为已访问，并将v入队。
（2）从队首取出一个顶点w，访问w的所有未被访问的邻接顶点，并将这些顶点标记为已访问，并将它们入队。
（3）重复步骤（2），直到队列为空。
三、图的遍历应用图的遍历算法在实际应用中有广泛的应用，下面介绍两个典型的应用场景。
1. 连通分量连通分量是指图中的一个子图，其中的任意两个顶点都是连通的，即存在一条路径可以从一个顶点到达另一个顶点。
图的遍历算法可以用来求解连通分量的个数及其具体的顶点集合。
具体步骤如下：（1）对图中的每一个顶点进行遍历，如果该顶点未被访问，则从该顶点开始进行深度优先搜索或者广度优先搜索，将访问到的顶点标记为已访问。
（2）重复步骤（1），直到所有顶点都被访问。
2. 最短路径最短路径是指图中两个顶点之间的最短路径，可以用图的遍历算法来求解。
第1章4．答案：（1）顺序存储结构顺序存储结构是借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系，通常借助程序设计语言的数组类型来描述。
（2）链式存储结构顺序存储结构要求所有的元素依次存放在一片连续的存储空间中，而链式存储结构，无需占用一整块存储空间。
但为了表示结点之间的关系，需要给每个结点附加指针字段，用于存放后继元素的存储地址。
所以链式存储结构通常借助于程序设计语言的指针类型来描述。
5. 选择题(1)~(6)：CCBDDA6．（1）O(1) （2）O(m*n) （3）O(n2)（4）O(log3n) （5）O(n2) （6）O(n)第2章1．选择题（1）~（5）：BABAD （6）~（10）：BCABD （11）~（15）：CDDAC 2．算法设计题（1）将两个递增的有序链表合并为一个递增的有序链表。
要求结果链表仍使用原来两个链表的存储空间, 不另外占用其它的存储空间。
表中不允许有重复的数据。
[题目分析]合并后的新表使用头指针Lc指向，pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的第一个结点，从第一个结点开始进行比较，当两个链表La和Lb均为到达表尾结点时，依次摘取其中较小者重新链接在Lc表的最后。
如果两个表中的元素相等，只摘取La表中的元素，删除Lb表中的元素，这样确保合并后表中无重复的元素。
当一个表到达表尾结点，为空时，将非空表的剩余元素直接链接在Lc表的最后。
void MergeList(LinkList &La,LinkList &Lb,LinkList &Lc){//合并链表La和Lb，合并后的新表使用头指针Lc指向pa=La->next; pb=Lb->next;//pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的第一个结点Lc=pc=La; //用La的头结点作为Lc的头结点while(pa && pb){ if(pa->data<pb->data){pc->next=pa; pc=pa; pa=pa->next;}//取较小者La中的元素，将pa链接在pc的后面，pa指针后移else if(pa->data>pb->data) {pc->next=pb; pc=pb; pb=pb->next;}//取较小者Lb中的元素，将pb链接在pc的后面，pb指针后移else //相等时取La中的元素，删除Lb中的元素{pc->next=pa;pc=pa;pa=pa->next;q=pb->next; delete pb ; pb =q;}}pc->next=pa?pa:pb; //插入剩余段delete Lb; //释放Lb的头结点}（5）设计算法将一个带头结点的单链表A分解为两个具有相同结构的链表B、C，其中B表的结点为A表中值小于零的结点，而C表的结点为A表中值大于零的结点（链表A中的元素为非零整数，要求B、C表利用A表的结点）。
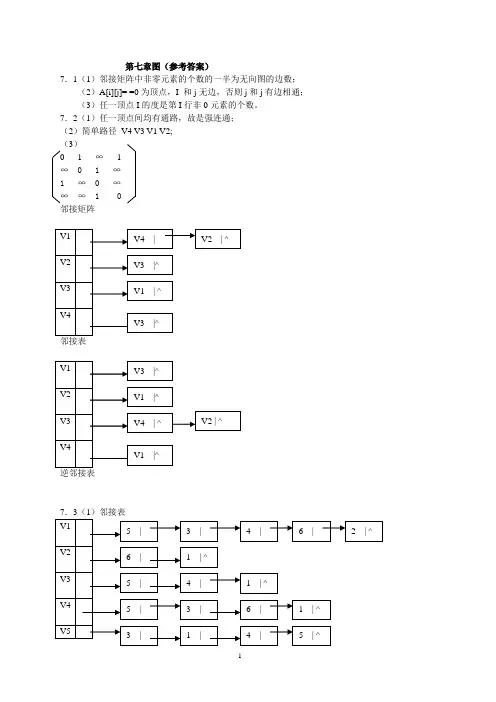
第七章图（参考答案）7．1（1）邻接矩阵中非零元素的个数的一半为无向图的边数；（2）A[i][j]= =0为顶点，I 和j无边，否则j和j有边相通；（3）任一顶点I的度是第I行非0元素的个数。
7．2（1）任一顶点间均有通路，故是强连通；（2）简单路径V4 V3 V1 V2;（3）0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表（2）从顶点4开始的DFS序列：V5,V3,V4,V6,V2,V1（3）从顶点4开始的BFS序列：V4,V5,V3,V6,V1,V27．4（1）①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j，则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路，退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if （!visited[k]）dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略，本算法判断一邻接表为存储结构的图g种，是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf （” 顶点”,i,”和顶点”,j,”有路径”）；else printf （” 顶点”,i,”和顶点”,j,”无路径”）；}// void connect_DFS(2)宽度优先遍历全程变量，调用函数与（1）相同，下面仅写宽度优先遍历部分。
第7章 《图》习题参考答案一、单选题（每题1分，共16分）（ C ）1. 在一个图中，所有顶点的度数之和等于图的边数的倍。
A ．1/2 B. 1 C. 2 D. 4 （B ）2. 在一个有向图中，所有顶点的入度之和等于所有顶点的出度之和的倍。
A ．1/2 B. 1 C. 2 D. 4 （ B ）3. 有8个结点的无向图最多有条边。
A ．14 B. 28 C. 56 D. 112 （ C ）4. 有8个结点的无向连通图最少有条边。
A ．5 B. 6 C. 7 D. 8 （ C ）5. 有8个结点的有向完全图有条边。
A ．14 B. 28 C. 56 D. 112 （B ）6. 用邻接表表示图进行广度优先遍历时，通常是采用来实现算法的。
A ．栈 B. 队列 C. 树 D. 图 （ A ）7. 用邻接表表示图进行深度优先遍历时，通常是采用来实现算法的。
A ．栈 B. 队列 C. 树 D. 图（ C ）8. 已知图的邻接矩阵，根据算法思想，则从顶点0出发按深度优先遍历的结点序列是（ D ）9. 已知图的邻接矩阵同上题8，根据算法，则从顶点0出发，按深度优先遍历的结点序列是A ． 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2 C. 0 4 2 3 1 6 5 D. 0 1 23465 （ D ）10. 已知图的邻接表如下所示，根据算法，则从顶点0出发按深度优先遍历的结点序列是（ A ）11. 已知图的邻接表如下所示，根据算法，则从顶点0出发按广度优先遍历的结点序列是A ．0 2 4 3 1 5 6B. 0 1 3 6 5 4 2C. 0 1 3 4 2 5 6D. 0 3 6 1 5 4 2⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0100011101100001011010110011001000110010011011110A ．0 1 3 2 B. 0 2 3 1 C. 0 3 2 1 D. 0 1 2 3A．0 3 2 1 B. 0 1 2 3C. 0 1 3 2D. 0 3 1 2（A）12. 深度优先遍历类似于二叉树的A．先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历（D）13. 广度优先遍历类似于二叉树的A．先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历（A）14. 任何一个无向连通图的最小生成树A．只有一棵 B. 一棵或多棵 C. 一定有多棵 D. 可能不存在（注，生成树不唯一，但最小生成树唯一，即边权之和或树权最小的情况唯一）二、填空题（每空1分，共20分）1. 图有邻接矩阵、邻接表等存储结构，遍历图有深度优先遍历、广度优先遍历等方法。
