专题03 导数-2018届浙江省高三数学优质金卷考卷分项(解析版)

绝密★启用前2018年普通高等学校招生全国统一考试（浙江卷）数 学本试题卷分选择题和非选择题两部分。

全卷共4页，选择题部分1至2页；非选择题部分3至4页。

满分150分。

考试用时120分钟。

考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。

2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

参考公式：若事件A ，B 互斥，则 若事件A ，B 相互独立，则 若事件A 在一次试验中发生的概率是p ，则n 次独立重复试验中事件A 恰好发生k 次的概率台体的体积公式其中分别表示台体的上、下底面积，表示台体的高柱体的体积公式其中表示柱体的底面积，表示柱体的高 锥体的体积公式其中表示锥体的底面积，表示锥体的高 球的表面积公式球的体积公式其中表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集U ={1，2，3，4，5}，A ={1，3}，则 A ．B ．{1，3}C ．{2，4，5}D ．{1，2，3，4，5}2．双曲线的焦点坐标是()()()P A B P A P B +=+()()()P AB P A P B =()C (1)(0,1,2,,)k k n k n n P k p p k n −=−=121()3V S S h =12,S S h V Sh =S h 13V Sh =S h 24S R =π343V R =πR =U A ð∅221 3=x y −A ．，0)，，0)B ．(−2，0)，(2，0)C ．(0，)，(0)D ．(0，−2)，(0，2)3．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm3）是A ．2B ．4C ．6D ．84．复数(i 为虚数单位)的共轭复数是 A ．1+iB ．1−iC ．−1+iD ．−1−i5．函数y =sin2x 的图象可能是A ．B ．C ．D ．6．已知平面α，直线m ，n 满足m α，n α，则“m ∥n ”是“m ∥α”的 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．设0<p <1，随机变量ξ的分布列是俯视图正视图21i−||2x ⊄⊂则当p 在（0，1）内增大时， A ．D （ξ）减小B ．D （ξ）增大C ．D （ξ）先减小后增大D ．D （ξ）先增大后减小 8．已知四棱锥S −ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S −AB −C 的平面角为θ3，则 A ．θ1≤θ2≤θ3B ．θ3≤θ2≤θ1C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ19．已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为，向量b 满足b 2−4e ·b +3=0，则|a −b |的最小值是 A 1B +1C ．2D ．210．已知成等比数列，且．若，则 A ．B ．C ．D ．非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

2018年浙江省高考数学试卷一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（4.00分）已知全集U={1，2，3，4，5}，A={1，3}，则∁U A=（）A．∅B．{1，3}C．{2，4，5}D．{1，2，3，4，5}2．（4.00分）双曲线﹣y2=1的焦点坐标是（）A．（﹣，0），（，0）B．（﹣2，0），（2，0）C．（0，﹣），（0，）D．（0，﹣2），（0，2）3．（4.00分）某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A．2 B．4 C．6 D．84．（4.00分）复数（i为虚数单位）的共轭复数是（）A．1+i B．1﹣i C．﹣1+i D．﹣1﹣i5．（4.00分）函数y=2|x|sin2x的图象可能是（）A．B．C．D．6．（4.00分）已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的（）A．充分不必要条件 B．必要不充分条件C．充分必要条件D．既不充分也不必要条件7．（4.00分）设0＜p＜1，随机变量ξ的分布列是则当p在（0，1）内增大时，（）A．D（ξ）减小B．D（ξ）增大C．D（ξ）先减小后增大D．D（ξ）先增大后减小8．（4.00分）已知四棱锥S﹣ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点）．设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S﹣AB﹣C的平面角为θ3，则（）A．θ1≤θ2≤θ3B．θ3≤θ2≤θ1C．θ1≤θ3≤θ2D．θ2≤θ3≤θ19．（4.00分）已知，，是平面向量，是单位向量．若非零向量与的夹角为，向量满足﹣4•+3=0，则|﹣|的最小值是（）A．﹣1 B．+1 C．2 D．2﹣10．（4.00分）已知a1，a2，a3，a4成等比数列，且a1+a2+a3+a4=ln（a1+a2+a3），若a1＞1，则（）A．a1＜a3，a2＜a4B．a1＞a3，a2＜a4C．a1＜a3，a2＞a4D．a1＞a3，a2＞a4二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

2018年高考理科数学全国卷三导数压轴题解析已知函数2()(2)ln(1)2f x x ax x x =+++-（1） 若0a =，证明：当10x -<<时，()0f x <；当0x >时，()0f x >；（2） 若0x =是()f x 的极大值点，求a .考点分析综合历年试题来看，全国卷理科数学题目中，全国卷三的题目相对容易。

但在2018年全国卷三的考察中，很多考生反应其中的导数压轴题并不是非常容易上手。

第1小问，主要通过函数的单调性证明不等式，第2小问以函数极值点的判断为切入点，综合考察复杂含参变量函数的单调性以及零点问题，对思维能力（化归思想与分类讨论）的要求较高。

具体而言，第1问，给定参数a 的值，证明函数值与0这一特殊值的大小关系，结合函数以及其导函数的单调性，比较容易证明，这也是大多数考生拿到题目的第一思维方式，比较常规。

如果能结合给定函数中20x +>这一隐藏特点，把ln(1)x +前面的系数化为1，判断ln(1)x +与2/(2)x x +之间的大小关系，仅通过一次求导即可把超越函数化为求解零点比较容易的代数函数，解法更加容易，思维比较巧妙。

总体来讲，题目设置比较灵活，不同能力层次的学生皆可上手。

理解什么是函数的极值点是解决第2问的关键。

极值点与导数为0点之间有什么关系：对于任意函数，在极值点，导函数一定等于0么（存在不存在）？导函数等于0的点一定是函数的极值点么？因此，任何不结合函数的单调性而去空谈函数极值点的行为都是莽撞与武断的。

在本题目中，0x =是()f x 的极大值点的充要条件是存在10δ<和20δ>使得对于任意1(,0)x δ∈都满足()(0)=0f x f <( 或者()f x 单调递增)，对于任意2(0,)x δ∈都满足()(0)=0f x f <( 或者()f x 单调递减)，因此解答本题的关键是讨论函数()f x 在0x =附近的单调性或者判断()f x 与(0)f 的大小关系。

2018届浙江省高三数学优质金卷考卷分项（11份，解析版）第一章 集合与常用逻辑用语一．基础题组1．【浙江省杭州市2018届高三上学期期末】设集合{|22}A x x =+≤， []0,4B =，则()R C A B ⋂=（ ）A. RB. {}0C. {|,0}x x R x ∈≠D. ∅ 【答案】C2. 【浙江省杭州市2018届高三上学期期末】设数列{}n a 的通项公式为()*2n a kn n N=+∈则“2k >”是“数列{}n a 为单调递增数列”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 【答案】A【解析】当2k >时12n n a a k --=>，则数列{}n a 为单调递增数列若数列{}n a 为单调递增数列，则10n n a a k --=>即可，所以“2k >”是“数列{}n a 为单调递增数列”的充分不必要条件 故选A .3. 【浙江省嘉兴市2018届高三上学期期末】已知,x y 是非零实数，则“x y >”是“11x y<”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 【答案】D【解析】因为11x y <,所以0{ 0x y x yxy xy>->⇒>或{ 0x y xy << ,所以x y >是“11x y <”的既不充分也不必要条件,选D点睛：充分、必要条件的三种判断方法．1．定义法：直接判断“若p 则q ”、“若q 则p ”的真假．并注意和图示相结合，例如“p ⇒q ”为真，则p 是q 的充分条件．2．等价法：利用p ⇒ q 与非q ⇒非p ， q ⇒ p 与非p ⇒非q ， p ⇔ q 与非q ⇔非p 的等价关系，对于条件或结论是否定式的命题，一般运用等价法．3．集合法：若A ⊆ B ，则A 是B 的充分条件或B 是A 的必要条件；若A ＝B ，则A 是B 的充要条件．4. 【浙江省嘉兴市2018届高三上学期期末】已知集合{|1}P x x =<， {}0Q x x =，则 A. P Q ⊆ B. Q P ⊆ C. P ⊆ R C Q D. R C P Q ⊆ 【答案】D5.【浙江省宁波市2018届高三上学期期末】已知集合2{|}M x x x =≤， {|lg 0}N x x ==，则M N ⋃=（ ）A. []0,1B. (]0,1C. [)0,1 D. {}0,1 【答案】A【解析】 {}2|M x x x =≤= {}|01x x =≤≤， {}{}|lg 01N x x ===，{}[]|010,1M N x x ∴⋃=≤≤=，故选A.6.【浙江省宁波市2018届高三上学期期末】已知a b >，则条件“0c ≥”是条件“ac bc >”的（ ）条件.A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件【解析】当21{0a b c =>==时， ac bc >不成立，所以充分性不成立，当{ ac bca b>>时，0c >成立， 0c ≥也成立，所以必要性成立，所以“0c ≥”是条件“ac bc >”的必要不充分条件，故选B.【方法点睛】本题通过不等式的基本性质主要考查充分条件与必要条件，属于中档题. 判断充要条件应注意：首先弄清条件p 和结论q 分别是什么，然后直接依据定义、定理、性质尝试,p q q p ⇒⇒，对于带有否定性的命题或比较难判断的命题，除借助集合思想化抽象为直观外，还可利用原命题和逆否命题、逆命题和否命题的等价性，转化为判断它的等价命题；对于范围问题也可以转化为包含关系来处理.7. 【浙江省台州市2018届高三上学期期末】已知R a ∈，则“1a ≤”是“112a a ++-=”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 【答案】B8. 【浙江省台州市2018届高三上学期期末】设集合{|11}M x x =-≤≤，{|124}x N x =<<，则M N ⋂=A. {|10}x x -≤<B. {|01}x x <≤C. {|12}x x ≤<D. {|12}x x -≤< 【答案】B【解析】因为{|11}M x x =-≤≤， {}|124{|02}xN x x x =<<=<<,所以{|01}M N x x ⋂=<≤，故选B.9.【浙江省台州中学2018届高三上学期第三次统练】已知集合{}2|x 320A x x =-+=，集合{}|log 42x B x ==，则A B = （ ）A ．{}2,1,2-B ．{}2,2-C ．{}1,2D ．{}2【解析】试题分析：由题设条件，得{1,2}A =，{2}B =，所以A B = {}1,2，故选C ． 考点：1、对数的运算；2、集合的并集运算．10．【浙江省台州中学2018届高三上学期第三次统练】“1a ≤”是“函数()241f x x ax =-+在区间[)4,+∞上为增函数”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 【答案】A【点睛】本题主要考查充分条件和必要条件的判断，根据二次函数的单调性求出a 的取值范围是解决本题的关键．11. 【2017年12月浙江省高三上学期期末热身】已知U R =， {}|0 2 A x x =<<，{}2|230 B x x x =+-≥，则U A C B ⋂=（ ）A. ∅B. {}|0 1 x x <<C. {}|0 2 x x <<D. {| 1 x x ≥或}3x ≤- 【答案】B【解析】∵{}2|230 B x x x =+-≥∴{|3B x x =≤-或1}x ≥ ∴{|31}U C B x x =-<< ∵{}|0 2 A x x =<< ∴{|01}U A C B x x ⋂=<< 故选B.12. 【浙江省部分市学校（新昌一中、台州中学等）2018届高三上学期9+1联考】“2m =”是“直线()2140x m y +++=与直线320mx y +-=平行”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 【答案】A【解析】当1m =-时，两直线不平行 当1m ≠-时，由两直线平行可得213m m -=-+，且4213m -≠+，解得2m =或3m =- ∴“2m =”是“直线()2140x m y +++=与直线320mx y +-=平行”的充分不必要条件 故选A.13. 【浙江省部分市学校（新昌一中、台州中学等）2018届高三上学期9+1联考】已知集合{}0P x x =， {}|11Q x x =-<<，那么()R P Q ⋂=ð（ ） A. ()1,-+∞ B. ()0,1 C. (]1,0- D. ()1,1- 【答案】C14.【浙江省嘉兴第一中学2018届高三9）A. D.【答案】A【解析】由题意得：故选：A点睛：1.用描述法表示集合，首先要弄清集合中代表元素的含义，再看元素的限制条件，明确集合类型，是数集、点集还是其他的集合．2．求集合的交、并、补时，一般先化简集合，再由交、并、补的定义求解．3．在进行集合的运算时要尽可能地借助Venn 图和数轴使抽象问题直观化．一般地，集合元素离散时用Venn 图表示；集合元素连续时用数轴表示，用数轴表示时要注意端点值的取舍．15．【浙江省嘉兴第一中学2018届高三9月基础知识测试】（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 【答案】D16. 【浙江省名校协作体2018届高三上学期测试】已知()cos ,sin a αα=，()()()cos ,sin b αα=-- ，那么“0?a b ⋅= 是“α= 4k ππ+ ()k Z ∈”的（ ）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件【答案】B【解析】2202a b cos cossin sin cos sin cos ααααααα⋅==⋅-+⋅-=-=（）（） ∵ 222k παπ∴=±，解得4k k Z παπ=±∈（）．故“0?a b ⋅= 是“α= 4k ππ+ ()k Z ∈”的必要不充分条件故选B ．17. 【浙江省镇海中学2018届高三上学期期中】设a ， b 是两条直线， a ， β表示两个平面，如果αa ⊂， α//β，那么“b β⊥”是“a b ⊥”的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件D. 既不充分又不必要条件 【答案】A【解析】如果a a ⊂， //αβ， b β⊥，则必有b a ⊥，充分性成立；如果a α⊂， //αβ， a b ⊥，不能保证b β⊥，有可能平行呢，必要性不成立. 故“b β⊥”是“a b ⊥”的充分不必要条件. 故选A.18. 【浙江省镇海中学2018届高三上学期期中】若集合2lgx M x y x -⎧⎫==⎨⎬⎩⎭， {}1N x x =<，则()M N ⋃=A. ()01，B. ()02，C. ()2-∞，D. ()0+∞， 【答案】C【解析】集合2lg{|02}x M x y x x x -⎧⎫===<<⎨⎬⎩⎭, {}1N x x =<. {}()|22M N x x ⋃=<=-∞，.故选C.19. 【浙江省温州市2018届高三9月高考适应测试（一模）】）D. 【答案】A 【解析】，选A.20 ）A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件 【答案】D21. 【浙江省清源中学2018届高三9月月考】已知,a b R ∈，则“||3a b +≤”是“||||3a b +≤”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 【答案】B 【解析】试题分析：设{}{}3),(,3),(≤+=≤+=b a b a B b a b a A ，如图涂色部分为A ，红色为B ，有B 是A 的真子集，故为必要不充分条件，选B ．考点：充分条件；必要条件．【易错点睛】本题考查了充分条件；必要条件．判断充分、必要条件时应注意的问题：（1）要弄清先后顺序：“A 的充分不必要条件是B ”是指B 能推出A ，且A 不能推出B ；而“A 是B 的充分不必要条件”则是指A 能推出B ，且B 不能推出A ；（2）要善于举出反例：如果从正面判断或证明一个命题的正确或错误不易进行，那么可以通过举出恰当的反例来说明．22. 【浙江省清源中学2018届高三9月月考】已知集合2{|20}A x x x =--<，{|10}B x x =-≤，则A B ⋂=（ ）A. (]1,1-B. ()1,1-C. ∅D. []1,2- 【答案】A23. 【浙江省嘉兴第一中学2018届高三上学期期中】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说，你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩，看后甲对大家说：我还是不知道我的成绩，根据以上信息，则A. 乙可以知道两人的成绩B. 丁可能知道两人的成绩C. 乙、丁可以知道对方的成绩D. 乙、丁可以知道自己的成绩 【答案】D【解析】四人所知只有自己看到，老师所说及最后甲说话，甲不知道自己的成绩→乙丙必有一优一良，（若为两优，甲会知道自己的成绩；若为两良，甲也会知道自己的成绩）→乙看到了丙的成绩，知道自己的成绩→丁看到甲，丁也为一优一良，丁知道自己的成绩故选D24. 【浙江省嘉兴第一中学2018届高三上学期期中】已知直线()12:210,:20l ax a y l x ay +++=++=，其中a R ∈，则“3a =-”是“12l l ⊥”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 【答案】A25. 【浙江省嘉兴第一中学2018届高三上学期期中】设全集U R =，集合{}{}| 3 ,|0 5 A x x B x x =≥=≤<则集合()U C A B ⋂=（ ）A. {}|0 3 x x <<B. {}|0 3 x x ≤≤C. {}|0 3 x x <≤D. {}|0 3 x x ≤< 【答案】D【解析】{3}U A x x =<ð， (){03}U A B x x ⋂=≤<ð，选D.第二章 函数一．基础题组1. 【浙江省杭州市2018届高三上学期期末】设函数()21xf x b a =+-（0a >且1a ≠）则函数()f x 的奇偶性（ ）A. 与a 无关，且与b 无关B. 与a 有关，且与b 有关C. 与a 有关，且与b 无关D. 与a 无关，但与b 有关 【答案】D2. 【浙江省杭州市2018届高三上学期期末】设函数()()2,f x x ax b a b R =++∈，记M为函数()y f x =在[]1,1-上的最大值， N 为a b +的最大值.（ ） A. 若13M =，则3N = B. 若12M =，则3N = C. 若2M =，则3N = D. 若3M =，则3N = 【答案】C【解析】由题意得()11f a b =++， ()11f a b -=-+ 则()(){}{}1111M maxf f max a b a b =-=++-+，，()()()11111112222M a b a b a b a b a a ≥+++-+≥++--+≥= 若2M =，则2a =，此时任意[]1,1x ∈-有222x ax b -≤++≤则31a b -≤+≤， 31b a -≤-≤， {}3a b max a b a b +=-+=，， 在12b a =-=，时与题意相符，故选C点睛：本题是道函数综合题目，考查了含有绝对值的最值问题，借助条件计算得最值情况，这里需要注意取最值时的讨论以及在运算过程中对于绝对值不等式的放缩求结果，本题有一定难度.3. 【浙江省嘉兴市2018届高三上学期期末】已知函数()()4log 4f x x =-，则()f x 的单调递增区间是______；()()204f f +=______．【答案】 (]4,0- 34. 【浙江省嘉兴市2018届高三上学期期末】若()2f x x bx c =++在()1,1m m -+内有两个不同的零点，则()1f m -和()1f m + A. 都大于1 B. 都小于1C. 至少有一个大于1D. 至少有一个小于1 【答案】D【解析】()1f m -+ ()1f m +=()22f m +，因为()2f x x bx c =++在()1,1m m -+内有两个不同的零点，所以()0f m <∴ ()1f m -+ ()1f m +<2,即()1f m -和()1f m + 至少有一个小于1，选D.5.【浙江省宁波市2018届高三上学期期末】已知4510a b==，则12a b+=__________． 【答案】2【解析】 4510a b==， 4511log 10,lg4,log 10,lg5a b a b∴====， 12lg42lg5lg4lg25lg1002a b∴+=+=+==，故答案为2. 6. 【浙江省宁波市2018届高三上学期期末】若函数()()22211f x ax a a x =+--+为偶函数，则实数a 的值为（ ） A. 1 B. 12- C. 1或12- D. 0 【答案】C【解析】0a =时， ()1f x x =-+不是偶函数， 0a ≠时，二次函数()()22211f x ax a a x =+--+的对称轴为2212a a x a--=，若()f x 为偶函数，则22102a a a---=，得1a =或12a =-，故选C.7. 【浙江省台州市2018届高三上学期期末】已知函数()21,0,{ 3,0,x x f x xx x +>=-+≤若函数()()()1g x f x k x =-+在(],1-∞恰有两个不同的零点，则实数k 的取值范围是A. [)1,3B. (]1,3C. [)2,3 D. ()3,+∞ 【答案】A【解析】【方法点睛】已知函数零点(方程根)的个数，求参数取值范围的三种常用的方法：(1)直接法，直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；(2)分离参数法，先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法，先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．一是转化为两个函数()(),y g x y h x ==的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，二是转化为(),y a y g x ==的交点个数的图象的交点个数问题 .8. 【浙江省台州中学2018届高三上学期第三次统练】已知函数()211,0{ 2log 1,0xx f x x x ⎛⎫-≤ ⎪=⎝⎭+>，则()()12f f +-=______________. 【答案】49. 【浙江省台州中学2018届高三上学期第三次统练】，的方程）A. 有两个B. 有一个C. 没有D. 上述情况都有可能 【答案】A【解析】由于函数单调递增，如图所示，，解，故的图象至少向左平移两个单位，才符合题意，即个交点，A.【方法点睛】本题主要考查函数的奇偶性、对称性以及函数图象的应用，属于难题.函数图象是函数的一种表达形式，它形象地揭示了函数的性质，为研究函数的数量关系提供了“形”的直观性．归纳起来，图象的应用常见的命题探究角度有：1、确定方程根的个数；2、求参数的取值范围；3、求不等式的解集；4、研究函数性质．解答本题的关键是根据把然后求出再利用数形结合将方程f(2x+1)=t 的根转化为函数.10. 【2017年12月浙江省高三上学期期末热身】已知函数241y x x =-+的定义域为[]1,t ，在该定义域内函数的最大值与最小值之和为-5，则实数t 的取值范围是（ ） A. (]1,3 B. []2,3 C. (]1,2 D. ()2,3 【答案】B11. 【浙江省部分市学校（新昌一中、台州中学等）2018届高三上学期9+1联考】16/17世纪之交，随着天文、航海、工程、贸易以及军事的发展，改进数字计算方法成了当务之急，约翰•纳皮尔正是在研究天文学的过程中，为了简化其中的计算而发明了对数.后来天才数学家欧拉发现了对数与指数的关系，即ba N = ⇔ log ab N =.现在已知23a =， 34b =，则ab =__________. 【答案】2【解析】∵23a =， 34b = ∴2log 3a =， 3log 4b = ∴23ln3ln4ln4log 3log 42ln2ln3ln2ab =⋅=⋅== 故答案为2.12. 【浙江省部分市学校（新昌一中、台州中学等）2018届高三上学期9+1联考】已知函数()3211132f x ax x x =+++（a R ∈），下列选项中不可能是函数()f x 图象的是（ ） A. B.C. D.【答案】D当104a <<时， 0∆>， ()f x '有两个不相等的负实数根， ()f x 先递增再递减然后再递增，故D 错误.故选D13. 【浙江省嘉兴第一中学2018届高三9月基础知识测试】，则________．【答案】f（f（a））=1，23a﹣1=1，解得（舍去）．综上故答案为：214. 【浙江省嘉兴第一中学2018届高三9）A. 2B. 3C. 4D. 5【答案】D【解析】∵故选：D15. 【浙江省名校协作体2018届高三上学期测试】已知函数()()22,0{ ,14,0x x f x xln x x +>=-+≤则关于x 的方程()246f x x -=的不同实根的个数为________．【答案】4个【解析】函数 ()f x 图像如图所示，()22424t x x x =-=-- ，由图像可知，当40t -≤≤ 时， ()6f t = 无解，当0t > 时，()6f t =由2个解，对应24t x x =-，各由2个解，故关于x 的方程()246f x x -=的不同实根的个数为为4 个16. 【浙江省名校协作体2018届高三上学期测试】函数y x =( ))).1)..(1,)A B C D ⎡+∞+∞+∞+∞⎣【答案】D由22123y x y -≤-＝，得y R ∈ ，由2232330022232y y y y x y y y y --+--≥⇒≥⇒>--＝．所以32y >．综上，所求函数的值域为(1,)+∞.选D17. 【浙江省镇海中学2018届高三上学期期中】设函数()3f x x a a x=--+， a R ∈，若关于x 的方程()2f x =有且仅有三个不同的实数根，且它们成等差数列，则实数a 的取值构成的集合__________．【答案】95⎧⎪-⎨⎪⎪⎩⎭.即5a -<，且35225a ++=，解得95a =-，满足题意； 当13a -<≤时， x a <时()2f x =有两根，设为12,x x ， x a ≥时()2f x =有一根为3，且有1232x x +=.322x a x--+=即()22230x a x --+=的两根为12,x x .有1222x x a +=-， 123x x =解得a =,因为13a -<≤，所以a =； 当3a >时， ()2f x =最多有两个根，不符合题意.综上实数a 的取值构成的集合为95⎧⎪-⎨⎪⎪⎩⎭.18. 【浙江省镇海中学2018届高三上学期期中】函数331x x y =-的图象大致是()A. B.C. D.【答案】C19. 【浙江省温州市2018届高三9月高考适应测试（一模）】已知函数且所有零点之和为3，__________．【答案】【解析】根据题意，有平均数为，于是函数单调递增，且取值范围是的大小关系，注意个公共点，,故答案为 .20. 【浙江省温州市2018届高三9月高考适应测试（一模）】．【答案】21. 【浙江省清源中学2018届高三9月月考】已知函数()240{3x x xf xxx-≥=<，，，若函数()()3g x f x x b=-+有三个零点，则实数的取值范围为_________.【答案】()1,6,04⎛⎤-∞-⋃-⎥⎝⎦【解析】函数()240{3x x xf xxx-≥=<，，,若函数()()3g x f x x b=-+有三个零点，就是()()3h x f x x =-与y b =-有3个交点，()22,0{7,4 33,0x x x h x x x x x x-≥=->--<，画出两个函数的图象如图：,当x<0时, 336x x--…，当且仅当x=−1时取等号，此时−b>6，可得b<−6； 当04x 剟时, 21,4x x -…当12x =时取得最大值,满足条件的1,04b ⎛⎤∈- ⎥⎝⎦. 综上, ()1,6,04b ⎛⎤∈-∞-⋃-⎥⎝⎦. 给答案为： ()1,6,04⎛⎤-∞-⋃-⎥⎝⎦. 点睛：已知函数有零点求参数常用的方法和思路：（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成函数的值域问题解决；（3）数形结合法：先对解析式变形，在同一个平面直角坐标系中，画出函数的图像，然后数形结合求解.22. 【浙江省嘉兴第一中学2018届高三上学期期中】设函数()f x a =，若存在唯一的整数0x 使得()00f x <，则实数a 的取值范围是（ ）A. ⎝⎭B. ⎝⎭C. 2,2⎛ ⎝⎦D. 2,2⎛ ⎝⎦【答案】A23. 【浙江省嘉兴第一中学2018届高三上学期期中】下列函数中，其图象既是轴对称图形又在区间(0,)+∞上单调递增的是 （ ）（A ）1y x= （B ）21y x =-+ （C ）2x y = （D ）lg |1|y x =+【答案】D. 【解析】试题分析：对于A ，函数1y x=是关于原点对称且在(,0)-∞和(0,)+∞上单调递减；对于B ，函数21y x =-+是关于y 轴对称且在(0,)+∞上单调递减；对于C ，函数2xy =无对称性且在R 上单调递增；对于D ，函数lg |1|y x =+是关于1x =-对称且在(1,)-+∞上单调递增；故选D .考点：1.函数的性质；2.常见函数的性质. 24.二．能力题组1. 【浙江省台州中学2018届高三上学期第三次统练】已知函数()2f x ax bx c =++．（1）当1,2a b ==时，若存在[]()1212,2,0x x x x ∈-≠，使得()()21,2i f x i ==，求实数c 的取值范围；（2）若,,a b c 为正整数，方程20ax bx c ++=的两个实数根12,x x 满足1211x x -<<<，求a b c ++的最小值．【答案】（1）21c -≤<-或23c ≤<.（2）11．试题解析：（1）当1,2a b ==时， ()()211f x x c =++-由题意可知， ()2f x =在[]2,0-上有两个不等实根，或()2f x =-在[]2,0-上有两个不等实根，则()()12{02f f -<≥或()()12{02f f -<-≥-,解得23c ≤<或21c -≤<-即实数c 的取值范围是21c -≤<-或23c ≤<.（2）设()2f x ax bx c =++，则由题意得()()21010{ 11240f f bab ac ->>-<-<∆=->，即21{21 41a b c a b b ac -+≥-≥-≥ ， 所以()212a b c a b c b b ++=-++≥+，由于2415b ac ≥+≥①当3b =时， 4a c +≥，且2124b ac -≤=无解， ②当4b =时， 5a c +≥，且211544b ac -≤=，于是3ac ≤无解， ③当5b =时， 6a c +≥，且2164b ac -≤=，由21a b -≥，得3a ≥，此时有解5,1a c ==， 综上所述， 11a b c ++≥，当5,5,1a b c ===时取等号，即a b c ++的最小值为11． 2.第三章 导数一．基础题组1.【浙江省杭州市2018届高三上学期期末】若函数()f x 的导函数()'f x 的图像如图所示，则（ ）A. 函数()f x 有1个极大值，2个极小值B. 函数()f x 有2个极大值，2个极小值C. 函数()f x 有3个极大值，1个极小值D. 函数()f x 有4个极大值，1个极小值 【答案】B2．【浙江省杭州市2018届高三上学期期末】若直线y x =与曲线x my e +=（m R ∈， e 为自然对数的底数）相切，则m =（ ） A. 1 B. 2 C. -1 D. -2 【答案】C【解析】设切点坐标为()00x mx e+，， x my e+=， ´x my e+=，则切线方程为()000y x m x m e e x x ++-=-，又因为切线为y x =过()00，代入得01x =，将()11，代入x m y e +=中得1m =-故选C3. 【浙江省嘉兴市2018届高三上学期期末】函数3y x x =-的图象与直线2y ax =+相切，则实数a =A. 1-B. 1C. 2D. 4 【答案】C 【解析】()233200000000031,23121,312y x a x x ax x x x x x a =-=-=+∴-=-+∴==-'=选C4. 【浙江省宁波市2018届高三上学期期末】已知()21cos 4f x x x =+， ()'f x 为()f x 的导函数，则()'f x 的图像是（ ）A. B. C. D.【答案】A【方法点晴】本题通过对多个图象的选择主要考查考查函数的图象与性质，属于中档题. 这类题型也是近年高考常见的命题方向，该题型的特点是综合性较强较强、考查知识点较多，但是并不是无路可循.解答这类题型可以从多方面入手，根据函数的定义域、值域、单调性、奇偶性、特殊点以及0,0,,x x x x +-→→→+∞→-∞时函数图象的变化趋势，利用排除法，将不合题意的选项一一排除.5. 【浙江省台州市2018届高三上学期期末】当[]1,4x ∈时，不等式322044ax bx a x≤++≤恒成立，则a b +的取值范围是A. []4,8-B. []2,8-C. []0,6D. []4,12 【答案】A【解析】1，若0a =，则2204bx x ≤≤， 04,04b a b ≤≤≤+≤；,2，若0a >，设()324f x ax bx a =++， ()2'32f x ax bx =+，（1）0b =时，由()'0f x >得， ()f x 在(),-∞∞上递增，只需()()014{0416f f ≤≤≤≤，得403{403a ab ≤≤≤+≤；（2）0b <时，()f x 在()2,0,,3b a ⎛⎫-∞-+∞ ⎪⎝⎭上递增，在20,3b a ⎛⎫- ⎪⎝⎭上递减，由()()014{ 0464f f ≤≤≤≤，得054{017416a b a b ≤+≤≤+≤，可得41a b -≤+≤；（3）当0b >时， ()f x 在()2,,0,3b a ⎛⎫-∞+∞ ⎪⎝⎭上递增， 0{054017416a b a b a b >>≤+≤≤+≤；3，若0a <，（1）0b ≤时，不合题意；（2）0b >， ()f x 在()2,0,,3b a ⎛⎫-∞-+∞ ⎪⎝⎭上递减，在20,3b a ⎛⎫-⎪⎝⎭上递增， 00{ 054017416a b a b a b <>∴≤+≤≤+≤，可得18a b ≤+≤，综上所述， ()min 175,,433a b a b =-=+=-，当168,33a b ==时， ()max 8a b +=，故选A. 【方法点睛】本题主要考查利用导数研究函数的单调性、分类讨论思想及方程的根与系数的关系， 属于难题. 分类讨论思想解决高中数学问题的一种重要思想方法，是中学数学四种重要的数学思想之一，尤其在解决含参数问题发挥着奇特功效，大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透，这样才能快速找准突破点. 充分利用分类讨论思想方法能够使问题条理清晰，进而顺利解答，希望同学们能够熟练掌握并应用与解题当中.6. 【浙江省台州中学2018届高三上学期第三次统练】若关于x 的不等式()x x a b a R -<∈在[]1,2上恒成立，则实数b 的取值范围是_______.【答案】2,3⎛⎫+∞⎪⎝⎭()0g x '=，得x =2≥，即4b ≥时， ()g x 在[]1,2上单调递减，()()min 222b g x g ==+，显然2222b b+>-成立，所以4b ≥1，即01b <≤时()g x 在[]1,2上单调递增， ()()min 11g x g b ==+，所以122b b +>-，所以213b <≤；当12<，即14b <<时， ()g x在⎡⎣上单调递减，在2⎤⎦上单调递增，()min g x g==22b>-，即240+>，所以2>，12b >-14b <<，综上23b >，故答案为2,3⎛⎫+∞ ⎪⎝⎭. 点睛：本题主要考查了绝对值不等式以及导数在不等式恒成立中的应用，属于难题；首先根据绝对值不等式的解法，将其转化为b bx a x x x-<<+在给定区间内恒成立问题，继而可转换为max minb b x a x x x ⎛⎫⎛⎫-<<+ ⎪ ⎪⎝⎭⎝⎭，分别将不等号两边看成两个不同的函数，然后利用导数与0的关系得其单调性，得其最值.7. 【浙江省台州中学2018届高三上学期第三次统练】已知ABC ∆的面积为S ，内角,,A B C 所对的边分别为,,a b c，且2sin C A 成等比数列，2213,218322b a c ac =≤+≤241c +的最小值为 .【答案】34【解析】()2222241414121144c a a aa a a a+++-===-++，令()()222212(2)(+1)4(4)a a af a f aa a a a---'=⇒=++，因为13a≤≤，可知当2a=时，()f a取得最大值，()124f=241c+的最小值为34.考点：等比数列的应用；余弦定理及三角形的面积公式；导数的应用.【方法点晴】本题主要考查了等比数列的通项公式，余弦定理及三角形的面积公式、导数的综合应用，试题有一点的难度，属于难题，着重考查了学生的推理、运算能力及转化与化归思想方法的应用，本题的解答中根据题设条件先得出c a=，在利用三角恒等变换和三角形的面积公式表示成三角形的面积，进而得到a241c+，利用导数研究其单调性确定最值即可.8. 【浙江省台州中学2018届高三上学期第三次统练】曲线()223f x x x=-在()1,1-处的切线方程为_________________________．【答案】20x y--=9. 【2017年12月浙江省高三上学期期末热身】已知a R∈，函数()1,0{,0xa xf x xe x-+><，若存在三个互不相等的实数123,,x x x ，使得()()()123123f x f x f x e x x x ===-成立，则a 的取值范围是__________．【答案】(,-∞-【解析】若存在三个互不相等的实数123,,x x x ，使得()()()123123f x f x f x e x x x ===-成立，则方程()f x ex =-存在三个不相等的实根 当0x <时， ()xf x eex -==-，令()(0)x g x e ex x -=+<，则()x g x e e --'=+令()0g x '=，得1x =-，当1x <-时， ()0g x '<，即()g x 在(),1-∞-上为减函数， 当10x -<<时， ()0g x '>，即()g x 在()1,0-上为增函数 ∴()()min 10g x g e e =-=-=，则()f x ex =-在(),0-∞上存在一个实根 ∴()f x ex =-在()0,+∞上存在两个不相等的实根，即1a ex x+=-， 210ex ax ++=有两个不相等的实根∴20{ 240a ea e ->∆=->∴a <-故答案为(,-∞-点睛：本题主要考查了函数与方程、函数的图像与性质和分段函数的应用，考查学生综合知识能力，属中高档题．其解题的一般思路为：分别利用导数及函数性质判断其各段的函数的单调性，进而得出其极值和最值，再结合函数的图像即可得出方程()f x ex =-的解的情况．其解题的关键是数形结合在分段函数中的应用．10. 【2017年12月浙江省高三上学期期末热身】已知点52,2A （）在曲线(),by ax a b R x=+∈上，且该曲线在点A 处的切线与直线4310x y +-=垂直，则方程20x ax b ++=的实数根的个数为（ ）A. 0个B. 1个C. 2个D. 不确定 【答案】A∴5222{344b a b a +=-=∴1{1a b ==∴方程20x ax b ++=为210x x ++=∵214130∆=-⨯=-<∴方程的实数根的个数为0个 故选A.11. 【浙江省名校协作体2018）【答案】A12. 【浙江省温州市2018届高三9月高考适应测试（一模）】）A. B. C. D.【答案】C13. 【浙江省清源中学2018届高三9月月考】已知函数()f x 的定义域为[)2,-+∞，且()()421f f =-=， ()f x '为()f x 的导函数，函数()y f x ='的图像如图所示，则平面区域()0{0 21a b f a b ≥≥+<所围成的面积是（ ）A. 2B. 4C. 5D. 8 【答案】B【解析】由函数()'y f x =的图象可得：当[)2,0x ∈-]时， ()'0f x <，此时函数f(x)单调递减；当x ∈(0,+∞)时， ()'0f x >，此时函数f(x)单调递增。

绝密★启用前2018年普通高等学校招生全国统一考试（浙江卷）数学本试题卷分选择题和非选择题两部分。

全卷共4页，选择题部分1至2页；非选择题部分3至4页。

满分150分。

考试用时120分钟。

考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。

2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

参考公式：若事件A，B互斥，则若事件A，B相互独立，则若事件A在一次试验中发生的概率是p，则n次独立重复试验中事件A恰好发生k次的概率台体的体积公式其中分别表示台体的上、下底面积，表示台体的高柱体的体积公式其中表示柱体的底面积，表示柱体的高锥体的体积公式其中表示锥体的底面积，表示锥体的高球的表面积公式球的体积公式其中表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知全集U={1，2，3，4，5}，A={1，3}，则A. B. {1，3} C. {2，4，5} D. {1，2，3，4，5}【答案】C【解析】分析:根据补集的定义可得结果.详解：因为全集，，所以根据补集的定义得,故选C.点睛：若集合的元素已知，则求集合的交集、并集、补集时，可根据交集、并集、补集的定义求解．2. 双曲线的焦点坐标是A. (−，0)，(，0)B. (−2，0)，(2，0)C. (0，−)，(0，)D. (0，−2)，(0，2)【答案】B【解析】分析:根据双曲线方程确定焦点位置，再根据求焦点坐标.详解：因为双曲线方程为，所以焦点坐标可设为，因为，所以焦点坐标为，选B.点睛：由双曲线方程可得焦点坐标为，顶点坐标为，渐近线方程为.3. 某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是A. 2B. 4C. 6D. 8【答案】C【解析】分析:先还原几何体为一直四棱柱，再根据柱体体积公式求结果.详解：根据三视图可得几何体为一个直四棱柱，高为2，底面为直角梯形，上下底分别为1，2，梯形的高为2，因此几何体的体积为选C.点睛：先由几何体的三视图还原几何体的形状,再在具体几何体中求体积或表面积等.4. 复数(i为虚数单位)的共轭复数是A. 1+iB. 1−iC. −1+iD. −1−i【答案】B【解析】分析:先分母实数化化简复数，再根据共轭复数的定义确定结果.详解：，∴共轭复数为，选B.点睛：本题重点考查复数的基本运算和复数的概念，属于基本题.首先对于复数的四则运算，要切实掌握其运算技巧和常规思路，如. 其次要熟悉复数的相关基本概念，如复数的实部为、虚部为、模为、对应点为、共轭复数为.5. 函数y=sin2x的图象可能是A. B.C. D.【答案】D【解析】分析:先研究函数的奇偶性，再研究函数在上的符号，即可判断选择.详解：令，因为，所以为奇函数，排除选项A,B; 因为时，，所以排除选项C，选D.点睛：有关函数图象的识别问题的常见题型及解题思路：（1）由函数的定义域，判断图象的左、右位置，由函数的值域，判断图象的上、下位置；（2）由函数的单调性，判断图象的变化趋势；（3）由函数的奇偶性，判断图象的对称性；（4）由函数的周期性，判断图象的循环往复．6. 已知平面α，直线m，n满足mα，nα，则“m∥n”是“m∥α”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】分析:根据线面平行的判定定理得充分性成立，而必要性显然不成立.详解：因为，所以根据线面平行的判定定理得.由不能得出与内任一直线平行，所以是的充分不必要条件，故选A.点睛：充分、必要条件的三种判断方法：（1）定义法：直接判断“若则”、“若则”的真假．并注意和图示相结合，例如“⇒”为真，则是的充分条件．（2）等价法：利用⇒与非⇒非，⇒与非⇒非，⇔与非⇔非的等价关系，对于条件或结论是否定式的命题，一般运用等价法．（3）集合法：若⊆，则是的充分条件或是的必要条件；若＝，则是的充要条件．7. 设0<p<1，随机变量ξ的分布列是ξ0 1 2P则当p在（0，1）内增大时，A. D（ξ）减小B. D（ξ）增大C. D（ξ）先减小后增大D. D（ξ）先增大后减小【答案】D【解析】分析:先求数学期望，再求方差，最后根据方差函数确定单调性.详解：，，，∴先增后减,因此选D.点睛：8. 已知四棱锥S−ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点），设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S−AB−C的平面角为θ3，则A. θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ1【答案】D【解析】分析:分别作出线线角、线面角以及二面角，再构造直角三角形，根据边的大小关系确定角的大小关系.详解：设O为正方形ABCD的中心，M为AB中点，过E作BC的平行线EF，交CD于F，过O作ON垂直EF于N，连接SO，SN，OM，则SO垂直于底面ABCD，OM垂直于AB，因此从而因为，所以即，选D.点睛：线线角找平行，线面角找垂直，面面角找垂面.9. 已知a，b，e是平面向量，e是单位向量．若非零向量a与e的夹角为，向量b满足b2−4e·b+3=0，则|a−b|的最小值是A. −1B. +1C. 2D. 2−【答案】A【解析】分析:先确定向量所表示的点的轨迹，一个为直线，一个为圆，再根据直线与圆的位置关系求最小值.详解：设，则由得，由得因此的最小值为圆心到直线的距离减去半径1，为选A.点睛：以向量为载体求相关变量的取值范围，是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系，是解决这类问题的一般方法.10. 已知成等比数列，且．若，则A. B. C. D.【答案】B【解析】分析:先证不等式，再确定公比的取值范围，进而作出判断.详解：令则，令得，所以当时，，当时，，因此，若公比，则，不合题意；若公比，则但，即，不合题意；因此，，选B.点睛：构造函数对不等式进行放缩，进而限制参数取值范围，是一个有效方法.如非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

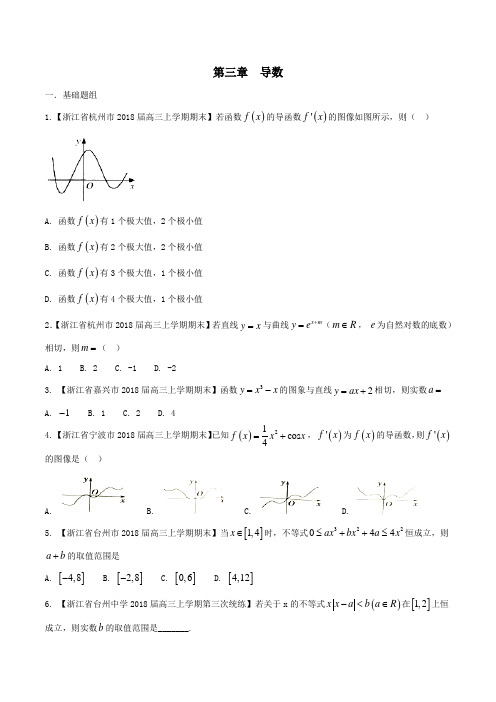
第三章 导数一．基础题组1.【浙江省杭州市2018届高三上学期期末】若函数()f x 的导函数()'f x 的图像如图所示，则（ ）A. 函数()f x 有1个极大值，2个极小值B. 函数()f x 有2个极大值，2个极小值C. 函数()f x 有3个极大值，1个极小值D. 函数()f x 有4个极大值，1个极小值2．【浙江省杭州市2018届高三上学期期末】若直线y x =与曲线x my e +=（m R ∈， e 为自然对数的底数）相切，则m =（ ）A. 1B. 2C. -1D. -23. 【浙江省嘉兴市2018届高三上学期期末】函数3y x x =-的图象与直线2y ax =+相切，则实数a = A. 1- B. 1 C. 2 D. 44. 【浙江省宁波市2018届高三上学期期末】已知()21cos 4f x x x =+，()'f x 为()f x 的导函数，则()'f x 的图像是（ ）A. B. C. D.5. 【浙江省台州市2018届高三上学期期末】当[]1,4x ∈时，不等式322044ax bx a x ≤++≤恒成立，则a b +的取值范围是A. []4,8-B. []2,8-C. []0,6D. []4,126. 【浙江省台州中学2018届高三上学期第三次统练】若关于x 的不等式()x x a b a R -<∈在[]1,2上恒成立，则实数b 的取值范围是_______.7. 【浙江省台州中学2018届高三上学期第三次统练】已知ABC ∆的面积为S ，内角,,A B C 所对的边分别为,,a b c，且2sin C A 成等比数列，2213,218322b a c ac =≤+≤的最小值为 .8. 【浙江省台州中学2018届高三上学期第三次统练】曲线()223f x x x =-在()1,1-处的切线方程为_________________________．9.【2017年12月浙江省高三上学期期末热身】已知a R ∈，函数()1,0{ ,0x a x f x xe x -+><，若存在三个互不相等的实数123,,x x x ，使得()()()123123f x f x f x e x x x ===-成立，则a 的取值范围是__________．10. 【2017年12月浙江省高三上学期期末热身】已知点52,2A （）在曲线(),by ax a b R x=+∈上，且该曲线在点A 处的切线与直线4310x y +-=垂直，则方程20x ax b ++=的实数根的个数为（ ） A. 0个 B. 1个 C. 2个 D. 不确定11. 【浙江省名校协作体2018届高三上学期测试】已知函数（）在上为增函数，则的取值范围是（ ） A.B.C.D.12. 【浙江省温州市2018届高三9月高考适应测试（一模）】已知函数的导函数的图象如图所示，则函数的图象可能是（ ）A. B.C. D.13. 【浙江省清源中学2018届高三9月月考】已知函数()f x 的定义域为[)2,-+∞，且()()421f f =-=，()f x '为()f x 的导函数，函数()y f x ='的图像如图所示，则平面区域()0{0 21a b f a b ≥≥+<所围成的面积是（ ）A. 2B. 4C. 5D. 8 二．能力题组1. 【浙江省杭州市2018届高三上学期期末】设函数()()221f x x R x =∈+. （Ⅰ）求证： ()21f x x x ≥-++；（Ⅱ）当[]1,0x ∈-时，函数()2f x ax ≥+恒成立，求实数a 的取值范围.2. 【浙江省嘉兴市2018届高三上学期期末】已知函数()()2e 1x f x x ax =⋅++， R a ∈（e 为自然对数的底数）．（Ⅰ）若e x =是()f x 的极值点，求实数a 的值； （Ⅱ）求()f x 的单调递增区间．3. 【浙江省宁波市2018届高三上学期期末】已知函数()()1xf x x e =-.（Ⅰ）若方程()f x a =只有一解，求实数a 的取值范围；（Ⅱ）设函数()()ln g x m x x =-，若对任意正实数12,x x ， ()()12f x g x ≥恒成立，求实数m 的取值范围. 4. 【浙江省台州市2018届高三上学期期末】已知函数()()21x f x x x e -=-+⋅． （Ⅰ）求函数()f x 的单调区间；（Ⅱ）当[]0,2x ∈时， ()22f x x x m ≥-++恒成立，求m 的取值范围．5. 【2017年12月浙江省高三上学期期末热身】已知函数()()ln f x x b a =-++． (),a b R ∈. ⑴若()y f x =图像在点()()2,2f 处的切线方程为3y x =-+，求,a b 的值；⑵当0b =时， ()f x ≥x 都成立，求a 的取值范围．6. 【浙江省部分市学校（新昌一中、台州中学等）2018届高三上学期9+1联考】已知函数()axf x e x =-.（1）讨论()f x 的单调性；（2）证明：当1a ≠时，存在实数0x ，使()01f x <.7. 【浙江省嘉兴第一中学2018届高三9月基础知识测试】已知函数()()21ln ,2f x x a x a R =-∈. （I ）若()y f x =在2x =处的切线方程为y x b =+，求,a b 的值； （II ）若()f x 在()1,+∞上为增函数，求a 得取值范围.8. 【浙江省名校协作体2018届高三上学期测试】设函数．（Ⅰ）当(为自然对数的底数)时，求的极小值；（Ⅱ）若对任意正实数a 、b （a b ≠），不等式()()2f a f b a b-≤-恒成立，求的取值范围．9. 【浙江省温州市2018届高三9月高考适应测试（一模）】已知函数．（1）求的单调递增区间；（2）当时，求证：．10. 【浙江省清源中学2018届高三9月月考】已知函数()ln f x x x =， ()()21g x x λ=-（λ为常数）. （1）若函数()y f x =与函数()y g x =在1x =处有相同的切线，求实数λ的值. （2）若12λ=，且1x ≥，证明： ()()f x g x ≤. 11. 【浙江省嘉兴第一中学2018届高三上学期期中】已知函数()()22xx f x ae a e x =+--.（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.。

绝密★启用前2018年普通高等学校招生全国统一考试（浙江卷）数 学本试题卷分选择题和非选择题两部分。

全卷共4页，选择题部分1至2页；非选择题部分3至4页。

满分150分。

考试用时120分钟。

考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。

2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

参考公式：互斥，则 相互独立，则分别表示台体的上、下底面积，台体的高柱体的体积公式表示柱体的底面积，表示柱体的高锥体的体积公式表示锥体的底面积，表示锥体的高球的体积公式其中表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知全集U ={1，2，3，4，5}，A ={1，3}，则A. B. {1，3} C. {2，4，5} D. {1，2，3，4，5}【答案】C【解析】分析:根据补集的定义可得结果.详解：因为全集，，所以根据补集的定义得,故选C.点睛：若集合的元素已知，则求集合的交集、并集、补集时，可根据交集、并集、补集的定义求解．2. 双曲线的焦点坐标是A. (−，0)，(，0)B. (−2，0)，(2，0)C. (0，−)，(0，)D. (0，−2)，(0，2)【答案】B【解析】分析:根据双曲线方程确定焦点位置，再根据求焦点坐标.详解：因为双曲线方程为，所以焦点坐标可设为，因为，所以焦点坐标为，选B.点睛：由双曲线方程可得焦点坐标为，顶点坐标为，渐近线方程为.3. 某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是A. 2B. 4C. 6D. 8【答案】C【解析】分析:先还原几何体为一直四棱柱，再根据柱体体积公式求结果.详解：根据三视图可得几何体为一个直四棱柱，高为2，底面为直角梯形，上下底分别为1，2，梯形的高为2，因此几何体的体积为选C.点睛：先由几何体的三视图还原几何体的形状,再在具体几何体中求体积或表面积等.4. 复数(i为虚数单位)的共轭复数是A. 1+iB. 1−iC. −1+iD. −1−i【答案】B【解析】分析:先分母实数化化简复数，再根据共轭复数的定义确定结果.详解：，∴共轭复数为，选B.点睛：本题重点考查复数的基本运算和复数的概念，属于基本题.首先对于复数的四则运算，要切实掌握其运算技巧和常规思路，如. 其次要熟悉复数的相关基本概念，如复数的实部为、虚部为、模为、对应点为、共轭复数为.5. 函数y=sin2x的图象可能是A. B.C. D.【答案】D【解析】分析:先研究函数的奇偶性，再研究函数在上的符号，即可判断选择.详解：令，因为，所以为奇函数，排除选项A,B;因为时，，所以排除选项C，选D.点睛：有关函数图象的识别问题的常见题型及解题思路：（1）由函数的定义域，判断图象的左、右位置，由函数的值域，判断图象的上、下位置；（2）由函数的单调性，判断图象的变化趋势；（3）由函数的奇偶性，判断图象的对称性；（4）由函数的周期性，判断图象的循环往复．6. 已知平面α，直线m，n满足mα，nα，则“m∥n”是“m∥α”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】分析:根据线面平行的判定定理得充分性成立，而必要性显然不成立.详解：因为，所以根据线面平行的判定定理得.由不能得出与内任一直线平行，所以是的充分不必要条件，故选A.点睛：充分、必要条件的三种判断方法：（1）定义法：直接判断“若则”、“若则”的真假．并注意和图示相结合，例如“⇒”为真，则是的充分条件．（2）等价法：利用⇒与非⇒非，⇒与非⇒非，⇔与非⇔非的等价关系，对于条件或结论是否定式的命题，一般运用等价法．（3）集合法：若⊆，则是的充分条件或是的必要条件；若＝，则是的充要条件．7. 设0<p<1，随机变量ξ的分布列是则当p在（0，1）内增大时，A. D（ξ）减小B. D（ξ）增大C. D（ξ）先减小后增大D. D（ξ）先增大后减小【答案】D【解析】分析:先求数学期望，再求方差，最后根据方差函数确定单调性.详解：，，，∴先增后减,因此选D.点睛：8. 已知四棱锥S−ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点），设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S−AB−C的平面角为θ3，则A. θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ1【答案】D【解析】分析:分别作出线线角、线面角以及二面角，再构造直角三角形，根据边的大小关系确定角的大小关系.详解：设O为正方形ABCD的中心，M为AB中点，过E作BC的平行线EF，交CD于F，过O作ON垂直EF于N，连接SO，SN，OM，则SO垂直于底面ABCD，OM垂直于AB，因此从而因为，所以即，选D.点睛：线线角找平行，线面角找垂直，面面角找垂面.9. 已知a，b，e是平面向量，e是单位向量．若非零向量a与e的夹角为，向量b满足b2−4e·b+3=0，则|a−b|的最小值是A. −1B. +1C. 2D. 2−【答案】A【解析】分析:先确定向量所表示的点的轨迹，一个为直线，一个为圆，再根据直线与圆的位置关系求最小值.详解：设，则由得，由得因此的最小值为圆心到直线的距离减去半径1，为选A.学|科|网...学|科|网...学|科|网...学|科|网...学|科|网...学|科|网...学|科|网...学|科|网...学|科|网...10. 已知成等比数列，且．若，则A. B. C. D.【答案】B【解析】分析:先证不等式，再确定公比的取值范围，进而作出判断.详解：令则，令得，所以当时，，当时，，因此，若公比，则，不合题意；若公比，则但，即，不合题意；因此，，选B.点睛：构造函数对不等式进行放缩，进而限制参数取值范围，是一个有效方法.如非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

1．A【解析】，故选2．B【解析】虚部为则，故选4．A【解析】圆心距为故两圆外离故选5．D【解析】作出可行域区域，如图由解得故选6．C【解析】不妨令，，代入：则故选7．A【解析】当增大时，也增大，也增大故选9．A【解析】由已知可得：，建立平面直角坐标系，，，可得：化简得点轨迹，则转化为圆上点与的距离故选点睛：本题主要考查的知识点是向量的数量积及模的关系。

通过建立平面直角坐标系将其转化为点与圆的位置关系，就可以求出距离的最值，解答本题的关键是转化，理解并掌握本题的解题方法。

有一定的难度。

10．A 【解析】过作垂直于平面，垂足为点图形中的阴影部分中，大小不定即，故选点睛：本题主要考查的知识点是面面角问题。

按照定义先作出三个面面角所成的平面角，然后由题意中的三边关系得到不等关系，利用正切，求出锐角二面角的正切值，从而比较大小，本题具有一定的难度。

11． y x =【解析】由2202x y -=可得双曲线2212x y -=的渐近线方程是y x =，且双曲线中， 2222222232,1,3,,2c a b c a b e e a ==∴=+====.12．3,162【解析】由题意可得：，代入得等比数列各项均为正数，解得，故14． -【解析】令，，则，15．32【解析】由题意，一次可以取球的个数为1，2，3，4，5，6个，则若一次取完可由1个6组成，有1种；二次取完可由1与5，2与4，3与3组成共5种；三次取完由1，1，4或1，2，3或2，2，2组成共10种；四次取完有1，1，1，3或1，1，2，2组成共10种；五次取完，由1，1，1，1，2个组成共5种；六次取完由6个1组成共有1种，综上得，共有32种.点睛：此题主要考查数学中计数原理在实际问题中的应用，属于中档题型，也是常考考点.计数原理是数学中的重要研究对象之一，分类加法计数原理、分步乘法计数原理是解计数问题最基本、最重要的方法，也称为基本计数原理，它们为解决很多实际问题提供了思想和工具. 16．【解析】即点睛：在解答三角形中关于边长的最值问题时，往往需要对其进行转化，转化为关于角的求值问题。

第三章 导数一．基础题组1.【浙江省杭州市2018届高三上学期期末】若函数()f x 的导函数()'f x 的图像如图所示，则（ ）A. 函数()f x 有1个极大值，2个极小值B. 函数()f x 有2个极大值，2个极小值C. 函数()f x 有3个极大值，1个极小值D. 函数()f x 有4个极大值，1个极小值 【答案】B2．【浙江省杭州市2018届高三上学期期末】若直线y x =与曲线x my e +=（m R ∈， e 为自然对数的底数）相切，则m =（ ）A. 1B. 2C. -1D. -2 【答案】C【解析】设切点坐标为()00x mx e+，， x my e+=， ´x my e+=，则切线方程为()000y x mx m ee x x ++-=-，又因为切线为y x =过()00，代入得01x =，将()11，代入x m y e +=中得1m =-故选C3. 【浙江省嘉兴市2018届高三上学期期末】函数3y x x =-的图象与直线2y ax =+相切，则实数a = A. 1- B. 1 C. 2 D. 4【答案】C【解析】()233200000000031,23121,312y x a x x ax x x x x x a =-=-=+∴-=-+∴==-'=Q 选C4. 【浙江省宁波市2018届高三上学期期末】已知()21cos 4f x x x =+，()'f x 为()f x 的导函数，则()'f x 的图像是（ ）A. B. C. D.【答案】A【方法点晴】本题通过对多个图象的选择主要考查考查函数的图象与性质，属于中档题. 这类题型也是近年高考常见的命题方向，该题型的特点是综合性较强较强、考查知识点较多，但是并不是无路可循.解答这类题型可以从多方面入手，根据函数的定义域、值域、单调性、奇偶性、特殊点以及0,0,,x x x x +-→→→+∞→-∞时函数图象的变化趋势，利用排除法，将不合题意的选项一一排除.5. 【浙江省台州市2018届高三上学期期末】当[]1,4x ∈时，不等式322044ax bx a x ≤++≤恒成立，则a b +的取值范围是A. []4,8-B. []2,8-C. []0,6D. []4,12 【答案】A【解析】1，若0a =，则2204bx x ≤≤， 04,04b a b ≤≤≤+≤；,2，若0a >，设()324f x ax bx a =++， ()2'32f x ax bx =+，（1）0b =时，由()'0f x >得， ()f x 在(),-∞∞上递增，只需()()014{0416f f ≤≤≤≤，得403{403a ab ≤≤≤+≤；（2）0b <时， ()f x 在()2,0,,3b a ⎛⎫-∞-+∞ ⎪⎝⎭上递增，在20,3b a ⎛⎫- ⎪⎝⎭上递减，由()()014{ 0464f f ≤≤≤≤，得054{ 017416a b a b ≤+≤≤+≤，可得41a b -≤+≤；（3）当0b >时， ()f x 在()2,,0,3b a ⎛⎫-∞+∞ ⎪⎝⎭上递增， 00{ 054017416a b a b a b >>≤+≤≤+≤； 3，若0a <，（1）0b ≤时，不合题意；（2）0b >， ()f x 在()2,0,,3b a ⎛⎫-∞-+∞ ⎪⎝⎭上递减，在20,3b a ⎛⎫- ⎪⎝⎭上递增， 00{ 054017416a b a b a b <>∴≤+≤≤+≤，可得18a b ≤+≤，综上所述， ()min 175,,433a b a b =-=+=-，当168,33a b ==时， ()max 8a b +=，故选A. 【方法点睛】本题主要考查利用导数研究函数的单调性、分类讨论思想及方程的根与系数的关系， 属于难题. 分类讨论思想解决高中数学问题的一种重要思想方法，是中学数学四种重要的数学思想之一，尤其在解决含参数问题发挥着奇特功效，大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透，这样才能快速找准突破点. 充分利用分类讨论思想方法能够使问题条理清晰，进而顺利解答，希望同学们能够熟练掌握并应用与解题当中.6. 【浙江省台州中学2018届高三上学期第三次统练】若关于x 的不等式()x x a b a R -<∈在[]1,2上恒成立，则实数b 的取值范围是_______. 【答案】2,3⎛⎫+∞⎪⎝⎭()0g x '=，得x b =2b ≥，即4b ≥时， ()g x 在[]1,2上单调递减， ()()min 222bg x g ==+，显然2222b b+>-成立，所以4b ≥1b ≤，即01b <≤时()g x 在[]1,2上单调递增，()()min 11g x g b ==+，所以122b b +>-，所以213b <≤；当12b <<，即14b <<时， ()g x 在b ⎡⎣上单调递减，在,2b ⎡⎤⎣⎦上单调递增， ()()min 2g x gb b ==，所以222bb >-，即()2440b b +->，所以222b >-， 1282b >-，所以14b <<，综上23b >，故答案为2,3⎛⎫+∞ ⎪⎝⎭. 点睛：本题主要考查了绝对值不等式以及导数在不等式恒成立中的应用，属于难题；首先根据绝对值不等式的解法，将其转化为b bx a x x x-<<+在给定区间内恒成立问题，继而可转换为max min b b x a x x x ⎛⎫⎛⎫-<<+ ⎪ ⎪⎝⎭⎝⎭，分别将不等号两边看成两个不同的函数，然后利用导数与0的关系得其单调性，得其最值.7. 【浙江省台州中学2018届高三上学期第三次统练】已知ABC ∆的面积为S ，内角,,A B C 所对的边分别为,,a b c ，且2sin ,sin ,cos C B A 成等比数列，2213,218322b a c ac =≤+≤，则2419216c S a++的最小值为 . 【答案】34【解析】()2222224141412114492162292169c a a a a a a aS aa a+++-===-+++⨯+，令()()222212(2)(+1)4(4)a a a f a f a a a a a ---'=⇒=++，因为13a ≤≤，可知当2a =时，()f a 取得最大值，()124f =2419216c S a++的最小值为34.考点：等比数列的应用；余弦定理及三角形的面积公式；导数的应用.【方法点晴】本题主要考查了等比数列的通项公式，余弦定理及三角形的面积公式、导数的综合应用，试题有一点的难度，属于难题，着重考查了学生的推理、运算能力及转化与化归思想方法的应用，本题的解答中根据题设条件先得出c a =，在利用三角恒等变换和三角形的面积公式表示成三角形的面积，进而得到a的取值范围，再代入2419216c S a++，利用导数研究其单调性确定最值即可.8. 【浙江省台州中学2018届高三上学期第三次统练】曲线()223f x x x =-在()1,1-处的切线方程为_________________________． 【答案】20x y --=9. 【2017年12月浙江省高三上学期期末热身】已知a R ∈，函数()1,0{ ,0x a x f x xe x -+><，若存在三个互不相等的实数123,,x x x ，使得()()()123123f x f x f x e x x x ===-成立，则a 的取值范围是__________．【答案】(,2e -∞-【解析】若存在三个互不相等的实数123,,x x x ，使得()()()123123f x f x f x e x x x ===-成立，则方程()f x ex =-存在三个不相等的实根当0x <时， ()xf x eex -==-，令()(0)x g x e ex x -=+<，则()x g x e e --'=+令()0g x '=，得1x =-，当1x <-时， ()0g x '<，即()g x 在(),1-∞-上为减函数， 当10x -<<时， ()0g x '>，即()g x 在()1,0-上为增函数 ∴()()min 10g x g e e =-=-=，则()f x ex =-在(),0-∞上存在一个实根 ∴()f x ex =-在()0,+∞上存在两个不相等的实根，即1a ex x+=-， 210ex ax ++=有两个不相等的实根∴20{ 240aea e ->∆=-> ∴2a e <-故答案为(),2e -∞-点睛：本题主要考查了函数与方程、函数的图像与性质和分段函数的应用，考查学生综合知识能力，属中高档题．其解题的一般思路为：分别利用导数及函数性质判断其各段的函数的单调性，进而得出其极值和最值，再结合函数的图像即可得出方程()f x ex =-的解的情况．其解题的关键是数形结合在分段函数中的应用．10. 【2017年12月浙江省高三上学期期末热身】已知点52,2A （）在曲线(),by ax a b R x=+∈上，且该曲线在点A 处的切线与直线4310x y +-=垂直，则方程20x ax b ++=的实数根的个数为（ ） A. 0个 B. 1个 C. 2个 D. 不确定 【答案】A∴5222{344b a b a +=-=∴1{1a b ==∴方程20x ax b ++=为210x x ++=∆=-⨯=-<∵214130∴方程的实数根的个数为0个故选A.11. 【浙江省名校协作体2018届高三上学期测试】已知函数（）在上为增函数，则的取值范围是（）A. B. C. D.【答案】A12. 【浙江省温州市2018届高三9月高考适应测试（一模）】已知函数的导函数的图象如图所示，则函数的图象可能是（）A. B. C.D.【答案】C13. 【浙江省清源中学2018届高三9月月考】已知函数()f x 的定义域为[)2,-+∞，且()()421f f =-=，()f x '为()f x 的导函数，函数()y f x ='的图像如图所示，则平面区域()0{0 21a b f a b ≥≥+<所围成的面积是（ ）A. 2B. 4C. 5D. 8 【答案】B【解析】由函数()'y f x =的图象可得：当[)2,0x ∈-]时， ()'0f x <，此时函数f(x)单调递减；当x ∈(0,+∞)时， ()'0f x >，此时函数f(x)单调递增。

2018年高考理科数学浙江卷导数压轴题解析【题目分析】此题综合考察了函数的单调性、极值和零点的分析。

解决第（I ）问中12()()f x f x +取值范围问题的关键在于成立1x 与2x 之间的关系将双变量转化为单变量，寻觅该单变量的取值范围，构造函数并依照函数的单调性和概念域讨论其值域，难度不大。

第（II ）问重点考察函数零点的寻觅，“零点存在性定理”与“函数单调性”的结合是解决“唯一零点”这种问题的常规套路——“零点存在性定理”解决有无的问题，“函数单调性”解决可能有几个的问题。

题目中需要构造()ln h x x kx a =--如此一个含有双参变量的函数，参数a 可不能阻碍“函数单调性”，也确实是意味着函数()h x 的单调性比较益处置，难点在于“零点存在性定理”的运用，()h x 是不是存在大于0或小于0的点是由参数k 和a 一起操纵的，关于如此一个既含有根号又含有对数的函数而言，处置起来比较棘手。

固然考虑()h x 在0x +=及x =+∞处的极限很容易患出()h x 存在零点的结论，可是需要强调的是求极限严格来讲不属于高中时期内的知识点（尽管高中教材中有涉及），高考时得不得分存在专门大争议，因此高考数学官方标准答案中都会带入“特殊值”，通过不等式的放缩来证明函数值是不是存在大于(小于)0的点，此题中官方标准答案中给出(||)a k m e -+=和22(||1)1n a k =++如此两个极为复杂的“特殊值”，让人望而生叹直呼好难想到。

本解答进程另辟蹊径，给出了两个超级简单的范围来讲明()h x 的正负号问题——将()h x 分为kx 与ln x a --两部份，现在参数k 和a 分开(k 和a 二者之间没有关系，彼此独立)，一一讨论范围以后再归并，从而确信()h x 的正负号。

【题目解答】（I ）21111(()2416f x x '-=-=-+，0x >；令12()()f x f x m ''==12(0)x x ≠>，是关于t的一元二次方程212t t m-+-=的两个不相等的正数根，从而1211612256mx xm⎧⎪<<⎪⎪⇒⎪>⎩121212()()ln lnf x f x x x x x+==；令()lng t t=-，那么14()4g tt t'=-=，()g t在(016)，上单调递减，在(16,)+∞上单调递增，因此当12256x x>时，12()(256)88ln2g x x g>=-，即12()()88ln2f x f x+>-，得证.（II）直线y kx b=+与曲线()f x有唯一公共点等价于函数()lnh x x kx a=--有唯一零点；(a)零点的存在性证明：当21(0,)xk∈时0kx>，当(0,)ax e-∈时ln0x a-->，因此当21(0,min(,))ax ek-∈时，(ln0h x kx x a-->；当21(+)xk∈∞，时0kx<，当(+)ax e-∈∞，时ln0x a--<，因此当21(max(,),)ax ek-∈+∞时，(ln0h x kx x a--<；依照零点存在性定理可知函数()h x在区间2211(min(,),max(,))a ae ek k--至少存在一个零点，从而()h x在(0,)+∞至少存在一个零点.(b)零点的唯一性证明：2111()416h x k kx'-=--+-；若116k≥，则()0h x'≤恒成立，()h x单调递减，现在()h x在(0,)+∞最多只有一个零点；若116k<<，()=0h x'有两个不相等正根3x和4x（设34x x<）且易知1142<<<<，从而()h x在3(0,)x上单调递减，34(,)x x上单调递增，4(,)x+∞上单调递减。