(贵阳专版)中考数学命题研究第一编教材知识梳理篇第四章图形的初步认识与三角形、四边形第二节三角形的基
- 格式:pdf
- 大小:2.00 MB
- 文档页数:17

第三节等腰三角形与直角三角形角三角形的性质.命题预测预计2021年中考,本节内容仍为重点考察内容,主要利用直角三角形的性质进展计算,题型仍以选择、填空题为主.,五年中考真题及模拟) 直角三角形的有关计算(5次)1.(20217题3分)如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,那么AP长不可能是( )A.BCD.72.(20218题3分)如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交于BC的延长线于F,假设∠F=30°,DE=1,那么EF的长是( )A.3 B.2 C. 3 D.13.(202115题4分)如图,等腰Rt△ABC的直角边长为1,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,……,依此类推到第五个等腰Rt△AFG,那么由这五个等腰直角三角形所构成的图形的面积为________.(第3题图)(第4题图)4.(202115题4分)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以2cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间是为t秒(0<t<8),那么t=________秒时,S1=2S2.5.(202124题12分)如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点.假设AB=62cm.(1)AE的长为________cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的间隔.勾股定理(1次)6.(202124题12分)在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC 是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).(1)当△ABC三边分别为6、8、9时,△ABC为________三角形;当△ABC三边分别为6、8、11时,△ABC为________三角形;(2)猜测,当a2+b2________c2时,△ABC为锐角三角形;当a2+b2________c2时,△ABC为钝角三角形;(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.等腰三角形的性质(1次)7.(202115题4分)如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;……,按此做法进展下去,∠A n的度数为________.(第7题图)(第8题图)8.(2021模拟)如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,那么∠B的度数为( )A.30°B.36°C.40°D.45°9.(2021模拟)如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为________.,中考考点清单) 等腰三角形的性质与断定(高频考点)1.等腰三角形定义有两边相等的三角形是等腰三角形,相等的两边叫腰,第三边为底性质(1)等腰三角形两腰相等(即AB=AC);(2)等腰三角形的两底角________(即∠B=________);(3)等腰三角形是轴对称图形,有一条对称轴;(4)等腰三角形顶角的平分线、底边上的高和底边的中线互相重合;(5)面积: S△ABC=12BC·AD断定假如一个三角形有两个角相等,那么这个三角形是等腰三角形,其中,两个相等的角所对的边相等.(简称“________〞)2.等边三角形定义三边相等的三角形是等边三角形性质(1)等边三角形三边相等(即AB=BC=AC);(2)等边三角形三角相等,且每一个角都等于________(即∠A=∠B=∠C=________);(3)等边三角形内、外心重合;(4)等边三角形是轴对称图形,有三条对称轴;(5)面积:S△ABC=12BC·AD断定(1)三边都相等的三角形是等边三角形;(2)三个角相等的三角形是等边三角形;(3)有一个角是60°的等腰三角形是等边三角形直角三角形的性质与断定(高频考点)直角三角形的性质与断定近8年考察3次,题型均为填空题,设问方式为:(1)求角度;(2)求线段长度;(3)求周长.结合的背景有:(1)与三角形折叠结合;(2)以赵爽弦图为背景;(3)利用三角形余角的性质求角度.3.直角三角形定义有一个角等于90°的三角形叫做直角三角形性质(1)直角三角形的两个锐角之和等于______;(2)直角三角形斜边上的____等于斜边的一半(即BD=12AC);(3)直角三角形中________角所对应的直角边等于斜边的一半(即AB=12AC);(4)勾股定理:假如直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2;(5)在直角三角形中,假如一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°断定(1)有一个角为90°的三角形是直角三角形;(2)一条边的中线等于这条边的一半的三角形是直角三角形;(3)有两个角互余的三角形是直角三角形4.等腰直角三角形定义顶角为90°的等腰三角形是等腰直角三角形性质等腰直角三角形的顶角是直角,两底角为45°断定(1)用定义断定;(2)有两个角为45°的三角形,中考重难点打破) 等腰三角形的相关计算【例1】如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,且∠DBC=15°,那么∠A =________.【解析】由线段垂直平分线定理知AD=BD,∴∠A=∠ABD,又∵AB=AC,∴∠ABC=∠ACB,设∠A =x,那么2(x+15°)+x=180°,∴∠A=x=50°.【学生解答】1.(2021中考)如图,∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,假设MN=2,那么OM=( )A.3 B.4 C.5 D.6,(第1题图)) ,(第2题图)) 2.(2021中考)如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,∠ADE=40°,那么∠DBC =________.直角三角形的相关计算【例2】(2021中考)如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,假设BD =4,CD=2,那么AB的长是________.,(例2题图)) ,(例2题解图)) 【解析】如解图,过D作DE⊥AB,∵∠ACB=90°,AD平分∠BAC,∴DE=CD=2,在Rt△BDE中,DE=2,BD=4,∴∠B=30°,在Rt△ABC中,BC=CD+BD=6,∴AC=63=23,∴AB=23·2=4 3.【学生解答】3.(2021中考)如图,△ABC中,∠C=45°,点D在AB上,点E在BC上.假设AD=DB=DE,AE =1,那么AC的长为( )A. 5 B.2 C. 3 D. 2(第3题图)(第4题图)4.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,假设BC=2,那么AC的长为( )A. 3 B.1 C. 2 D.25.(2021考试说明):如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,D为△ABC外一点,连接AD,BD,过D作DH⊥AB,垂足为H,交AC于E.假设△ABD是等边三角形,求DE的长.制卷人:打自企;成别使;而都那。

第五节多边形与平行四边形1.(2016长沙中考)六边形的内角和是( B )A.540°B.720°C.900°D.360°2.(2016益阳中考)将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( D )A.360°B.540°C.720°D.900°3.(2016丽水中考)如图,▱ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( B )A.13 B.17 C.20 D.26,(第3题图)) ,(第4题图)) 4.(2016泰安中考)如图,在▱ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则AE+AF的值等于( C )A.2 B.3 C.4 D.65.(2016原创)如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( B )A.8 B.10 C.12 D.14,(第5题图)) ,(第6题图)) 6.(2016绍兴中考)小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( D )A.①②B.①④C.③④D.②③7.(2016原创)如图,将▱ABCD沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( C ) A.66°B.104°C.114°D.124°,(第7题图)) ,(第9题图))8.(2016扬州中考)若多边形的每个内角均为135°,则这个多边形的边数为__8__.9.(2016河南中考)如图,在▱ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数是__110°__.10.(2016原创)如图,在▱ABCD中,AC=8,BD=6,AD=a,则a的取值范围是__1<a<7__.11.(2016巴中中考)已知:如图,四边形ABCD 是平行四边形,延长BA 至点E ,使AE +CD =AD.连接CE ,求证:CE 平分∠BCD.证明:∵四边形ABCD 是平行四边形,∴AB∥CD,AB =CD ,AD =BC ,∴∠E=∠DCE,∵AE+CD =AD ,∴BE=BC ,∴∠E=∠BCE ,∴∠DCE=∠BCE ,即CE 平分∠BCD.12.(2016宿迁中考)如图,已知BD 是△ABC 的角平分线,点E ,F 分别在边AB ,BC 上,ED ∥BC ,EF ∥AC.求证:BE =CF.证明:∵BD 是∠ABC 的平分线,∴∠EBD=∠DBC ,又∵ED ∥BC ,∴∠EDB=∠DBC ,∴∠EBD=∠EDB ,∴BE=ED.又∵EF ∥AC ,∴四边形EFCD 是平行四边形,∴CF=ED ,∴BE=CF.13.(2016凉山中考)如图,▱ABCD 的对角线AC ,BD 交于点O ,EF 过点O 且与BC ,AD 分别交于点E ,F.试猜想线段AE ,CF 的关系,并说明理由.解:AE =CF ,AE∥CF.理由如下:∵四边形ABCD 是平行四边形,∴AD∥BC,OA =OC ,∴∠ACB=∠CAD ,在△AOF 和△COE 中,∠AOF =∠COE ,OA =OC ,∴△AOF≌△COE(ASA ),∴OE=OF.∵OA =OC ,∴四边形AECF 是平行四边形,∴AE=CF ,AE∥CF.14.(2016陕西中考)如图,在▱ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF,CE.求证:AF∥CE.证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠1=∠2.又∵BF=DE,∴BF+BD=DE+BD,∴DF=BE,∴△ADF≌△CBE,∴∠AFD=∠CEB,∴AF∥CE.15.(2016梅州中考)如图,在平行四边形ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE =DF,连接EF交BD于点O.(1)求证:BO=DO;(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.∠BOE=∠DOF,解:(1)∵四边形ABCD是平行四边形,∴DC∥AB,∴∠OBE=∠ODF.在△OBE与△ODF中,BE=DF,∴△OBE≌△ODF(AAS),∴BO=DO;(2)∵EF⊥AB,AB∥DC,∴∠GEA=∠GFD=90°.∵∠A=45°,∴∠G=∠A=45°.∴AE=GE.∵BD⊥AD,∴∠ADB=∠GDO=90°.∴∠GOD=∠G=45°,∴DG=DO,∴OF=FG=1.由(1)可知,OE=OF=1,∴GE=OE+OF+FG=3,∴AE=3.。

第五节多边形与平行四边形制卷人:打自企;成别使;而都那。
审核人:众闪壹;春壹阑;各厅……日期:2022年二月八日。
年份题型题号考察点考察内容分值总分2021未考2021未考2021未考2021未考2021选择9 图形的镶嵌几种特殊正多边形图形镶嵌的判断3 3命题规律纵观5年中考,其中2021-2021年均未单独考察本节.命题预测预计2021年中考,本节内容会与特殊的平行四边形结合在一起进展考察.,五年中考真题及模拟)图形的镶嵌(1次)1.(20219题3分)有以下五种正多边形地砖:①正三角形;②正方形;③正五边形;④正六边形;⑤正八边形,现要用同一种大小一样、形状一样的正多边形地砖铺设地面,其中能做到此之间不留空隙、不重叠地铺设的地砖有( )A.4种B.3种C.2种D.1种2.如图,在▱ABCD中,E在AB上,CE、BD交于F,假设AE∶BE=4∶3,且BF=2,那么DF=________.,(第2题图)) ,(第3题图)) 3.(2021考试说明)如图,在▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,那么AB的长是________.4.(2021模拟)如图,在▱ABCD中,过点C的直线CE⊥AB于点E,交AD于点F,假设∠EAD=53°,那么∠BCE的度数为( )A.53°B.37°C.47°D.123°,(第4题图)) ,(第5题图)) 5.(2021模拟)如图,▱ABCD中,点E在边AD上,以BE为折痕,将△ABE向上折叠,使点A正好与CD上的F点重合,假设△FDE的周长为16,三角形FCB的周长为28,那么FC的长为( ) A.4 B.5 C.6 D.76.(2021考试说明)如图①,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,以OB为边,在△OAB 外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.(1)求证:四边形ABCE是平行四边形;(2)如图②,将图①中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.,中考考点清单)多边形1.n 边形(n≥3)内角和定理 n 边形的内角和为________外角和定理n 边形的外角和为________对角线过n(n >3)边形一个顶点可引(n -3)条对角线,n 边形一共有n 〔n -3〕2条对角线正n 边形n≥3定义在平面内,边相等,角也相等的多边形叫做正多边形性质(1)正n 边形的每一个内角为______(2)正(2n -1)边形是轴对称图形,对称轴有(2n -1)条;正2n 边形既是轴对称图形,又是中心对称图形,对称轴有2n 条平行四边形的性质与断定(高频考点)2.定义:两组对边分别平行的四边形叫做平行四边形.如图(1)所示. 3.性质文字描绘字母表示[参考图(1)](1)对边________ AB綊CD ,AD綊BC(2)对角________∠DAB=∠DCB,∠ADC =∠ABC(3)对角线________ OA=OC,OB=OD(4)平行四边形是中心对称图形,对称中心是两条对角线的交点,O为对称中心4.断定文字描绘字母表示[(参考图(1))] (1)两组对边分别平行的四边形是平行四边形⇒(2)两组对边分别相等的四边形是平行四边形⇒(3)一组对边平行且相等的四边形是平行四边形⇒(4)两组对角分别相等的四边形是平行四边形⇒四边形ABCD是平行四边形(5)两条对角线互相平分的四边形是平行四边形⇒,中考重难点打破) 多边形的相关计算【例1】如图,正三角形与正六边形的边长分别为2和1,正六边形的顶点O是正三角形的中心,那么四边形OABC的面积等于________.(例1题图)(例1题解图)【解析】过点O 作三角形两边的垂线,垂足为E 、F.∵O 为正三角形的中心,∴OE =OF ,所求四边形OABC 的面积等于四边形OEBF 的面积,即正三角形面积的13.∵正三角形的面积为12×2×3=3,故四边形OABC 的面积为=33. 【学生解答】1.(2021中考)假设一个正多边形的每个内角为156°,那么这个正多边形的边数是( )A .13B .14C .15D .16平行四边形的相关计算【例2】(2021中考)在▱ABCD 中,BC 边上的高为4,AB =5,AC =25,那么▱ABCD 的周长等于________. 【解析】如解图(1)所示,∵在▱ABCD 中,BC 边上的高为4,AB =5,AC =25,∴EC=AC 2-AE 2=2,BE =AB 2-AE 2=3,∴AD =BC =BE +EC =5,∴▱ABCD 的周长等于20;如解图(2)所示,∵在▱ABCD 中,BC 边上的高为4,AB =5,AC =25,∴EC =AC 2-AE 2=2,BE =AB 2-AE 2=3,∴BC =3-2=1,∴▱ABCD ▱ABCD 的周长等于12或者20.【学生解答】2.如图,平行四边形ABCD 的对角线交于点O ,且AB =5,△OCD 的周长为23,那么平行四边形ABCD 的两条对角线的和是( )A .18B .28C .36D .46(第2题图)(第3题图)3.(2021中考)如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,那么EF∶FC等于( )A.3∶2 B.3∶1 C.1∶1 D.1∶24.(2021中考)如图,在▱ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,那么CE的长等于________.(第4题图)(第5题图)5.(2021中考)如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,那么▱ABCD的周长等于________.制卷人:打自企;成别使;而都那。
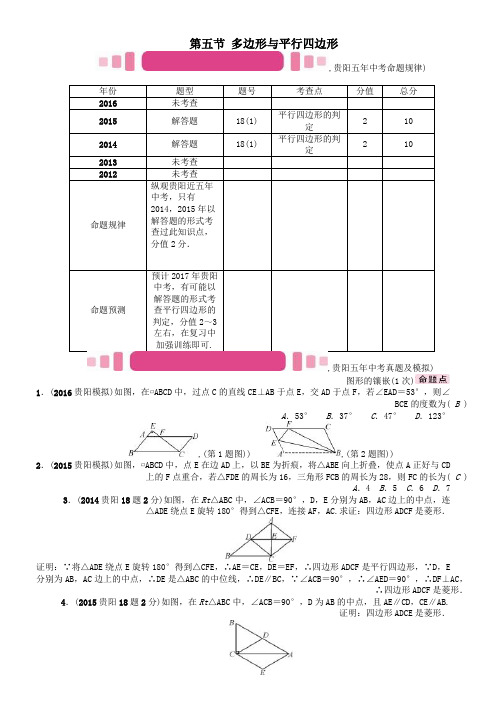
第五节多边形与平行四边形,贵阳五年中考命题规律)年份题型题号考查点分值总分2016未考查2015解答题18(1)平行四边形的判定2102014解答题18(1)平行四边形的判定2102013未考查2012未考查命题规律纵观贵阳近五年中考,只有2014,2015年以解答题的形式考查过此知识点,分值2分.命题预测预计2017年贵阳中考,有可能以解答题的形式考查平行四边形的判定,分值2~3左右,在复习中加强训练即可.,贵阳五年中考真题及模拟)图形的镶嵌(1次)1.(2016贵阳模拟)如图,在▱ABCD中,过点C的直线CE⊥AB于点E,交AD于点F,若∠EAD=53°,则∠BCE的度数为( B )A.53°B.37°C.47° D.123°,(第1题图)) ,(第2题图))2.(2015贵阳模拟)如图,▱ABCD中,点E在边AD上,以BE为折痕,将△ABE向上折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,三角形FCB的周长为28,则FC的长为( C )A.4 B.5 C.6 D.7 3.(2014贵阳18题2分)如图,在Rt△ABC中,∠ACB=90°,D,E分别为AB,AC边上的中点,连△ADE绕点E旋转180°得到△CFE,连接AF,AC.求证:四边形ADCF是菱形.证明:∵将△ADE绕点E旋转180°得到△CFE,∴AE=CE,DE=EF,∴四边形ADCF是平行四边形,∵D,E分别为AB,AC边上的中点,∴DE是△ABC的中位线,∴DE∥BC,∵∠ACB=90°,∴∠AED=90°,∴DF⊥AC,∴四边形ADCF是菱形.4.(2015贵阳18题2分)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.证明:四边形ADCE是菱形.证明:∵AE ∥CD ,CE∥AB,∴四边形ADCE 是平行四边形,又∵∠ACB =90°,D 是AB 的中点,∴CD =21AB=BD =AD ,∴平行四边形ADCE 是菱形.,中考考点清单)多边形1.平行四边形的性质与判定2.定义:两组对边分别平行的四边形叫做平行四边形.如图(1)所示.4。
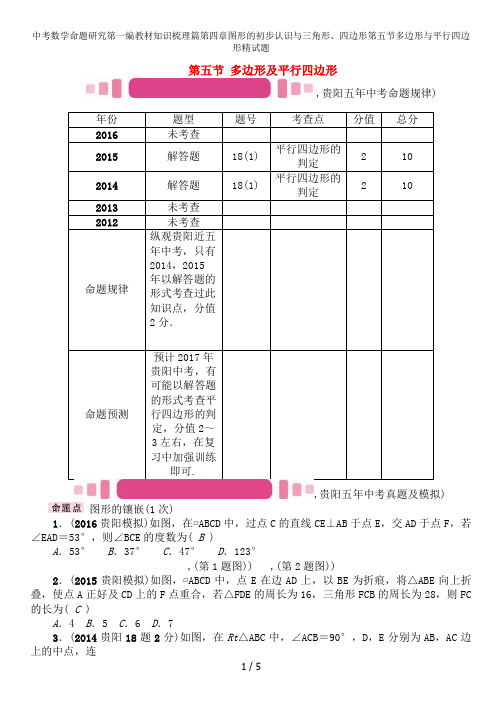
第五节多边形及平行四边形,贵阳五年中考命题规律)年份题型题号考查点分值总分2016未考查2015解答题18(1)平行四边形的判定2102014解答题18(1)平行四边形的判定2102013未考查2012未考查命题规律纵观贵阳近五年中考,只有2014,2015年以解答题的形式考查过此知识点,分值2分.命题预测预计2017年贵阳中考,有可能以解答题的形式考查平行四边形的判定,分值2~3左右,在复习中加强训练即可.,贵阳五年中考真题及模拟)图形的镶嵌(1次)1.(2016贵阳模拟)如图,在▱ABCD中,过点C的直线CE⊥AB于点E,交AD于点F,若∠EAD=53°,则∠BCE的度数为( B )A.53°B.37°C.47° D.123°,(第1题图)) ,(第2题图))2.(2015贵阳模拟)如图,▱ABCD中,点E在边AD上,以BE为折痕,将△ABE向上折叠,使点A正好及CD上的F点重合,若△FDE的周长为16,三角形FCB的周长为28,则FC 的长为( C )A.4 B.5 C.6 D.73.(2014贵阳18题2分)如图,在Rt△ABC中,∠ACB=90°,D,E分别为AB,AC边上的中点,连△ADE 绕点E 旋转180°得到△CFE ,连接AF ,AC.求证:四边形ADCF 是菱形.证明:∵将△ADE 绕点E 旋转180°得到△CFE ,∴AE=CE ,DE =EF ,∴四边形ADCF 是平行四边形,∵D,E 分别为AB ,AC 边上的中点,∴DE 是△ABC 的中位线,∴DE∥BC,∵∠ACB=90°,∴∠AED=90°,∴DF⊥AC,∴四边形ADCF 是菱形.4.(2015贵阳18题2分)如图,在Rt △ABC 中,∠ACB =90°,D 为AB 的中点,且AE ∥CD ,CE ∥AB.证明:四边形ADCE 是菱形.证明:∵AE ∥CD ,CE∥AB,∴四边形ADCE 是平行四边形,又∵∠ACB =90°,D 是AB 的中点,∴CD =21AB =BD =AD ,∴平行四边形ADCE 是菱形.,中考考点清单)多边形1.n 边形 (n ≥3) 内角和定理 n 边形的内角和为__(n -2)·180°__外角和定理 n 边形的外角和为__360°__对角线 过n(n >3)边形一个顶点可引(n -3)条对角线,n 边形共有2n (n -3)条对角线正n 边 形(n ≥3)定义在平面内,边相等,角也相等的多边形叫做正多边形性质(1)正n 边形的每一个内角为__n (n -2)×180°__(2)正(2n -1)边形是轴对称图形,对称轴有(2n -1)条;正2n 边形既是轴对称图形,又是中心对称图形,对称轴有2n 条平行四边形的性质及判定2.定义:两组对边分别平行的四边形叫做平行四边形.如图(1)所示. 3文字描述 字母表示[参考图(1)](1)对边__平行且相等__AB 綊CD ,AD 綊BC (2)对角__相等__ ∠DAB =∠DCB ,∠ADC =∠ABC(3)对角线__互相平分__OA =OC ,OB =OD(4)平行四边形是中心对称图形,对称中心是两条对角线的交点,O 为对称中心4文字描述字母表示[参考图(1)](1)两组对边分别平行的四边形是平行四边形AD ∥BC AB ∥CD ⇒是平行四边形四边形ABCD (2)两组对边分别相等的四边形是平行四边形AD =BC AB =CD ⇒是平行四边形四边形ABCD (3)一组对边平行且相等的四边形是平行四边形AB =CD AB ∥CD ⇒是平行四边形四边形ABCD(4)两组对角分别相等的四边形是平行四边形∠ADC =∠ABC ∠DAB =∠DCB ⇒四边形ABCD 是平行四边形(5)两条对角线互相平分的四边形是平行四边形 BO =DO AO =CO ⇒是平行四边形四边形ABCD,中考重难点突破)多边形的相关计算【例1】(2016长沙中考)六边形的内角和是( ) A .540° B .720° C .900° D .360°【解析】六边形的内角和度数为(6-2)×180°=720°. 【学生解答】B1.(2016北京中考)内角和为540°的多边形是( C ),A ) ,B ) ,C ) ,D )2.(2016临沂中考)一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( C )A .108°B .90°C .72°D .60°3.(2016宜昌中考)设四边形的内角和等于a ,五边形的外角和等于b ,则a 及b 的关系是( B )A .a>bB .a =bC .a<bD .b =a +180°平行四边形的性质及判定【例2】(2016襄阳模拟)在▱ABCD 中,BC 边上的高为4,AB =5,AC =2,求▱ABCD 的周长.【解析】如图(1)所示,∵在▱ABCD中,BC边上的高为4,AB=5,AC=2,∴EC==2,BE==3,∴AD=BC=BE+EC=5,∴▱ABCD的周长等于20;如图(2)所示,∵在▱ABCD中,BC边上的高为4,AB=5,AC=2,∴EC==2,BE==3,∴BC=3-2=1,∴▱ABCD的周长等于1+1+5+5=12.则▱ABCD的周长等于12或20.【学生解答】12或204.(2016衢州中考)如图,在▱ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( A )A.45°B.55°C.65°D.75°,(第4题图)) ,(第5题图))5.(2016内江中考)如图,▱ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( B )A.10 B.14 C.20 D.226.(2016宁夏中考)在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于__2__.7.(2016北京中考)如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.证明:∵四边形ABCD是平行四边形,AB∥DC,∴∠AED=∠BAE.∵AE平分∠BAD,∴∠BAE=∠EAD,∴∠EAD=∠AED,∴DA=DE.8.(2016益阳中考)如图,在▱ABCD中,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE.求证:AF=CE.证明:∵四边形ABCD是平行四边形,∴AD綊BC,∴∠ADB=∠CBD.又∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB,AE∥CF.∴△AED≌△CFB.∴AE=CF.∴四边形AECF是平行四边形.∴AF=CE.9.(2016西宁中考)如图,在▱ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:CF=AB;(2)连接DE,若AD=2AB,求证:DE⊥AF.证明:(1)∵四边形ABCD是平行四边形,∴AB∥DF,∴∠BAE=∠F.∵E是BC中点,∴BE=CE ,在△AEB 和△FEC中,BE =EC ,∠AEB =∠FEC ,∴△AEB≌△FEC,∴AB=CF ;(2)∵四边形ABCD 是平行四边形,∴AB=CD.∵AB =CF ,DF =DC +CF ,∴DF=2CF ,∴DF=2AB.∵AD =2AB ,∴AD=DF.∵△AEB ≌△FEC ,∴AE=EF ,∴ED⊥AF.10.(2016连云港中考)在四边形ABCD 中,AD =BC ,BE =DF ,AE ⊥BD ,CF ⊥BD ,垂足分别为点E ,F.(1)求证:△ADE ≌△CBF ;(2)若AC 及BD 相交于点O ,求证:AO =CO.证明:(1)∵在四边形ABCD 中,BE =DF ,∴BE-EF =DF -EF ,即BF =DE.∵AE ⊥BD ,CF⊥BD,∴∠AED=∠CFB =90°,又AD =BC ,∴△ADE≌△CBF;(2)连接AC 交BD 于点O.∵△ADE ≌△CBF ,∴AE=CF.又∵AE ⊥BD ,CF⊥BD,∴AE∥CF,∴四边形AECF 为平行四边形,∴AO=CO.11.(2016菏泽中考)如图,点O 是△ABC 内一点,连接OB ,OC ,并将AB ,OB ,OC ,AC 的中点D ,E ,F ,G 依次连接,得到四边形DEFG.(1)求证:四边形DEFG 是平行四边形;(2)若点M 为EF 的中点,OM =3,∠OBC 和∠OCB 互余,求DG 的长度.解:(1)∵点D ,G 分别是AB ,AC的中点,∴DG∥BC,DG =21BC.∵点E ,F 分别是OB ,OC 的中点,∴EF∥BC,EF =21BC ,∴DG=EF ,DG∥EF,∴四边形DEFG 是平行四边形;(2)∵∠OBC 和∠OCB 互余,∴∠OBC+∠OCB =90°,∴∠BOC=90°.∵点M 为EF 的中点,OM =3,∴EF=2OM =6,由(1)知,四边形DEFG 是平行四边形,∴DG=EF =6.。
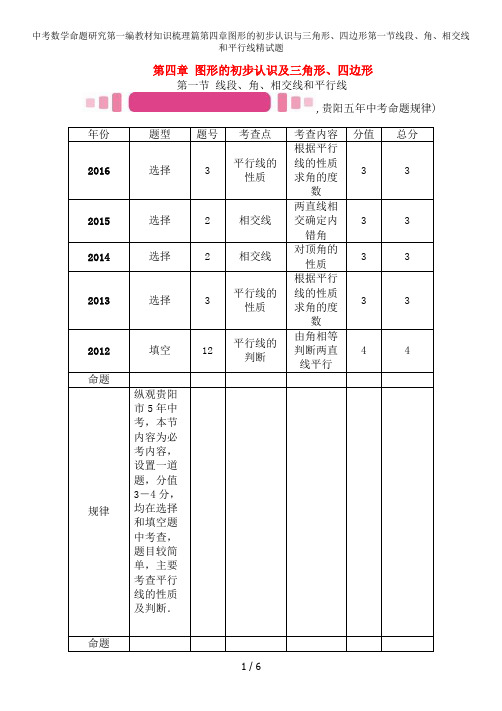
第四章图形的初步认识及三角形、四边形第一节线段、角、相交线和平行线,贵阳五年中考命题规律)年份题型题号考查点考查内容分值总分2016选择3平行线的性质根据平行线的性质求角的度数332015选择2相交线两直线相交确定内错角332014选择2相交线对顶角的性质332013选择3平行线的性质根据平行线的性质求角的度数332012填空12平行线的判断由角相等判断两直线平行44命题规律纵观贵阳市5年中考,本节内容为必考内容,设置一道题,分值3-4分,均在选择和填空题中考查,题目较简单,主要考查平行线的性质及判断.命题预测预计2017年贵阳市中考,本节内容仍然会考查,且以利用平行线的性质进行计算角度为主,题型仍会是选择、填空.,贵阳五年中考真题及模拟)相交线(2次)1.(2015贵阳2题3分)如图,∠1的内错角是( D )A.∠2 B.∠3 C.∠4 D .∠5(第1题图)(第2题图)2.(2014贵阳2题3分)如图,直线a,b相交于点O,若∠1等于50°,则∠2等于( A )A.50°B.40°C.140°D.130°平行线的性质及判断(3次)3.(2016贵阳3题3分)如图,直线a∥b,点B在直线a上,AB⊥BC.若∠1=38°,则∠2的度数为( B )A.38°B.52°C.76°D.142°(第3题图)(第4题图)4.(2013贵阳3题3分)如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是( B )A.40°B.50°C.90°D.130°(第5题图)(第6题图)5.(2015贵阳适应性考试)如图,直线c 及直线a ,b 交于点A ,B ,且a ∥b ,线段AC 垂直于直线b ,垂足为点C ,若∠1=55°,则∠2的度数是( B )A .25°B .35°C .45°D .55°6.(2016贵阳模拟)如图,AB ∥CD ,CE 平分∠ACD ,∠A =100°,则∠ECD 等于( B ) A .50° B .40° C .30° D .20°7.(2012贵阳12题4分)如图,已知∠1=∠2,则图中互相平行的线段是__AB ∥CD__.,(第7题图)) ,(第8题图))8.(2016贵阳适应性考试)如图,BC ⊥AE 于点C ,CD ∥AB ,∠B =40°,则∠ECD 的度数__50°__.,中考考点清单)线段及直线1.线段(1)定义:线段的直观形象是拉直的一段线.(2)基本事实:两点之间的所有连线中,线段最短.(3)线段的和及差:如图(1),已知两条线段a 和b ,且a>b ,在直线l 上画线段AB =a ,BC =b ,则线段AC 就是线段a 及b 的和,即AC =__a +b__.如图(2),在直线l 上画线段AB =a ,在AB 上画线段AD =b ,则线段DB 就是线段a 及b 的差,即DB =a -b.(4)线段的中点:如图(3),线段AB 上的一点M ,把线段AB 分成两条线段AM 及MB.如果AM =MB ,那么点M 就叫做线段AB的中点,此时有__AM__=MB =21AB ,AB =2AM =2MB.2.直线(1)定义:沿线段向两方无限延伸所形成的图形.(2)基本事实:经过两点有一条直线,并且只有一条直线.角及角平分线3.角的分类 分类 锐角 直角 钝角平角 周角 度数 0°<α<90° α=90°90°<α<180°α=180° α=360°1周角=2平角=4直角=360°,1平角=2直角=180°,1直角=90°,1°=60′,1′=60″,1′=(601)°,1″=(601)′.4.角平分线的概念及性质(1)定义:如果一条射线把一个角分成两个相等的角,那么这条射线叫做这个角的角平分线.(2)性质:角平分线上的点到角两边的距离相等. 警示:到角两边距离相等的点在角平分线上. 5.余角、补角、邻补角(1)余角:如果两个角的和为__90°__,那么这两个角互为余角;同角(等角)的余角相等.(2)补角:如果两个角的和为__180°__,那么这两个角互为补角;同角(等角)的补角相等.(3)邻补角:两个角有一个公共顶点和一条公共边,另一边互为反向延长线的两个角互为邻补角;互为邻补角的两个角的和为180°.相交线三线八角(如图)6.同位角有:∠1及__∠5__,∠2及∠6,∠4及∠8,∠3及∠7. 7.内错角有:∠2及__∠8__,∠3及∠5. 8.同旁内角有:∠3及∠8,∠2及__∠5__.9.对顶角:∠1及∠3为对顶角,∠2及__∠4__为对顶角,∠5及∠7为对顶角,∠6及__∠8__为对顶角.垂线及其性质10.定义:两条直线相交所成的四个角中,如果有一个角是直角,我们就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.11.基本事实:经过直线上或直线外一点,有且只有一条直线及已知直线垂直. 12.性质:直线外一点及直线上各点连接的所有线段中,垂线段最短. 13.点到直线的距离:从直线外一点到这条直线的垂线段长度.14.线段的垂直平分线:(1)定理:线段垂直平分线上的点到这条线段两端的距离__相等__.(2)逆定理:到一条线段的两端点的距离相等的点在这条线段的垂直平分线上.平行线的判定及性质(高频考点)15.定义:在同一平面内,不相交的两条直线叫做平行线. 16.两条平行线之间的距离处处相等.17.性质:(1)两直线平行,同位角相等,即∠1=__∠2__. (2)两直线平行,内错角相等,即∠2=__∠3__.(3)两直线平行,同旁内角互补,即∠3+__∠4__=180°.18.判定:(1)基本事实:经过已知直线外一点,有且只有一条直线和已知直线平行. (2)同位角相等,两直线平行. (3)内错角相等,两直线平行. (4)同旁内角互补,两直线平行.(5)平行于同一条直线的两条直线平行.,中考重难点突破)补角、余角的计算【例1】(2016原创)一个角的度数是40°,那么它的余角的补角度数是( ) A .130° B .140° C .50° D .90°【解析】若两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.依此求出度数.【学生解答】A1.(2016长沙中考)下列各图中,∠1及∠2互为余角的是( B ),A ) ,B ) ,C ) ,D )2.(2016贵阳模拟)将直角三角尺的直角顶点靠在直尺上,且斜边及这把直尺平行,那么,在形成的这个图中及∠α互余的角共有( C )A .4个B .3个C .2个D .1个(第2题图) (第3题图)平行线的性质【例2】(2016陕西中考)如图,AB ∥CD ,AE 平分∠CAB 交CD 于点E.若∠C =50°,则∠AED =( )A .65°B .115°C .125°D .130°【解析】∵AB ∥CD ,∠C =50°,∴∠BAC +∠C =180°,∴∠BAC =130°.∵AE 平分∠BAC ,∴∠BAE =21∠BAC =65°,∵AB ∥CD ,∴∠BAE +∠AED =180°,∴∠AED =115°.【学生解答】B3.如图,直线a ∥b ,射线DC 及直线a 相交于点C ,过点D 作DE ⊥b 于点E ,已知∠1=25°,则∠2的度数为( A )A .115°B .125°C .155°D .165°4.(2016贺州中考)如图,已知∠1=60°,如果CD ∥BE ,那么∠B 的度数为( D ) A .70° B .100° C .110° D .120°,(第4题图)) ,(第5题图))5.(2016苏州中考)如图,直线a ∥b ,直线l 及a 、b 分别相交于A 、B 两点,过点A 作直线l 的垂线交直线b 于点C.若∠1=58°,则∠2的度数为( C )A .58°B .42°C .32°D .28°6.(2016连云港中考)如图,直线AB ∥CD ,BC 平分∠ABD ,若∠1=54°,则∠2=__72°__.,(第6题图)) ,(第7题图))7.(2016扬州中考)如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=2∠2,则∠1=__80°__.8.(2016西宁中考)如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD=__2__.9.(2016原创)如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2=__31°__.,(第9题图)) ,(第10题图))10.(2016菏泽中考)如图,将一副三角板和一张对边平行的纸条按如图所示的方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边及纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是__15°__.。